Analytical Evaluation and Experiment of the Dynamic Characteristics of Double-Thimble-Type Fiber Bragg Grating Temperature Sensors
Abstract
:1. Introduction
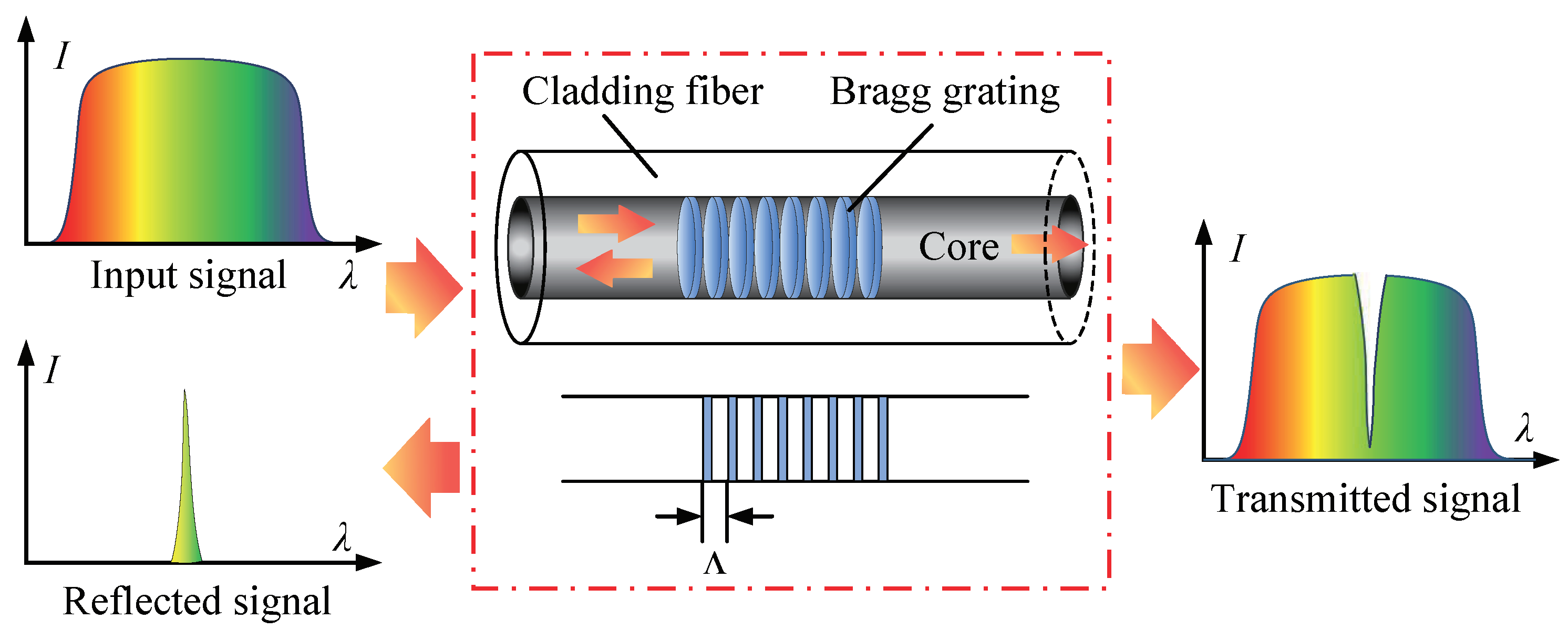
2. Structure and Principle
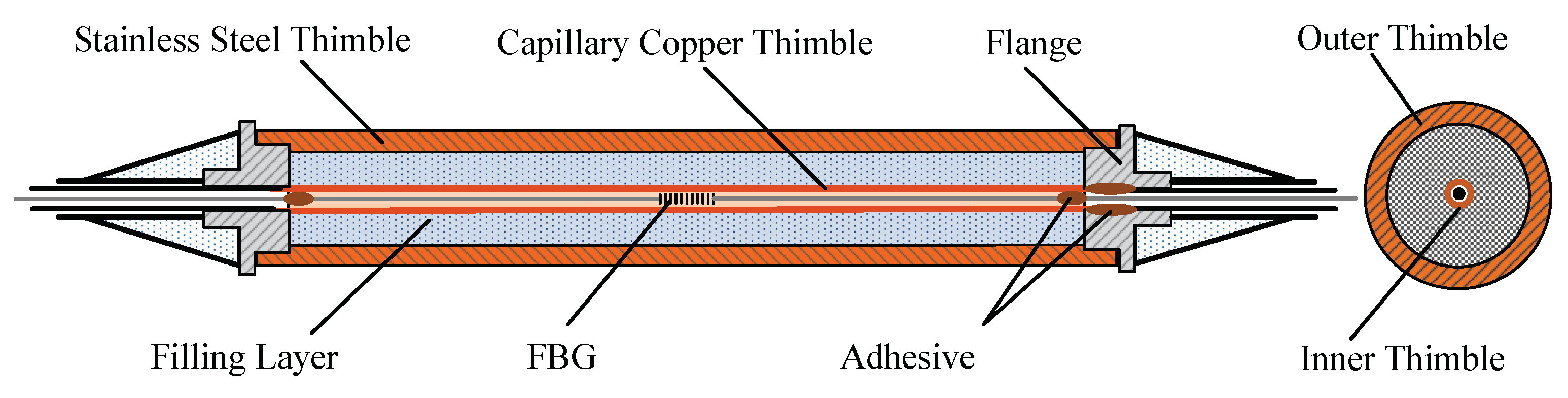
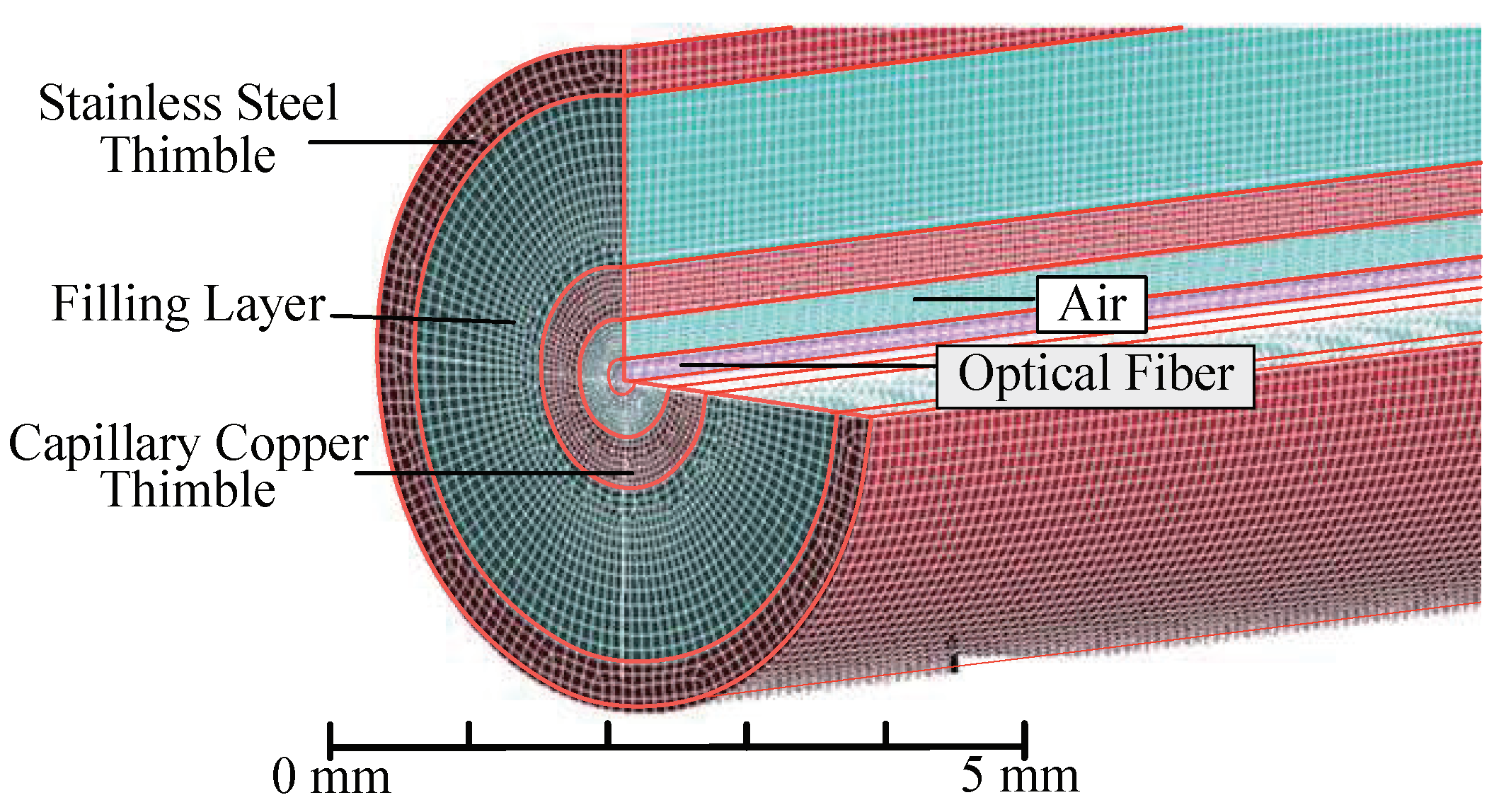
2.1. Structure and Encapsulation
2.2. Theoretical Derivations of Temperature Sensitivity
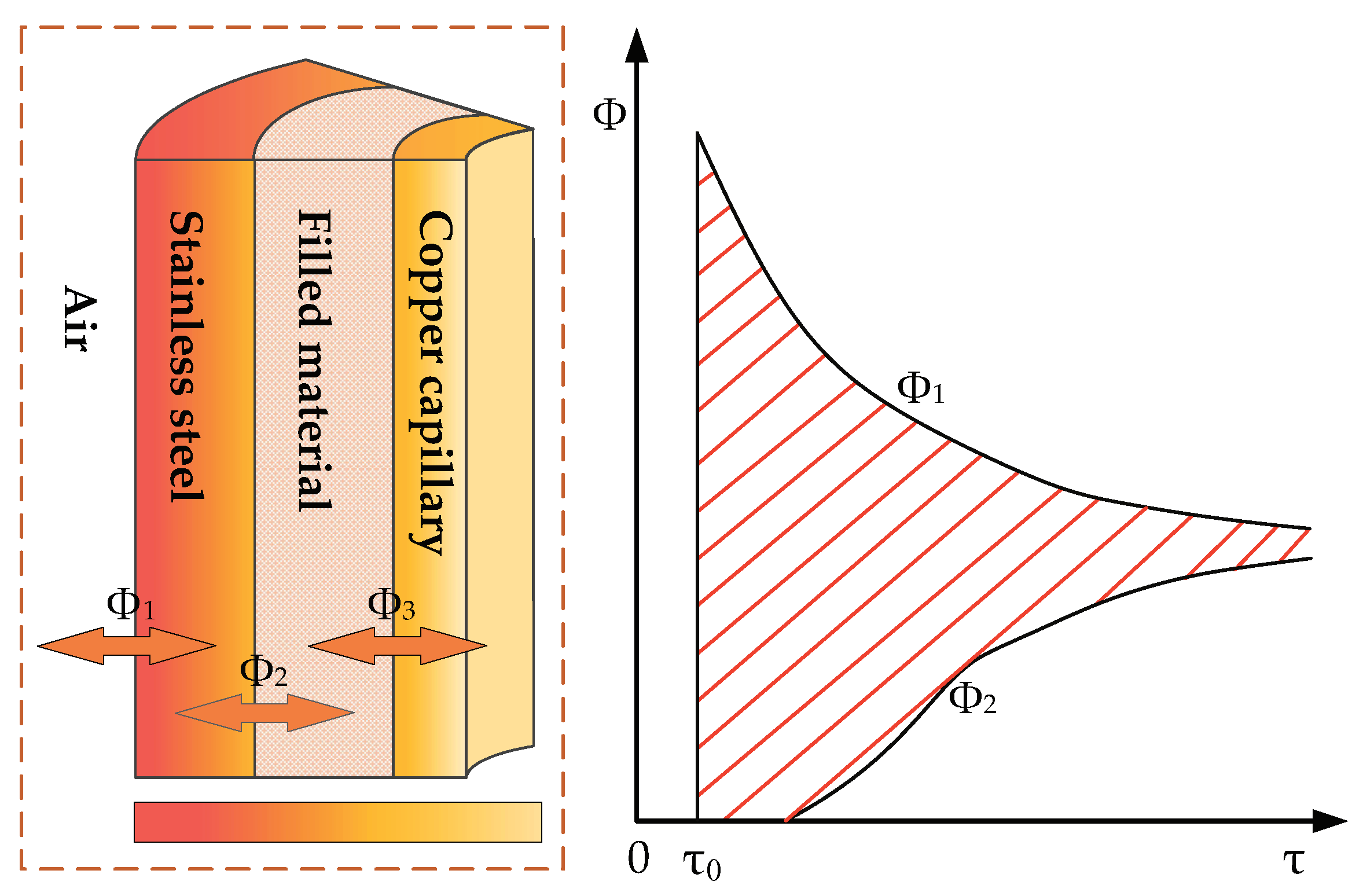
2.3. Dynamic Heat Transfer Process
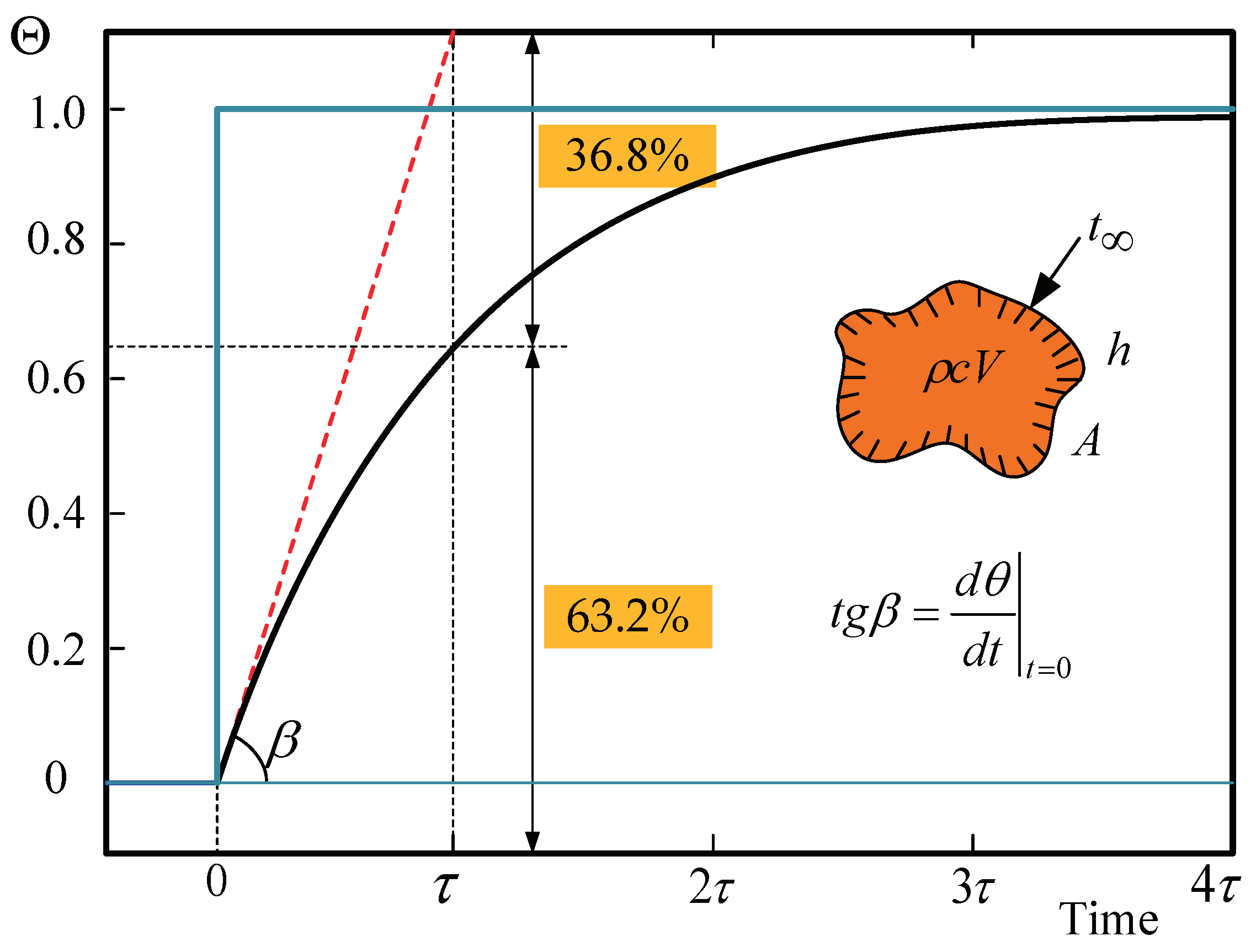
2.4. Theoretical Derivations of Temperature Sensor Dynamic Response
3. Numerical Simulation and Experiments
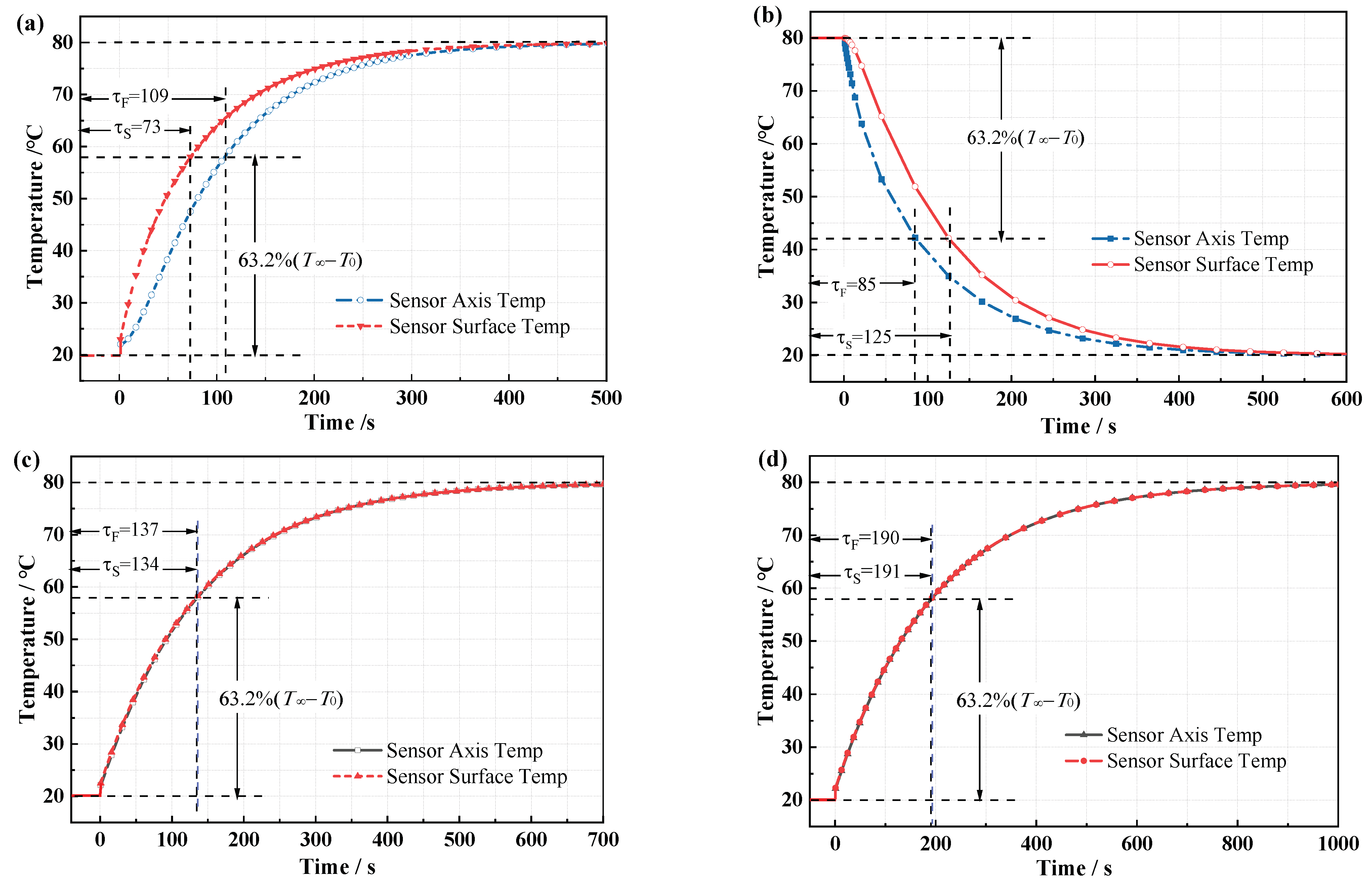
3.1. Simulation of Temperature Sensor Dynamic Response
- The fiber grating, outer thimble, filling material, and inner thimble are considered as isotropic materials, and their thermophysical parameters are constant. The material characteristics are shown in Table 1.
- The outer thimble surface of the sensor is in contact with air, and it is set as a fluid–solid interface coupling surface, and the natural convection heat transfer coefficient of air is set to 20 . The interface between the sensor surface and the air is set as a nonslip boundary condition.
- To calculate the time required for the response process of the sensor by setting the ambient temperature to 80 C and the sensor temperature to 20 C, a solution is performed every 0.2 s to calibrate the sensor.
- To calculate the time required for the recovery process of the sensor by setting the ambient temperature to 20 C and the sensor temperature to 80 C, a solution is performed every 0.2 s to get the heat dissipation process of the sensor.
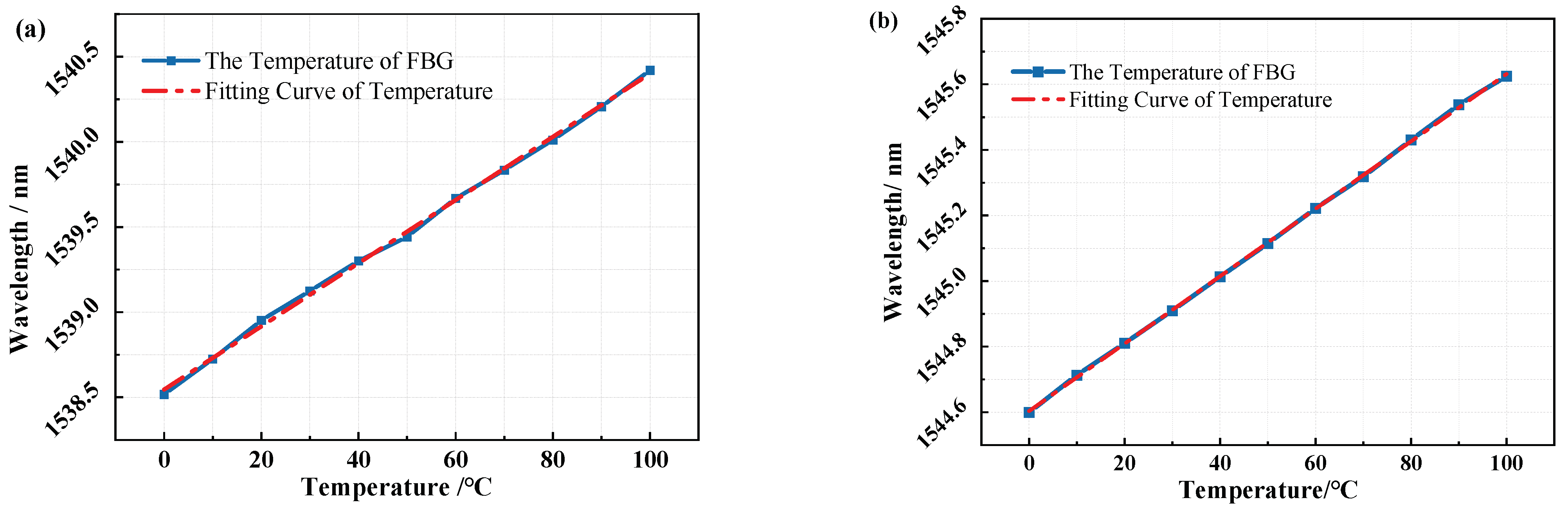
3.2. Experiment of FBG Temperature Sensitivity
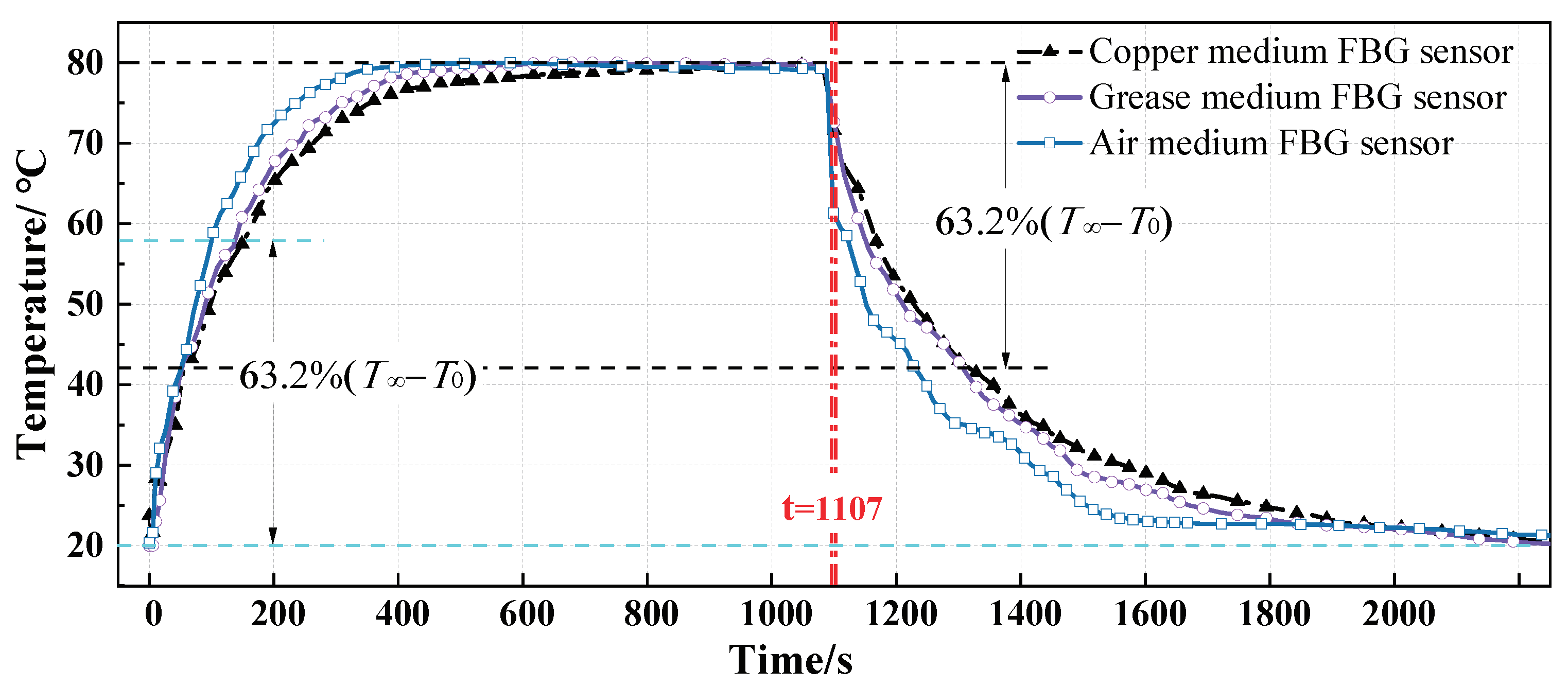
3.3. Experiment of Response Time
4. Discussion
- In the production of the copper-medium FBG sensor, there is a certain gap between the copper thimble and the inner thimble, and between the copper thimble and the outer thimble. There is a large contact thermal resistance on these contact surfaces, and the heat transfer is greatly affected. Based on this, the established equal-scale three-dimensional simulation model also has two gaps. However, this structure is not considered in the transient heat conduction mathematical model, the ideal contact model (the copper is in good contact with the inner and outer thimble) is applied, so the time constant obtained by the mathematical model is smaller than that of the other two methods.
- It can be seen that the time response of the sensor is related to the heat storage capacity and thermal conductivity of the packaging material. In different research methods, the response speed of the air-medium FBG temperature sensor is more than 20% faster than that of the grease-medium FBG sensor, and more than 30% faster than that of the copper-medium FBG sensor. The smaller the heat storage capacity and the larger the heat transfer coefficient, the faster the response of the sensor.
- In the heating process, the system has an infinite external heat source, but in the cooling process, the heat source is the finite heat absorbed by the sensor. So, in the heating and cooling process, the difference in heat density causes the time constant is shorter during the heating phase than the cooling phase.
- For the same encapsulation structure, the response and recovery times obtained by different research methods are consistent and the deviation is within the acceptable range (except the copper-medium FBG sensor), indicating that the analytical solution and finite element simulation of the transient heat conduction model have certain engineering application value.
- The model of the sensor is based on an air bath, that is, the heat exchange method with the external environment is natural convection heat exchange. In actual engineering applications, the environment the double-thimble FBG temperature sensor is exposed to is water or concrete with a larger contact heat transfer coefficient, so the sensor has a faster response speed.
5. Conclusions
- The response speed depends on the thermal properties of the sensor encapsulation materials.
- The time constant depends on whether the sensor is heated or cooled, heating time response for the sensor is shorter than the cooling time response.
- The dynamic performance of the sensor can be verified quickly and effectively by establishing a transient differential equation and finite element model based on heat balance.
- This work can provide inspections for the trial manufacture and dynamic calibration of FBG temperature sensors.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wen, J.; Wang, J.; Yang, L.; Hou, Y.; Huo, D.; Cai, E.; Xiao, Y.; Wang, S. Response Time of Microfiber Temperature Sensor in Liquid Environment. IEEE Sensors J. 2020, 20, 6400–6407. [Google Scholar] [CrossRef]
- Du, C.; Xie, W.; Huo, S.; Meng, S.; Xu, K.; Jiao, L. The response of high-temperature optical fiber sensor applied to different materials. In Fourth International Conference on Smart Materials and Nanotechnology in Engineering; Epaarachchi, J.A., Lau, A.K., Leng, J., Eds.; SPIE-Int Soc Optical Engineering: Bellingham, WA, USA; Gold Coast, Australia, 2013; Volume 8793, p. 87930. [Google Scholar]
- Ganziy, D.; Rose, B.; Bang, O. Performance of low-cost few-mode fiber Bragg grating sensor systems: Polarization sensitivity and linearity of temperature and strain response. Appl. Opt. 2016, 55, 6156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C.; You, J.; Li, Y.; Wan, Z.; Chen, Y.; Xu, X.; Xu, J. Double thimble type fiber Bragg grating temperature sensor. Opt. Tech. 2010, 36, 244–247. [Google Scholar]
- Liu, Y.; Guo, Z.; Zhang, Y.; Chiang, K.S.; Dong, X. Simultaneous pressure and Temperature Measurement With Polymer-Coated Fibre Bragg grating. Electron. Lett. 2000, 36, 564–566. [Google Scholar] [CrossRef]
- McCary, K.M.; Wilson, B.A.; Birri, A.; Blue, T.E. Response of Distributed Fiber Optic Temperature Sensors to High-Temperature Step Transients. IEEE Sensors J. 2018, 18, 8755–8761. [Google Scholar] [CrossRef]
- Yu, Y.; Li, D.; Zhang, L. Experimental study on the characteristics of fiber Bragg grating temperature sensor packaged with metal tube. J. Nat. Sci. Heilongjiang Univ. 2011, 28, 737–740. [Google Scholar]
- Barrera, D.; Finazzi, V.; Villatoro, J.; Sales, S.; Pruneri, V. Packaged Optical Sensors Based on Regenerated Fiber Bragg Gratings for High Temperature Applications. IEEE Sensors J. 2012, 12, 107–112. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J.; Wang, Y.; Dai, X. A fast response temperature sensor based on fiber Bragg grating. Meas. Sci. Technol. 2014, 25, 075105. [Google Scholar] [CrossRef]
- Chen, X.; Xu, X.; Li, Y.; Zhao, Z.; Xie, T.; Li, C.L. Simulation design and development of double thimble type fiber Bragg grating temperature sensor. Opt. Tech. 2015, 41, 208–211. [Google Scholar] [CrossRef]
- Rinaudo, P.; Paya-Zaforteza, I.; Calderón, P.; Sales, S. Experimental and analytical evaluation of the response time of high temperature fiber optic sensors. Sens. Actuators A Phys. 2016, 243, 167–174. [Google Scholar] [CrossRef]
- Barreto, R.C.; Abe, I.; Kamikawachi, R.C. An Empirical Study of In-Fiber Mach-Zehnder Interferometer’s Nonlinear Temperature Response. IEEE Sens. J. 2018, 18, 8338–8344. [Google Scholar] [CrossRef]
- Her, S.; Chung, S. Dynamic Responses Measured by Optical Fiber Sensor for Structural Health Monitoring. Appl. Sci. 2019, 9, 2956. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Deng, S.; Geng, T.; Sun, C.; Niu, H.; Li, X.; Wang, Z.; Li, X.; Ma, Y.; Yang, W.; et al. A miniature ultra long period fiber grating for simultaneous measurement of axial strain and temperature. Opt. Laser Technol. 2020, 126, 106121. [Google Scholar] [CrossRef]
- Da Silva, G.E.; Santos, J.C.; de Almeida, V.R.; Caso, R.M. Dynamic response of optical fiber Bragg grating temperature sensors. In Fourth European Workshop on Optical Fibre Sensors; Santos, J.L., Culshaw, B., López-Higuera, J.M., MacPherson, W.N., Eds.; SPIE-Int Soc Optical Engineering: Bellingham, WA, USA; Porto, Portugal, 2010; Volume 7653, p. 76531A. [Google Scholar]
- Siqueira Dias, J.A.; Leite, R.L.; Ferreira, E.C. Electronic technique for temperature compensation of fibre Bragg gratings sensors. AEU Int. J. Electron. Commun. 2008, 62, 72–76. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, G.; Zhu, Y.; Sheng, Q.; Wang, X.; Liu, Y.; Jing, Z.; Peng, W.; Han, M. Unambiguous Peak Identification of a Silicon Fabry-Perot Temperature Sensor Assisted with an In-Line Fiber Bragg Grating. J. Light. Technol. 2019, 37, 4210–4215. [Google Scholar] [CrossRef]
- Patrick, H.J.; Williams, G.M.; Kersey, A.D.; Pedrazzani, J.R.; Vengsarkar, A.M. Hybrid fiber Bragg grating/long period fiber grating sensor for strain/temperature discrimination. IEEE Photonics Technol. Lett. 1996, 8, 1223–1225. [Google Scholar] [CrossRef]
- Chen, L. Fluid mechanics and Basics of Thermal Engineering, 2nd ed.; Tsinghua University Press: Beijing, China, 2012; p. 215. [Google Scholar]
- Chehura, E.; Ye, C.-C.; Staines, S.E.; James, S.W.; Tatam, R.P. Characterization of the response of fibre Bragg gratings fabricated in stress and geometrically induced high birefringence fibres to temperature and transverse load. Smart Mater. Struct. 2004, 13, 888–895. [Google Scholar] [CrossRef]
- Reddy, P.S.; Prasad, R.L.N.S.; Sengupta, D.; Kishore, P.; Shankar, M.S.; Narayana, K.S.; Tiwari, U.K. Method for Enhancing and Controlling Temperature Sensitivity of Fiber Bragg Grating Sensor Based on Two Bimetallic Strips. IEEE Photonics J. 2012, 4, 1035–1041. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Jiang, S.; Li, K. Research on the calibration algorithm of temperature sensitivity coefficient of fiber Bragg grating sensor. Electron. Des. Eng. 2020, 28, 64–68, 73. [Google Scholar]
- Van Wyk, A.J.; Swart, P.L.; van Rooyen, J.A.; Chtcherbakov, A.A. Dynamic temperature measurements with a Bragg grating sensor. Int. Conf. Opt. Fibre Sens. 2005, 5855, 751. [Google Scholar]
- Wang, X.; Yu, F.; Yang, S.; Qi, M.; Ye, S. Study of TFTC dynamic character based on lumped capacitance method. Chin. J. Sens. Actuators 2014, 27, 1627–1631. [Google Scholar]
- Pawlus, D. Stability of three-layered annular plate in stationary temperature field. Thin-Walled Struct. 2019, 144, 106280. [Google Scholar] [CrossRef]
- Campo, A. He lumped capacitance model for unsteady heat conduction in regular solid bodies with natural convection to nearby fluids engages the nonlinear Bernoulli equation. J. Therm. Sci. Eng. Appl. 2018, 10, 1–5. [Google Scholar] [CrossRef]
- Tegenaw, P.D.; Gebrehiwot, M.G.; Vanierschot, M. On the comparison between computational fluid dynamics (CFD) and lumped capacitance modeling for the simulation of transient heat transfer in solar dryers. Sol. Energy 2019, 184, 417–425. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Machado, J.A.T.; Babaei, A. A computationally efficient method for tempered fractional differential equations with application. Comput. Appl. Math. 2018, 37, 3657–3671. [Google Scholar] [CrossRef]
- Luo, C.; Zhao, Z.; Zhang, D.; Li, C.; Liu, C.; Li, Y.; Zhang, J. Temperature effect on the thermal properties of insulation paper. Electr. Eng. 2020. [Google Scholar] [CrossRef]
- Pan, Y.; Jiang, J.; Liu, K.; Wang, S.; Liu, T. Note: Response time characterization of fiber Bragg grating temperature sensor in water medium. Rev. Sci. Instruments 2016, 87, 116102. [Google Scholar] [CrossRef]
- Akpobi, J.A.; Akele, S. Finite Element Analysis to Predict Temperature and Velocity Distribution in Radiator Tubes. Int. J. Eng. Manag. Res. 2019, 9, 102–116. [Google Scholar]
- Ren, Z.; Yuan, J.; Su, X.; Mangla, S.; Nam, C.Y.; Lu, M.; Tenney, S.A.; Shi, Y. Electro-thermal modeling and experimental validation for multilayered metallic microstructures. Microsyst. Technol. 2020. [Google Scholar] [CrossRef]



| Physical Parameters | Outer Thimble | Inner Thimble | Filling Layer | ||
|---|---|---|---|---|---|
| 304# Stainless Steel | Red Copper | Air | Thermal Grease | Red Copper | |
| 3.46 | 1.01 | 7.85 | 7.85 | 7.85 | |
| 1.13 | 3.77 | 9.65 | 9.65 | 9.65 | |
| 16.2 | 401 | 0.026 | 10 | 401 | |
| 8055 | 8900 | 1.1614 | 2013 | 8900 | |
| 480 | 385 | 1007 | 850 | 385 | |
| 4.67 | 1.34 | 6.26 | 6.78 | 4.06 | |
| Type of FBG Sensor | Mathematical Model/s | Simulation Results/s | Experiments Results/s | ||
|---|---|---|---|---|---|
| Air | 116 | 109 | 123 | 100 | 120 |
| Grease | 146 | 137 | 149 | 136 | 196 |
| Copper | 78 | 190 | 209 | 153 | 214 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Wang, H.; Zhang, D.; Zhao, Z.; Li, Y.; Li, C.; Liang, K. Analytical Evaluation and Experiment of the Dynamic Characteristics of Double-Thimble-Type Fiber Bragg Grating Temperature Sensors. Micromachines 2021, 12, 16. https://doi.org/10.3390/mi12010016
Luo C, Wang H, Zhang D, Zhao Z, Li Y, Li C, Liang K. Analytical Evaluation and Experiment of the Dynamic Characteristics of Double-Thimble-Type Fiber Bragg Grating Temperature Sensors. Micromachines. 2021; 12(1):16. https://doi.org/10.3390/mi12010016
Chicago/Turabian StyleLuo, Chuan, Han Wang, Dacheng Zhang, Zhengang Zhao, Yingna Li, Chuan Li, and Ke Liang. 2021. "Analytical Evaluation and Experiment of the Dynamic Characteristics of Double-Thimble-Type Fiber Bragg Grating Temperature Sensors" Micromachines 12, no. 1: 16. https://doi.org/10.3390/mi12010016
APA StyleLuo, C., Wang, H., Zhang, D., Zhao, Z., Li, Y., Li, C., & Liang, K. (2021). Analytical Evaluation and Experiment of the Dynamic Characteristics of Double-Thimble-Type Fiber Bragg Grating Temperature Sensors. Micromachines, 12(1), 16. https://doi.org/10.3390/mi12010016






