Start-Up Electroosmotic Flow of Multi-Layer Immiscible Maxwell Fluids in a Slit Microchannel
Abstract
1. Introduction
2. Mathematical Modeling
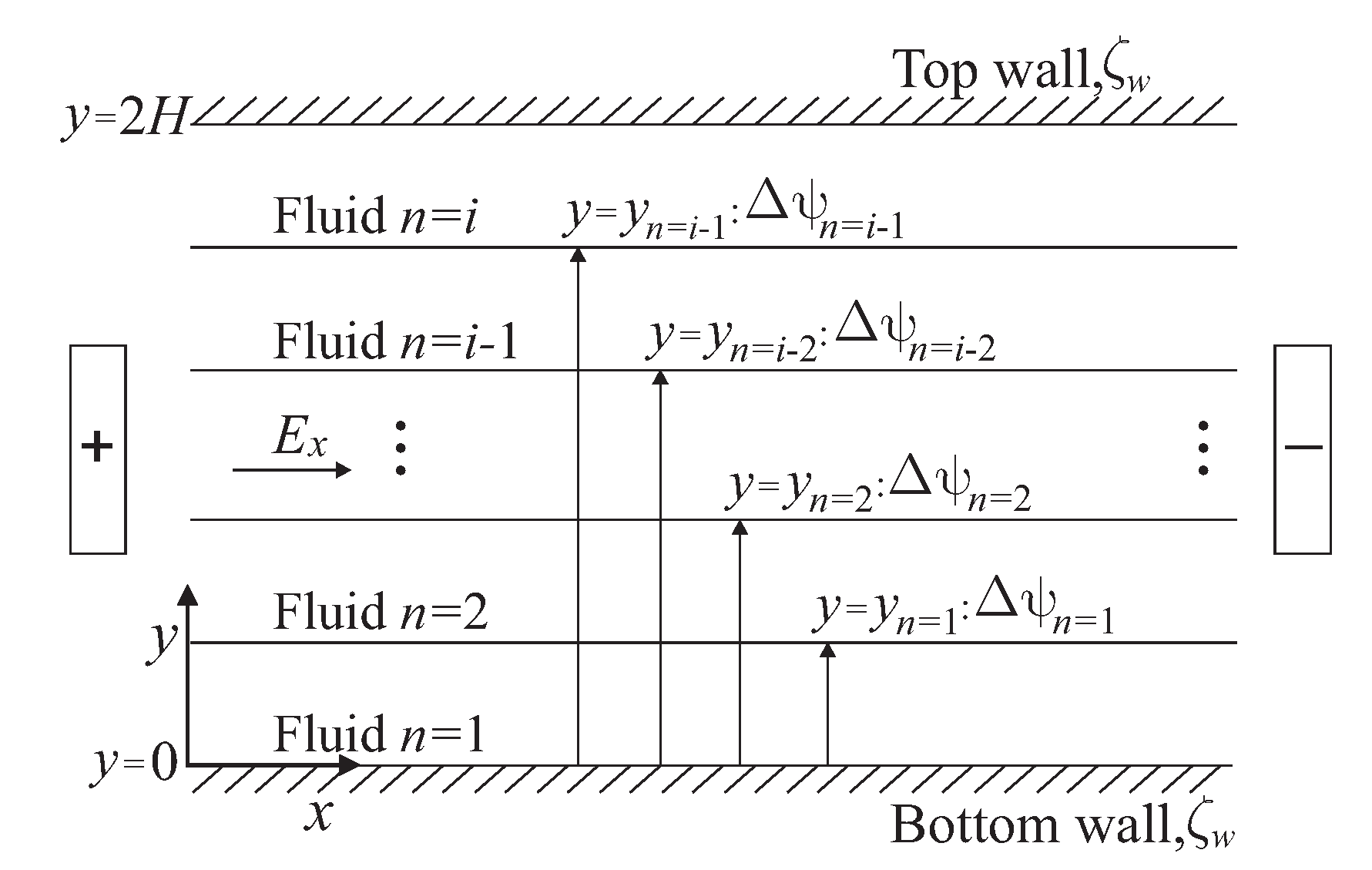
2.1. Physical Model Description
2.2. Governing and Constitutive Equations
2.3. Simplified Mathematical Model
- Fully-developed flow [35].
- Impermeable interfaces between the fluids and ideally polarizable to electric charges [5,54,55,56]. The electric double layers at the liquid-liquid interfaces are composed of two diffuse charge layers separated by a central compact layer, characterized by a potential difference drop due to the orientation of the solvent molecules; also, the continuity of electrical displacements on both sides of the central inner layer, in absence of ions in the inner layer is considered [5,55,56,57,58].
- Flat interfaces between the fluids [44,59,60,61]. This is assumed when considering that there is: (i) creeping flow for low Reynolds numbers, being , resulting in parallel flows with laminar fluid interfaces [43], and (ii) uniform zeta potentials along the microchannel. Here, the characteristic velocity of flow is the well-known Helmholtz-Smoluchowski velocity defined by , where the subscript “” indicates physical properties referred to electrolytes in aqueous solutions at 298.15 K (25 C) [5,62].
- The gravitational forces are neglected [60].
- Long microchannel neglecting any end effects; hence, the electric potential , is the algebraic sum of the potential due to the electric double layer, , and the potential due to the imposed electric field, , as [5]:where ; being the electric potential at the inlet of the microchannel at and is the external electric field independent of the position and constant along the axial direction.
- The local distribution of the free charges, that is, ions, is governed by the electrical potential into the electric double layer, , through the Boltzmann distribution as [5]where is the valence of electrolyte, e is the electron charge, is the ionic number concentration in the bulk solution, is the Boltzmann constant and is the fluid temperature.
- There is no imposed pressure gradient on microchannel.
- The electric double layers do not overlap.
2.4. Dimensionless Mathematical Model
3. Solution Methodology
3.1. Electric Potential Distribution
3.2. Velocity Distribution
4. Results and Discussion
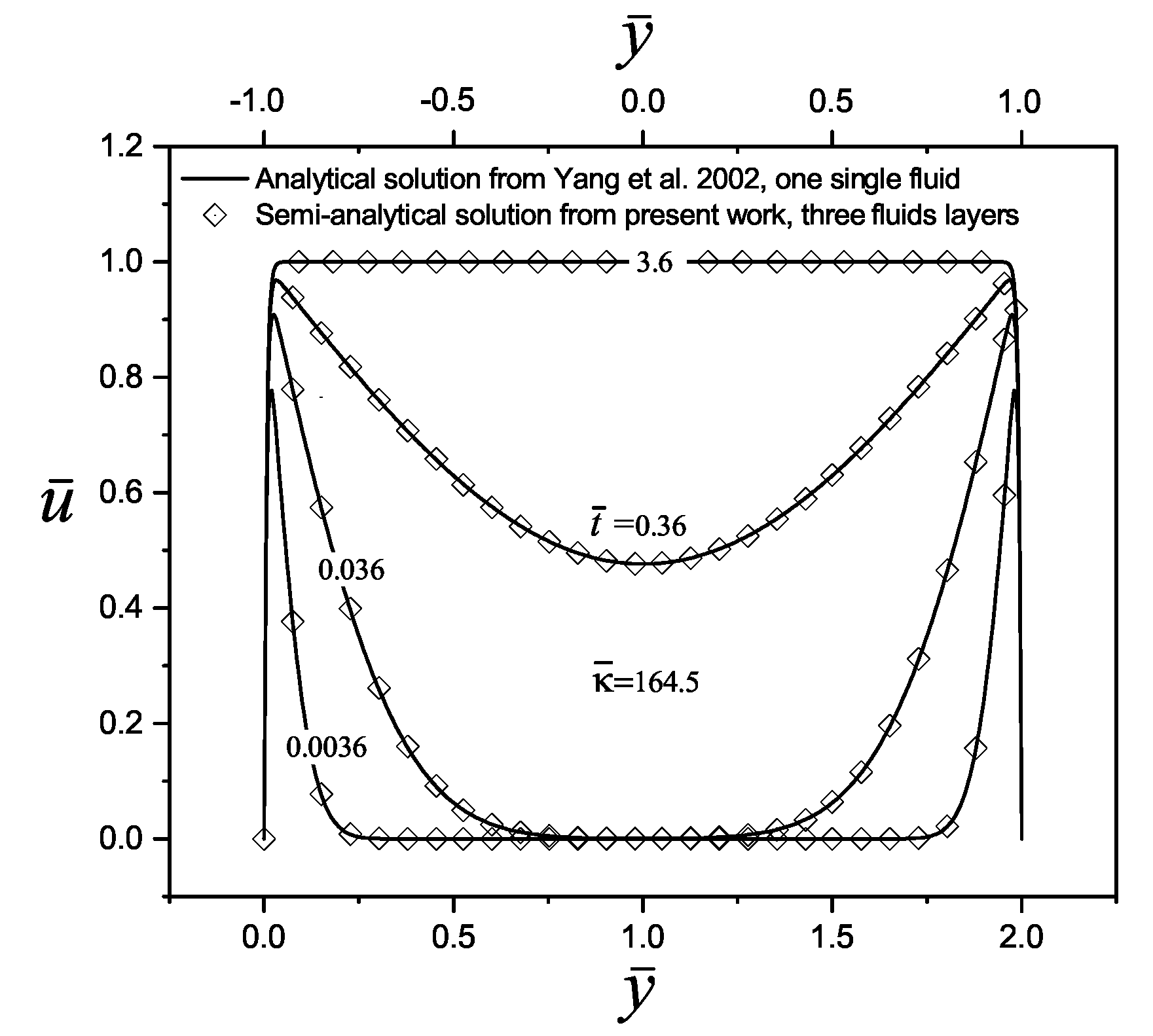
4.1. Solution Validation
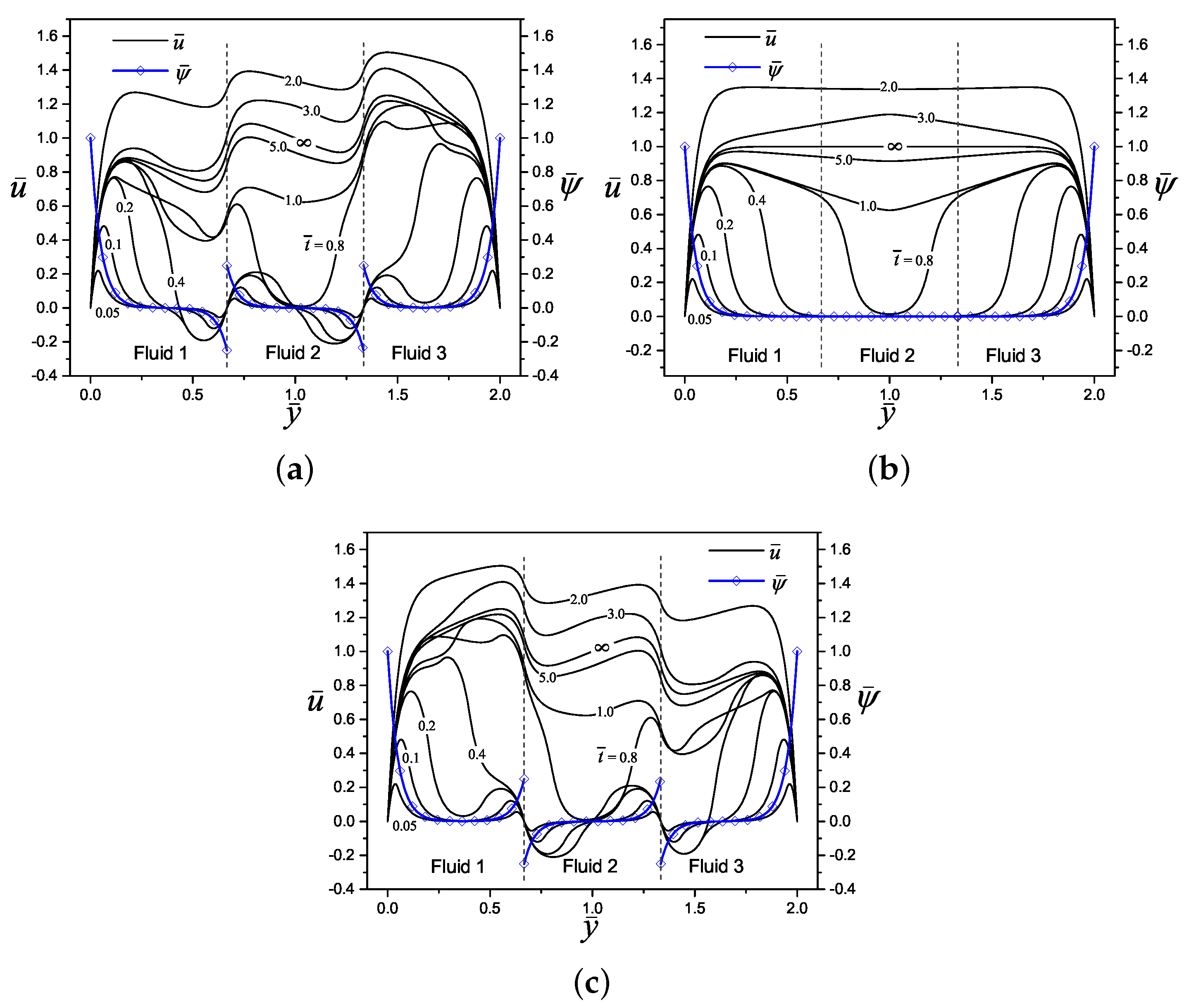
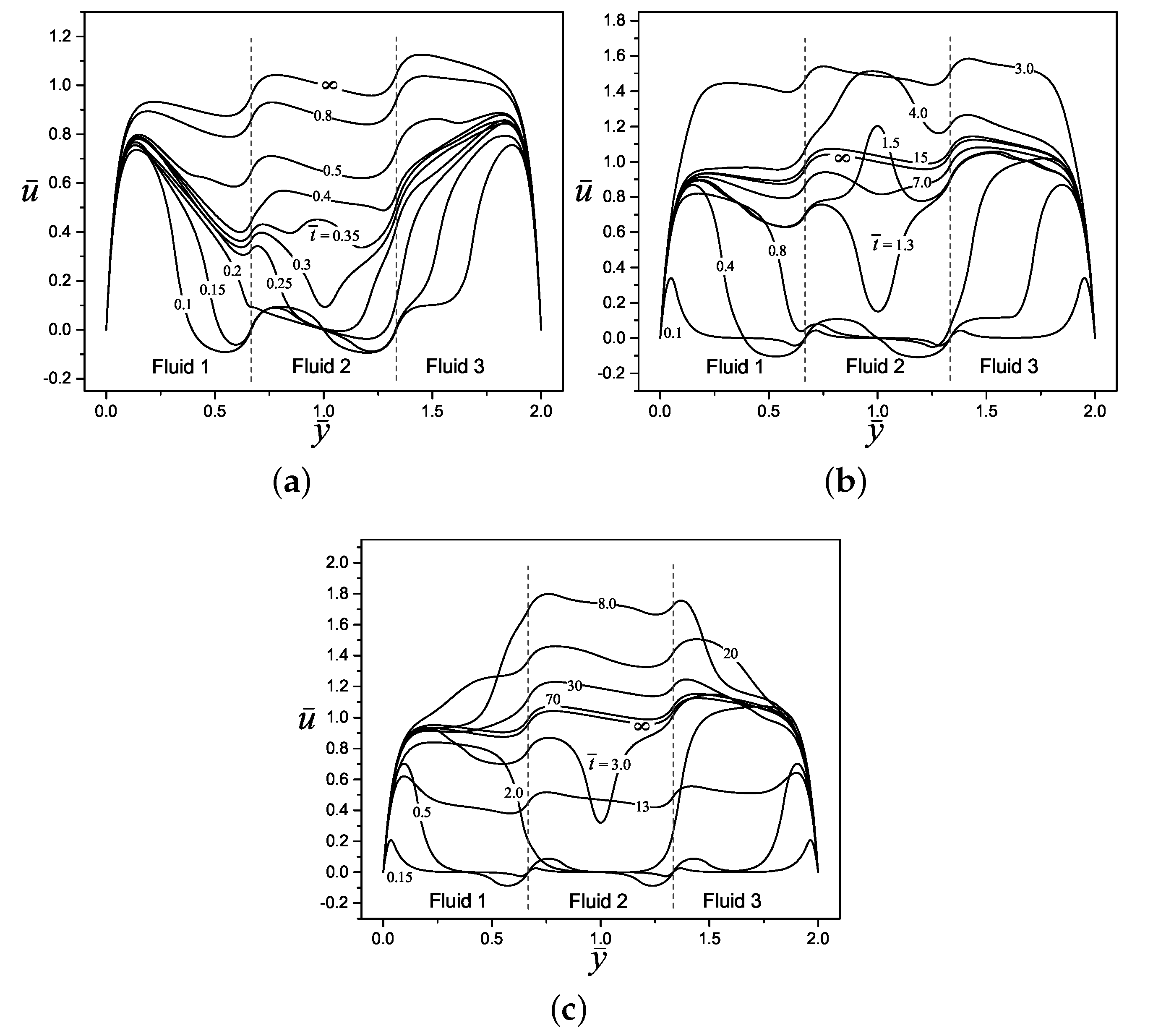
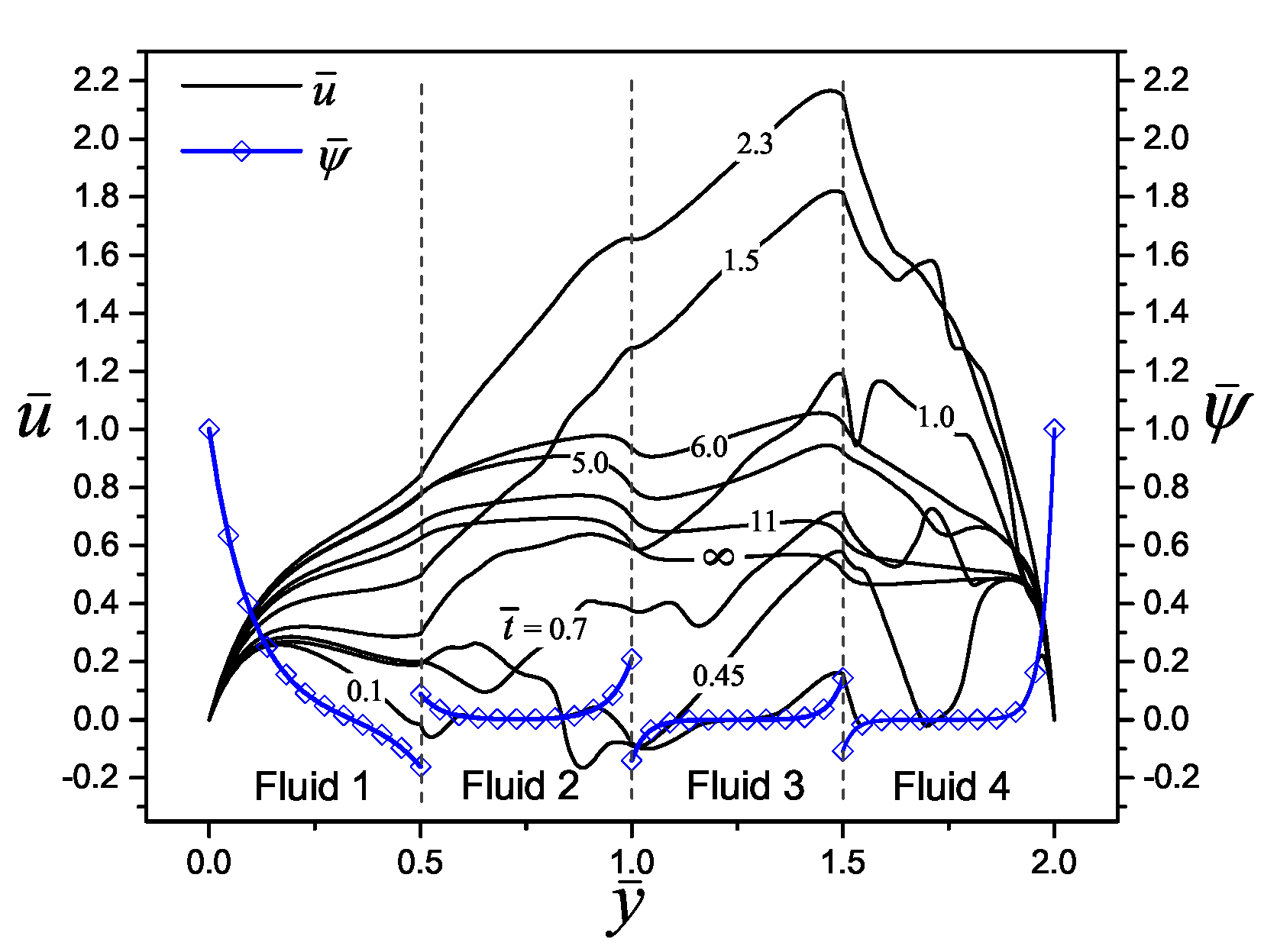
4.2. Velocity Profiles
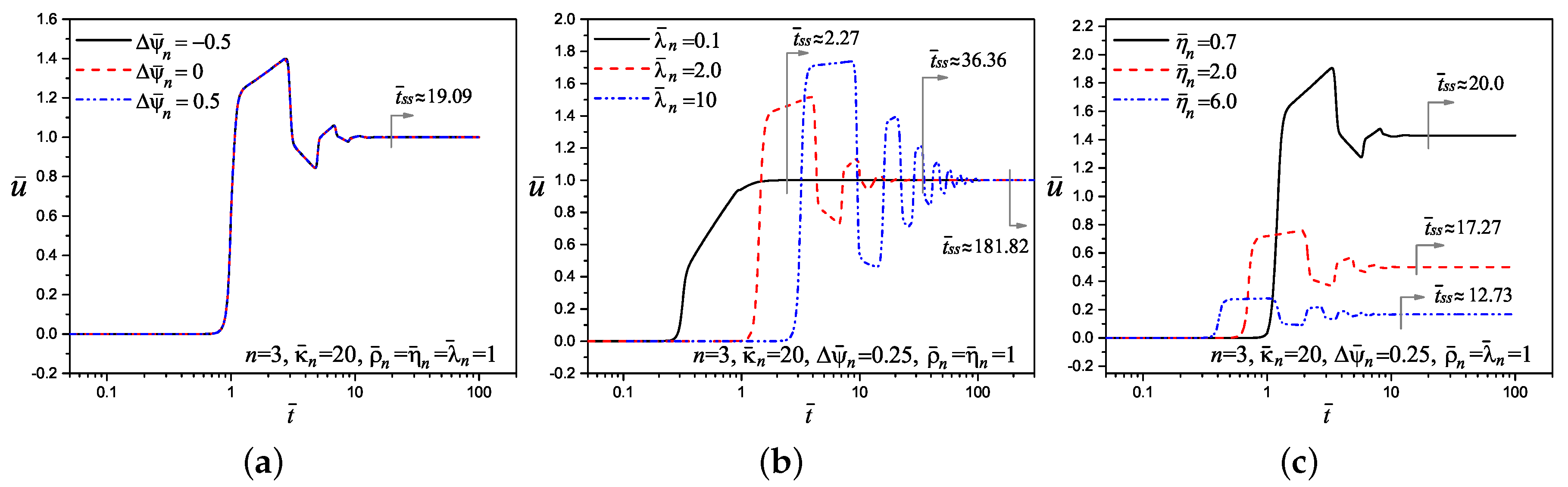
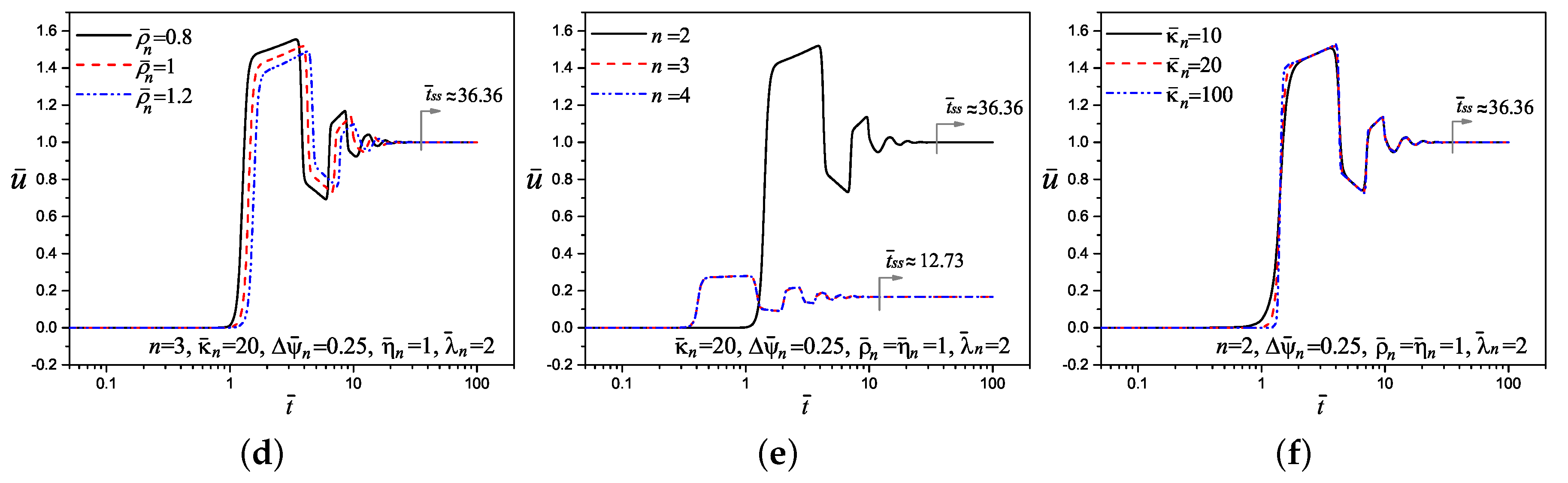
5. Tracking of the Velocity
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kleinstreuer, C. Microfluidics and Nanofluidics. Theory and Selected Applications; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Sengupta, P.; Khanra, K.; Chowdhury, A.R.; Datta, P. Lab-on-a-chip sensing devices for biomedical applications. In Bioelectronics and Medical Devices. From Materials to Devices-Fabrication, Applications and Reliability; Pal, K., Kraatz, H.B., Khasnobish, A., Bag, S., Banerjee, I., Kuruganti, U., Eds.; Elsevier: Cambridge, MA, USA, 2019. [Google Scholar]
- Badilescu, S.; Packirisamy, M. BioMEMS Science and Engineering Perspertives; CRC Press and Taylor & Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Meng, E. Biomedical Microsystems; CRC Press and Taylor & Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Masliyah, J.H.; Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Burgreen, D.; Nakache, F.R. Electrokinetic flow in ultrafine capillary slits. J. Phys. Chem. 1964, 68, 1084–1091. [Google Scholar] [CrossRef]
- Rice, C.L.; Whitehead, R. Electrokinetic flow in a narrow cylindrical capillary. J. Phys. Chem. 1965, 69, 4017–4024. [Google Scholar] [CrossRef]
- Yang, C.; Li, D. Electrokinetic effects on pressure-driven liquid flows in rectangular microchannels. J. Colloid Interface Sci. 1997, 194, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Keh, H.J.; Tseng, H.C. Transient electrokinetic flow in fine capillaries. J. Colloid Interface Sci. 2001, 242, 450–459. [Google Scholar] [CrossRef]
- Yang, C.; Ng, C.B.; Chan, V. Transient analysis of electroosmotic flow in a slit microchannel. J. Colloid Interface Sci. 2002, 248, 524–527. [Google Scholar] [CrossRef] [PubMed]
- Miller, A.; Villegas, A.; Diez, F.J. Characterization of the startup transient electrokinetic flow in rectangular channels of arbitrary dimensions, zeta potential distribution, and time-varying pressure gradient. Electrophoresis 2015, 36, 692–702. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.I.; Dutta, P. Analytical solution of time-periodic electroosmotic flow through cylindrical microchannel with non-uniform surface potential. Micromachines 2019, 10, 498. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Tang, G.H.; Li, X.F.; He, Y.L.; Tao, W.Q. Electroosmotic flow of non-Newtonian fluid in microchannels. J. Non-Newton. Fluid Mech. 2009, 157, 133–137. [Google Scholar] [CrossRef]
- Dhinakaran, S.; Afonso, A.M.; Alves, M.A.; Pinho, F.T. Steady viscoelastic fluid flow between parallel plates under electro-osmotic forces: Phan-Thien-Tanner model. J. Colloid Interface Sci. 2010, 344, 513–520. [Google Scholar] [CrossRef]
- Escandón, J.; Jiménez, E.; Hernández, C.; Bautista, O.; Méndez, F. Transient electroosmotic flow of Maxwell fluids in a slit microchannel with asymmetric zeta potentials. Eur. J. Mech. B Fluids 2015, 53, 180–189. [Google Scholar] [CrossRef]
- Hamedi, A.; Shamshiri, M.; Charmiyan, M.; Shirani, E. Investigation of nonlinear electrokinetic and rheological behaviors of typical Non-Newtonian biofluids through annular microchannels. J. Appl. Fluid Mech. 2016, 9, 367–378. [Google Scholar] [CrossRef]
- Sarma, R.; Deka, N.; Sarma, K.; Mondal, P.K. Electroosmotic flow of Phan-Thien-Tanner fluids at high zeta potentials: An exact analytical solution. Phys. Fluids 2018, 30, 062001. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Bag, N. Enhanced electroosmotic flow of Herschel-Bulkley fluid in a channel patterned with periodically arranged slipping surfaces. Phys. Fluids 2019, 31, 072007. [Google Scholar] [CrossRef]
- Aota, A.; Mawatari, K.; Kitamori, T. Parallel multiphase microflows: Fundamental physics, stabilization methods and applications. Lab Chip 2009, 9, 2470–2476. [Google Scholar] [CrossRef]
- Minakov, A.V.; Shebeleva, A.A.; Yagodnitsyna, A.A.; Kovalev, A.V.; Bilsky, A.V. Flow regimes of viscous immiscible liquids in T-type microchannels. Chem. Eng. Technol. 2019, 42, 1037–1044. [Google Scholar] [CrossRef]
- Meng, S.-X.; Xue, L.-H.; Xie, C.-Y.; Bai, R.-X.; Yang, X.; Qiu, Z.-P.; Guo, T.; Wang, Y.-L.; Meng, T. Enhanced enzymatic reaction by aqueous two-phase systems using parallel-laminar flow in a double Y-branched microfluidic device. Chem. Eng. J. 2018, 335, 392–400. [Google Scholar] [CrossRef]
- Hu, Y.; Peng, H.; Yan, Y.; Guan, S.; Wang, S.; Li, P.C.H.; Sun, Y. Integration of laminar flow extraction and capillary electrophoretic separation in one microfluidic chip for detection of plant alkaloids in blood samples. Anal. Chim. Acta 2017, 985, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Kazoe, Y.; Ugajin, T.; Ohta, R.; Mawatari, K.; Kitamori, T. Parallel multiphase nanofluidics utilizing nanochannels with partial hydrophobic surface modification and application to femtoliter solvent extraction. Lab Chip 2019, 19, 3844–3852. [Google Scholar] [CrossRef]
- Priest, C.; Zhou, J.; Klink, S.; Sedev, R.; Ralston, J. Microfluidic solvent extraction of metal ions and complexes from leach solutions containing nanoparticles. Chem. Eng. Technol. 2012, 35, 1312–1319. [Google Scholar] [CrossRef]
- Huh, Y.S.; Jeon, S.J.; Lee, E.Z.; Park, H.S.; Hong, W.H. Microfluidic extraction using two phase laminar flow for chemical and biological applications. Korean J. Chem. Eng. 2011, 28, 633–642. [Google Scholar] [CrossRef]
- Reddy, V.; Zahn, J.D. Interfacial stabilization of organic-aqueous two-phase microflows for a miniaturized DNA extraction module. J. Colloid Interface Sci. 2005, 286, 158–165. [Google Scholar] [CrossRef]
- Hisamoto, H.; Shimizu, Y.; Uchiyama, K.; Tokeshi, M.; Kikutani, Y.; Hibara, A.; Kitamori, T. Chemicofunctional membrane for integrated chemical processes on a microchip. Anal. Chem. 2003, 75, 350–354. [Google Scholar] [CrossRef]
- Desir, P.; Chen, T.-Y.; Bracconi, M.; Saha, B.; Maestri, M.; Vlachos, D.G. Experiments and computations of microfluidic liquid-liquid flow patterns. React. Chem. Eng. 2020, 5, 39–50. [Google Scholar] [CrossRef]
- Vladisavljevi<i>c</i>´, G.T.; Khalid, N.; Neves, M.A.; Kuroiwa, T.; Nakajima, M.; Uemura, K.; Ichikawa, S.; Kobayashi, I. Industrial lab-on-a-chip: Design, applications and scale-up for drug discovery and delivery. Adv. Drug Deliv. Rev. 2013, 65, 1626–1663. [Google Scholar]
- Pan, Y.-J.; Ren, C.-M.; Yang, R.-J. Electrokinetic flow focusing and valveless switching integrated with electrokinetic instability for mixing enhancement. J. Micromech. Microeng. 2007, 17, 820–827. [Google Scholar] [CrossRef]
- Jiang, H.; Weng, X.; Li, D. A novel microfluidic flow focusing method. Biomicrofluidics 2014, 8, 054120. [Google Scholar] [CrossRef]
- Li, H.; Wong, T.N.; Nguyen, N.T. Microfluidic switch based on combined effect of hydrodynamics and electroosmosis. Microfluid. Nanofluid. 2011, 10, 965–976. [Google Scholar] [CrossRef][Green Version]
- Jia, Y.; Ren, Y.; Jiang, H. Continuous-flow focusing of microparticles using induced-charge electroosmosis in a microfluidic device with 3D AgPDMS electrodes. RSC Adv. 2015, 5, 66602–66610. [Google Scholar] [CrossRef]
- Gao, Y.; Wong, T.N.; Yang, C.; Ooi, K.T. Transient two-liquid electroosmotic flow with electric charges at the interface. Colloid Surf. A Physicochem. Eng. Asp. 2005, 266, 117–128. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Y.; Guo, Q.; Yang, J. Modeling of electroosmotic pumping of nonconducting liquids and biofluids by a two-phase flow method. J. Electroanal. Chem. 2009, 636, 86–92. [Google Scholar] [CrossRef]
- Movahed, S.; Khani, S.; Wen, J.Z.; Li, D. Electroosmotic flow in a water column surrounded by an immiscible liquid. J. Colloid Interface Sci. 2012, 372, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Afonso, A.M.; Alves, M.A.; Pinho, F.T. Analytical solution of two-fluid electro-osmotic flows of viscoelastic fluids. J. Colloid Interface Sci. 2013, 395, 277–286. [Google Scholar] [CrossRef]
- Huang, Y.; Li, H.; Wong, T.N. Two immiscible layers of electro-osmotic driven flow with a layer of conducting non-Newtonian fluid. Int. J. Heat Mass Transf. 2014, 74, 368–375. [Google Scholar] [CrossRef]
- Moghadam, A.J. Two-fluid electrokinetic flow in a circular microchannel. Int. J. Eng. Trans. A 2016, 29, 1469–1477. [Google Scholar]
- Gaikwad, H.; Basu, D.N.; Mondal, P.K. Electroosmotic transport of immiscible binary system with a layer of non-conducting fluid under interfacial slip: The role applied pressure gradient. Electrophoresis 2016, 37, 1998–2009. [Google Scholar] [CrossRef]
- Matías, A.; Méndez, F.; Bautista, O. Interfacial electric effects on a non-isothermal electroosmotic flow in a microcapillary tube filled by two immiscible fluids. Micromachines 2017, 8, 232. [Google Scholar] [CrossRef]
- Haiwang, L.; Wong, T.N.; Nguyen, N.-T. Time-dependent model of mixed electroosmotic/pressure-driven three immiscible fluids in a rectangular microchanne. Int. J. Heat Mass Transf. 2010, 53, 772–785. [Google Scholar] [CrossRef]
- Choi, W.; Sharma, A.; Qian, S.; Lim, G.; Joo, S.W. On steady two-fluid electroosmotic flow with full interfacial electrostatics. J. Colloid Interface Sci. 2011, 357, 521–526. [Google Scholar] [CrossRef]
- Su, J.; Jian, Y.-J.; Chang, L.; Liu, Q.-S. Transient electro-osmotic and pressure driven flows of two-layer fluids through a slit microchannel. Acta Mech. Sin. 2013, 29, 534–542. [Google Scholar] [CrossRef]
- Jian, Y.; Su, J.; Chang, L.; Liu, Q.; He, G. Transient electroosmotic flow of general Maxwell fluids through a slit microchannel. Z. Angew. Math. Phys. 2014, 65, 435–447. [Google Scholar] [CrossRef]
- Shit, G.C.; Mondal, A.; Sinha, A.; Kundu, P.K. Two-layer electro-osmotic flow and heat transfer in a hydrophobic micro-channel with fluid-solid interfacial slip and zeta potential difference. Colloid Surf. A Physicochem. Eng. Asp. 2016, 506, 535–549. [Google Scholar] [CrossRef]
- Li, J.; Sheeran, P.S.; Kleinstreuer, C. Analysis of multi-layer immiscible fluid flow in a microchannel. ASME J. Fluids Eng. 2011, 133, 111202. [Google Scholar] [CrossRef]
- Escandón, J.P.; Gómez, J.R.; Hernández, C.G. Multilayer analysis of Phan-Thien-Tanner immiscible fluids under electro-osmotic and pressure-driven effects in a slit microchannel. ASME J. Fluids Eng. 2020, 142, 061205. [Google Scholar] [CrossRef]
- Torres, D.; Escandón, J. Transient analysis of combined electroosmotic and pressure-driven flow with multi-layer immiscible fluids in a narrow capillary. Rev. Mex. Fis. 2020, 66, 137–152. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids. Volume 1 Fluid Mechanics; Wiley-Interscience: Hoboken, NJ, USA, 1987. [Google Scholar]
- Morrison, F.A. Understanding Rheology; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Gao, Y.; Wong, T.N.; Yang, C.; Ooi, K.T. Two-fluid electroosmotic flow in microchannels. J. Colloid Interface Sci. 2005, 284, 306–314. [Google Scholar] [CrossRef]
- Samec, Z. Electrical double layer at the interface between two immiscible electrolyte solutions. Chem. Rev. 1988, 88, 617–632. [Google Scholar] [CrossRef]
- Wandlowsky, T.; Holub, K.; Mareček, V.; Samec, Z. The double layer at the interface between two immiscible electrolyte solutions-IV. Solvent effect. Electrochim. Acta 1995, 40, 2887–2895. [Google Scholar] [CrossRef]
- Volkov, A.G.; Deamer, D.W.; Tanelian, D.L.; Markin, V.S. Electrical double layers at the oil/water interface. Prog. Surf. Sci. 1996, 53, 1–134. [Google Scholar] [CrossRef]
- Das, S.; Hardt, S. Electric-double-layer potential distribution in multiple-layer immiscible electrolytes. Phys. Rev. E 2011, 84, 022502. [Google Scholar] [CrossRef]
- Gavach, C.; Seta, P.; D’epenoux, B. The double layer and ion adsorption at the interface between two non miscible solutions. Part I. interfacial tension measurements for the water-nitrobenzene tetraalkylammonium bromide systems. J. Electroanal. Chem. 1977, 83, 225–235. [Google Scholar] [CrossRef]
- Middleman, S. Modeling Axisymmetric Flows: Dynamics of Films, Jets, and Drops; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Ngoma, G.D.; Erchiqui, F. Pressure gradient and electroosmotic effects on two immiscible fluids in a microchannel between two parallel plates. J. Micromech. Microeng. 2006, 16, 83–91. [Google Scholar] [CrossRef]
- Lee, J.S.H.; Barbulovic-Nad, I.; Wu, Z.; Xuan, X.; Li, D. Electrokinetic flow in a free surface-guided microchannel. J. Appl. Phys. 2006, 99, 054905. [Google Scholar] [CrossRef]
- Zhang, H.-L.; Han, S.-J. Viscosity and density of water + sodium chloride + potassium chloride solutions at 298.15 K. J. Chem. Eng. Data 1996, 41, 502–516. [Google Scholar] [CrossRef]
- Probstein, R.F. Physicochemical Hydrodynamics: An introduction; Wiley-Interscience: Hobooken, NJ, USA, 2003. [Google Scholar]
- Goswami, P.; Chakraborty, S. Semi-analytical solutions for electroosmotic flows with interfacial slip in microchannels of complex cross-sectional shapes. Microfluid. Nanofluid. 2011, 11, 255–267. [Google Scholar] [CrossRef]
- Hoffman, J.D. Numerical Methods for Engineers and Scientists; Marcel Dekker, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Horváth, G.; Horváth, I.; Almousa, S.A.-D.; Telek, M. Numerical inverse Laplace transformation using concentrated matrix exponential distributions. Perform. Eval. 2020, 137, 102067. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escandón, J.; Torres, D.; Hernández, C.; Vargas, R. Start-Up Electroosmotic Flow of Multi-Layer Immiscible Maxwell Fluids in a Slit Microchannel. Micromachines 2020, 11, 757. https://doi.org/10.3390/mi11080757
Escandón J, Torres D, Hernández C, Vargas R. Start-Up Electroosmotic Flow of Multi-Layer Immiscible Maxwell Fluids in a Slit Microchannel. Micromachines. 2020; 11(8):757. https://doi.org/10.3390/mi11080757
Chicago/Turabian StyleEscandón, Juan, David Torres, Clara Hernández, and René Vargas. 2020. "Start-Up Electroosmotic Flow of Multi-Layer Immiscible Maxwell Fluids in a Slit Microchannel" Micromachines 11, no. 8: 757. https://doi.org/10.3390/mi11080757
APA StyleEscandón, J., Torres, D., Hernández, C., & Vargas, R. (2020). Start-Up Electroosmotic Flow of Multi-Layer Immiscible Maxwell Fluids in a Slit Microchannel. Micromachines, 11(8), 757. https://doi.org/10.3390/mi11080757






