PIV-Based Acoustic Pressure Measurements of a Single Bubble near the Elastic Boundary
Abstract
1. Introduction
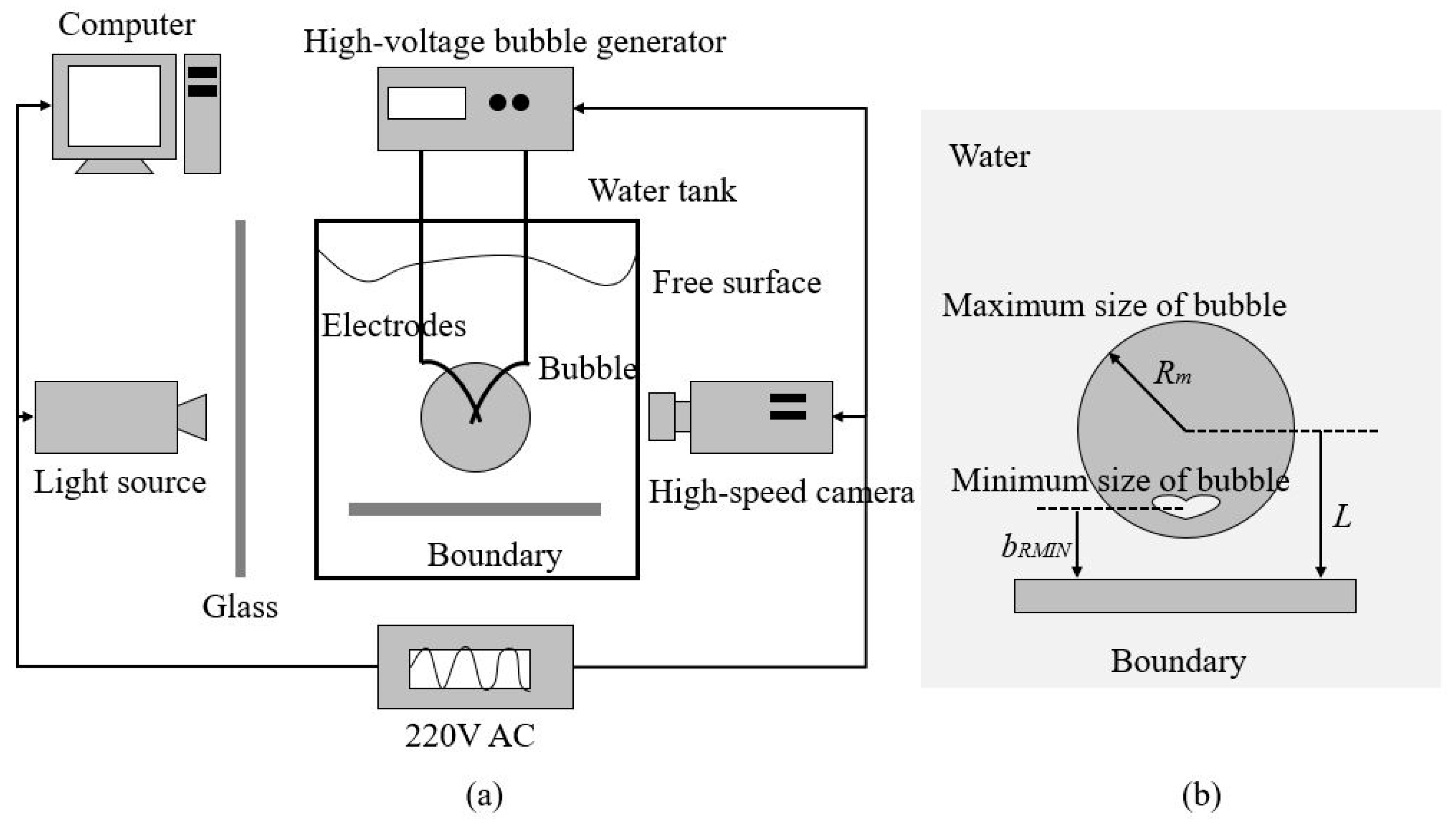
2. Experimental Method
2.1. Bubble Generation
2.2. Boundary Information
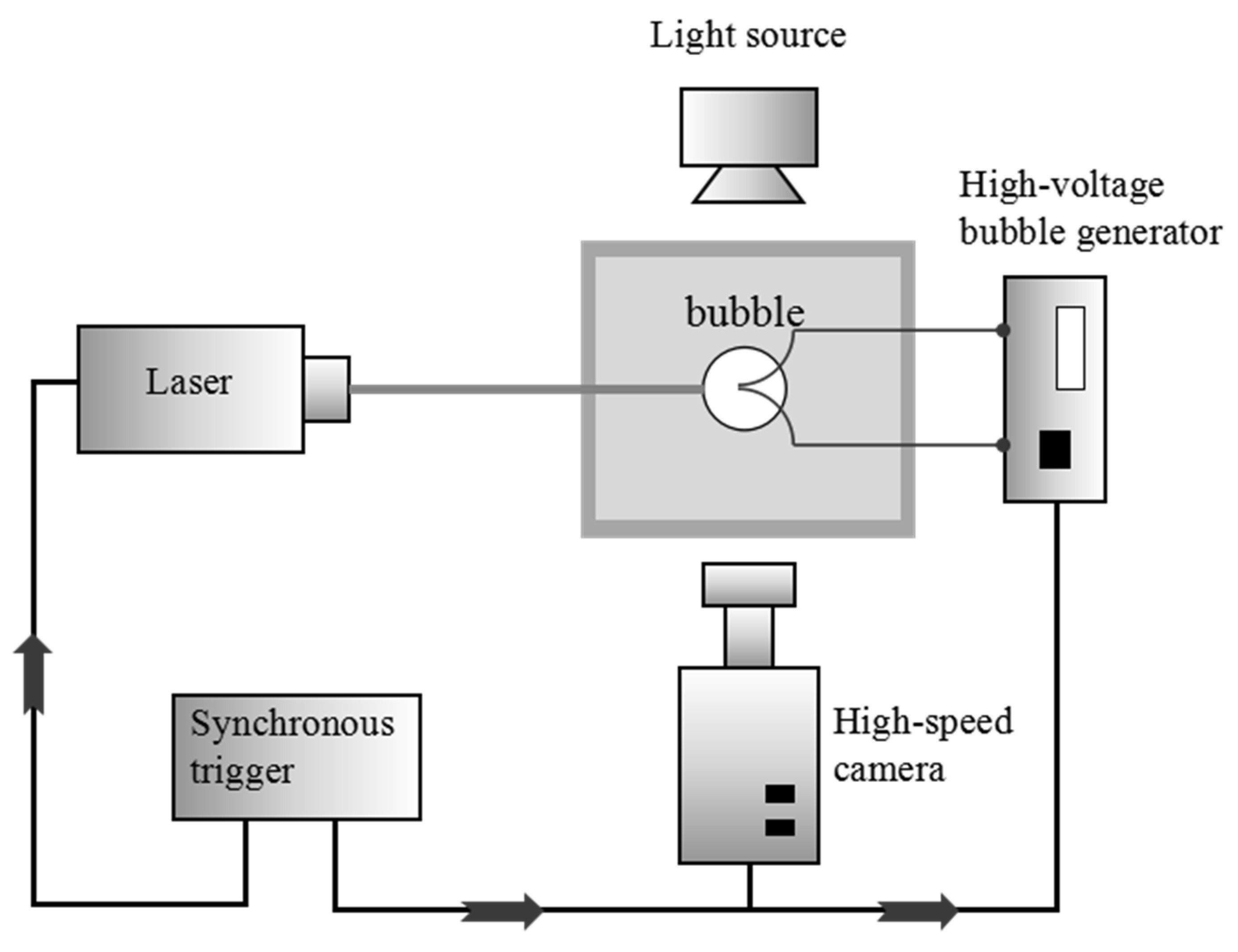
2.3. High-Speed Photography
2.4. PIV System
3. Acoustic Pressure Prediction Method
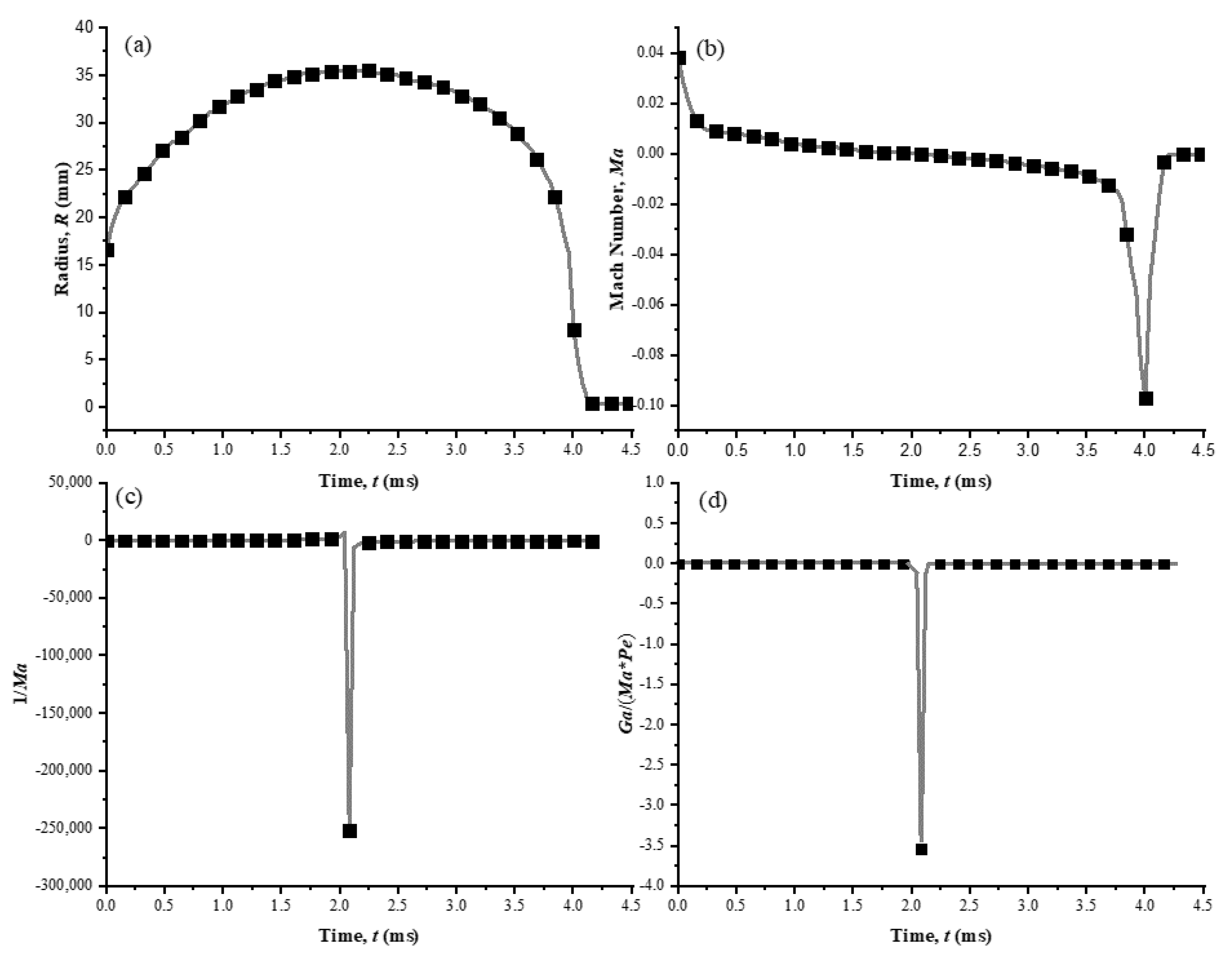
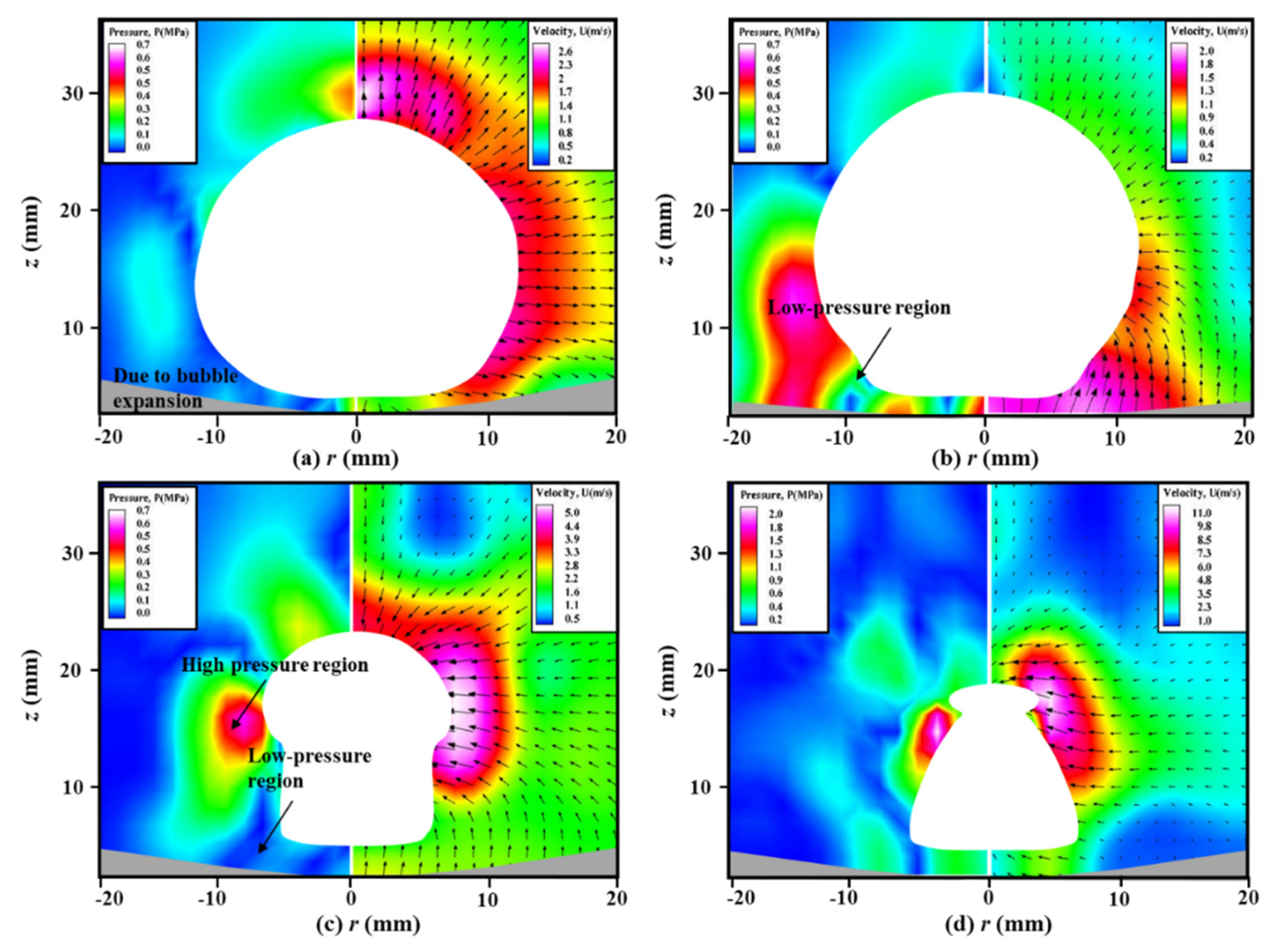
4. Results and Discussions
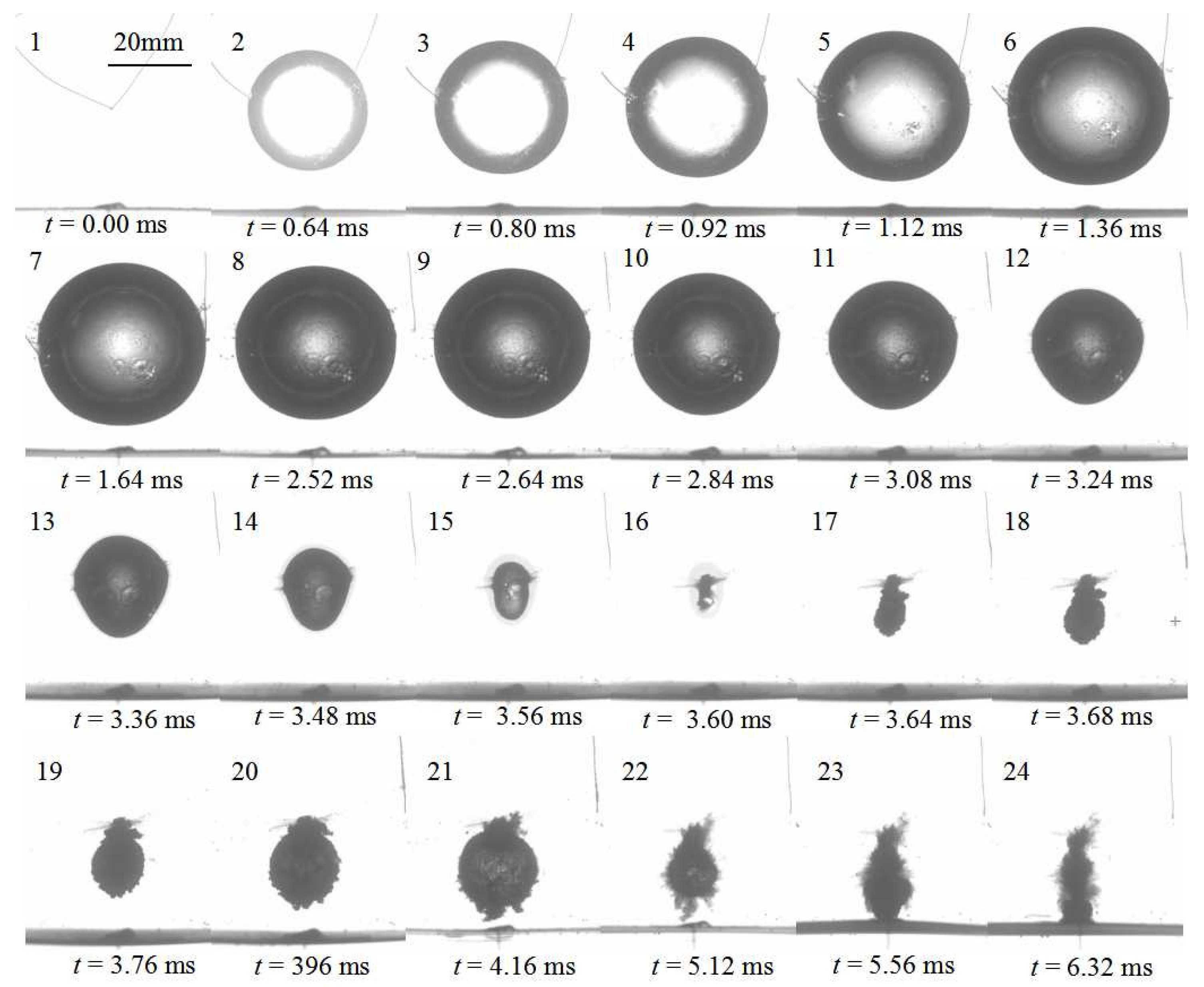
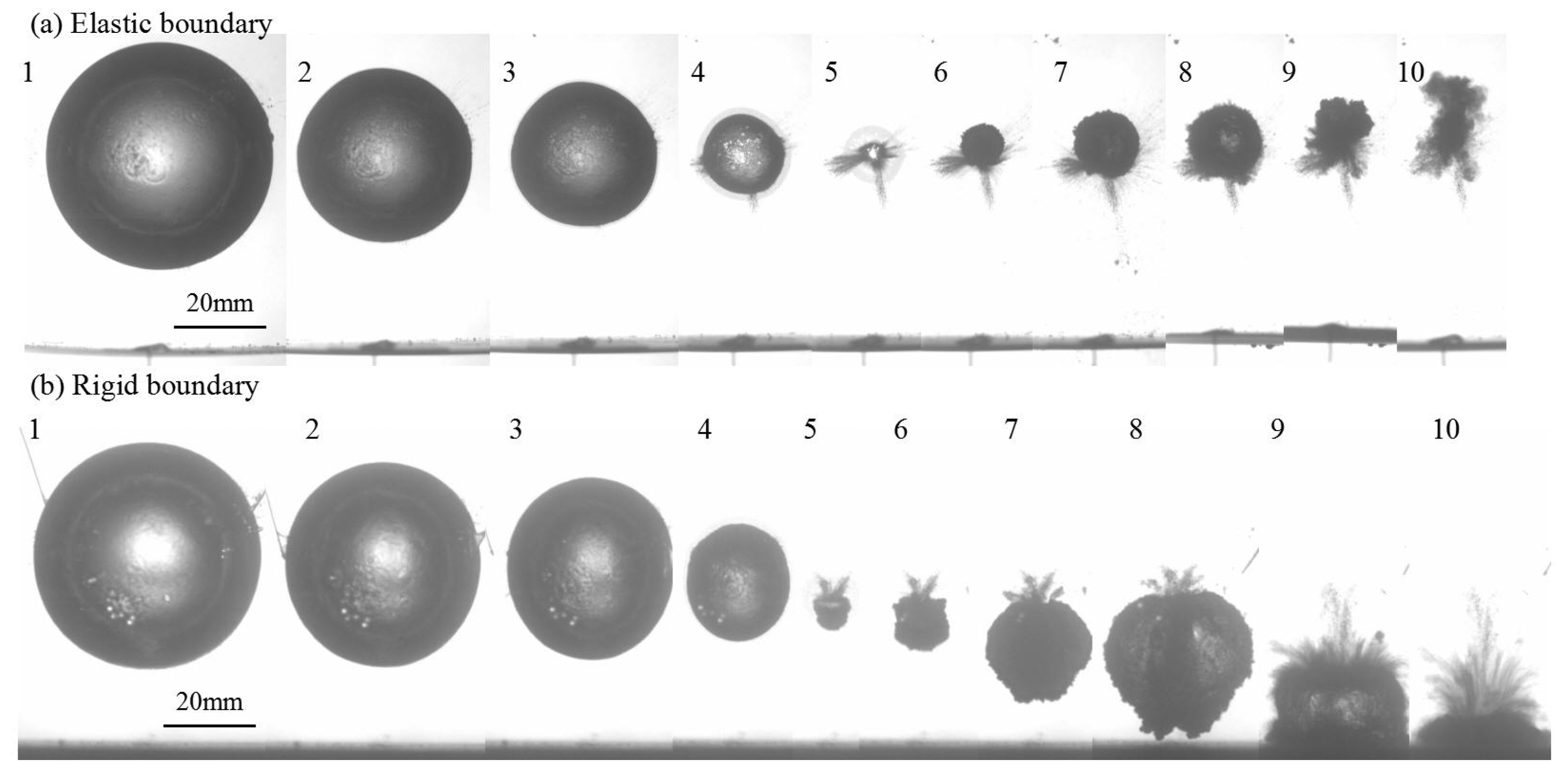
4.1. The Formation of “Mushroom” Bubble
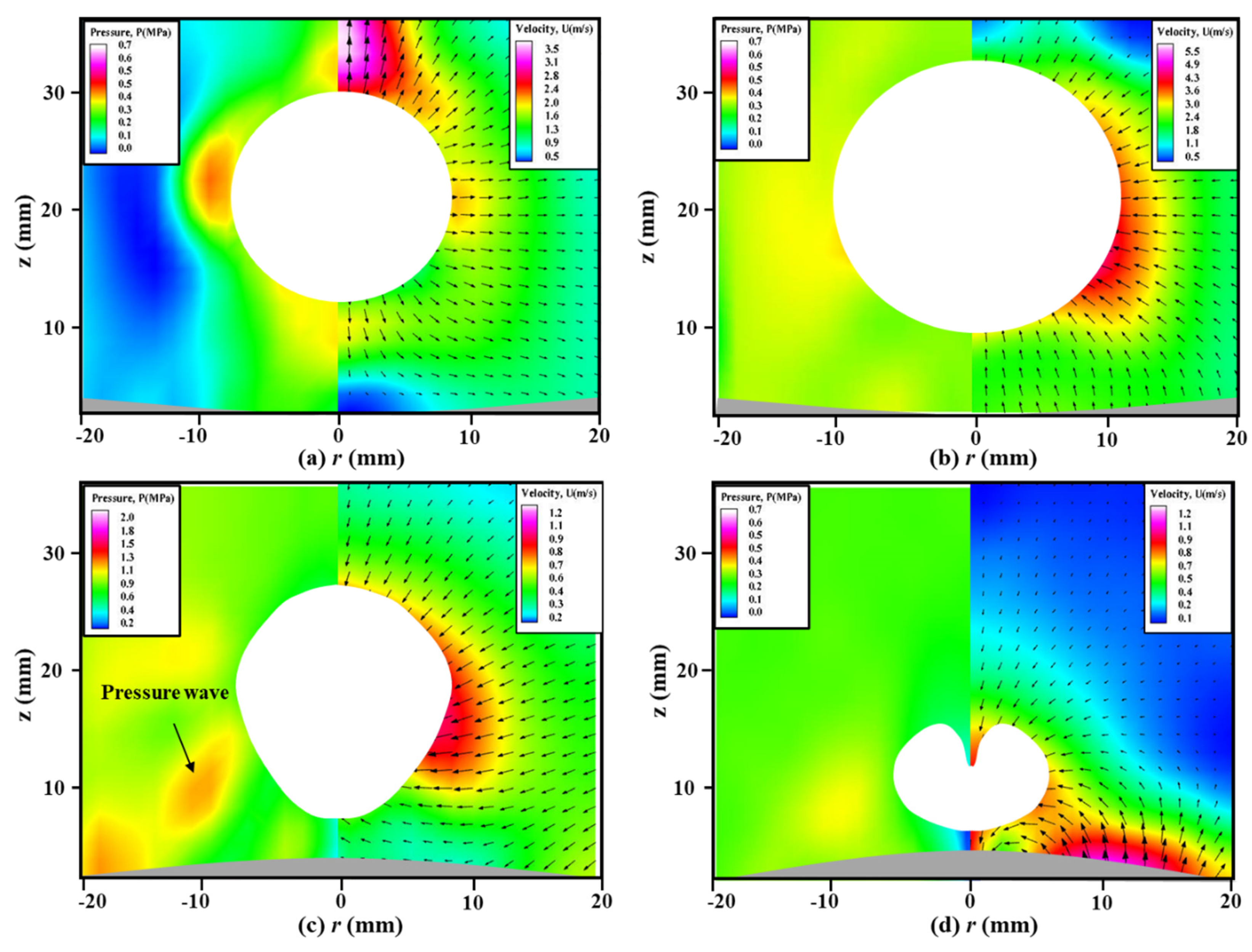
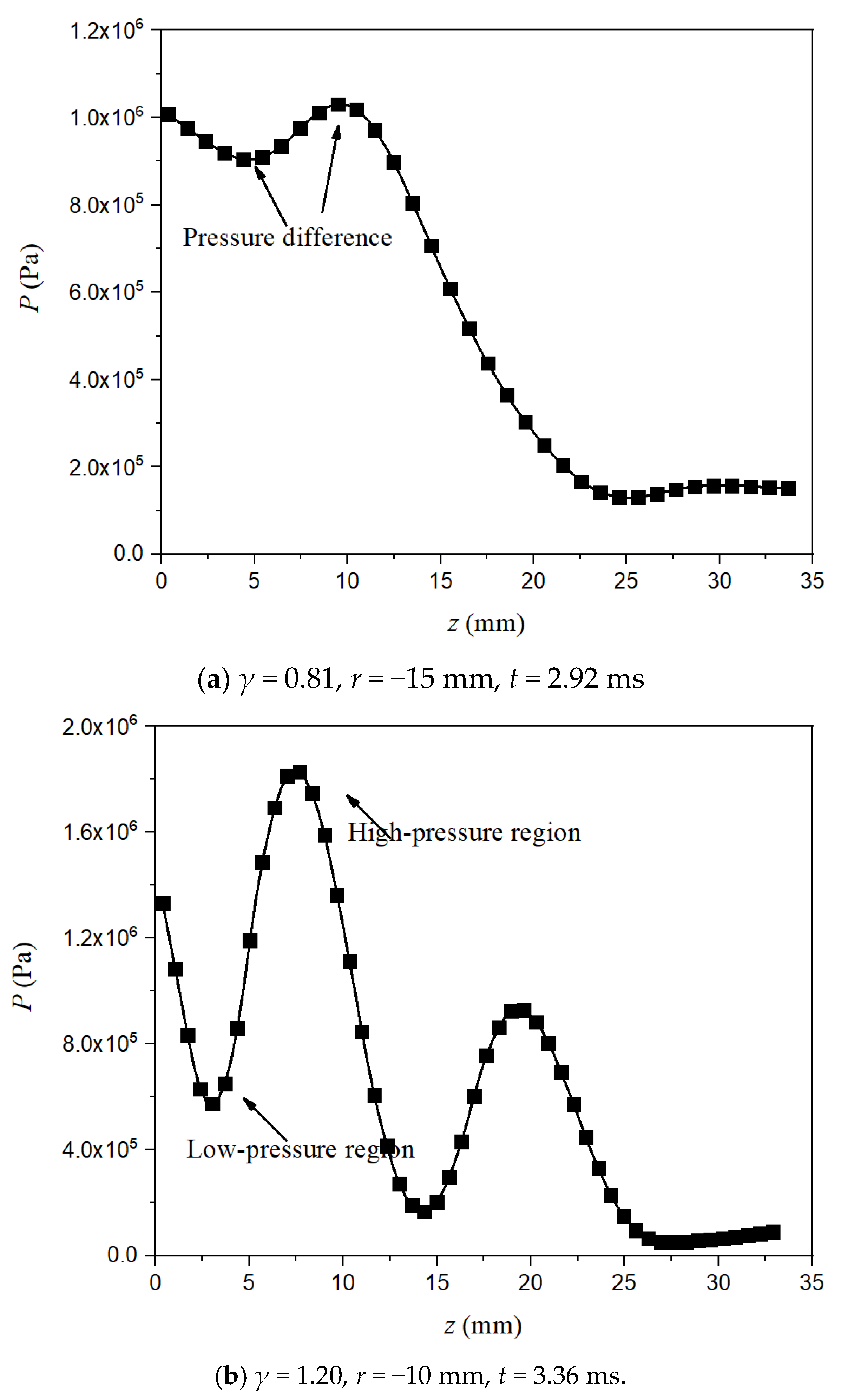
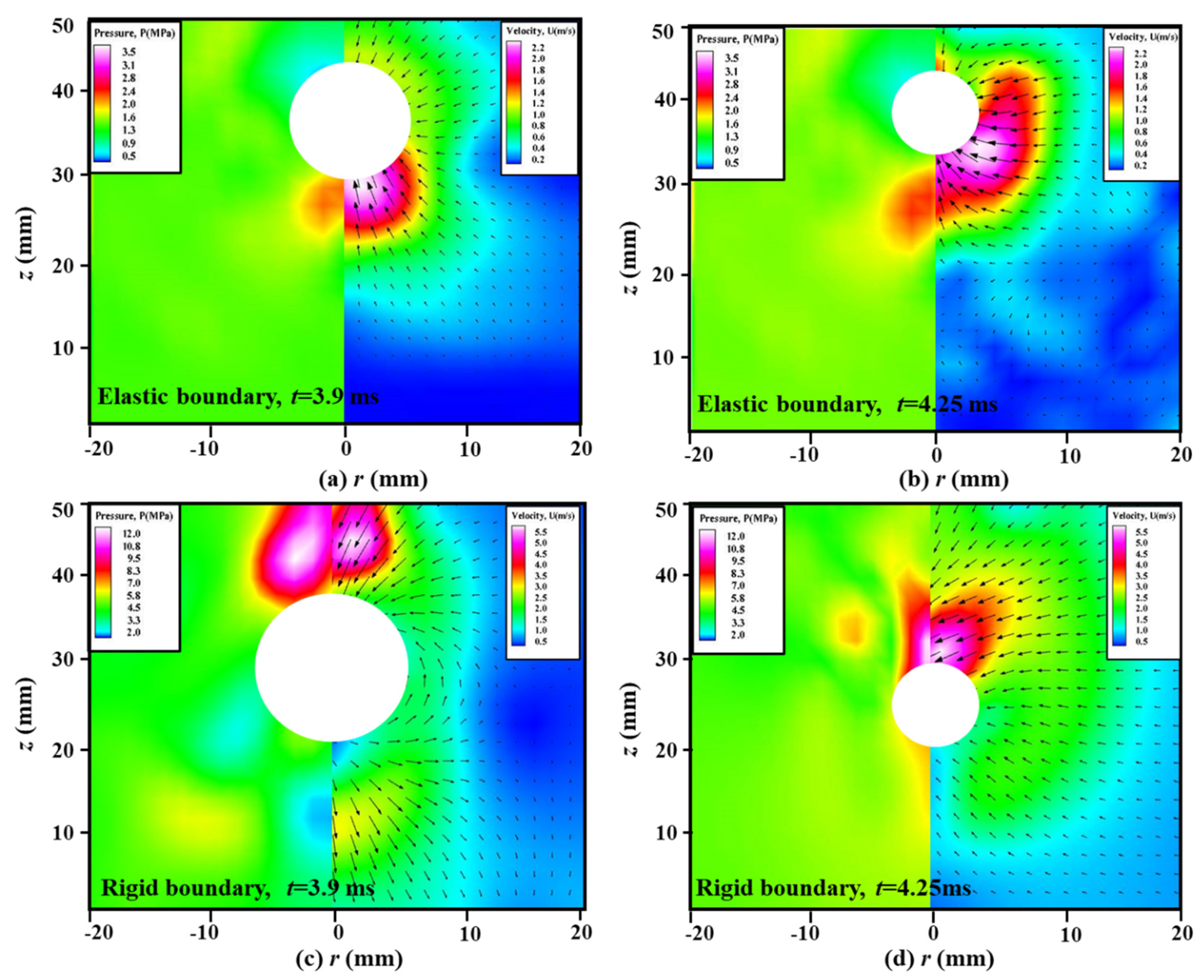
4.1.1. The Case of γ = 0.81
4.1.2. The Case of γ = 1.20
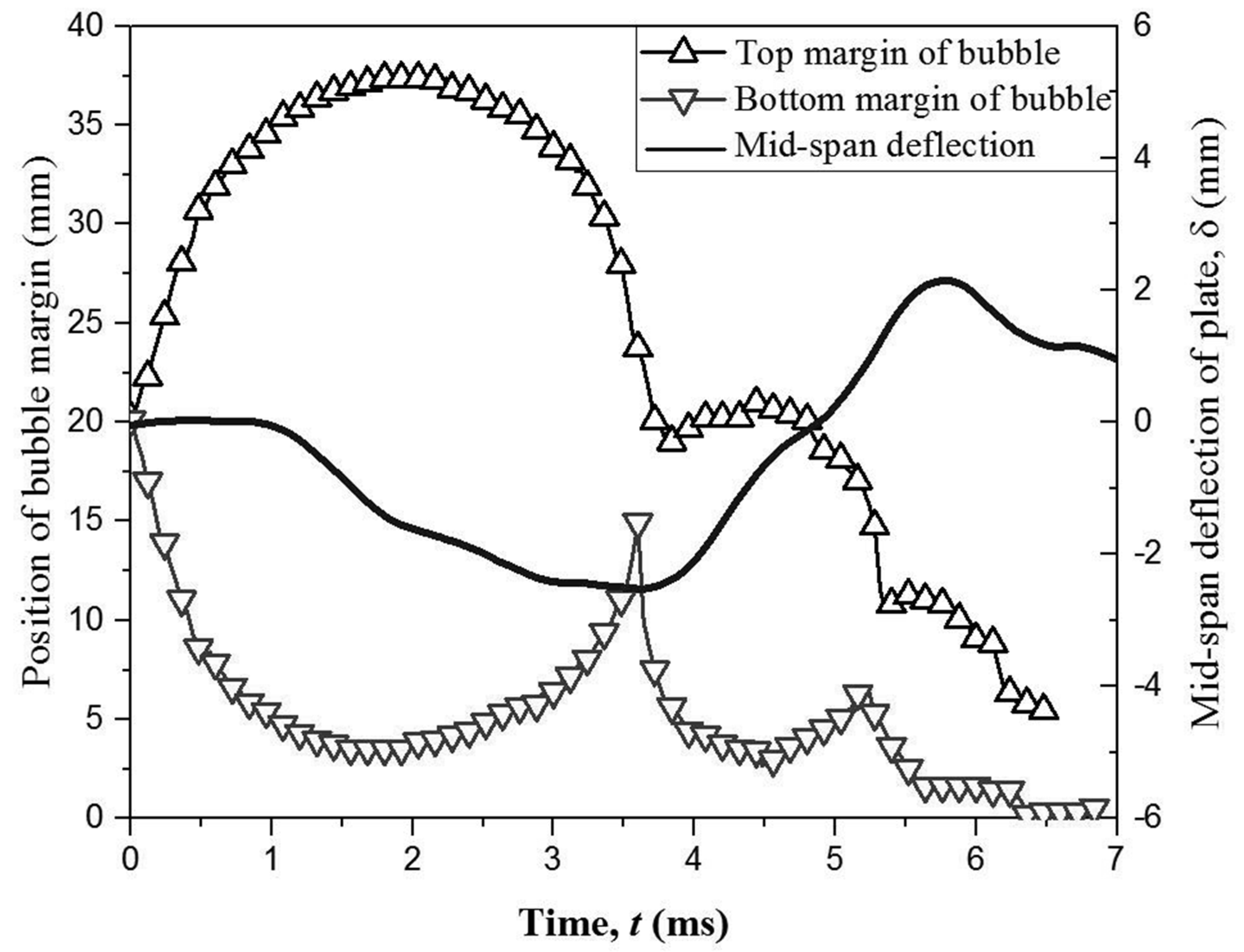
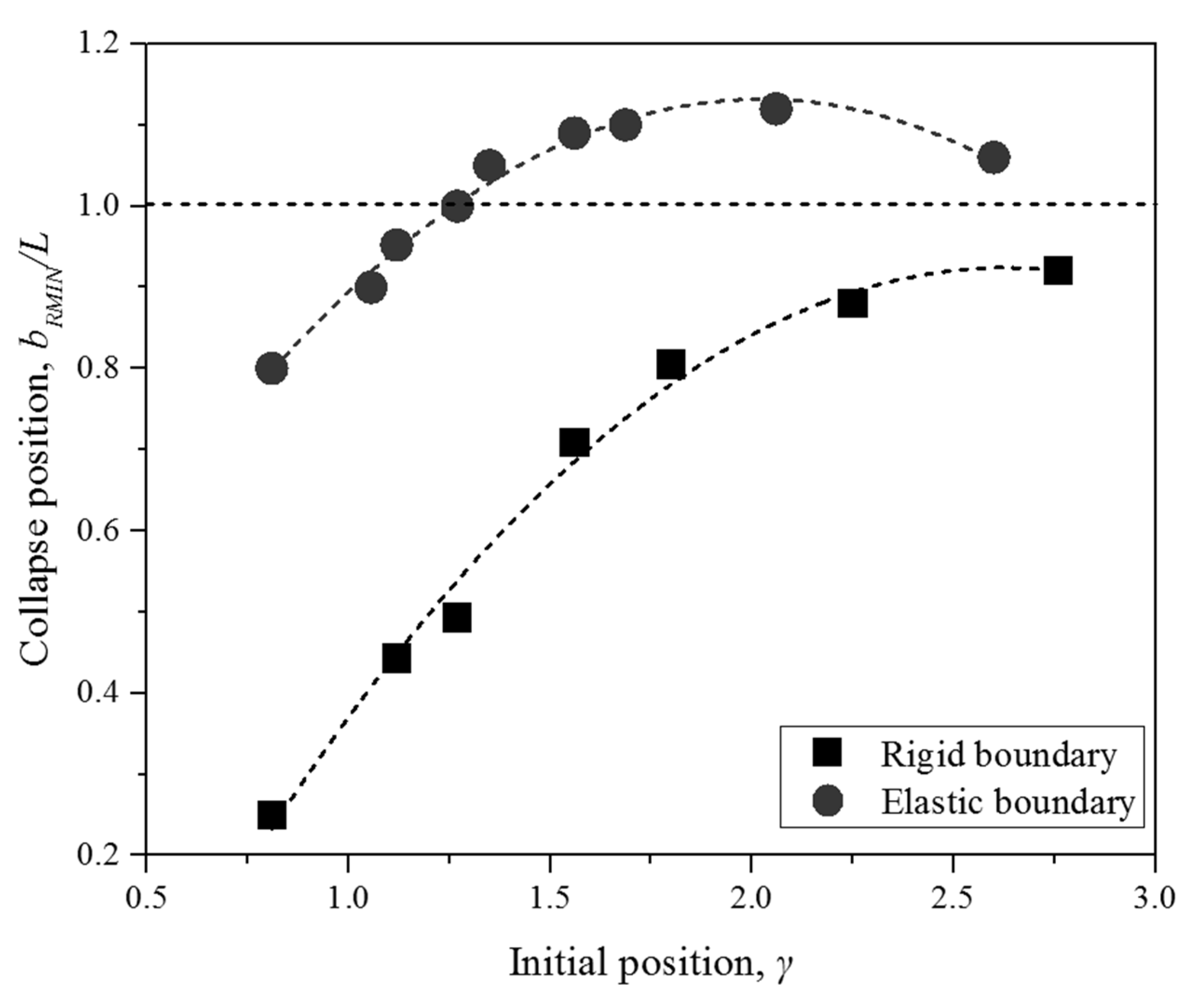
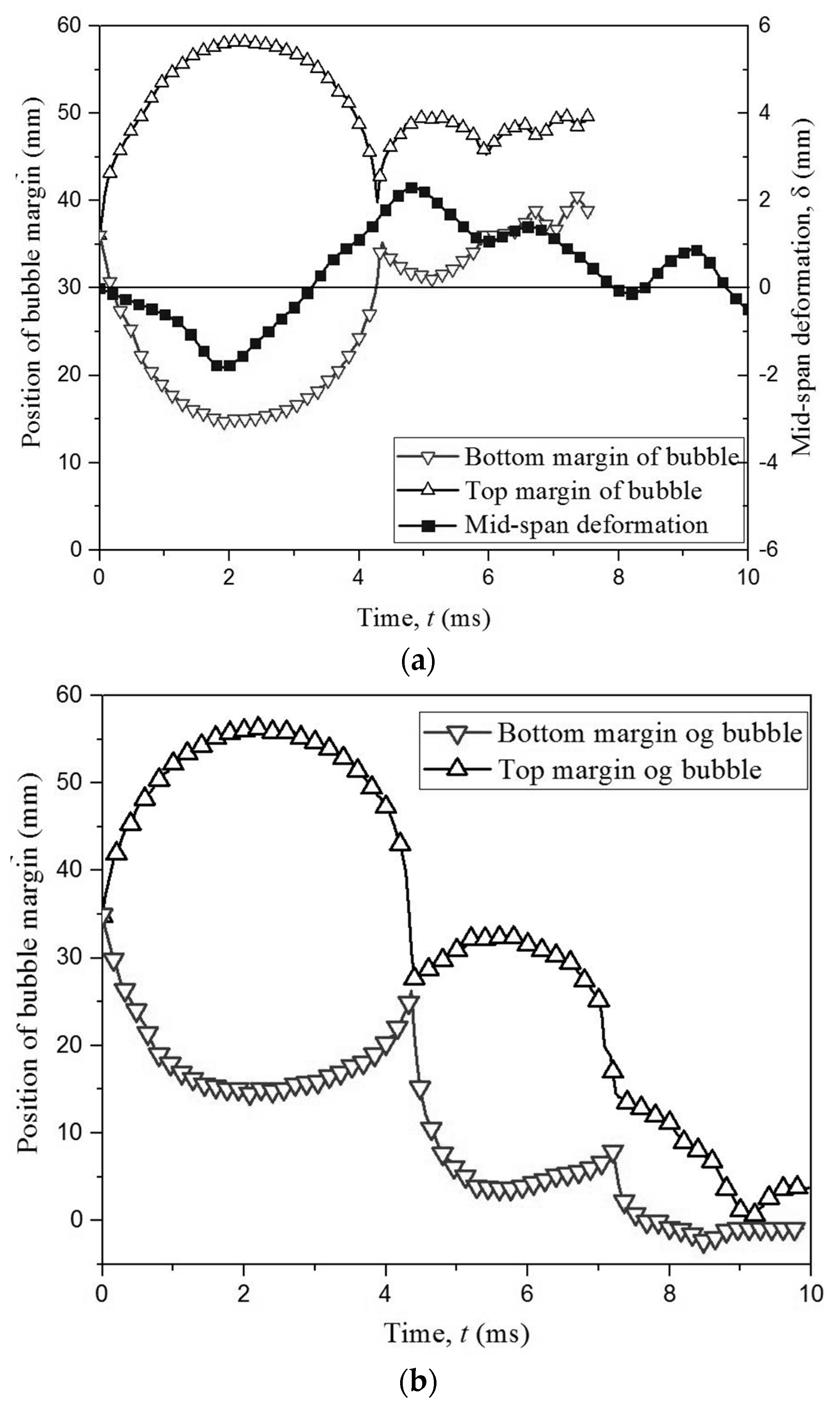
4.2. The Bubble Migration
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Harrison, M. An experimental study of single bubble cavitation noise. J. Acoust. Soc. Am. 1952, 24, 776–782. [Google Scholar] [CrossRef]
- Akhatov, I.S.; Lindau, O.; Topolnikov, A.; Mettin, R.; Vakhitova, N.; Lauterborn, W. Collapse and rebound of a laser-induced cavitation bubble. Phys. Fluids 2001, 13, 2805–2819. [Google Scholar] [CrossRef]
- Tomita, Y.; Shima, A. Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 1986, 169, 535–564. [Google Scholar] [CrossRef]
- Ma, X.; Huang, B.; Wang, G.; Zhang, M. Experimental investigation of conical bubble structure and acoustic flow structure in ultrasonic field. Ultrason. Sonochem. 2017, 34, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.-W.; Ji, B.; Tsujimoto, Y. A review of cavitation in hydraulic machinery. J. Hydrodyn. 2016, 28, 335–358. [Google Scholar] [CrossRef]
- Bratukhin, Y.K.; Kostarev, K.G.; Viviani, A.; Zuev, A.L. Experimental study of Marangoni bubble migration in normal gravity. Exp. Fluids 2005, 38, 594–605. [Google Scholar]
- Hickling, R.; Plesset, M.S. Collapse and Rebound of a Spherical Bubble in Water. Phys. Fluids 1964, 7, 7. [Google Scholar] [CrossRef]
- Liu, L.T.; Yao, X.; Zhang, A.-M.; Chen, Y.Y. Numerical analysis of the jet stage of bubble near a solid wall using a front tracking method. Phys. Fluids 2017, 29, 012105. [Google Scholar] [CrossRef]
- Brujan, E.A.; Nahen, K.; Schmidt, P. Dynamics of Laser-Induced Cavitation Bubbles Near an Elastic Boundary Used as a Tissue Phantom; American Institute of Physics: University Park, MD, USA, 2000; pp. 381–384. [Google Scholar]
- Brujan, E.-A.; Nahen, K.; Schmidt, P.; Vogel, A. Dynamics of laser-induced cavitation bubbles near elastic boundaries: Influence of the elastic modulus. J. Fluid Mech. 2001, 433, 283–314. [Google Scholar] [CrossRef]
- Klaseboer, E.; Khoo, B.C. An oscillating bubble near an elastic material. J. App. Phys. 2004, 96, 5808–5818. [Google Scholar] [CrossRef]
- Wang, Q. Oscillation of a bubble in a liquid confined in an elastic solid. Phys. Fluids 2017, 29, 072101. [Google Scholar] [CrossRef]
- Bai, L.; Chen, X.; Zhu, G.; Xu, W.; Lin, W.; Wu, P.; Li, C.; Xu, D.; Yan, J. Surface tension and quasi-emulsion of cavitation bubble cloud. Ultrason. Sonochem. 2017, 35, 405–414. [Google Scholar] [CrossRef] [PubMed]
- Hua, C.; Johnsen, E. Nonlinear oscillations following the Rayleigh collapse of a gas bubble in a linear viscoelastic (tissue-like) medium. Phys. Fluids 2013, 25, 083101. [Google Scholar] [CrossRef]
- Kalumuck, K.; Duraiswami, R.; Chahine, G. Bubble Dynamics Fluid-Structure Interaction Simulation by Coupling Fluid Bem and Structural Fem Codes. J. Fluids Struct. 1995, 9, 861–883. [Google Scholar] [CrossRef]
- Ma, X.; Huang, B.; Li, Y.; Chang, Q.; Qiu, S.; Su, Z.; Fu, X.; Wang, G. Numerical simulation of single bubble dynamics under acoustic travelling waves. Ultrason. Sonochem. 2018, 42, 619–630. [Google Scholar] [CrossRef]
- Klaseboer, E.; Turangan, C.; Fong, S.W.; Liu, T.G.; Hung, K.C.; Khoo, B.C. Simulations of pressure pulse–bubble interaction using boundary element method. Comput. Methods Appl. Mech. Eng. 2006, 195, 4287–4302. [Google Scholar] [CrossRef]
- Turangan, C.K.; Klaseboer, E.; Khoo, B.C.; Ong, G.P. Experimental and numerical study of transient bubble-elastic membrane interaction. J. Appl. Phys. 2006, 100, 54910. [Google Scholar] [CrossRef]
- Brujan, E.; Nahen, K.; Schmidt, P. Dynamics of laser-induced cavitation bubbles near an elastic boundary. J. Fluid Mech. 2001, 433, 251–281. [Google Scholar] [CrossRef]
- Blake, J.R.; Robinson, P.B.; Shima, A.; Tomita, Y. Interaction of two cavitation bubbles with a rigid boundary. J. Fluid Mech. 1993, 255, 707–721. [Google Scholar] [CrossRef]
- Wu, P.; Bai, L.; Lin, W.; Yan, J.; Pengfei, W.; Lixin, B.; Weijun, L.; Jiuchun, Y. Stability of cavitation structures in a thin liquid layer. Ultrason. Sonochem. 2017, 38, 75–83. [Google Scholar] [CrossRef]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 1975, 72, 391. [Google Scholar] [CrossRef]
- Klaseboer, E.; Khoo, B.C. Boundary integral equations as applied to an oscillating bubble near a fluid-fluid interface. Comput. Mech. 2004, 33, 129–138. [Google Scholar] [CrossRef]
- Shima, A.; Takayama, K.; Tomita, Y. An Experimental Study on Effects of a Solid Wall on the Motion of Bubbles and Shock Waves in Bubble Collapse. Acta Acust. United Acust. 1981, 48, 293–301. [Google Scholar]
- Ma, X.; Huang, B.; Zhao, X.; Wang, Y.; Chang, Q.; Qiu, S.; Fu, X.; Wang, G. Comparisons of spark-charge bubble dynamics near the elastic and rigid boundaries. Ultrason. Sonochem. 2018, 43, 80–90. [Google Scholar] [CrossRef]
- Kröninger, D.; Köhler, K.; Kurz, T.; Lauterborn, W. Particle tracking velocimetry of the flow field around a collapsing cavitation bubble. Exp. Fluids 2009, 48, 395–408. [Google Scholar] [CrossRef]
- Vogel, A.; Lauterborn, W. Time resolved particle image velocimetry. Opt. Lasers Eng. 1988, 9, 277–294. [Google Scholar] [CrossRef]
- Shangguan, H.; Casperson, L.W.; Shearin, A.; Prahl, S.A. Investigation of cavitation bubble dynamics using particle image velocimetry: Implications for photoacoustic drug delivery. Photonics West 1996, 2671, 104–115. [Google Scholar] [CrossRef]
- Curtin, D.M.; Newport, D.; Davies, M.R. Utilising μ-PIV and pressure measurements to determine the viscosity of a DNA solution in a microchannel. Exp. Therm. Fluid Sci. 2006, 30, 843–852. [Google Scholar] [CrossRef]
- Azijli, I.; Sciacchitano, A.; Ragni, D.; Palha, A.; Dwight, R.P. A posteriori uncertainty quantification of PIV-based pressure data. Exp. Fluids 2016, 57. [Google Scholar] [CrossRef][Green Version]
- Yang, H.; Shen, W.Z.; Sørensen, J.N.; Zhu, W.J. Extraction of airfoil data using PIV and pressure measurements. Wind. Energy 2010, 14, 539–556. [Google Scholar] [CrossRef]
- Auteri, F.; Carini, M.; Zagaglia, D.; Montagnani, D.; Gibertini, G.; Merz, C.B.; Zanotti, A. A novel approach for reconstructing pressure from PIV velocity measurements. Exp. Fluids 2015, 56, 45. [Google Scholar] [CrossRef]
- Morris, S.C. Shear-Layer Instabilities: Particle Image Velocimetry Measurements and Implications for Acoustics. Ann. Rev. Fluid Mech. 2011, 43, 529–550. [Google Scholar] [CrossRef]
- Kat, R.D.; Oudheusden, B.W.V. Instantaneous planar pressure determination from PIV in turbulent flow. Exp. Fluids 2012, 52, 1089–1106. [Google Scholar] [CrossRef]
- Hung, C.F.; Hwangfu, J.J. Experimental study of the behaviour of mini-charge underwater explosion bubbles near different boundaries. J. Fluid Mech. 2010, 651, 55. [Google Scholar] [CrossRef]
- Caltagirone, J.-P.; Vincent, S.; Caruyer, C. A multiphase compressible model for the simulation of multiphase flows. Comput. Fluids 2011, 50, 24–34. [Google Scholar] [CrossRef]
- Ma, X.-J.; Zhao, X.; Huang, B.; Fu, X.-Y.; Wang, G.-Y. Physical investigation of non-spherical bubble collapse near a rigid boundary. J. Hydrodyn. 2019, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.; Chang, Q.; Ma, X.; Wang, G.; Huang, B. Physical investigation of the counterjet dynamics during the bubble rebound. Ultrason. Sonochem. 2019, 58, 104706. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C.; Huang, B.; Wang, G. Application of two-branch deep neural network to predict bubble migration near elastic boundaries. Phys. Fluids 2019, 31, 102003. [Google Scholar] [CrossRef]
- Blake, J.R. The Kelvin impulse: Application to cavitation bubble dynamics. J. Aust. Math. Soc. Ser. B 1988, 30, 127–146. [Google Scholar] [CrossRef]


| Items | Materials | Length a (mm) | Width b (mm) | Height c (mm) | Elastic Modulus E (GPa) | Density ρ (kg/m3) |
|---|---|---|---|---|---|---|
| Elastic boundary | Carbon fiber composite | 120.0 | 80.0 | 0.5 | 66.2 | 1286 |
| Rigid boundary | Aluminum | 120.0 | 80.0 | 3.0 | 70.0 | 2700 |
| Values of elastic modulus, density of the boundary samples at 298 K | ||||||
| Seeding | Type | Hollow glass micro sphere | |
| Diameter | 50 | μm | |
| Type | Gas bubbles | ||
| Light sheet | Laser type | RayPower 5000 | |
| Laser power | 5 | W | |
| Wave length | 532 | nm | |
| Laser light mode | Continuous mode | ||
| Camera | Type | SpeedSence M310 | |
| Resolution | 800 × 512 | Pixels2 | |
| Interframe time | 0.25 | ms | |
| Pixel size | 20 | μm | |
| Pixel depth | 12 | bit | |
| Memory | 6 | GB | |
| PIV analysis | Interrogation area | 32 × 32 | Pixels2 |
| Overlap IA | 50% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Xu, Z.; Zhao, J.; Zhang, M.; Ma, X. PIV-Based Acoustic Pressure Measurements of a Single Bubble near the Elastic Boundary. Micromachines 2020, 11, 637. https://doi.org/10.3390/mi11070637
Yu Q, Xu Z, Zhao J, Zhang M, Ma X. PIV-Based Acoustic Pressure Measurements of a Single Bubble near the Elastic Boundary. Micromachines. 2020; 11(7):637. https://doi.org/10.3390/mi11070637
Chicago/Turabian StyleYu, Qidong, Zhicheng Xu, Jing Zhao, Mindi Zhang, and Xiaojian Ma. 2020. "PIV-Based Acoustic Pressure Measurements of a Single Bubble near the Elastic Boundary" Micromachines 11, no. 7: 637. https://doi.org/10.3390/mi11070637
APA StyleYu, Q., Xu, Z., Zhao, J., Zhang, M., & Ma, X. (2020). PIV-Based Acoustic Pressure Measurements of a Single Bubble near the Elastic Boundary. Micromachines, 11(7), 637. https://doi.org/10.3390/mi11070637





