Adaptive Tracking Control for the Piezoelectric Actuated Stage Using the Krasnosel’skii-Pokrovskii Operator
Abstract
1. Introduction
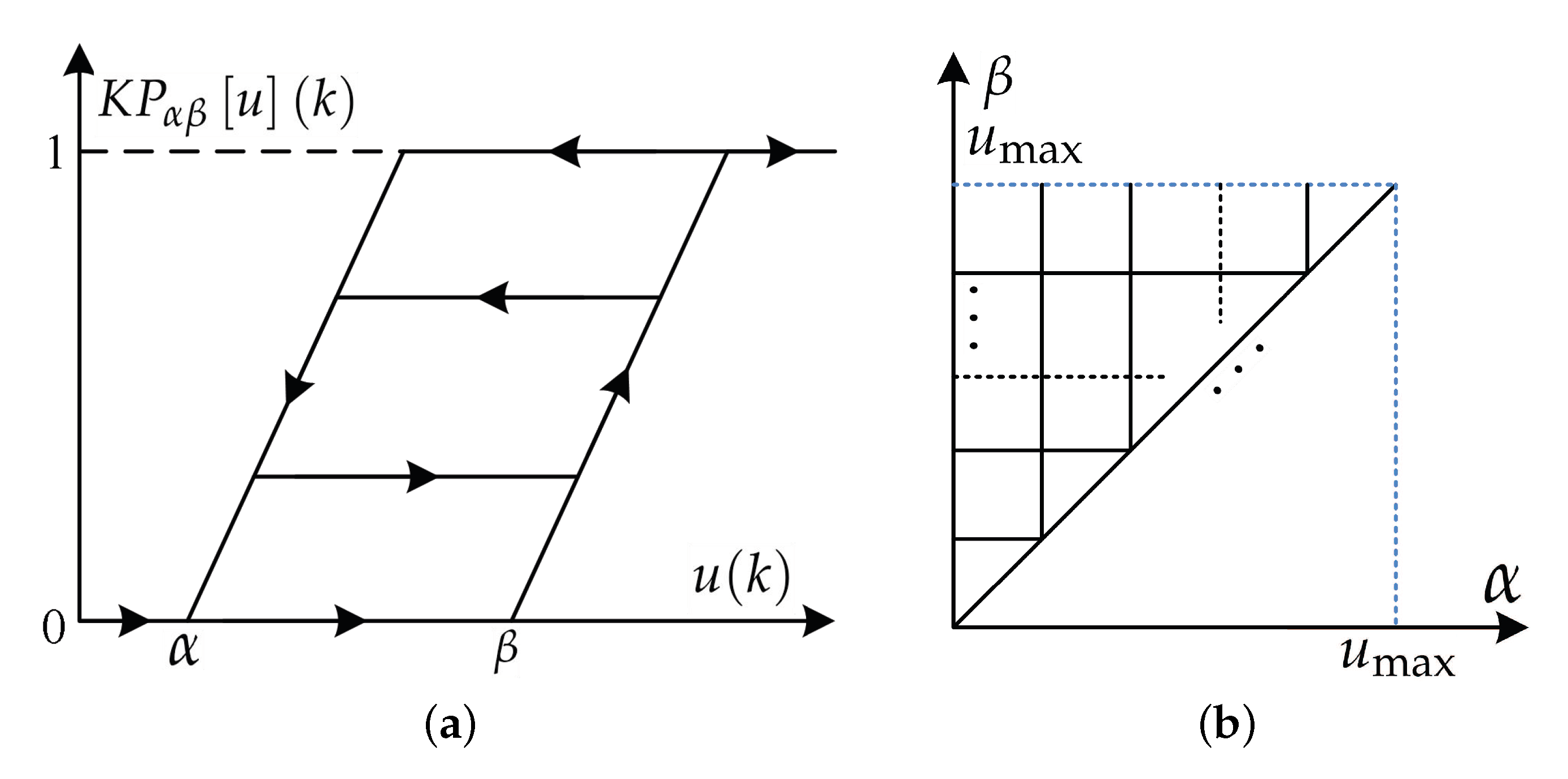
2. Hysteresis Modeling of the Piezoelectric Actuated Stage
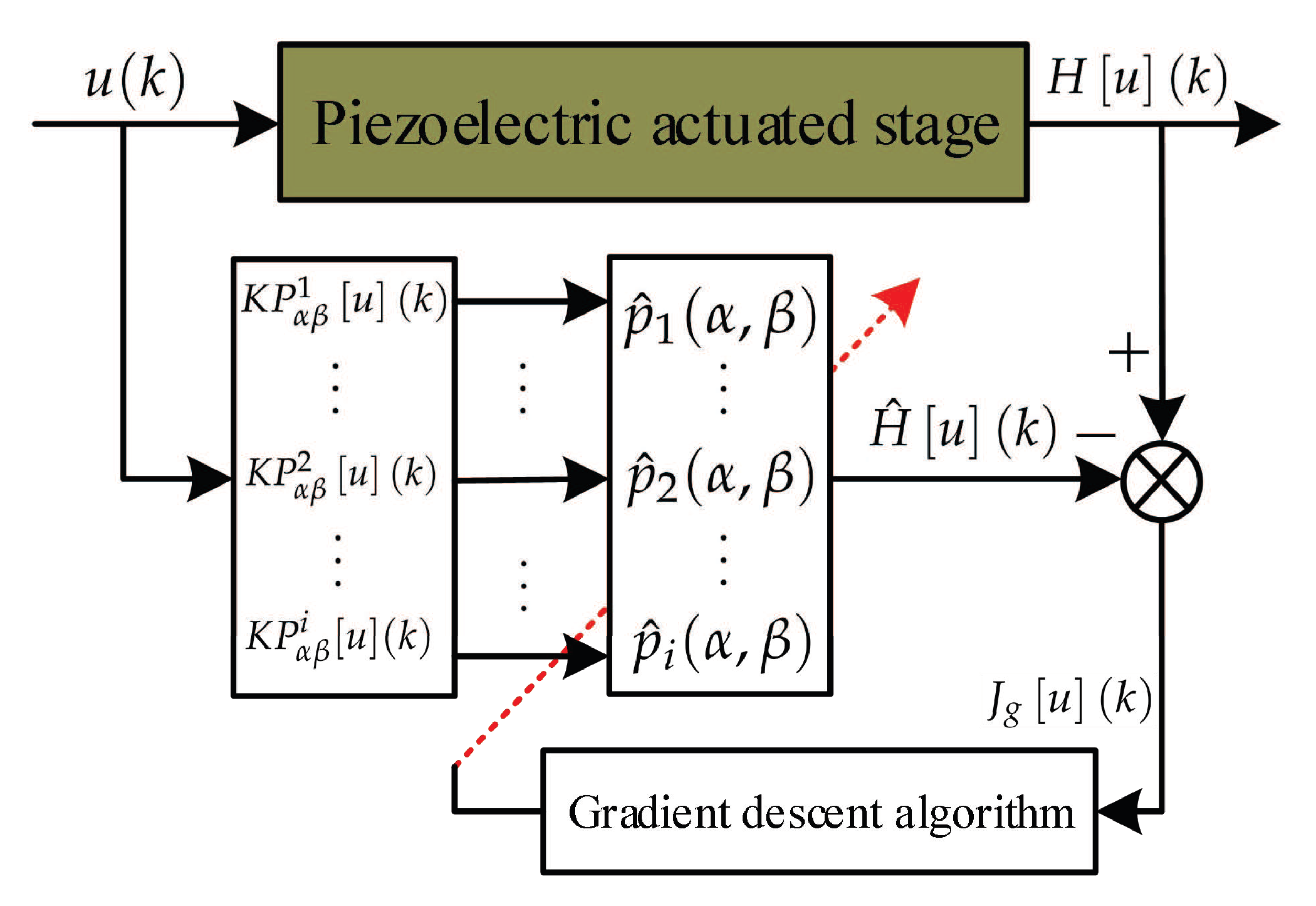
3. Adaptive Tracking Control Law Design
4. Simulation and Experimental Results
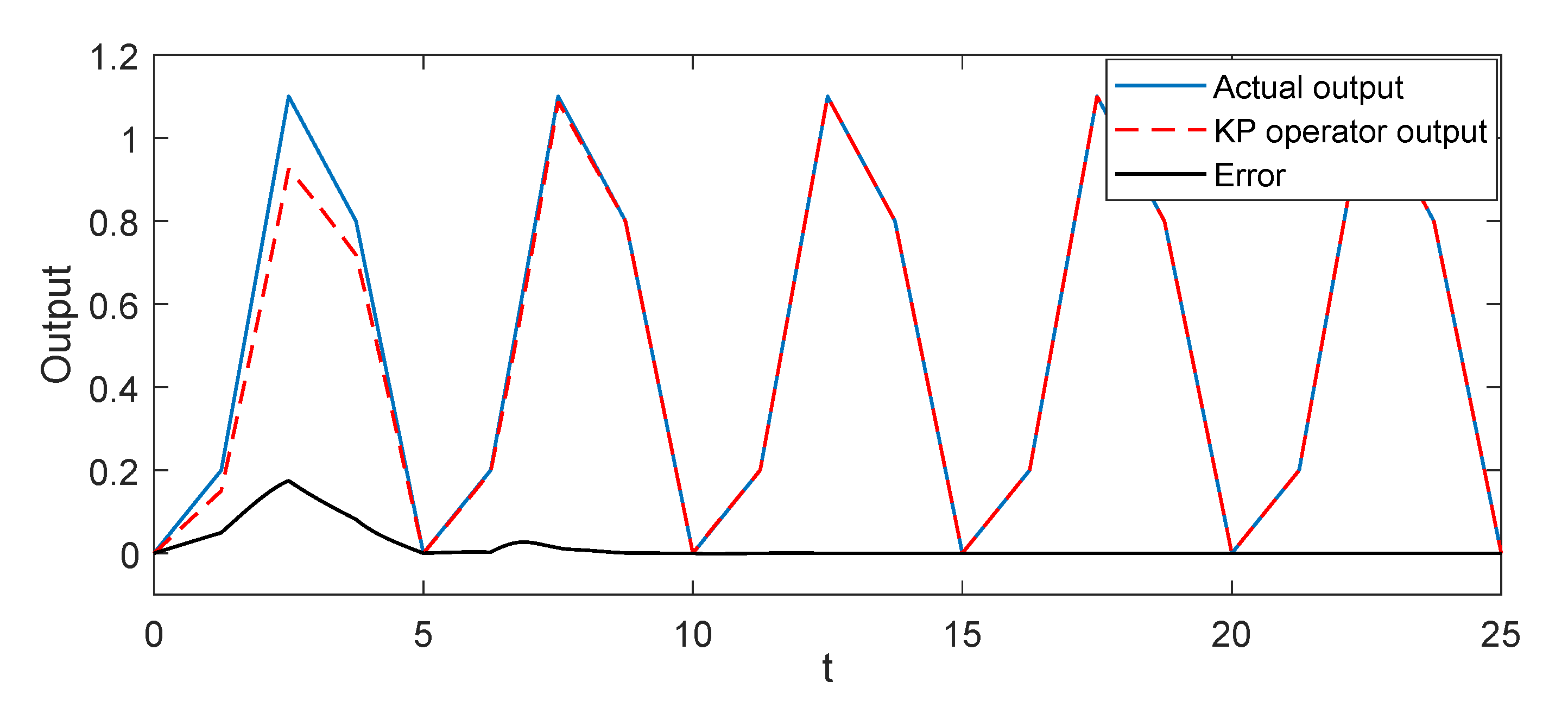
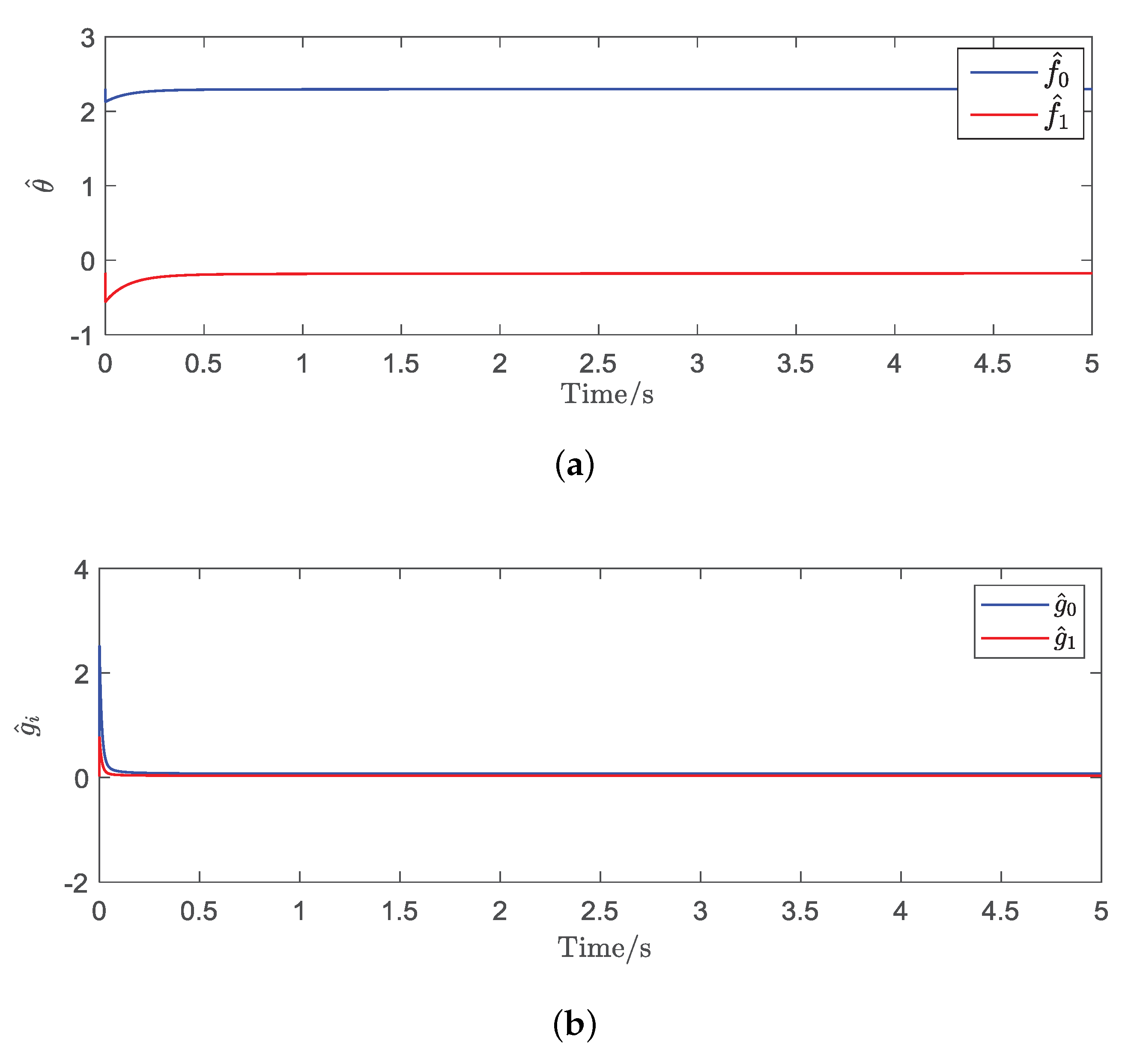
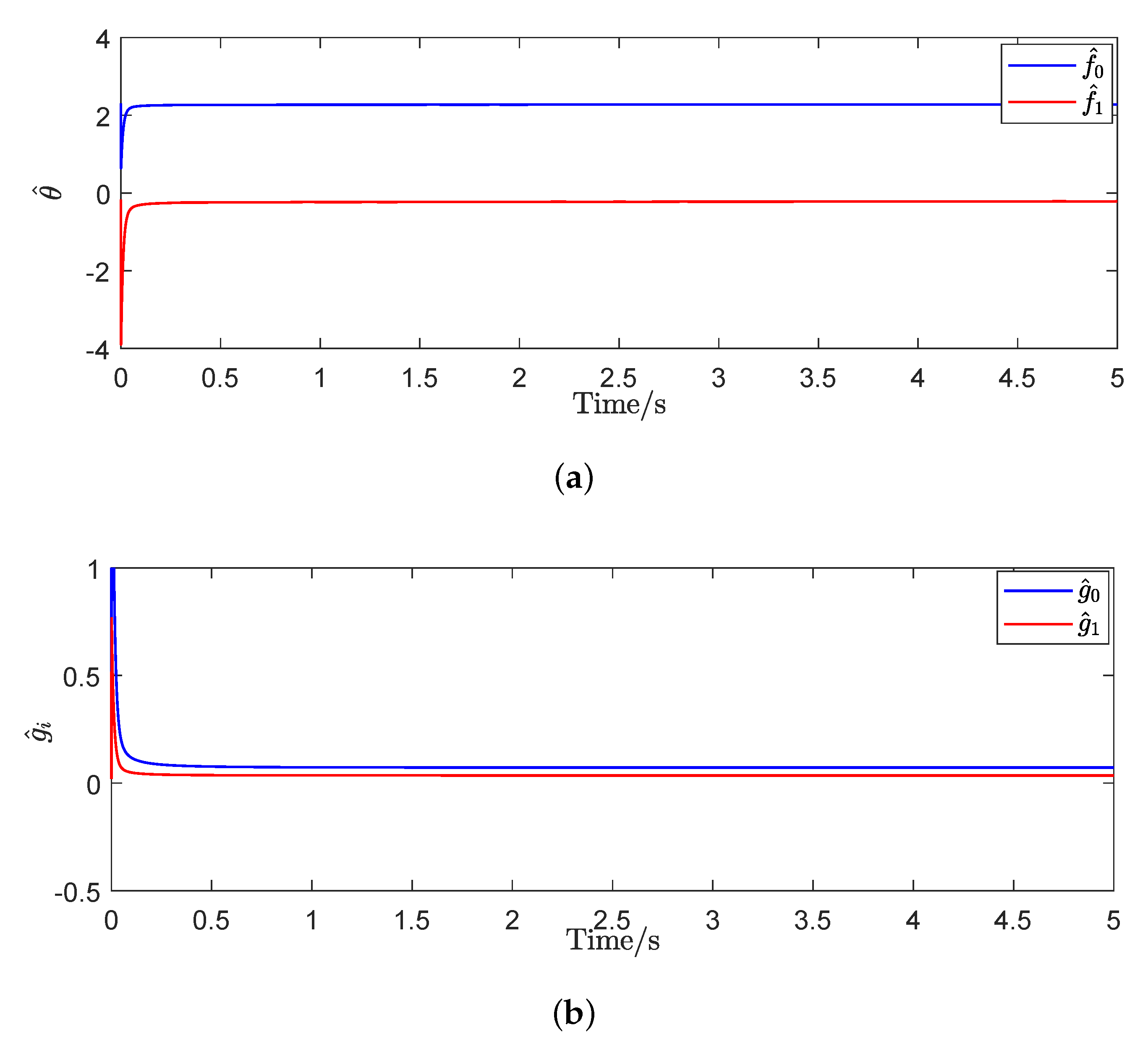
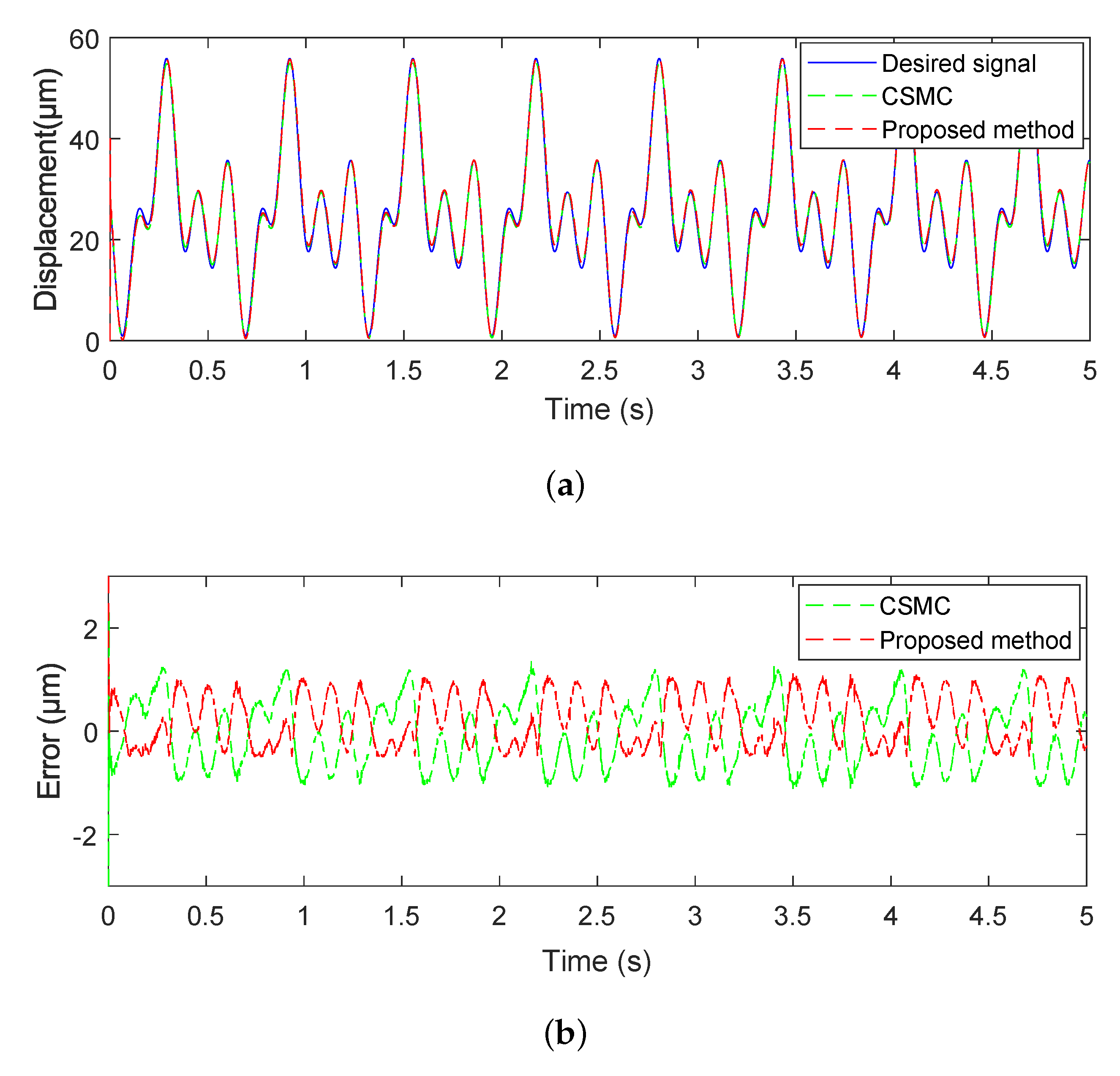
4.1. Simulation Results
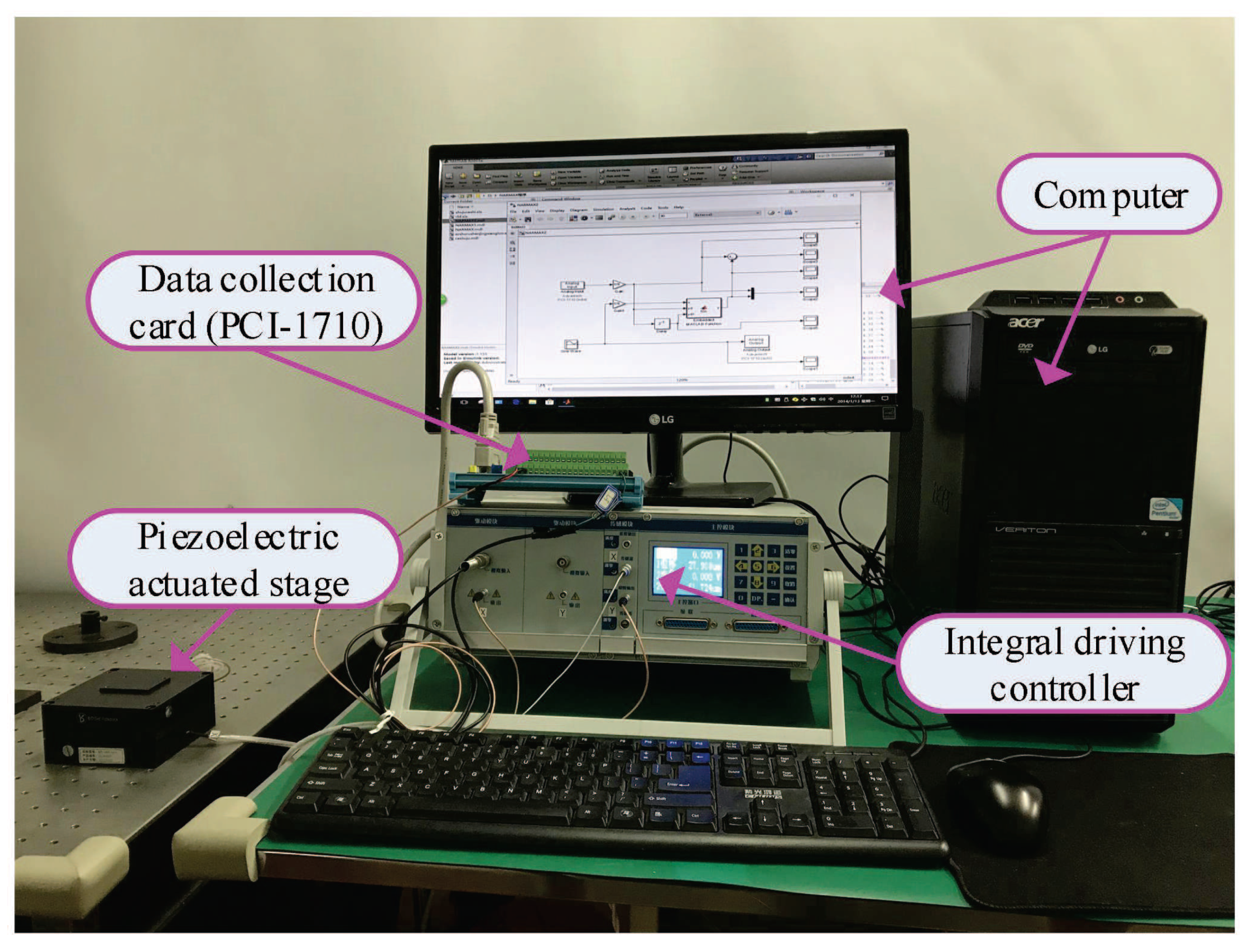
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zawierta, M.; Fleming, A.; Putrino, G.; Yong, Y. Multimodal atomic force microscopy with optimized higher eigenmode sensitivity using on-chip piezoelectric actuation and sensing. Nanotechnology 2019, 8, 085503. [Google Scholar]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y. Modeling and compensation of asymmetric hysteresis nonlinearity for piezoceramic actuators with a modified Prandtl-Ishlinskii model. IEEE Trans. Ind. Electron. 2014, 61, 1583–1595. [Google Scholar] [CrossRef]
- Qin, Y.D.; Duan, H. Single-Neuron adaptive hysteresis compensation of piezoelectric actuator based on hebb learning rules. Micromachines 2020, 11, 84. [Google Scholar] [CrossRef] [PubMed]
- Ding, B.X.; Li, Y.M. Hysteresis compensation and sliding mode control with perturbation estimation for piezoelectric actuators. Micromachines 2018, 9, 241. [Google Scholar] [CrossRef]
- Ounissi, A.; Landry, M.; Kaddouri, A.; Abdessemed, R. PSO based parameter identification of Colman-Hodgdon hysteresis model of a piezoelectric actuator and PID feedback controller. Contemp. Eng. Sci. 2014, 7, 179–192. [Google Scholar] [CrossRef][Green Version]
- Lin, C.J.; Lin, P.T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Comput. Math. Appl. 2012, 64, 766–787. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, X.Y.; Guo, H.Y.; Zhou, M.L. Sliding mode tracking control with perturbation estimation for hysteresis nonlinearity of piezo-actuated stages. IEEE Access 2018, 6, 30617–30629. [Google Scholar] [CrossRef]
- Li, Z.; Su, C.Y.; Chai, T.Y. Compensation of hysteresis nonlinearity in magnetostrictive actuators with inverse multiplicative structure for Preisach model. IEEE Trans. Autom. Sci. Eng. 2014, 11, 613–619. [Google Scholar] [CrossRef]
- Li, C.T.; Tan, Y.H. Adaptive output feedback control of systems preceded by the Preisach-type hysteresis. IEEE Trans. Syst. Man Cybern. B Cybern. 2005, 35, 130–135. [Google Scholar] [CrossRef]
- Xiao, S.L.; Li, Y.M. Modeling and high dynamic compensating the rate-dependent hysteresis of piezoelectric actuators via a novel modified inverse Preisach model. IEEE Trans. Control Syst. Technol. 2013, 21, 1549–1557. [Google Scholar] [CrossRef]
- Liu, S.N.; Su, C.Y.; Li, Z. Robust adaptive inverse control of a class of nonlinear systems with Prandtl-Ishlinskii hysteresis model. IEEE Trans. Autom. Control. 2014, 59, 2170–2175. [Google Scholar] [CrossRef]
- Wang, Y.F.; Xu, R.; Zhou, M.L. Prandtl-Ishlinskii modeling for giant magnetostrictive actuator based on internal time-delay recurrent neural network. IEEE Trans. Magn. 2018, 54, 7301004. [Google Scholar]
- Janaideh, M.A.; EI-Shaer, A.H. Performance enhancement for a class of hysteresis nonlinearities using disturbance observers. Int. J. Control Autom. Syst. 2014, 12, 283–293. [Google Scholar] [CrossRef]
- Kuhnen, K. Modeling, identification and compensation of complex hysteretic nonlinearities: A modified Prandtl-Ishlinskii approach. Eur. J. Control 2003, 9, 407–418. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, M.L. Elman neural network-based identification of Krasnosel’skii-Pokrovskii model for magnetic shape memory alloys actuator. IEEE Trans. Magn. 2017, 53, 2002004. [Google Scholar] [CrossRef]
- Zakerzadeh, M.R.; Sayyaadi, H.; Zanjani, M.A.V. Characterizing hysteresis nonlinearity behavior of SMA actuators by KP model. Appl. Math. 2011, 1, 28–38. [Google Scholar] [CrossRef]
- Wang, Y.; Su, C.Y.; Hong, H. Model reference control including adaptive inverse hysteresis for systems with unknown input hysteresis. In Proceedings of the 2007 IEEE International Conference on Networking, Sensing and Control, London, UK, 15–17 April 2007; pp. 70–75. [Google Scholar]
- Pan, W.; Xu, R.; Zhou, M.L. Modeling of hysteresis for piezo-driven stages using a rate-dependent Krasnosel’skii-Pokrovskii model. In Proceedings of the 2019 Chinese Control Conference (CCC2019), Guangzhou, China, 27–31 July 2019; pp. 1604–1609. [Google Scholar]
- Li, Z.; Shan, J.J.; Gabbert, U. Inverse compensation of hysteresis using Krasnoselskii-Pokrovskii model. IEEE/ASME Trans. Mechatron. 2018, 2, 966–971. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, P. Adaptive observer-based integral sliding mode control of a piezoelectric nano-manipulator. IET Control Theory Appl. 2019, 14, 2173–2180. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, M.L. Sliding mode control with sigmoid function for the motion tracking control of the piezo-actuated stages. Electron. Lett. 2017, 53, 75–77. [Google Scholar] [CrossRef]
- Kim, I.; Kim, Y.S.; Park, E.C. Sliding mode control of the inchworm displacement with hysteresis compensation. Int. J. Precis. Eng. Man 2009, 3, 43–49. [Google Scholar] [CrossRef]
- Nie, Z.; Ma, Y.; Liu, R.; Guo, D. Improved disturbance rejection control for piezoelectric actuators based on combination of ESO and Q-filter. Electron. Lett. 2018, 54, 872–874. [Google Scholar]
- Merry, R.; Uyanik, M.; Van, D.M.R.; Koops, R.; Veghel, M.V.; Steinbuch, M. Identification control and hysteresis compensation of a 3 DOF metrological AFM. Asian J. Control 2009, 11, 130–143. [Google Scholar] [CrossRef]
- Yang, M.J.; Li, C.X.; Gu, G.Y.; Zhu, L.M. Modeling and compensating the dynamic hysteresis of piezoelectric actuators via a modified rate-dependent Prandtl-Ishlinskii model. Smart Mater. Struct. 2015, 12. [Google Scholar] [CrossRef]
- Nguyen, M.L.; Chen, X.K.; Yang, F. Discrete-time quasi-sliding-mode control with prescribed performance function and its application to piezo-actuated positioning systems. IEEE Tans. Ind. Electron. 2018, 65, 942–950. [Google Scholar] [CrossRef]
- Shan, J.J.; Yang, L.; Li, Z. Output feedback integral control for nano-positioning using piezoelectric actuators. Smart Mater. Struct. 2015, 24, 045001. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, X.B. Integrated inversion-feedforward and PID-based-sliding-mode-control for piezoelectric actuators. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 869–874. [Google Scholar]
- Ge, P.; Jouaneh, M. Generalized Preisach model for hysteresis nonlinearity of piezoceramic actuators. Precis. Eng. 1977, 20, 99–111. [Google Scholar] [CrossRef]
- Lin, F.J.; Lee, S.Y. Intelligent integral backstepping sliding-mode control for piezo-flexural nanopositioning stage. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; pp. 1–6. [Google Scholar]
- Xu, Q.S. Digital integral terminal sliding mode predictive control of piezoelectric-driven motion system. IEEE Trans. Ind. Electron. 2016, 6, 3976–3984. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Sin, K.S. Adaptive Filtering, Prediction and Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Tian, D.; Wang, Z. Adaptive Tracking Control for the Piezoelectric Actuated Stage Using the Krasnosel’skii-Pokrovskii Operator. Micromachines 2020, 11, 537. https://doi.org/10.3390/mi11050537
Xu R, Tian D, Wang Z. Adaptive Tracking Control for the Piezoelectric Actuated Stage Using the Krasnosel’skii-Pokrovskii Operator. Micromachines. 2020; 11(5):537. https://doi.org/10.3390/mi11050537
Chicago/Turabian StyleXu, Rui, Dapeng Tian, and Zhongshi Wang. 2020. "Adaptive Tracking Control for the Piezoelectric Actuated Stage Using the Krasnosel’skii-Pokrovskii Operator" Micromachines 11, no. 5: 537. https://doi.org/10.3390/mi11050537
APA StyleXu, R., Tian, D., & Wang, Z. (2020). Adaptive Tracking Control for the Piezoelectric Actuated Stage Using the Krasnosel’skii-Pokrovskii Operator. Micromachines, 11(5), 537. https://doi.org/10.3390/mi11050537






