Investigation on the Stability of Random Vortices in an Ion Concentration Polarization Layer with Imposed Normal Fluid Flow
Abstract
1. Introduction
2. Numerical Formulation
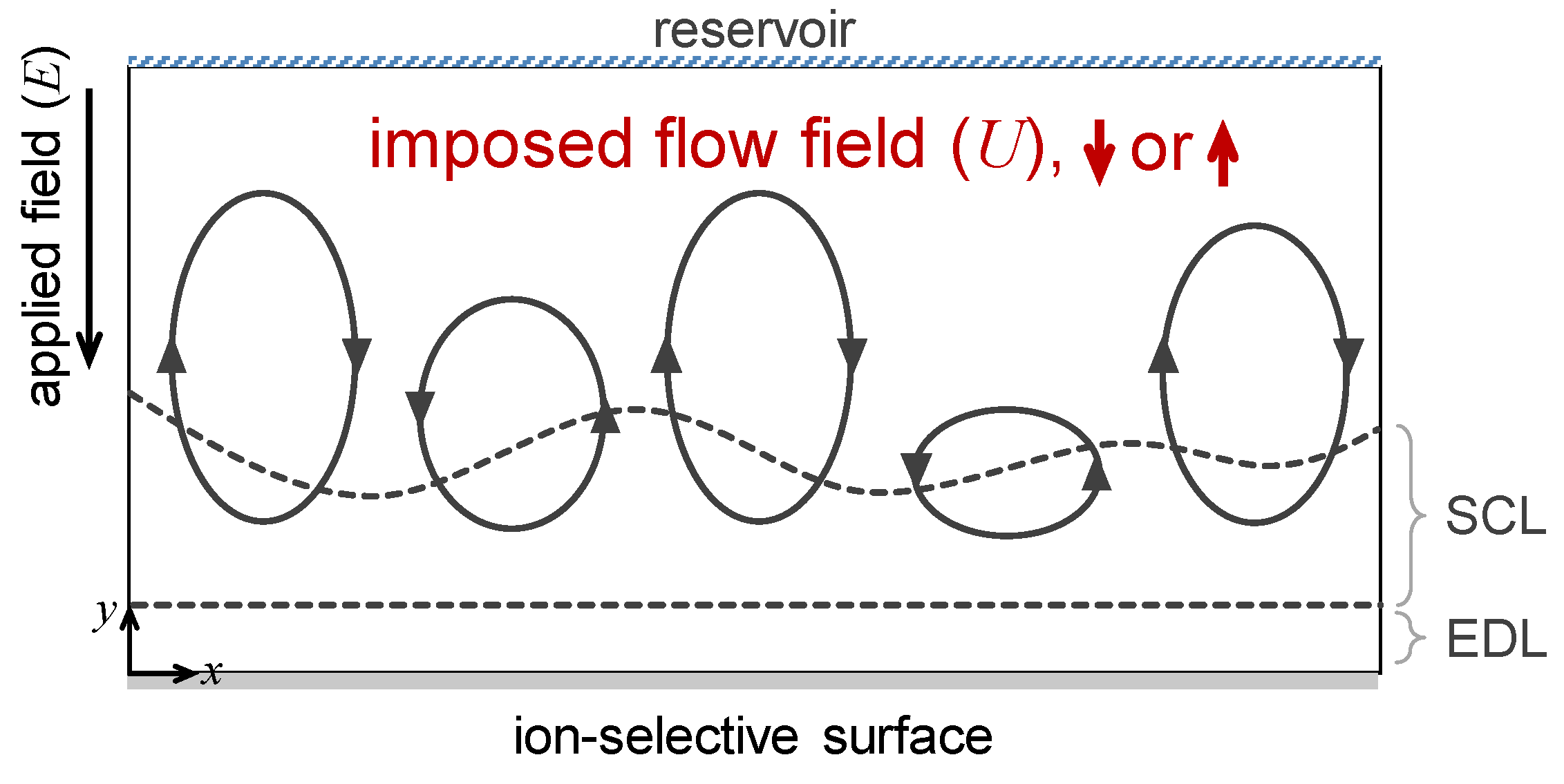
2.1. Domain Description
2.2. Governing Equations and Boundary Conditions
3. Results and Discussions
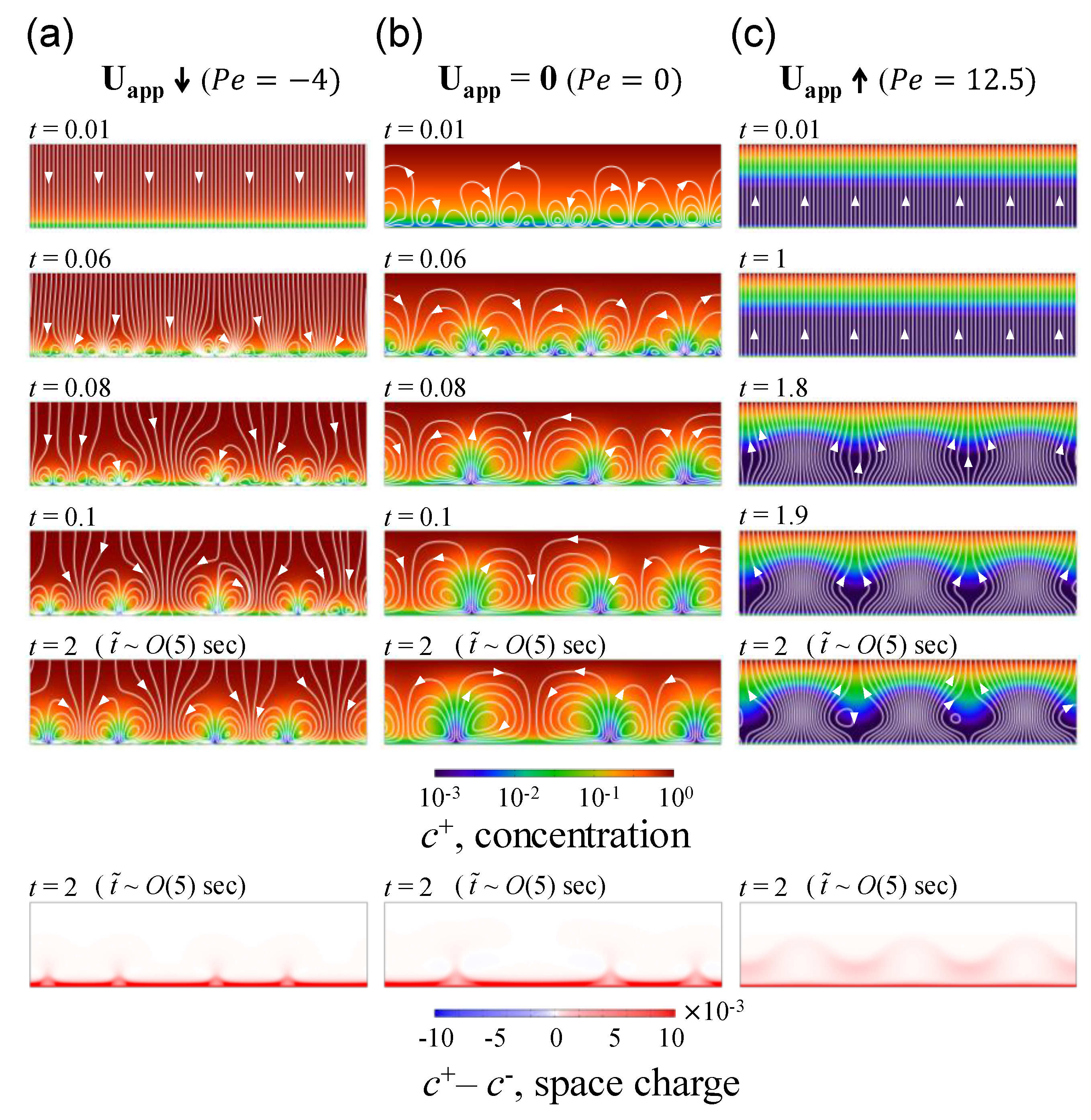
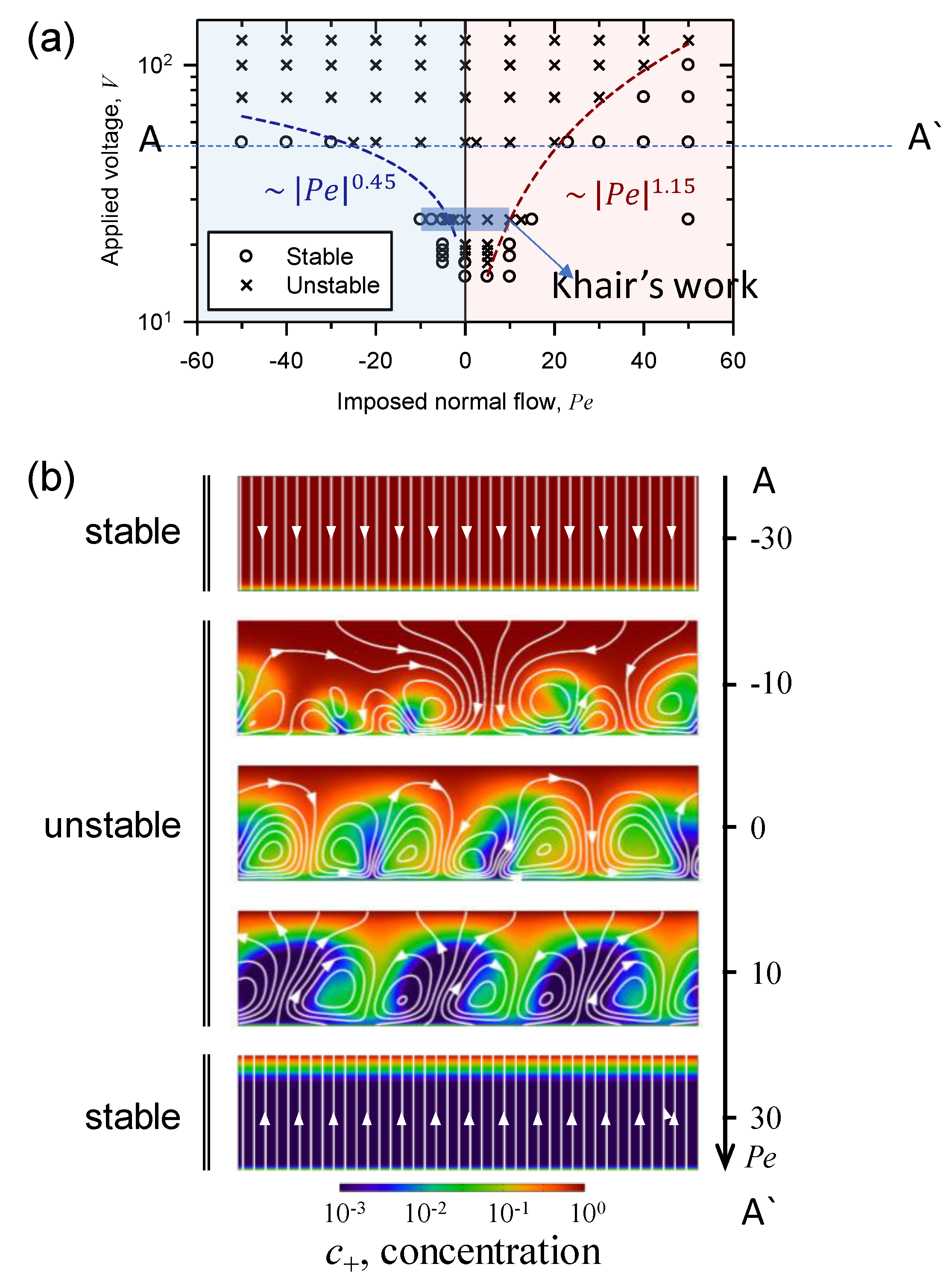
3.1. The Effect of Space Charge Layer on Electro-Convection with Admitted Normal Flow
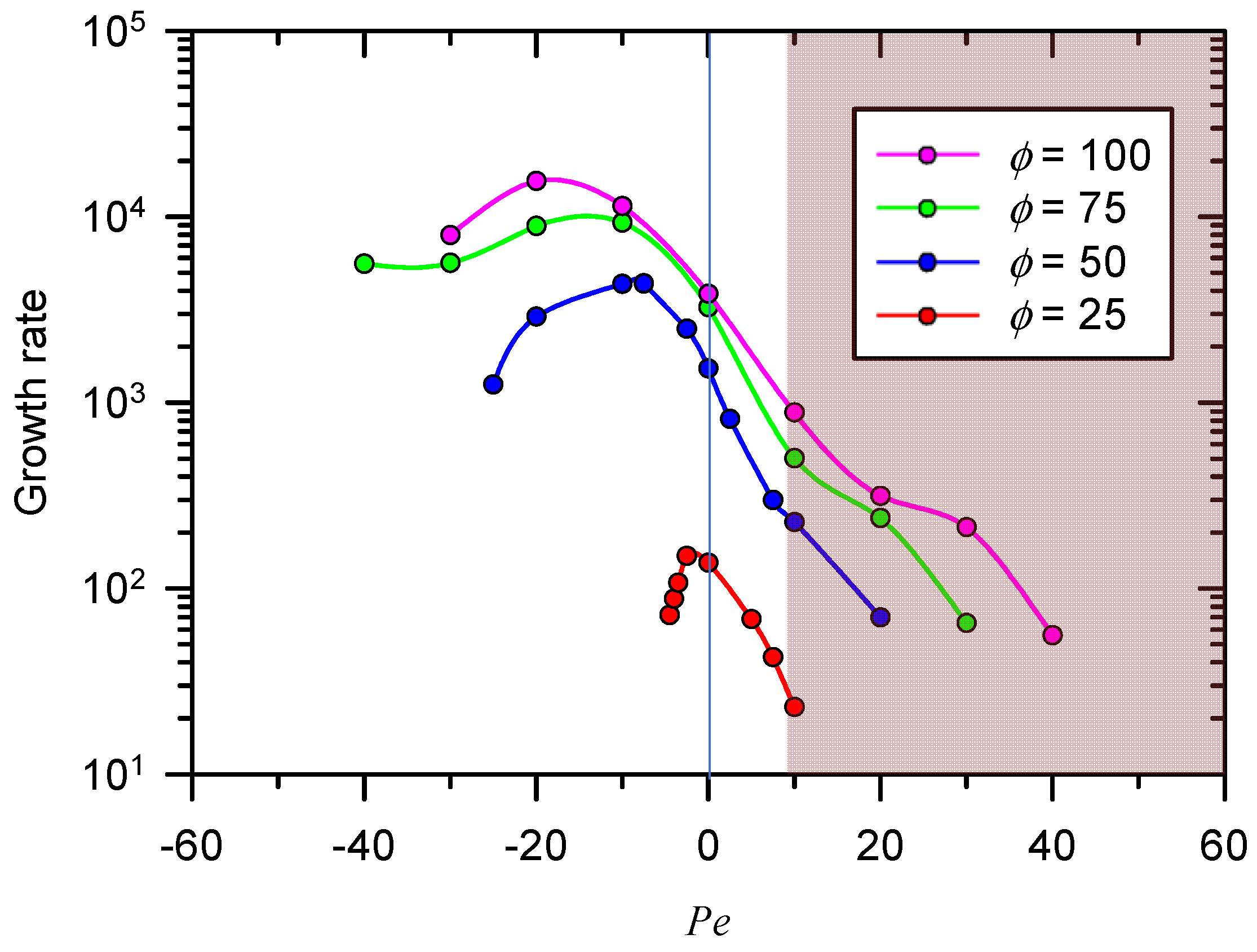
3.2. Growth Rate of Electro-Convective Instability
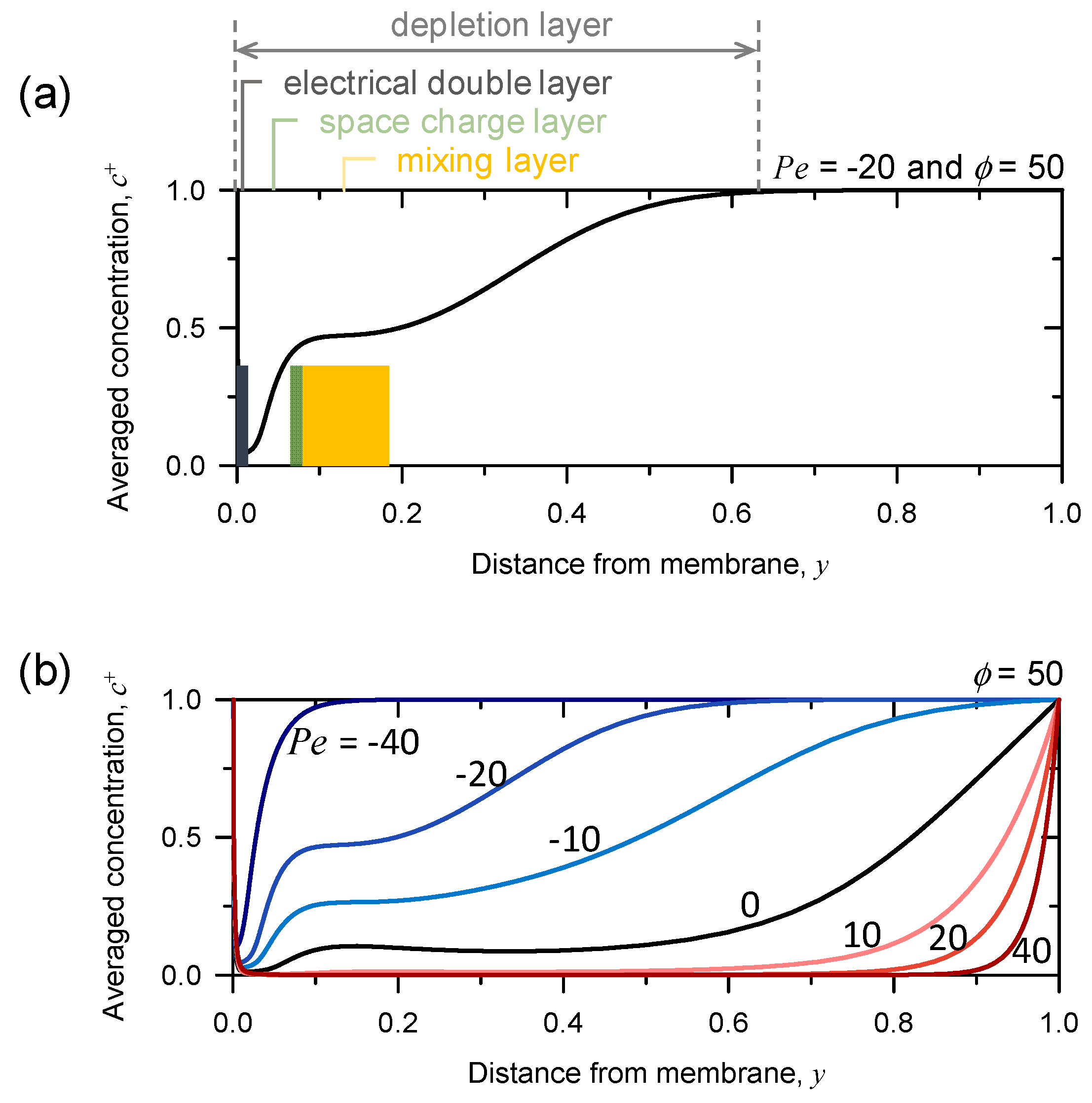
3.3. Rearrangement of Space Charge Layer and Mixing Layer Depending on Pe
3.4. Asymmetric Transition of Electro-Convective Instability
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zabolotsky, V.; Nikonenko, V.; Pismenskaya, N.; Laktionov, E.; Urtenov, M.K.; Strathmann, H.; Wessling, M.; Koops, G. Coupled transport phenomena in over-limiting current electrodialysis. Sep. Purif. Technol. 1998, 14, 255–267. [Google Scholar] [CrossRef]
- Choi, J.; Huh, K.; Moon, D.J.; Lee, H.; Son, S.Y.; Kim, K.; Kim, H.C.; Chae, J.-H.; Sung, G.Y.; Kim, H.-Y.; et al. Selective preconcentration and online collection of charged molecules using ion concentration polarization. RSC Adv. 2015, 5, 66178–66184. [Google Scholar] [CrossRef]
- Choi, J.; Baek, S.; Kim, H.C.; Chae, J.-H.; Koh, Y.; Seo, S.W.; Lee, H.; Kim, S.J. Nanoelectrokinetic selective preconcentration based on ion concentration polarization. BioChip J. 2020, 14, 100–109. [Google Scholar] [CrossRef]
- Baek, S.; Choi, J.; Son, S.Y.; Kim, J.; Hong, S.; Kim, H.C.; Chae, J.-H.; Lee, H.; Kim, S.J. Dynamics of driftless preconcentration using ion concentration polarization leveraged by convection and diffusion. Lab Chip 2019, 19, 3190–3199. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Choi, J.; Jeong, E.; Baek, S.; Kim, H.C.; Chae, J.-H.; Koh, Y.; Seo, S.W.; Kim, J.-S.; Kim, S.J. Dcas9-mediated nanoelectrokinetic direct detection of target gene for liquid biopsy. Nano Lett. 2018, 18, 7642–7650. [Google Scholar] [CrossRef] [PubMed]
- Son, S.Y.; Lee, S.; Lee, H.; Kim, S.J. Engineered nanofluidic preconcentration devices by ion concentration polarization. BioChip J. 2016, 10, 251–261. [Google Scholar] [CrossRef]
- Kim, S.J.; Song, Y.-A.; Han, J. Nanofluidic concentration devices for biomolecules utilizing ion concentration polarization: Theory, fabrication, and application. Chem. Soc. Rev. 2010, 39, 912–922. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotic slip of the second kind and instability in concentration polarization at electrodialysis membranes. Math. Models Methods Appl. Sci. 2001, 11, 263–300. [Google Scholar] [CrossRef]
- Yossifon, G.; Chang, H.-C. Selection of nonequilibrium over-limiting currents: Universal depletion layer formation dynamics and vortex instability. Phys. Rev. Lett. 2008, 101, 254501. [Google Scholar] [CrossRef]
- De Valença, J.C.; Wagterveld, R.M.; Lammertink, R.G.; Tsai, P.A. Dynamics of microvortices induced by ion concentration polarization. Phys. Rev. E 2015, 92, 031003. [Google Scholar] [CrossRef]
- Li, L.; Kim, D. Effect of poly-dispersed nanostructures on concentration polarization phenomena in ion exchange membranes. J. Membr. Sci. 2016, 520, 639–645. [Google Scholar] [CrossRef]
- Kim, S.J.; Ko, S.H.; Kang, K.H.; Han, J. Direct seawater desalination by ion concentration polarization. Nat. Nanotechnol. 2010, 5, 297. [Google Scholar] [CrossRef] [PubMed]
- Benneker, A.M.; Gumuscu, B.; Derckx, E.G.; Lammertink, R.G.; Eijkel, J.C.; Wood, J.A. Enhanced ion transport using geometrically structured charge selective interfaces. Lab Chip 2018, 18, 1652–1660. [Google Scholar] [CrossRef] [PubMed]
- Gumuscu, B.; Haase, A.S.; Benneker, A.M.; Hempenius, M.A.; van den Berg, A.; Lammertink, R.G.; Eijkel, J.C. Desalination by electrodialysis using a stack of patterned ion-selective hydrogels on a microfluidic device. Adv. Funct. Mater. 2016, 26, 8685–8693. [Google Scholar] [CrossRef]
- Cheow, L.F.; Ko, S.H.; Kim, S.J.; Kang, K.H.; Han, J. Increasing the sensitivity of enzyme-linked immunosorbent assay using multiplexed electrokinetic concentrator. Anal. Chem. 2010, 82, 3383–3388. [Google Scholar] [CrossRef]
- Cheow, L.F.; Han, J. Continuous signal enhancement for sensitive aptamer affinity probe electrophoresis assay using electrokinetic concentration. Anal. Chem. 2011, 83, 7086–7093. [Google Scholar] [CrossRef][Green Version]
- Cheow, L.F.; Sarkar, A.; Kolitz, S.; Lauffenburger, D.; Han, J. Detecting kinase activities from single cell lysate using concentration-enhanced mobility shift assay. Anal. Chem. 2014, 86, 7455–7462. [Google Scholar] [CrossRef]
- Kim, K.; Kim, W.; Lee, H.; Kim, S.J. Stabilization of ion concentration polarization layer using micro fin structure for high-throughput applications. Nanoscale 2017, 9, 3466–3475. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Stevens, A.L.; Han, J. Million-fold preconcentration of proteins and peptides by nanofluidic filter. Anal. Chem. 2005, 77, 4293–4299. [Google Scholar] [CrossRef]
- Jia, M.; Kim, T. Multiphysics simulation of ion concentration polarization induced by a surface-patterned nanoporous membrane in single channel devices. Anal. Chem. 2014, 86, 10365–10372. [Google Scholar] [CrossRef]
- Ehlert, S.; Hlushkou, D.; Tallarek, U. Electrohydrodynamics around single ion-permselective glass beads fixed in a microfluidic device. Microfluid. Nanofluidics 2008, 4, 471–487. [Google Scholar] [CrossRef]
- Kwak, R.; Pham, V.S.; Lim, K.M.; Han, J. Shear flow of an electrically charged fluid by ion concentration polarization: Scaling laws for electroconvective vortices. Phys. Rev. Lett. 2013, 110, 114501. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Lee, J.A.; Lee, H.; Kim, S.J. Spontaneous selective preconcentration leveraged by ion exchange and imbibition through nanoporous medium. Sci. Rep. 2019, 9, 2336. [Google Scholar] [CrossRef]
- Lee, J.A.; Lee, D.; Park, S.; Lee, H.; Kim, S.J. Non-negligible water-permeance through nanoporous ion exchange medium. Sci. Rep. 2018, 8, 12842. [Google Scholar] [CrossRef]
- Kwon, H.J.; Kim, B.; Lim, G.; Han, J. A multiscale-pore ion exchange membrane for better energy efficiency. J. Mater. Chem. A 2018, 6, 7714–7723. [Google Scholar] [CrossRef]
- Ko, S.H.; Song, Y.A.; Kim, S.J.; Kim, M.; Han, J.; Kang, K.H. Nanofluidic preconcentration device in a straight microchannel using ion concentration polarization. Lab Chip 2012, 12, 4472–4482. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.; Kim, W.; Moon, S.; Kim, H.-Y.; Lee, H.; Kim, S.J. Nanoelectrokinetic bufferchannel-less radial preconcentrator and online extractor by tunable ion depletion layer. Biomicrofluidics 2019, 13, 034113. [Google Scholar] [CrossRef]
- Subramanian, V.; Lee, S.; Jena, S.; Jana, S.K.; Ray, D.; Kim, S.J.; Thalappil, P. Enhancing the sensitivity of point-of-use electrochemical microfluidic sensors by ion concentration polarization—A case study on arsenic. Sens. Actuators B Chem. 2020, 304, 127340. [Google Scholar] [CrossRef]
- Kim, M.; Jia, M.; Kim, T. Ion concentration polarization in a single and open microchannel induced by a surface-patterned perm-selective film. Analyst 2013, 138, 1370–1378. [Google Scholar] [CrossRef]
- Van der Bruggen, B.; Vandecasteele, C.; Van Gestel, T.; Doyen, W.; Leysen, R. A review of pressure-driven membrane processes in wastewater treatment and drinking water production. Environ. Prog. 2003, 22, 46–56. [Google Scholar] [CrossRef]
- Sun, L.; Ying, Y.; Huang, H.; Song, Z.; Mao, Y.; Xu, Z.; Peng, X. Ultrafast molecule separation through layered ws2 nanosheet membranes. ACS Nano 2014, 8, 6304–6311. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. Concentration polarization in ion exchange membrane electrodialysis. J. Membr. Sci. 1991, 57, 217–235. [Google Scholar] [CrossRef]
- Hsu, J.-P.; Yang, K.-L.; Ting, K.-C. Effect of convective boundary layer on the current efficiency of a membrane bearing nonuniformly distributed fixed charges. J. Phys. Chem. B 1997, 101, 8984–8989. [Google Scholar] [CrossRef]
- Khair, A.S. Concentration polarization and second-kind electrokinetic instability at an ion-selective surface admitting normal flow. Phys. Fluids 2011, 23, 072003. [Google Scholar] [CrossRef]
- Demekhin, E.; Nikitin, N.; Shelistov, V. Direct numerical simulation of electrokinetic instability and transition to chaotic motion. Phys. Fluids 2013, 25, 122001. [Google Scholar] [CrossRef]
- Druzgalski, C.; Andersen, M.; Mani, A. Direct numerical simulation of electroconvective instability and hydrodynamic chaos near an ion-selective surface. Phys. Fluids 2013, 25, 110804. [Google Scholar] [CrossRef]
- Masliyah, J.H.; Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Karatay, E.; Druzgalski, C.L.; Mani, A. Simulation of chaotic electrokinetic transport: Performance of commercial software versus custom-built direct numerical simulation codes. J. Colloid Interface Sci. 2015, 446, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kim, S.J.; Ko, S.H.; Kwak, R.; Posner, J.D.; Kang, K.H.; Han, J. Multi-vortical flow inducing electrokinetic instability in ion concentration polarization layer. Nanoscale 2012, 4, 7406–7410. [Google Scholar] [CrossRef]
- Dydek, E.V.; Zaltzman, B.; Rubinstein, I.; Deng, D.S.; Mani, A.; Bazant, M.Z. Over-limiting current in a microchannel. Phys. Rev. Lett. 2011, 107, 118301. [Google Scholar] [CrossRef]
- Nam, S.; Cho, I.; Heo, J.; Lim, G.; Bazant, M.Z.; Moon, D.J.; Sung, G.Y.; Kim, S.J. Experimental verification of over-limiting current by surface conduction and electro-osmotic flow in microchannels. Phys. Rev. Lett. 2015, 114, 114501. [Google Scholar] [CrossRef]
- Sohn, S.; Cho, I.; Kwon, S.; Lee, H.; Kim, S.J. Surface conduction in a microchannel. Langmuir 2018, 34, 7916–7921. [Google Scholar] [CrossRef] [PubMed]
- Huh, K.; Yang, S.-Y.; Park, J.S.; Lee, J.A.; Lee, H.; Kim, S.J. Surface conduction and electroosmotic flow around charged dielectric pillar arrays in microchannels. Lab Chip 2020, 20, 675–686. [Google Scholar] [CrossRef] [PubMed]
| Physical Quantity | Characteristic Scale | Description |
|---|---|---|
| Length | y-directional length of numerical domain | |
| Time | Diffusion time scale | |
| Electric potential | Thermal voltage | |
| Concentration | Bulk concentration | |
| Pressure | Diffusion-scaled pressure | |
| Flow velocity | Diffusion-scaled velocity | |
| Current density | Diffusion-limited current density |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Mani, A.; Lee, H.; Kim, S.J. Investigation on the Stability of Random Vortices in an Ion Concentration Polarization Layer with Imposed Normal Fluid Flow. Micromachines 2020, 11, 529. https://doi.org/10.3390/mi11050529
Choi J, Mani A, Lee H, Kim SJ. Investigation on the Stability of Random Vortices in an Ion Concentration Polarization Layer with Imposed Normal Fluid Flow. Micromachines. 2020; 11(5):529. https://doi.org/10.3390/mi11050529
Chicago/Turabian StyleChoi, Jihye, Ali Mani, Hyomin Lee, and Sung Jae Kim. 2020. "Investigation on the Stability of Random Vortices in an Ion Concentration Polarization Layer with Imposed Normal Fluid Flow" Micromachines 11, no. 5: 529. https://doi.org/10.3390/mi11050529
APA StyleChoi, J., Mani, A., Lee, H., & Kim, S. J. (2020). Investigation on the Stability of Random Vortices in an Ion Concentration Polarization Layer with Imposed Normal Fluid Flow. Micromachines, 11(5), 529. https://doi.org/10.3390/mi11050529





