The Effect of Streaming Potential and Viscous Dissipation in the Heat Transfer Characteristics of Power-Law Nanofluid Flow in a Rectangular Microchannel
Abstract
1. Introduction
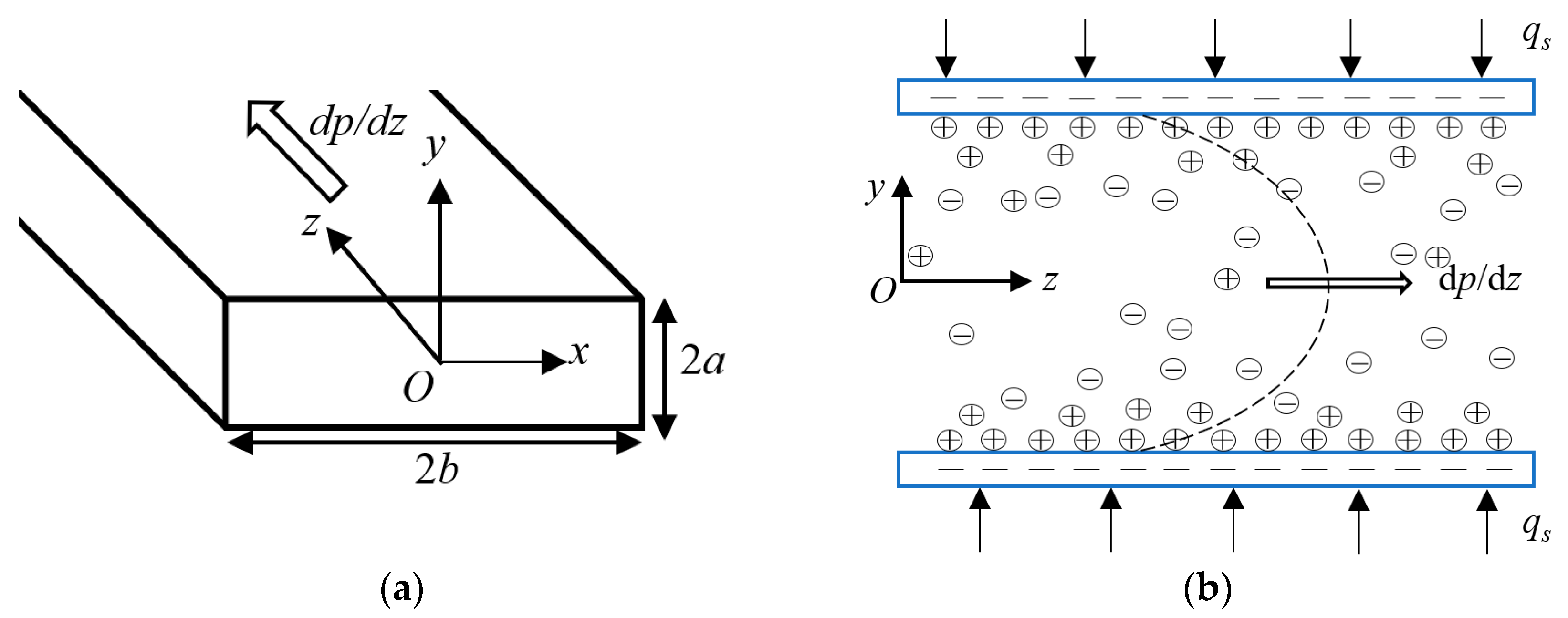
2. Mathematical Modeling
2.1. Electric Potential Field
2.2. Hydrodynamic Field
2.3. Thermal Field
3. Solution Methodology
3.1. In the Case of Newtonian Nanofluid Flow
3.2. In the Ccase of Power-Law Nanofluid
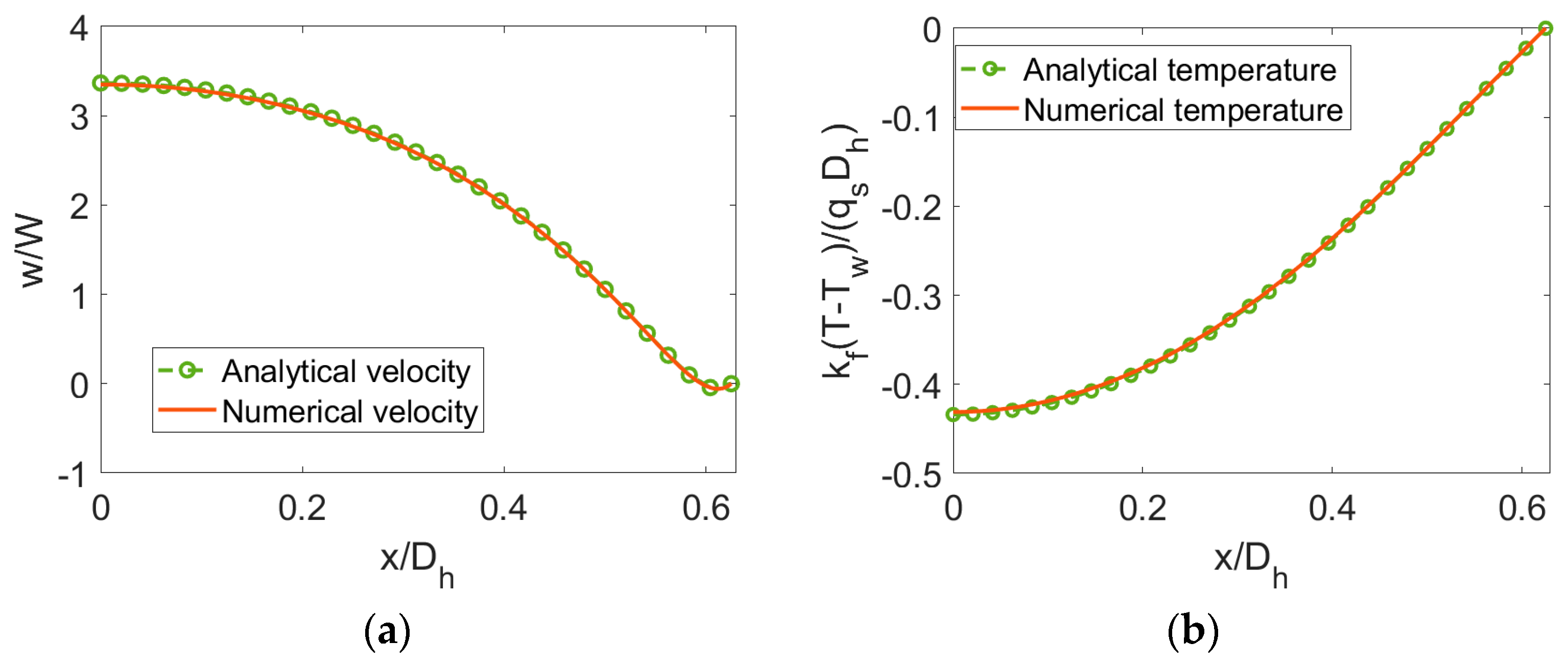
4. Method Validation
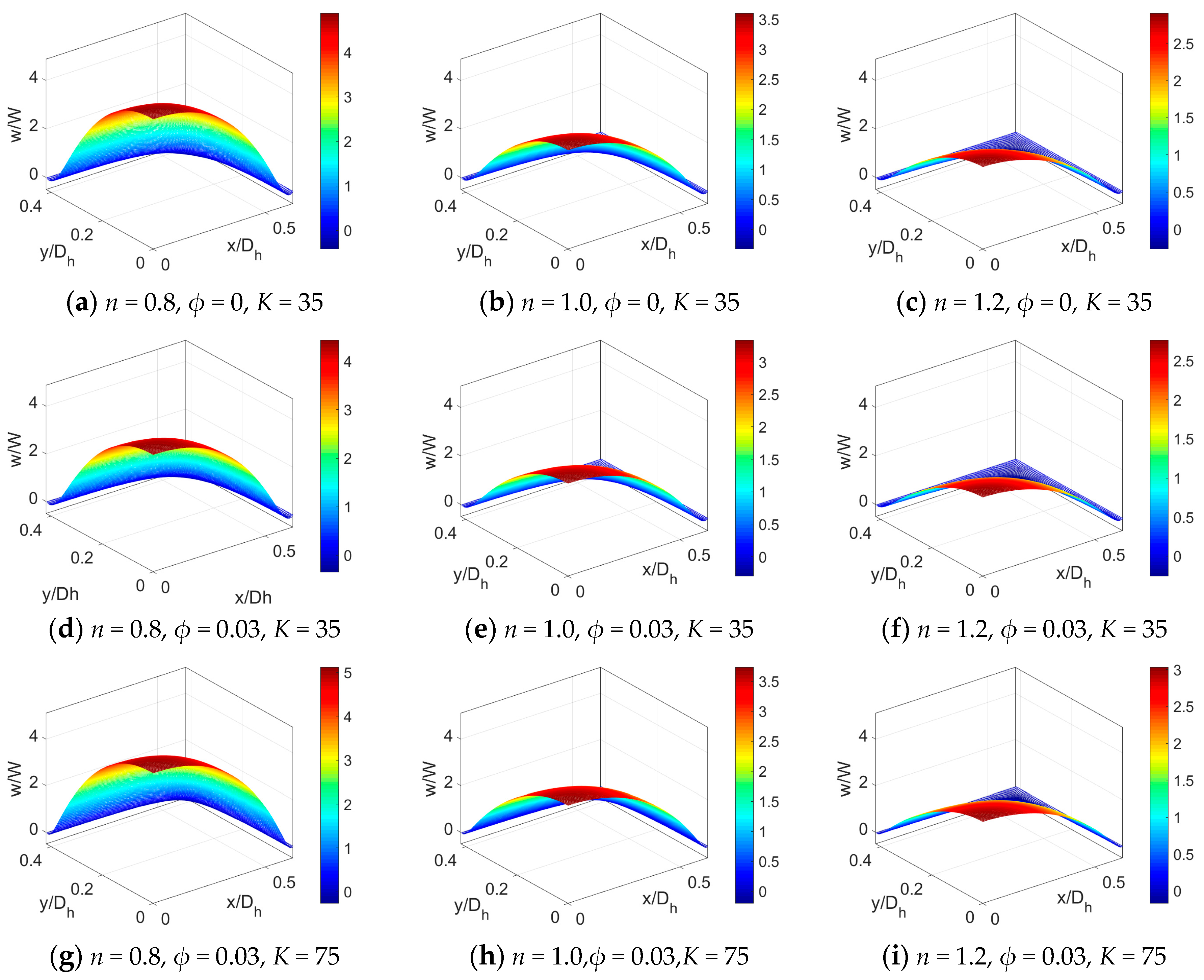
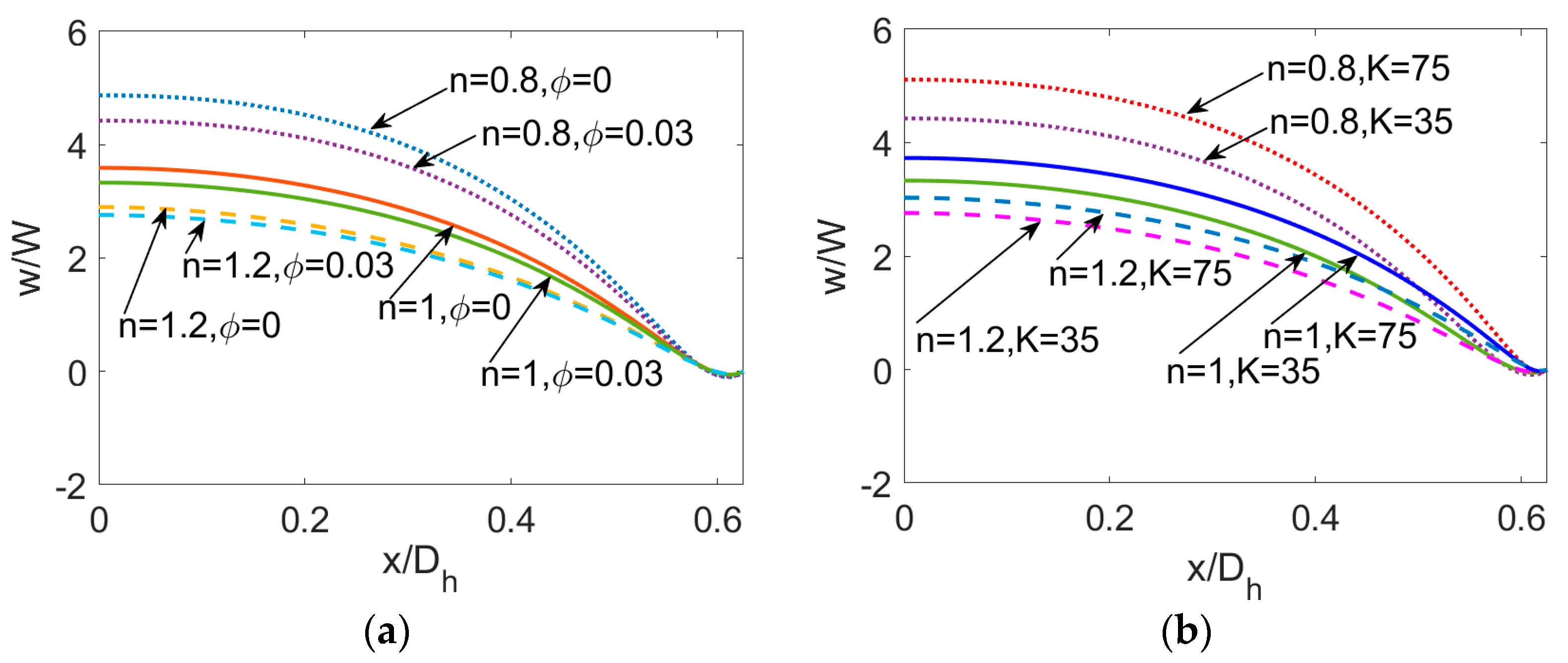
5. Results and Discussion
6. Conclusions
- For electrokinetic flow of power-law nanofluid, the streaming potential effect not only reduces and retards velocity distribution, but also narrows temperature difference between the bulk flow and channel wall, which in further reduces the Nusselt number. Thus, when considering the streaming potential effect on PDF in microchannels, increasing the electrokinetic width K is an effective approach to improve heat transfer performance of PDF.
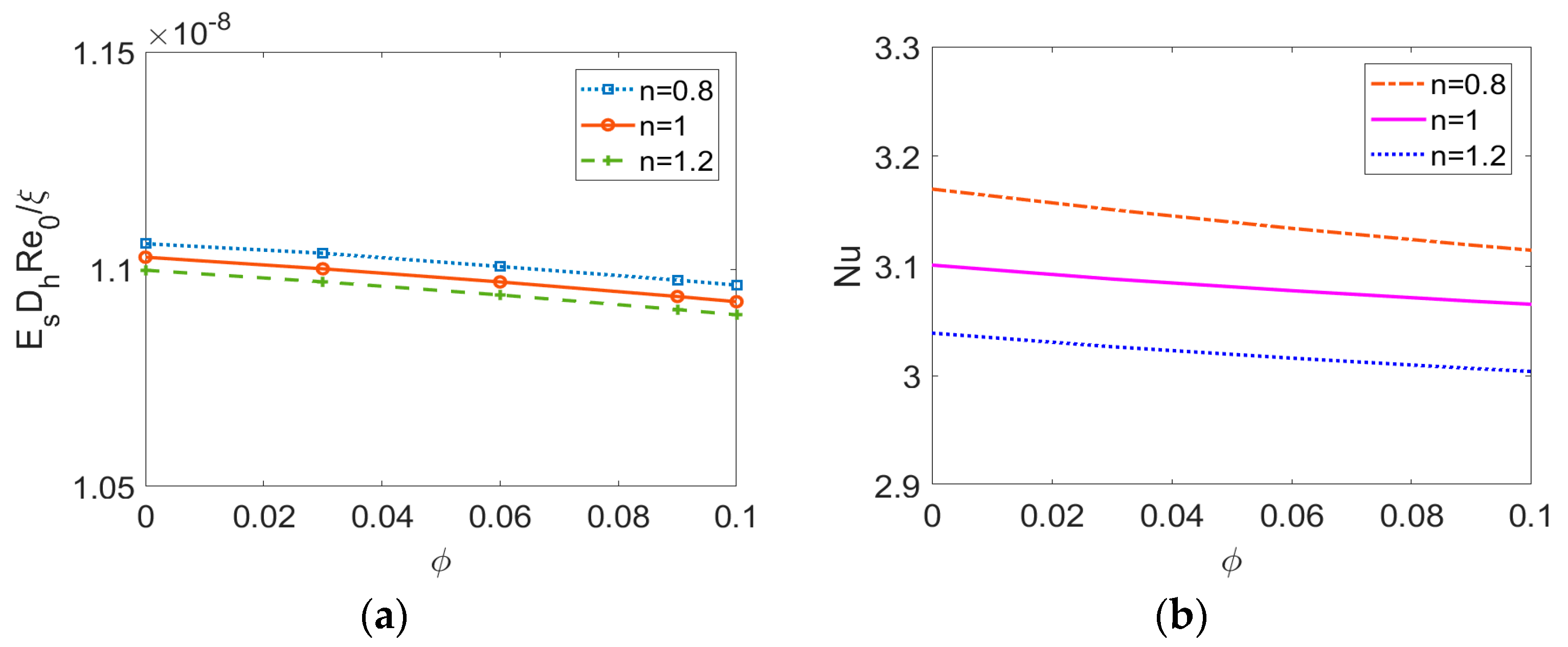
- The bulk mean temperature rises as the volume fraction of nanoparticle ϕ increases no matter what fluid type is considered. However, a slight decrease of Nusselt number Nu with ϕ is observed and thus one should have a second thought when adding nanoparticles to liquid to enhance the heating transfer rate.
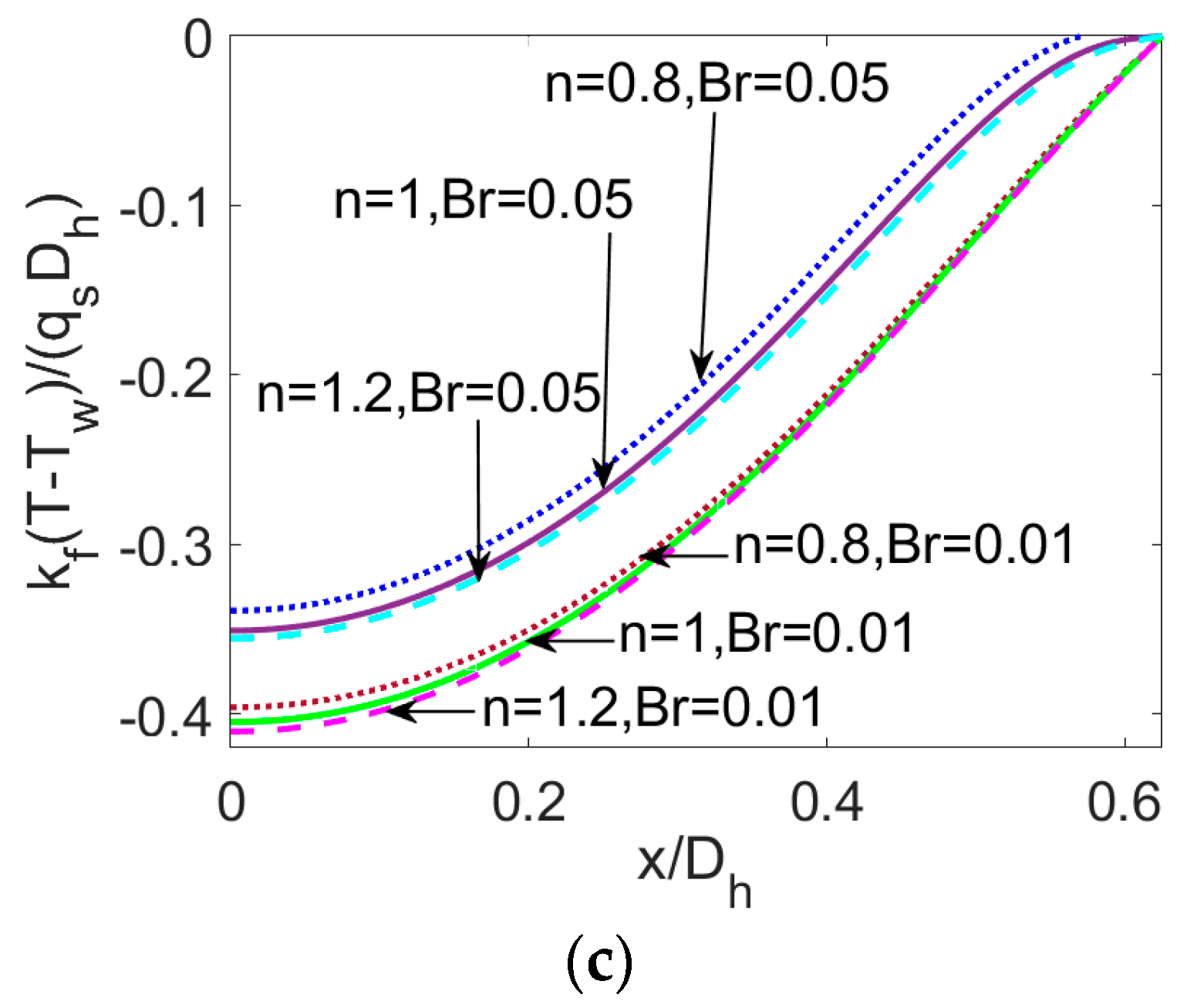
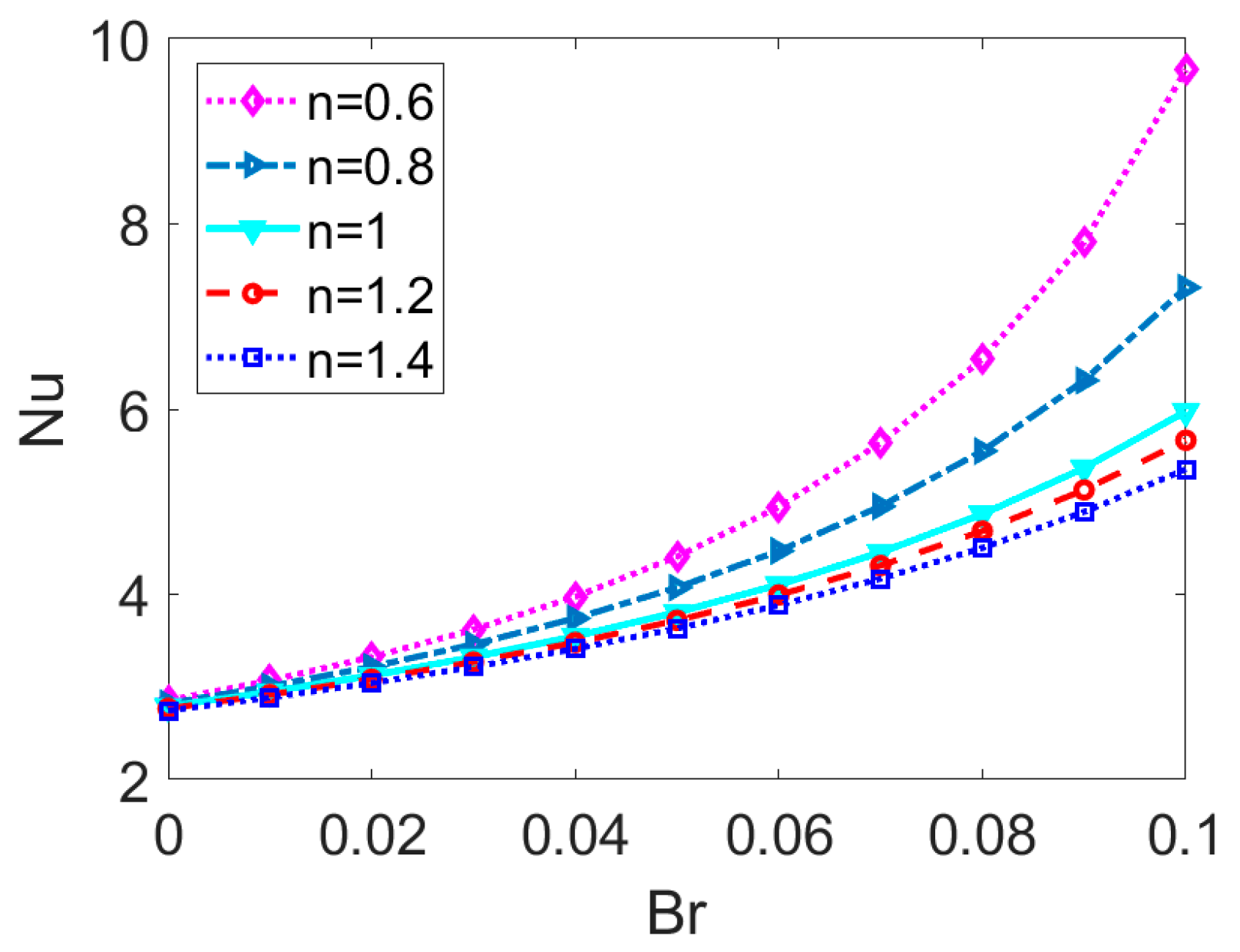
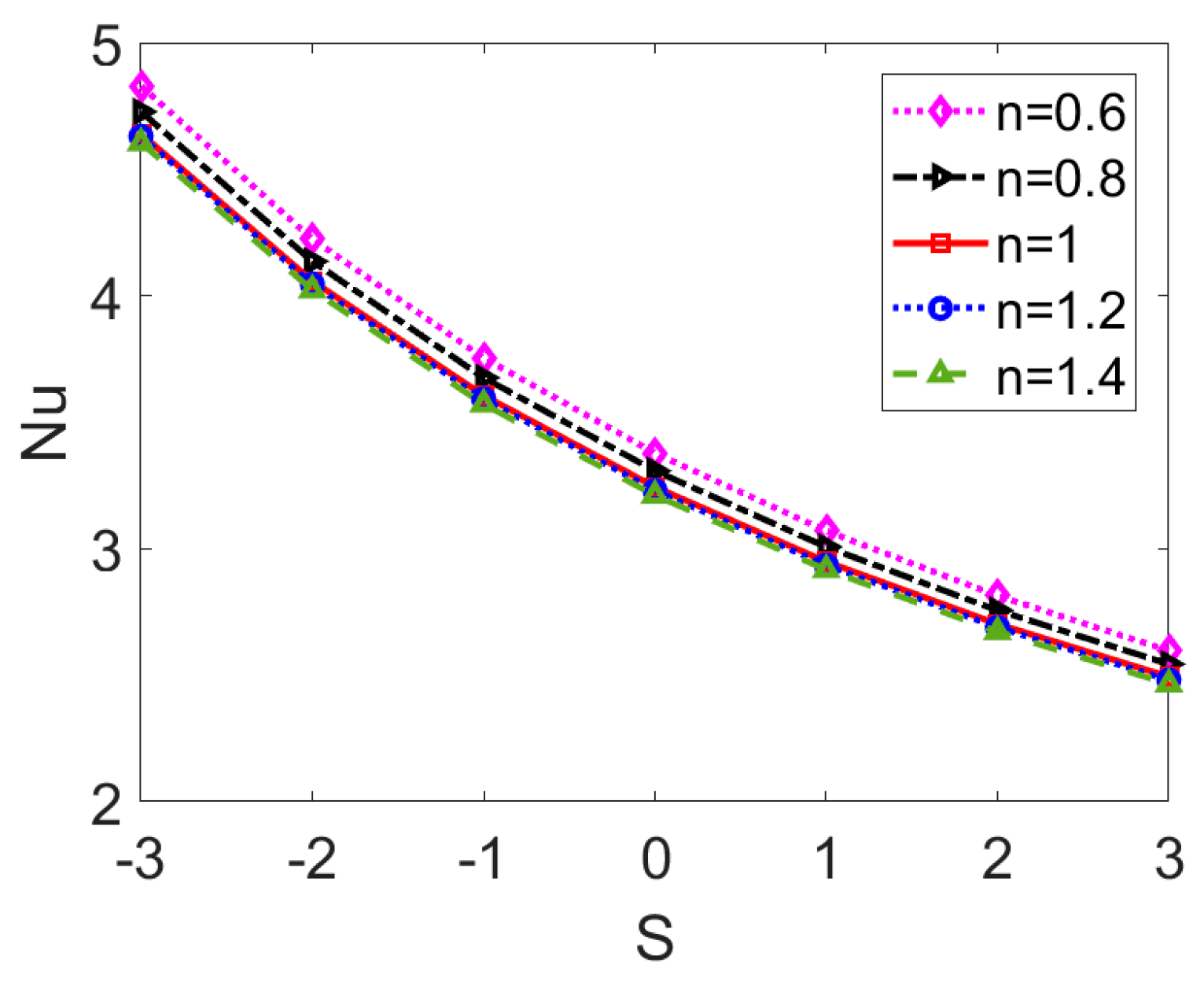
- Regarding the nanofluid type, it is notable that temperature distribution is a weak function of flow behavior index n. Compared to the Newtonian nanofluid and especially the shear thickening nanofluid, the shear thinning nanofluid exhibits greater heat transfer rate, indicating it to be more sensitive to the introduction of nanoparticles, the effects of streaming potential, and viscous dissipation. Therefore, to obtain higher heat transfer rate in engineering application, the working liquid can be chosen as shear thinning power-law nanofluid. Moreover, one should carefully consider the heat transfer characteristics when treating biofluids and other liquids with long chain molecules as Newtonian fluids.
- When the Brinkman number Br is augmented, the temperature distribution especially in the vicinity of channel wall increases and Nu is enhanced correspondingly. It reveals that the viscous dissipation effect plays a part on both temperature profile and Nusselt number, which is more pronounced in the case of shear thinning nanofluid. Therefore, the consideration of viscous dissipation for non-Newtonian fluids is worth the discussion above.
- The Nusselt number Nu shows a decreasing trend with Joule heating parameter S. The evident difference of Nu with and without consideration of Joule heating effect indicates that the Joule heating needs to be carefully considered when studying the heat transfer characteristics in electrokinetic flow of power-law nanofluid.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering Flows in Small Devices. Ann. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Chen, C.H.; Ding, C.Y. Study on the thermal behavior and cooling performance of a nanofluid-cooled microchannel heat sink. Int. J. Therm. Sci. 2011, 50, 378–384. [Google Scholar] [CrossRef]
- Krishnan, M.; Mojarad, N.; Kukura, P.; Sandoghdar, V. Geometry-induced electrostatic trapping of nanometric objects in a fluid. Nature 2010, 467, 692–695. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Das, S.; Chakraborty, S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Datta, S.; Ghosal, S.; Patankar, N.A. Electroosmotic flow in a rectangular channel with variable wall zeta-potential: Comparison of numerical simulation with asymptotic theory. Electrophoresis 2006, 27, 611–619. [Google Scholar] [CrossRef]
- Deng, S.Y.; Jian, Y.J.; Bi, Y.H.; Chang, L.; Wang, H.J.; Liu, Q.S. Unsteady electroosmotic flow of power-law fluid in a rectangular microchannel. Mech. Res. Commun. 2012, 39, 9–14. [Google Scholar] [CrossRef]
- Srinivas, B. Electroosmotic flow of a power law fluid in an elliptic microchannel. Colloids Surf. A Physicochem. Eng. Asp. 2016, 492, 144–151. [Google Scholar] [CrossRef]
- Zhao, C.L.; Yang, C. Joule heating induced heat transfer for electroosmotic flow of power-law fluids in a microcapillary. Int. J. Heat Mass Transf. 2012, 55, 2044–2051. [Google Scholar] [CrossRef]
- Li, F.Q.; Jian, Y.J.; Xie, Z.Y.; Liu, Y.B.; Liu, Q.S. Transient alternating current electroosmotic flow of a Jeffrey fluid through a polyelectrolyte-grafted nanochannel. Rsc Adv. 2017, 7, 782–790. [Google Scholar] [CrossRef]
- Si, D.Q.; Jian, Y.J.; Chang, L.; Liu, Q.S. Unsteady Rotating Electroosmotic Flow through a Slit Microchannel. J. Mech. 2016, 32, 603–611. [Google Scholar] [CrossRef]
- Qi, C.; Ng, C.O. Rotating electroosmotic flow of viscoplastic material between two parallel plates. Colloids Surf. A Physicochem. Eng. Asp. 2017, 513, 355–366. [Google Scholar] [CrossRef][Green Version]
- Mondal, A.; Shit, G.C. Transport of magneto-nanoparticles during electro-osmotic flow in a micro-tube in the presence of magnetic field for drug delivery application. J. Magn. Magn. Mater. 2017, 442, 319–328. [Google Scholar] [CrossRef]
- Vakili, M.A.; Sadeghi, A.; Saidi, M.H. Pressure effects on electroosmotic flow of power-law fluids in rectangular microchannels. Theor. Comput. Fluid Dyn. 2014, 28, 409–426. [Google Scholar] [CrossRef]
- Afonso, A.M.; Alves, M.A.; Pinho, F.T. Analytical solution of two-fluid electro-osmotic flows of viscoelastic fluids. J. Colloid Interface Sci. 2013, 395, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Soong, C.Y.; Wang, S.H. Theoretical analysis of electrokinetic flow and heat transfer in a microchannel under asymmetric boundary conditions. J. Colloid Interface Sci. 2003, 265, 202–213. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Deng, S.Y.; Chen, Y.Q. Periodical pressure-driven electrokinetic flow of power-law fluids through a rectangular microchannel. J. Non-Newtonian Fluid Mech. 2014, 203, 38–50. [Google Scholar] [CrossRef]
- Gong, L.; Wu, J.; Wang, L.; Cao, K. Streaming potential and electroviscous effects in periodical pressure-driven microchannel flow. Phys. Fluids 2008, 20, 063603. [Google Scholar] [CrossRef]
- Chen, G.; Das, S. Streaming potential and electroviscous effects in soft nanochannels beyond Debye-Huckel linearization. J. Colloid Interface Sci. 2015, 445, 357–363. [Google Scholar] [CrossRef]
- Shamshiri, M.; Khazaeli, R.; Ashrafizaadeh, M.; Mortazavi, S. Electroviscous and thermal effects on non-Newtonian liquid flows through microchannels. J. Non-Newtonian Fluid Mech. 2012, 173–174, 1–12. [Google Scholar] [CrossRef]
- Tan, D.K.; Liu, Y. Combined effects of streaming potential and wall slip on flow and heat transfer in microchannels. Int. Commun. Heat Mass 2014, 53, 39–42. [Google Scholar] [CrossRef]
- Habibi Matin, M. Electroviscous effects on thermal transport of electrolytes in pressure driven flow through nanoslit. Int. J. Heat Mass Transf. 2017, 106, 473–481. [Google Scholar] [CrossRef]
- Vakili, M.A.; Saidi, M.H.; Sadeghi, A. Thermal transport characteristics pertinent to electrokinetic flow of power-law fluids in rectangular microchannels. Int. J. Therm. Sci. 2014, 79, 76–89. [Google Scholar] [CrossRef]
- Babaie, A.; Saidi, M.H.; Sadeghi, A. Heat transfer characteristics of mixed electroosmotic and pressure driven flow of power-law fluids in a slit microchannel. Int. J. Therm. Sci. 2012, 53, 71–79. [Google Scholar] [CrossRef]
- Sarkar, S.; Ganguly, S.; Dutta, P. Electrokinetically induced thermofluidic transport of power-law fluids under the influence of superimposed magnetic field. Chem. Eng. Sci. 2017, 171, 391–403. [Google Scholar] [CrossRef]
- Shit, G.C.; Mondal, A.; Sinha, A.; Kundu, P.K. Electro-osmotic flow of power-law fluid and heat transfer in a micro-channel with effects of Joule heating and thermal radiation. Phys. A Stat. Mech. Its Appl. 2016, 462, 1040–1057. [Google Scholar] [CrossRef]
- Chen, C.-H. Fully-developed thermal transport in combined electroosmotic and pressure driven flow of power-law fluids in microchannels. Int. J. Heat Mass Transf. 2012, 55, 2173–2183. [Google Scholar] [CrossRef]
- Choi, U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME FED 1995, 231, 99–103. [Google Scholar]
- Ganguly, S.; Sarkar, S.; Kumar Hota, T.; Mishra, M. Thermally developing combined electroosmotic and pressure-driven flow of nanofluids in a microchannel under the effect of magnetic field. Chem. Eng. Sci. 2015, 126, 10–21. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. A study of heat transfer in power law nanofluid. Therm. Sci. 2016, 20, 2015–2026. [Google Scholar] [CrossRef]
- Si, X.; Li, H.; Zheng, L.; Shen, Y.; Zhang, X. A mixed convection flow and heat transfer of pseudo-plastic power law nanofluids past a stretching vertical plate. Int. J. Heat Mass Transf. 2017, 105, 350–358. [Google Scholar] [CrossRef]
- Zhao, G.P.; Jian, Y.J.; Li, F.Q. Heat transfer of nanofluids in microtubes under the effects of streaming potential. Appl. Therm. Eng. 2016, 100, 1299–1307. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R. Electroosmotic Flow of MHD Power Law Al2O3-PVC Nanouid in a Horizontal Channel: Couette-Poiseuille Flow Model. Commun. Theor. Phys. 2018, 69, 655. [Google Scholar] [CrossRef]
- Deng, S. Thermally Fully Developed Electroosmotic Flow of Power-Law Nanofluid in a Rectangular Microchannel. Micromachines 2019, 10, 363. [Google Scholar] [CrossRef]
- Brinkman, H.C. The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Liu, K.; Ding, T.; Li, J.; Chen, Q.; Xue, G.; Yang, P.; Xu, M.; Wang, Z.L.; Zhou, J. Thermal-Electric Nanogenerator Based on the Electrokinetic Effect in Porous Carbon Film. Adv. Energy Mater. 2018, 8, 1702481. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Saedodin, S.; Mahian, O.; Wongwises, S. Thermal conductivity of Al2O3/water nanofluids. J. Therm. Anal. Calorim. 2014, 117, 675–681. [Google Scholar] [CrossRef]
- Yu, W.; Choi, S.U.S. The role of interfacial layer in the enhanced thermal conductivity of nanofluids a renovated Maxwell model. J. Nanopart. Res. 2004, 6, 355–361. [Google Scholar] [CrossRef]
- Jian, Y.J.; Liu, Q.S.; Yang, L.G. AC electroosmotic flow of generalized Maxwell fluids in a rectangular microchannel. J. Non Newton. Fluid Mech. 2011, 166, 1304–1314. [Google Scholar] [CrossRef]


| Parameters (notation) | Value (unit) |
|---|---|
| The permittivity in vacuum ε | 8.85 × 10−12 C·V−1·m−1 |
| Boltzmann constant kB | 1.38 × 10−23 J·K−1 |
| Absolute temperature Ta | 293 K |
| Elementary charge e | 1.6 × 10−19 C |
| Half channel height a | 1 × 10−6 m |
| Half channel width b | 1.5 × 10−6 m |
| Total electrical conductivity σ | 1.2639 × 10−7 S·m−1 |
| Flow consistency index of power-law fluid m | 9 × 10−4 N·m−2·sn |
| Viscosity of Newtonian fluid μ0 | 9 × 10−4 N·m−2·s |
| Zeta potential ξ | 0.025 V |
| Thermal conductivity of the solid nanoparticle ks | 40 W·m−1·K−1 |
| Thermal conductivity of the base fluid kf | 0.618 W·m−1·K−1 |
| The pressure gradient dp/dz | −1 × 104 Pa |
| The relative permittivity ε0 | 80 |
| Valence of ions zv | 1 |
| Electrokinetic width K | 15–75 |
| Flow behavior index n | 0.6–1.4 |
| Nanoparticle volume fraction ϕ | 0.0–0.1 |
| Joule heating Parameter S | −3 – 3 |
| Brinkman number Br | 0–0.1 |
| Ratio of nanolayer thickness to original particle radius ω | 1.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, S.; An, Q.; Li, M. The Effect of Streaming Potential and Viscous Dissipation in the Heat Transfer Characteristics of Power-Law Nanofluid Flow in a Rectangular Microchannel. Micromachines 2020, 11, 421. https://doi.org/10.3390/mi11040421
Deng S, An Q, Li M. The Effect of Streaming Potential and Viscous Dissipation in the Heat Transfer Characteristics of Power-Law Nanofluid Flow in a Rectangular Microchannel. Micromachines. 2020; 11(4):421. https://doi.org/10.3390/mi11040421
Chicago/Turabian StyleDeng, Shuyan, Quan An, and Mingying Li. 2020. "The Effect of Streaming Potential and Viscous Dissipation in the Heat Transfer Characteristics of Power-Law Nanofluid Flow in a Rectangular Microchannel" Micromachines 11, no. 4: 421. https://doi.org/10.3390/mi11040421
APA StyleDeng, S., An, Q., & Li, M. (2020). The Effect of Streaming Potential and Viscous Dissipation in the Heat Transfer Characteristics of Power-Law Nanofluid Flow in a Rectangular Microchannel. Micromachines, 11(4), 421. https://doi.org/10.3390/mi11040421




