Detailed Experiment-Theory Comparison of Mid-Infrared Metasurface Perfect Absorbers
Abstract
1. Introduction
2. Experiments
2.1. Fabrication and Characterization of MIM Metasurfaces
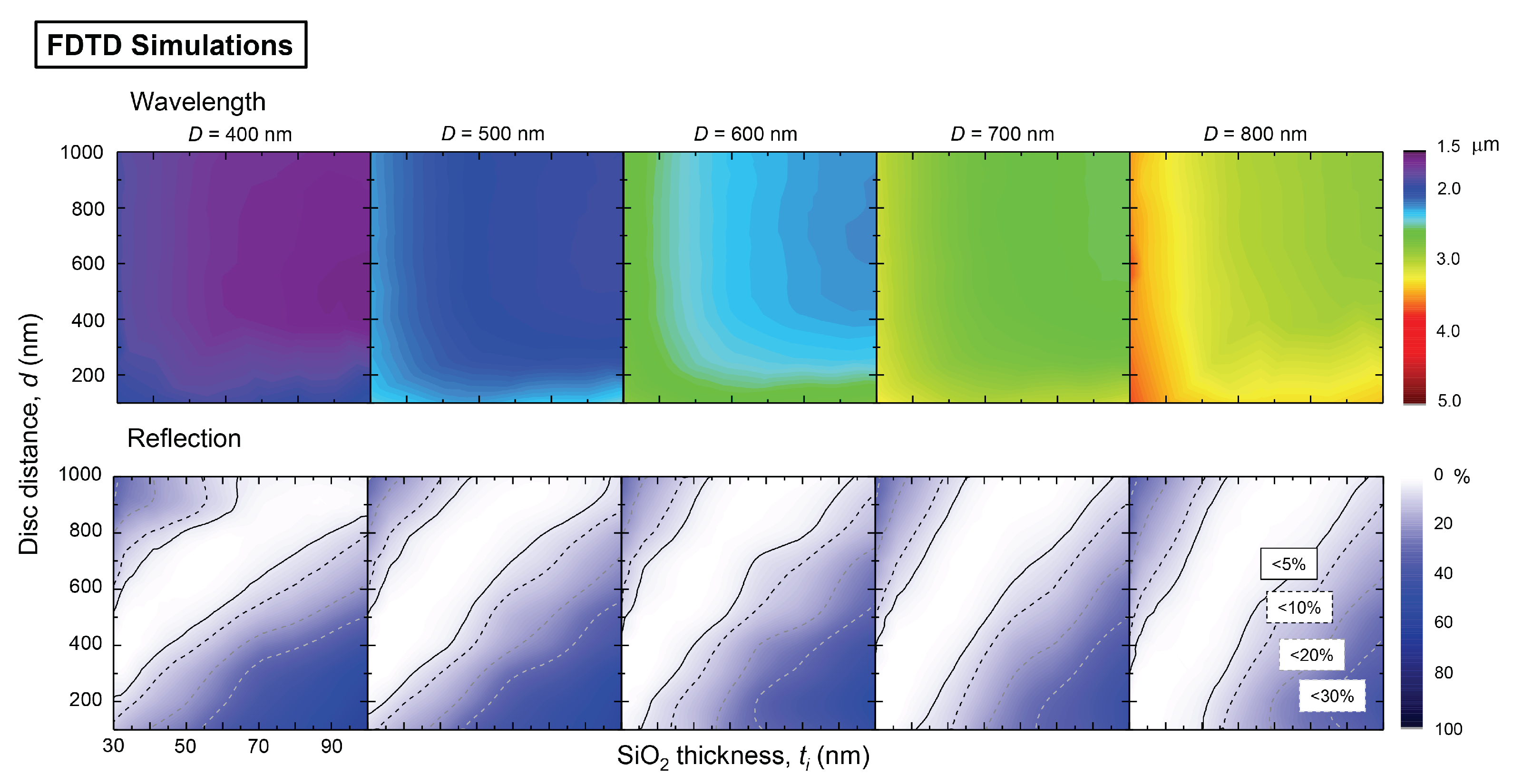
2.2. FDTD Simulations
3. Results and Discussions
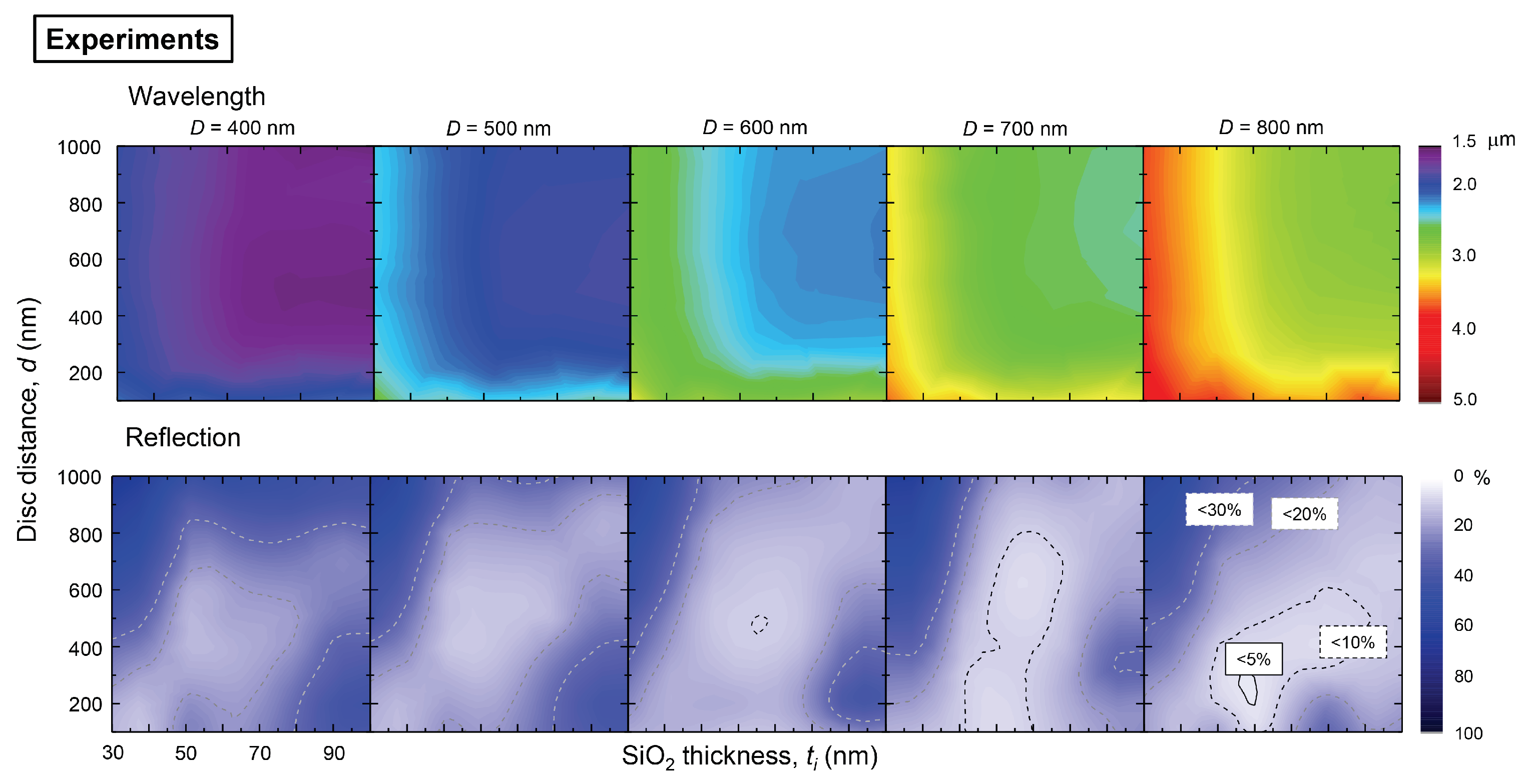
3.1. Comparison of Experimental and Numerical Optical Properties
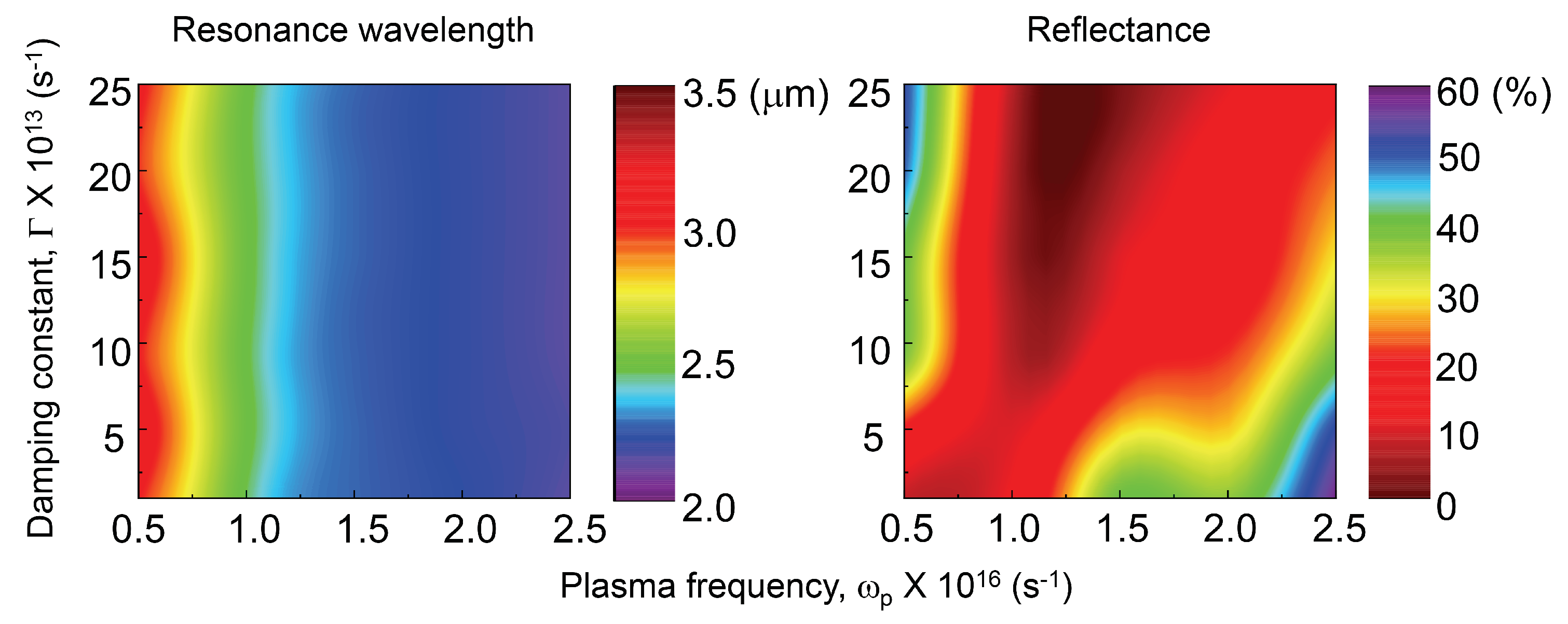
3.2. Effects of Metal Permittivity
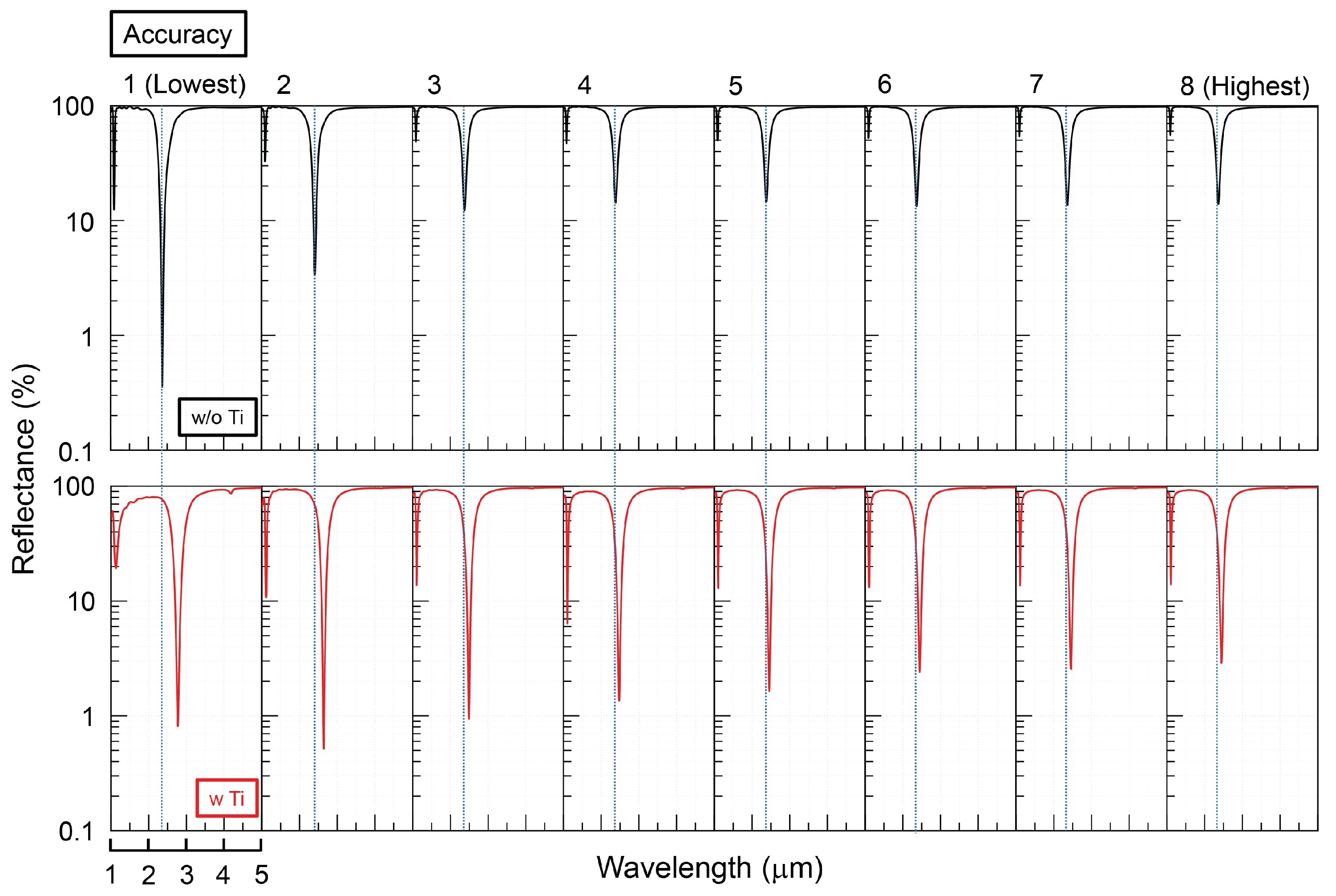
3.3. The Effect of Adhesion Layer
4. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Ding, F.; Yang, Y.; Deshpande, R.A.; Bozhevolnyi, S.I. A review of gap-surface plasmon metasurfaces: Fundamentals and applications. Nanophotonics 2018, 7, 1129–1156. [Google Scholar] [CrossRef]
- Lochbaum, A.; Fedoryshyn, Y.; Dorodnyy, A.; Koch, U.; Hafner, C.; Leuthold, J. On-Chip Narrowband Thermal Emitter for Mid-IR Optical Gas Sensing. ACS Photonics 2017, 4, 1371–1380. [Google Scholar] [CrossRef]
- Tsai, M.W.; Chuang, T.H.; Meng, C.Y.; Chang, Y.T.; Lee, S.C. High performance midinfrared narrow-band plasmonic thermal emitter. Appl. Phys. Lett. 2006, 89, 2–5. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Ishii, S.; Yokoyama, T.; Dao, T.D.; Sun, M.G.; Pankin, P.S.; Timofeev, I.V.; Nagao, T.; Chen, K.P. Narrowband wavelength selective thermal emitters by confined tamm plasmon polaritons. ACS Photonics 2017, 4, 2212–2219. [Google Scholar] [CrossRef]
- Yu, W.; Lu, Y.; Chen, X.; Xu, H.; Shao, J.; Chen, X.; Sun, Y.; Hao, J.; Dai, N. Large-Area, Broadband, Wide-Angle Plasmonic Metasurface Absorber for Midwavelength Infrared Atmospheric Transparency Window. Adv. Opt. Mat. 2019, 7, 1900841. [Google Scholar] [CrossRef]
- Dharmavarapu, R.; Ng, S.H.; Eftekhari, F.; Juodkazis, S.; Bhattacharya, S. MetaOptics: Opensource software for designing metasurface optical element GDSII layouts. Opt. Express 2020, 28, 3505–3516. [Google Scholar] [CrossRef]
- Ding, F.; Dai, J.; Chen, Y.; Zhu, J.; Jin, Y.; Bozhevolnyi, S.I. Broadband near-infrared metamaterial absorbers utilizing highly lossy metals. Sci. Rep. 2016, 6, 39445. [Google Scholar] [CrossRef]
- Qu, C.; Ma, S.; Hao, J.; Qiu, M.; Li, X.; Xiao, S.; Miao, Z.; Dai, N.; He, Q.; Sun, S.; et al. Tailor the Functionalities of Metasurfaces Based on a Complete Phase Diagram. Phys. Rev. Lett. 2015, 115, 235503. [Google Scholar] [CrossRef]
- Zou, Y.; Cao, J.; Gong, X.; Qian, R.; An, Z. Ultrathin and Electrically Tunable Metamaterial with Nearly Perfect Absorption in Mid-Infrared. Appl. Sci. 2019, 9, 3358. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application As Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Liu, X.; Padilla, W.J.; Zhou, L.; Qiu, M. High performance optical absorber based on a plasmonic metamaterial. Appl. Phys. Lett. 2010, 96, 251104. [Google Scholar] [CrossRef]
- Nishijima, Y.; Balčytis, A.; Naganuma, S.; Seniutinas, G.; Juodkazis, S. Kirchhoff’s metasurfaces towards efficient photo-thermal energy conversion. Sci. Rep. 2019, 9, 8284. [Google Scholar] [CrossRef] [PubMed]
- Nishijima, Y.; Balčytis, A.; Naganuma, S.; Seniutinas, G.; Juodkazis, S. Tailoring metal and insulator contributions in plasmonic perfect absorber metasurfaces. ACS Appl. Nano Mater. 2018, 1, 3557–3564. [Google Scholar] [CrossRef]
- Beni, T.; Yamasaku, N.; Kurotsu, T.; To, N.; Okazaki, S.; Arakawa, T.; Balčytis, A.; Seniutinas, G.; Juodkazis, S.; Nishijima, Y. Metamaterial for Hydrogen Sensing. ACS Sens. 2019, 4, 2389–2394. [Google Scholar] [CrossRef] [PubMed]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Washington, DC, USA, 1985; pp. 286–295. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 1985; Volume 73, pp. 111–114. [Google Scholar]
- McPeak, K.M.; Jayanti, S.V.; Kress, S.J.P.; Meyer, S.; Iotti, S.; Rossinelli, A.; Norris, D.J. Plasmonic films can easily be better: Rules and recipes. ACS Photon. 2015, 2, 326–333. [Google Scholar] [CrossRef]
- Olmon, R.L.; Slovick, B.; Johnson, T.W.; Shelton, D.; Oh, S.H.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of gold. Phys. Rev. B 2012, 86, 235147. [Google Scholar] [CrossRef]
- Werner, W.S.M.; Glantschnig, K.; Ambrosch-Draxl, C. Optical constants and inelastic electron-scattering data for 17 elemental metals. J. Phys. Chem. Ref. Data 2009, 38, 1013–1092. [Google Scholar] [CrossRef]
- Yakubovsky, D.I.; Stebunov, Y.V.; Kirtaev, R.V.; Ermolaev, G.A.; Mironov, M.S.; Novikov, S.M.; Arsenin, A.V.; Volkov, V.S. Ultrathin and ultrasmooth gold films on monolayer MoS2. Adv. Mater. Interfaces 2019, 6, 1900196. [Google Scholar] [CrossRef]
- Gao, L.; Lemarchand, F.; Lequime, M. Comparison of different dispersion models for single layer optical thin film index determination. Thin Solid Films 2011, 520, 501–509. [Google Scholar] [CrossRef]
- Babar, S.; Weaver, J.H. Optical constants of Cu, Ag, and Au revisited. Appl. Opt. 2015, 54, 477–481. [Google Scholar] [CrossRef]
- Hashimoto, Y.; Seniutinas, G.; Balčytis, A.; Juodkazis, S.; Nishijima, Y. Au-Ag-Cu nano-alloys: Tailoring of permittivity. Sci. Rep. 2016, 2, 25010. [Google Scholar] [CrossRef] [PubMed]
- Nishijima, Y.; Hashimoto, Y.; Seniutinas, G.; Rosa, L.; Juodkazis, S. Engineering gold alloys for plasmonics. Appl. Phys. A 2014, 117, 641–645. [Google Scholar] [CrossRef]
- Nishijima, Y.; Akiyama, S. Unusual optical properties of the Au/Ag alloy at the matching mole fraction. Opt. Mater. Express 2012, 2, 1226–1235. [Google Scholar] [CrossRef]
- Cai, W.; Shalaev, V. Optical Metamaterials; Springer: New York, NY, USA, 2010. [Google Scholar]
- Gall, D. Electron mean free path in elemental metals. J. Appl. Phys. 2016, 119, 085101. [Google Scholar] [CrossRef]
- Lundgaard, S.; Ng, S.; Nishijima, Y.; Mazilu, M.; Juodkazis, S. Black Metals: Optical Absorbers. Micromachines 2020, 11, 256. [Google Scholar] [CrossRef]
- Stockmann, U.; Adams, M.A.; Crawford, J.W.; Field, D.J.; Henakaarchchi, N.; Jenkins, M.; Minasny, B.; McBratney, A.B.; Courcelles, V.; Singh, K.; et al. The knowns, known unknowns and unknowns of sequestration of soil organic carbon. Agricul. Ecosyst. Environ. 2013, 164, 80–99. [Google Scholar] [CrossRef]
- Seet, K.; Mizeikis, V.; Juodkazis, S.; Misawa, H. Three-dimensional horizontal circular spiral photonic crystals with stop gaps below 1 micrometer. Appl. Phys. Lett. 2006, 88, 221101. [Google Scholar] [CrossRef]
- Kondo, T.; Juodkazis, S.; Mizeikis, V.; Matsuo, S.; Misawa, H. Fabrication of three-dimensional periodic microstructures in photoresist SU-8 by phase-controlled holographic lithography. New J. Phys. 2006, 8, 250. [Google Scholar] [CrossRef]
- Žukauskas, A.; Malinauskas, M.; Kadys, A.; Gervinskas, G.; Seniutinas, G.; Kandasamy, S.; Juodkazis, S. Black silicon: Substrate for laser 3D micro/nano-polymerization. Opt. Express 2013, 21, 6901–6909. [Google Scholar] [CrossRef]
- Zhou, L.; Tan, Y.; Ji, D.; Zhu, B.; Zhang, P.; Xu, J.; Gan, Q.; Yu, Z.; Zhu, J. Self-assembly of highly efficient, broadband plasmonic absorbers for solar steam generation. Adv. Sci. 2016, 2, e1501227. [Google Scholar] [CrossRef] [PubMed]
- Kaur, M.; Ishii, S.L.S.; Nagao, T. All-ceramic solar-driven water purifier based on anodized aluminum oxide and plasmonic titanium nitride. Adv. Sustain. Syst. 2019, 3, 1800112. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
To, N.; Juodkazis, S.; Nishijima, Y. Detailed Experiment-Theory Comparison of Mid-Infrared Metasurface Perfect Absorbers. Micromachines 2020, 11, 409. https://doi.org/10.3390/mi11040409
To N, Juodkazis S, Nishijima Y. Detailed Experiment-Theory Comparison of Mid-Infrared Metasurface Perfect Absorbers. Micromachines. 2020; 11(4):409. https://doi.org/10.3390/mi11040409
Chicago/Turabian StyleTo, Naoki, Saulius Juodkazis, and Yoshiaki Nishijima. 2020. "Detailed Experiment-Theory Comparison of Mid-Infrared Metasurface Perfect Absorbers" Micromachines 11, no. 4: 409. https://doi.org/10.3390/mi11040409
APA StyleTo, N., Juodkazis, S., & Nishijima, Y. (2020). Detailed Experiment-Theory Comparison of Mid-Infrared Metasurface Perfect Absorbers. Micromachines, 11(4), 409. https://doi.org/10.3390/mi11040409





