Air-Bubble Induced Mixing: A Fluidic Mixer Chip
Abstract
1. Introduction
2. Fabrication and Experiments
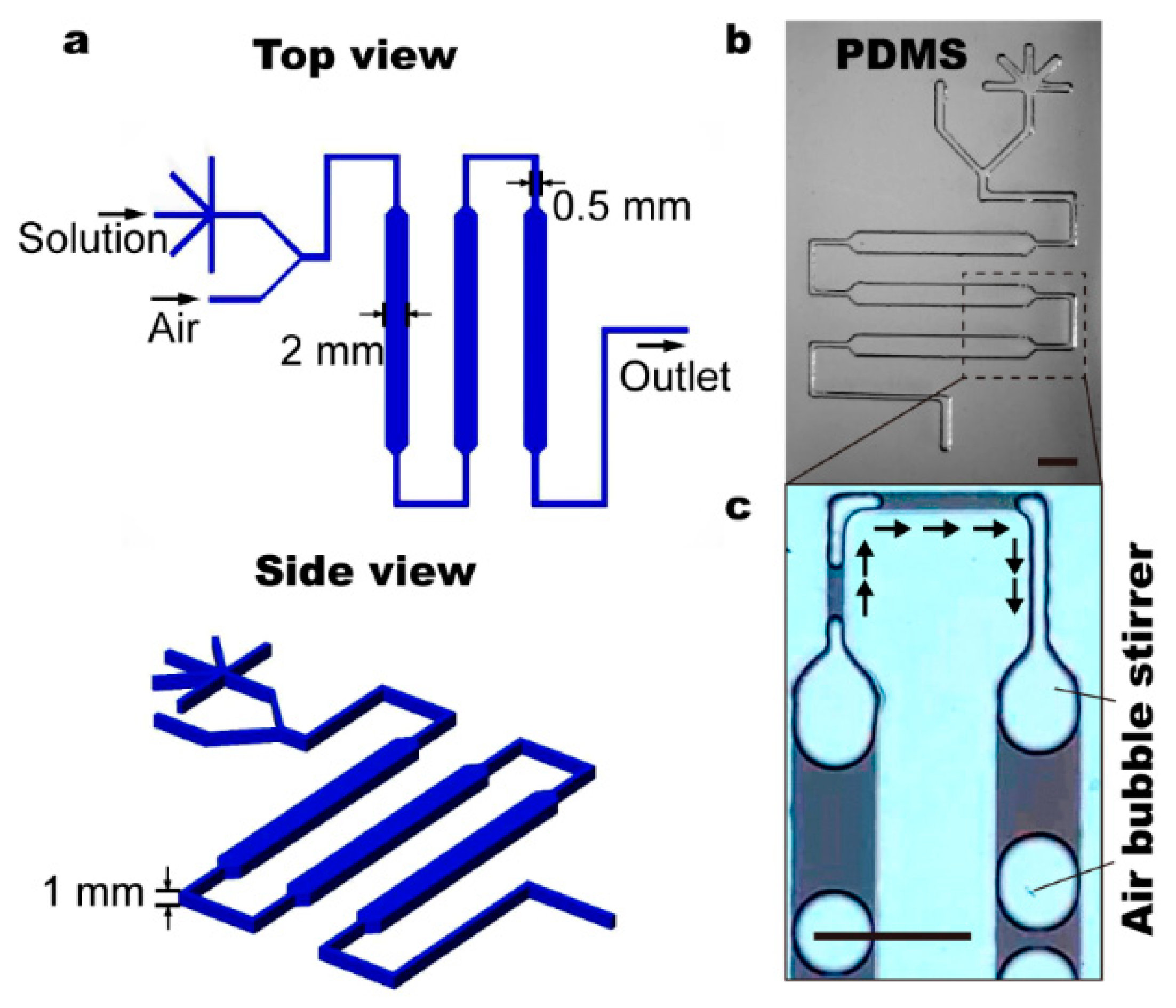
2.1. Chip Fabrication
2.2. Chip Control and Operation
2.3. Data Analysis
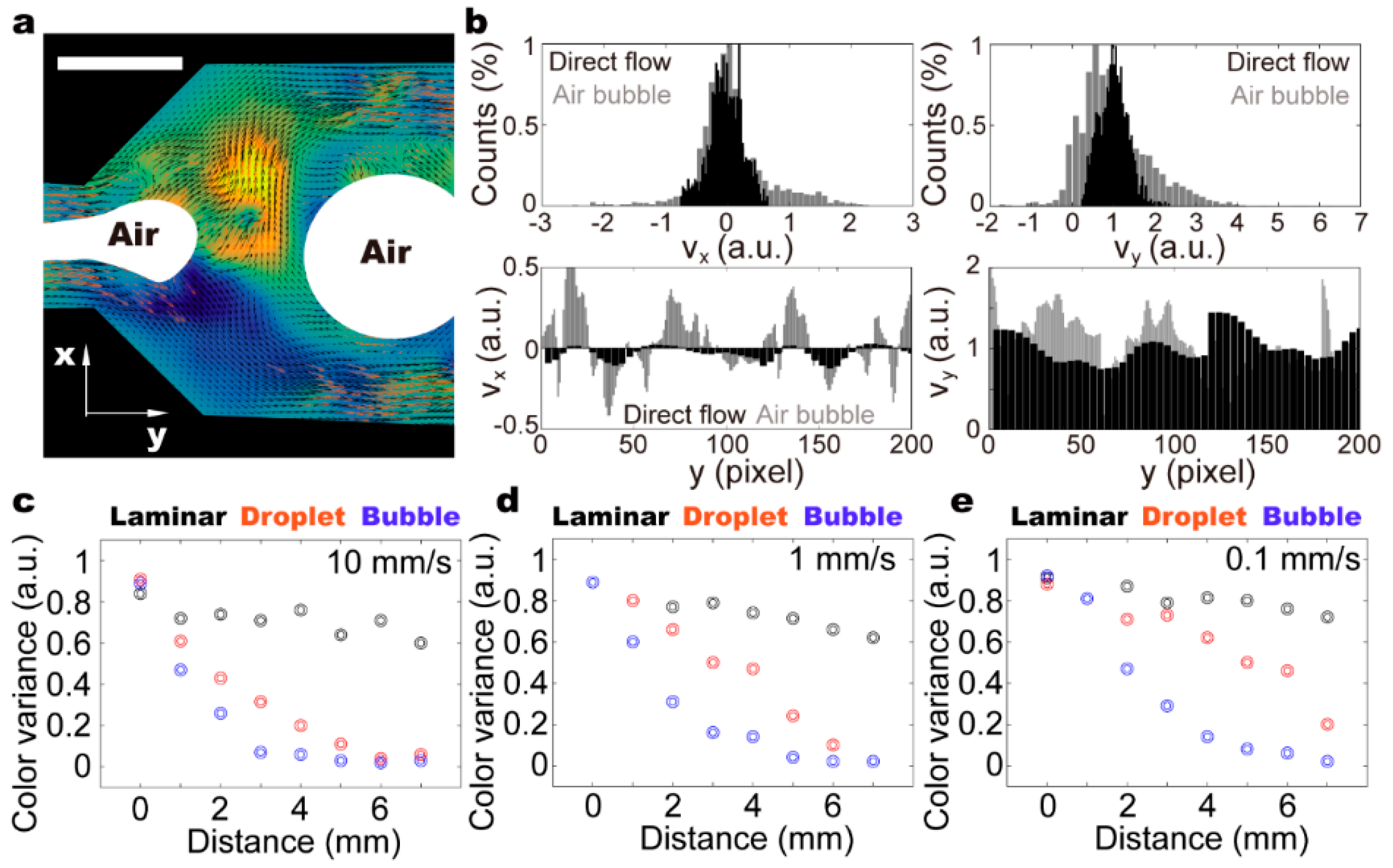
3. Results and Discussion
3.1. The Theory
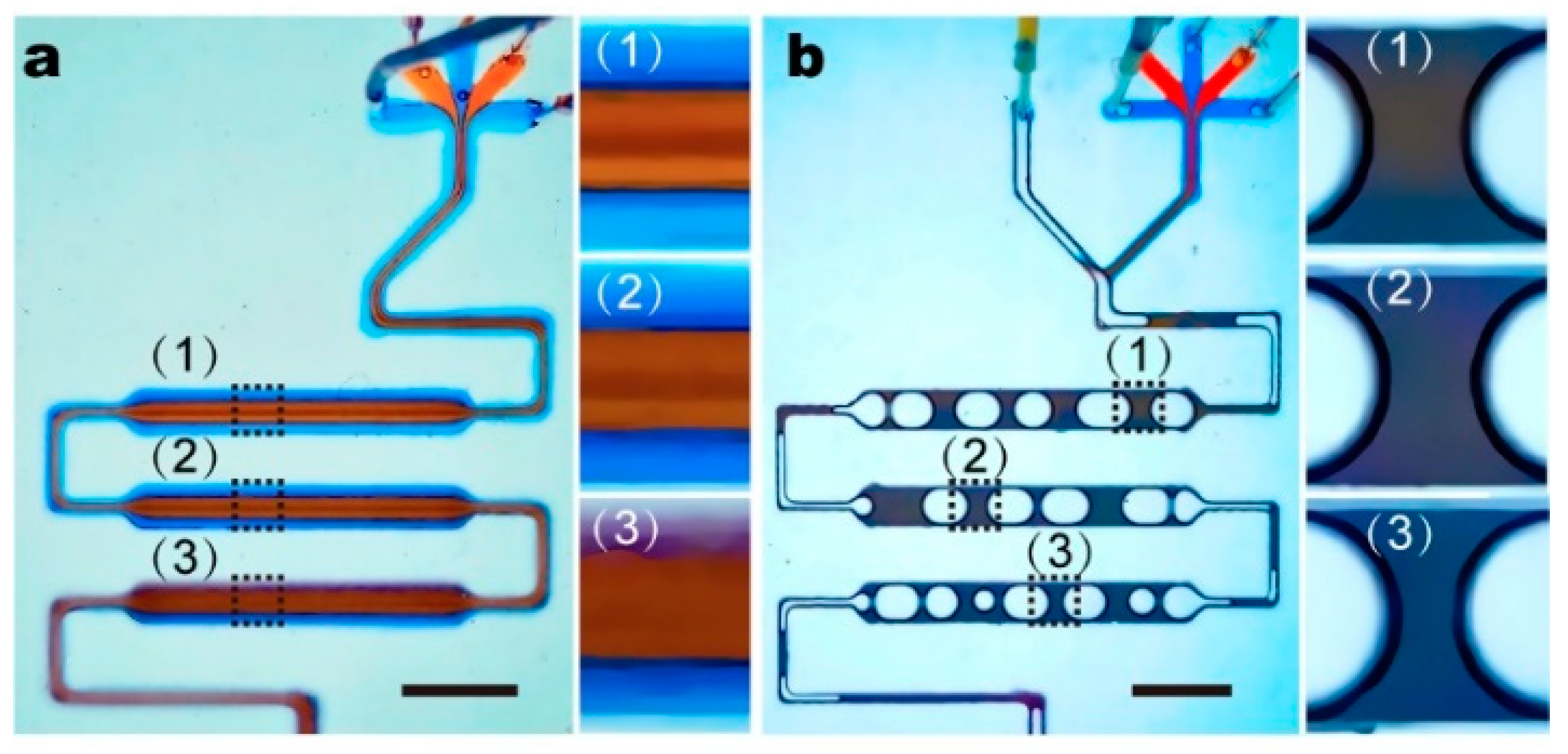
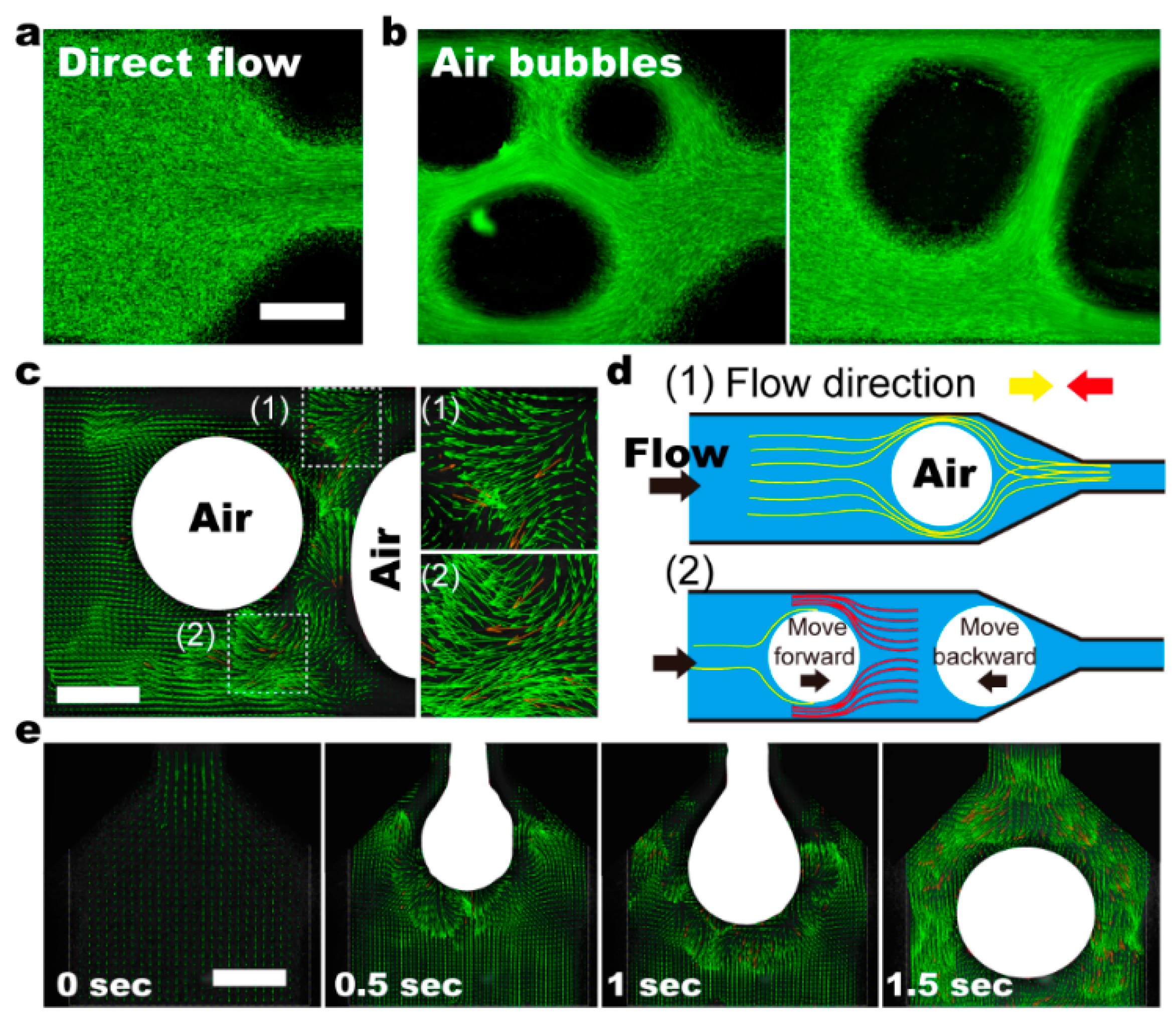
3.2. The Fluidic Mixer
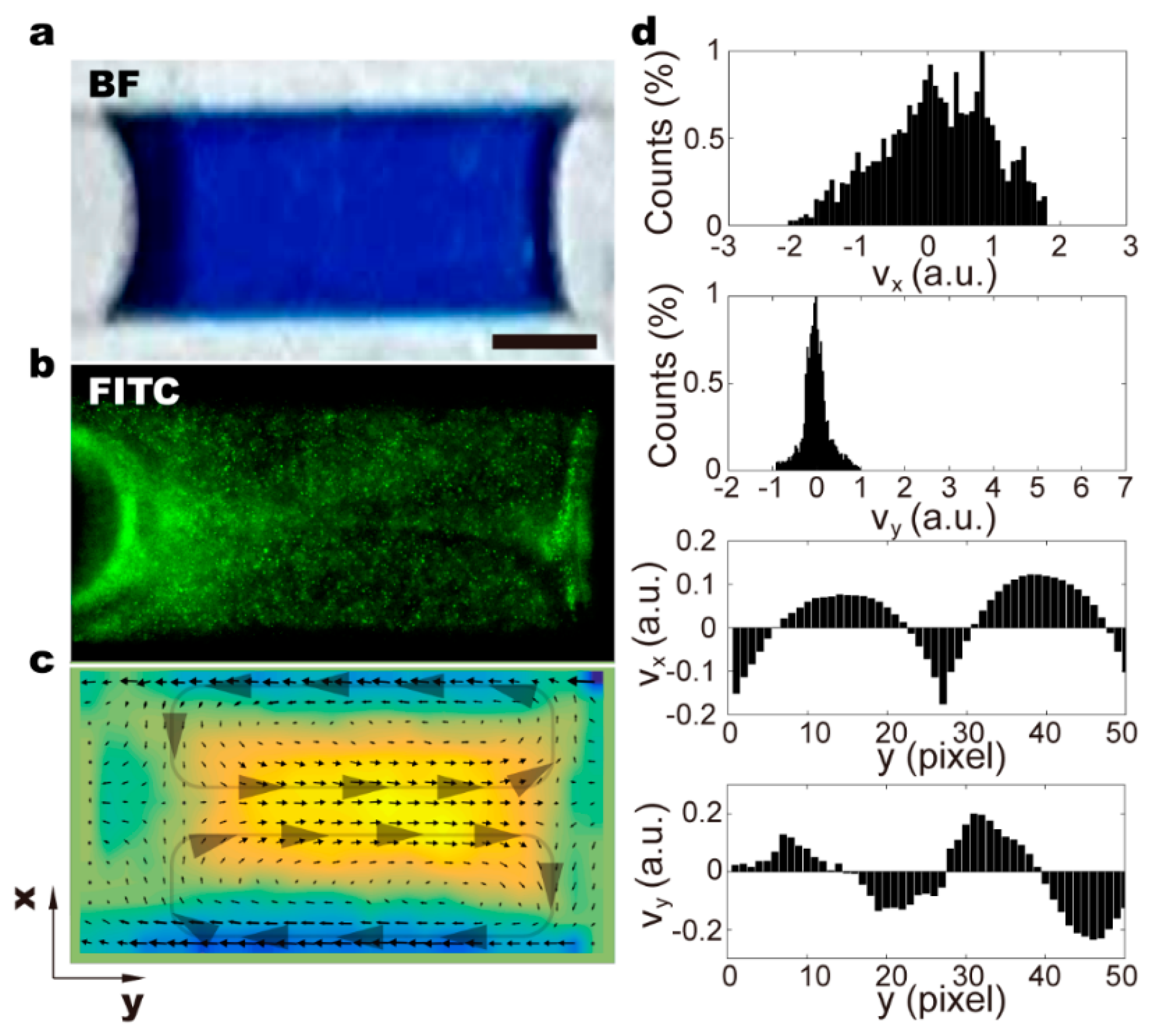
3.3. Recirculating Flow in the Moving Droplet
3.4. Small Air-Bubbles as Stirrers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices: Microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid. Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977. [Google Scholar] [CrossRef]
- Dittrich, P.S.; Manz, A. Lab-on-a-chip: Microfluidics in drug discovery. Nat. Rev. Drug Discov. 2006, 5, 210. [Google Scholar] [CrossRef] [PubMed]
- Duncombe, T.A.; Tentori, A.M.; Herr, A.E. Microfluidics: Reframing biological enquiry. Nat. Rev. Mol. Cell Biol. 2015, 16, 554–567. [Google Scholar] [CrossRef] [PubMed]
- Shang, L.; Cheng, Y.; Zhao, Y. Emerging droplet microfluidics. Chem. Rev. 2017, 117, 7964–8040. [Google Scholar] [CrossRef]
- Ahn, J.; Ko, J.; Lee, S.; Yu, J.; Kim, Y.; Jeon, N.L. Microfluidics in nanoparticle drug delivery; From synthesis to pre-clinical screening. Adv. Drug Deliv. Rev. 2018, 128, 29–53. [Google Scholar] [CrossRef]
- Aref, H. Stirring by chaotic advection. J. Fluid Mech. 1984, 143, 1–21. [Google Scholar] [CrossRef]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Tofteberg, T.; Skolimowski, M.; Andreassen, E.; Geschke, O. A novel passive micromixer: Lamination in a planar channel system. Microfluid. Nanofluid. 2010, 8, 209–215. [Google Scholar] [CrossRef]
- Jones, S.W.; Thomas, O.M.; Aref, H. Chaotic advection by laminar flow in a twisted pipe. J. Fluid Mech. 1989, 209, 335–357. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.; Ajdari, A.; Mezić, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef]
- Simonnet, C.; Groisman, A. Chaotic mixing in a steady flow in a microchannel. Phys. Rev. Lett. 2005, 94, 134501. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.R.; Jun, H.S.; Kwon, T.H. Experiments on chaotic mixing in a screw channel flow. AIChE J. 2002, 48, 1621–1630. [Google Scholar] [CrossRef]
- Alvarez-Hernández, M.M.; Shinbrot, T.; Zalc, J.; Muzzio, F.J. Practical chaotic mixing. Chem. Eng. Sci. 2002, 57, 3749–3753. [Google Scholar] [CrossRef]
- Ansari, M.A.; Kim, K.Y.; Anwar, K.; Kim, S.M. Vortex micro T-mixer with non-aligned inputs. Chem. Eng. J. 2012, 181, 846–850. [Google Scholar] [CrossRef]
- Li, J.; Xia, G.; Li, Y. Numerical and experimental analyses of planar asymmetric split-and-recombine micromixer with dislocation sub-channels. J. Chem. Technol. Biotechnol. 2013, 88, 1757–1765. [Google Scholar] [CrossRef]
- Afzal, A.; Kim, K.Y. Convergent-divergent micromixer coupled with pulsatile flow. Sens. Actuators B Chem. 2015, 211, 198–205. [Google Scholar] [CrossRef]
- Lim, T.W.; Son, Y.; Jeong, Y.J.; Yang, D.Y.; Kong, H.J.; Lee, K.S.; Kim, D.P. Three-dimensionally crossing manifold micro-mixer for fast mixing in a short channel length. Lab Chip 2011, 11, 100–103. [Google Scholar] [CrossRef]
- Li, L.; Chen, Q.D.; Tsai, C.T. Three dimensional triangle chaotic micromixer. Adv. Mater. Res. 2014, 875, 1189–1193. [Google Scholar] [CrossRef]
- Wu, S.J.; Hsu, H.C.; Feng, W.J. Novel design and fabrication of a geometrical obstacle-embedded micromixer with notched wall. Jpn. J. Appl. Phys. 2014, 53, 97201. [Google Scholar] [CrossRef]
- Cubaud, T.; Ho, C.M. Transport of bubbles in square microchannels. Phys. Fluids 2004, 16, 4575–4585. [Google Scholar] [CrossRef]
- Bottausci, F.; Mezić, I.; Meinhart, C.D.; Cardonne, C. Mixing in the shear superposition micromixer: Three-dimensional analysis. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1818, 362, 1001–1018. [Google Scholar] [CrossRef] [PubMed]
- Niu, X.; Lee, Y.K. Efficient spatial-temporal chaotic mixing in microchannels. J. Micromech. Microeng. 2003, 13, 454. [Google Scholar] [CrossRef]
- Okkels, F.; Tabeling, P. Spatiotemporal resonances in mixing of open viscous fluids. Phys. Rev. Lett. 2004, 92, 38301. [Google Scholar] [CrossRef] [PubMed]
- Oddy, M.H.; Santiago, J.G.; Mikkelsen, J.C. Electrokinetic instability micromixing. Anal. Chem. 2001, 73, 5822–5832. [Google Scholar] [CrossRef]
- Ho, C.M. Fluidics-the link between micro and nano sciences and technologies. In Proceedings of the 14th IEEE International Conference on Micro Electro Mechanical Systems, Interlaken, Switzerland, 25 January 2001. [Google Scholar]
- Song, H.; Tice, J.D.; Ismagilov, R.F. A microfluidic system for controlling reaction networks in time. Angew. Chem. Int. Ed. 2003, 42, 768–772. [Google Scholar] [CrossRef]
- Song, H.; Bringer, M.R.; Tice, J.D.; Gerdts, C.J.; Ismagilov, R.F. Experimental test of scaling of mixing by chaotic advection in droplets moving through microfluidic channels. Appl. Phys. Lett. 2003, 83, 4664–4666. [Google Scholar] [CrossRef]
- Feng, Y.B.; Wang, B.Q.; Tian, Y.; Chen, H.; Liu, Y.G.; Fan, H.M.; Wang, K.G.; Zhang, C. Active fluidic chip produced using 3D-printing for combinatorial therapeutic screening on liver tumor spheroid. Biosens. Bioelectron. 2020, 151, 111966. [Google Scholar] [CrossRef]
- Smolianski, A.; Haario, H.; Luukka, P. Numerical study of dynamics of single bubbles and bubble swarms. Appl. Math. Model. 2008, 32, 641–659. [Google Scholar] [CrossRef]
- Handique, K.; Burns, M.A. Mathematical modeling of drop mixing in a slit-type microchannel. J. Micromech. Microeng. 2001, 11, 548. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Che, B.; Jing, G.; Zhang, C. Air-Bubble Induced Mixing: A Fluidic Mixer Chip. Micromachines 2020, 11, 195. https://doi.org/10.3390/mi11020195
Jia X, Che B, Jing G, Zhang C. Air-Bubble Induced Mixing: A Fluidic Mixer Chip. Micromachines. 2020; 11(2):195. https://doi.org/10.3390/mi11020195
Chicago/Turabian StyleJia, Xiaoyu, Bingchen Che, Guangyin Jing, and Ce Zhang. 2020. "Air-Bubble Induced Mixing: A Fluidic Mixer Chip" Micromachines 11, no. 2: 195. https://doi.org/10.3390/mi11020195
APA StyleJia, X., Che, B., Jing, G., & Zhang, C. (2020). Air-Bubble Induced Mixing: A Fluidic Mixer Chip. Micromachines, 11(2), 195. https://doi.org/10.3390/mi11020195




