Optical Micromachines for Biological Studies
Abstract
1. Introduction
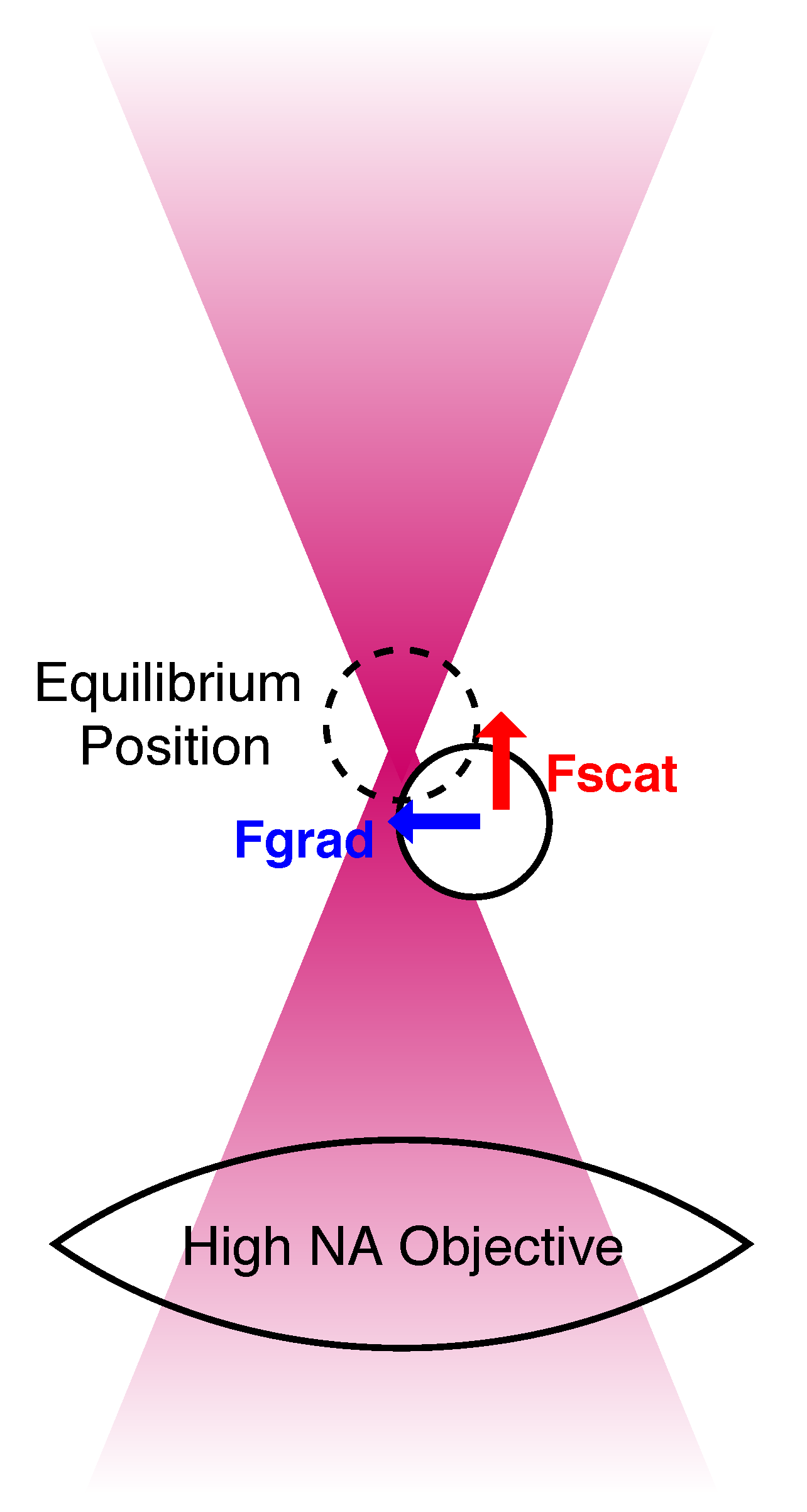
2. An Introduction to the Theory of Optical Tweezers
3. First Applications and Impact on Fields
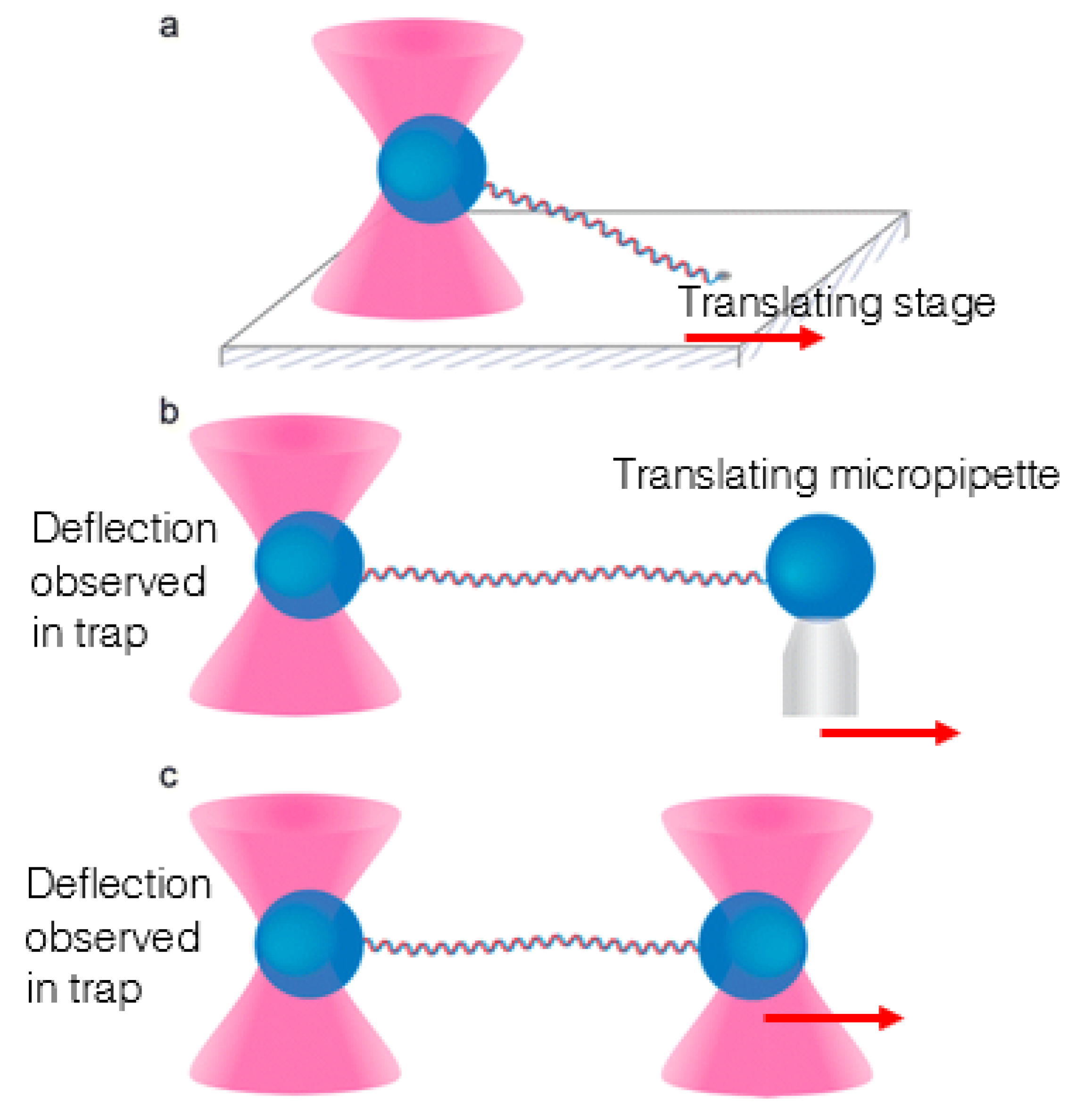
4. Optical Trapping: Concerns for Biological Research
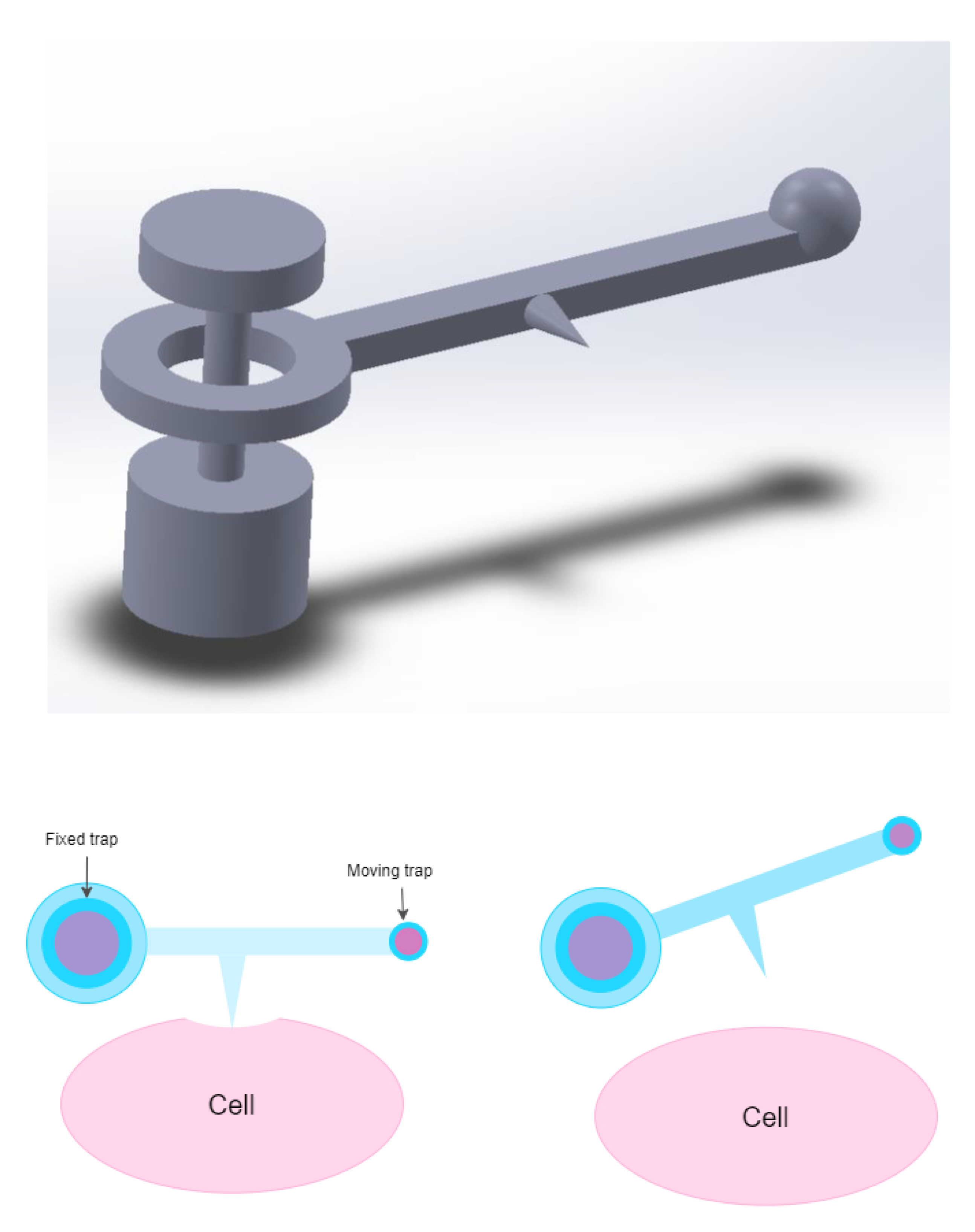
5. Optical Microrobots: Potential Tools for Biological Studies
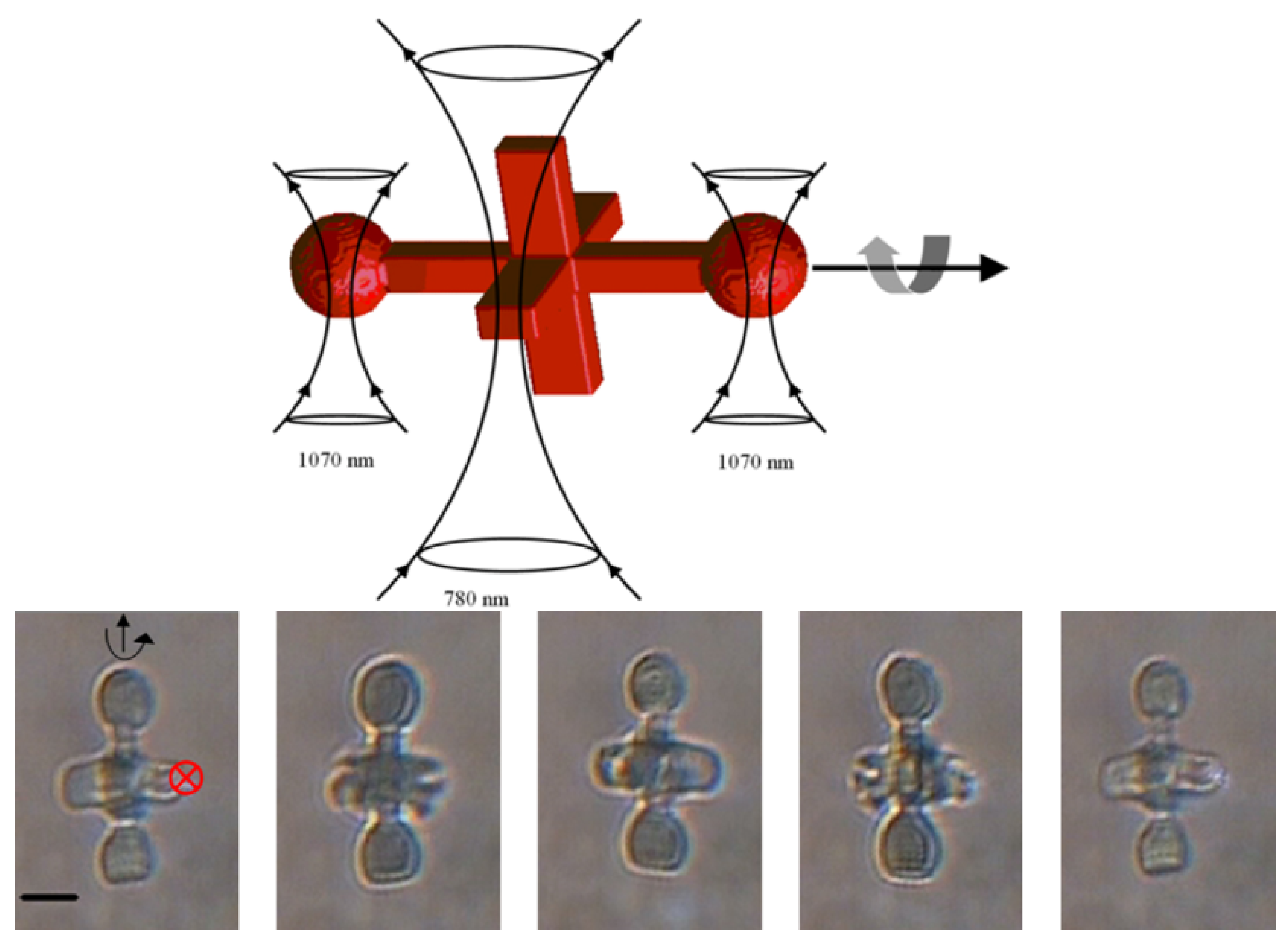
6. Optical Microrobots: Achievements to Date and Challenges
7. Effects of Microrobot Shape
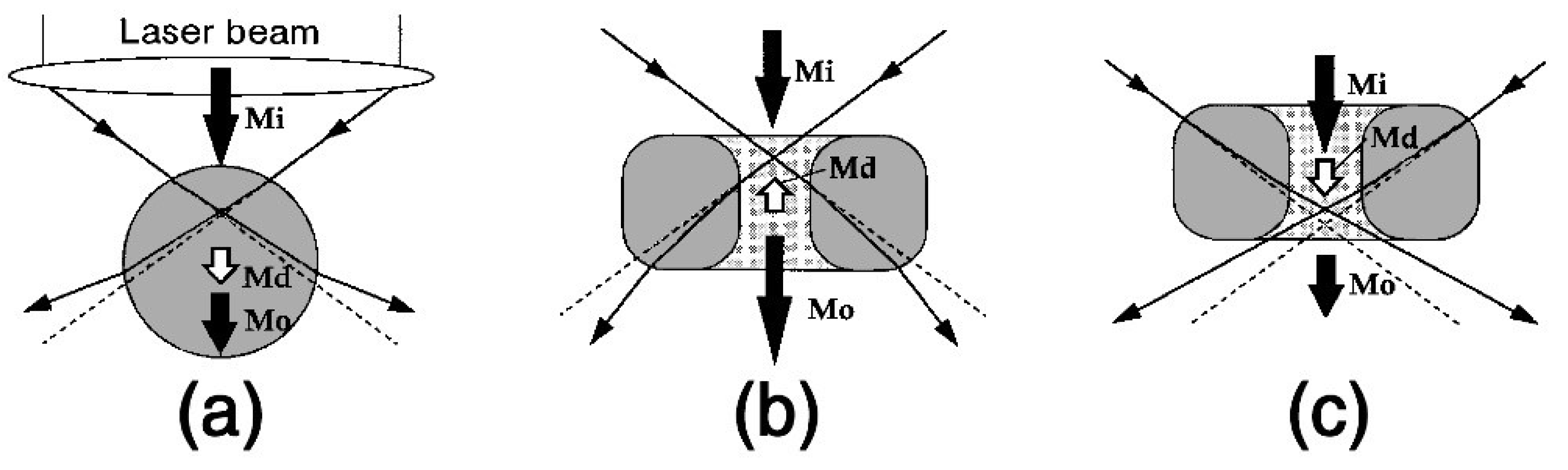
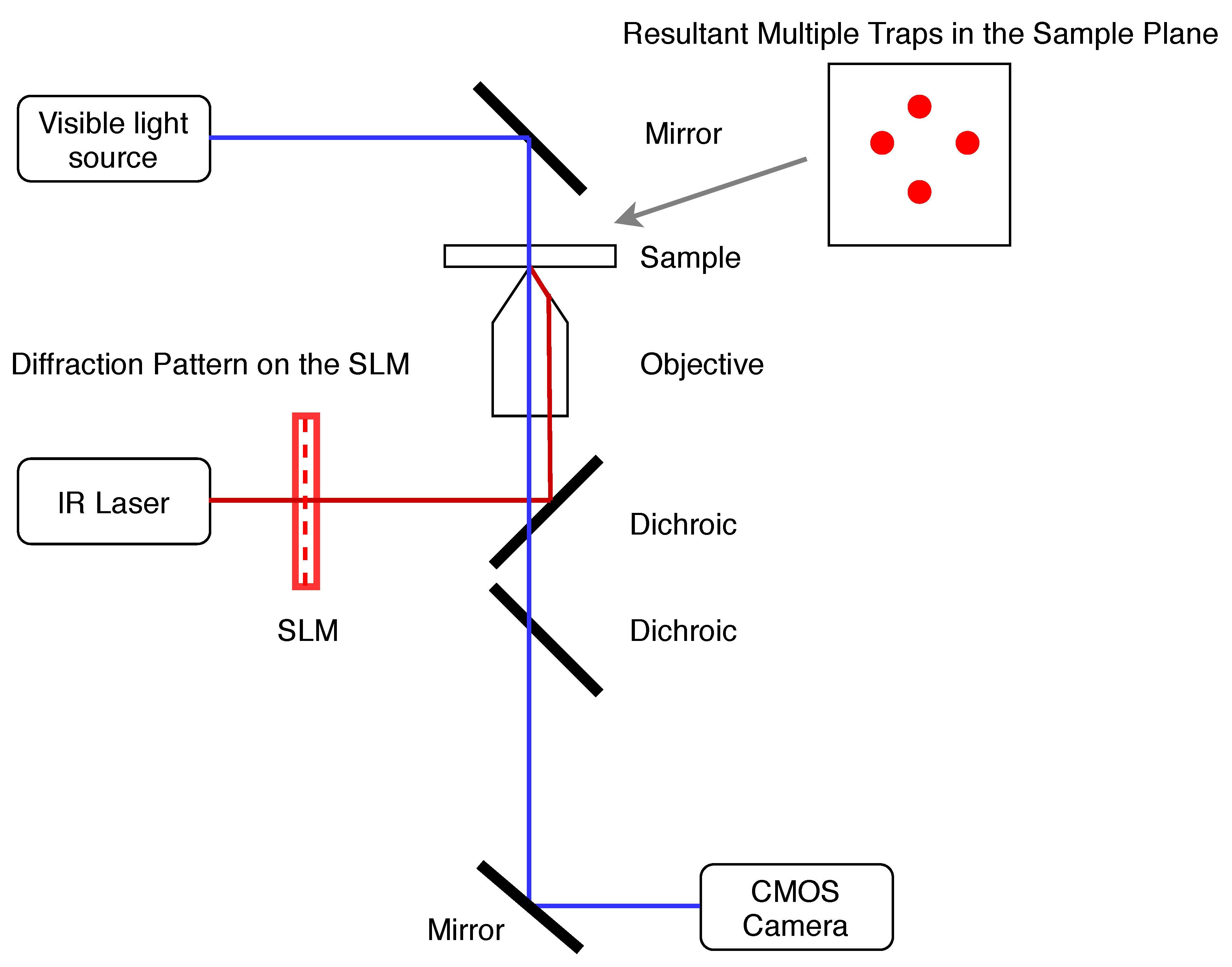
8. Choice of Optical Tweezers for Microrobotics
9. Looking to the Future
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Avci, E. Dynamic releasing of biological cells at high speed using parallel mechanism to control adhesion forces. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, 31 May–5 June 2014; IEEE: Hong Kong, China, 2019; pp. 3789–3794. [Google Scholar]
- Gauthier, M.; Alvo, S.; Dejeu, J.; Tamadazte, B.; Rougeot, P.; Régnier, S. Analysis and Specificities of Adhesive Forces Between Microscale and Nanoscale. IEEE Trans. Autom. Sci. Eng. 2013, 10, 562–570. [Google Scholar] [CrossRef]
- Neuman, K.C.; Nagy, A. Single Molecule Force Spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2014, 10, 491–505. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical Levitation by Radiation Pressure. Appl. Phys. Lett. 1971, 19, 283–285. [Google Scholar] [CrossRef]
- Gordon, J.P.; Ashkin, A. Motion of atoms in a radiation trap. Phys. Rev. A 1980, 21, 1606–1617. [Google Scholar] [CrossRef]
- Ashkin, A. Applications of Laser Radiation Pressure. Science 1980, 210, 1081–1088. [Google Scholar] [CrossRef]
- Ashkin, A. Trapping of Atoms by Resonance Radiation Pressure. Phys. Rev. Lett. 1978, 40, 729–732. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical Levitation of Liquid Drops by Radiation Pressure. Science 1975, 187, 1073–1075. [Google Scholar] [CrossRef]
- Nichols, E.F.; Hull, G.F. A Preliminary Communication on the Pressure of Heat and Light Radiation. Phys. Rev. 1901, 13, 307–320. [Google Scholar] [CrossRef]
- Nichols, E.F.; Hull, G.F. The Pressure Due to Radiation (Second Paper). Phys. Rev. 1903, 17, 26–50. [Google Scholar] [CrossRef]
- Jones, R.V.; Richards, J.C.S.; Lindemann, F.A. The Pressure of Radiation in a Refractive Medium. Proc. R. Soc. Lond. 1954, 221, 480–498. [Google Scholar] [CrossRef]
- Lebedev, P.N. Experimental Examination of Light Pressure. Ann. Phys. 1901, 301, 433–458. [Google Scholar]
- Schawlow, A.L.; Townes, C.H. Infrared and Optical Masers. Phys. Rev. 1958, 112, 1940–1949. [Google Scholar] [CrossRef]
- Kogelnik, H.; Li, T. Laser Beams and Resonators. Appl. Opt. 1966, 5, 1550–1567. [Google Scholar] [CrossRef] [PubMed]
- Draegert, D. Single-diode end-pumped Nd:YAG laser. IEEE J. Quantum Electron. 1973, 9, 1146–1149. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical Trapping and Manipulation of Viruses and Bacteria. Science 1987, 235, 1517–1520. [Google Scholar] [CrossRef]
- Ashkin, A. Force generation or organelle transport measured in vivo by inrared laser trap. Nature 1990, 348, 346–348. [Google Scholar] [CrossRef]
- Ikin, L.; Carberry, D.M.; Gibson, G.M.; Padgett, M.J.; Miles, M.J. Assembly and force measurement with SPM-like probes in holographic optical tweezers. New J. Phys. 2009, 11, 023012:1–023012:8. [Google Scholar] [CrossRef]
- Xie, M.; Chen, S.; Mills, J.K.; Wang, Y.; Liu, Y.; Sun, D. Cell out-of-plane rotation control using a cell surgery robotic system equipped with optical tweezers manipulators. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 31 July–4 August 2016; IEEE: Ningbo, China, 2016; pp. 103–108. [Google Scholar]
- Aekbote, B.L.; Fekete, T.; Jacak, J.; Vizsnyiczai, G.; Ormos, P.; Kelemen, L. Surface-modified complex SU-8 microstructures for indirect optical manipulation of single cells. Biomed. Opt. Express 2016, 7, 45–56. [Google Scholar] [CrossRef]
- Hu, S.; Hu, R.; Dong, X.; Wei, T.; Chen, S.; Sun, D. Translational and rotational manipulation of filamentous cells using optically driven microrobots. Opt. Express 2019, 27, 16475–16482. [Google Scholar] [CrossRef] [PubMed]
- Fukada, S.; Maruyama, H.; Masuda, T.; Arai, F. 3D fabrication and manipulation of hybrid nanorobots by laser for single cell analysis. In Proceedings of the 2012 International Symposium on Micro-NanoMechatronics and Human Science (MHS), Nagoya, Japan, 4–7 November 2012; pp. 479–481. [Google Scholar]
- Lin, C.-L.; Lee, Y.-H.; Lin, C.-T.; Liu, Y.-J.; Hwang, J.-L.; Chung, T.-L.; Baldeck, P.L. Multiplying optical tweezers force using a micro-lever. Opt. Express 2011, 19, 20604–20609. [Google Scholar] [CrossRef] [PubMed]
- Jeong, Y.J.; Lim, T.W.; Son, Y.; Yang, D.-Y.; Kong, H.-J.; Lee, K.-S. Proportional enlargement of movement by using an optically driven multi-link system with an elastic joint. Opt. Express 2010, 18, 13745–13753. [Google Scholar] [CrossRef]
- Ushiba, S.; Masui, K.; Taguchi, N.; Hamano, T.; Kawata, S.; Shoji, S. Size dependent nanomechanics of coil spring shaped polymer nanowires. Sci. Rep. 2015, 5, 17152:1–17152:8. [Google Scholar] [CrossRef] [PubMed]
- Bui, A.A.M.; Stilgoe, A.B.; Lenton, I.C.D.; Gibson, L.J.; Kashchuk, A.V.; Zhang, S.; Rubinsztein-Dunlop, H.; Nieminen, T.A. Theory and practice of simulation of optical tweezers. J. Quant. Spectrosc. Radiat. 2017, 195, 66–75. [Google Scholar] [CrossRef]
- Nieminen, T.A.; Stilgoe, A.B.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Approximate and exact modelling of optical trapping. In Proceedings of the SPIE NanoScience + Engineering, San Diego, CA, USA, 27 August 2010; pp. 1–8. [Google Scholar]
- Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Computational modelling of optical tweezers. In Proceedings of the Volume 5514, Optical Trapping and Optical Micromanipulation, Optical Science and Technology, the SPIE 49th Annual Meeting, Denver, CO, USA, 2–6 August 2004; pp. 514–523. [Google Scholar]
- Ashkin, A. History of optical trapping and manipulation of small-neutral particles, atoms and molecules. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 841–856. [Google Scholar] [CrossRef]
- Ashkin, A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys. J. 1992, 61, 569–582. [Google Scholar] [CrossRef]
- Lvovsky, A.I. Fresnel Equations. In Encyclopedia of Optical Engineering; Hoffman, C., Driggers, R., Eds.; Taylor and Francis: New York, NY, USA, 2013; pp. 1–6. [Google Scholar]
- Neuman, K.C.; Block, S.M. Optical Trapping. Rev. Sci. Instrum. 2004, 75, 2787–2809. [Google Scholar] [CrossRef]
- Harada, Y.; Asakura, T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun. 1996, 124, 529–541. [Google Scholar] [CrossRef]
- Smith, P.W.; Ashkin, A.; Tomlinson, W.J. Four-wave mixing in an artificial Kerr medium. Opt. Lett. 1981, 6, 284–286. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Salandrino, A.; Fardad, S.; Christodoulides, D.N. Generalized Mie theory of optical forces. J. Opt. Soc. Am. B 2012, 29, 855–866. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Observation of light scattering from nonspherical particles using optical levitation. Appl. Opt. 1980, 19, 660–668. [Google Scholar] [CrossRef]
- Xu, F.; Ren, K.; Gouesbet, G.; Gréhan, G.; Cai, X. Generalized Lorenz-Mie theory for an arbitrarily oriented, located and shaped beam scattered by a homogeneous spheroid. J. Opt. Soc. Am. A 2007, 24, 119–131. [Google Scholar] [CrossRef] [PubMed]
- Ren, K.; Gréhan, G.; Gouesbet, G. Prediction of reverse radiation pressure by generalized Lorenz-Mie theory. Appl. Opt. 1996, 35, 2702–2710. [Google Scholar] [CrossRef]
- Sun, B.; Roichman, Y.; Grier, D.G. Theory of holographic optical trapping. Opt. Express 2008, 16, 15765–15776. [Google Scholar] [CrossRef]
- Waterman, P.C. Matrix formulation of electromagnetic scattering. Proc. IEEE 1965, 53, 805–812. [Google Scholar] [CrossRef]
- Qi, X.; Nieminen, T.A.; Stilgoe, A.B.; Loke, V.L.Y.; Rubinsztein-Dunlop, H. Comparison of T-matrix calculation methods for scattering by cylinders in optical tweezers. Opt. Lett 2014, 39, 4827–4830. [Google Scholar] [CrossRef]
- Nieminen, T.A.; Rubinsztein-Dunlop, H.; Heckenberg, N.R.; Bishop, A.I. Numerical modelling of optical trapping. Comput. Phys. Commun. 2001, 142, 468–471. [Google Scholar] [CrossRef]
- Nieminen, T.A.; Rubinsztein-DUnlop, H.; Heckenberg, N.R. Calculation of the T-matrix: General considerations and application of the point-matching method. J. Quant. Spectrosc. Radiat. 2003, 79, 1019–1029. [Google Scholar] [CrossRef]
- Loke, V.L.Y.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. T-matrix calculation via discrete dipole approximation, point matching and exploiting symmetry. J. Quant. Spectrosc. Radiat. 2009, 110, 1460–1471. [Google Scholar] [CrossRef]
- Nieminen, T.A.; Loke, V.L.Y.; Stilgoe, A.B.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. T-matrix method for modelling optical tweezers. J. Mod. Opt. 2011, 58, 528–544. [Google Scholar] [CrossRef]
- Gouesbet, G. T-matrix formulation and generalized Lorenz-Mie theories in spherical coordinates. Opt. Commun. 2010, 283, 517–521. [Google Scholar] [CrossRef]
- Nieminen, T.A.; du Preez-Wilkinson, N.; Stilgoe, A.B.; Loke, V.L.Y.; Bui, A.A.M.; Rubinsztein-Dunlop, H. Optical tweezers: Theory and modelling. J. Quant. Spectrosc. Radiat. Transf. 2014, 146, 59–80. [Google Scholar] [CrossRef]
- Svoboda, K.; Schmidt, C.F.; Schnapp, B.J.; Block, S.M. Direct observation of kinesin stepping by optical trapping interferometry. Nature 1993, 365, 721–727. [Google Scholar] [CrossRef]
- Ghislain, L.P.; Webb, W.W. Scanning-force microscope based on an optical trap. Opt. Lett. 1993, 18, 1678–1680. [Google Scholar] [CrossRef]
- Bui, A.A.M.; Kashchuk, A.V.; Balanant, M.A.; Nieminen, T.A.; Rubinsztein-Dunlop, H.; Stilgoe, A.B. Calibration of force detection for arbitrarily shaped particles in optical tweezers. Sci. Rep. 2018, 8, 10798:1–10798:12. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The Elastic Response of Individual Double-Stranded and Single-Stranded DNA Molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef]
- Berg-Sørensen, K.; Flyvbjerg, H. Power spectrum analysis for optical tweezers. Rev. Sci. Instrum. 2004, 75, 594–612. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Optical-trap force transducer that operates by direct measurement of light momentum. Methods Enzymol. 2003, 361, 134–162. [Google Scholar] [CrossRef]
- Farr’e, A.; Montes-Usategui, M. A force detection technique for single-beam optical traps based on direct measurement of light momentum changes. Opt. Express 2010, 18, 11955–11968. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M.; Yamane, T. Optical trapping and manipulation of single cells using infrared laser beams. Nature 1987, 330, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, K.; Block, S.M. Biological Applications of Optical Forces. Annu. Rev. Biophys. 1994, 23, 247–285. [Google Scholar] [CrossRef] [PubMed]
- Mills, J.; Qie, L.; Dao, M.; Lim, C.; Suresh, S. Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers. Mech. Chem. Biosyst. 2004, 1, 169–180. [Google Scholar] [CrossRef]
- Capitanio, M.; Pavone, F.S. Interrogating Biology with Force: Single Molecule High-Resolution Measurements with Optical Tweezers. Biophys. J. 2013, 105, 1293–1303. [Google Scholar] [CrossRef]
- Grigaravicius, P.; Greulich, K.O.; Monajembashi, S. Laser Microbeams and Optical Tweezers in Ageing Research. ChemPhysChem 2009, 10, 79–85. [Google Scholar] [CrossRef]
- Suei, S.; Raudsepp, A.; Kent, L.M.; Keen, S.A.J.; Filichev, V.V.; Williams, M.A.K. DNA visualization in single molecule studies carried out with optical tweezers: Covalent versus non-covalent attachment of fluorophores. Biochem. Biophys. Res. Commun. 2015, 466, 226–231. [Google Scholar] [CrossRef]
- Sischka, A.; Toensing, K.; Eckel, R.; Wilking, S.D.; Sewald, N.; Ros, R.; Anselmetto, D. Molecular mechanisms and kinetics between DNA and DNA binding ligands. Biophys. J. 2005, 88, 404–411. [Google Scholar] [CrossRef]
- McCauley, M.J.; Wiliams, M.C. Mechanisms of DNA binding determined in optical tweezers experiments. Biopolymers 2007, 85, 154–168. [Google Scholar] [CrossRef]
- Smith, S.B.; Finzi, L.; Bustamante, C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science 1992, 258, 1122–1126. [Google Scholar] [CrossRef]
- Simmons, R.M.; Finer, J.T.; Chu, S.; Spudich, J.A. Quantitative measurements of force and displacement using an optical trap. Biophys. J. 1996, 70, 1813–1822. [Google Scholar] [CrossRef]
- Lien, C.-H.; Wei, M.-T.; Tseng, T.-Y.; Lee, C.-D.; Wang, C.; Wang, T.-F.; Ou-Yang, H.D.; Chiou, A. Probing the dynamic differential stiffness of dsDNA interacting with RecA in the enthalpic regime. Opt. Express 2009, 17, 20376–20385. [Google Scholar] [CrossRef] [PubMed]
- Bouchiat, C.; Wang, M.D.; Allemand, J.F.; Strick, T.; Block, S.M.; Croquette, V. Estimating the persistance length of a worm-like chain molecule from force-extension measurements. Biophys. J. 1999, 76, 409–413. [Google Scholar] [CrossRef]
- Wang, M.D.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Stretching DNA with optical tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef]
- Bustamante, C.; Marko, J.F.; Siggia, E.D.; Smith, S. Entropic elasticity of lambda-phage DNA. Science 1994, 265, 1599–1600. [Google Scholar] [CrossRef]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Shivashankar, G.V.; Feingold, M.; Krichevsky, O.; Libchaber, A. RecA polymerization on double-stranded DNA by using single-molecule manipulation: The role of ATP hydrolysis. Proc. Natl. Acad. Sci. USA 1999, 96, 7916–7921. [Google Scholar] [CrossRef]
- van Mameren, J.; Gross, P.; Farge, G.; Hoojiman, P.; Modesti, M.; Falkenberg, M.; Wuite, G.J.L.; Peterman, E.J.G. Unraveling the structure of DNA during overstretching by using multicolor, single-molecule fluorescence imaging. Proc. Natl. Acad. Sci. USA 2009, 106, 18231–18236. [Google Scholar] [CrossRef]
- Heller, I.; Hoekstra, T.P.; King, G.A.; Peterman, E.J.G.; Wuite, G.J.L. Optical tweezers analysis of DNA-protein complexes. Chem. Rev. 2014, 114, 3087–3119. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Rapp, A.; Monajembashi, S.; Gupta, P.K.; Greulich, K.O. Comet assay measurements of DNA damage in cells by laser microbeams and trapping beams with wavelengths spanning a ramge of 308 nm to 1064 nm. Radiat. Res. 2002, 157, 378–385. [Google Scholar] [CrossRef]
- Liang, H.; Vu, K.T.; Krishnan, P.; Trang, T.C.; Shin, D.; Kimel, S.; Berns, M.W. Wavelength dependence of cell cloning efficiency after optical trapping. Biophys. J. 1996, 70, 1529–1533. [Google Scholar] [CrossRef]
- Neuman, K.C.; Chadd, E.H.; Liou, G.F.; Bergman, K.; Block, S.M. Characterization of photodamage to escherichia coli in optical traps. Biophys. J. 1999, 77, 2856–2863. [Google Scholar] [CrossRef]
- Landry, M.P.; McCall, P.M.; Qi, Z.; Chemla, Y.R. Characterization of photoactivated singlet oxygen damage in single-molecule optical trap experiments. Biophys. J. 2009, 97, 2128–2136. [Google Scholar] [CrossRef] [PubMed]
- Bl’azquez-Castro, A. Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules. Micromachines 2019, 10, 507. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, D.K.; Sonek, G.J.; Berns, M.W.; Chapman, C.F.; Tromberg, B.J. Evidence for localized cell heating induced by infrared optical tweezers. Biophys. J. 1995, 68, 2137–2144. [Google Scholar] [CrossRef]
- Peterman, E.J.G.; Gittes, F.; Schmidt, C.F. Laser-induced heating in optical traps. Biophys. J. 2003, 84, 1308–1316. [Google Scholar] [CrossRef]
- Nagar, H.; Admon, T.; Goldman, D.; Eyal, A.; Roichman, Y. Optical trapping below the diffraction limit with a tunable beam waist using super-oscillating beams. Opt. Lett. 2019, 44, 2430–2433. [Google Scholar] [CrossRef]
- Jeffries, G.D.M.; Edgars, J.S.; Zhao, Y.; Shelby, J.P.; Fong, C.; Chiu, D.T. Using polarization-shaped optical vortex traps for single-cell nanosurgery. Nano Lett. 2007, 7, 415–420. [Google Scholar] [CrossRef]
- Kairdolf, B.A.; Smith, A.M.; Stokes, T.H.; Wang, M.D.; Young, A.N.; Nie, S. Semiconductor quantum dots for bioimaging and biodiagnostic applications. Annu. Rev. Anal. Chem. 2013, 6, 143–162. [Google Scholar] [CrossRef]
- Chowdhury, A.; Waghmare, D.; Dasgupta, R.; Majumder, S.K. Red blood cell membrance damage by light-induced thermal gradient under optical trap. J. Biophotonics 2018, 11, 201700222:1–201700222:10. [Google Scholar] [CrossRef]
- König, K.; Tadir, Y.; Patrizio, P.; Berns, M.W.; Tromberg, B.J. Effects of ultraviolet exposure and near infrared laser tweezers on human spermatozoa. Hum. Reprod. 1996, 11, 2162–2164. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, L.; Zhang, Y.; Liu, C.; Wu, J.; Zhang, Y.; Yang, X.; Zhang, J.; Yang, J.; Yuam, L. Optical funnel for living cells trap. Opt. Commun. 2019, 431, 196–198. [Google Scholar] [CrossRef]
- Shao, B.; Shi, L.Z.; Nascimento, J.M.; Botvinick, E.L.; Ozkan, M.; Berns, M.W.; Esener, S.C. High-throughput sorting and analysis of human sperm with a ring-shaped laser trap. Biomed. Microdevices 2007, 9, 361–369. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cizmar, T.; Siler, M.; Zemanek, P. An optical nanotrap array movable over a milimetre range. Appl. Phys. 2006, 84, 197–203. [Google Scholar] [CrossRef]
- Shao, B.; Esener, S.C.; Nascimento, J.M.; Berns, M.W.; Botvinivk, E.L.; Ozkan, M. Size tunable three-dimensional annular laser trap based on axicons. Opt. Lett. 2006, 31, 3375–3377. [Google Scholar] [CrossRef] [PubMed]
- Manek, I.; Ovchinnikov, Y.B.; Grimm, R. Generation of a hollow laser beam for atom trapping using an axicon. Opt. Commun. 1998, 147, 67–70. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K.; Soneson, J.; Wright, E.M. Optical dipole traps and atomic waveguides based on Bessel light beams. Phys. Rev. A 2001, 63, 063602:1–063602:8. [Google Scholar] [CrossRef]
- Dao, M.; Lim, C.T.; Suresh, S. Mechanics of the human red blood cell deformed by optical tweezers. J. Mech. Phys. Solids 2003, 51, 2259–2280. [Google Scholar] [CrossRef]
- Pollard, M.R.; Botchway, S.W.; Chichkov, B.; Freeman, E.; Halsall, R.N.J.; Jenkins, D.W.K.; Loader, I.; Ovsianikov, A.; Parker, A.W.; Stevens, R.; et al. Optically trapped probes with nanometer-scale tips for femto-Newton force measurement. New J. Phys. 2010, 12, 113056:1–113056:15. [Google Scholar] [CrossRef]
- Phillips, D.B.; Simpson, S.H.; Grieve, J.A.; Bowman, R.; Gibson, G.M.; Padgett, M.J.; Rarity, J.G.; Hanna, S.; Miles, M.J.; Carberry, D.M. Force sensing with a shaped dielectric micro-tool. EPL 2012, 99, 58004:1–58004:6. [Google Scholar] [CrossRef]
- Avci, E.; Ohara, K.; Nguyen, C.N.; Theeravithayangkura, C.; Kojima, M.; Tanikawa, T.; Mae, Y.; Arai, T. High-Speed Automated Manipulation of Microobjects Using a Two-Fingered Microhand. IEEE Trans. Ind. Electron. 2015, 62, 1070–1079. [Google Scholar] [CrossRef]
- Mittas, A.; Dickey, F.M.; Holswade, S.C. Modeling an optical micromachine probe. In Proceedings of the Conference: Annual meeting of the Society of Photo-Optical Instrumentation Engineers, San Diego, CA, USA, 27 July–1 August 1997. [Google Scholar]
- Rodrigo, P.J.; Gammelgaard, L.; Bøggild, P.; Perch-Nielsen, I.R.; Glückstad, J. Actuation of microfabricated tools using multiple GPC-based counterpropagating-beam traps. Opt. Express 2005, 13, 6899–6904. [Google Scholar] [CrossRef]
- Probst, M.; Hürzeler, C.; Borer, R.; Nelson, B.J. A Microassembly System for the Flexible Assembly of Hybrid Robotic Mems Devices. Int. J. Optomechatron. 2009, 3, 69–90. [Google Scholar] [CrossRef]
- Gerratt, A.P.; Penskiy, I.; Bergbreiter, S. Integrated silicon-PDMS process for microrobot mechanisms. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3153–3158. [Google Scholar]
- Hull, C.W. Apparatus for Production of Three-Dimensional Objects by Stereolithography. U.S. Patent US4575330A, 17 August 1986. [Google Scholar]
- Galajda, P.; Ormos, P. Complex micromachines produced and driven by light. Appl. Phys. Lett. 2001, 78, 249–251. [Google Scholar] [CrossRef]
- Göppert-Mayer, M. Über Elementarakte mit zwei Quantensprüngen. Ann. Phys. 1931, 401, 273–294. [Google Scholar] [CrossRef]
- La Porta, A.; Offrein, B.J.; Soganci, I.M. Method of Manufacturing a Three Dimensional Photonic Device by Two Photon Absorption Polymerization. U.S. Pantent US13,898,869, 7 April 2015. [Google Scholar]
- Hohmann, J.K.; Renner, M.; Waller, E.H.; von Freymann, G. Three-Dimensional μ-Printing: An Enabling Technology. Adv. Opt. Mater. 2015, 3, 1488–1507. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, W.; Zhang, S.; Feng, D.; Jia, T.; Sun, Z.; Qiu, J. Coherent quantum control of two-photon absorption and polymerization by shaped ultrashort laser pulses. Laser Phys. Lett. 2013, 10, 085304:1–085304:7. [Google Scholar] [CrossRef]
- Kim, J.M.; Muramatsu, H. Two-Photon Photopolymerized Tips for Adhesion-Free Scanning-Probe Microscopy. Nano Lett. 2005, 5, 309–314. [Google Scholar] [CrossRef]
- Kawata, S.; Sun, H.-B.; Tanaka, T.; Takada, K. Finer features for functional microdevices. Nature 2001, 412, 697–698. [Google Scholar] [CrossRef]
- Accardo, A.; Blatché, M.-C.; Courson, R.; Loubinoux, I.; Vieu, C.; Malaquin, L. Two-photon lithography and microscopy of 3D hydrogel scaffolds for neuronal cell growth. Biomed. Phys. Eng. Express 2018, 4, 027009:1–027009:8. [Google Scholar] [CrossRef]
- Inukai, R.; Takao, H.; Shimokawa, F.; Terao, K. On-site manipulation of single DNA molecules using optically-driven microchopsticks. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 585–588. [Google Scholar]
- Avci, E.; Grammatikopoulou, M.; Yang, G.-Z. Laser-Printing and 3D Optical-Control of Untethered Microrobots. Adv. Opt. Mater. 2017, 5, 1700031:1–1700031:6. [Google Scholar] [CrossRef]
- Koss, B.; Chowdhury, S.; Aabo, T.; Gupta, S.K.; Losert, W. Indirect optical gripping with triplet traps. J. Opt. Soc. Am. B 2011, 28, 982–985. [Google Scholar] [CrossRef]
- Nakanishi, S.; Sun, H.-B.; Kawata, S. Elasticity of two-photon-fabricated nano-wires. In Proceedings of the Volume 6645, Nanoengineering: Fabrication, Properties, Optics, and Devices IV, NanoScience + Engineering, San Diego, CA, USA, 11 December 2007; Volume 6645, pp. 14–15. [Google Scholar]
- Sun, H.-B.; Takada, K.; Kawata, S. Elastic force analysis of functional polymer submicron oscillators. Appl. Phys. Lett. 2001, 79, 3173–3175. [Google Scholar] [CrossRef]
- Lemma, E.D.; Rizzi, F.; Dattoma, T.; Spagnolo, B.; Sileo, L.; Qualtieri, A.; De Vittorio, M.; Pisanello, F. Mechanical Properties Tunability of Three-Dimensional Polymeric Structures in Two-Photon Lithography. IEEE Trans. Nanotechnol. 2017, 16, 23–31. [Google Scholar] [CrossRef]
- Raudsepp, A.; Kent, L.M.; Hall, S.B.; Williams, M.A.K. Overstretching partially alkyne functionalized dsDNA using near infrared optical tweezers. Biochem. Biophys. Res. Commun. 2018, 496, 989–995. [Google Scholar] [CrossRef]
- Griffiths, M.R.; Raudsepp, A.; McGrath, K.M.; Williams, M.A.K. Measuring the interaction between a pair of emulsion droplets using dual-trap optical tweezers. RSC Adv. 2016, 6, 14538–14546. [Google Scholar] [CrossRef]
- Crimp, D.P.; Avci, E. Development of a Micromanipulation Platform with Passive-Active Hybrid Release Strategy for Single-Cell Separation. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; pp. 986–990. [Google Scholar]
- Arai, F.; Ando, D.; Fukuda, T.; Nonoda, Y.; Oota, T. Micro manipulation based on micro physics-strategy based on attractive force reduction and stress measurement. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; pp. 236–241. [Google Scholar]
- Bergström, L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 1997, 70, 125–169. [Google Scholar] [CrossRef]
- Badman, R.P.; Ye, F.; Caravan, W.; Wang, M.D. High Trap Stiffness Microcylinders for Nanophotonic Trapping. ACS Appl. Mater. Interfaces 2019, 11, 25074–25080. [Google Scholar] [CrossRef]
- Bunea, A.-I.; Engay, E.L.; Chouliara, M.; Bañas, A.R.; Glückstad, J. Rational design of light-controlled microrobots. In Proceedings of the Volume 10804, Advanced Manufacturing Technologies for Micro- and Nanosystems in Security and Defence, Berlin, Germany, 8 October 2018. [Google Scholar]
- Glückstad, J. Sculpting the object. Nat. Photonics 2011, 5, 7–8. [Google Scholar] [CrossRef]
- Phillips, D.B.; Gibson, G.M.; Bowman, R.; Padgett, M.J.; Hanna, S.; Carberry, D.M.; Miles, M.J.; Simpson, S.H. An optically actuated surface scanning probe. Opt. Express 2012, 20, 29679–29693. [Google Scholar] [CrossRef]
- Wang, W.; Chiou, A.E.; Sonek, G.J.; Berns, M.W. Self-aligned dual-beam optical laser trap using photorefractive phase conjugation. J. Opt. Soc. Am. B 1997, 14, 697–704. [Google Scholar] [CrossRef]
- Woerdemann, M.; Berghoff, K.; Denz, C. Dynamic multiple-beam counter-propagating optical traps using optical phase-conjugation. Opt. Express 2010, 18, 22348–22357. [Google Scholar] [CrossRef] [PubMed]
- Villangca, M.J.; Palima, D.; Bañas, A.R.; Glückstad, J. Light-driven micro-tool equipped with a syringe function. Light Sci. Appl. 2016, 5, e16148:1–e16148:7. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhao, Q.; Du, X. Light-Powered Micro/Nanomotors. Micromachines 2018, 9, 41:1–41:19. [Google Scholar] [CrossRef] [PubMed]
- Ukita, H.; Nagatomi, K. Optical tweezers and fluid characteristics of an optical rotator with slopes on the surface upon which light is incident and a cylindrical body. Appl. Opt. 2003, 42, 2708–2715. [Google Scholar] [CrossRef]
- Maruo, S.; Inoue, H. Optically driven micropump produced by three-dimensional two-photon microfabrication. Appl. Phys. Lett. 2006, 89, 144101. [Google Scholar] [CrossRef]
- Asavei, T.; Nieminen, T.A.; Loke, V.L.Y.; Stilgoe, A.B.; Bowman, R.; Preece, D.; Padgett, M.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Optically trapped and driven paddle-wheel. New J. Phys. 2013, 15, 063016:1–063016:17. [Google Scholar] [CrossRef]
- Kashchuk, A.V.; Bui, A.A.M.; Zhang, S.; Houillot, A.; Carberry, D.; Stilgoe, A.B.; Nieminen, T.A. Rubinsztein-Dunlop, Halina Chapter 4–Optically driven rotating micromachines. In Light Robotics: Structure-Mediated Nanobiophotonics; Glückstad, J., Palima, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 99–128. [Google Scholar]
- Lin, C.-L.; Vitrant, G.; Bouriau, M.; Casalegno, R.; Baldeck, P.L. Optically driven Archimedes micro-screws for micropump application. Opt. Express 2011, 19, 8267–8276. [Google Scholar] [CrossRef]
- Galajda, P.; Ormos, P. Rotors produced and driven in laser tweezers with reversed direction of rotation. Appl. Phys. Lett. 2002, 80, 4653–4655. [Google Scholar] [CrossRef]
- La Porta, A.; Wang, M.D. Optical Torque Wrench: Angular Trapping, Rotation, and Torque Detection of Quartz Microparticles. Phys. Rev. Lett. 2004, 92, 190801. [Google Scholar] [CrossRef]
- Inman, J.; Forth, S.; Wang, M.D. Passive torque wrench and angular position detection using a single-beam optical trap. Opt. Lett. 2010, 35, 2949–2951. [Google Scholar] [CrossRef] [PubMed]
- Chapin, S.C.; Germain, V.; Dufresne, E.R. Automated trapping, assembly, and sorting with holographic optical tweezers. Opt. Express 2006, 14, 13095–13100. [Google Scholar] [CrossRef]
- Tanaka, Y.; Kawada, H.; Hirano, K.; Ishikawa, M.; Kitajima, H. Automated manipulation of non-spherical micro-objects using optical tweezers combined with image processing techniques. Opt. Express 2008, 16, 15115–15122. [Google Scholar] [CrossRef] [PubMed]
- Maruo, S.; Takaura, A.; Saito, Y. Optically driven micropump with a twin spiral microrotor. Opt. Express 2009, 17, 18525–18532. [Google Scholar] [CrossRef] [PubMed]
- Higurashi, E.; Ohguchi, O.; Ukita, H. Optical trapping of low-refractive-index microfabricated objects using radiation pressure exerted on their inner walls. Opt. Lett. 1995, 20, 1931–1933. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, R.C. Trapping model for the low-index ring-shaped micro-object in a focused, lowest-order Gaussian laser-beam profile. J. Opt. Soc. Am. B 1997, 14, 782–789. [Google Scholar] [CrossRef]
- Grier, D.G.; Roichman, Y. Holographic optical trapping. Appl. Opt. 2006, 45, 880–887. [Google Scholar] [CrossRef]
- Brouhard, G.J.; Schek, H.T.; Hunt, A.J. Advanced optical tweezers for the study of cellular and molecular biomechanics. IEEE Trans. Biomed. Eng. 2003, 50, 121–125. [Google Scholar] [CrossRef]
- van der Horst, A.; Forde, N.R. Calibration of Holographic Optical Tweezers for Force Measurements on Biomaterials. Biophys. J. 2009, 96, 20987–21003. [Google Scholar] [CrossRef][Green Version]
- Gerchberg, R.W.; Saxton, W.O. Practical Algorithm for Determination of Phase From Image and Diffraction Plane Pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Di Leonardo, R.; Ianni, F.; Ruocco, G. Computer generation of optimal holograms for optical trap arrays. Opt. Express 2007, 15, 1913–1922. [Google Scholar] [CrossRef] [PubMed]
- Pleguezuelos, E.; Carnicer, A.; Andilla, J.; Martin-Badosa, E.; Montes-Usategui, M. HoloTrap: Interactive hologram design for multiple dynamic optical trapping. Comput. Phys. Commun. 2007, 176, 701–709. [Google Scholar] [CrossRef]
- Pozzi, P.; Maddalena, L.; Ceffa, N.; Soloviev, O.; Vdovin, G.; Carroll, E.; Verhaegen, M. Fast Calculation of Computer Generated Holograms for 3D Photostimulation through Compressive-Sensing Gerchberg-Saxton Algorithm. Methods Protoc. 2018, 2, 2:1–2:11. [Google Scholar] [CrossRef]
- Bowman, R.W.; Gibson, G.M.; Linnenberger, A.; Phillips, D.B.; Grieve, J.A.; Carberry, D.M.; Serati, S.; Miles, M.J.; Padgett, M.J. “Red Tweezers”: Fast, customisable hologram generation for optical tweezers. Comput. Phys. Commun. 2014, 185, 268–273. [Google Scholar] [CrossRef]
- Mack, A.H.; Trias, M.K.; Mochrie, S.G.J. Precision optical trapping via a programmable direct-digital-synthesis-based controller for acousto-optic deflectors. Rev. Sci. Instrum. 2009, 80, 016101:1–016101:3. [Google Scholar] [CrossRef] [PubMed]
- Valentine, M.T.; Guydosh, N.R.; Gutiérrez-Medina, B.; Fehr, A.N.; Andreasson, J.O.; Block, S.M. Precision steering of an optical trap by electro-optic deflection. Opt. Lett. 2008, 33, 599–601. [Google Scholar] [CrossRef] [PubMed]
- Antonov, S.N. Acousto-Optic Deflector with a High Diffraction Efficiency and Wide Angular Scanning Range. Acoust. Phys. 2018, 64, 432–436. [Google Scholar] [CrossRef]
- Antonov, S.N. Paratellurite-Based Acoustooptical Deflectors. Methods for Increasing their Efficiency and Widening the Scanning Angle. Instrum. Exp. Tech. 2019, 62, 386–392. [Google Scholar] [CrossRef]
- Constable, A.; Kim, J.; Mervis, J.; Zarinetchi, F.; Prentiss, M. Demonstration of a fiber-optical light-force trap. Opt. Lett. 1993, 18, 1867–1869. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, N.; Shi, Y.; Xin, H.; Li, B. Optical Fiber Tweezers: A Versatile Tool for Optical Trapping and Manipulation. Micromachines 2020, 11, 114. [Google Scholar] [CrossRef]
- Oh, M.-J.; Kuhr, F.; Byfield, F.; Levitan, I. Micropipette aspiration of substrate-attached cells to estimate cell stiffness. J. Vis. Exp. 2012, 67, e3886. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. Double-arm optical tweezer system for precise and dexterous handling of micro-objects in 3D workspace. Opt. Lasers Eng. 2018, 111, 65–70. [Google Scholar] [CrossRef]
- Bianchi, S.; Di Leonardo, R. Real-time optical micro-manipulation using optimized holograms generated on the GPU. Comput. Phys. Commun. 2010, 181, 1444–1448. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrew, P.-K.; Williams, M.A.K.; Avci, E. Optical Micromachines for Biological Studies. Micromachines 2020, 11, 192. https://doi.org/10.3390/mi11020192
Andrew P-K, Williams MAK, Avci E. Optical Micromachines for Biological Studies. Micromachines. 2020; 11(2):192. https://doi.org/10.3390/mi11020192
Chicago/Turabian StyleAndrew, Philippa-Kate, Martin A. K. Williams, and Ebubekir Avci. 2020. "Optical Micromachines for Biological Studies" Micromachines 11, no. 2: 192. https://doi.org/10.3390/mi11020192
APA StyleAndrew, P.-K., Williams, M. A. K., & Avci, E. (2020). Optical Micromachines for Biological Studies. Micromachines, 11(2), 192. https://doi.org/10.3390/mi11020192






