Design and Implementation of a GaN-Based Three-Phase Active Power Filter
Abstract
1. Introduction
2. Gallium Nitride (GaN) High Electron-Mobility Transistor (HEMT) and Its Driving Requirements
3. Mathematical Modeling and Control Algorithms of GaN-Based Active Power Filter (APF)
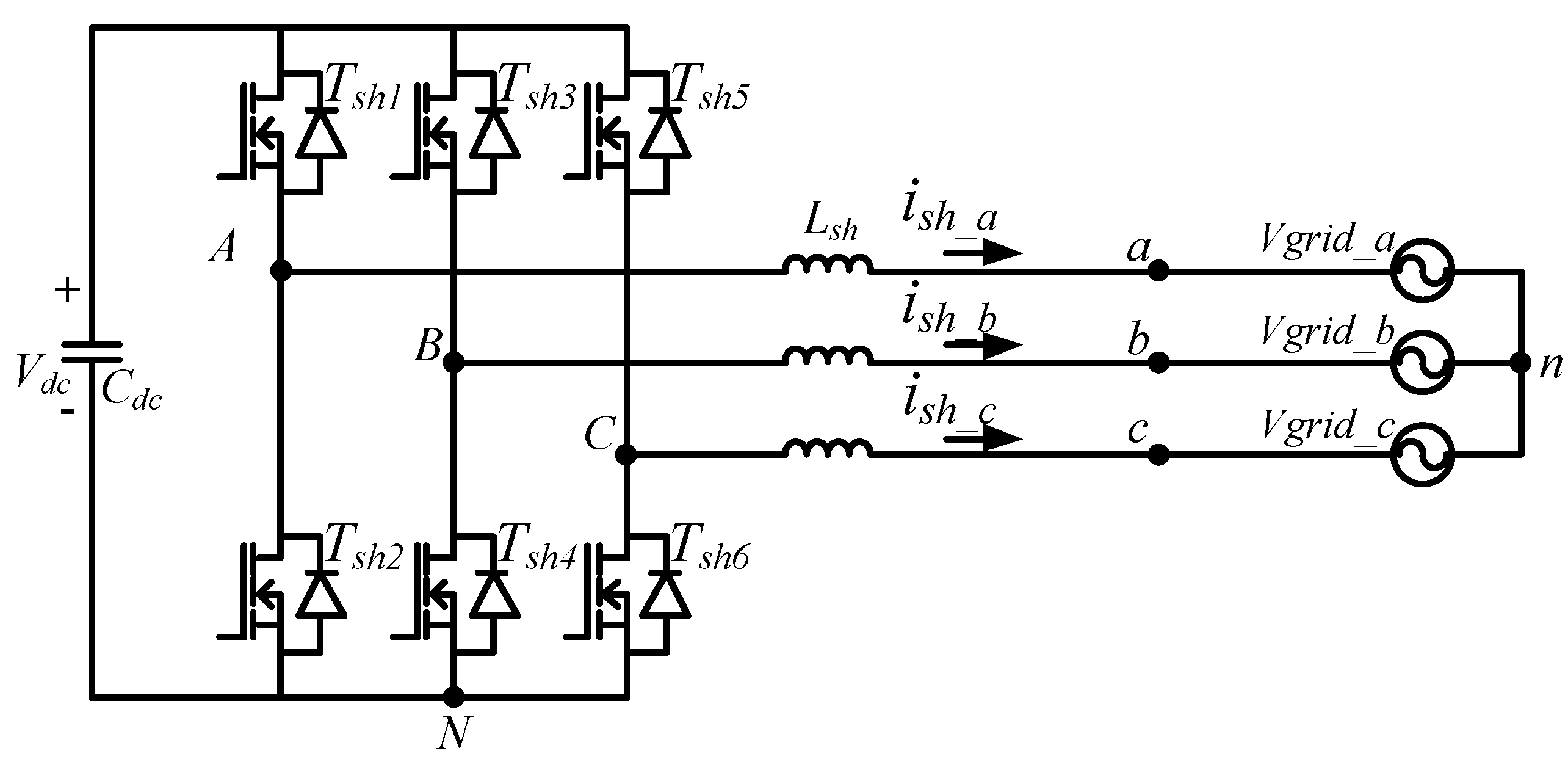
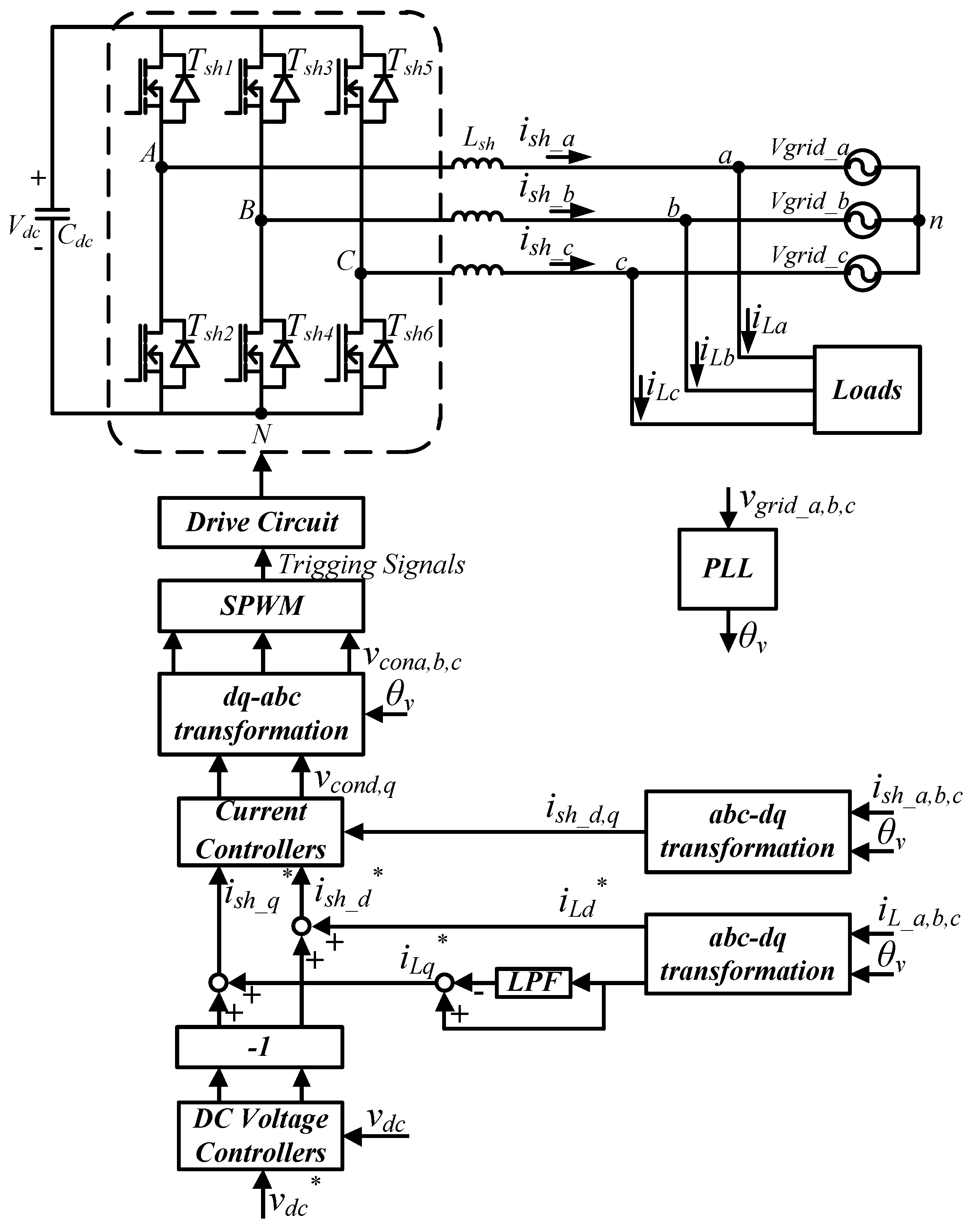
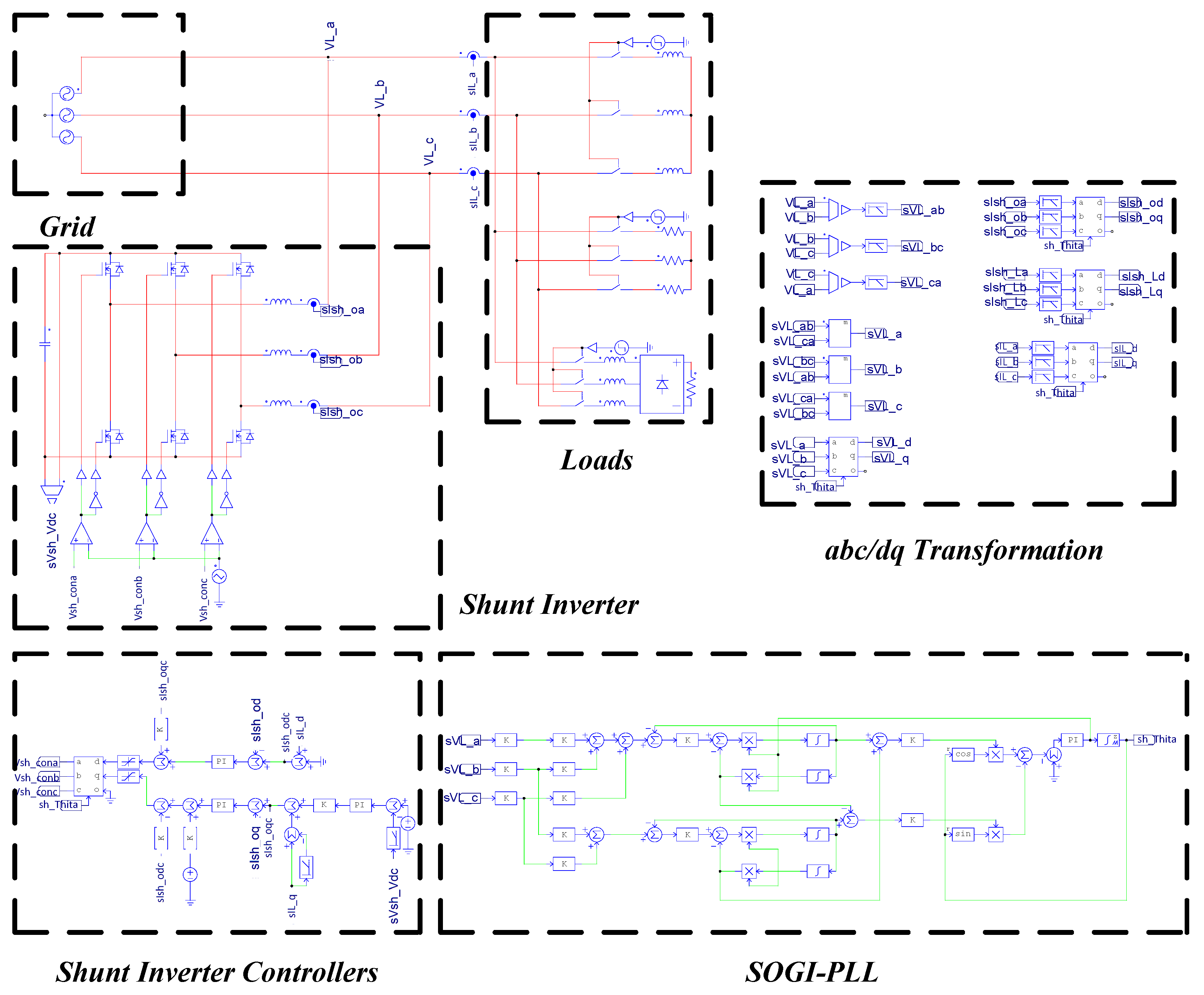
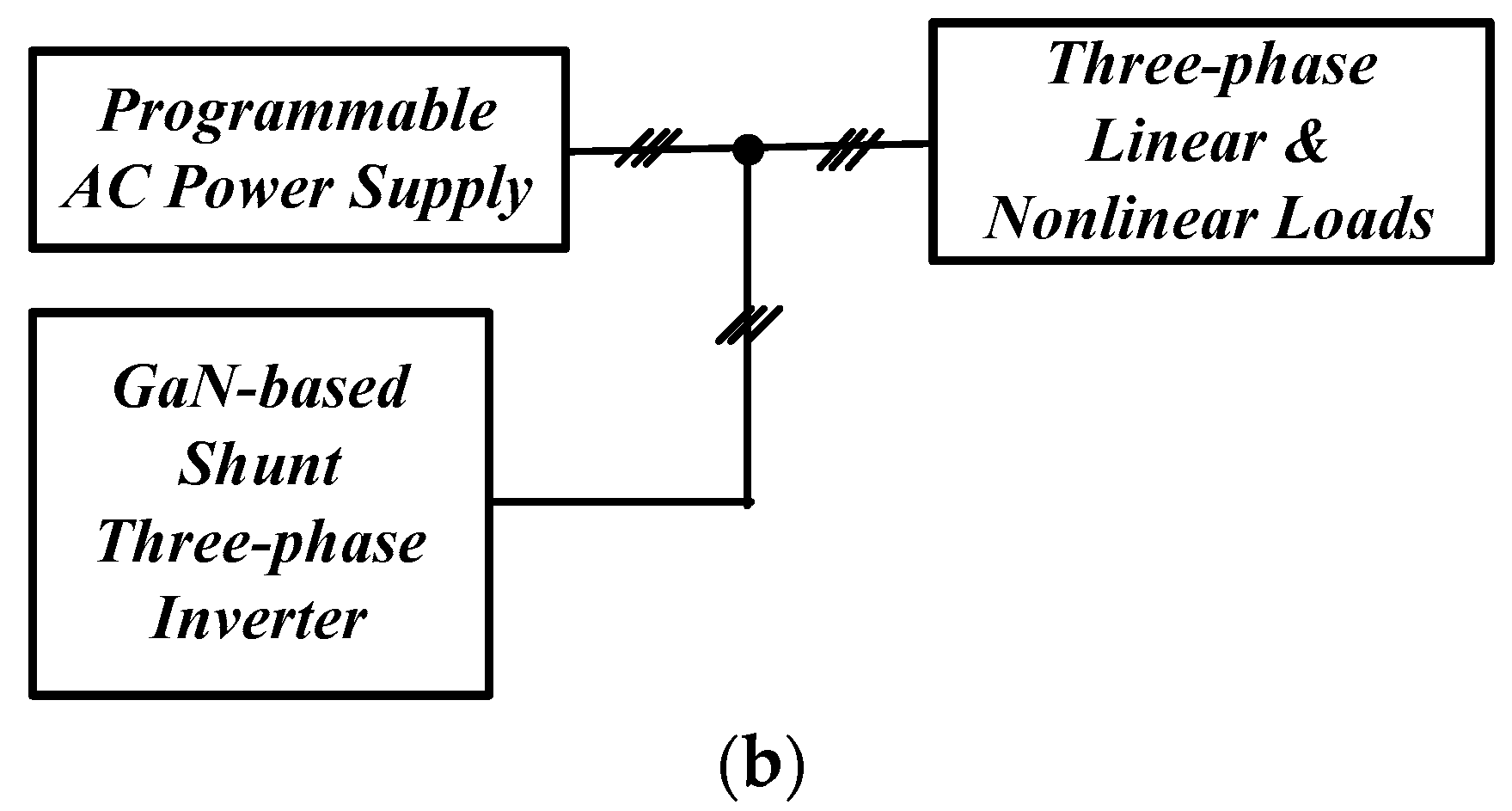
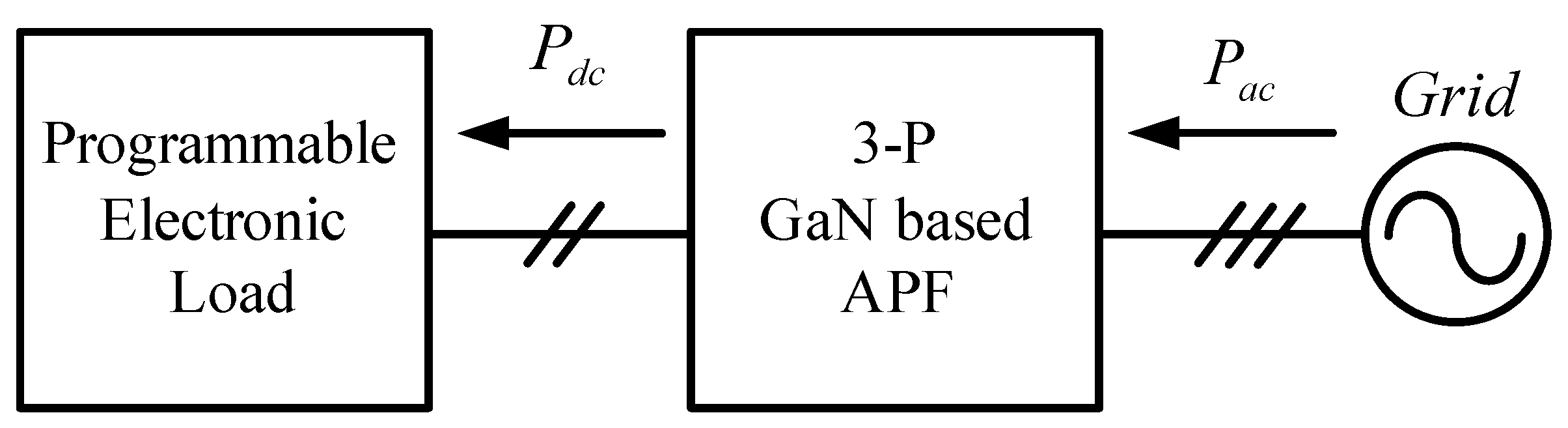
3.1. GaN-Based Three-Phase Active Power Filter
3.2. Design of Direct Current (DC) Capacitor and Filter Inductors
3.3. Mathematical Modeling and Controller’s Design for GaN-Based Shunt APF
3.3.1. Mathematical Modeling
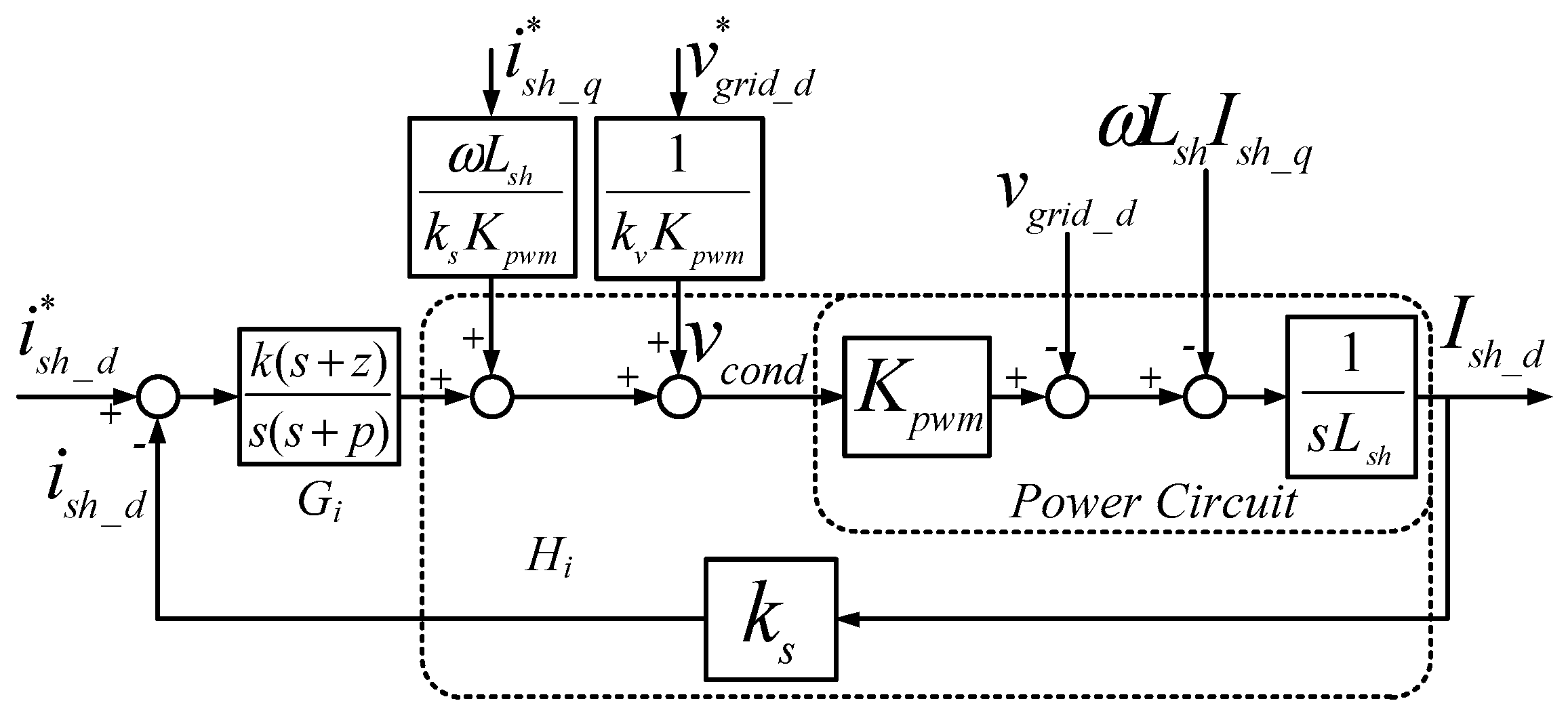
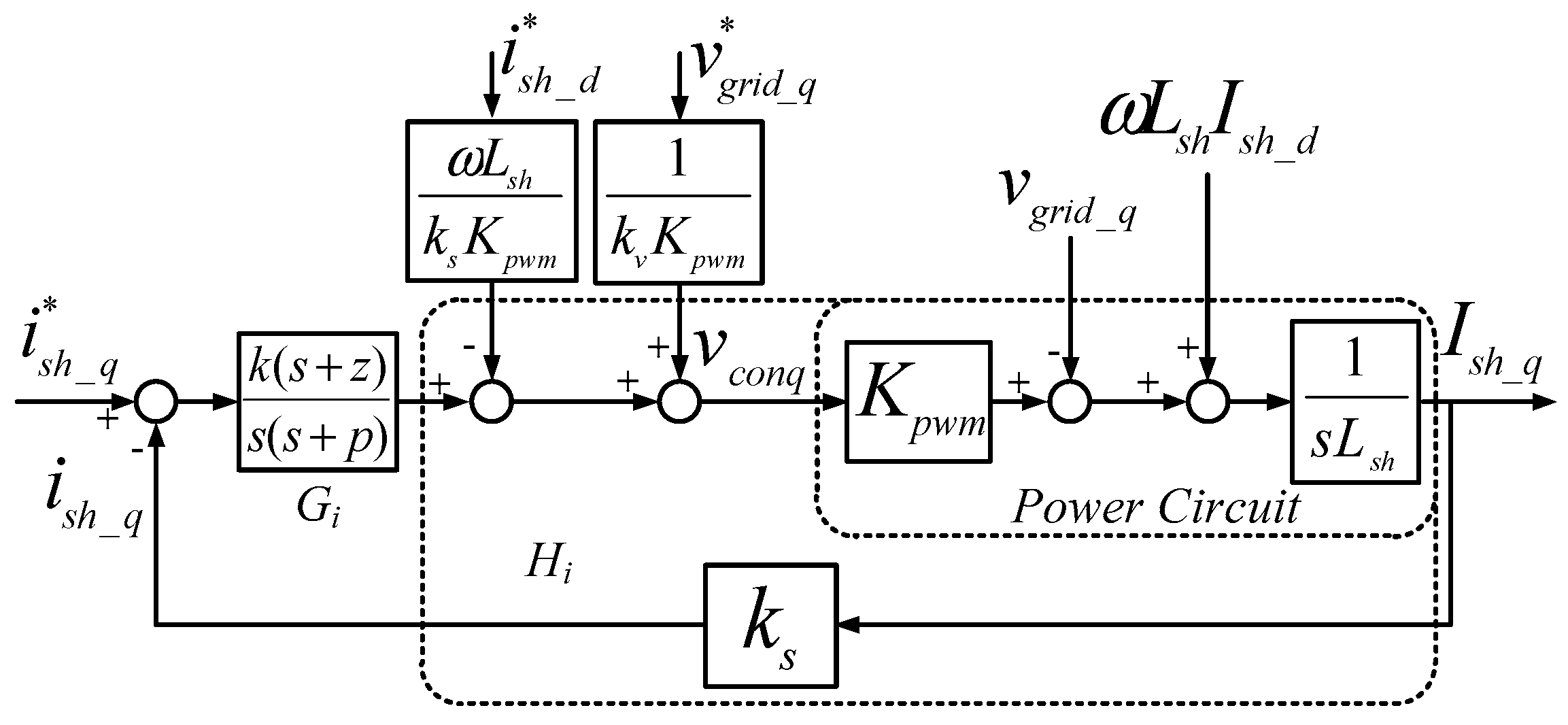
3.3.2. Design of Current Controllers
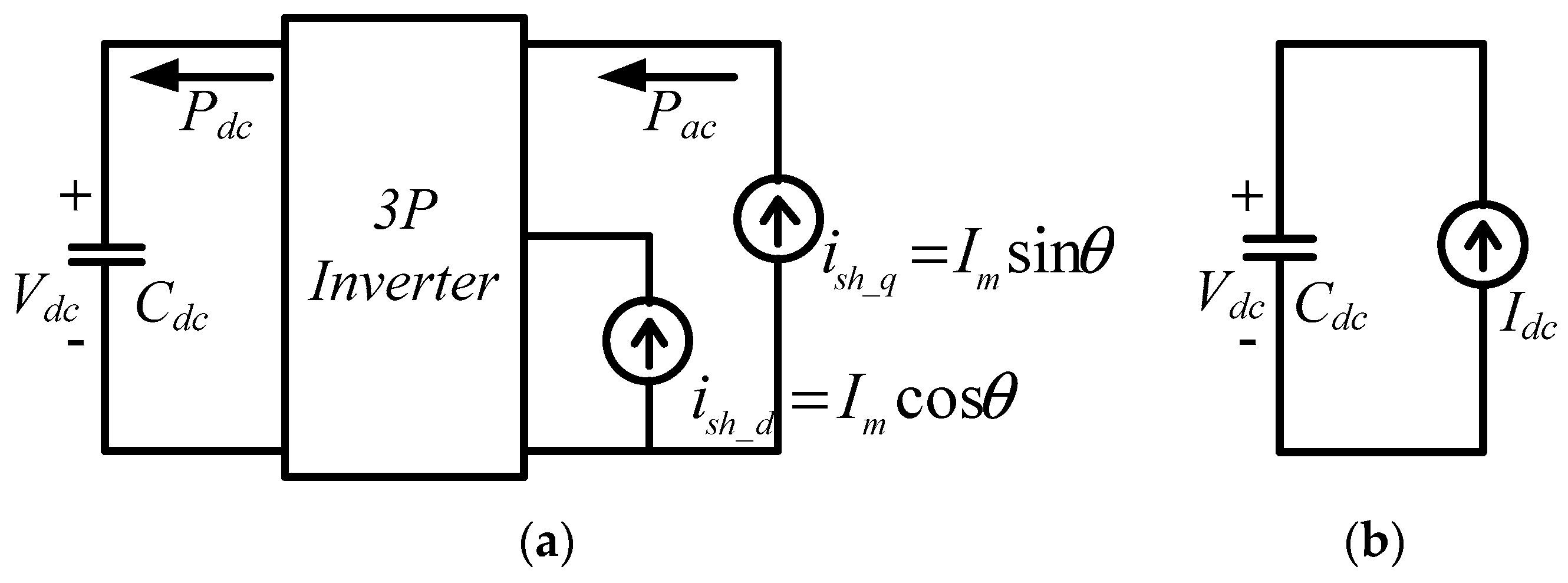
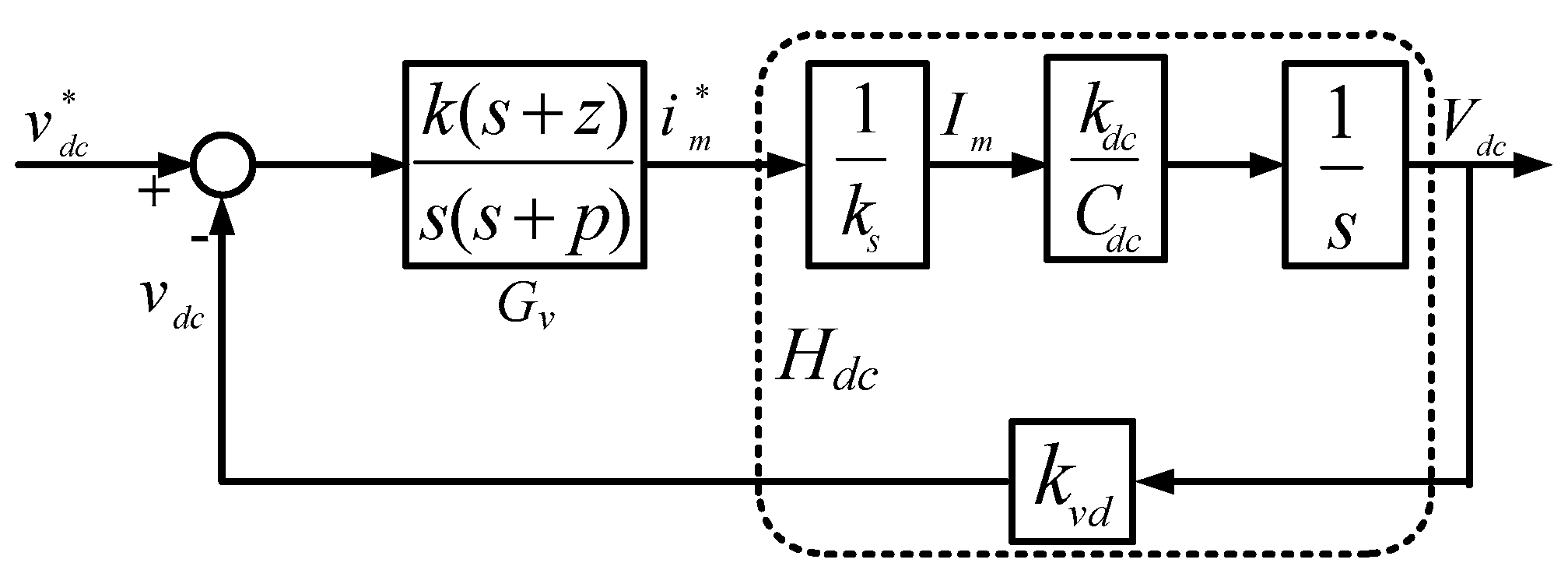
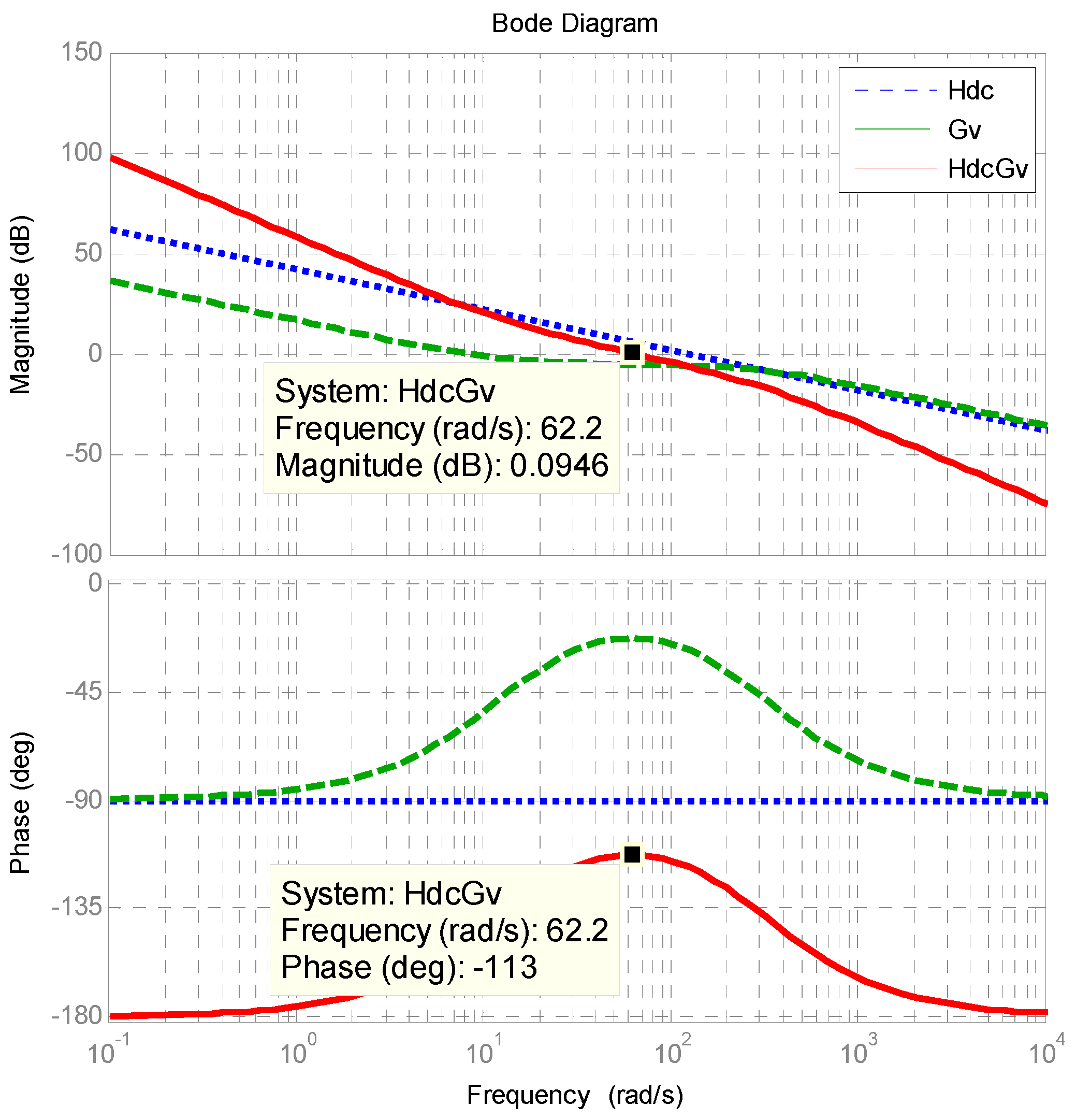
3.3.3. Design of DC Link Voltage Controller
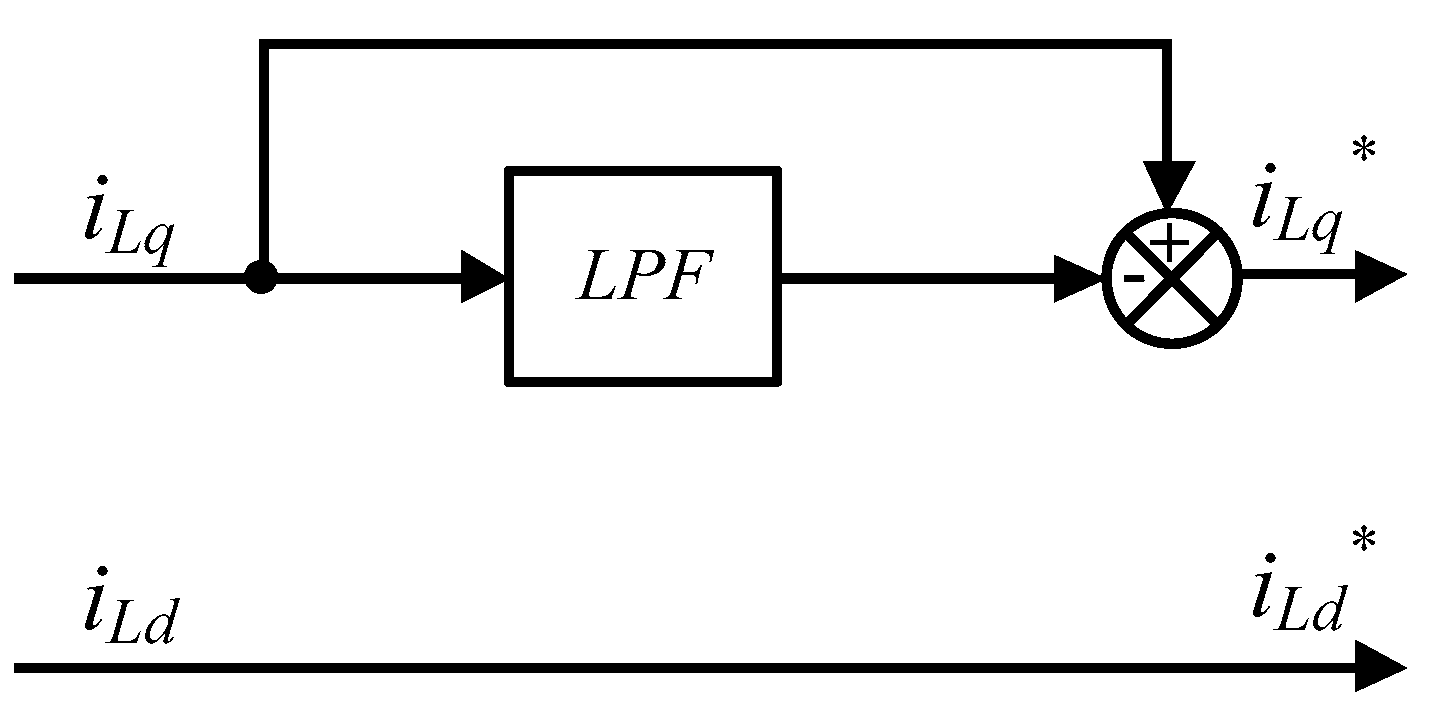
3.3.4. Load Current Compensation Signals of APF
3.4. Complete System of GaN-Based Shunt APF
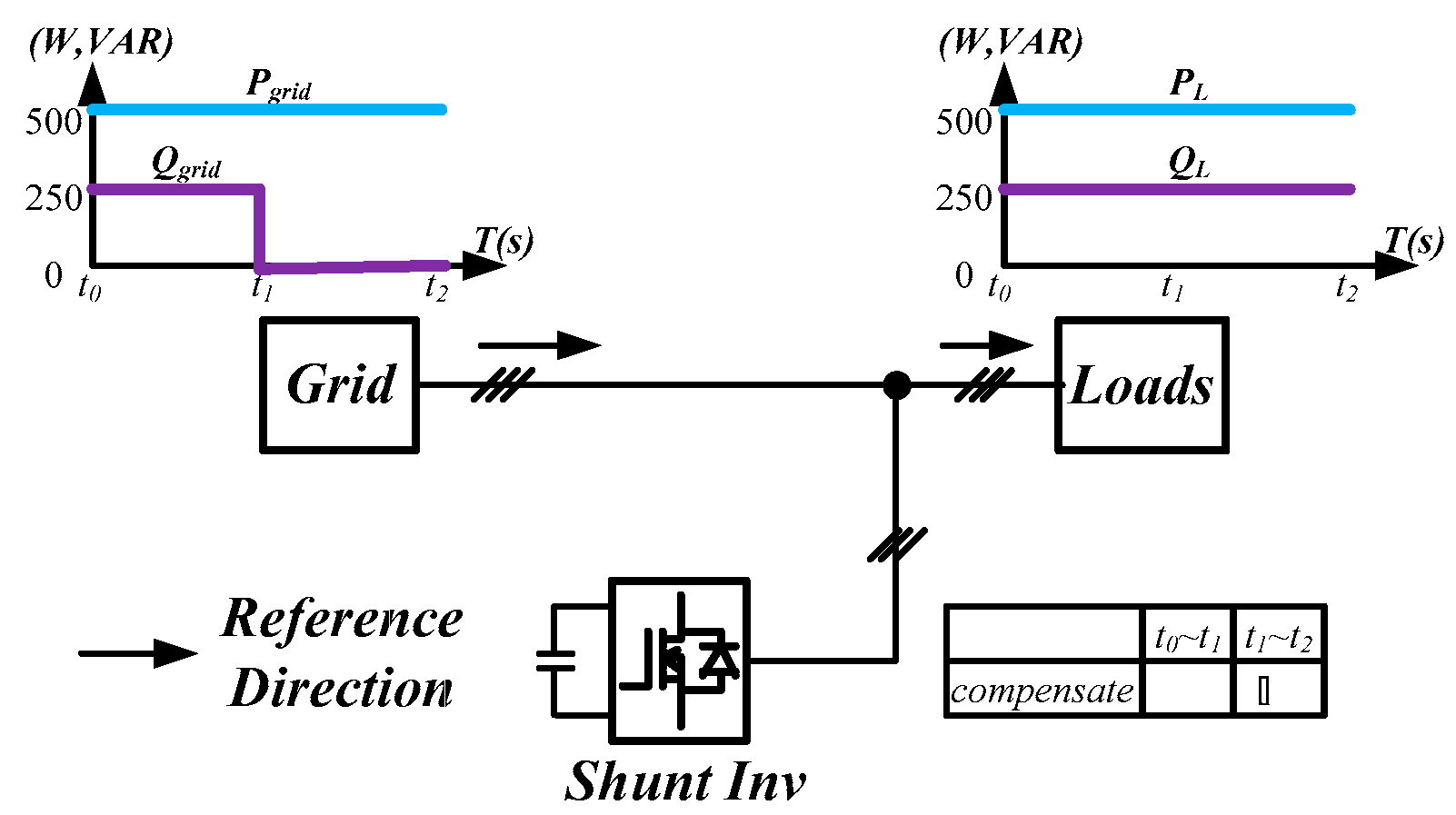
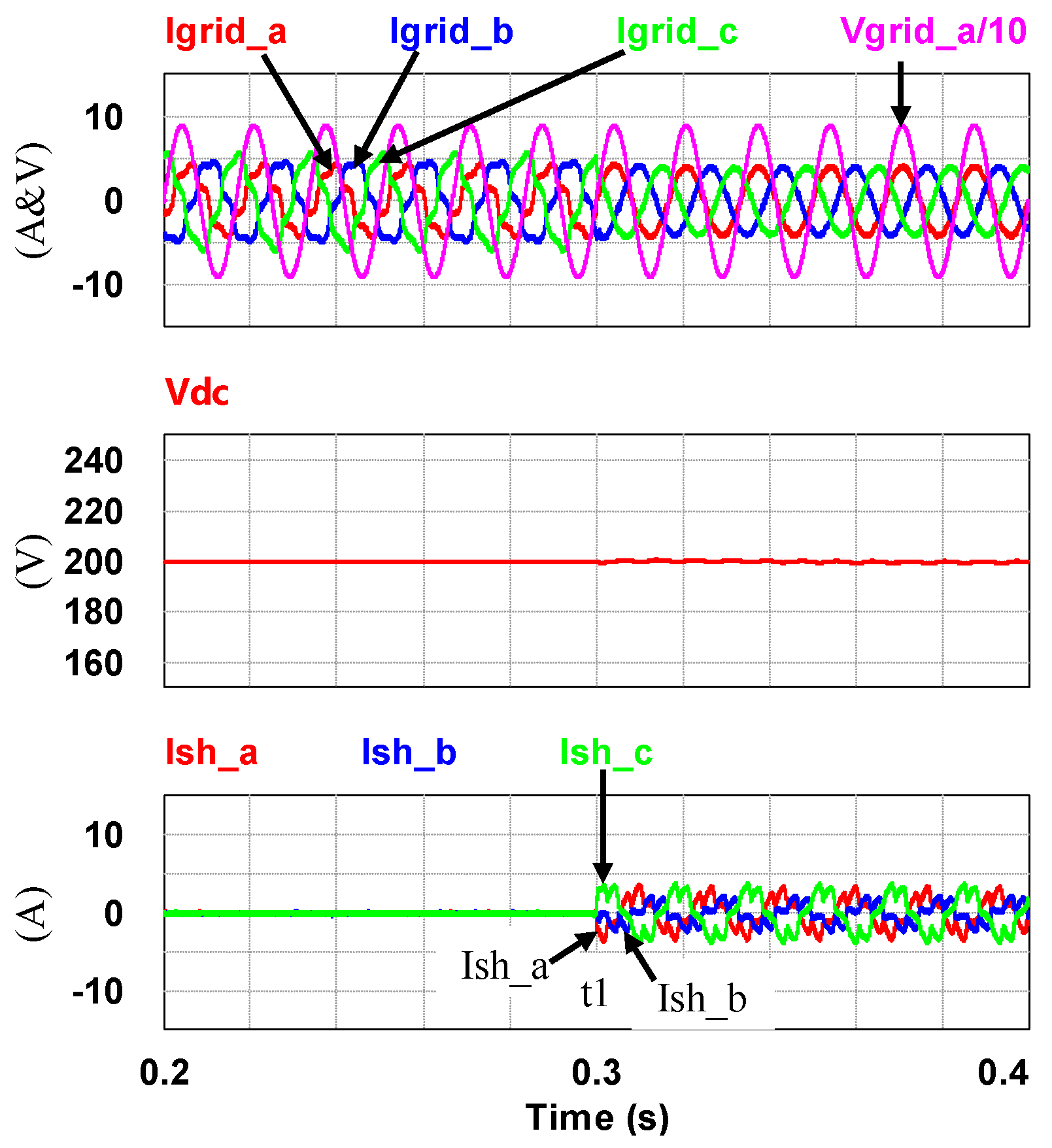
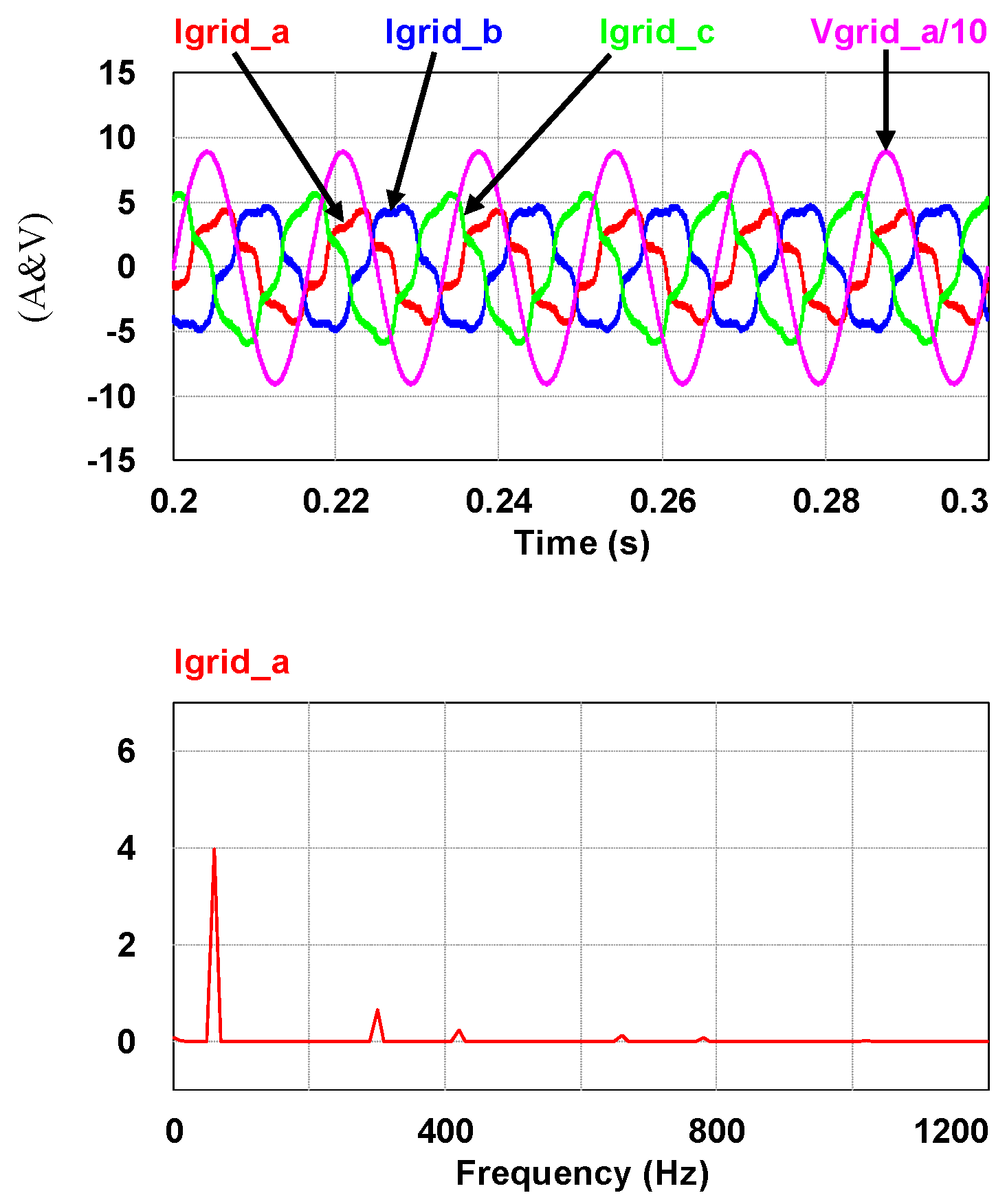
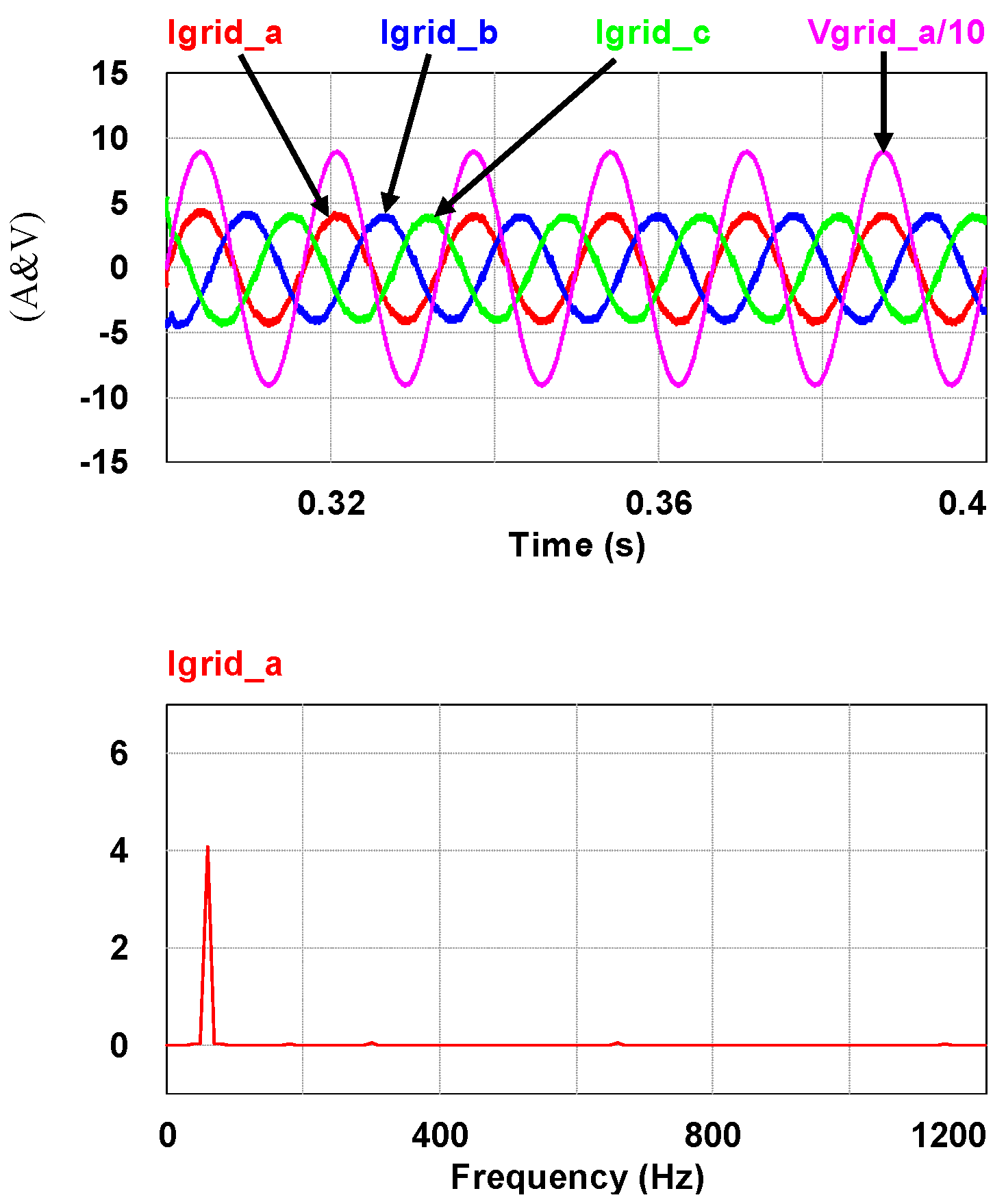
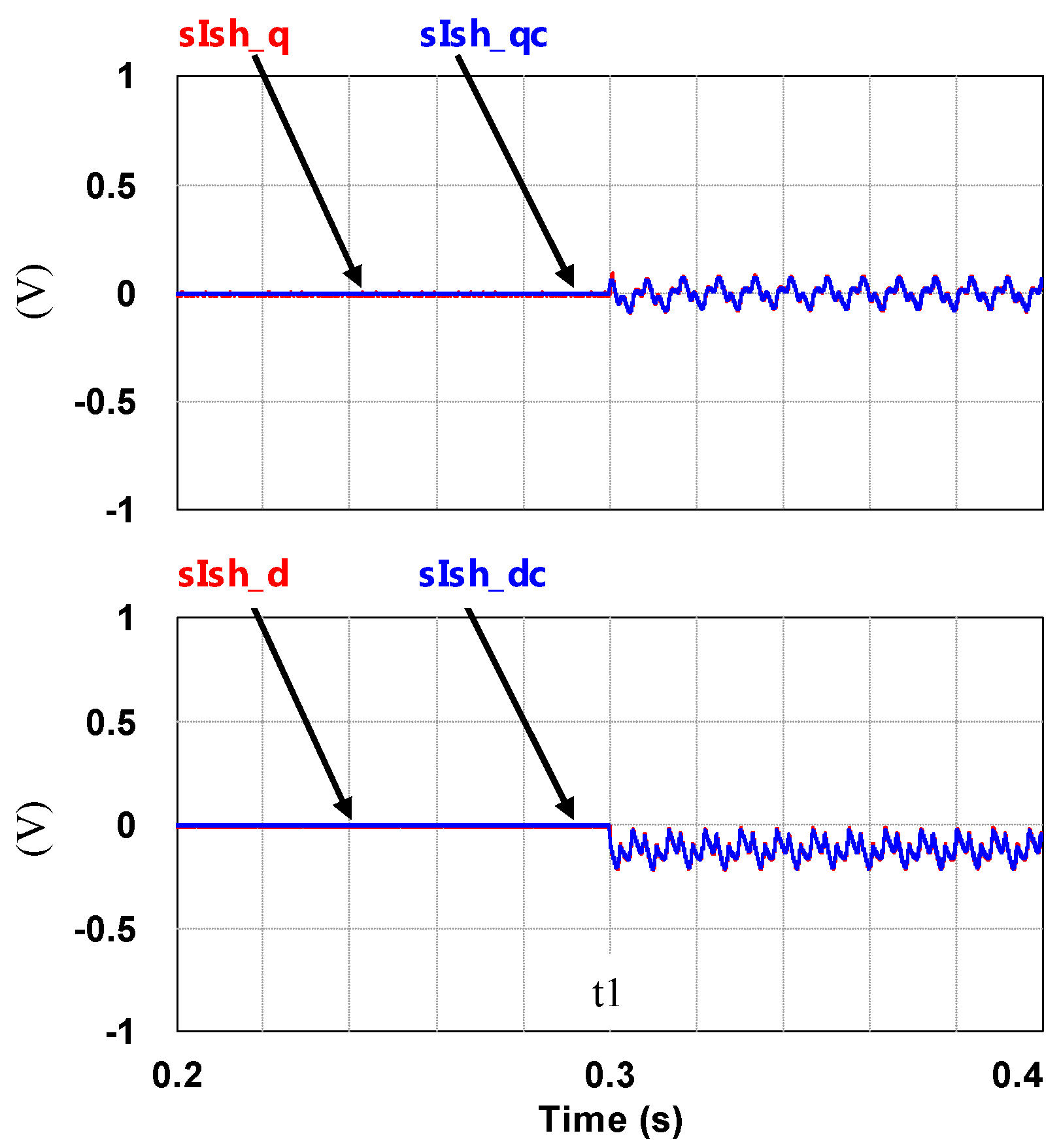
4. Simulation Study and Results
4.1. Simulation Scenario
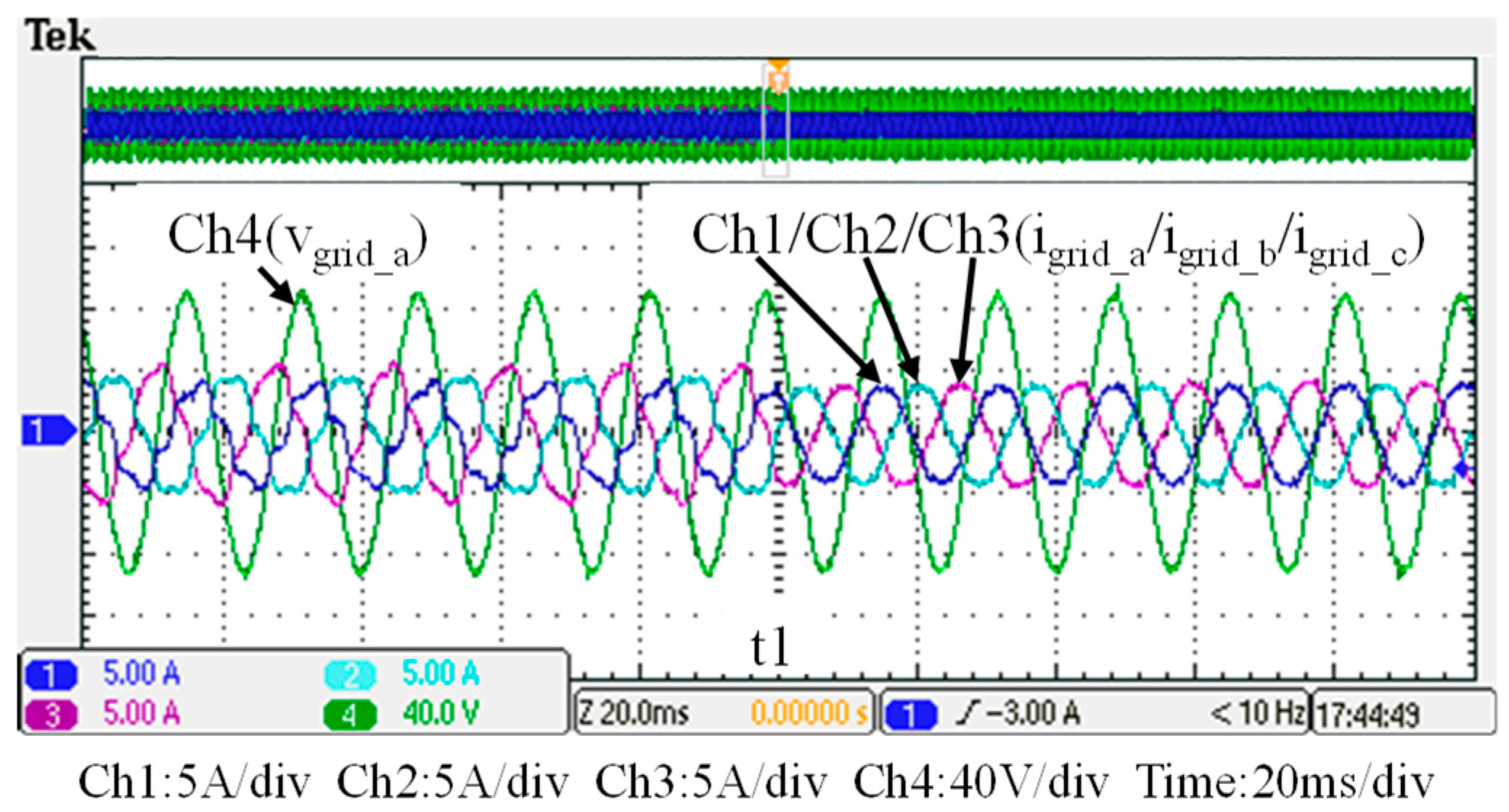
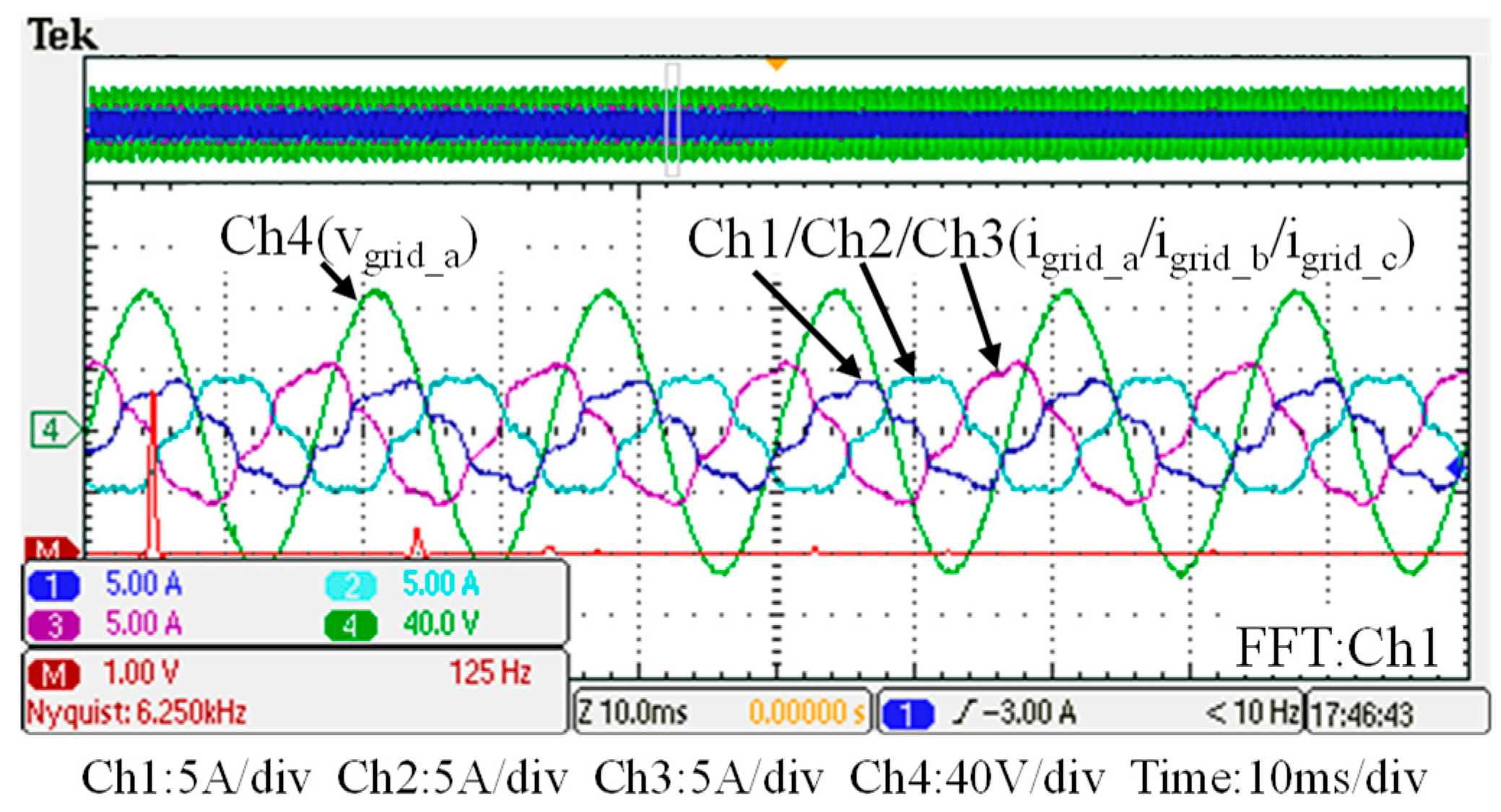
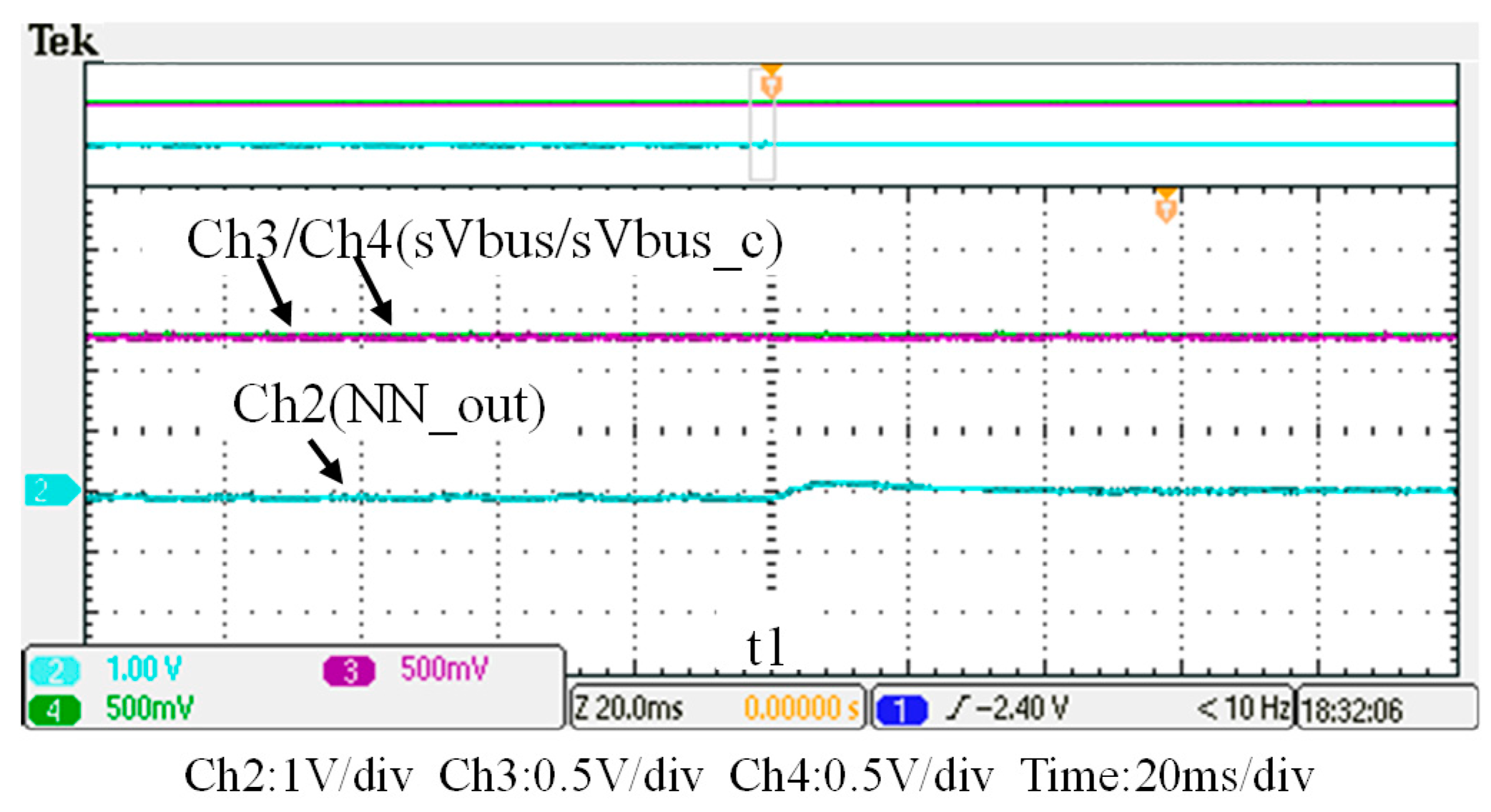
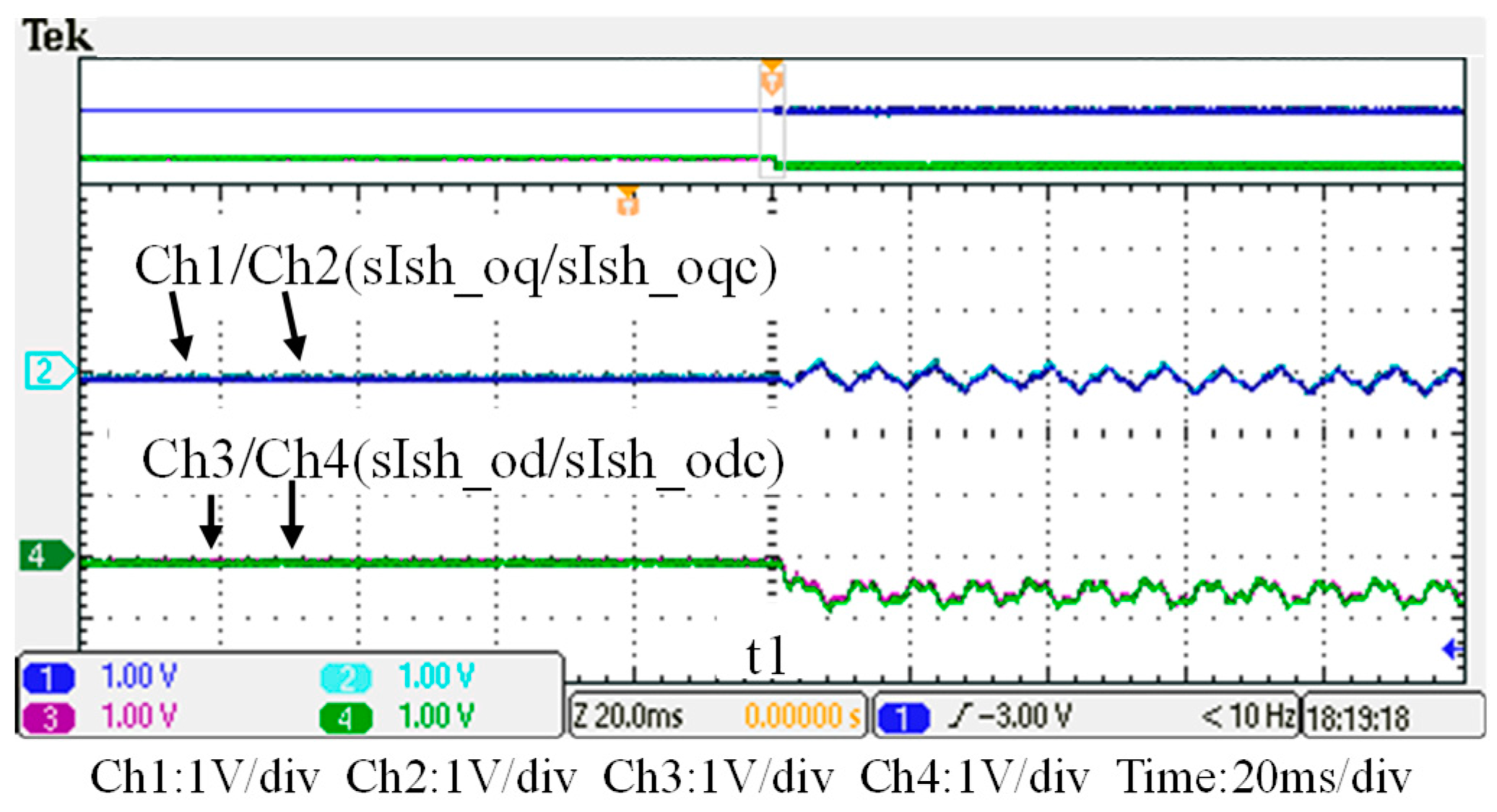
5. Hardware Implementation and Test Results
6. Discussion
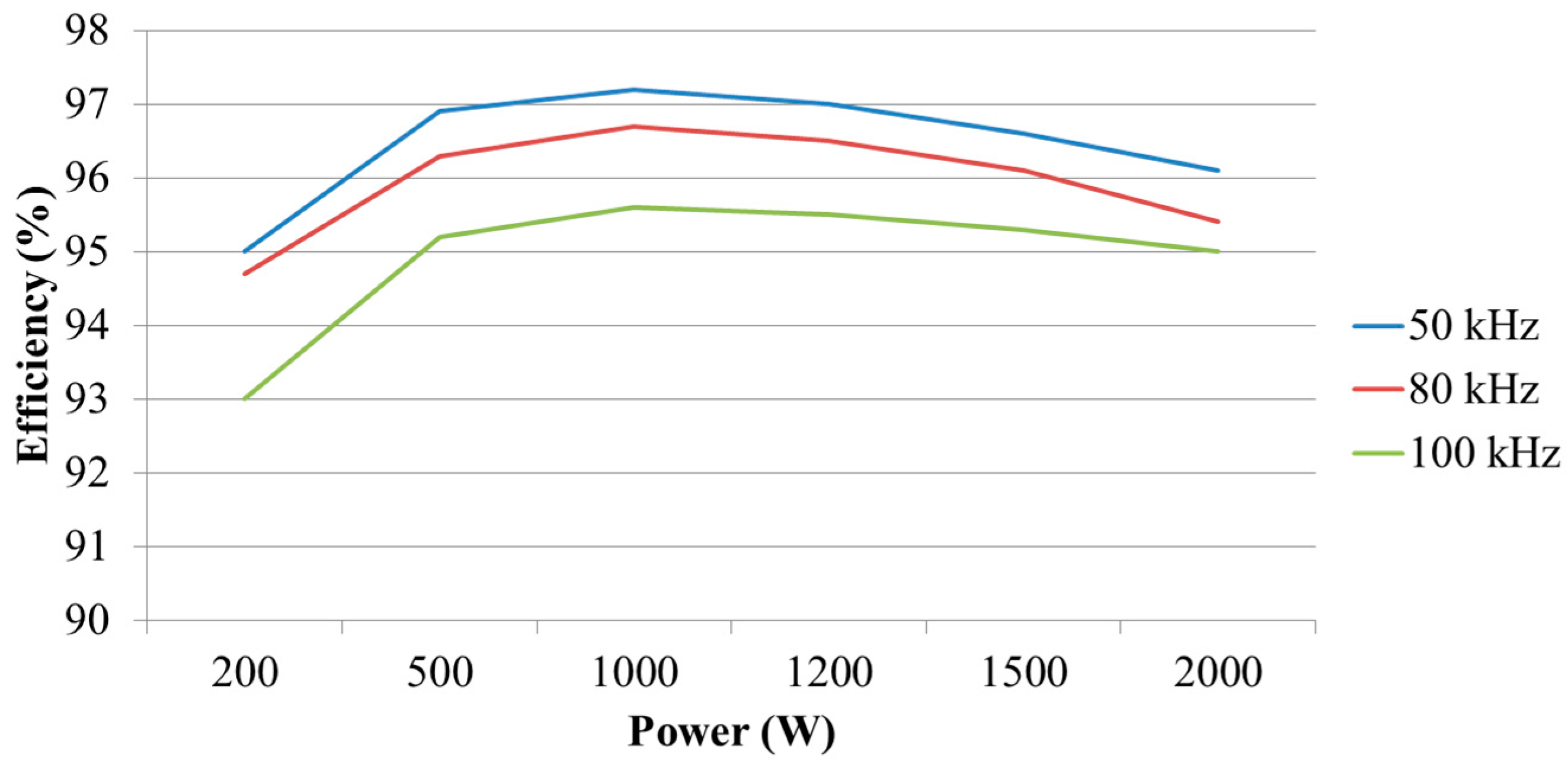
6.1. The Analysis of System Efficiency
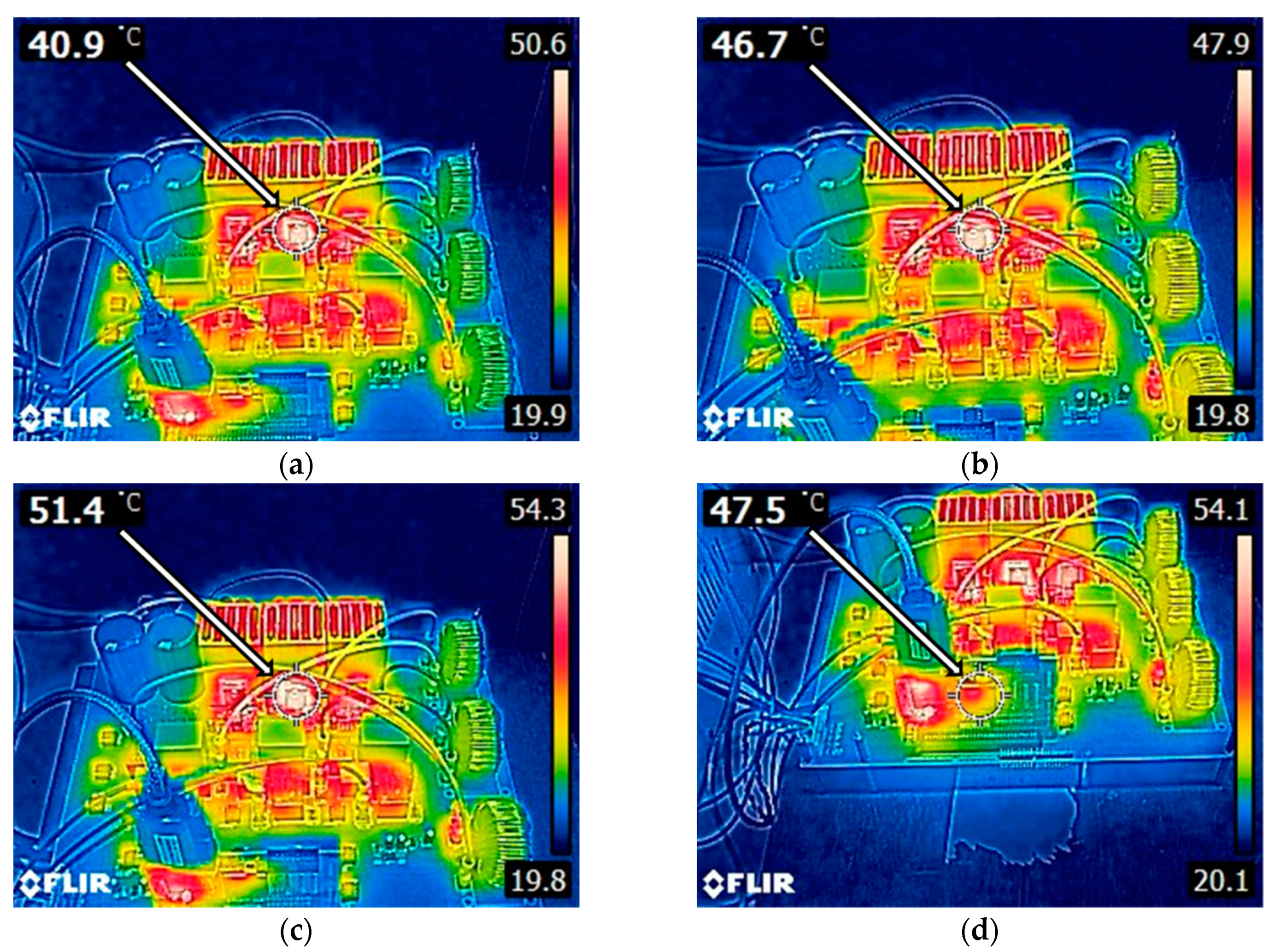
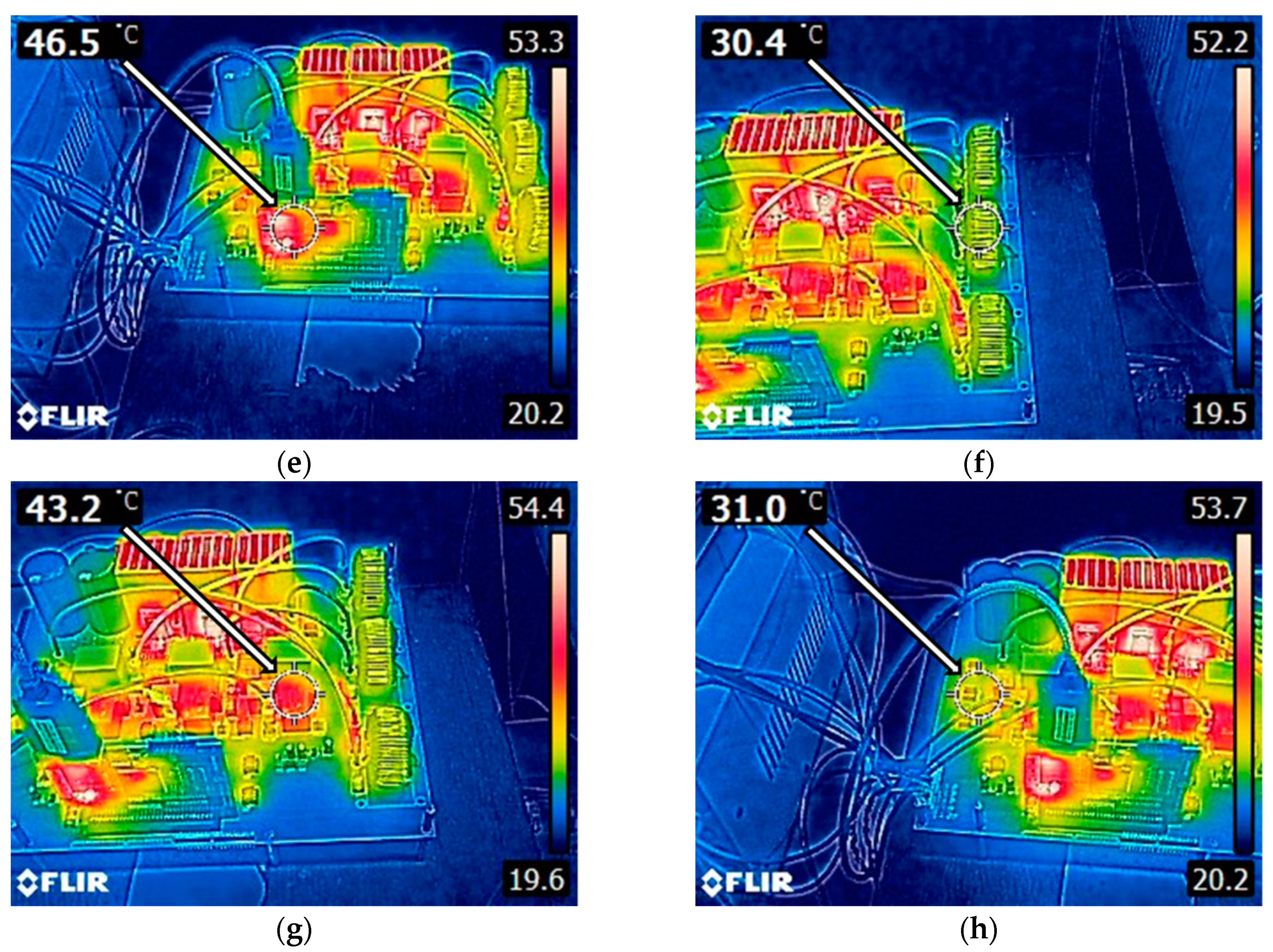
6.2. The Thermographic Analysis of the System
6.3. Related Technical Issues
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gayatri, M.T.L.; Parimi, A.M.; Pavan Kumar, A.V. A review of reactive power compensation techniques in microgrids. Renew. Sustain. Energy Rev. 2018, 81, 1030–1036. [Google Scholar] [CrossRef]
- Naderi, Y.; Hosseini, S.H.; Zadeh, S.G.; Mohammadi-Ivatloo, B.; Vasquez, J.C.; Guerrero, J.M. An overview of power quality enhancement techniques applied to distributed generation in electrical distribution networks. Renew Sustain. Energy Rev. 2018, 93, 201–214. [Google Scholar] [CrossRef]
- Kumar, R.; Bansal, H.O. Shunt active power filter: Current status of control techniques and its integration to renewable energy sources. Sustain. Cities Soc. 2018, 42, 574–592. [Google Scholar] [CrossRef]
- Baimel, D. Implementation of DQ0 control methods in high power electronics devices for renewable energy sources, energy storage and FACTS. Sustain. Energy Grids 2019, 18, 100218. [Google Scholar] [CrossRef]
- Swain, S.; Subudhi, B. Grid integration scheme for a three phase single stage photovoltaic system employing EKF. IFAC-PapersOnLine 2018, 51, 279–282. [Google Scholar] [CrossRef]
- Chauhan, S.; Singh, B. Grid-interfaced solar PV powered electric vehicle battery system with novel adaptive digital control algorithm. IET Power Electron. 2019, 12, 3470–3478. [Google Scholar] [CrossRef]
- Zhai, H.; Zhuo, F.; Zhu, C.; Yi, H.; Wang, Z.; Tao, R.; Wei, T. An optimal compensation method of shunt active power filters for system-wide voltage quality improvement. IEEE Trans. Ind. Electron. 2020, 67, 1270–1281. [Google Scholar] [CrossRef]
- Badoni, M.; Singh, A.; Singh, V.P.; Tripathi, R.N. Grid interfaced solar photovoltaic system using ZA-LMS based control algorithm. Electr Power Syst. Res. 2018, 160, 261–272. [Google Scholar] [CrossRef]
- Prasad, V.; Jayasree, P.R.; Sruthy, V. Active power sharing and reactive power compensation in a grid-tied photovoltaic system. Mater. Today: Proc. 2018, 5, 1537–1544. [Google Scholar] [CrossRef]
- Viswan, V. A review of silicon carbide and gallium nitride power semiconductor devices. IJRESM 2018, 1, 224–225. [Google Scholar]
- Jones, E.A.; Wang, F.; Costinett, D. Review of commercial GaN power devices and GaN-based converter design challenges. IEEE J. Emerg. Sel. Topics Power Electron. 2016, 4, 707–719. [Google Scholar] [CrossRef]
- Spaziani, L.; Lu, L. Silicon, GaN and SiC: There’s room for all: An application space overview of device considerations. In Proceedings of the 2018 IEEE 30th International Symposium on Power Semiconductor Devices and ICs (ISPSD), Chicago, IL, USA, 13–17 May 2018; pp. 8–11. [Google Scholar]
- Ma, C.T.; Gu, Z.H. Review of GaN HEMT Applications in Power Converters over 500 W. Electronics 2019, 8, 1401. [Google Scholar] [CrossRef]
- Gwóždž, M. Active power filter with sigma-delta modulator in control section. In Proceedings of the 2017 19th International Conference on Electrical Drives and Power Electronics (EDPE), Dubrovnik, Croatia, 4–6 October 2017; pp. 128–132. [Google Scholar]
- Otero-De-Leon, R.; Liu, L.; Bala, S.; Manchia, G. Hybrid active power filter with GaN power stage for 5kW single phase inverter. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 692–697. [Google Scholar]
- Uğur, M.; Saraç, H.; Keysan, O. Comparison of Inverter Topologies Suited for Integrated Modular Motor Drive Applications. In Proceedings of the 2018 IEEE 18th International Power Electronics and Motion Control Conference (PEMC), Budapest, Hungary, 26–30 August 2018; pp. 524–530. [Google Scholar]
- Mahmoudian, M.; Gitizadeh, M.; Rajaei, A.H.; Tehrani, V.M. Common mode voltage suppression in three-phase voltage source inverters with dynamic load. IET Power Electron. 2019, 12, 3141–3148. [Google Scholar] [CrossRef]
- Fu, Y.; Li, Y.; Huang, Y.; Bai, H.; Zou, K.; Lu, X.; Chen, C. Design methodology of a three-phase four-wire EV charger operated at the autonomous mode. IEEE Trans. Transp. Electr. 2019, 5, 1169–1181. [Google Scholar] [CrossRef]

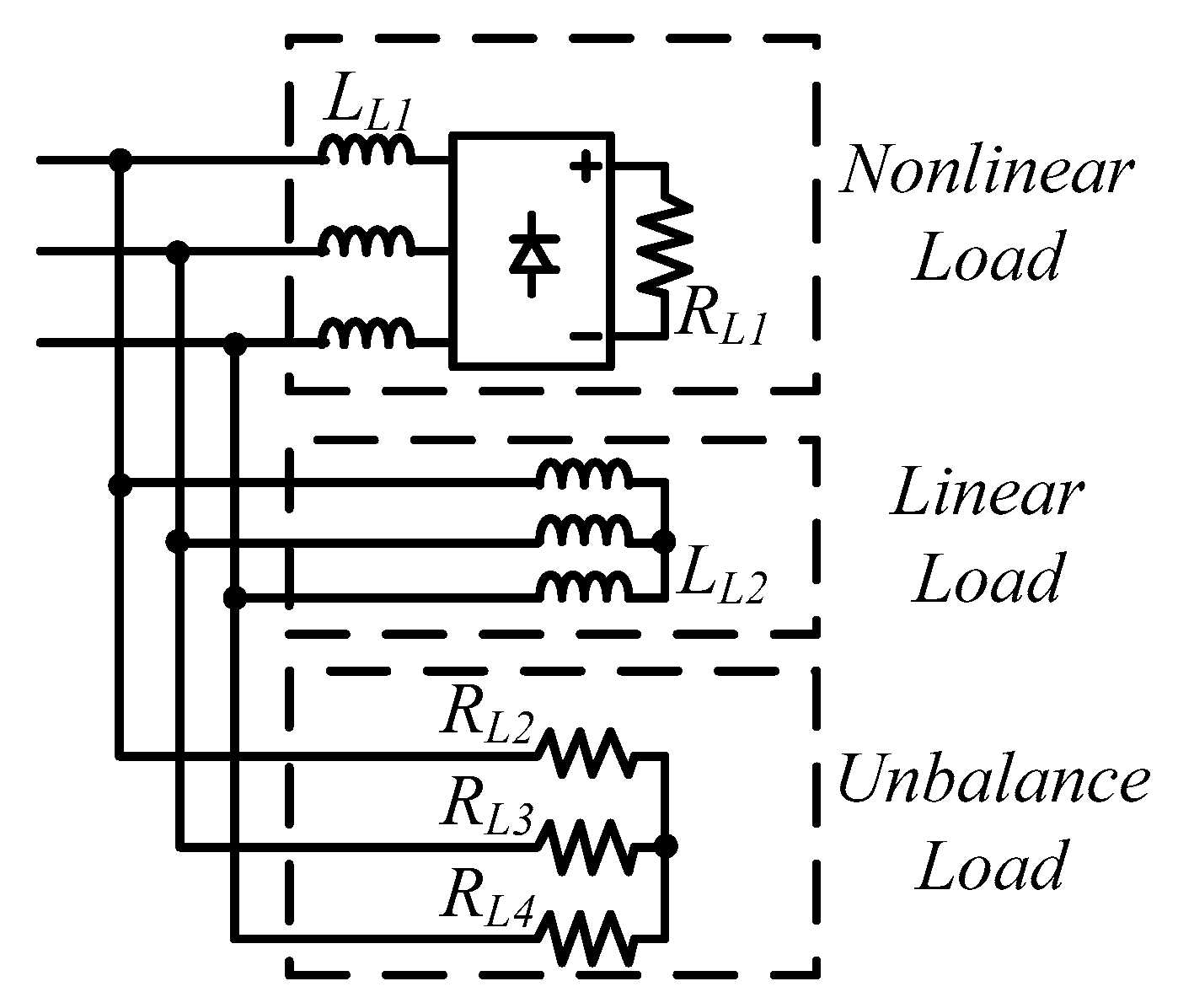



| Nonlinear Load | Linear Load | Unbalanced Load | ||||
|---|---|---|---|---|---|---|
| RL1 | LL1 | LL2 | RL2 | RL3, RL4 | ||
| 50 Ω | 6 mH × 3 | 152 mH × 3 | ∞ Ω | 50 Ω | ||
| Power Grid Currents and Unbalance Ratio (UR) | |||
|---|---|---|---|
| Item | Without APF (t0–t1) | With APF (t1–t2) | |
| igrid_a (A) | 2.9 | 2.84 | |
| igrid_b (A) | 3.42 | 2.87 | |
| igrid_c (A) | 3.87 | 2.89 | |
| UR (%) | 14.91 | 0.94 | |
| THD | |||
| Item | Without APF (t0–t1) | With APF (t1–t2) | |
| THD (igrid_a) (%) | 19.18 | 3.91 | |
| THD (igrid_b) (%) | 15.56 | 3.94 | |
| THD (igrid_c) (%) | 13.89 | 3.94 | |
| Number | Device | Value/Part Number |
|---|---|---|
| (1) | Microcontroller | TMS320F28335 |
| (2) | Interface circuit of the microcontroller | N/A |
| (3)–(5) | GaN HEMT pairs | TPH3207 |
| (6) and (7) | DC link capacitors | 680 mF/450 V |
| (8)–(10) | Filter inductors | 0.5 mH |
| (11)–(13) | Filter capacitors | 10 μF/300 V |
| Power Grid Currents and Unbalance Ratio (UR) | ||
|---|---|---|
| Item | Without APF (t0–t1) | With APF (t1–t2) |
| igrid_a (A) | 2.93 | 2.91 |
| igrid_b (A) | 3.43 | 2.94 |
| igrid_c (A) | 3.95 | 3.02 |
| UR (%) | 14.83 | 2.13 |
| THD | ||
| Item | Without APF (t0–t1) | With APF (t1–t2) |
| THD (igrid_a) (%) | 20.23 | 4.15 |
| THD (igrid_b) (%) | 16.57 | 4.08 |
| THD (igrid_c) (%) | 15.48 | 4.05 |
| Paper | Switching Device | Function | Power | Switching Frequency | Efficiency |
|---|---|---|---|---|---|
| [16] | IGBT | Motor drive | 8 kW | 20 kHz | 95.5% |
| [17] | MOSFET | Motor drive | 1.5 kW | 15 kHz | 92% |
| [18] | SiC | Electric vehicle | 8.8 kW | 50 kHz | 97% |
| proposed | GaN | Active power filter | 2 kVA | 50 kHz | 97.2% |
| 80 kHz | 96.7% | ||||
| 100 kHz | 95.6% |
| Sensed Object | Operating Temperature (°C) |
|---|---|
| TPH3207 @ 50kHz switching frequency | 40.9 |
| TPH3207 @ 80kHz switching frequency | 46.7 |
| TPH3207 @ 100kHz switching frequency | 51.4 |
| DSP | 47.5 |
| Communication interface | 46.5 |
| Inductors | 30.4 |
| Relays | 43.2 |
| Signal processing integrated circuits (ICs) | 31.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.-T.; Gu, Z.-H. Design and Implementation of a GaN-Based Three-Phase Active Power Filter. Micromachines 2020, 11, 134. https://doi.org/10.3390/mi11020134
Ma C-T, Gu Z-H. Design and Implementation of a GaN-Based Three-Phase Active Power Filter. Micromachines. 2020; 11(2):134. https://doi.org/10.3390/mi11020134
Chicago/Turabian StyleMa, Chao-Tsung, and Zhen-Huang Gu. 2020. "Design and Implementation of a GaN-Based Three-Phase Active Power Filter" Micromachines 11, no. 2: 134. https://doi.org/10.3390/mi11020134
APA StyleMa, C.-T., & Gu, Z.-H. (2020). Design and Implementation of a GaN-Based Three-Phase Active Power Filter. Micromachines, 11(2), 134. https://doi.org/10.3390/mi11020134





