Fully-Differential TPoS Resonators Based on Dual Interdigital Electrodes for Feedthrough Suppression
Abstract
1. Introduction
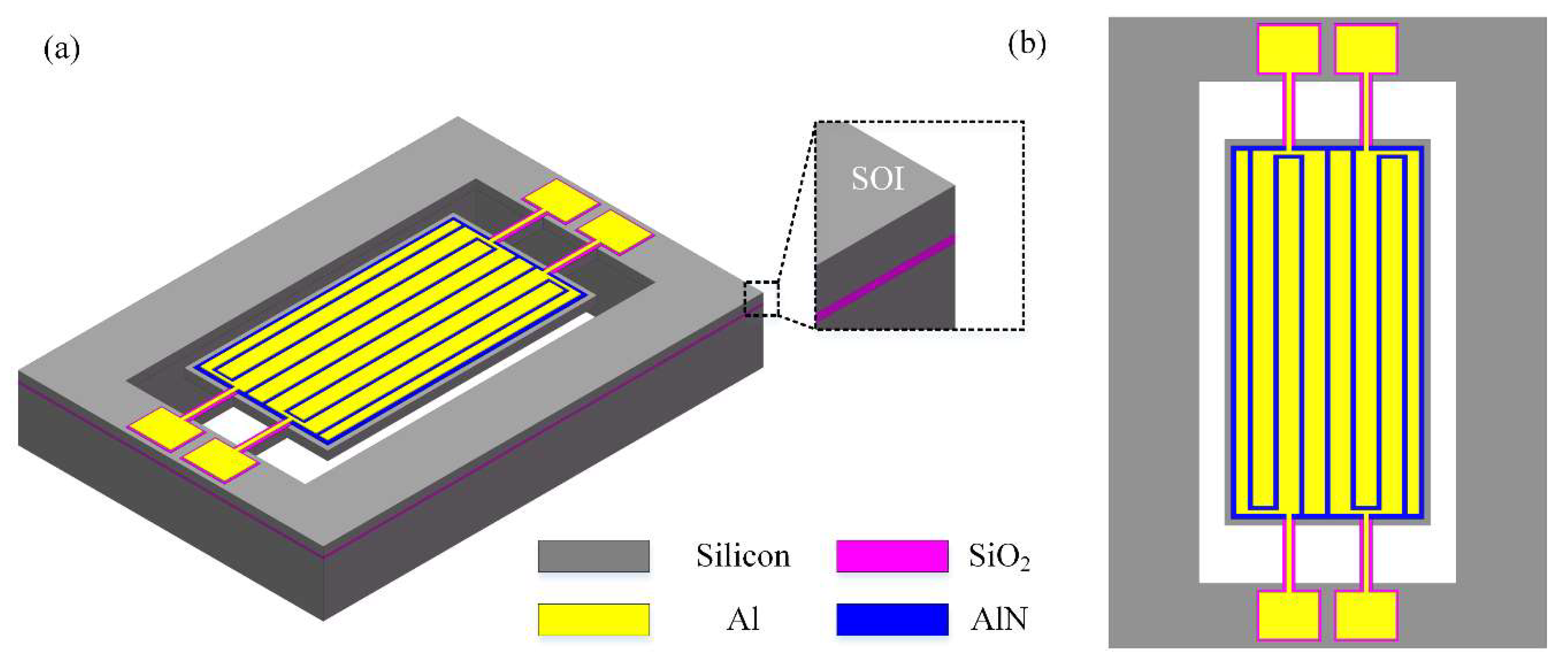
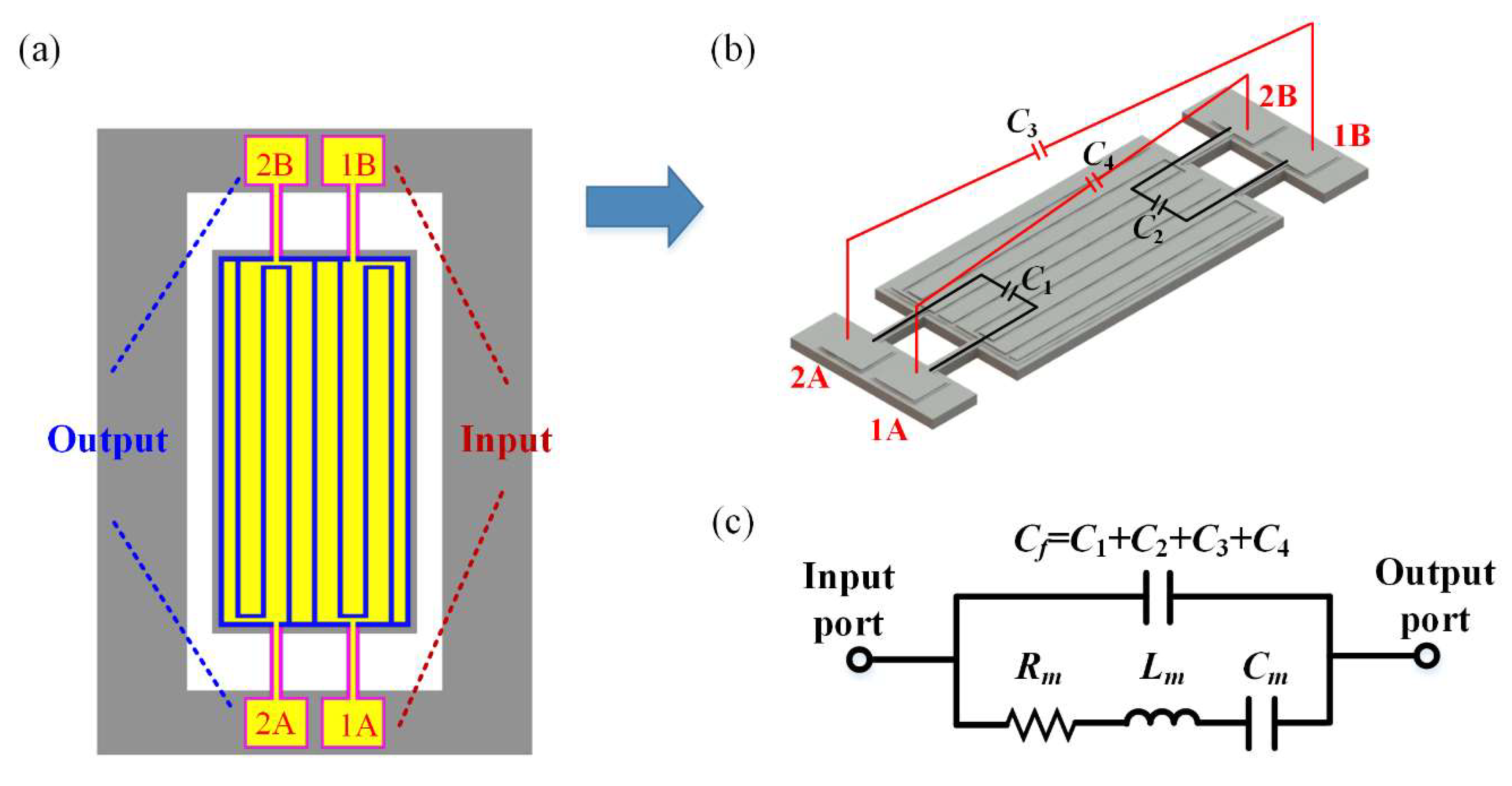
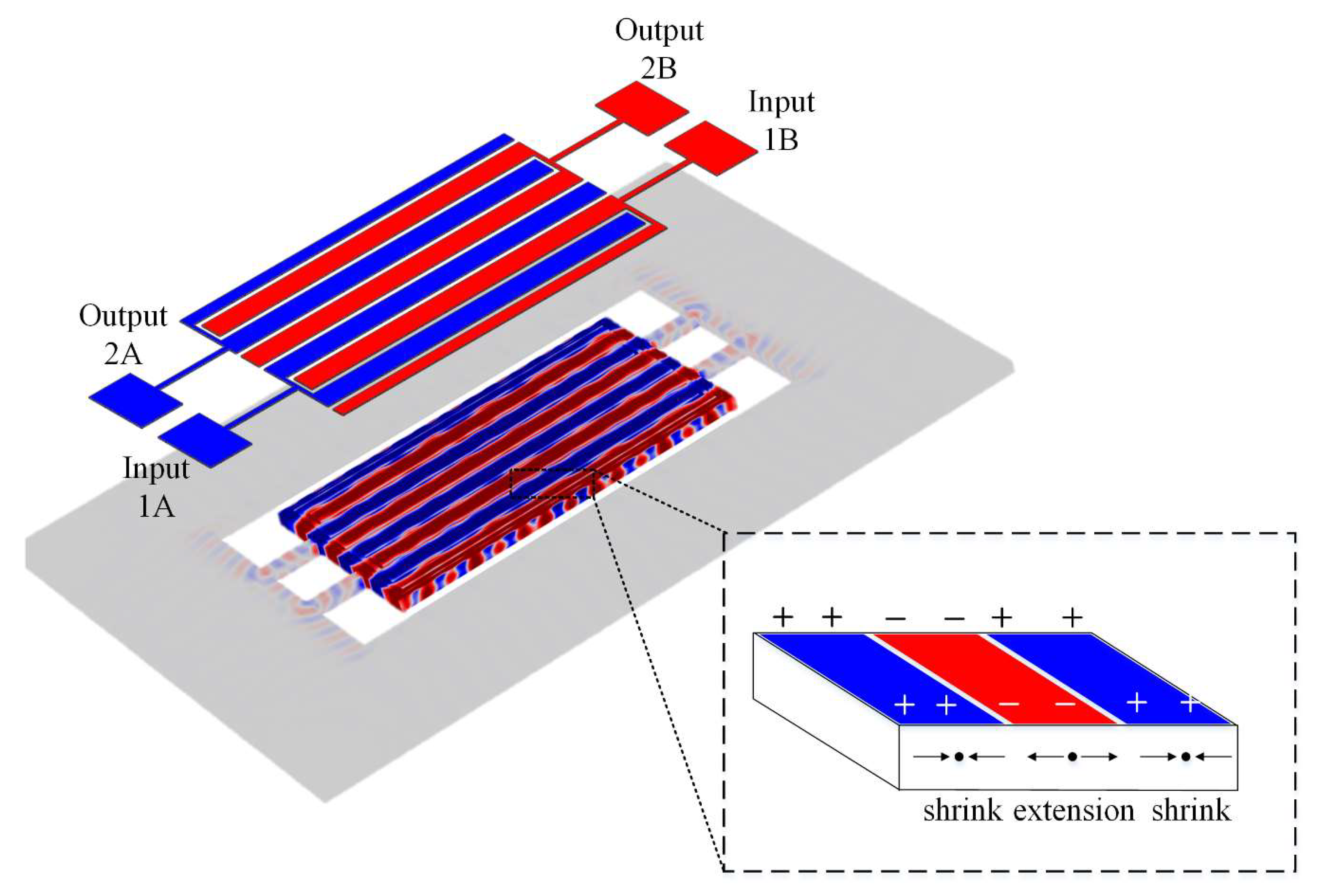
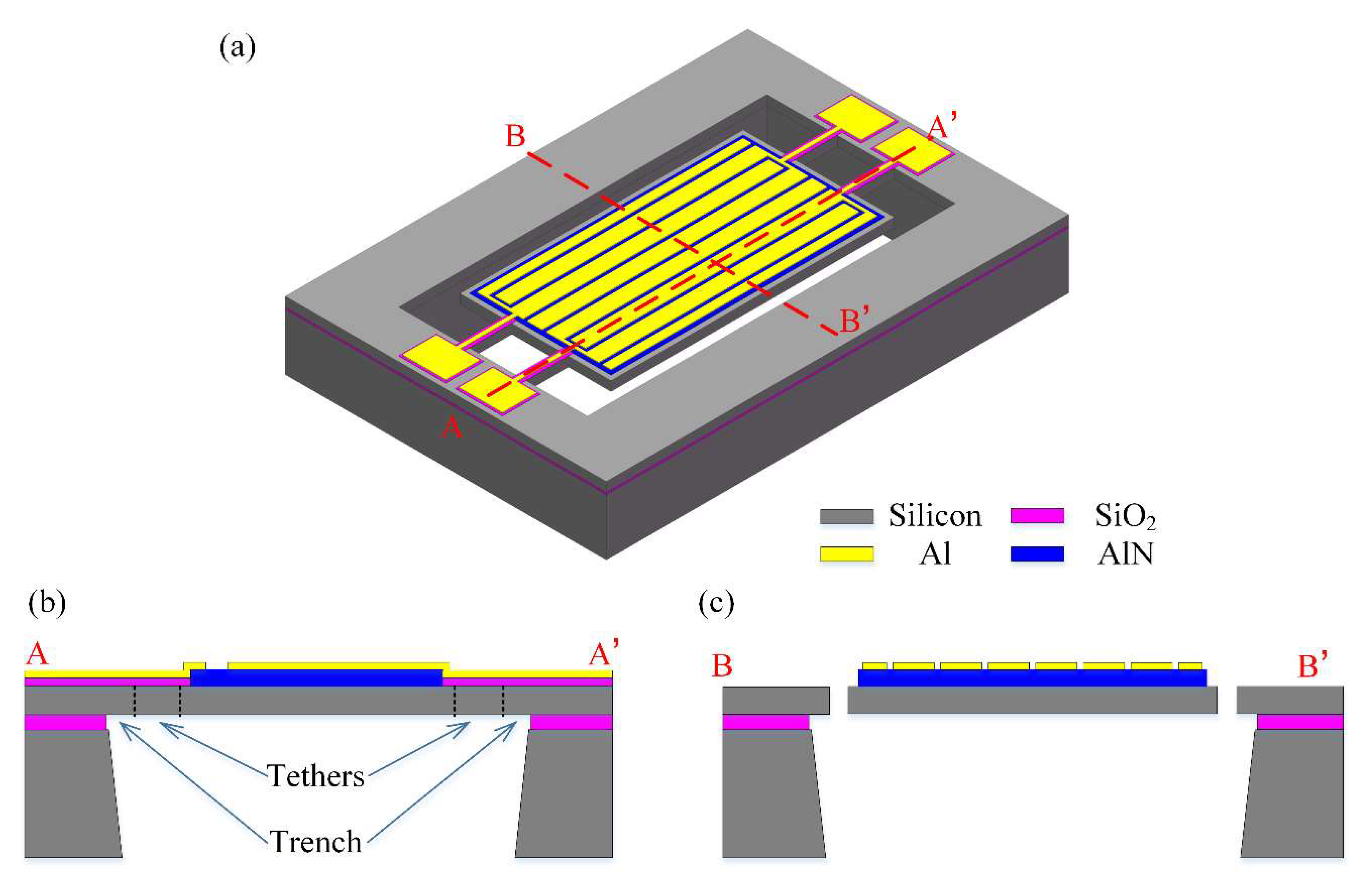
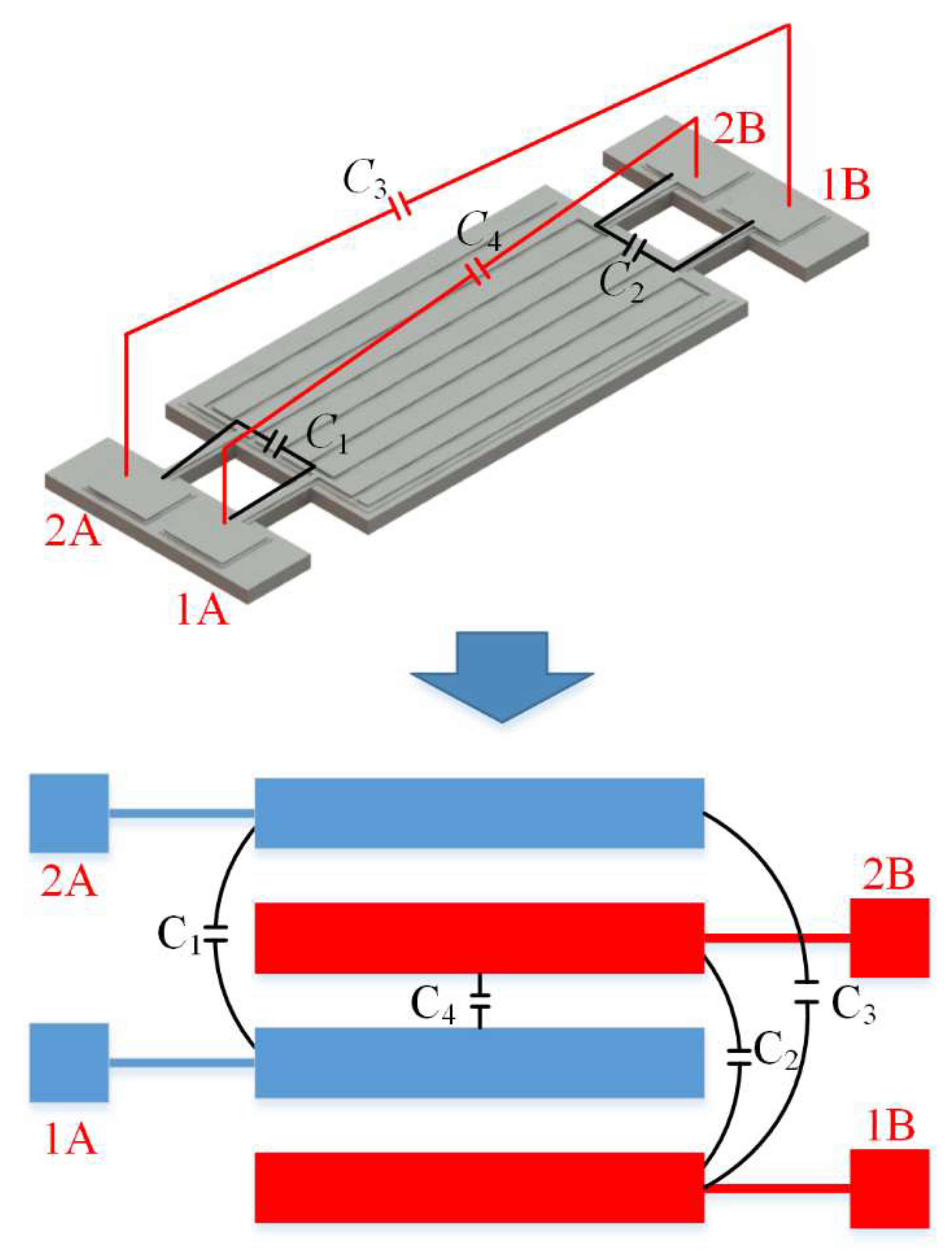
2. Resonator Model and Design
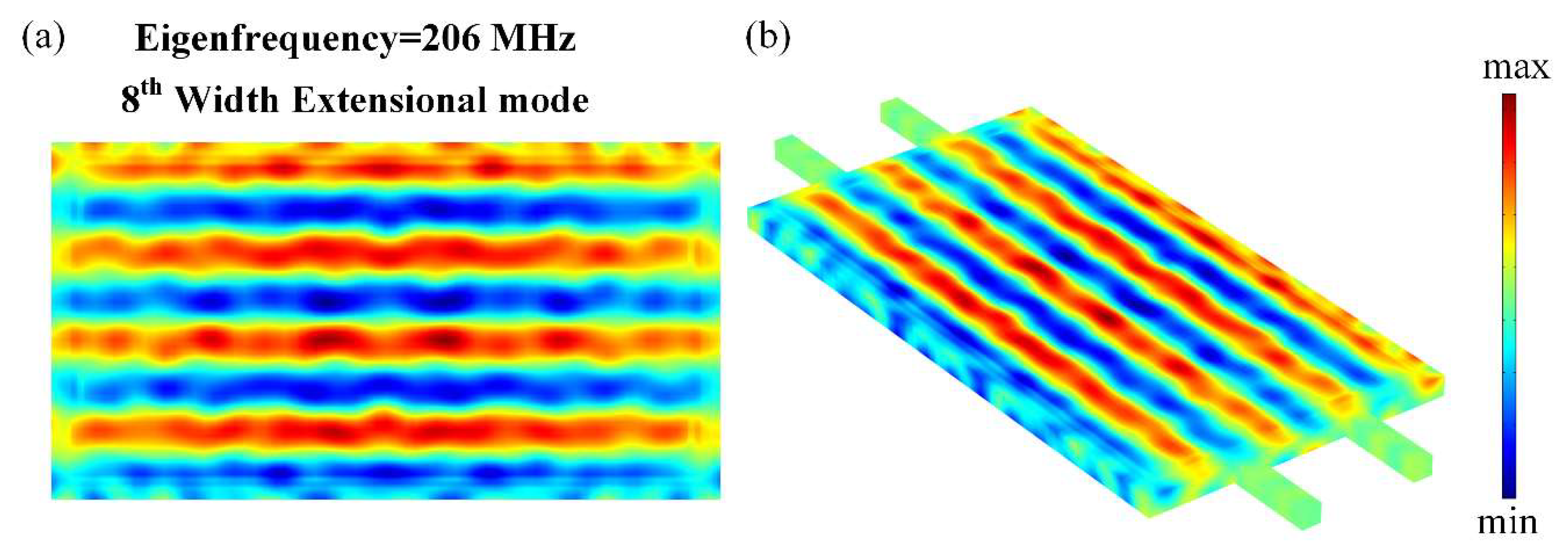
3. Results and Discussion
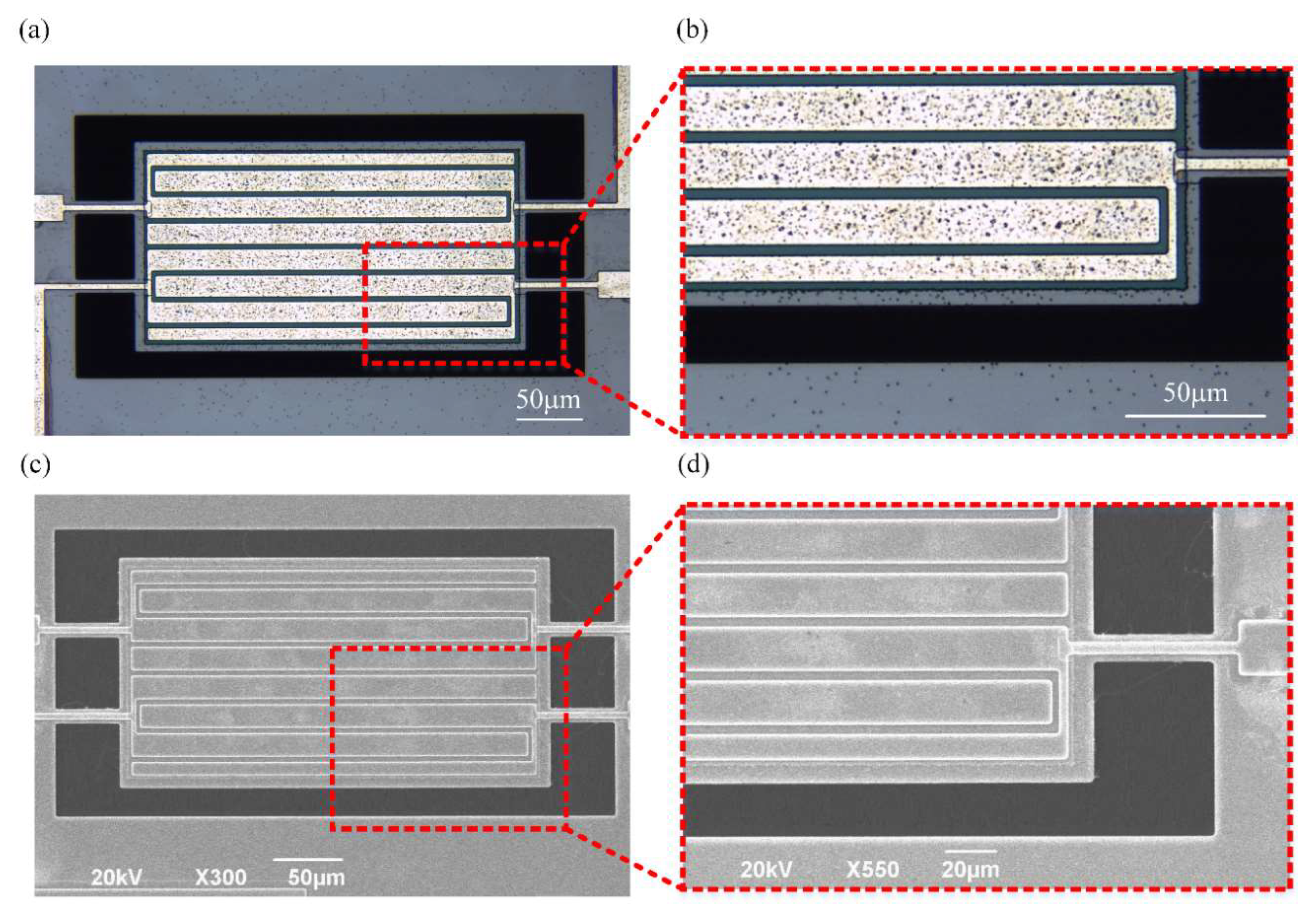
3.1. Fabrication
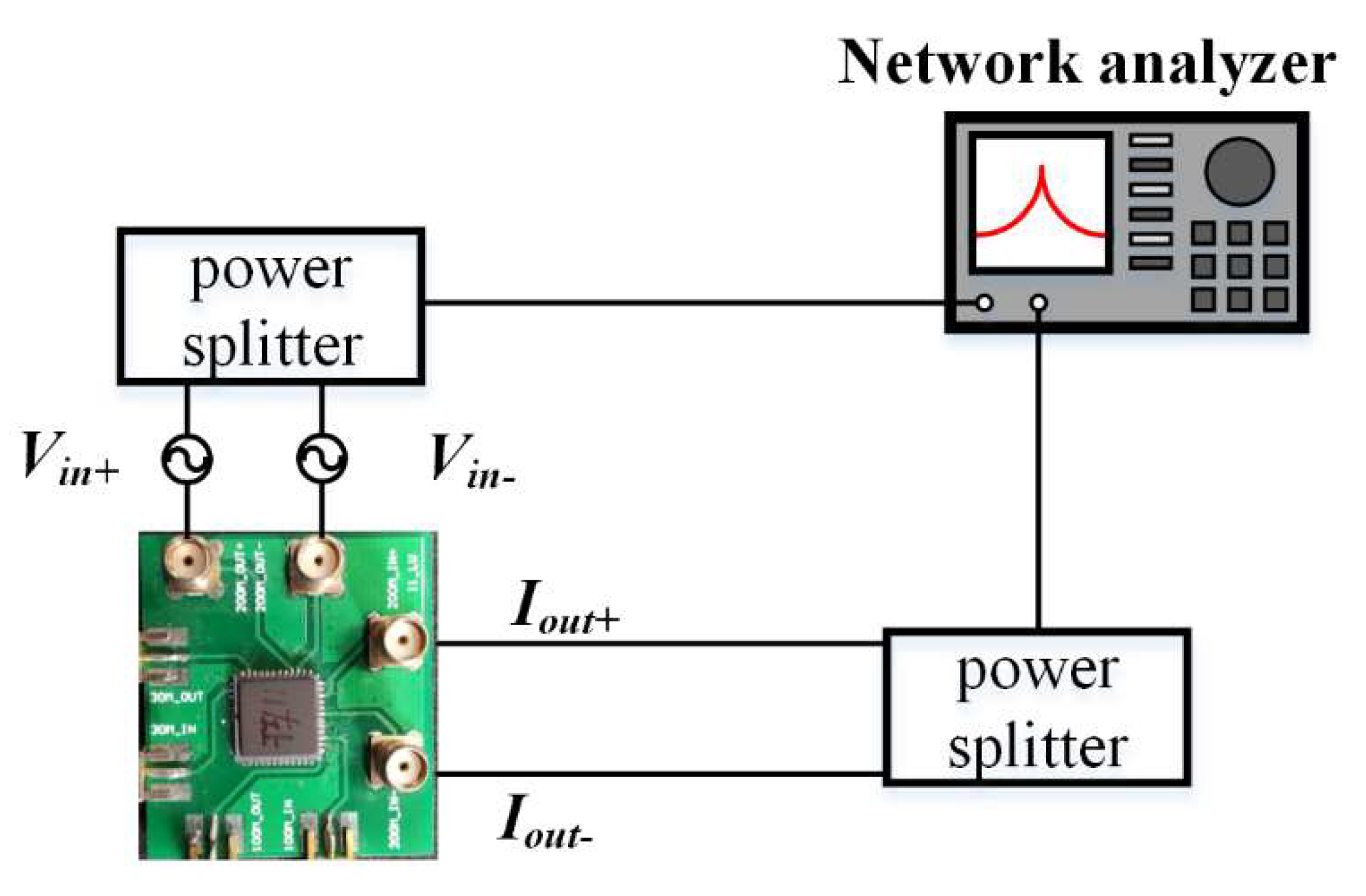
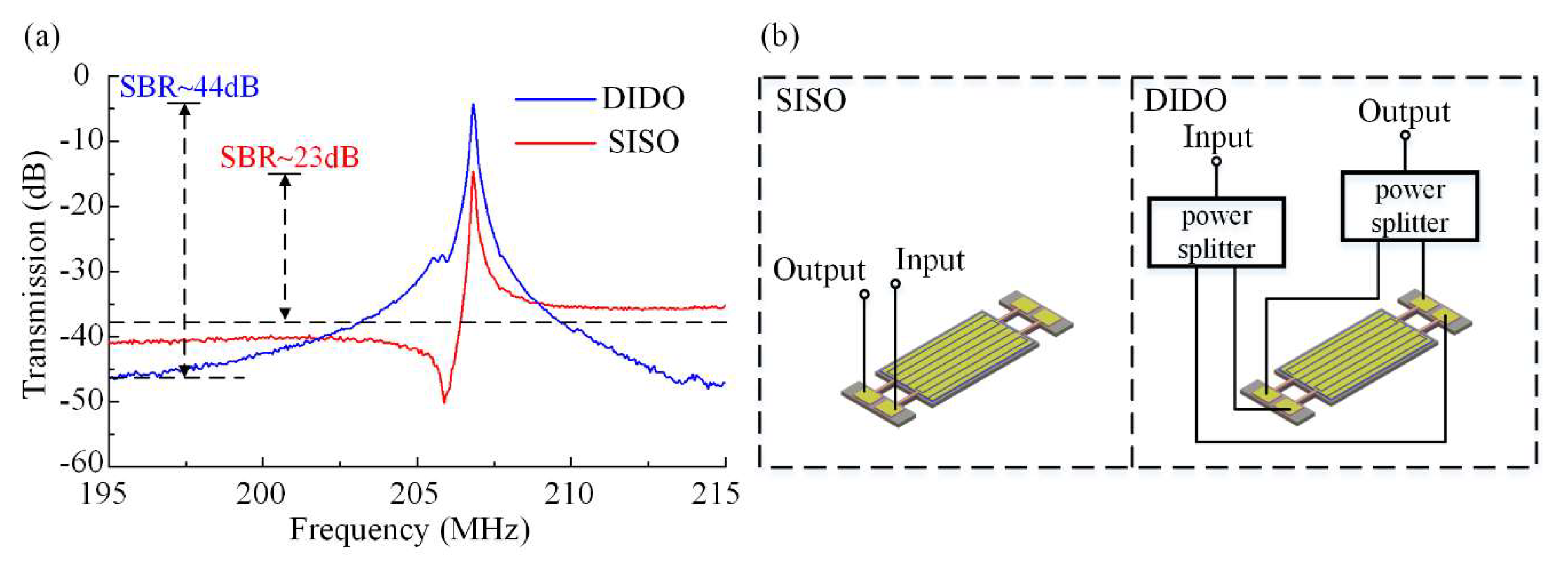
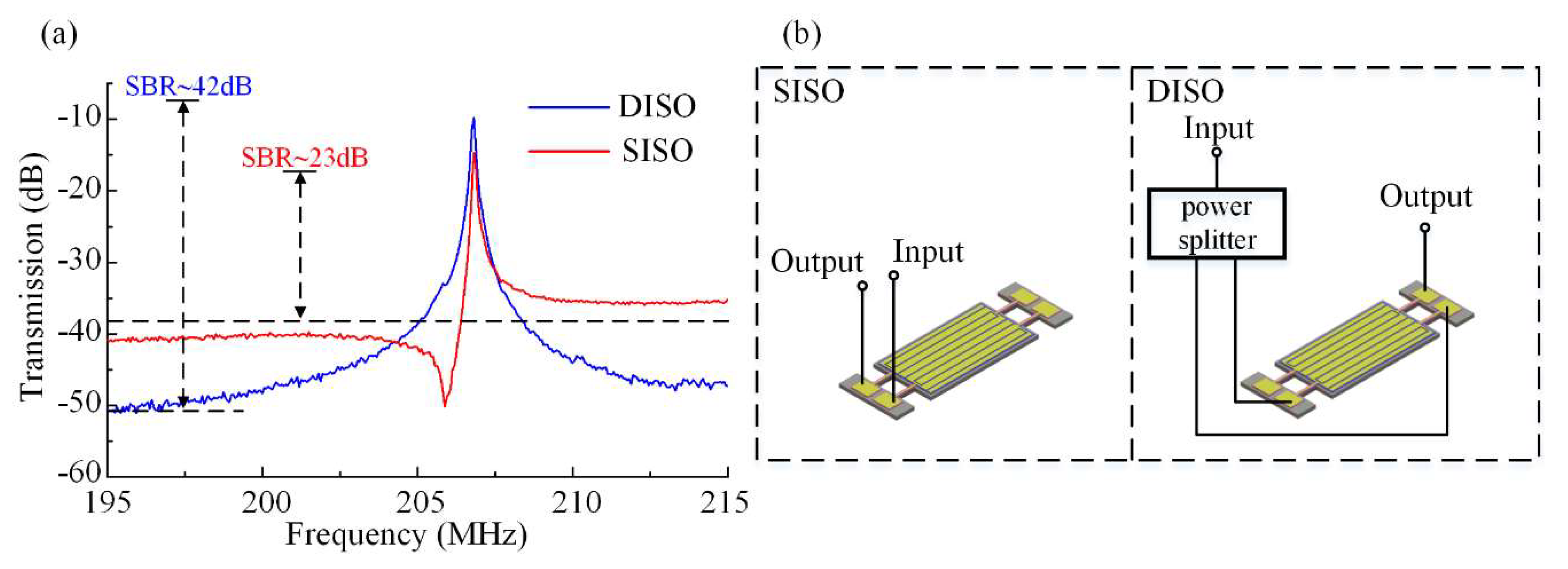
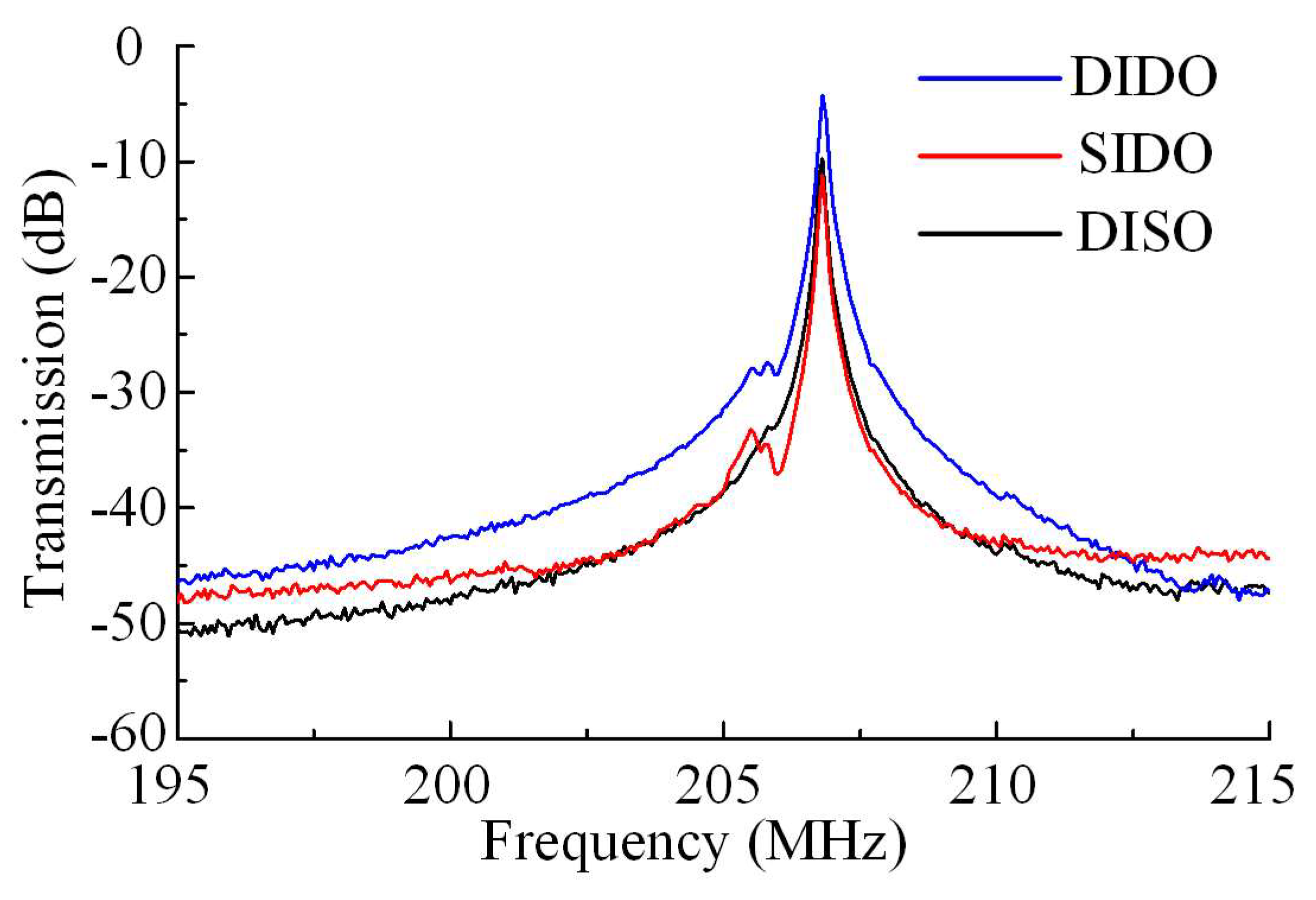
3.2. Measurement and Results
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.Y.; Nabki, F. Micromachined Resonators: A Review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef]
- Lee, J.E.Y.; Yan, J.; Seshia, A.A. Low loss HF band SOI wine glass bulk mode capacitive square-plate resonator. J. Micromech. Microeng. 2009, 19, 074003. [Google Scholar] [CrossRef]
- Lee, J.E.Y.; Seshia, A.A. 5.4-MHz single-crystal silicon wine glass mode disk resonator with quality factor of 2 million. Sens. Actuator A Phys. 2009, 156, 28–35. [Google Scholar] [CrossRef]
- Li, X.Y.; Bao, J.F.; Huang, Y.L.; Ling, Y.; Zheng, Y.B.; Du, Y.J. A 9.45 MHz micromechanical disk resonator with movable electrodes for gap reduction. Sens. Actuator A Phys. 2016, 243, 66–70. [Google Scholar] [CrossRef]
- Ghosh, S.; Lee, J.E.Y. Piezoelectric-on-silicon Lorentz force magnetometers based on radial contour mode disk resonators. Sens. Actuator A Phys. 2018, 281, 185–195. [Google Scholar] [CrossRef]
- Abdolvand, R.; Lavasani, H.M.; Ho, G.K.; Ayazi, F. Thin-Film Piezoelectric-on-Silicon Resonators for High-Frequency Reference Oscillator Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2596–2606. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.P.; Bao, J.F.; Ling, Y.; Li, X.Y. Design of a novel RF MEMS square resonator. Microsyst. Technol. 2015, 21, 1805–1810. [Google Scholar] [CrossRef]
- Nguyen, C.T.C. MEMS technology for timing and frequency control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 251–270. [Google Scholar] [CrossRef]
- Pillai, G.; Zope, A.A.; Li, S.S. Piezoelectric-Based Support Transducer Design to Enable High-Performance Bulk Mode Resonators. J. Microelectromech. Syst. 2019, 28, 4–13. [Google Scholar] [CrossRef]
- Ali, A.; Lee, J.E.Y. Fully-differential Piezoelectric Button-like Mode Disk Resonator for Liquid Phase Sensing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 600–608. [Google Scholar] [CrossRef]
- Ali, A.; Lee, J.E.Y. Fully-Differential AlN-on-Si Wine Glass Mode Resonator for Enhanced Characterization in Water. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–2 November 2016. [Google Scholar] [CrossRef]
- Ali, A.; Lee, J.E.Y. Single device on-chip feedthrough cancellation for enhanced electrical characterization of piezoelectric-on-silicon resonators in liquid. Sens. Actuator A Phys. 2017, 260, 131–138. [Google Scholar] [CrossRef]
- Ali, A.; Lee, J.E.Y. Electrical characterization of piezoelectric-on-silicon contour mode resonators fully immersed in liquid. Sens. Actuator A Phys. 2016, 241, 216–223. [Google Scholar] [CrossRef]
- Lee, J.E.Y.; Zhu, Y.; Seshia, A.A. A bulk acoustic mode single-crystal silicon microresonator with a high-quality factor. J. Micromech. Microeng. 2008, 18, 064001. [Google Scholar] [CrossRef]
- Xu, Y.J.; Lee, J.E.Y. Characterization and modeling of a contour mode mechanical resonator using piezoresistive sensing with quasi-differential inputs. J. Micromech. Microeng. 2012, 22, 125018. [Google Scholar] [CrossRef]
- Nguyen, C.T.C.; Howe, R.T. An integrated CMOS micromechanical resonator high-Q oscillator. IEEE J. Solid State Circuits 1999, 34, 440–455. [Google Scholar] [CrossRef]
- Xu, Y.J.; Lee, J.E.Y. Single-Device and On-Chip Feedthrough Cancellation for Hybrid MEMS Resonators. IEEE Trans. Ind. Electron. 2012, 59, 4930–4937. [Google Scholar] [CrossRef]
- Tanaka, K.; Kihara, R.; Sanchez-Amores, A.; Montserrat, J.; Esteve, J. Parasitic effect on silicon MEMS resonator model parameters. Microelectron. Eng. 2007, 84, 1363–1368. [Google Scholar] [CrossRef]
- Clark, J.R.; Hsu, W.T.; Abdelmoneum, M.A.; Nguyen, C.T.C. High-Q UHF micromechanical radial-contour mode disk resonators. J. Microelectromech. Syst. 2005, 14, 1298–1310. [Google Scholar] [CrossRef]
- Lee, J.E.Y.; Seshia, A.A. Parasitic feedthrough cancellation techniques for enhanced electrical characterization of electrostatic microresonators. Sens. Actuator A Phys. 2009, 156, 36–42. [Google Scholar] [CrossRef]
- Tu, C.; Zhu, H.S.; Xu, Y.J.; Lee, J.E.Y. Differential-capacitive-input and differential-piezoresistive-output enhanced transduction of a silicon bulk-mode microelectromechanical resonator. Sens. Actuator A Phys. 2014, 210, 41–50. [Google Scholar] [CrossRef]
- Li, C.S.; Chin, C.H.; Liu, Y.C.; Li, S.S. Capacitively-Driven and Piezoresistively-Sensed CMOS-MEMS Resonators. In Proceedings of the 2012 IEEE 25th International Conference on Micro Electro Mechanical Systems (MEMS 2012), Paris, France, 29 January–2 February 2012; pp. 539–542. [Google Scholar]
- Li, C.S.; Li, M.H.; Li, S.S. Differential Measurement of Piezoresistive Transduction for Silicon-Based MEMS Resonators. In Proceedings of the 2012 IEEE International Frequency Control Symposium, Baltimore, MD, USA, 21–24 May 2012; pp. 593–596. [Google Scholar]
- Ho, G.K.; Abdolvand, R.; Sivapurapu, A.; Humad, S.; Ayazi, F. Piezoelectric-on-Silicon Lateral Bulk Acoustic Wave Micromechanical Resonators. J. Microelectromech. Syst. 2008, 17, 512–520. [Google Scholar] [CrossRef]
- Ali, A.; Lee, J.E.Y. Square-Extensional Mode Piezoelectric-on-Silicon Resonator for Physical Measurements of Liquids. In Proceedings of the 2016 IEEE International Frequency Control Symposium, New Orleans, LA, USA, 9–12 May 2016; pp. 427–430. [Google Scholar]
- Humad, S.; Abdolvand, R.; Ho, G.K.; Piazza, G.; Ayazi, F. High frequency micromechanical piezo-on-silicon block resonators. In Proceedings of the 2003 IEEE International Electron Devices Meeting, Technical Digest, Washinton, DC, USA, 8–10 December 2003; pp. 957–960. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Bao, J.-F.; Li, X.-Y.; Zhou, X.; Wu, Z.-H.; Zhang, X.-S. Fully-Differential TPoS Resonators Based on Dual Interdigital Electrodes for Feedthrough Suppression. Micromachines 2020, 11, 119. https://doi.org/10.3390/mi11020119
Zhang Y, Bao J-F, Li X-Y, Zhou X, Wu Z-H, Zhang X-S. Fully-Differential TPoS Resonators Based on Dual Interdigital Electrodes for Feedthrough Suppression. Micromachines. 2020; 11(2):119. https://doi.org/10.3390/mi11020119
Chicago/Turabian StyleZhang, Yi, Jing-Fu Bao, Xin-Yi Li, Xin Zhou, Zhao-Hui Wu, and Xiao-Sheng Zhang. 2020. "Fully-Differential TPoS Resonators Based on Dual Interdigital Electrodes for Feedthrough Suppression" Micromachines 11, no. 2: 119. https://doi.org/10.3390/mi11020119
APA StyleZhang, Y., Bao, J.-F., Li, X.-Y., Zhou, X., Wu, Z.-H., & Zhang, X.-S. (2020). Fully-Differential TPoS Resonators Based on Dual Interdigital Electrodes for Feedthrough Suppression. Micromachines, 11(2), 119. https://doi.org/10.3390/mi11020119





