Performance Analysis of a Microfluidic Pump Based on Combined Actuation of the Piezoelectric Effect and Liquid Crystal Backflow Effect
Abstract
1. Introduction
2. Theory and Methods
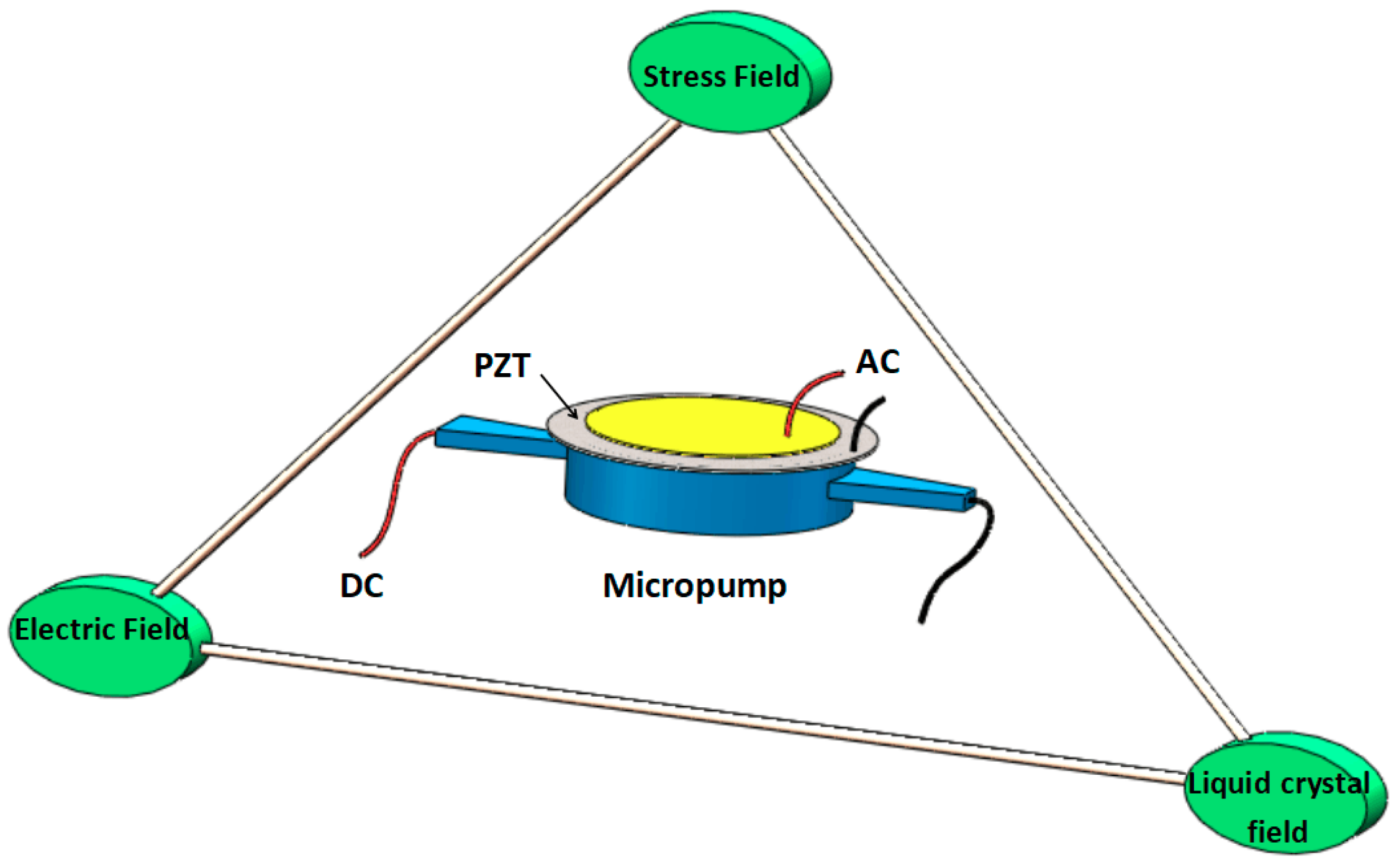
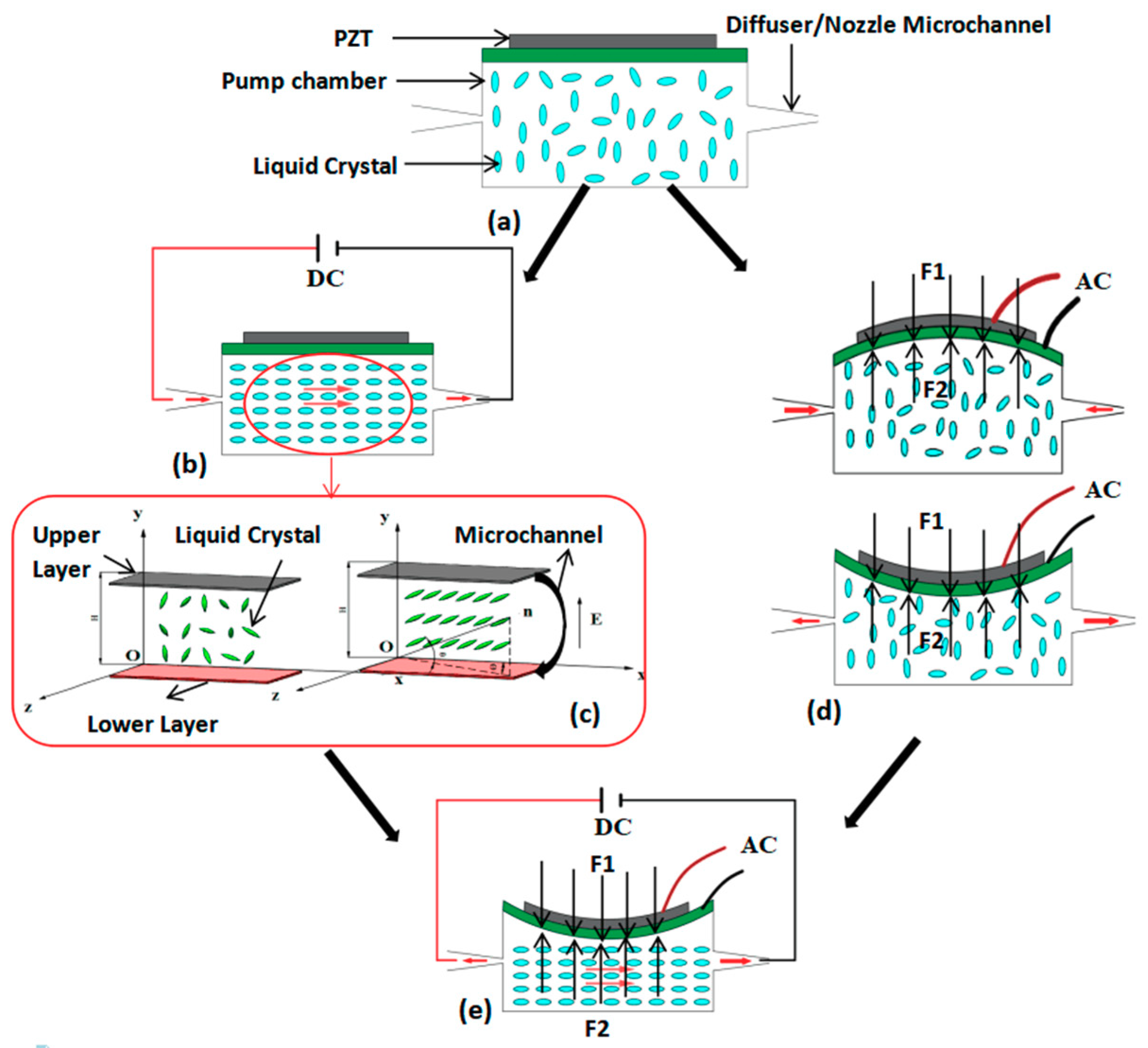
2.1. Combined Driving Mechanism
2.2. The Establishment of Multi-Field Coupling Numerical Model
2.3. Revising of Movement Equation under Combined Driving Mode
2.4. Initial and Boundary Conditions for Numerical Analysis
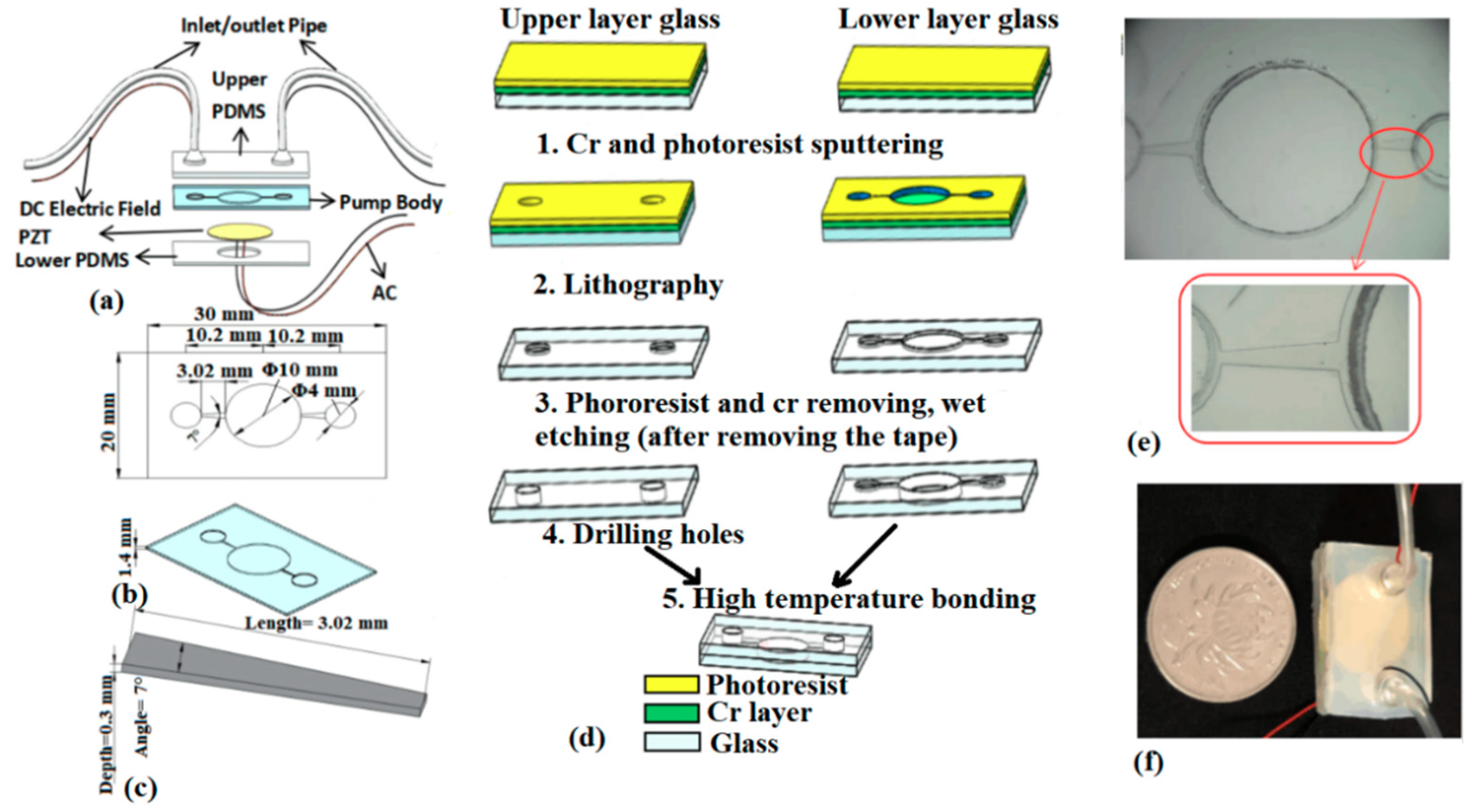
2.5. Structural Design
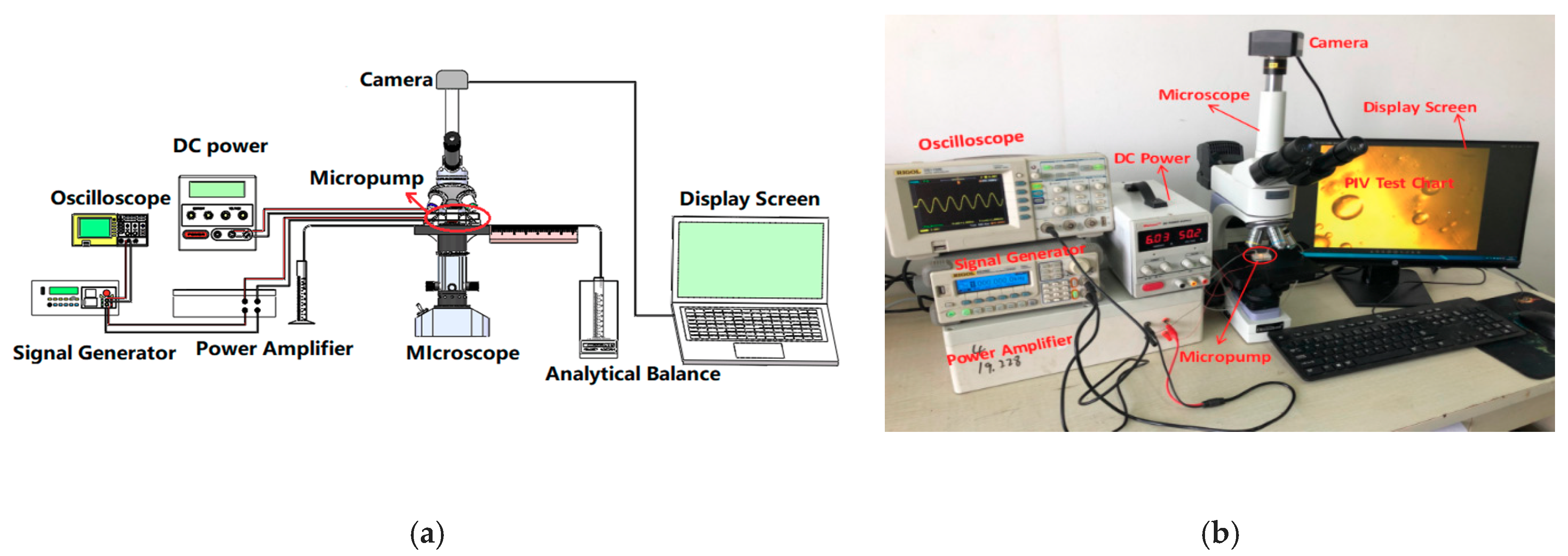
2.6. Layout of Experiment
3. Results and Discussion
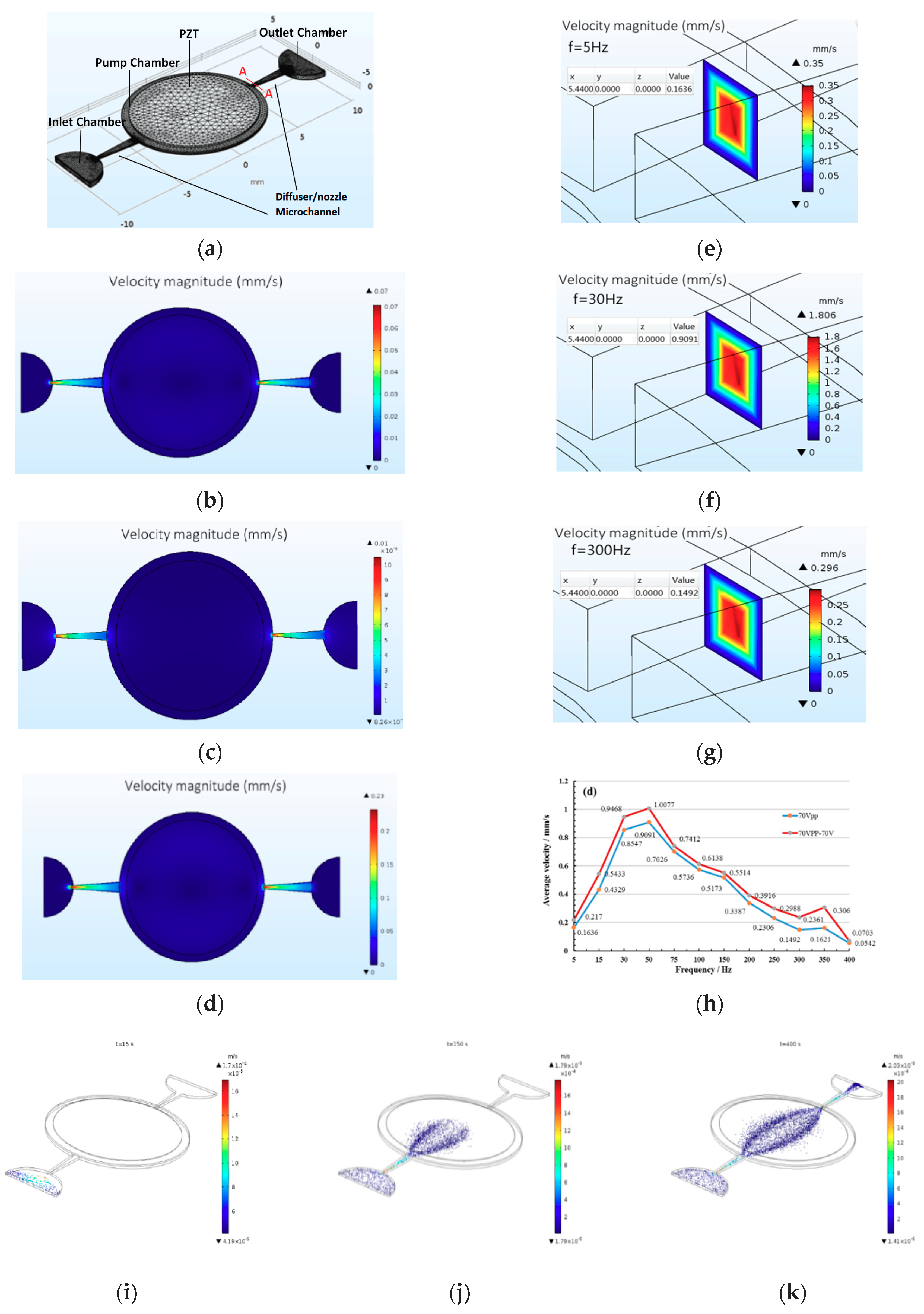
3.1. Analysis of Numerical Results
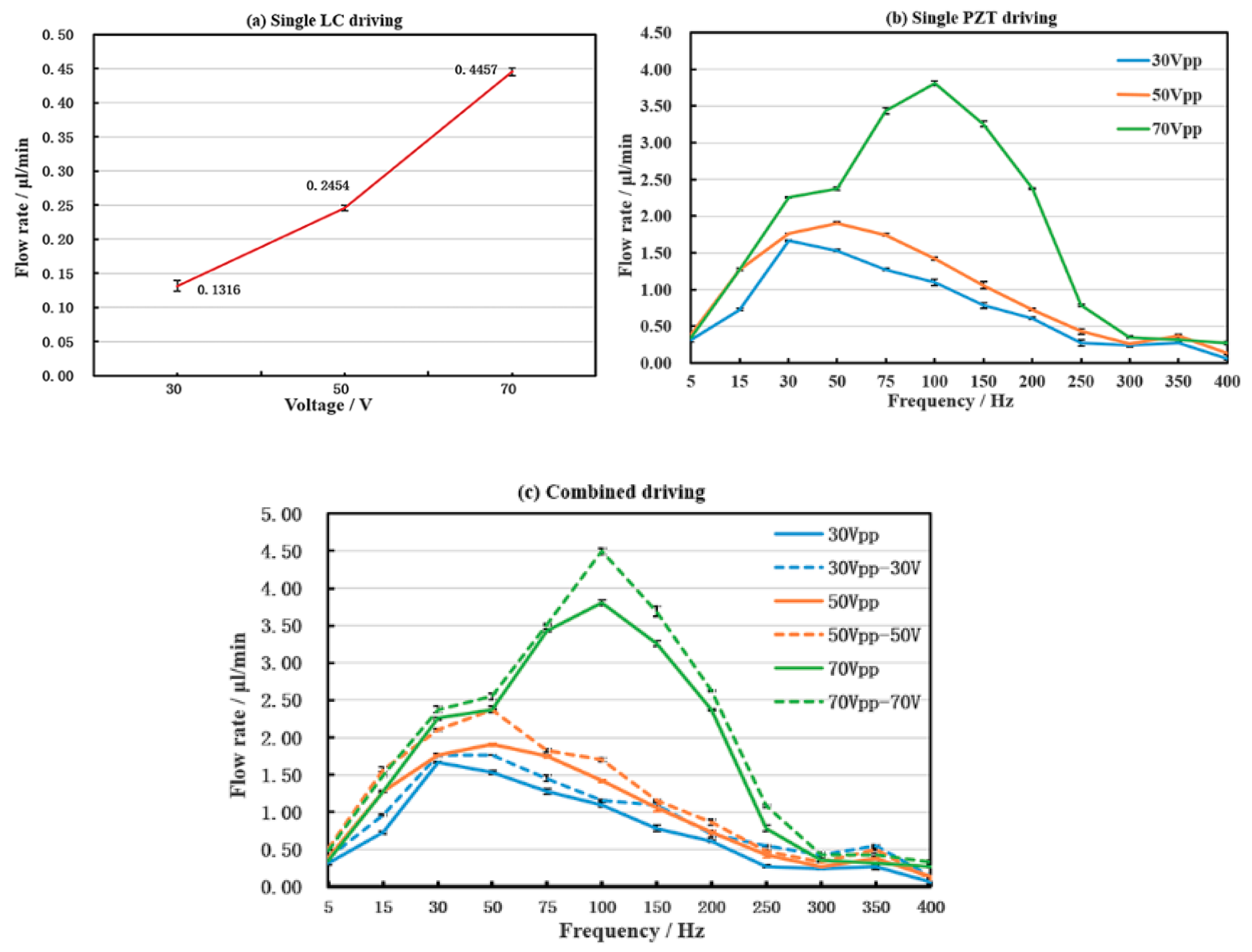
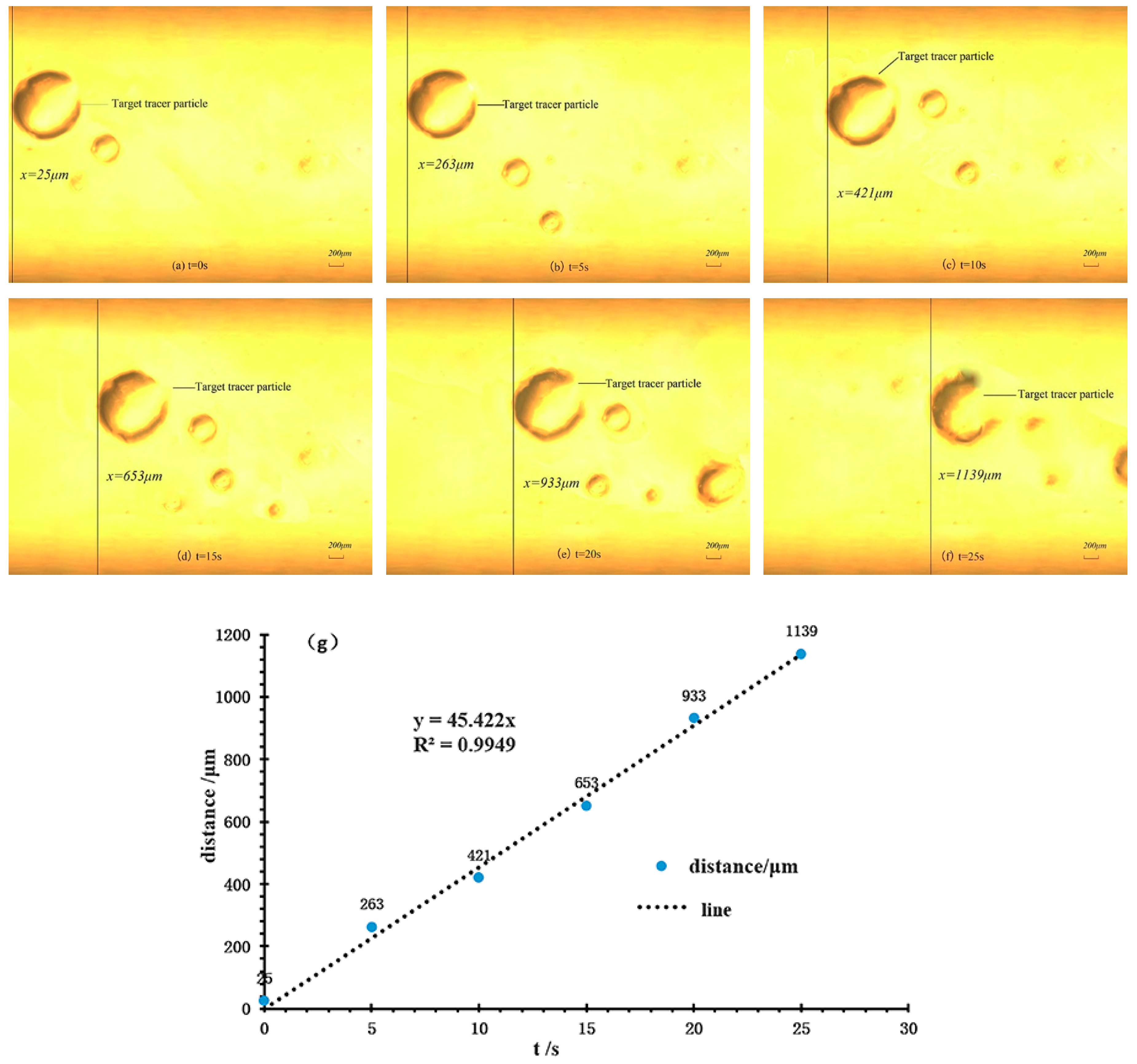
3.2. Experiment Results Discussion
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Milad, S.; Alireza, S. Nonlinear vibration analysis of a circular micro-plate in two-sided NEMS/MEMS capacitive system by using harmonic balance method. Acta Mech. Sin. 2019, 35, 129–143. [Google Scholar]
- Thuau, D.; Laval, C.; Dufour, I.; Poulin, P.; Ayela, C.; Salmon, J.-B. Engineering polymer MEMS using combined microfluidic pervaporation and micro-molding. Microsyst. Nanoeng. 2018, 4, 15. [Google Scholar] [CrossRef] [PubMed]
- Cesewki, E.; Haring, A.P.; Tong, Y.; Singh, M.; Thakur, R.; Laheri, S.; Read, K.A.; Powell, M.D.; Oestreich, K.J.; Johnson, B.N. Additive manufacturing of three-dimensional (3D) microfluidic-based microelectromechanical systems (MEMS) for acoustofluidic applications. Lab Chip 2018, 18, 2087–2098. [Google Scholar] [CrossRef] [PubMed]
- Sima, R.; Mostafa, K.M. Microfluidic assisted synthesis of PLGA drug delivery systems. RSC Adv. 2019, 9, 2055–2072. [Google Scholar]
- Li, Z.G.; Zhao, J.; Wu, X.; Zhu, C.; Liu, Y.; Wang, A.; Deng, G.; Zhu, L. A rapid microfluidic platform with real-time fluorescence detection system for molecular diagnosis. Biotechnol. Biotechnol. Equip. 2019, 1–8. [Google Scholar] [CrossRef]
- Shi, Y.; Wu, Q.; Sun, D.; Gao, C. An analytic model of microfluidic system triggered by thermal expansion. Biomed. Microdevices 2019, 21, 4. [Google Scholar] [CrossRef] [PubMed]
- Chung, B.G. Microfluidic fabrication of microengineered hydrogels and their application in tissue engineering. Lab Chip 2012, 12, 45–49. [Google Scholar] [CrossRef]
- Das, P.K.; Hasan, A.B.M. Mechanical Micropumps and their application: A review. AIP Conf. Proc. 2017, 1851, 020110. [Google Scholar]
- Li, M.T.; Su, Y.; Zhang, H.; Dong, B. Light-powered direction-controlled micropump. Nano Res. 2018, 11, 1810–1821. [Google Scholar] [CrossRef]
- Chu, L.Y.; Wang, W. Microfluidic fabrication of membrane-in-a-chip with self-regulated permeability. Microfluid. Adv. Funct. Polym. Mater. 2017, 253–266. [Google Scholar] [CrossRef]
- Gidde, R.R.; Pawar, P.M.; Ronge, B.P.; Dhamgaye, V.P. Design optimization of an electromagnetic actuation based valveless micropump for drug delivery application. Microsyst. Technol. 2019, 25, 509–519. [Google Scholar] [CrossRef]
- Zhang, C.S.; Xing, D.; Li, Y.Y. Micropumps, microvalves, and micromixers within PCR microfluidic chips, Adcances and trends. Biotechnol. Adv. 2007, 25, 483–514. [Google Scholar] [CrossRef] [PubMed]
- Aksoy, B.; Besse, N.; jan Boom, R.; Hoogenberg, B.-J.; Blom, M.; Shea, H. Latchable microfluidic valve arrays based on shape memory polymer actuators. Lab Chip 2019, 19, 608–617. [Google Scholar] [CrossRef] [PubMed]
- Hossan, M.R.; Dutta, D.; Islam, N.; Dutta, P. Review: Electric field driven pumping in microfluidic device. Electrophoresis 2018, 39, 702–731. [Google Scholar] [CrossRef] [PubMed]
- Jayavel, P.; Jhorar, R.; Tripathi, D.; Azese, M.N. Electroosmotic flow of pseudoplastic nanoliquids via peristaltic pumping. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 61. [Google Scholar] [CrossRef]
- Gorbacheva, E.V.; Ganchenko, G.S.; Demekhin, E.A. Stability of the electroosmotic flow of a two-layer electrolyte-dielectric system with external pressure gradient. Eur. Phys. J. E 2018, 41, 40–44. [Google Scholar] [CrossRef] [PubMed]
- Babaie, A.; Saidi, M.H.; Sadeghi, A. Electroosmotic flow of power-law fluids with temperature dependent properties. J. Non-Newton. Fluid Mech. 2012, 185–186, 49–57. [Google Scholar] [CrossRef]
- Giouroudi, I.; Kokkinis, G. Recent advances in magnetic microfluidic biosensors. Nanomaterials 2017, 7, 171. [Google Scholar] [CrossRef]
- Bienzeisler, J.; Ludtke-Buzug, K.; Schemberg, J. Magnetic Flow Field Separation of Superparamagnetic Dextran Coated Iron Oxide Nanoparticles. In Proceedings of the 5th International Workshop on Magnetic Particle Imaging (IWMPI), Istanbul, Turkey, 26–28 March 2015. [Google Scholar]
- Miccio, L.; Merola, F.; Finizio, A.; Paturzo, M.; Grilli, S.; Ferraro, P. Holographic Microscope for Quantitative Phase-Contrast Imaging of Particles Driven by Optical Forces in Microfluidics. In Proceedings of the IEEE Photonic Society 24th Annual Meeting, Arlington, VA, USA, 9–13 October 2011. [Google Scholar]
- Baigl, D. Photo-actuation of liquids for light-driven microfluidics: State of the art and perspectives. Lab Chip 2012, 12, 3637–3653. [Google Scholar] [CrossRef]
- Maruo, S.; Inoue, H. Optically driven micropump produced by three-dimensional two-photo microfabrication. Appl. Phys. Lett. 2006, 89, 144101. [Google Scholar] [CrossRef]
- Liu, B.; Sun, J.; Li, D.; Zhe, J.; Oh, K.W. A high flow rate thermal bubble-driven micropump with induction heating. Microfluid. Nanofluid. 2016, 20, 155. [Google Scholar] [CrossRef]
- Stubble, M.; Gimsa, J. A short review on AC electro-thermal micropumps based on smeared structural polarizations in the presence of a temperature gradient. Colloid. Surf. A 2010, 376, 97–101. [Google Scholar] [CrossRef]
- Kasai, Y.; Sakuma, S.; Hayakawa, T.; Arai, F. High-speed On-Chip Local Flow Control by Synchronized Actuation of Piezo-Driven Dual Membrane Pumps. In Proceedings of the 2016 International Symposium on Micro-Nanomechatronics and Human Science (MHS), Nagoya, Japan, 20–30 November 2016. [Google Scholar]
- Munas, F.R.; Melroy, G.; Abeynayake, C.B.; Chathuranga, H.L.; Amarasinghe, R.; Kumarage, P.; Dau, V.; Dao, D.V. Development of PZT actuated valveless micropump. Sensors 2018, 18, 1302. [Google Scholar] [CrossRef] [PubMed]
- He, X.H.; Zhu, J.; Zhang, X.; Yang, L.X. The analysis of internal transient flow and the performance of valveless piezoelectric micropump with planar diffuser/nozzles elements. Microsyst. Technol. 2017, 23, 23–37. [Google Scholar] [CrossRef]
- Jiang, Y.B.; Wang, Y.; Lin, G.-L.; Weng, C.-E.; Lu, W.-H. An automatic feeding system with a linear piezoelectric actuator, driving circuit position sensors. Microsyst. Technol. 2018, 24, 1909–1917. [Google Scholar] [CrossRef]
- Guan, Y.F.; Liu, C.B. Structural parameter analysis and experimental study of micropumps with saw-tooth microchallel. Sens. Actuators A 2015, 201, 195–205. [Google Scholar]
- Demori, M.; Baù, M.; Ferrari, M.; Ferrari, V. Particle Manipulation by Means of Piezoelectric Actuators for Microfluidic Applications. In Proceedings of the AISEM Annual Conference on Sensors and Microsystems, Lecce, Italy, 1–23 February 2017; Volume 223–228. [Google Scholar]
- Peng, Y.; Wang, W. Design and Development of Megascopic System and Its Application to PZT Nano Powder Dispersion. In Proceedings of the International Technology and Innovation Conference, Xi’an, China, 12–14 December 2009. [Google Scholar]
- Ueno, T.; Miura, H.; Yamada, S. Evaluation of a miniature magnetostrictive actuator using galfenol under tensile stress. J. Phys. D 2011, 44, 064017. [Google Scholar] [CrossRef]
- Guo, J.; Lee, D.; Song, J. Chirality Transfer Technique between Liquid Crystal Microdroplets Using Microfluidic Systems. In Proceedings of the Emerging Liquid Crystal Technologies XIII, International Society for Optics and Photonics, San Francisco, CA, USA, 8 February 2018. [Google Scholar]
- Yoshitaka, M.; Katsushi, F. Two-dimensional micromanipulation using liquid crystals. Appl. Phys. Lett. 2005, 86, 101901. [Google Scholar]
- Priest, C.; Quinn, A.; Postma, A.; Zelikin, A.N.; Ralstona, J.; Caruso, F. Microfluidic polymer multilayer adsorption on liquid crystal droplets for microcapsule synthesis. Lab Chip 2008, 8, 2182–2187. [Google Scholar] [CrossRef]
- Deng, J.N.; Wang, X.; Liang, W.; Richardson, D.; Lu, Q.; Fang, J. Surface modified liquid crystal droplets as an optical probe for the detection of bile acids in microfluidic channels. Colloid. Surf. A 2018, 542, 52–58. [Google Scholar] [CrossRef]
- Chono, S.; Tsuji, T. Simulation of the liquid crystalline backflow and the proposal of the micro actuators. Jpn. Soc. Mech. Eng. 2003, 15, 47–48. [Google Scholar]
- Liu, J.H.; Cao, F.; Zhou, C.; Yan, W.; Zhao, Y.; Fu, Z. A Novel Miniature Spatial Hybrid Compliant-Parallel Mechanism Foe Film Micropump. In Proceedings of the IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 2010–2015. [Google Scholar]
- Chakraborty, J.; Ray, S.; Chakraborty, S. Role of streaming potential on pulsating mass flow rate control in combined electroosmotic and pressure-driven microfluidic devices. Electrophoresis 2012, 33, 419–444. [Google Scholar] [CrossRef] [PubMed]
- Sandip, S.; Suvankar, G. Fully developed thermal transport in combined pressure and electroosmotically driven flow of nanofluid in a microchannel under the effect of a magnetic field. Microfluid. Nanofluid. 2015, 18, 623–636. [Google Scholar]
- Li, X.T.; Liu, J.F.; Li, J.Q. Theoretical Research and Design of a New Piezoelectric/Electrorheological Hybrid Hydraulic Step Actuator. In Proceedings of the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; pp. 455–458. [Google Scholar]
- Zhang, X.Y.; Uchiyama, K.K.; Ishizuka, T. High-speed, high-precision magnetic/piezoelectric hybrid drive actuator for micro electrical discharge machining. Adv. Mater. Res. 2014, 941–944, 2112–2115. [Google Scholar] [CrossRef]
- Zheng, Q.; Shi, B.J.; Wang, Z.L. Recent progress on piezoelectric and triboelectric energy harvesters in biomedical systems. Adv. Sci. 2017, 4, 1700029. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Kim, Y.J.; Kim, S.J. Drop-on-demand hybrid printing using a piezoelectric MEMS printhead at various waveforms, high voltages and jetting frequencies. J. Micromech. Microeng. 2013, 23, 065011. [Google Scholar] [CrossRef]
- Koyuncuoglu, A.; Özyurt, O.; Okutucu, T.; Külah, H.; Zorlu, O. Hybrid Energy Harvester Using Piezoelectric and Pyroelectric Properties of PZT-5A Ceramics. In Proceedings of the 11th International Energy Conversion Engineering Conference, San Jose, CA, USA, 15 July 2013. [Google Scholar]
- Hamed, R.; Mansour, N.B.; Aghil, Y.K. Static characterization and pull-in voltage of a micro-switch underboth electrostatic and piezoelectric excitations. Eur. J. Mech. A/Solids 2014, 44, 116–124. [Google Scholar]
- Zhou, S.G.; Xi, J.T. Simulation and experiment study on piezoelectric actuated diaphragm-driven microdroplet jetting. J. Mech. Eng. 2013, 49, 178–185. [Google Scholar] [CrossRef]
- Becker, R.; Feng, X.B.; Prohl, A. Finite element approximations of the Ericksen-Leslie model for nematic liquid crystal flow. SIAM J. Numer. Anal. 2008, 46, 1704–1731. [Google Scholar] [CrossRef]
- Li, J.K.; Titi, E.S.; Xin, Z.P. On the uniqueness of weak solutions to the Ericksen-Leslie liquid crystal model in R2. Math. Models Meth. Appl. Sci. 2016, 26, 803–822. [Google Scholar] [CrossRef]
- Sirohi, J.; Chopra, I. Fundamental understanding of piezoelectric strain sensors. J. Intell. Mater. Syst. Struct. 2000, 11, 246–257. [Google Scholar] [CrossRef]
- Gambhire, P.; Atwell, S.; Iss, C.; Bedu, F.; Ozerov, I.; Badens, C.; Helfer, E.; Viallat, A.; Charrier, A. High aspect ratio sub-micrometer channels using wet etching: Application to the dynamics of red blood cell transiting through biomimetic splenic slits. Small 2017, 13, 1700967. [Google Scholar] [CrossRef] [PubMed]
- Iliescu, C.; Chen, B.; Miao, J. Deep Wet Etching-Through 1 mm Pyrex Glass Wafer for Microfluidic Applications. In Proceedings of the IEEE 20th International Conference on Micro Electro Mechanical Systems, Hyogo, Japan, 21–25 January 2007; pp. 393–396. [Google Scholar]
| Content | Value |
|---|---|
| Density/ | 0.85 kg/m3 |
| Dynamic viscosity/ | 32 Pa·s |
| Rotational viscosity/ | 229 |
| Temperature/T | 300 K |
| Electric permittivity/ and | , |
| Refractive index/ | 0.12–0.15 |
| Elastic constant/, | |
| Conductivity of the ionic solution/ |
| Piezoelectric Material | PZT-5H | Copper |
|---|---|---|
| Diameters (mm) | 9 | 12 |
| Thickness (mm) | 0.05 | 0.12 |
| Young’s modulus (MPa) | 2000 | 1 |
| Poisson’s ratio | 0.3 | 0.32 |
| (pC/N) | –274 | |
| (pC/N) | –274 | |
| (pC/N) | 593 | |
| Density (kg/m3) | 7500 | 1150 |
| Electromechanical coupling factor k | 0.39 | |
| Relative permittivity | 4 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y. Performance Analysis of a Microfluidic Pump Based on Combined Actuation of the Piezoelectric Effect and Liquid Crystal Backflow Effect. Micromachines 2019, 10, 584. https://doi.org/10.3390/mi10090584
Guan Y. Performance Analysis of a Microfluidic Pump Based on Combined Actuation of the Piezoelectric Effect and Liquid Crystal Backflow Effect. Micromachines. 2019; 10(9):584. https://doi.org/10.3390/mi10090584
Chicago/Turabian StyleGuan, Yanfang. 2019. "Performance Analysis of a Microfluidic Pump Based on Combined Actuation of the Piezoelectric Effect and Liquid Crystal Backflow Effect" Micromachines 10, no. 9: 584. https://doi.org/10.3390/mi10090584
APA StyleGuan, Y. (2019). Performance Analysis of a Microfluidic Pump Based on Combined Actuation of the Piezoelectric Effect and Liquid Crystal Backflow Effect. Micromachines, 10(9), 584. https://doi.org/10.3390/mi10090584





