Experimental Study on Microfluidic Mixing with Different Zigzag Angles
Abstract
1. Introduction
2. Method
2.1. Overview
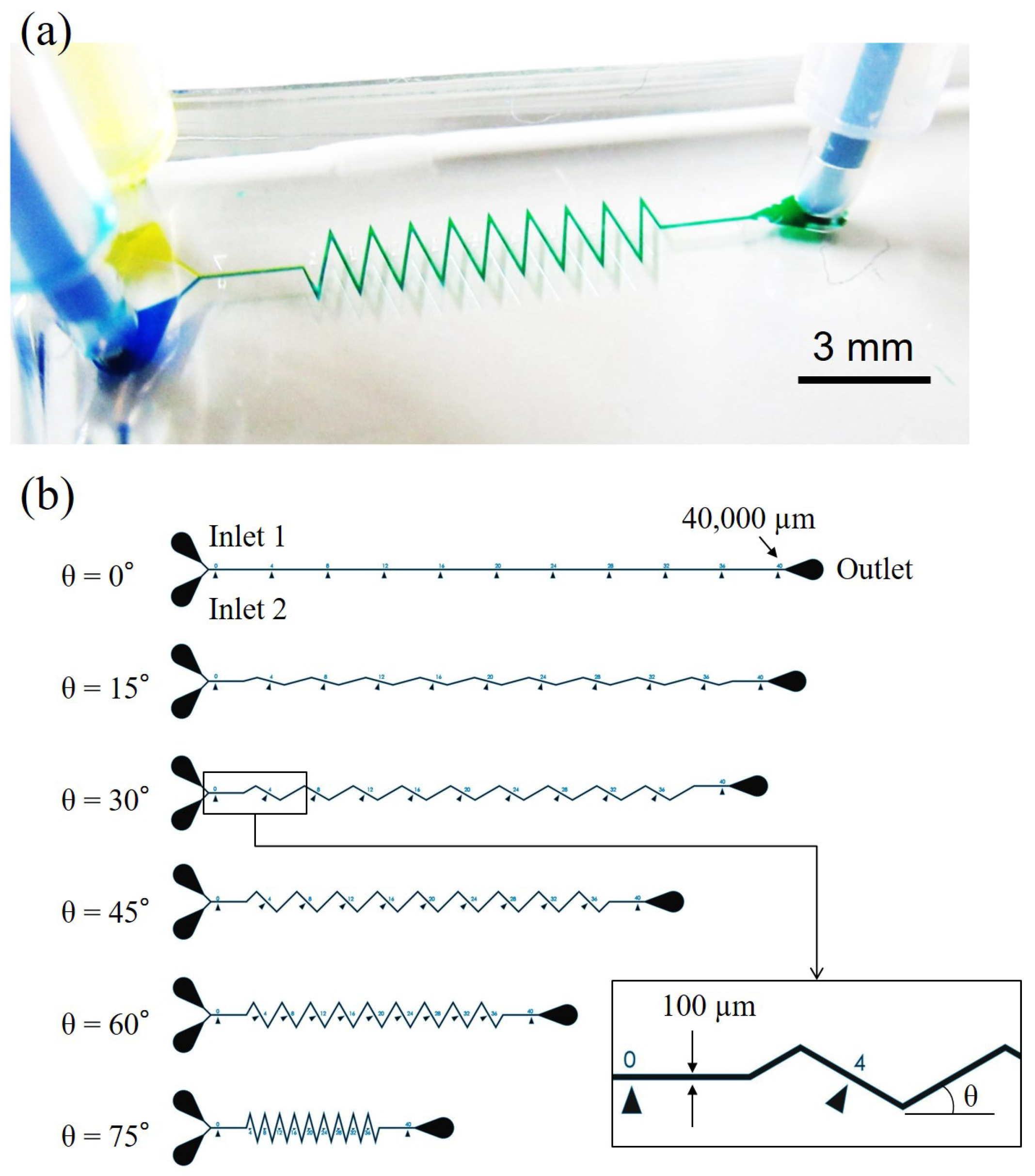
2.2. Experimental System
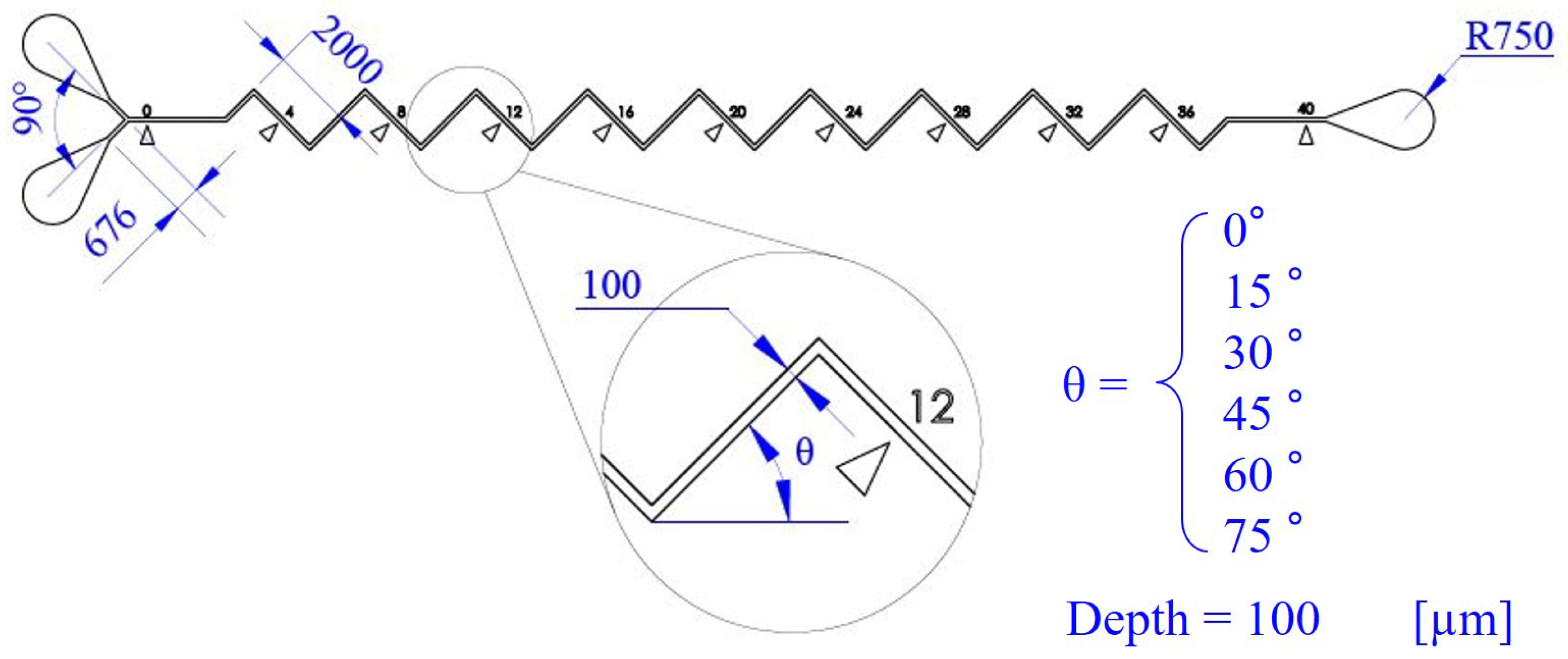
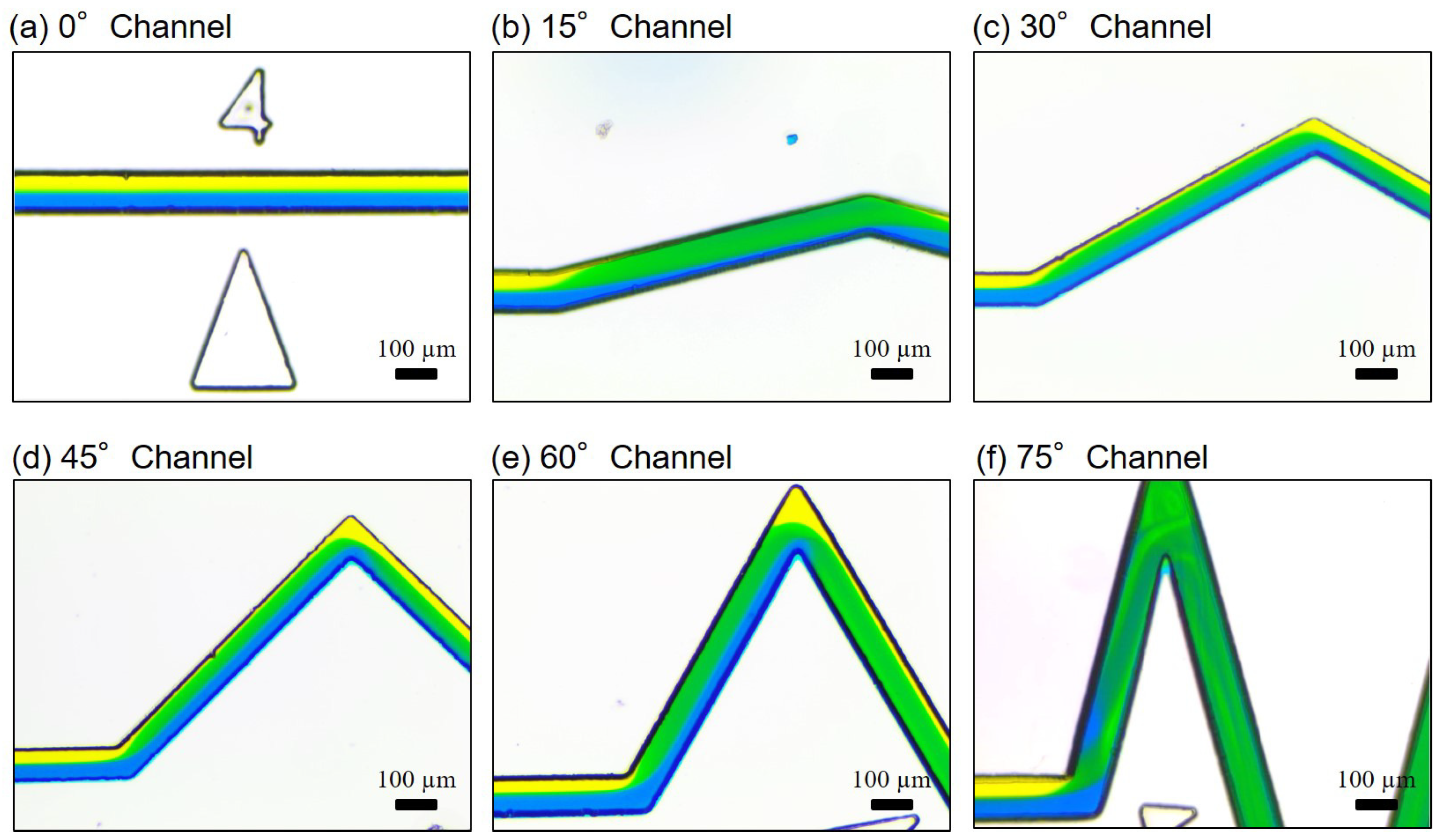
2.3. Dimensions and Fabrication of Microfluidic Channels
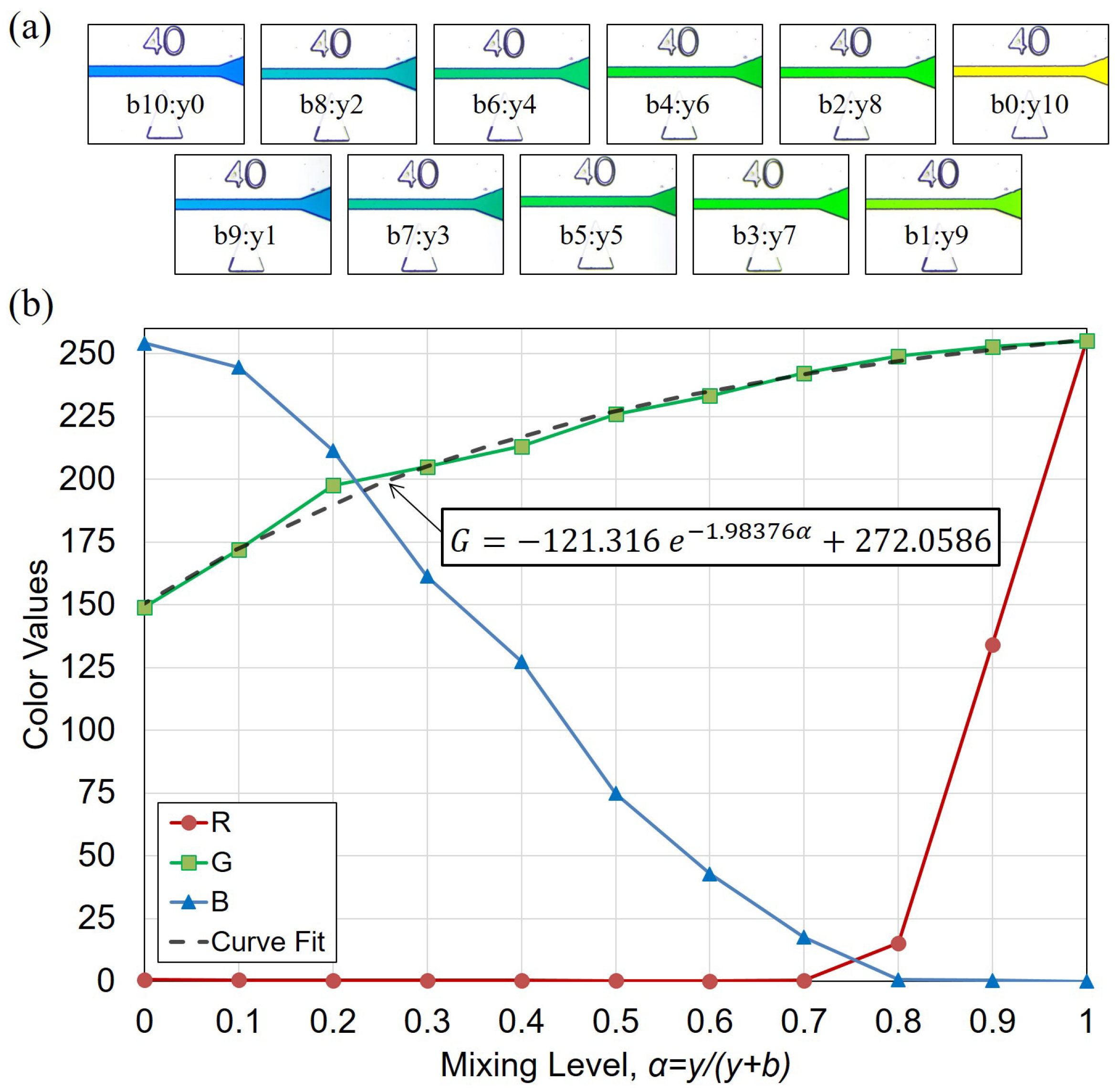
2.4. Image-based Evaluation for Mixing Performance
2.5. Calculation of Reynolds Number,
3. Results
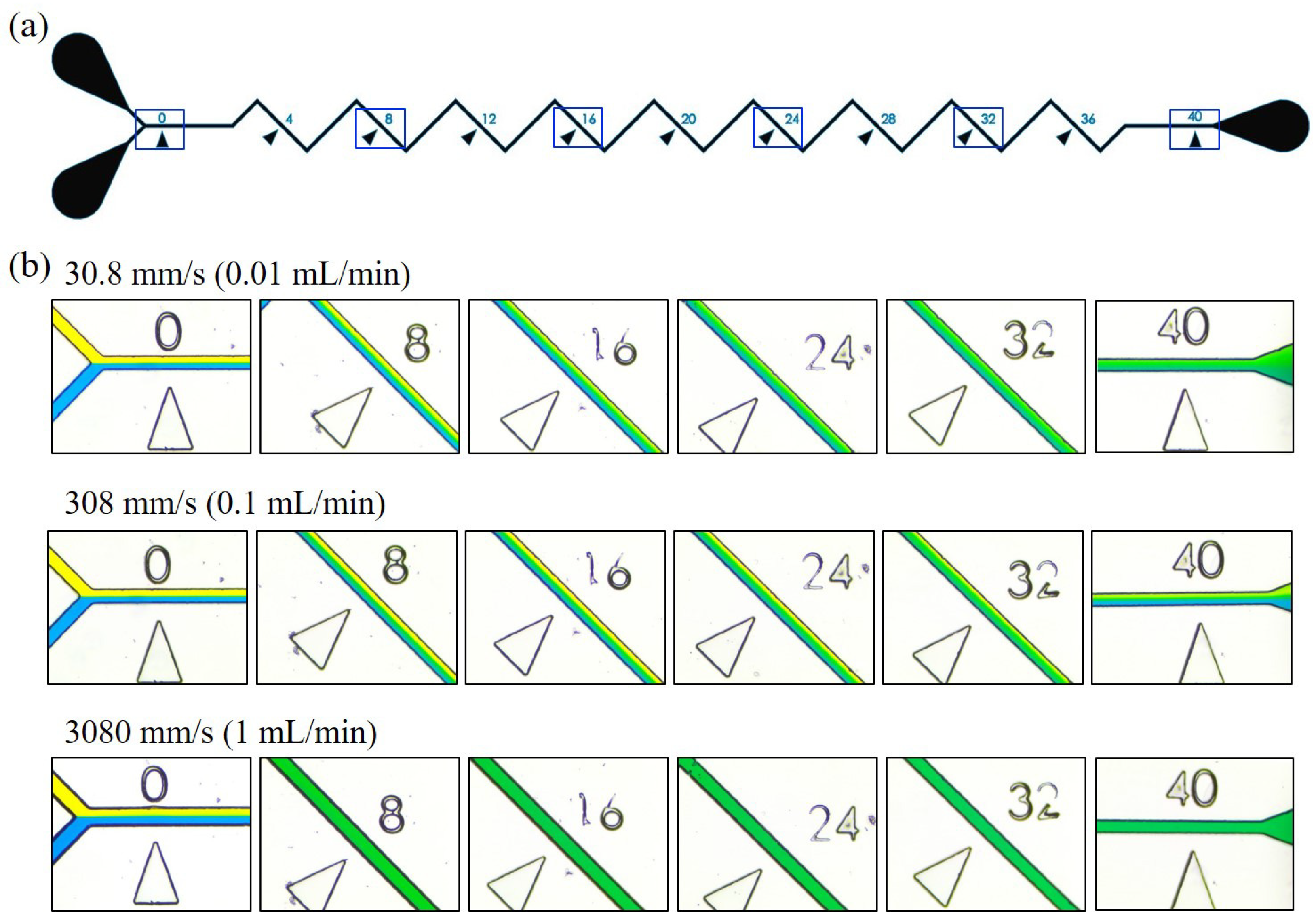
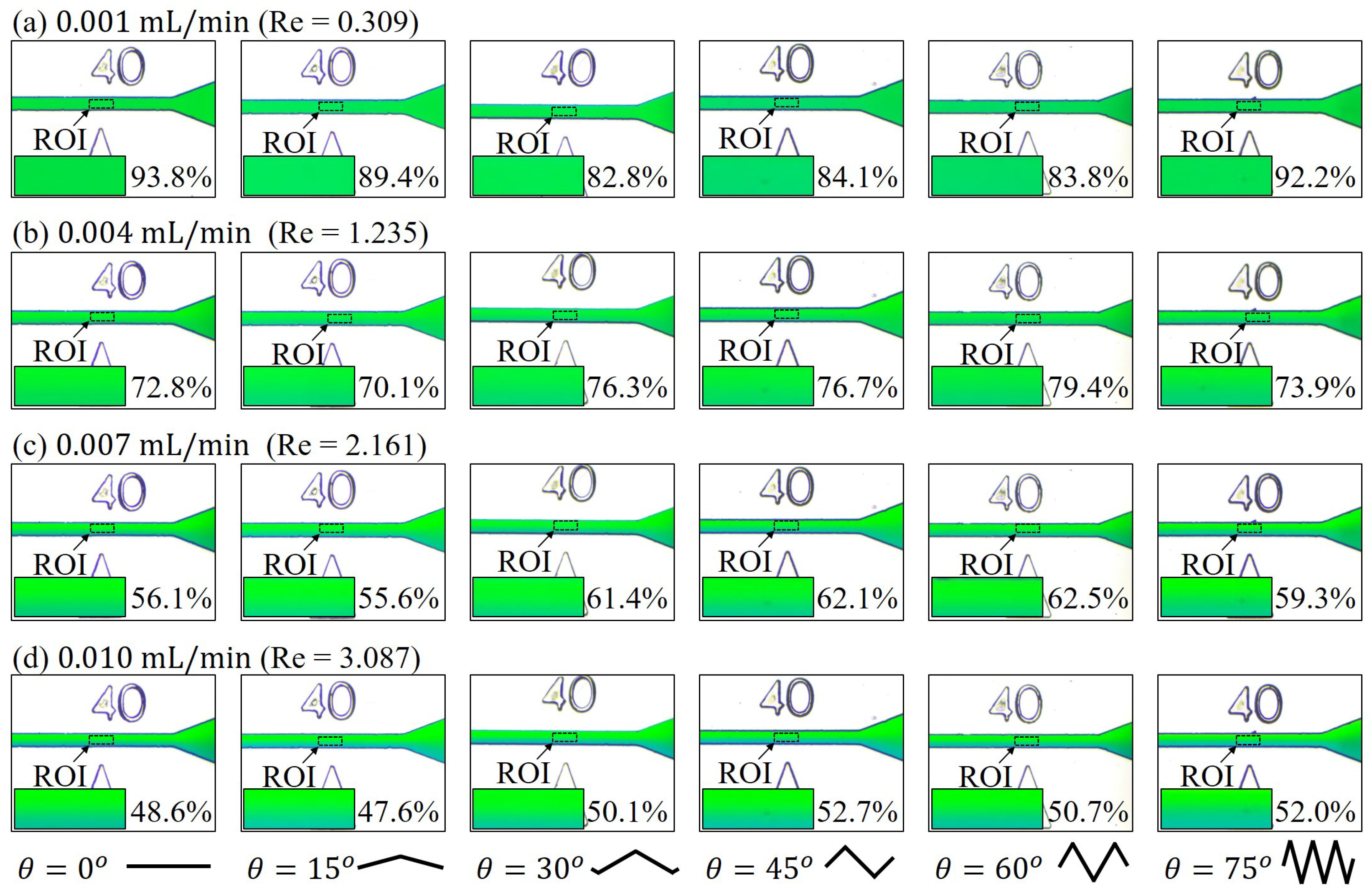
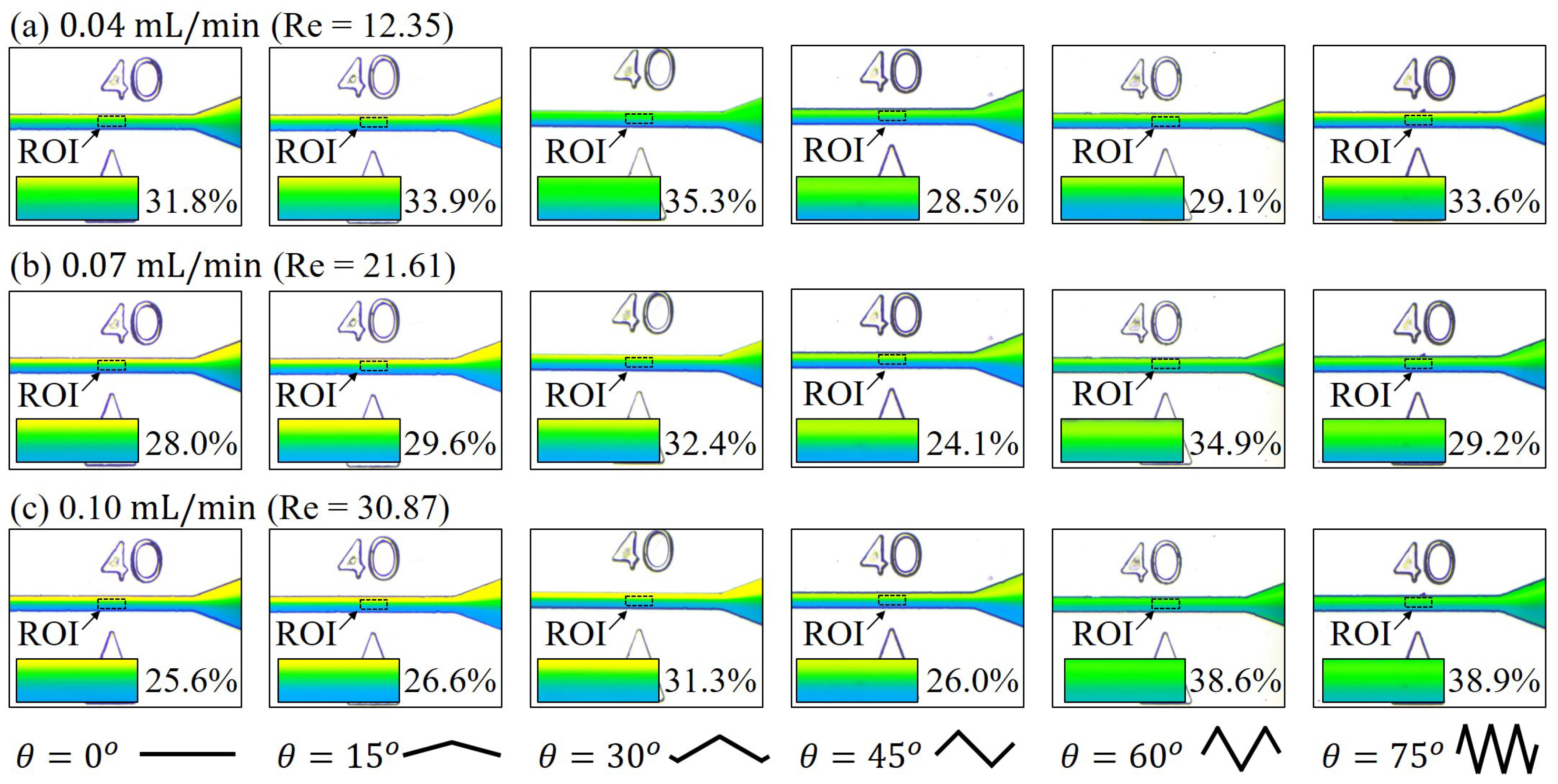
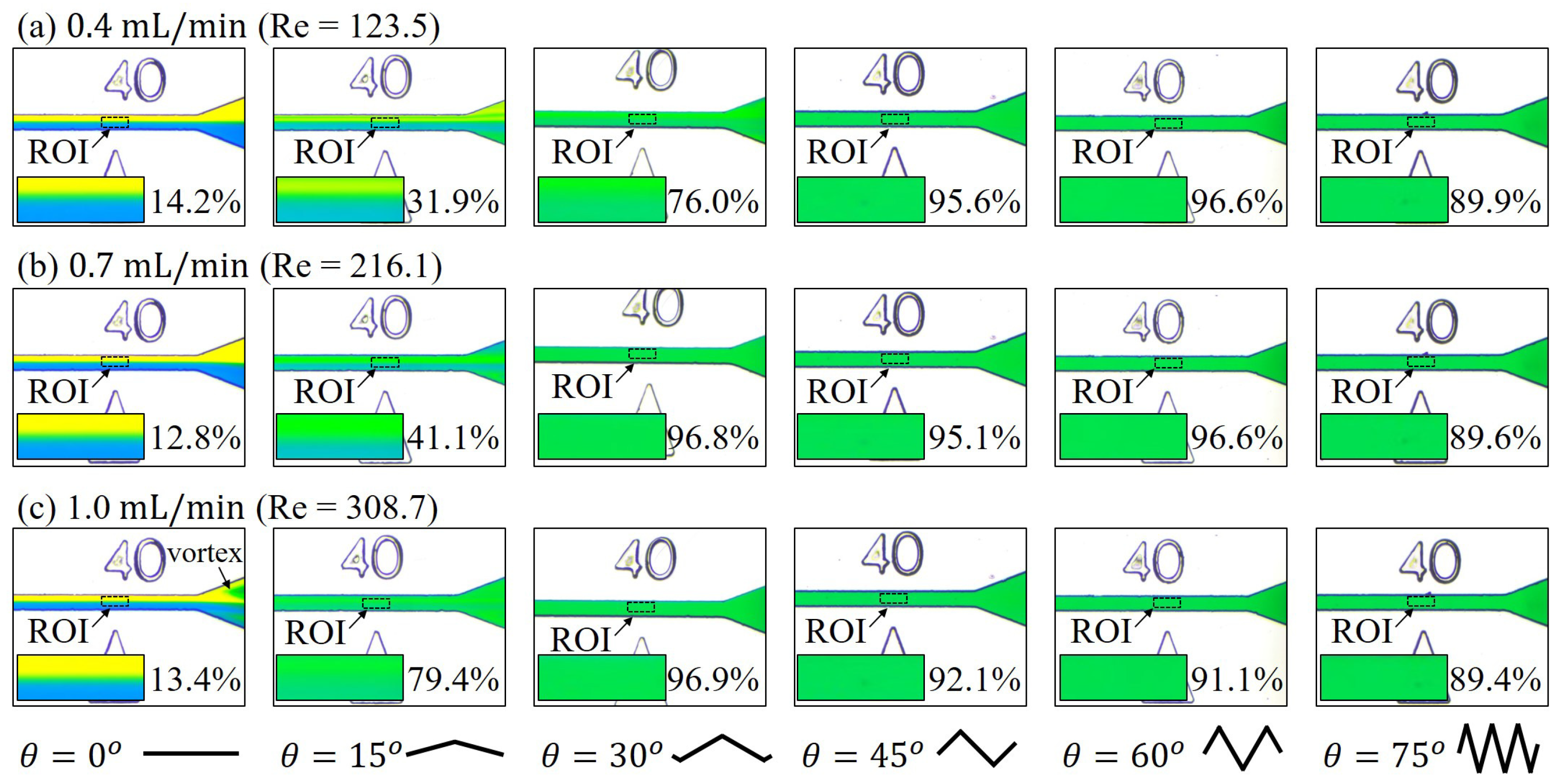
3.1. Mixing at Different Locations along the Channel
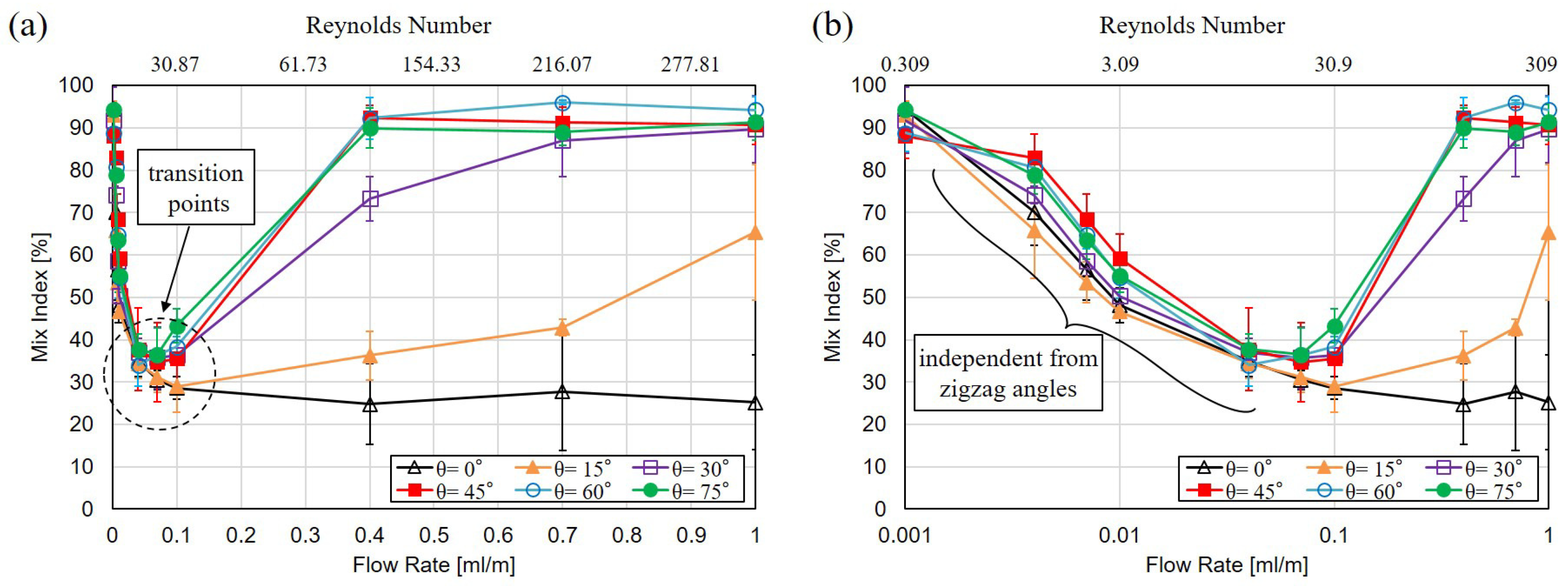
3.2. Mixing with Different Zigzag Angles at Different Flow Rates
4. Discussion
4.1. Mixing of Zigzag Angles in Different Speed Regimes
4.2. Experimental Errors in Flow Control and Channel Dimensions
4.3. Spiral-Like Advection in Different Zigzag Angles
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LOC | lab on a chip |
| ROI | region of interest |
References
- Abate, A.R.; Agresti, J.J.; Weitz, D.A. Microfluidic sorting with high-speed single-layer membrane valves. Appl. Phys. Lett. 2010, 96, 203509. [Google Scholar] [CrossRef]
- Adamo, A.; Sharei, A.; Adamo, L.; Lee, B.; Mao, S.; Jensen, K.F. Microfluidics-based assessment of cell deformability. Anal. Chem. 2012, 84, 6438–6443. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, B.; Maeda, H.; Kawahara, T.; Arai, F. Microrobotic Platform for Single Motile Microorganism Investigation. Micromachines 2017, 8, 295. [Google Scholar] [CrossRef] [PubMed]
- Dhar, M.; Pao, E.; Renier, C.; Go, D.E.; Che, J.; Montoya, R.; Conrad, R.; Matsumoto, M.; Heirich, K.; Triboulet, M.; et al. Label-free enumeration, collection and downstream cytological and cytogenetic analysis of circulating tumor cells. Sci. Rep. 2016, 96, 117A. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.Y.; Chang, C.L.; Wang, Y.N.; Fu, L.M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [PubMed]
- Cheaib, F.; Kekejian, G.; Antoun, S.; Cheikh, M.; Lakkis, I. Microfluidic mixing using pulsating flows. Microfluid. Nanofluid. 2016, 20, 1–19. [Google Scholar] [CrossRef]
- Shang, X.; Huang, X.; Yang, C. Vortex generation and control in a microfluidic chamber with actuations. Phys. Fluids 2016, 28, 122001. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, W.; Syed, A.A.; Chau, Y.; Chen, L.; Chew, B.; Yassine, O.; Wu, X.; Gao, Y.; Zhang, J.; et al. Design and fabrication of magnetically functionalized flexible micropillar arrays for rapid and controllable microfluidic mixing. Lab Chip 2015, 15, 2125–2132. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.C.; Lai, Y.W.; Ben, Y.; Chang, H.C. Microfluidic mixing by dc and ac nonlinear electrokinetic vortex flows. Ind. Eng. Chem. Res. 2004, 43, 2902–2911. [Google Scholar] [CrossRef]
- Chen, C.K.; Cho, C.C. A combined active/passive scheme for enhancing the mixing efficiency of microfluidic devices. Chem. Eng. Sci. 2008, 63, 3081–3087. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, S.W.; Kwon, T.H.; Lee, S.S. A barrier embedded chaotic micromixer. J. Micromechan. Microeng. 2004, 14, 798–805. [Google Scholar] [CrossRef]
- Takayama, T.; Hosokawa, N.; Tsai, C.H.D.; Kaneko, M. On-Chip Super High Speed Mixer. In Proceedings of the 22nd International Conference on Miniaturized Systems for Chemistry and Life Sciences, Kaohsiung, Taiwan, 11–15 November 2018; pp. 487–490. [Google Scholar]
- Lee, C.Y.; Wang, W.T.; Liu, C.C.; Fu, L.M. Passive mixers in microfluidic systems: A review. Chem. Eng. J. 2016, 288, 146–160. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesides, G.M. Chaotic Mixer for Microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.T.; Huang, K.J.; Tung, K.Y.; Hu, I.C.; Lyu, P.C. A chaotic micromixer modulated by constructive vortex agitation. J. Micromechan. Microeng. 2007, 17, 2084–2092. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chung, Y.C.; Wu, C.Y. Mixing enhancement of the passive microfluidic mixer with J-shaped baffles in the tee channel. Biomed. Microdevices 2007, 9, 215–221. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.C.; Hsu, Y.L.; Jen, C.P.; Lu, M.C.; Lin, Y.C. Design of passive mixers utilizing microfluidic self-circulation in the mixing chamber. Lab Chip 2004, 4, 70–77. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.M.; Fang, W.C.; Hou, H.H.; Wang, Y.N.; Hong, T.F. Rapid vortex microfluidic mixer utilizing double-heart chamber. Chem. Eng. J. 2014, 249, 246–251. [Google Scholar] [CrossRef]
- Chen, X.; Li, T. A novel passive micromixer designed by applying an optimization algorithm to the zigzag microchannel. Chem. Eng. J. 2017, 313, 1406–1414. [Google Scholar] [CrossRef]
- The, H.L.; Ta, B.Q.; Thanh, H.L.; Dong, T.; Thoi, T.N.; Karlsen, F. Geometric effects on mixing performance in a novel passive micromixer with trapezoidal-zigzag channels. J. Micromechan. Microeng. 2015, 25, 094004. [Google Scholar] [CrossRef]
- Su, Y.; Chen, G.; Kenig, E.Y. An experimental study on the numbering-up of microchannels for liquid mixing. Lab Chip 2015, 15, 179–187. [Google Scholar] [CrossRef]
- Chen, J.K.; Yang, R.J. Electroosmotic flow mixing in zigzag microchannels. Electrophoresis 2007, 28, 975–983. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, D.; Feng, X.; Xu, Y.; Liu, B.F. A microsecond microfluidic mixer for characterizing fast biochemical reactions. Talanta 2012, 88, 175–180. [Google Scholar] [CrossRef] [PubMed]
- Mengeaud, V.; Josserand, J.; Girault, H.H. Mixing processes in a zigzag microchannel: Finite element simulations and optical study. Anal. Chem. 2002, 74, 4279–4286. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Leung, W.W.F. Flow and mixing in rotating zigzag microchannel. Chem. Eng. J. 2013, 215–216, 561–578. [Google Scholar] [CrossRef]
- Tsai, C.H.D.; Kaneko, M. On-chip pressure sensor using single-layer concentric chambers. Biomicrofluidics 2016, 10, 024116. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, P.J.; Leylegian, J.C. Fox and McDonald’s Introduction to Fluid Mechanics, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tsai, C.H.D.; Takayama, T.; Shimozyo, Y.; Akai, T.; Kaneko, M. Virtual vortex gear: Unique flow patterns driven by microfluidic inertia leading to pinpoint injection. Biomicrofluidics 2018, 12, 034114. [Google Scholar] [CrossRef]
- Di Carlo, D.; Edd, J.F.; Irimia, D.; Tompkins, R.G.; Toner, M. Equilibrium separation and filtration of particles using differential inertial focusing. Anal. Chem. 2008, 80, 2204–2211. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Mak, S.Y.; Sauret, A.; Shum, H.C. Syringe-pump-induced fluctuation in all-aqueous microfluidic system implications for flow rate accuracy. Lab Chip 2014, 14, 744–749. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, C.-H.D.; Lin, X.-Y. Experimental Study on Microfluidic Mixing with Different Zigzag Angles. Micromachines 2019, 10, 583. https://doi.org/10.3390/mi10090583
Tsai C-HD, Lin X-Y. Experimental Study on Microfluidic Mixing with Different Zigzag Angles. Micromachines. 2019; 10(9):583. https://doi.org/10.3390/mi10090583
Chicago/Turabian StyleTsai, Chia-Hung Dylan, and Xin-Yu Lin. 2019. "Experimental Study on Microfluidic Mixing with Different Zigzag Angles" Micromachines 10, no. 9: 583. https://doi.org/10.3390/mi10090583
APA StyleTsai, C.-H. D., & Lin, X.-Y. (2019). Experimental Study on Microfluidic Mixing with Different Zigzag Angles. Micromachines, 10(9), 583. https://doi.org/10.3390/mi10090583





