Numerical Determination of the Secondary Acoustic Radiation Force on a Small Sphere in a Plane Standing Wave Field
Abstract
1. Introduction
2. Methods
2.1. Theoretical Expression for the Primary Acoustic Radiation Force
2.2. Theoretical Expression for the Potential of the Secondary Force
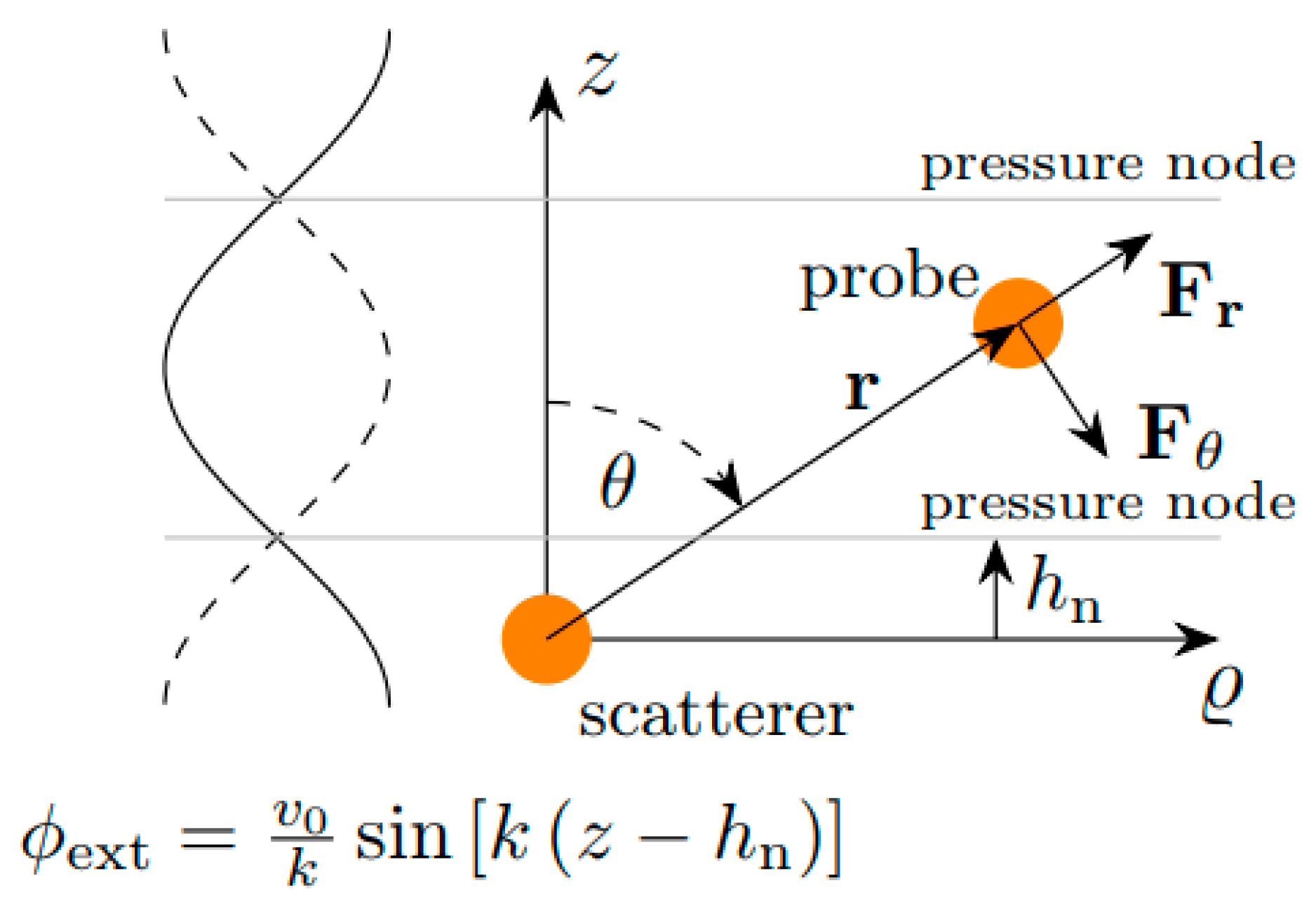
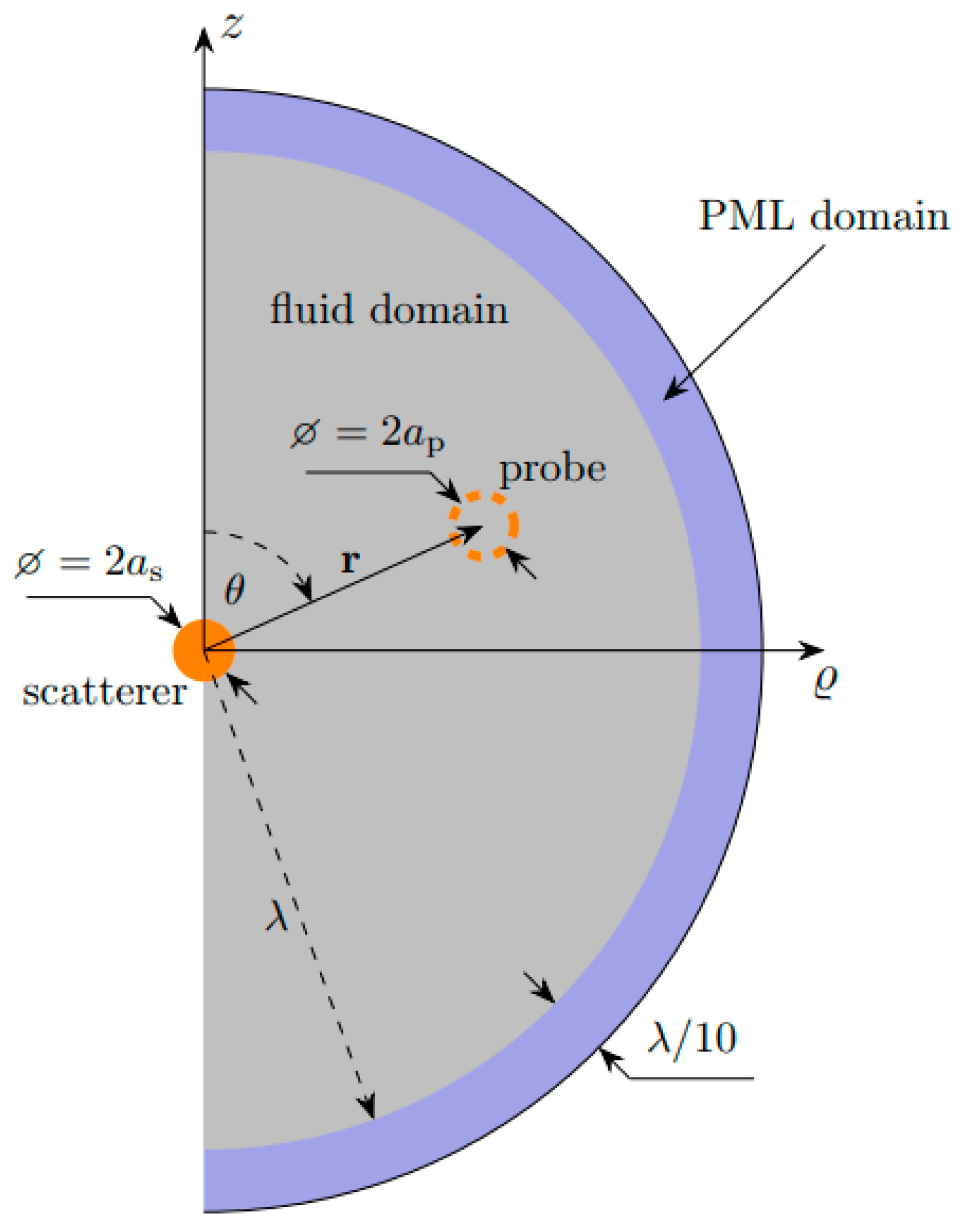
2.3. Determination of the Secondary Force by the Finite Element Method
2.4. Simplified Numerical Approach
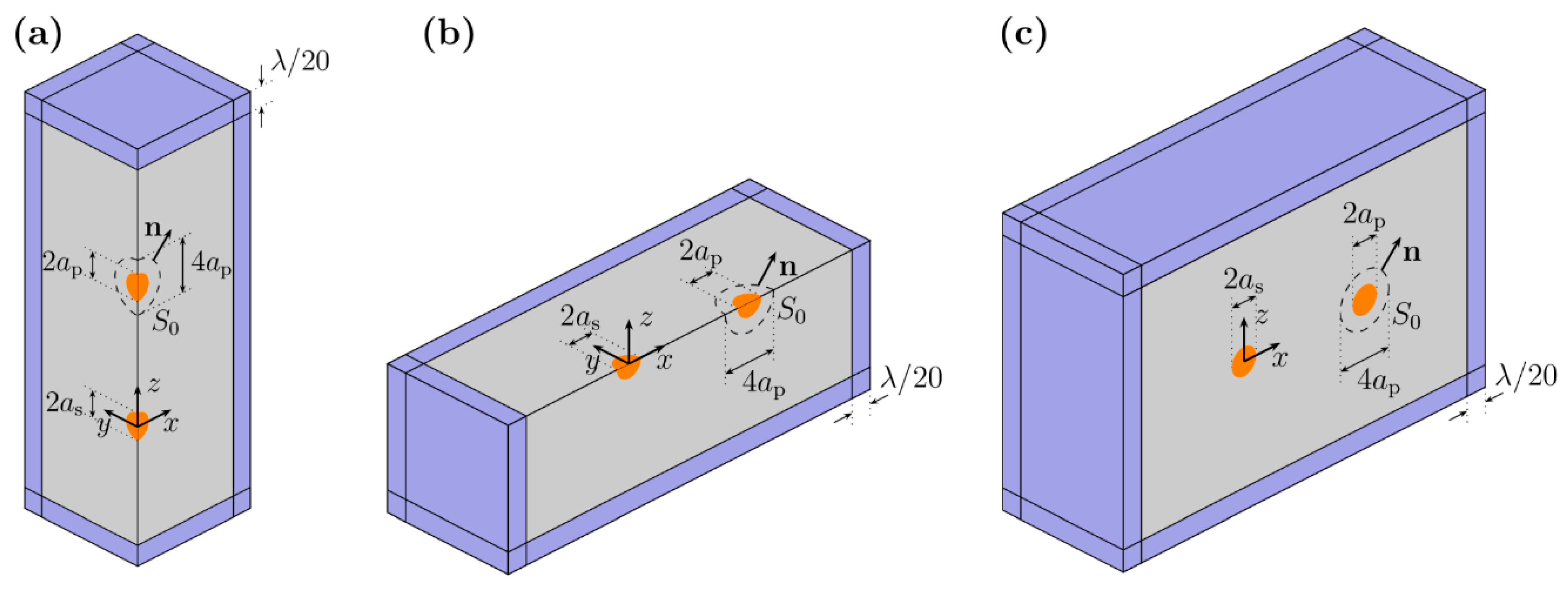
2.5. Complete Finite Element Model Incorporating Re-Scattering Effects
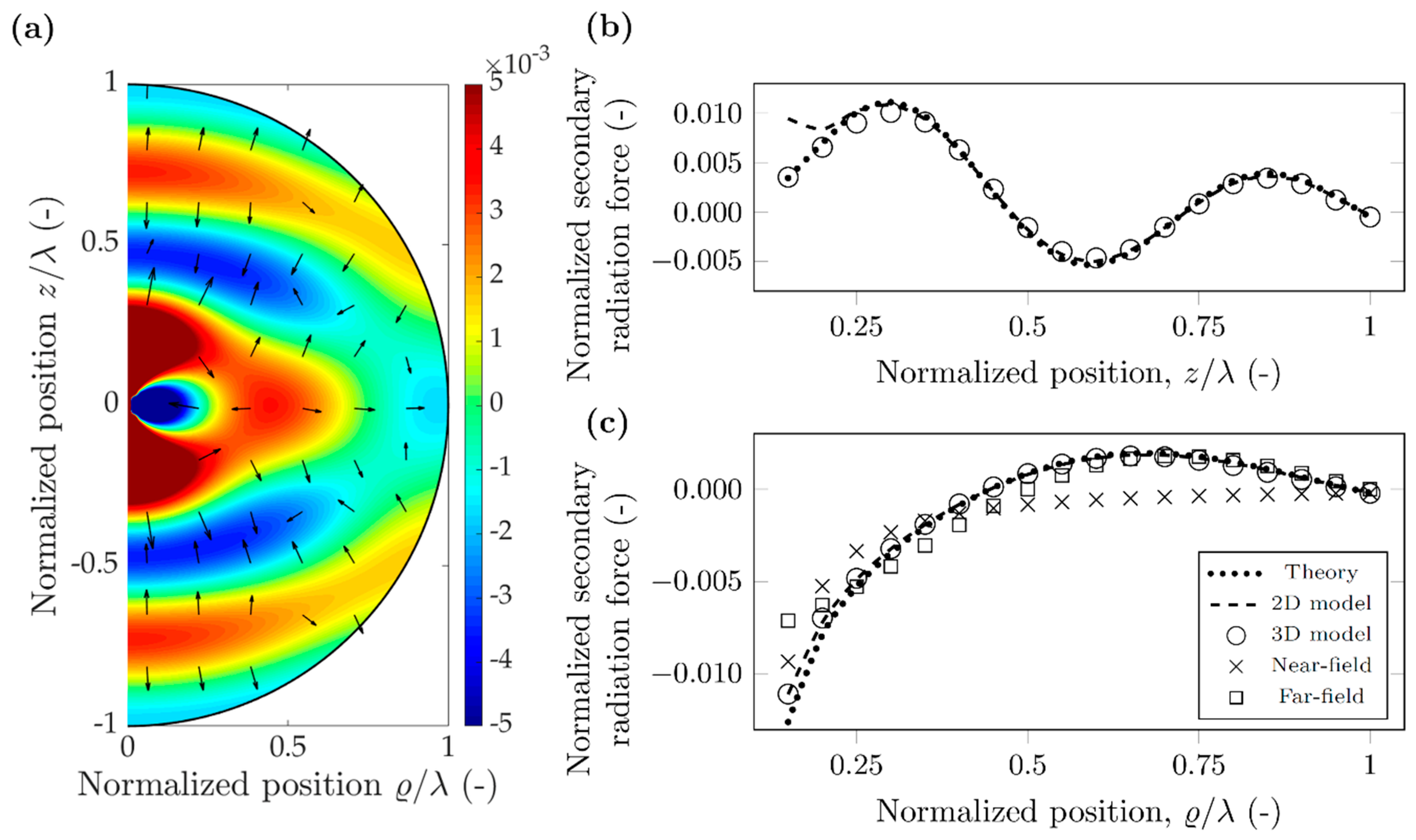
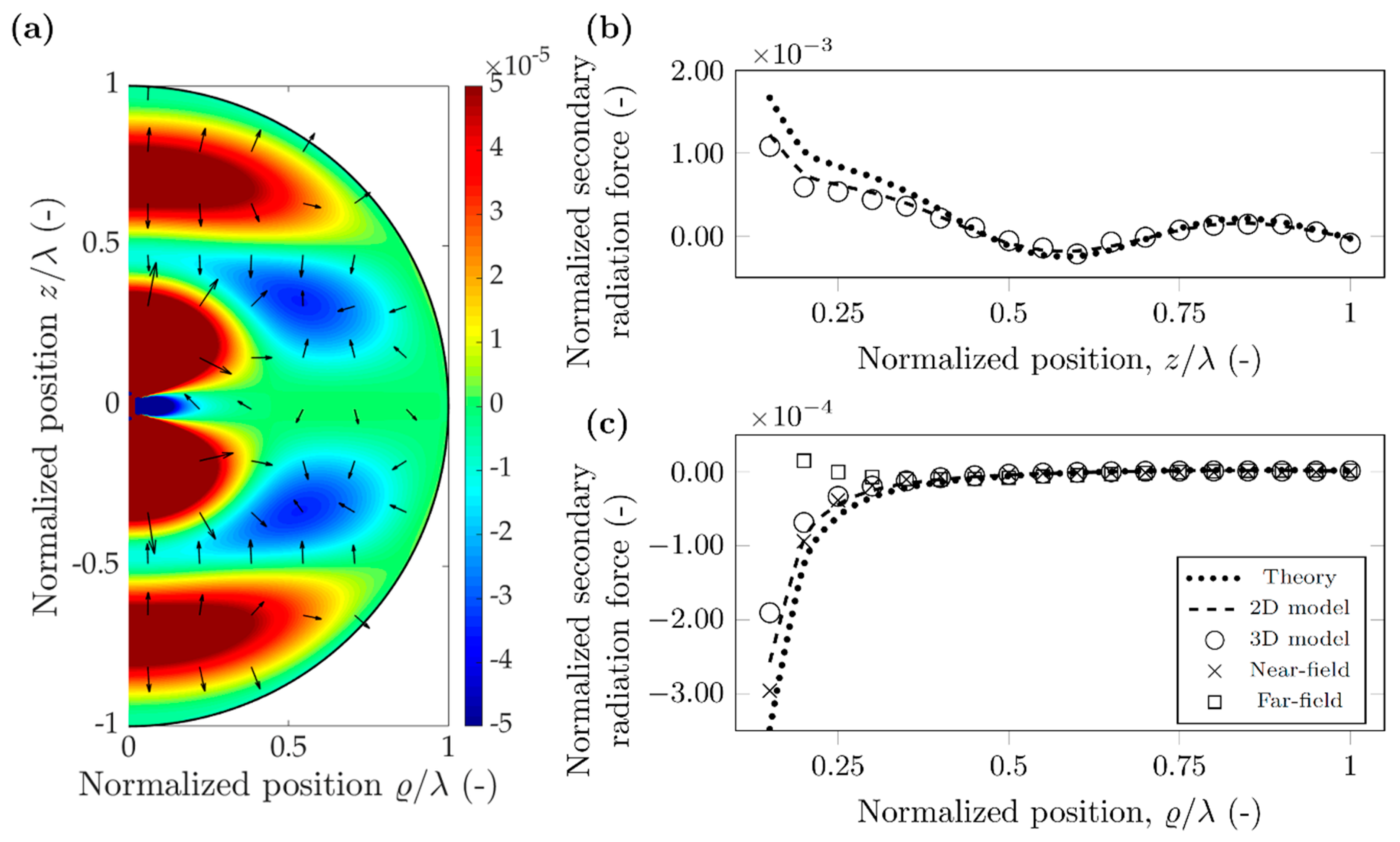
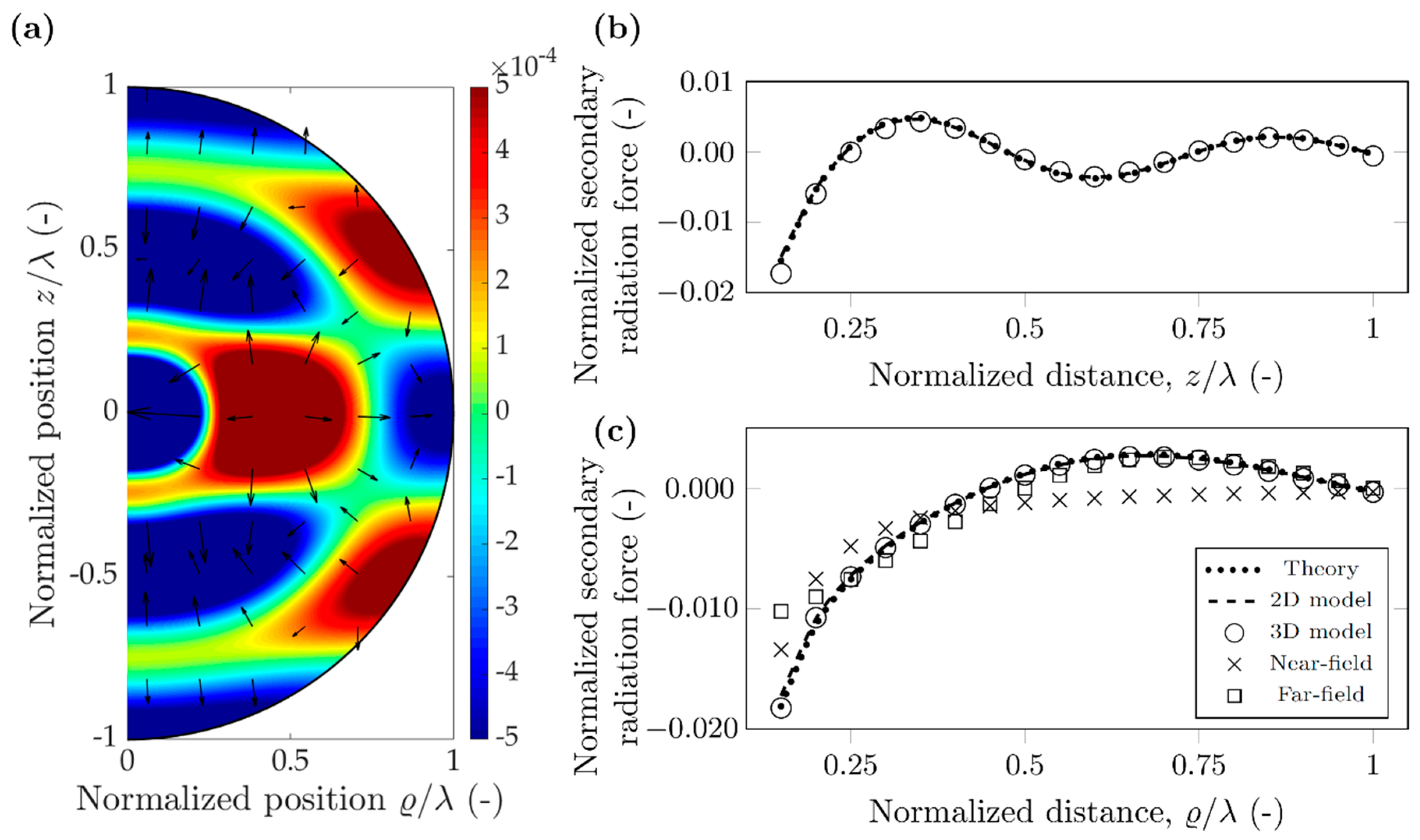
3. Results
3.1. Polystyrene Particle in Air
3.2. Polystyrene Particle in Water
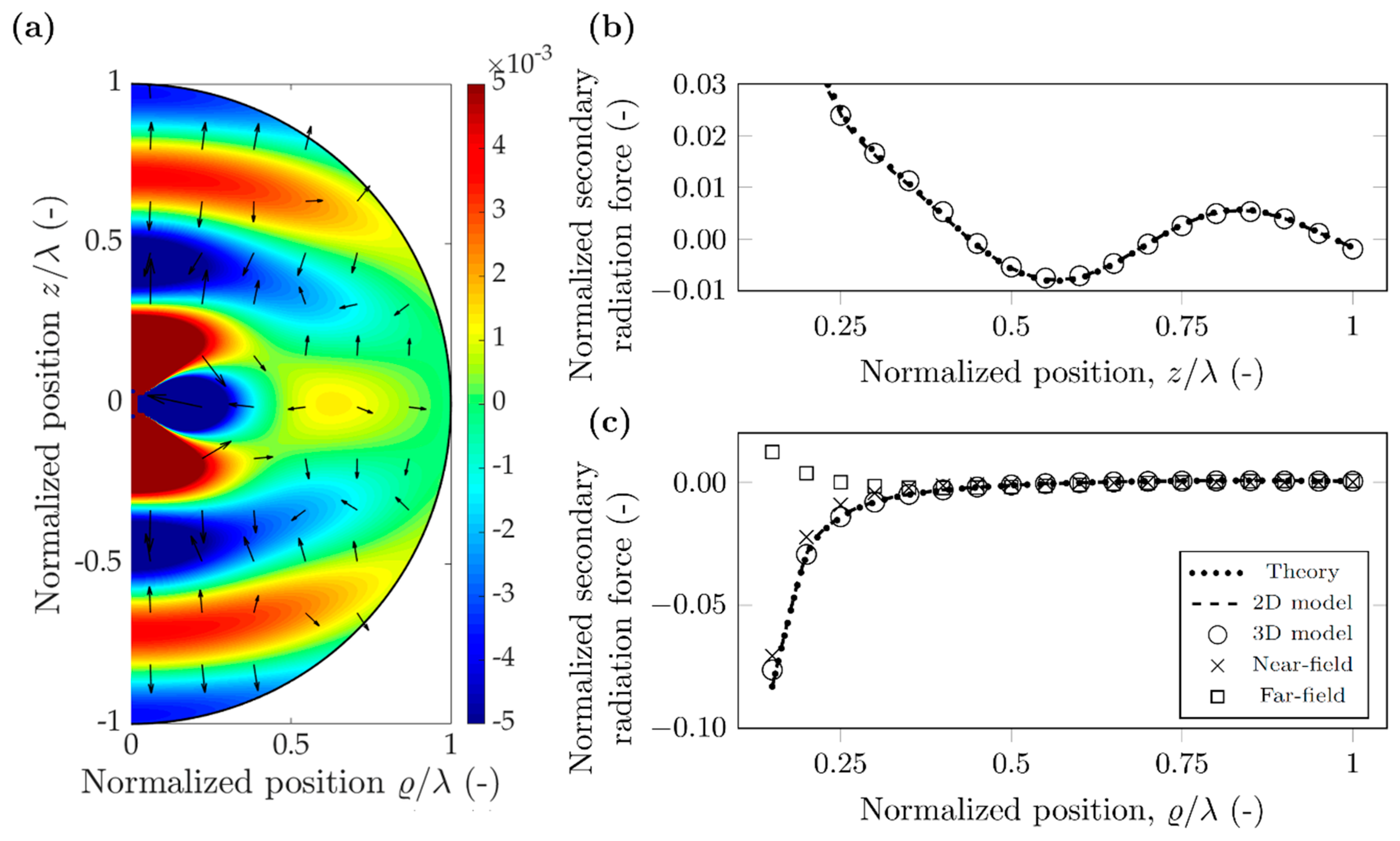
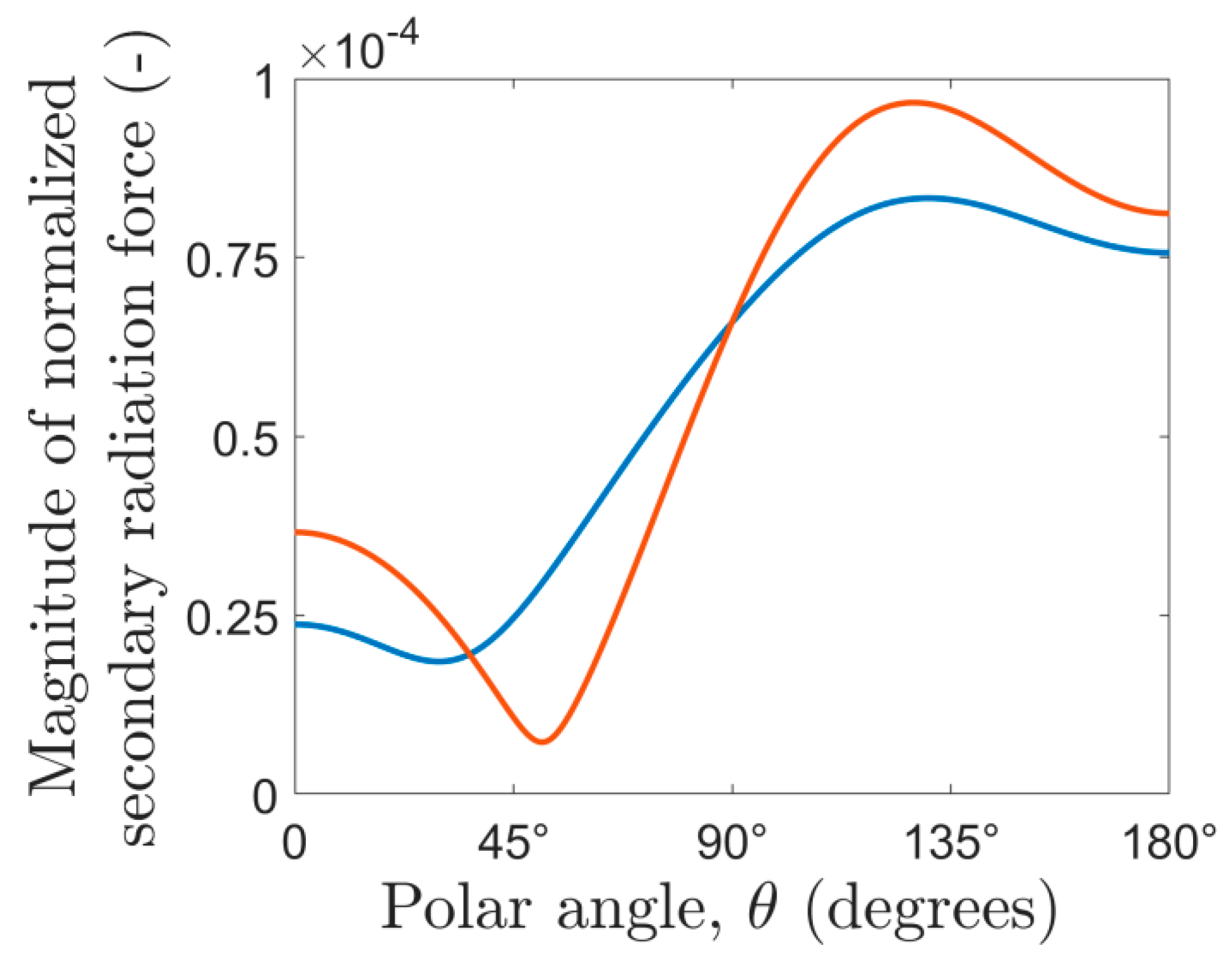
3.3. Properties of the Secondary Radiation Force
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Li, S.; Feng, G.; Yuchao, C.; Xiaoyun, D.; Peng, L.; Lin, W.; Cameron, C.E.; Huang, T.J. Standing Surface Acoustic Wave Based Cell Coculture. Anal. Chem. 2014, 86, 9853–9859. [Google Scholar] [CrossRef] [PubMed]
- Ng, J.W.; Devendran, C.; Neild, A. Acoustic tweezing of particles using decaying opposing travelling surface acoustic waves (DOTSAW). Lab Chip 2017, 17, 3489–3497. [Google Scholar] [CrossRef] [PubMed]
- Simon, G.; Andrade, M.A.B.; Reboud, J.; Marques-Hueso, J.; Desmulliez, M.P.Y.; Cooper, J.M.; Riehle, M.O.; Bernassau, A.L. Particle separation by phase modulated surface acoustic waves. Biomicrofluidics 2017, 11, 054115. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Zhou, W.; Lin, Z.; Cai, F.; Li, F.; Wu, J.; Meng, L.; Niu, L.; Zheng, H. Sorting of tumour cells in a microfluidic device by multi-stage surface acoustic waves. Sens. Actuators B Chem. 2017, 258, 1174–1183. [Google Scholar] [CrossRef]
- King, L.V. On the Acoustic Radiation Pressure on Spheres. Proc. R. Soc. A Math. Phys. Eng. Sci. 1934, 147, 212–240. [Google Scholar] [CrossRef]
- Yosioka, K.; Kawasima, Y. Acoustic radiation pressure on a compressible sphere. Acustica 1955, 5, 167–173. [Google Scholar]
- Gor’kov, L.P. On the Forces Acting on a Small Particle in an Acoustical Field in an Ideal Fluid. Solviet Phys. Dokl. 1962, 6, 773–775. [Google Scholar]
- Doinikov, A.A. Acoustic radiation force on a spherical particle in a viscous heat-conducting fluid. I. General formula. J. Acoust. Soc. Am. 1997, 101, 713–721. [Google Scholar] [CrossRef]
- Settnes, M.; Bruus, H. Forces acting on a small particle in an acoustical field in a viscous fluid. Phys. Rev. E. Stat. Nonlinear Soft Matter Phys. 2012, 85, 016327. [Google Scholar] [CrossRef]
- Leão-Neto, J.P.; Silva, G.T. Acoustic radiation force and torque exerted on a small viscoelastic particle in an ideal fluid. Ultrasonics 2016, 71, 1–11. [Google Scholar] [CrossRef]
- Mitri, F.G. Theoretical calculation of the modulated acoustic radiation force on spheres and cylinders in a standing plane wave-field. Phys. D Nonlinear Phenom. 2005, 212, 66–81. [Google Scholar] [CrossRef]
- Mitri, F.G. Acoustic radiation force of high-order Bessel beam standing wave tweezers on a rigid sphere. Ultrasonics 2009, 49, 794–798. [Google Scholar] [CrossRef] [PubMed]
- Mitri, F.G. Axial acoustic radiation force on rigid oblate and prolate spheroids in Bessel vortex beams of progressive, standing and quasi-standing waves. Ultrasonics 2017, 74, 62–71. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Baasch, T.; Dual, J. Acoustofluidic particle dynamics: Beyond the Rayleigh limit. J. Acoust. Soc. Am. 2018, 143, 509–519. [Google Scholar] [CrossRef] [PubMed]
- Collino, R.R.; Ray, T.R.; Fleming, R.C.; Sasaki, C.H.; Haj-Hariri, H.; Begley, M.R. Acoustic field controlled patterning and assembly of anisotropic particles. Extrem. Mech. Lett. 2015, 5, 37–46. [Google Scholar] [CrossRef]
- Nyborg, W.L. Theoretical criterion for acoustic aggregation. Ultrasound Med. Biol. 1989, 15, 93–99. [Google Scholar] [CrossRef]
- Baasch, T.; Leibacher, I.; Dual, J. Multibody dynamics in acoustophoresis. J. Acoust. Soc. Am. 2017, 141, 1664–1674. [Google Scholar] [CrossRef]
- Bjerknes, V.F.K. Fields of Force; Columbia University: New York, NY, USA, 1906. [Google Scholar]
- Crum, L.A. Bjerknes forces on bubbles in a stationary sound field. J. Acoust. Soc. Am. 1975, 57, 1363–1370. [Google Scholar] [CrossRef]
- Pelekasis, N.A.; Gaki, A.; Doinikov, A.; Tsamopoulos, J.A. Secondary Bjerknes forces between two bubbles and the phenomenon of acoustic streamers. J. Fluid Mech. 2004, 500, 313–347. [Google Scholar] [CrossRef]
- Pelekasis, N.A.; Tsamopoulos, J.A. Bjerknes forces between two bubbles. Part 1. Response to a step change in pressure. J. Fluid Mech. 1993, 254, 467–499. [Google Scholar] [CrossRef]
- Pelekasis, N.A.; Tsamopoulos, J.A. Bjerknes forces between two bubbles. Part 2. Response to an oscillatory pressure field. J. Fluid Mech. 1993, 254, 501–527. [Google Scholar] [CrossRef]
- Yasui, K.; Iida, Y.; Tuziuti, T.; Kozuka, T.; Towata, A. Strongly interacting bubbles under an ultrasonic horn. Phys. Rev. E Stat. Nonlinear. Soft Matter Phys. 2008, 77, 016609. [Google Scholar] [CrossRef] [PubMed]
- Zhuk, A.P. Hydrodynamic interaction of two spherical particles due to sound waves propagating perpendicularly to the center line. Sov. Appl. Mech. 1985, 21, 307–312. [Google Scholar] [CrossRef]
- Garcia-Sabaté, A.; Castro, A.; Hoyos, M.; González-Cinca, R. Experimental study on inter-particle acoustic forces. J. Acoust. Soc. Am. 2014, 135, 1056–1063. [Google Scholar] [CrossRef] [PubMed]
- Silva, G.T.; Bruus, H. Acoustic interaction forces between small particles in an ideal fluid. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 063007. [Google Scholar] [CrossRef] [PubMed]
- Doinikov, A.A. Acoustic radiation interparticle forces in a compressible fluid. J. Fluid Mech. 2001, 444, 1–21. [Google Scholar] [CrossRef]
- Sepehrirahnama, S.; Lim, K.-M.; Chau, F.S. Numerical study of interparticle radiation force acting on rigid spheres in a standing wave. J. Acoust. Soc. Am. 2015, 137, 2614–2622. [Google Scholar] [CrossRef]
- Wijaya, F.B.; Sepehrirahnama, S.; Lim, K.M. Interparticle force and torque on rigid spheroidal particles in acoustophoresis. Wave Motion 2018, 81, 28–45. [Google Scholar] [CrossRef]
- Glynne-Jones, P.; Mishra, P.P.; Boltryk, R.J.; Hill, M. Efficient finite element modeling of radiation forces on elastic particles of arbitrary size and geometry. J. Acoust. Soc. Am. 2013, 133, 1885–1893. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Bruus, H. Acoustofluidics 7: The acoustic radiation force on small particles. Lab Chip 2012, 12, 1014–1021. [Google Scholar] [CrossRef]
- Martin, P.A. Multiple Scattering: Interaction of Time-Harmonic Waves with N Obstacles; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Zhang, P.; Li, T.; Zhu, J.; Zhu, X.; Yang, S.; Wang, Y.; Yin, X.; Zhang, X. Generation of acoustic self-bending and bottle beams by phase engineering. Nat. Commun. 2014, 5, 4316. [Google Scholar] [CrossRef] [PubMed]
- Andrade, M.A.B.; Okina, F.T.A.; Bernassau, A.L.; Adamowski, J.C. Acoustic levitation of an object larger than the acoustic wavelength. J. Acoust. Soc. Am. 2017, 141, 4148–4154. [Google Scholar] [CrossRef] [PubMed]
- Nama, N.; Barnkob, R.; Mao, Z.; Kähler, C.J.; Costanzo, F.; Huang, T.J. Numerical study of acoustophoretic motion of particles in a PDMS microchannel driven by surface acoustic waves. Lab Chip 2015, 15, 2700–2709. [Google Scholar] [CrossRef] [PubMed]
- Bernassau, A.L.; Courtney, C.R.P.; Beeley, J.; Drinkwater, B.W.; Cumming, D.R.S. Interactive manipulation of microparticles in an octagonal sonotweezer. Appl. Phys. Lett. 2013, 102, 164101. [Google Scholar] [CrossRef]
- Lenshof, A.; Magnusson, C.; Laurell, T. Acoustofluidics 8: Applications of acoustophoresis in continuous flow microsystems. Lab Chip 2012, 12, 1210–1223. [Google Scholar] [CrossRef] [PubMed]
- Skotis, G.D.; Cumming, D.R.S.; Roberts, J.N.; Riehle, M.O.; Bernassau, A.L. Dynamic acoustic field activated cell separation (DAFACS). Lab Chip 2015, 15, 802–810. [Google Scholar] [CrossRef] [PubMed]
- Muller, P.B.; Barnkob, R.; Jensen, M.J.H.; Bruus, H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab Chip 2012, 12, 4617–4627. [Google Scholar] [CrossRef]
- Devendran, C.; Albrecht, T.; Brenker, J.; Alan, T.; Neild, A. The importance of travelling wave components in standing surface acoustic wave (SSAW) systems. Lab Chip 2016, 16, 3756–3766. [Google Scholar] [CrossRef]

| Symbol | Description | Value |
|---|---|---|
| f | Frequency | 10 kHz |
| c0 | Speed of sound in air a | 343 m/s |
| λ | Wavelength in air | 34.3 mm |
| ρ0 | Density of air | 1.225 kg/m3 |
| as, ap | Radius of scatterer and probe particle () | 1.715 mm |
| ρs, ρp | Density of scatterer and probe particle b | 1050 kg/m3 |
| cs, cp | Speed of sound of scatterer and probe b | 2350 m/s |
| f0,s, f0,p | Monopole scattering coefficient c | 0.99998 |
| f1,s, f1,p | Dipole scattering coefficient d | 0.99825 |
| p0 | Acoustic pressure amplitude | 50 kPa |
| ΦAC | Acoustic contrast factor | 2.4974 |
| Symbol | Description | Value |
|---|---|---|
| f | Frequency | 10 MHz |
| c0 | Speed of sound in water a | 1480 m/s |
| λ | Wavelength in air | 148 µm |
| ρ0 | Density of water | 998 kg/m3 |
| as, ap | Radius of scatterer and probe particle () | 7.4 µm |
| ρs, ρp | Density of scatterer and probe particle b | 1050 kg/m3 |
| cs, cp | Speed of sound of scatterer and probe b | 2350 m/s |
| f0,s, f0,p | Monopole scattering coefficient c | 0.623 |
| f1,s, f1,p | Dipole scattering coefficient d | 0.034 |
| p0 | Acoustic pressure amplitude | 50 kPa |
| ΦAC | Acoustic contrast factor | 0.6734 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, G.; Andrade, M.A.B.; Desmulliez, M.P.Y.; Riehle, M.O.; Bernassau, A.L. Numerical Determination of the Secondary Acoustic Radiation Force on a Small Sphere in a Plane Standing Wave Field. Micromachines 2019, 10, 431. https://doi.org/10.3390/mi10070431
Simon G, Andrade MAB, Desmulliez MPY, Riehle MO, Bernassau AL. Numerical Determination of the Secondary Acoustic Radiation Force on a Small Sphere in a Plane Standing Wave Field. Micromachines. 2019; 10(7):431. https://doi.org/10.3390/mi10070431
Chicago/Turabian StyleSimon, Gergely, Marco A. B. Andrade, Marc P. Y. Desmulliez, Mathis O. Riehle, and Anne L. Bernassau. 2019. "Numerical Determination of the Secondary Acoustic Radiation Force on a Small Sphere in a Plane Standing Wave Field" Micromachines 10, no. 7: 431. https://doi.org/10.3390/mi10070431
APA StyleSimon, G., Andrade, M. A. B., Desmulliez, M. P. Y., Riehle, M. O., & Bernassau, A. L. (2019). Numerical Determination of the Secondary Acoustic Radiation Force on a Small Sphere in a Plane Standing Wave Field. Micromachines, 10(7), 431. https://doi.org/10.3390/mi10070431






