Intensity Switchable and Wide-Angle Mid-Infrared Perfect Absorber with Lithography-Free Phase-Change Film of Ge2Sb2Te5
Abstract
1. Introduction
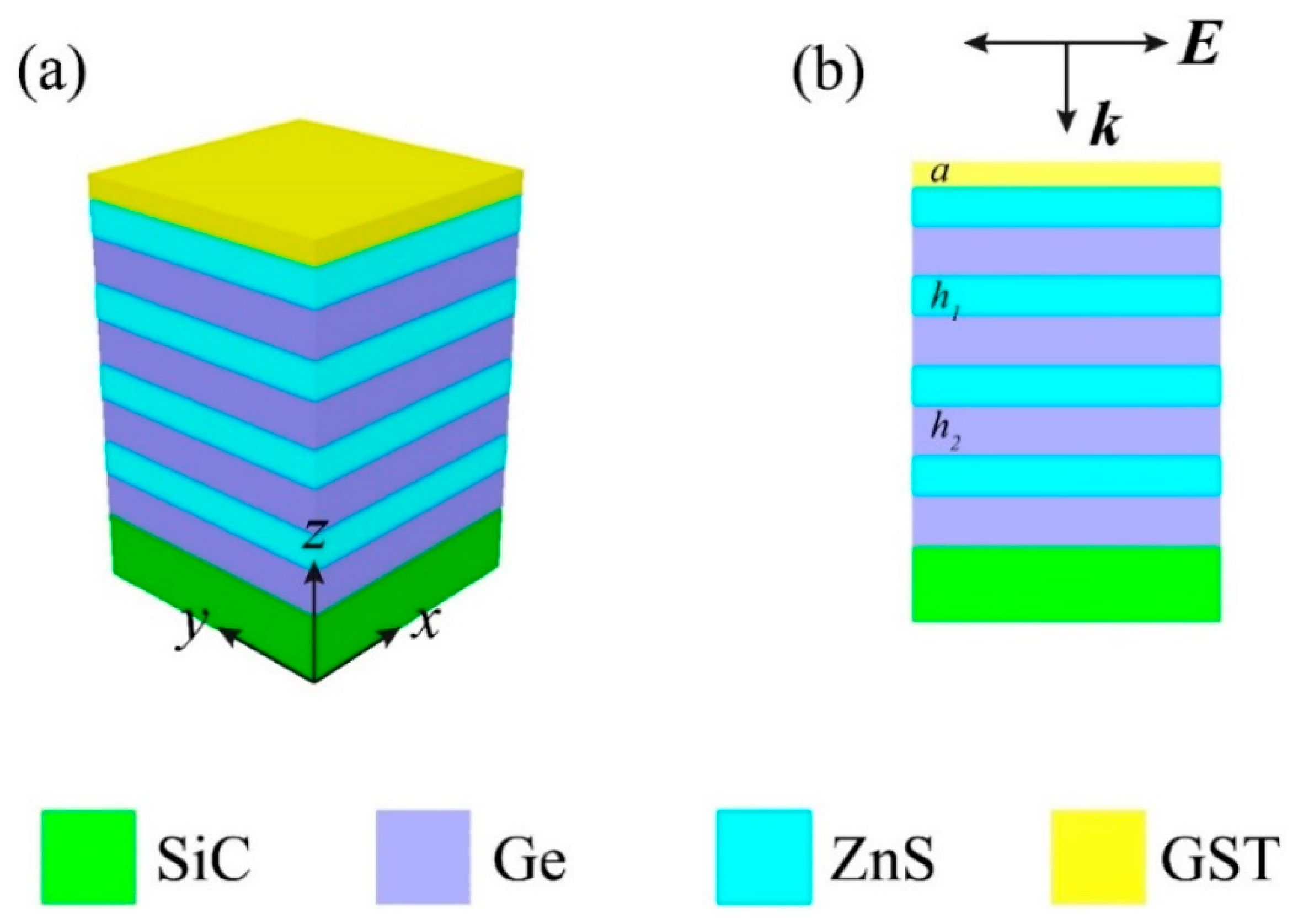
2. Model and Methods
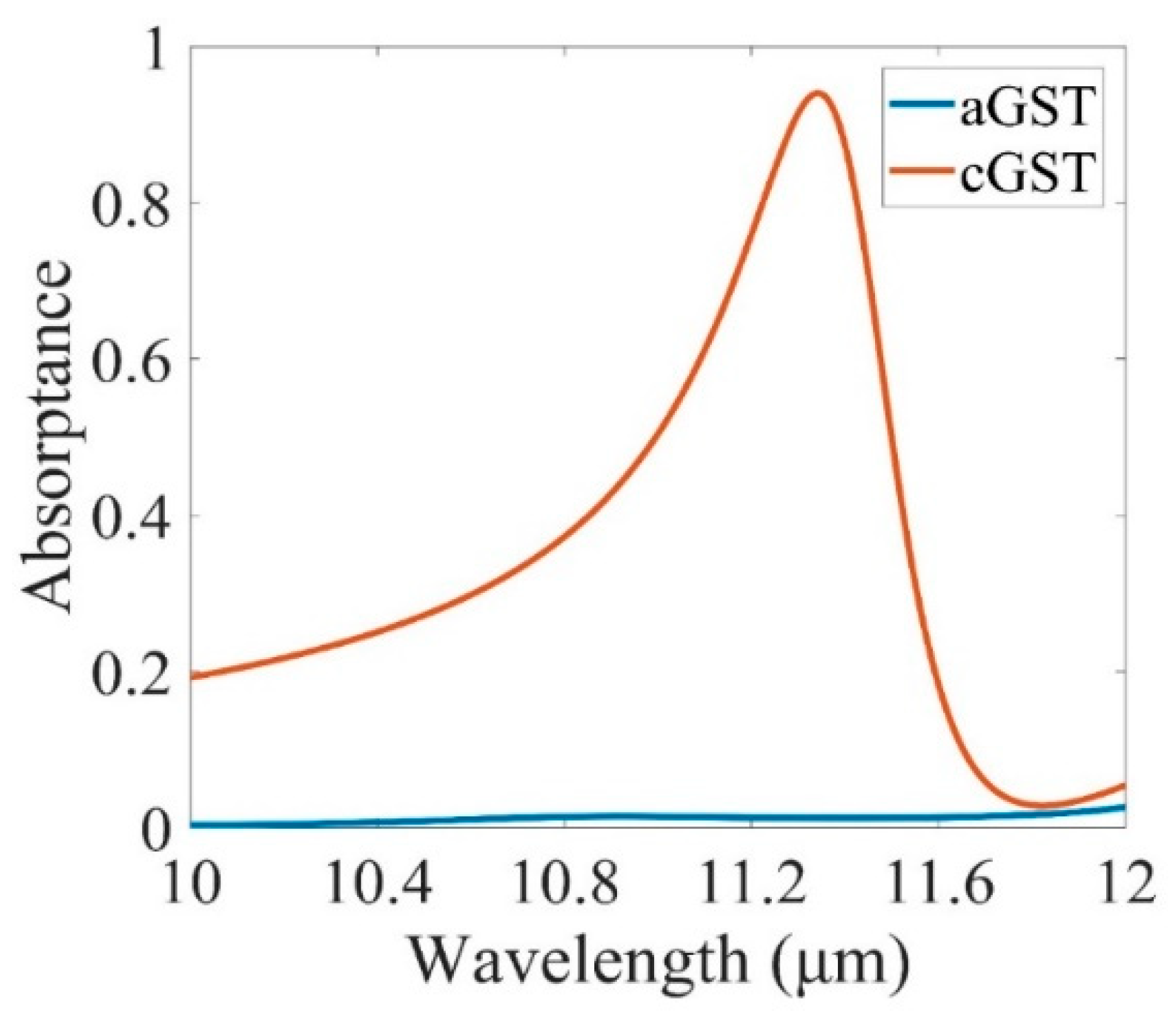
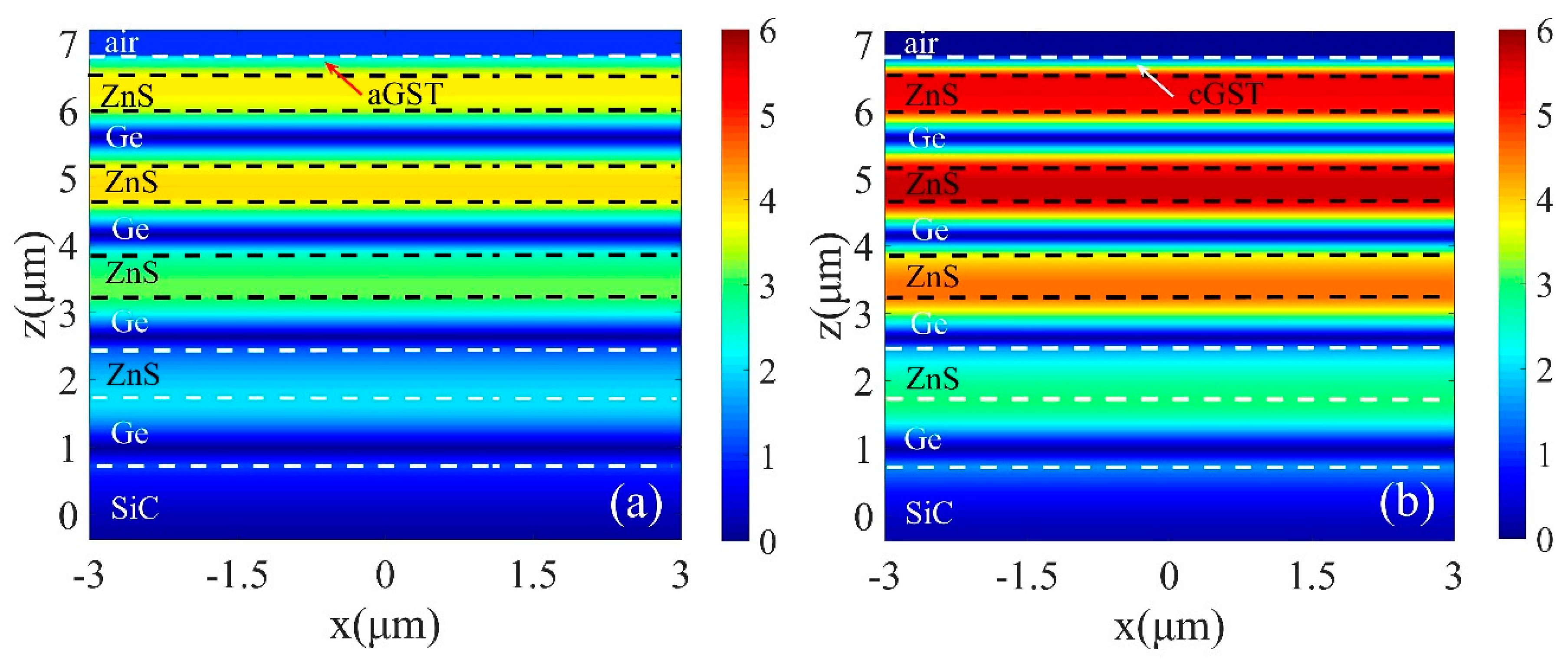
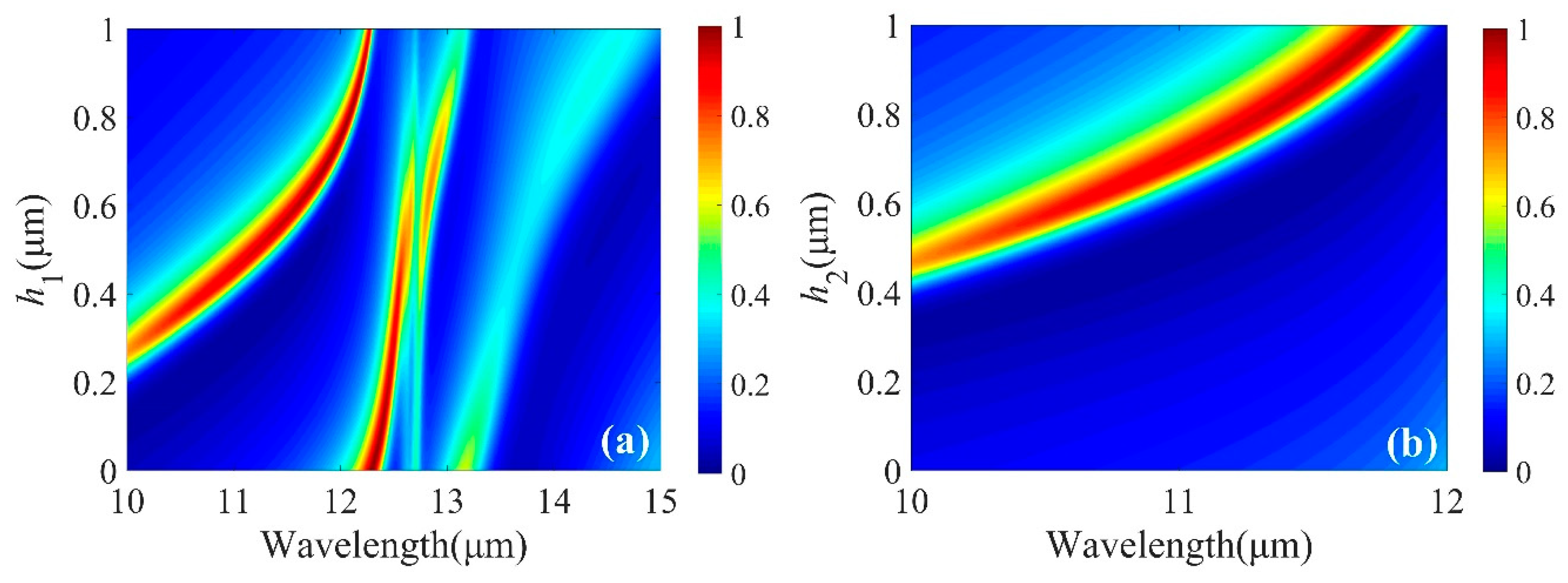
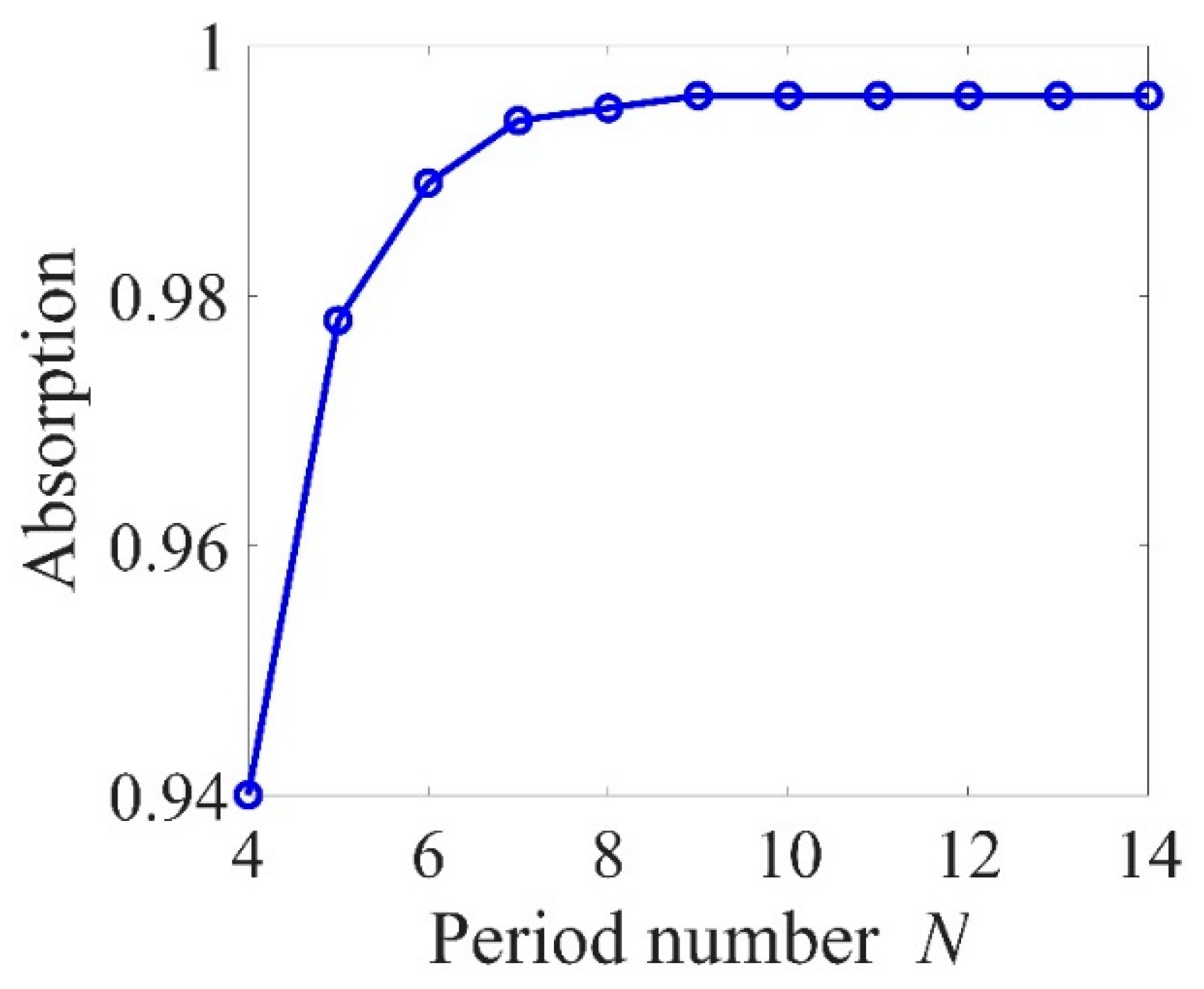
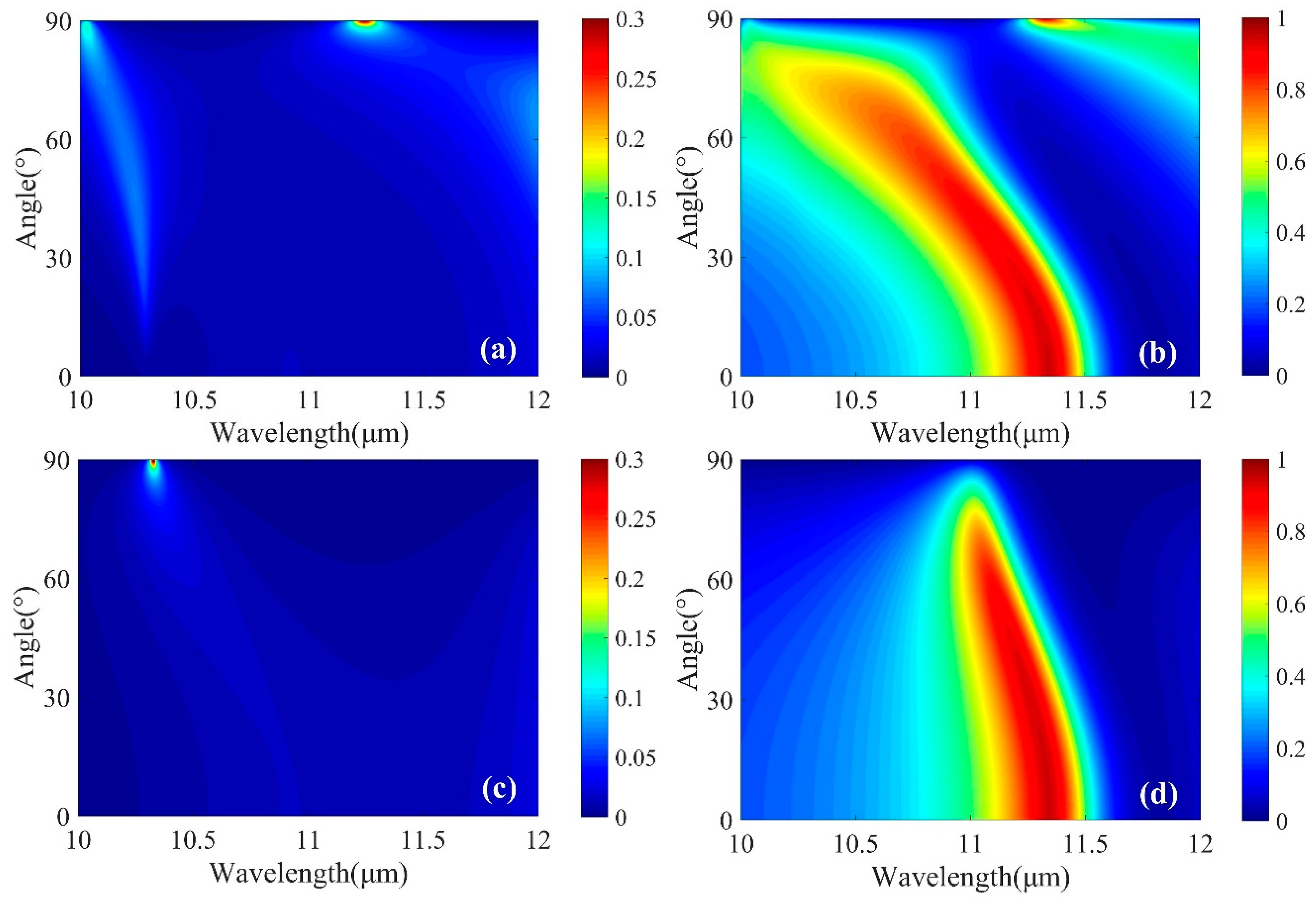
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cao, L.; White, J.S.; Park, J.S.; Park, J.-S.; Schuller, J.A.; Clemens, B.M.; Brongersma, M.L. Engineering light absorption in semiconductor nanowire devices. Nat. Mater. 2009, 8, 643–647. [Google Scholar] [CrossRef]
- Aydin, K.; Ferry, V.; Briggs, R.M.; Atwater, H.A. Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat. Commun. 2011, 2, 517–524. [Google Scholar] [CrossRef]
- Liu, X.; Starr, T.; Starr, A.F.; Padilla, W.J. Infrared spatial and frequency selective metamaterial with near-unity absorbance. Phys. Rev. Lett. 2010, 104, 207403. [Google Scholar]
- Tittl, A.; Mai, P.; Taubert, R.; Dregely, D.; Liu, N.; Giessen, H. Palladium-based plasmonic perfect absorber in the visible wavelength range and its application to hydrogen sensing. Nano Lett. 2011, 11, 4366–4369. [Google Scholar] [CrossRef]
- Aslan, E.; Aslan, E.; Turkmen, M.; Saracoglu, O.G. Experimental and numerical characterization of a mid-infrared plasmonic perfect absorber for dual-band enhanced vibrational spectroscopy. Opt. Mater. 2017, 73, 213–222. [Google Scholar] [CrossRef]
- Bang, S.H.; Kim, J.; Yoon, G.; Tanaka, T.; Rho, J. Recent advances in tunable and reconfigurable metamaterials. Micromachines 2018, 9, 560. [Google Scholar] [CrossRef]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial electromagnetic wave absorbers. Adv. Mater. 2012, 24, 98–120. [Google Scholar] [CrossRef]
- Gu, J.; Singh, R.; Liu, X.; Zhang, X.; Ma, Y.; Zhang, S.; Maier, S.; Tian, Z.; Azad, A.K.; Chen, H.-T.; et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 2012, 3, 1151–1157. [Google Scholar] [CrossRef]
- Fan, K.; Padilla, W. Dynamic electromagnetic metamaterials. Mater. Today 2015, 18, 39–50. [Google Scholar]
- Liu, L.; Kang, L.; Mayer, T.S.; Werner, D.H. Hybrid metamaterials for electrically triggered multifunctional control. Nat. Commun. 2016, 7, 13236. [Google Scholar]
- Zhao, X.; Fan, K.; Zhang, J.; Keiser, G.R.; Duang, G.; Averitt, R.D.; Zhang, X. Voltage-tunable dual-layer terahertz metamaterials. Microsyst. Nanoeng. 2016, 2, 16025–16033. [Google Scholar]
- Jung, Y.U.; Bendoym, I.; Crose, D.T. Numerical study of near-, mid-, and long-infrared photon trapping in crystalline and amorphous HgCdTe metamaterials. Appl. Phys. A 2016, 122, 376–382. [Google Scholar]
- Yi, Z.; Chen, J.; Cen, C.; Chen, X.; Zhou, Z.; Tang, Y.; Ye, X.; Xiao, S.; Luo, W.; Wu, P. Tunable graphene-based plasmonic perfect metamaterial absorber in the THz region. Micromachines 2019, 10, 194–205. [Google Scholar]
- Dave, V.; Sorathiya, V.; Guo, T.; Patel, S.K. Graphene based tunable broadband far-infrared absorber. Superlattices Microst. 2018, 124, 113–120. [Google Scholar]
- Yang, L.; Fan, F.; Chen, M.; Zhang, X.; Chang, S.-J. Active terahertz metamaterials based on liquid-crystal induced transparency and absorption. Opt. Commun. 2017, 382, 42–48. [Google Scholar]
- Cao, T.; Wei, C.W.; Simpson, R.E.; Zhang, L.; Cryan, M.J. Broadband polarization-independent perfect absorber using a phase-change metamaterial at visible frequencies. Sci. Rep. 2014, 4, 3955–3963. [Google Scholar]
- Wutting, M.; Bhaskaran, H.; Taubner, T. Phase-change materials for non-volatile photonic applications. Nat. Photon 2017, 11, 465–476. [Google Scholar]
- Torres, D.; Zhang, J.; Dooley, S.; Tan, X.; Sepúlveda, N. Modeling of MEMS mirrors actuated by phase-change mechanism. Micromachines 2017, 8, 138. [Google Scholar] [CrossRef]
- Wang, Q.; Rogers, E.T.F.; Gholipour, B.; Wang, C.-M.; Yuan, G.; Teng, J.; Zheludev, N.I. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat. Photon. 2016, 10, 60–65. [Google Scholar]
- Tittl, A.; Michel, A.-K.U.; Schaferling, M.; Yin, X.; Gholipour, B.; Cui, L.; Wuttig, M.; Taubner, T.; Neubrech, F.; Giessen, H. A switchable mid-infrared plasmonic perfect absorber with multispectral thermal imaging capability. Adv. Mater. 2015, 27, 4597–4603. [Google Scholar]
- Ding, F.; Zhong, S.; Bozhevolnyi, S.I. Vanadium dioxide integrated metasurfaces with switchable functionalities at terahertz frequencies. Adv. Opt. Mater. 2018, 6, 1701204. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, J.; Zhang, D.; Pang, W.; Zhang, H. A novel bulk acoustic wave resonator for filters and sensors applications. Micromachines 2015, 6, 1306–1316. [Google Scholar] [CrossRef]
- Mohr, D.A.; Yoo, D.; Chen, C.; Li, M.; Oh, S.H. Waveguide-integrated mid-infrared plasmonics with high-efficiency coupling for ultracompact surface-enhanced infrared absorption spectroscopy. Opt. Express 2018, 26, 23540–23549. [Google Scholar] [CrossRef]
- Qu, Y.; Li, Q.; Du, K.; Cai, L.; Lu, J.; Qiu, M. Dynamic thermal emission control based on ultrathin plasmonic metamaterials including phase-changing material GST. Laser Photonics Rev. 2017, 11, 1700091. [Google Scholar] [CrossRef]
- Zhu, N.; Chen, J.; Deng, H.; Di, Y. A graphene-coated mo tip array for highly-efficient nanostructured electron field emitters. Micromachines 2018, 9, 12. [Google Scholar] [CrossRef]
- Zhu, Z.; Evans, P.G.; Haglund, R.F.; Valentine, J.G. Dynamically reconfigurable metadevice employing nanostructured phase-change materials. Nano Lett. 2017, 17, 4881–4885. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, X.; Shen, F.; Zhou, Q.; Gao, J.; Guo, K. Active-tuning and polarization-independent absorber and sensor in the infrared region based on the phase change material of Ge2Sb2Te5 (GST). Sci. Rep. 2018, 8, 12433–12441. [Google Scholar] [CrossRef]
- Cai, L.; Du, K.; Qu, Y.; Luo, H.; Pan, M.; Qiu, M.; Li, Q. Nonvolatile tunable silicon-carbide-based midinfrared thermal emitter enabled by phase-changing materials. Opt. Lett. 2018, 43, 1295–1298. [Google Scholar] [CrossRef]
- Palik, E. (Ed.) Handbook of Optical Constants of Solids; Academic Press: Waltham, MA, USA, 1998. [Google Scholar]
- Bhargava, R.N.; Gallagher, D.; Hong, X.; Nurmikko, A. Optical properties of manganese-doped nanocrystals of ZnS. Phys. Rev. Lett. 1994, 72, 416–419. [Google Scholar] [CrossRef]
- Neuner, B.; Korobkin, D.; Fietz, C.; Carole, D.; Ferro, G.; Shvets, G. Critically coupled surface phonon-polarition excitation in silicon carbide. Opt. Lett. 2009, 34, 2667–2669. [Google Scholar] [CrossRef]
- Kim, T.Y.; Badsha, M.A.; Yoon, J.; Lee, S.Y.; Jun, Y.C.; Hwangbo, C.K. General strategy for broadband coherent perfect absorption and multi-wavelength all-optical switching based on epsilon-near-zero multilayer films. Sci. Rep. 2016, 6, 22941–22952. [Google Scholar] [CrossRef]
- Bhattarai, K.; Ku, Z.; Silva, S.; Jeon, J.; Kim, J.O.; Lee, S.J. A large-area mushroom-capped plasmonic perfect absorber: Refractive index sensing and Fabry-Perot cavity mechanism. Adv. Opt. Mater. 2015, 3, 1179–1786. [Google Scholar] [CrossRef]
- Rude, M.; Simpson, R.; Quidant, R.; Pruneri, V.; Renger, J. Active control of surface plasmon waveguides with a phase change material. ACS Photon. 2015, 2, 669–674. [Google Scholar] [CrossRef]
- Tian, X.; Li, Z. Visible-near infrared ultra-broadband polarization-independent metamaterial perfect absorber involving phase-change materials. Photo Res. 2016, 4, 146–152. [Google Scholar] [CrossRef]
- Ding, F.; Yang, Y.; Bozhevolnyi, S.I. Dynamic metasurfaces using phase-change chalcogenides. Adv. Opt. Mater. 2019. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, X.; Zheng, G. Intensity Switchable and Wide-Angle Mid-Infrared Perfect Absorber with Lithography-Free Phase-Change Film of Ge2Sb2Te5. Micromachines 2019, 10, 374. https://doi.org/10.3390/mi10060374
Hua X, Zheng G. Intensity Switchable and Wide-Angle Mid-Infrared Perfect Absorber with Lithography-Free Phase-Change Film of Ge2Sb2Te5. Micromachines. 2019; 10(6):374. https://doi.org/10.3390/mi10060374
Chicago/Turabian StyleHua, Xiaomin, and Gaige Zheng. 2019. "Intensity Switchable and Wide-Angle Mid-Infrared Perfect Absorber with Lithography-Free Phase-Change Film of Ge2Sb2Te5" Micromachines 10, no. 6: 374. https://doi.org/10.3390/mi10060374
APA StyleHua, X., & Zheng, G. (2019). Intensity Switchable and Wide-Angle Mid-Infrared Perfect Absorber with Lithography-Free Phase-Change Film of Ge2Sb2Te5. Micromachines, 10(6), 374. https://doi.org/10.3390/mi10060374



