New Logic-In-Memory Paradigms: An Architectural and Technological Perspective
Abstract
1. Introduction
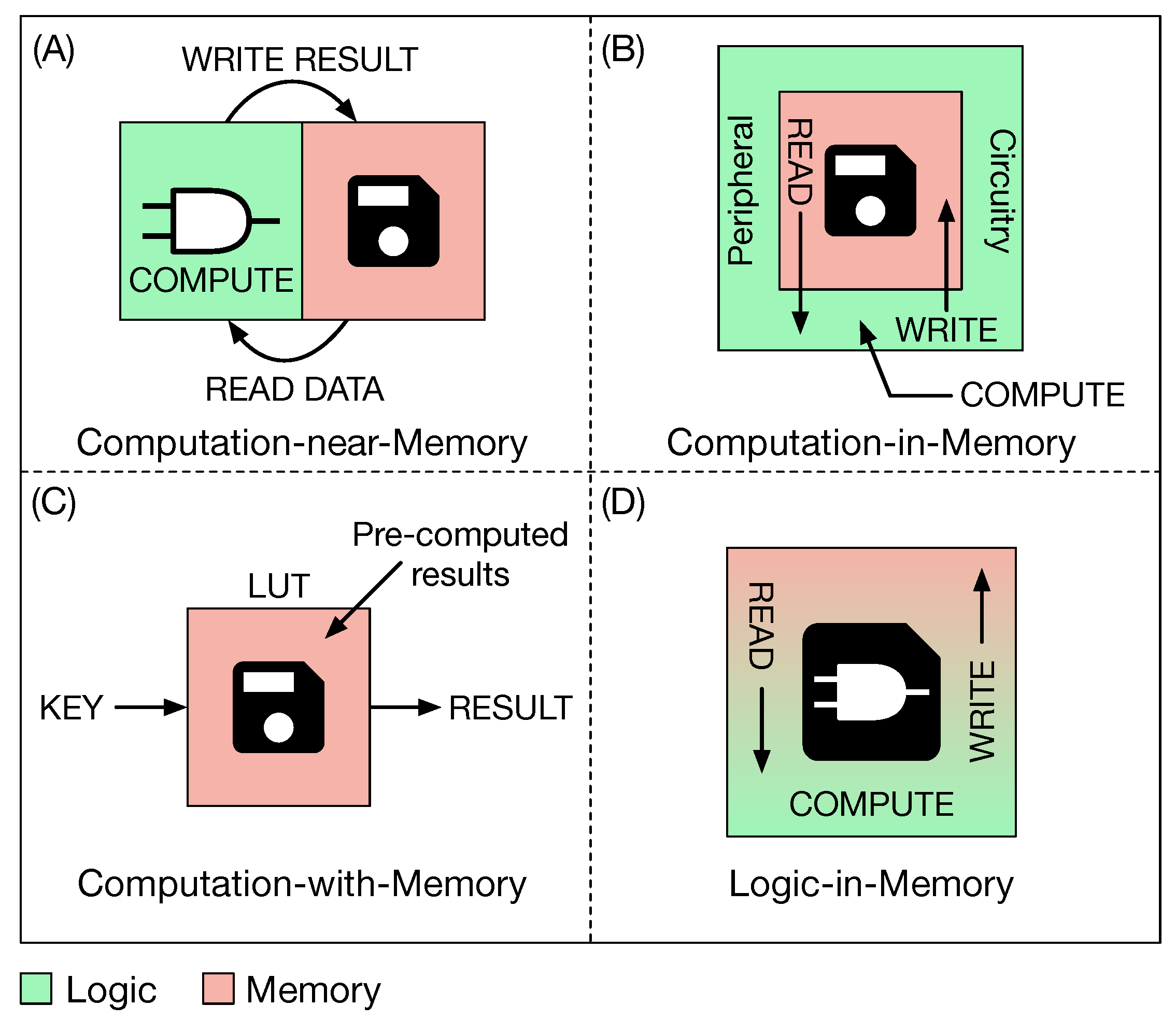
2. State of the Art
- (A)
- Computation-near-Memory (CnM, Figure 1A): Thanks to the 3D Stacked Integrated Circuit technology (3D-SIC) [2], computation and storage are brought closer together, from which the name CnM, by stacking the two units one on top of the other. This technique has a two-fold advantage: Reducing the length of the interconnections and widening the memory bandwidth. However, this approach cannot be considered as true in-memory computing, since computation and storage are still two separate entities, but more as an evolution of conventional architectures based on the von Neumann model. Works belonging to this category are [3,4,5,6,7,8].
- (B)
- Computation-in-Memory (CiM, Figure 1B): The structure of the memory array is not modified, while its intrinsic analog functionality is exploited to perform computation. In particular, in-memory computation is achieved by reading data from the memory which is then sensed by sense amplifiers (SAs). SAs are specifically modified in order to support the computation of a few simple logic operations (AND, OR, ...). The result is then written back in the memory array. Decoders are also adapted in order to read more than one data from the array and execute row-wise (between data on different rows) or column-wise (between data on different columns) operations. Works belonging to this class are [9,10,11,12,13,14] and they all use a resistive non-volatile memory technology (RRAM). The approach followed in [15] is the same but here authors use a commodity volatile memory (DRAM, Dynamic Random Access Memory).
- (C)
- Computation-with-Memory (CwM, Figure 1C): This approach uses memory as a Content Addressable Memory (CAM) to retrieve pre-computed results by means of a Look Up Table (LUT). The working principle of this kind of computation is that any Boolean function involving two or more inputs can be encoded in a memory by storing its truth table. In particular, input combinations are stored in a LUT, while results are stored in a CAM. Then the LUT is accessed through an input combination and an address is retrieved. These addresses are used to access the CAM and obtain the final result. Works that follows this approach are [16,17,18,19,20].
- (D)
- Logic-in-Memory (LiM, Figure 1D): In this case logic is directly integrated inside the memory cell. Differently from the other three approaches, here data are computed locally without the need to move them outside the array (towards a close computing unit as in a CnM approach or towards the peripheral circuitry as in a CiM approach). Internal readings are performed in order to execute operations on data stored in different cells, by exploiting inter-cells connections. Internal writings are executed to locally save the result of the operation. There are a few works belonging to this category, such as [21,22,23,24].
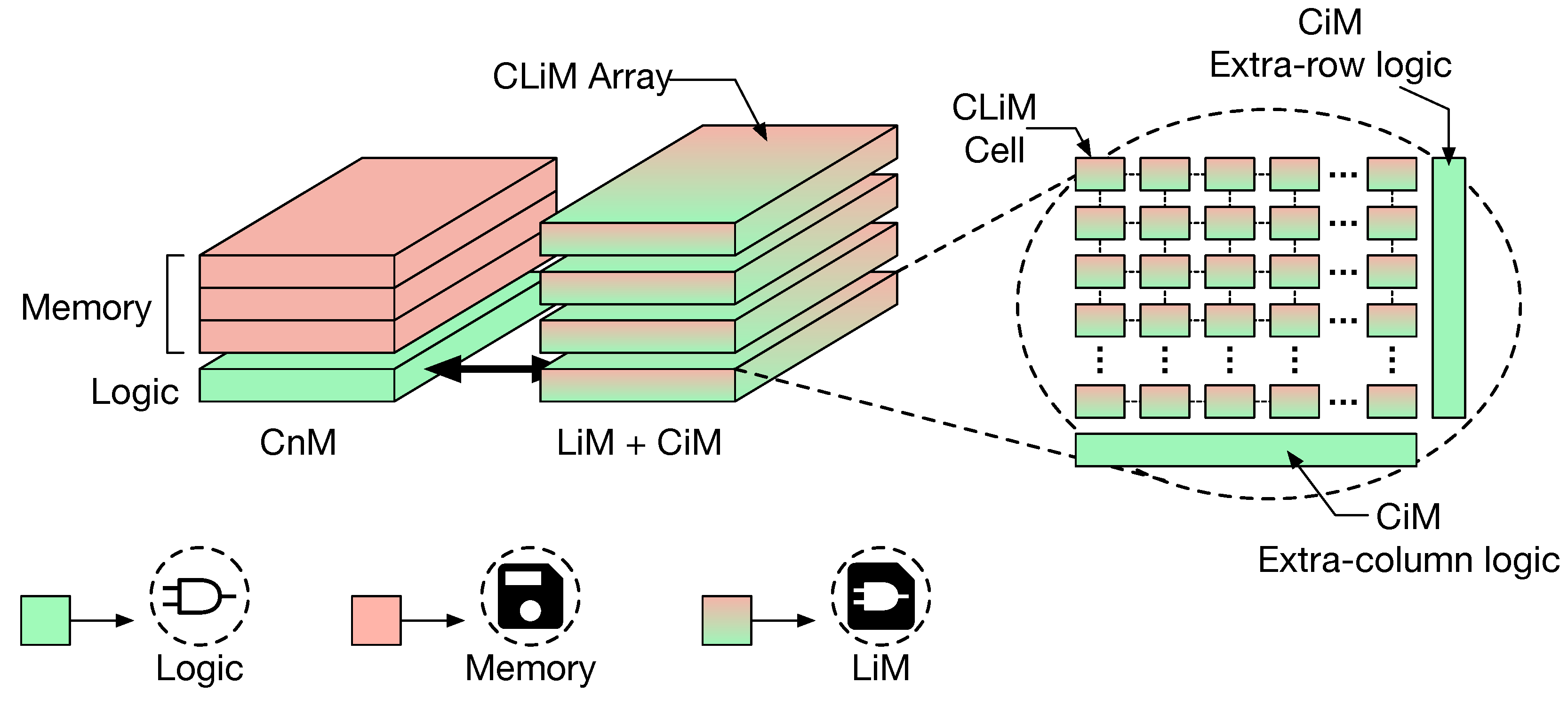
3. Configurable Logic-In-Memory Architecture (CLiMA): Main Ideas
- The idea of an architecture that exploits various approaches to in-memory computing in order to adapt to different requirements and applications (Section 3);
- Configurability, hence flexibility, at different levels:
- -
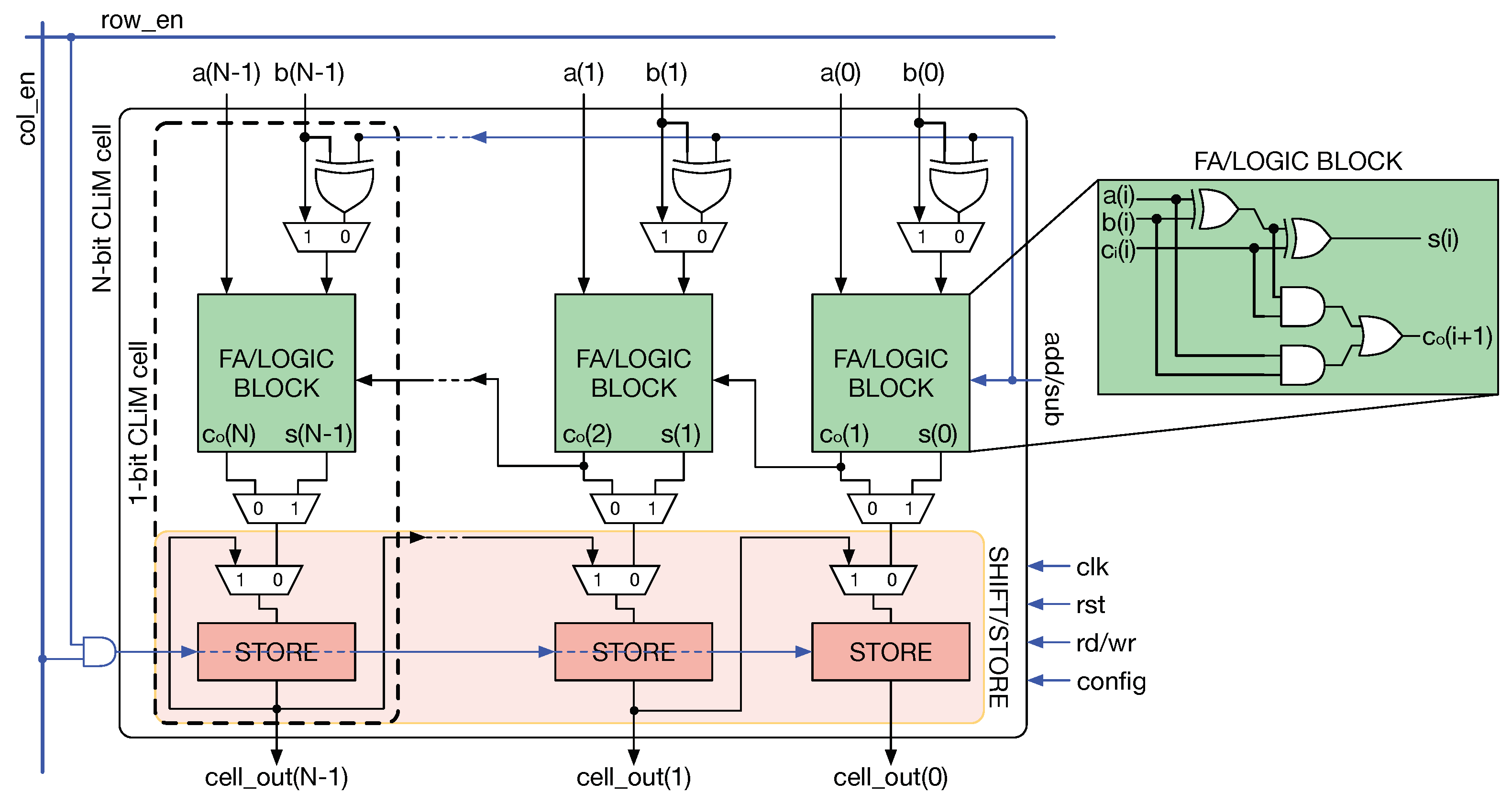
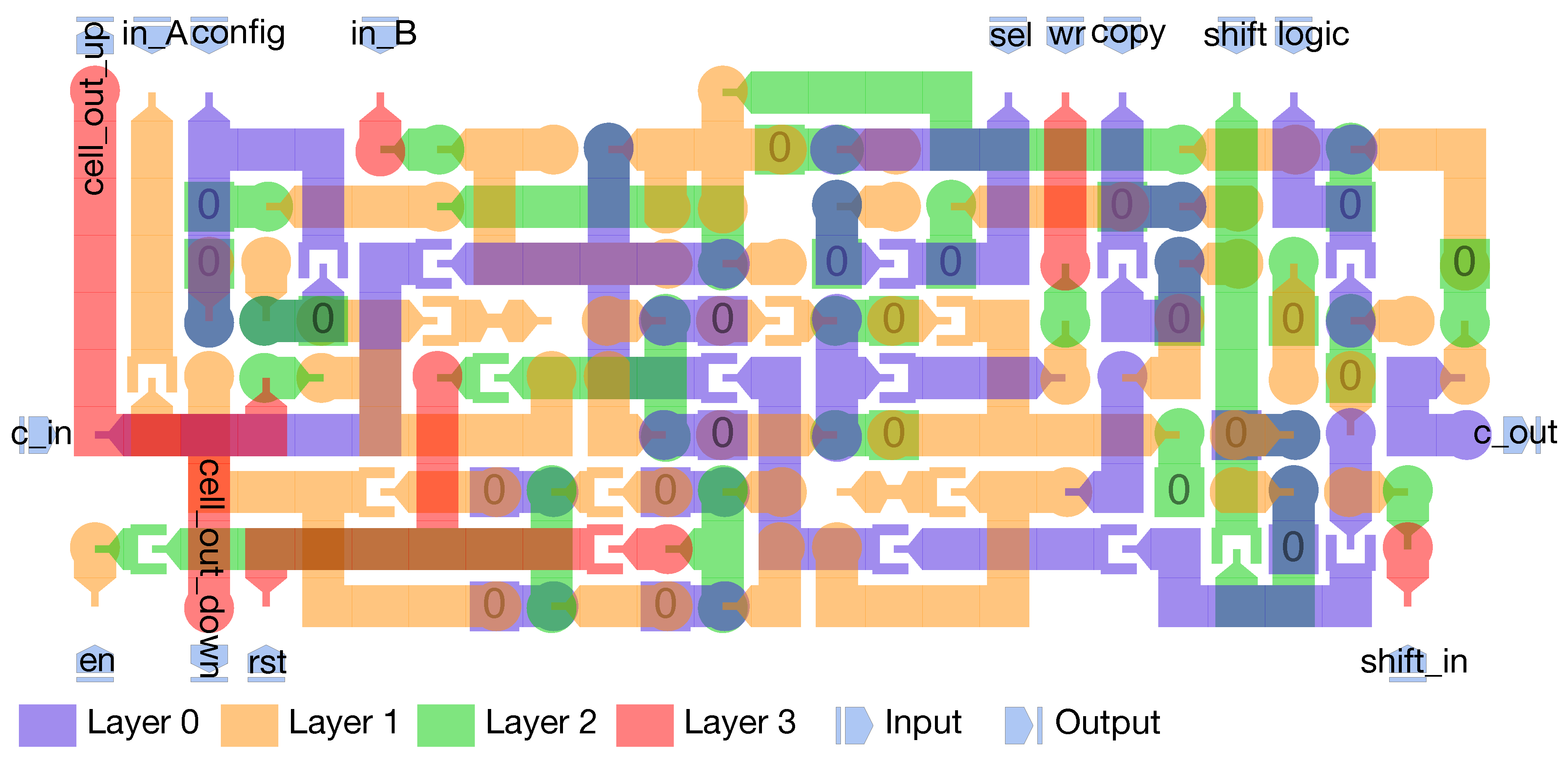
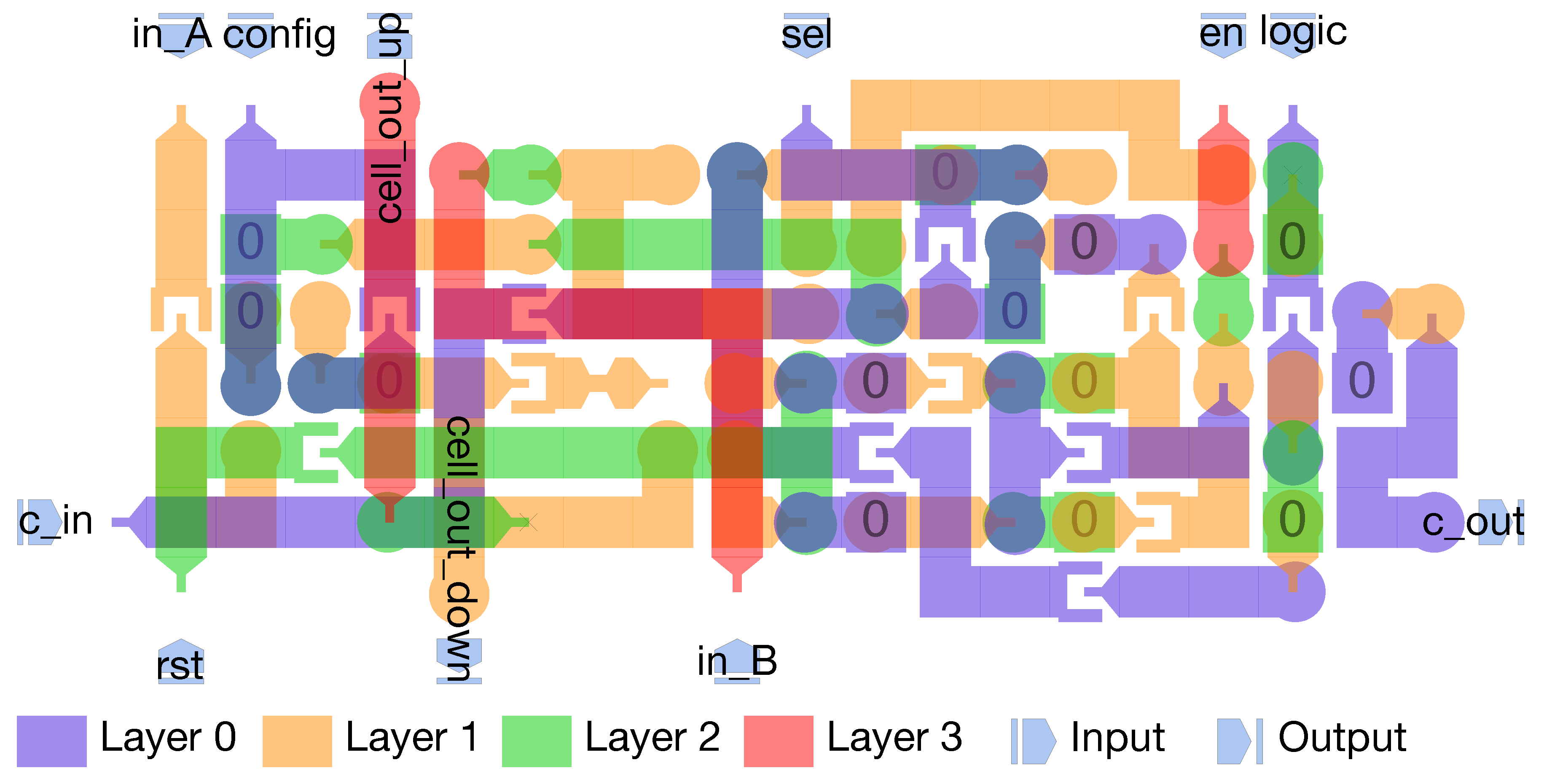
- The basic block of CLiMA is a 1-bit Configurable LiM (CLiM) cell that can be programmed to perform different logic and arithmetic operations (Section 4.4);
- -
- More 1-bit CLiM cells can be grouped together to from a multi-bit CLiM cell that supports more complex operations such as bit-wise logic operations, multi-bit addition/subtraction, multiplication, shifts (Section 3 and Section 4.4);
- A data flow for Convolutional Neural Networks workload and an inter-cells connection fabric specifically optimized to minimize memory accesses outside CLiMA, to maximize data-reuse inside the CLiM array and to support high parallelism (Section 4.3, Section 4.4 and Section 4.5);
- A pNML-based design of the 1-bit and multi-bit CLiM cells and a small version of the CLiM array (Section 6).
3.1. Overview
- Type of operations (logic, arithmetic);
- Complexity of operations (e.g., a logic function with respect to division);
- Data movement.
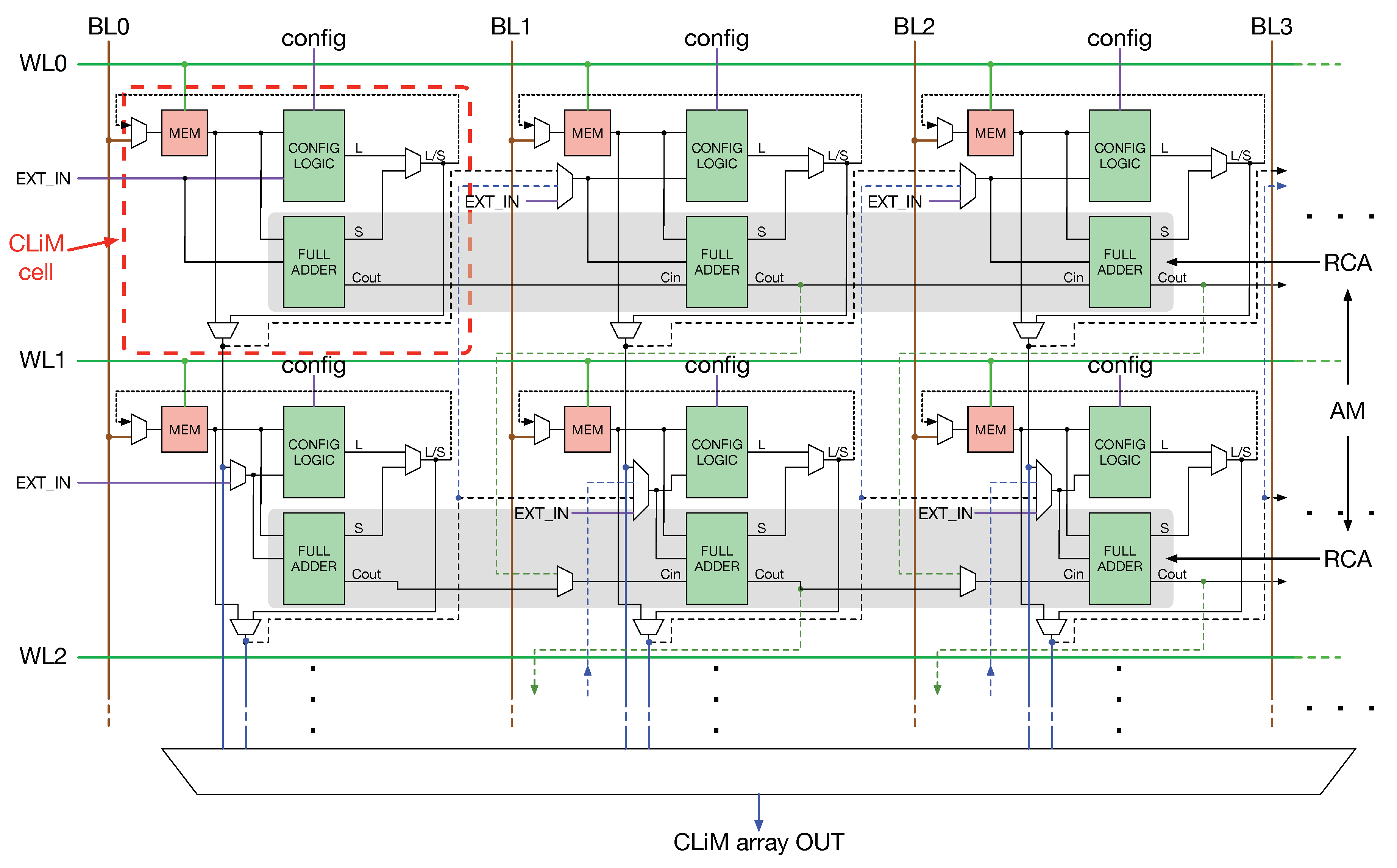
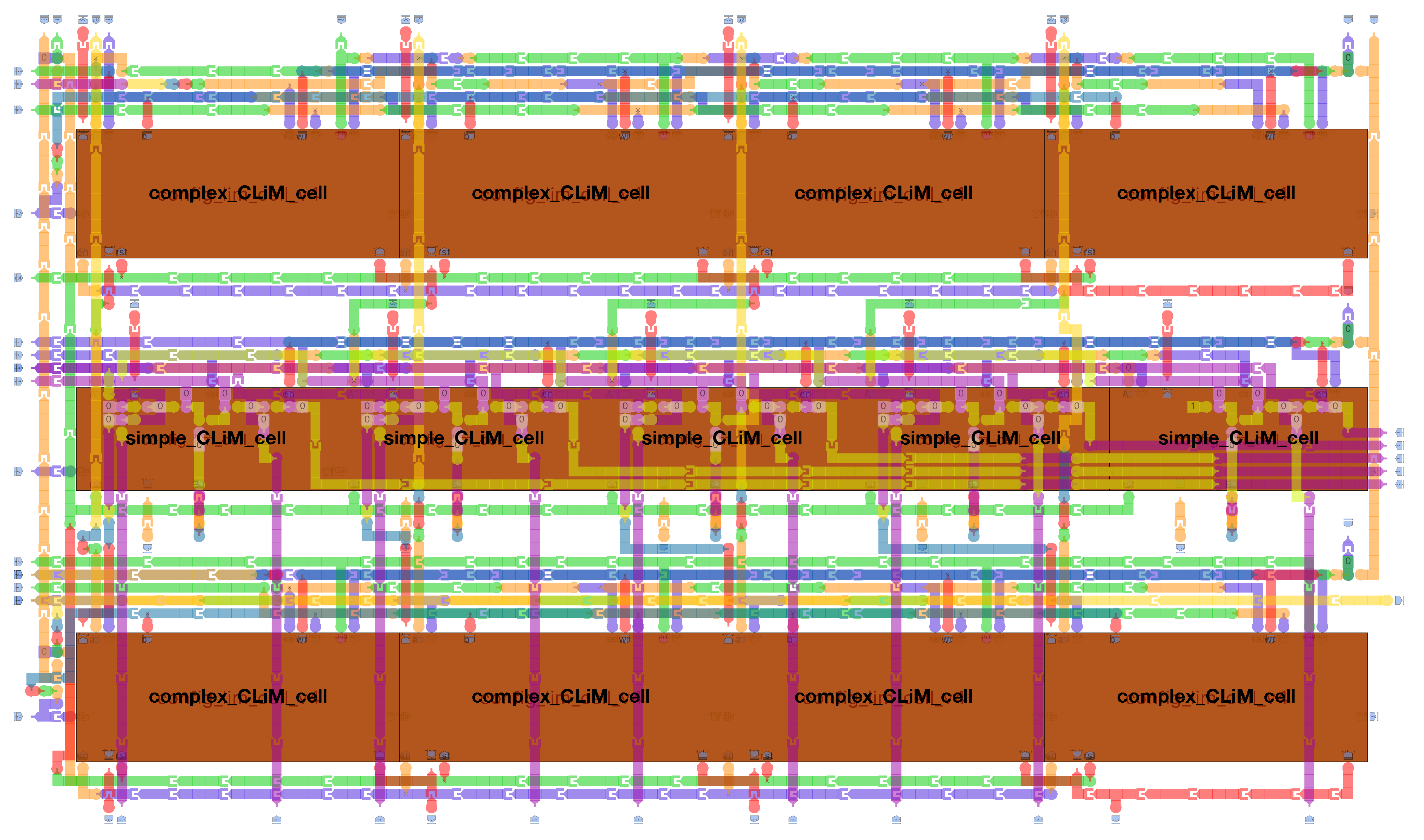
3.2. Type of Operations and Data Movement in CLiM Array
- Intra-row computation between cells in the same row (black dashed arrow in Figure 4);
- Intra-column computation between cells in the same column (black solid arrow in Figure 4);
- Inter-row computation between two rows, an instance being an operation between a data stored in row 0 and one stored in row 1;
- Inter-column computation between two columns, an instance being an operation between a data stored in column 0 and one stored in column 1.
4. CLiMA for Quantized Convolutional Neural Networks
- CNNs are an extremely popular application nowadays because they are a powerful method for solving many complex problems such as image recognition and classification, language processing, etc.;
- CNNs are data-intensive, hence, memory accesses represent the bottleneck;
- CNNs are computational-intensive, hence, they require hardware acceleration.
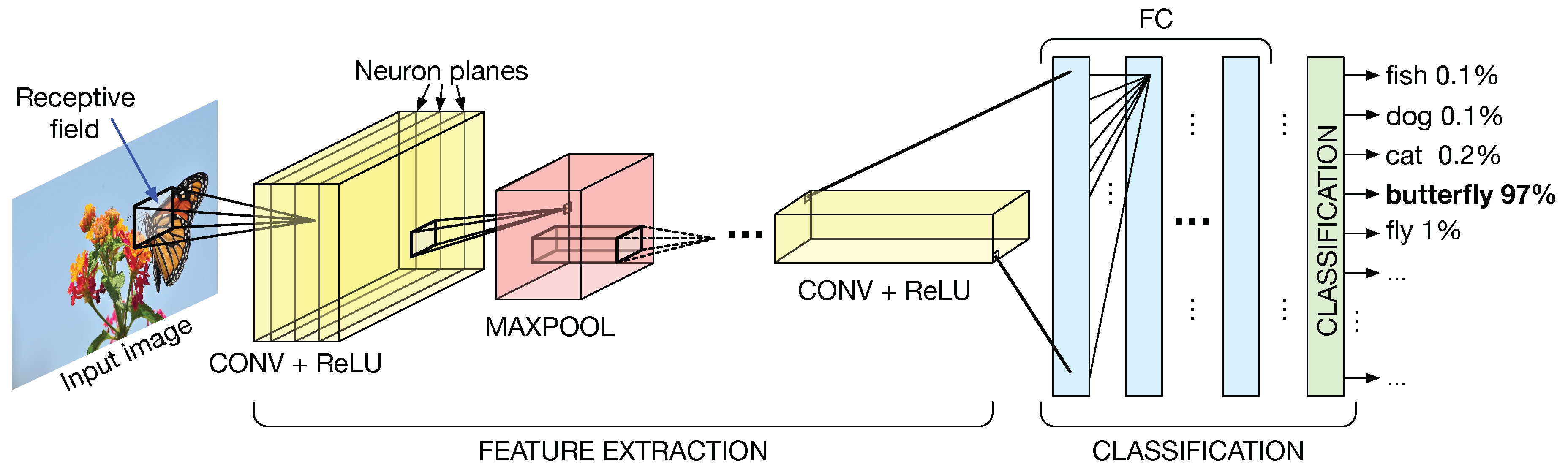
4.1. Convolutional Neural Networks (CNNs)
4.2. ShiftCNN: A Quantized CNN
4.3. CNN Data Flow Mapping Scheme for CLiMA
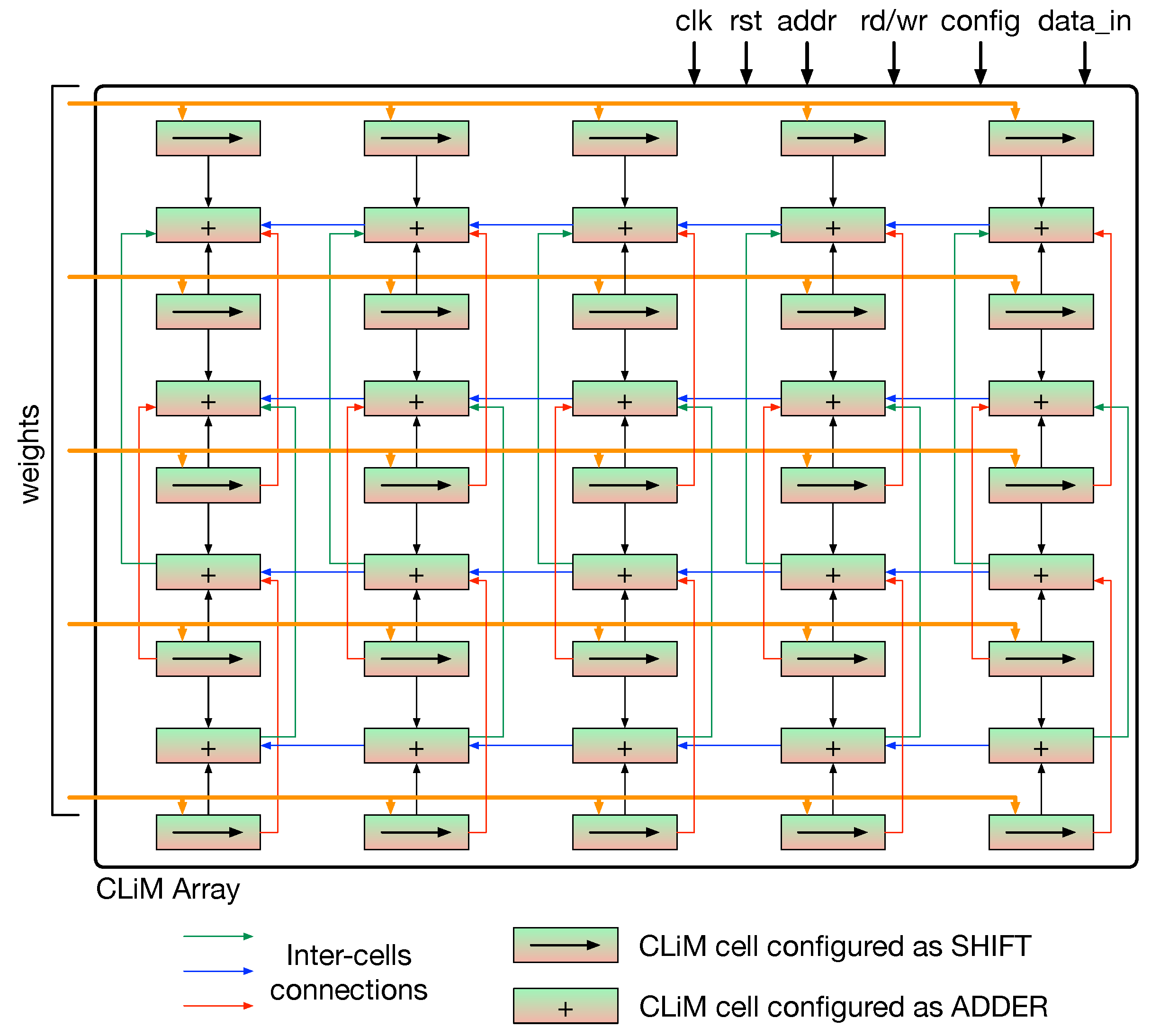
4.4. CLiM Array Structure
4.5. Weight Dispatching Mechanism
4.6. Data Reuse Possibilities
5. Results and Discussion
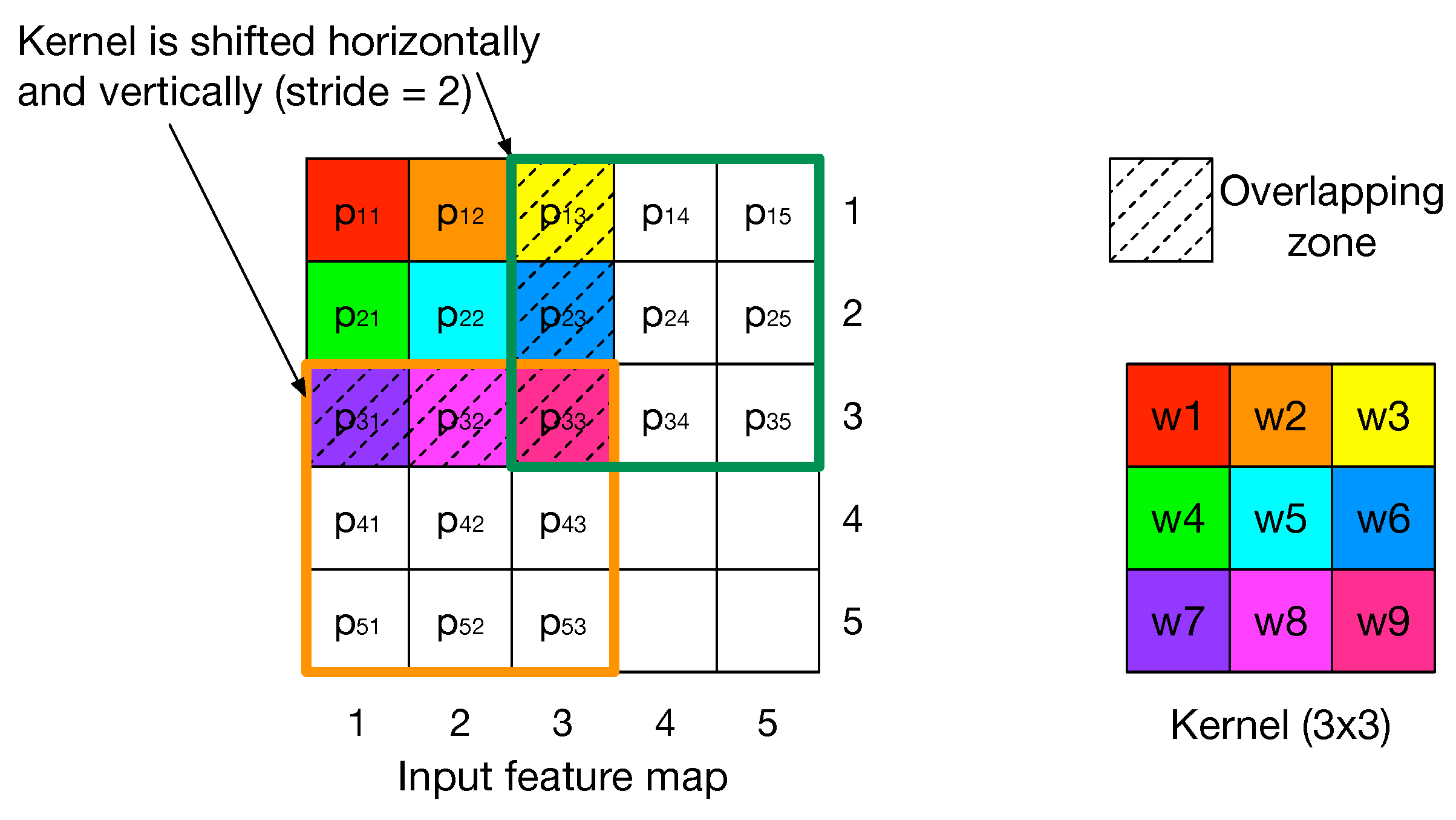
- Convolutional layer parameters including input feature map dimensions (), kernel dimensions (K), stride (S) and output feature map dimensions ();
- The number of parallel non overlapping convolution windows;
- The number of execution cycles needed to complete a convolution window.
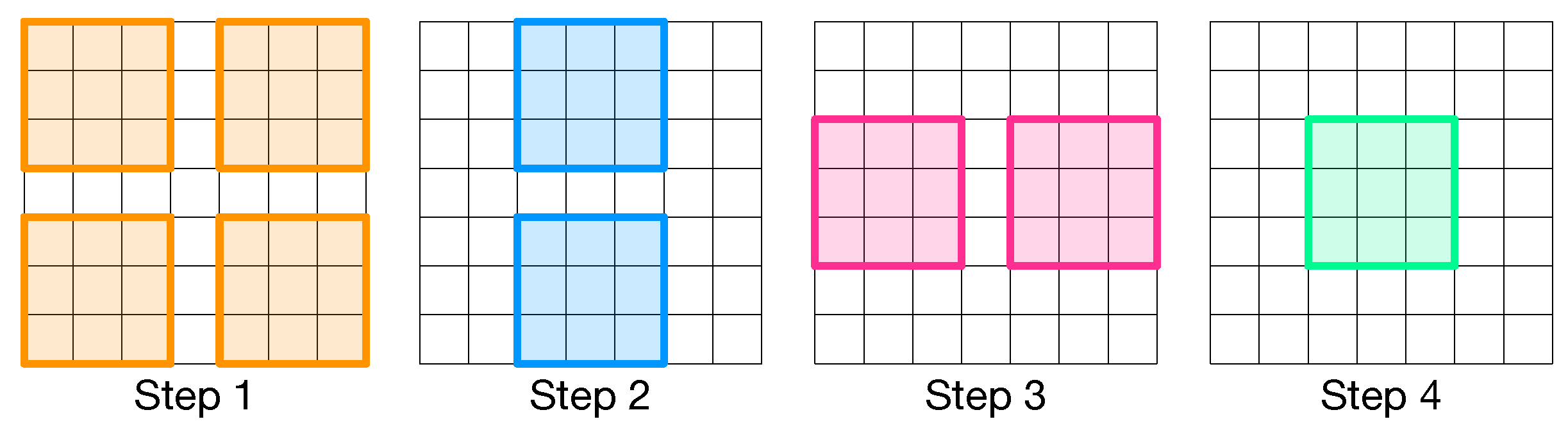
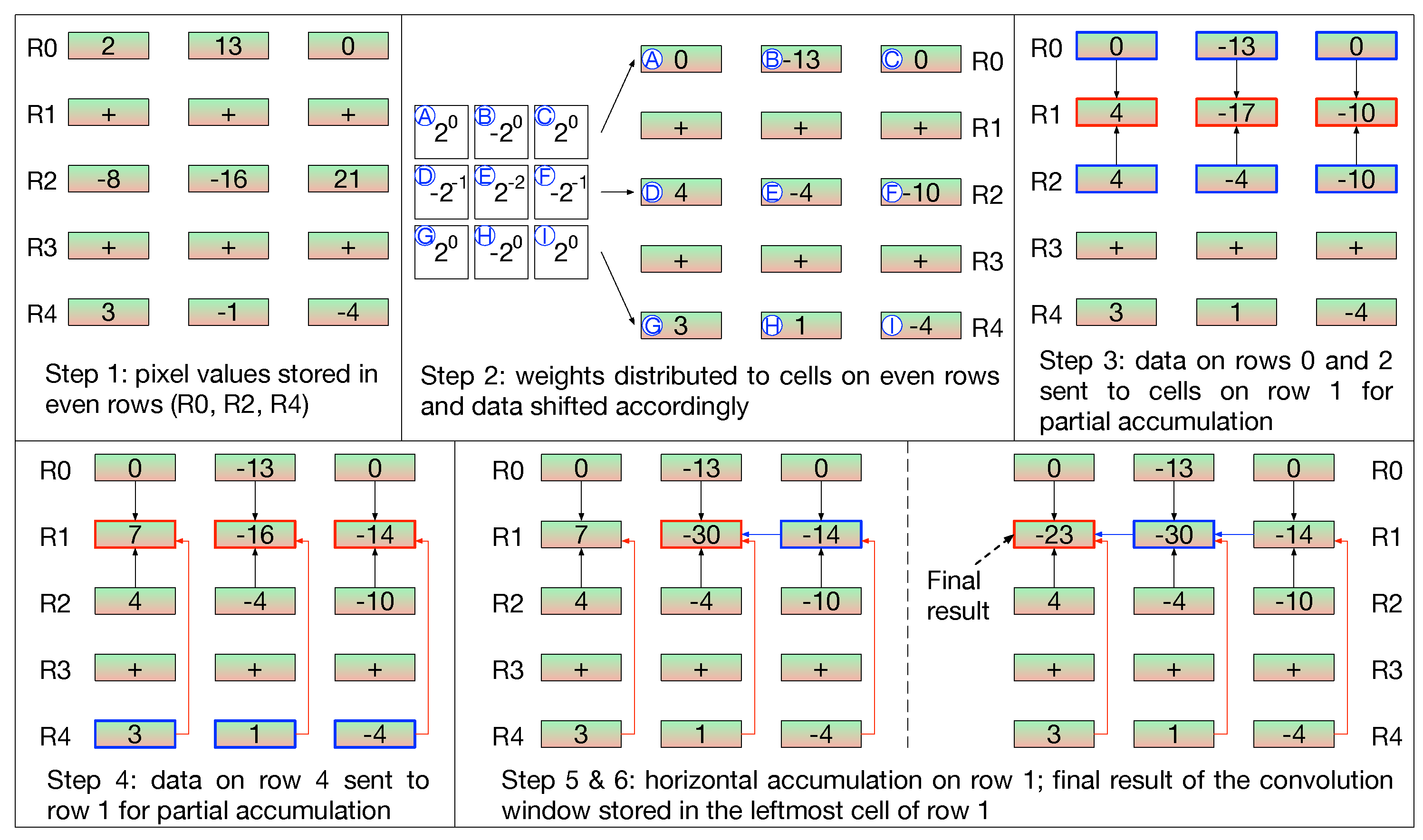
- The number of cycles to execute shift operations; in CLiMA data are shifted 1 bit at a time. Since weights are 8-bit long, in the worst case scenario eight cycles are needed to complete the operation;
- The number of cycles to execute accumulations:
- -
- One cycle for partial accumulation of data couples (Figure 13, step 3); this term does not depend on the size of the kernel because these accumulations can always be done in parallel;
- -
- cycles for partial accumulation of non-adjacent data (Figure 13, step 4); this term depends on the size of the kernel, in fact, as the convolution window dimension changes the number of non-adjacent data to accumulate changes as well;
- -
- cycles to perform final horizontal accumulations (Figure 13, steps 5 and 6); similarly to the previous term, also this one depends on the size of the kernel.
- read accesses to the input buffer to retrieve input features and weights;
- write accesses to the output buffer to store the convolution results.
6. Beyond CMOS: A pNML Implementation
6.1. pNML Basics
6.2. pNML-Based CLiM Array
7. Conclusions
- In-memory computation: Data are processed directly inside the memory, drastically reducing the need of data movement and favoring their reusing for further computation;
- Parallelism: The array is intrinsically highly parallel and perfect for accelerating compute and data intensive applications;
- Flexibility: The configurability of the cells and the possibility of exploiting inter-cells connections to build complex in-memory functions make CLiMA adaptable to different applications.
- Not all data-flows can be supported in an array-like structure because moving data from any source to any destination is not easy and would require a very complex (but flexible) network of interconnections;
- The control of data movement between cells is complex and must be managed carefully in order to avoid cells receiving/sending wrong data from/to wrong cells.
Author Contributions
Funding
Conflicts of Interest
References
- 2013 International Technology Roadmap for Semiconductors (ITRS). Available online: http://www.itrs2.net/2013-itrs.html (accessed on 31 May 2013).
- 2009 International Technology Roadmap for Semiconductors (ITRS). Available online: https://www.semiconductors.org/wp-content/uploads/2018/09/Interconnect.pdf (accessed on 31 May 2009).
- Kim, D.H.; Athikulwongse, K.; Healy, M.B.; Hossain, M.M.; Jung, M.; Khorosh, I.; Kumar, G.; Lee, Y.; Lewis, D.L.; Lin, T.; et al. Design and Analysis of 3D-MAPS (3D Massively Parallel Processor with Stacked Memory). IEEE Trans. Comput. 2015, 64, 112–125. [Google Scholar] [CrossRef]
- Zhu, Q.; Akin, B.; Sumbul, H.E.; Sadi, F.; Hoe, J.C.; Pileggi, L.; Franchetti, F. A 3D-Stacked Logic-in-Memory Accelerator for Application-Specific Data Intensive Computing. In Proceedings of the 2013 IEEE International 3D Systems Integration Conference (3DIC), San Francisco, CA, USA, 2–4 October 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Ahn, J.; Hong, S.; Yoo, S.; Mutlu, O.; Choi, K. A Scalable Processing-in-Memory Accelerator for Parallel Graph Processing. In Proceedings of the 2015 ACM/IEEE 42nd Annual International Symposium on Computer Architecture (ISCA), Portland, OR, USA, 13–17 June 2015; pp. 105–117. [Google Scholar] [CrossRef]
- Zhang, D.; Jayasena, N.; Lyashevsky, A.; Greathouse, J.L.; Xu, L.; Ignatowski, M. TOP-PIM: Throughput-oriented Programmable Processing in Memory. In Proceedings of the 23rd International Symposium on High-performance Parallel and Distributed ComputingVancouver, BC, Canada, 23–27 June 2014; pp. 85–98. [Google Scholar] [CrossRef]
- Xie, C.; Song, S.L.; Wang, J.; Zhang, W.; Fu, X. Processing-in-Memory Enabled Graphics Processors for 3D Rendering. In Proceedings of the 2017 IEEE International Symposium on High Performance Computer Architecture (HPCA), Austin, TX, USA, 4–8 February 2017; pp. 637–648. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Y.; Li, H.; Li, X. ApproxPIM: Exploiting realistic 3D-stacked DRAM for energy-efficient processing in-memory. In Proceedings of the 2017 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Chiba, Japan, 16–19 January 2017; pp. 396–401. [Google Scholar] [CrossRef]
- Angizi, S.; He, Z.; Fan, D. PIMA-Logic: A Novel Processing-in-Memory Architecture for Highly Flexible and Energy-Efficient Logic Computation. In Proceedings of the 2018 55th ACM/ESDA/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24–29 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Chi, P.; Li, S.; Xu, C.; Zhang, T.; Zhao, J.; Liu, Y.; Wang, Y.; Xie, Y. PRIME: A Novel Processing-in-Memory Architecture for Neural Network Computation in ReRAM-Based Main Memory. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016; pp. 27–39. [Google Scholar] [CrossRef]
- Han, L.; Shen, Z.; Shao, Z.; Huang, H.H.; Li, T. A novel ReRAM-based processing-in-memory architecture for graph computing. In Proceedings of the 2017 IEEE 6th Non-Volatile Memory Systems and Applications Symposium (NVMSA), Taiwan, China, 16–18 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Gaillardon, P.; Amarú, L.; Siemon, A.; Linn, E.; Waser, R.; Chattopadhyay, A.; De Micheli, G. The Programmable Logic-in-Memory (PLiM) computer. In Proceedings of the 2016 Design, Automation Test in Europe Conference Exhibition (DATE), Dresden, Germany, 14–18 March 2016; pp. 427–432. [Google Scholar]
- Li, S.; Xu, C.; Zou, Q.; Zhao, J.; Lu, Y.; Xie, Y. Pinatubo: A processing-in-memory architecture for bulk bitwise operations in emerging non-volatile memories. In Proceedings of the 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Papandroulidakis, G.; Vourkas, I.; Abusleme, A.; Sirakoulis, G.C.; Rubio, A. Crossbar-Based Memristive Logic-in-Memory Architecture. IEEE Trans. Nanotechnol. 2017, 16, 491–501. [Google Scholar] [CrossRef]
- Seshadri, V.; Lee, D.; Mullins, T.; Hassan, H.; Boroumand, A.; Kim, J.; Kozuch, M.A.; Mutlu, O.; Gibbons, P.B.; Mowry, T.C. Ambit: In-memory Accelerator for Bulk Bitwise Operations Using Commodity DRAM Technology. In Proceedings of the 50th Annual IEEE/ACM International Symposium on Microarchitecture, Cambridge, MA, USA, 14–18 October 2017; pp. 273–287. [Google Scholar] [CrossRef]
- Huangfu, W.; Li, S.; Hu, X.; Xie, Y. RADAR: A 3D-ReRAM based DNA Alignment Accelerator Architecture. In Proceedings of the 2018 55th ACM/ESDA/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kaplan, R.; Yavits, L.; Ginosar, R.; Weiser, U. A Resistive CAM Processing-in-Storage Architecture for DNA Sequence Alignment. IEEE Micro 2017, 37, 20–28. [Google Scholar] [CrossRef]
- Yavits, L.; Kvatinsky, S.; Morad, A.; Ginosar, R. Resistive Associative Processor. IEEE Comput. Archit. Lett. 2015, 14, 148–151. [Google Scholar] [CrossRef]
- Imani, M.; Rosing, T. CAP: Configurable resistive associative processor for near-data computing. In Proceedings of the 2017 18th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 14–15 March 2017; pp. 346–352. [Google Scholar] [CrossRef]
- Imani, M.; Gupta, S.; Arredondo, A.; Rosing, T. Efficient query processing in crossbar memory. In Proceedings of the 2017 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), Taiwan, China, 24–26 July 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Matsunaga, S.; Hayakawa, J.; Ikeda, S.; Miura, K.; Hasegawa, H.; Endoh, T.; Ohno, H.; Hanyu, T. Fabrication of a Nonvolatile Full Adder Based on Logic-in-Memory Architecture Using Magnetic Tunnel Junctions. Appl. Phys. Express 2008, 1, 091301. [Google Scholar] [CrossRef]
- Jarollahi, H.; Onizawa, N.; Gripon, V.; Sakimura, N.; Sugibayashi, T.; Endoh, T.; Ohno, H.; Hanyu, T.; Gross, W.J. A Nonvolatile Associative Memory-Based Context-Driven Search Engine Using 90 nm CMOS/MTJ-Hybrid Logic-in-Memory Architecture. IEEE J. Emerg. Sel. Top. Circuits Syst. 2014, 4, 460–474. [Google Scholar] [CrossRef]
- Yang, K.; Karam, R.; Bhunia, S. Interleaved logic-in-memory architecture for energy-efficient fine-grained data processing. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 409–412. [Google Scholar] [CrossRef]
- Cofano, M.; Vacca, M.; Santoro, G.; Causapruno, G.; Turvani, G.; Graziano, M. Exploiting the Logic-In-Memory paradigm for speeding-up data-intensive algorithms. Integration 2019. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. The Handbook of Brain Theory and Neural Networks; Chapter Convolutional Networks for Images, Speech, and Time Series; MIT Press: Cambridge, MA, USA, 1998; pp. 255–258. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 253–256. [Google Scholar]
- Gudovskiy, D.A.; Rigazio, L. ShiftCNN: Generalized Low-Precision Architecture for Inference of Convolutional Neural Networks. arXiv 2017, arXiv:1706.02393. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems—Volume 1; Curran Associates Inc.: Lake Tahoe, NV, USA, 2012; pp. 1097–1105. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Santoro, G.; Casu, M.R.; Peluso, V.; Calimera, A.; Alioto, M. Energy-performance design exploration of a low-power microprogrammed deep-learning accelerator. In Proceedings of the 2018 Design, Automation Test in Europe Conference Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 1151–1154. [Google Scholar] [CrossRef]
- Santoro, G.; Casu, M.R.; Peluso, V.; Calimera, A.; Alioto, M. Design-Space Exploration of Pareto-Optimal Architectures for Deep Learning with DVFS. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Becherer, M.; Csaba, G.; Porod, W.; Emling, R.; Lugli, P.; Schmitt-Landsiedel, D. Magnetic Ordering of Focused-Ion-Beam Structured Cobalt-Platinum Dots for Field-Coupled Computing. IEEE Trans. Nanotechnol. 2008, 7, 316–320. [Google Scholar] [CrossRef]
- Nikonov, D.E.; Young, I.A. Benchmarking of Beyond-CMOS Exploratory Devices for Logic Integrated Circuits. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 3–11. [Google Scholar] [CrossRef]
- Cairo, F.; Turvani, G.; Riente, F.; Vacca, M.; Gamm, S.B.V.; Becherer, M.; Graziano, M.; Zamboni, M. Out-of-plane NML modeling and architectural exploration. In Proceedings of the 2015 IEEE 15th International Conference on Nanotechnology (IEEE-NANO), Rome, Italy, 27–30 July 2015; pp. 1037–1040. [Google Scholar] [CrossRef]
- Causapruno, G.; Riente, F.; Turvani, G.; Vacca, M.; Roch, M.R.; Zamboni, M.; Graziano, M. Reconfigurable Systolic Array: From Architecture to Physical Design for NML. IEEE Trans. Very Large Scale Integr. (VLSI) Systems 2016. [Google Scholar] [CrossRef]
- Chiolerio, A.; Allia, P.; Graziano, M. Magnetic dipolar coupling and collective effects for binary information codification in cost-effective logic devices. J. Magn. Magn. Mater. 2012, 324, 3006–3012. [Google Scholar] [CrossRef]
- Breitkreutz, S.; Kiermaier, J.; Ju, X.; Csaba, G.; Schmitt-Landsiedel, D.; Becherer, M. Nanomagnetic Logic: Demonstration of directed signal flow for field-coupled computing devices. In Proceedings of the European Solid-State Device Research Conference (ESSDERC), Helsinki, Finland, 12–16 September 2011; pp. 323–326. [Google Scholar] [CrossRef]
- Kimling, J.; Gerhardt, T.; Kobs, A.; Vogel, A.; Wintz, S.; Im, M.Y.; Fischer, P.; Peter Oepen, H.; Merkt, U.; Meier, G. Tuning of the nucleation field in nanowires with perpendicular magnetic anisotropy. J. Appl. Phys. 2013, 113, 163902. [Google Scholar] [CrossRef]
- Becherer, M.; Kiermaier, J.; Breitkreutz, S.; Eichwald, I.; Žiemys, G.; Csaba, G.; Schmitt-Landsiedel, D. Towards on-chip clocking of perpendicular Nanomagnetic Logic. Solid-State Electron. 2014, 102, 46–51. [Google Scholar] [CrossRef]
- Goertz, J.J.W.; Ziemys, G.; Eichwald, I.; Becherer, M.; Swagten, H.J.M.; Breitkreutz-v. Gamm, S. Domain wall depinning from notches using combined in- and out-of-plane magnetic fields. AIP Adv. 2016, 6, 056407. [Google Scholar] [CrossRef]
- Ferrara, A.; Garlando, U.; Gnoli, L.; Santoro, G.; Zamboni, M. 3D design of a pNML random access memory. In Proceedings of the 2017 13th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Giardini Naxos, Italy, 12–15 June 2017; pp. 5–8. [Google Scholar] [CrossRef]
- Riente, F.; Ziemys, G.; Mattersdorfer, C.; Boche, S.; Turvani, G.; Raberg, W.; Luber, S.; Breitkreutz-v Gamm, S. Controlled data storage for non-volatile memory cells embedded in nano magnetic logic. AIP Adv. 2017, 7, 055910. [Google Scholar] [CrossRef]
- Becherer, M.; Gamm, S.B.V.; Eichwald, I.; Žiemys, G.; Kiermaier, J.; Csaba, G.; Schmitt-Landsiedel, D. A monolithic 3D integrated nanomagnetic co-processing unit. Solid-State Electron. 2016, 115, 74–80. [Google Scholar] [CrossRef]
- Eichwald, I.; Kiermaier, J.; Breitkreutz, S.; Wu, J.; Csaba, G.; Schmitt-Landsiedel, D.; Becherer, M. Towards a Signal Crossing in Double-Layer Nanomagnetic Logic. IEEE Trans. Magn. 2013, 49, 4468–4471. [Google Scholar] [CrossRef]
- Eichwald, I.; Breitkreutz, S.; Kiermaier, J.; Csaba, G.; Schmitt-Landsiedel, D.; Becherer, M. Signal crossing in perpendicular nanomagnetic logic. J. Appl. Phys. 2014, 115, 17E510. [Google Scholar] [CrossRef]
- Eichwald, I.; Breitkreutz, S.; Ziemys, G.; Csaba, G.; Porod, W.; Becherer, M. Majority logic gate for 3D magnetic computing. Nanotechnology 2014, 25, 335202. [Google Scholar] [CrossRef] [PubMed]
- Cofano, M.; Santoro, G.; Vacca, M.; Pala, D.; Causapruno, G.; Cairo, F.; Riente, F.; Turvani, G.; Roch, M.R.; Graziano, M.; et al. Logic-in-Memory: A Nano Magnet Logic Implementation. In Proceedings of the 2015 IEEE Computer Society Annual Symposium on VLSI, Montpellier, France, 8–10 July 2015; pp. 286–291. [Google Scholar] [CrossRef]
- Riente, F.; Ziemys, G.; Turvani, G.; Schmitt-Landsiedel, D.; Gamm, S.B.; Graziano, M. Towards Logic-In-Memory circuits using 3D-integrated Nanomagnetic logic. In Proceedings of the 2016 IEEE International Conference on Rebooting Computing (ICRC), San Diego, CA, USA, 17–19 October 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Garlando, U.; Riente, F.; Turvani, G.; Ferrara, A.; Santoro, G.; Vacca, M.; Graziano, M. Architectural exploration of perpendicular Nano Magnetic Logic based circuits. Integration 2018, 63, 275–282. [Google Scholar] [CrossRef]
- Santoro, G.; Vacca, M.; Bollo, M.; Riente, F.; Graziano, M.; Zamboni, M. Exploration of multilayer field-coupled nanomagnetic circuits. Microelectron. J. 2018, 79, 46–56. [Google Scholar] [CrossRef]
- Vacca, M.; Graziano, M.; Wang, J.; Cairo, F.; Causapruno, G.; Urgese, G.; Biroli, A.; Zamboni, M. NanoMagnet Logic: An Architectural Level Overview; LNCS, Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2014; Volume 8280, pp. 223–256. [Google Scholar]
- Riente, F.; Garlando, U.; Turvani, G.; Vacca, M.; Roch, M.R.; Graziano, M. MagCAD: A Tool for the Design of 3D Magnetic Circuits. IEEE J. Explor. Solid-State Comput. Devices Circuits 2017, 3, 65–73. [Google Scholar] [CrossRef]
- Turvani, G.; Riente, F.; Graziano, M.; Zamboni, M. A quantitative approach to testing in Quantum dot Cellular Automata: NanoMagnet Logic case. In Proceedings of the 2014 10th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Grenoble, France, 30 June–3 July 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Turvani, G.; Tohti, A.; Bollo, M.; Riente, F.; Vacca, M.; Graziano, M.; Zamboni, M. Physical design and testing of Nano Magnetic architectures. In Proceedings of the 2014 9th IEEE International Conference on Design & Technology of Integrated Systems in Nanoscale Era (DTIS), Santorini, Greece, 6–8 May 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Turvani, G.; Riente, F.; Cairo, F.; Vacca, M.; Garlando, U.; Zamboni, M.; Graziano, M. Efficient and reliable fault analysis methodology for nanomagnetic circuits. Int. J. Circuit Theory Appl. 2016, 45, 660–680. [Google Scholar] [CrossRef]








| Fixed Input | S | Cout |
|---|---|---|
| A = 0 | B ⊕ Cin | B Cin |
| A = 1 | B + Cin | |
| A = 0 & B = 1 | Cin | |
| A = 1 & B = 0 | Cin |
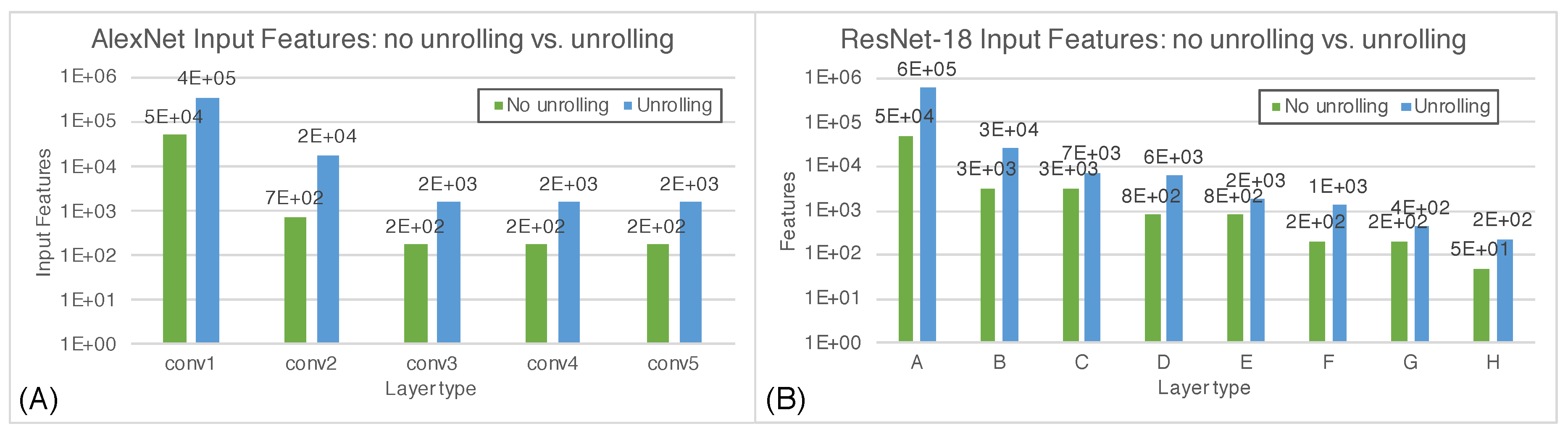
| CNN Type | Architecture | Average Cycles | Texec (s) |
|---|---|---|---|
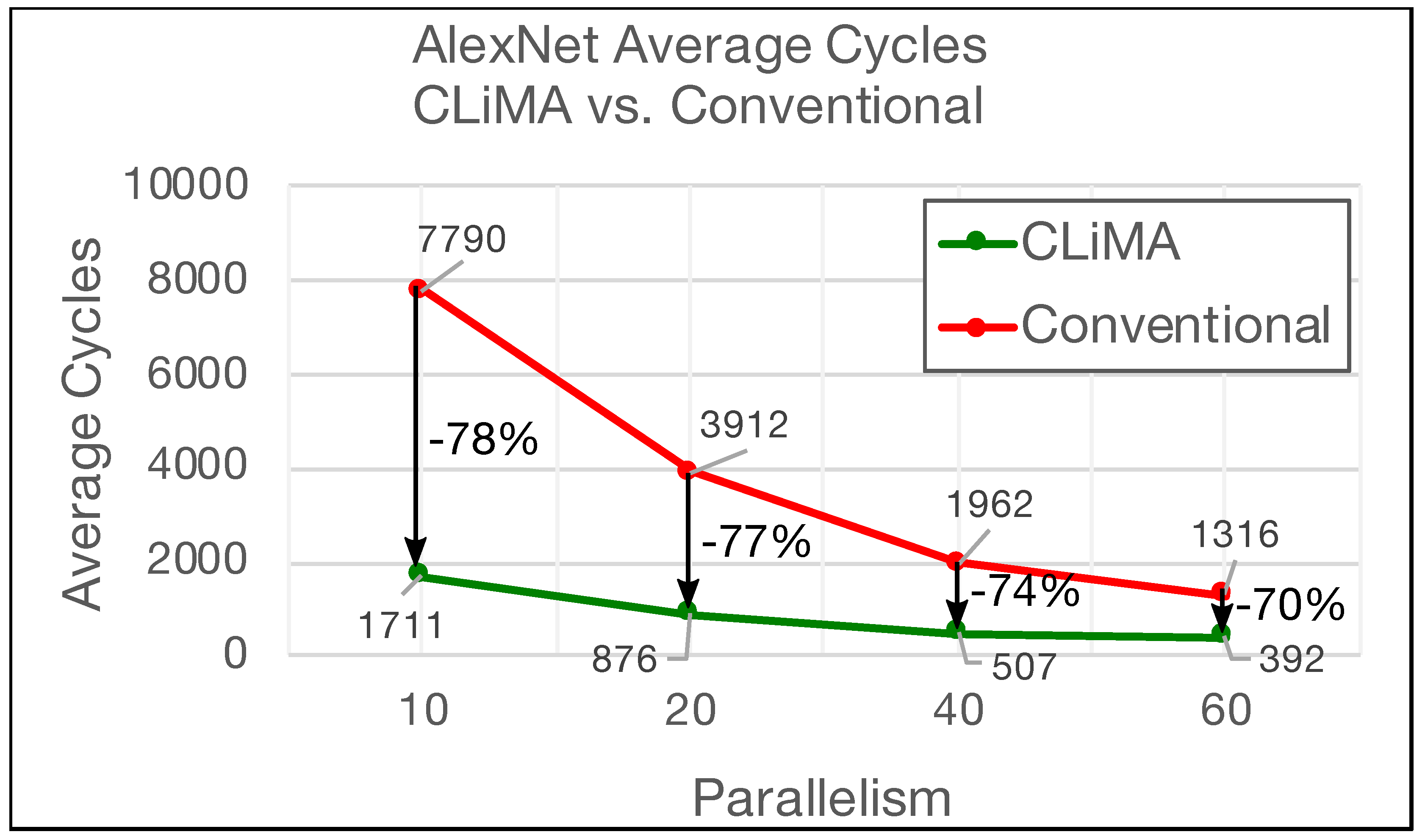
| AlexNet | CLiMA DL Acc. | 1711 7790 | 0.95 43.2 |
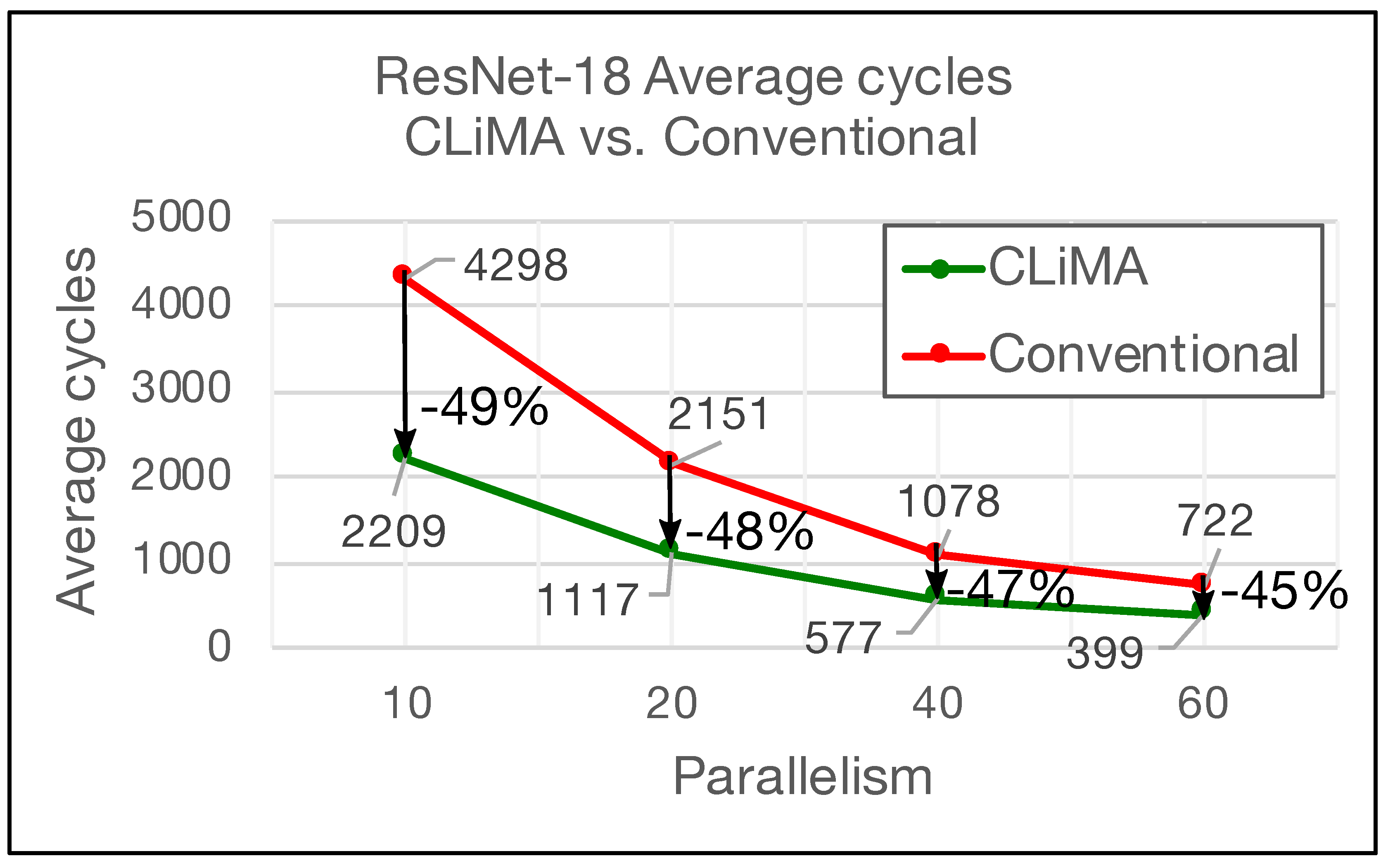
| ResNet-18 | CLiMA DL Acc. | 2209 42,939 | 1.2 24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santoro, G.; Turvani, G.; Graziano, M. New Logic-In-Memory Paradigms: An Architectural and Technological Perspective. Micromachines 2019, 10, 368. https://doi.org/10.3390/mi10060368
Santoro G, Turvani G, Graziano M. New Logic-In-Memory Paradigms: An Architectural and Technological Perspective. Micromachines. 2019; 10(6):368. https://doi.org/10.3390/mi10060368
Chicago/Turabian StyleSantoro, Giulia, Giovanna Turvani, and Mariagrazia Graziano. 2019. "New Logic-In-Memory Paradigms: An Architectural and Technological Perspective" Micromachines 10, no. 6: 368. https://doi.org/10.3390/mi10060368
APA StyleSantoro, G., Turvani, G., & Graziano, M. (2019). New Logic-In-Memory Paradigms: An Architectural and Technological Perspective. Micromachines, 10(6), 368. https://doi.org/10.3390/mi10060368





