Continuous Phase Plate Structuring by Multi-Aperture Atmospheric Pressure Plasma Processing
Abstract
1. Introduction
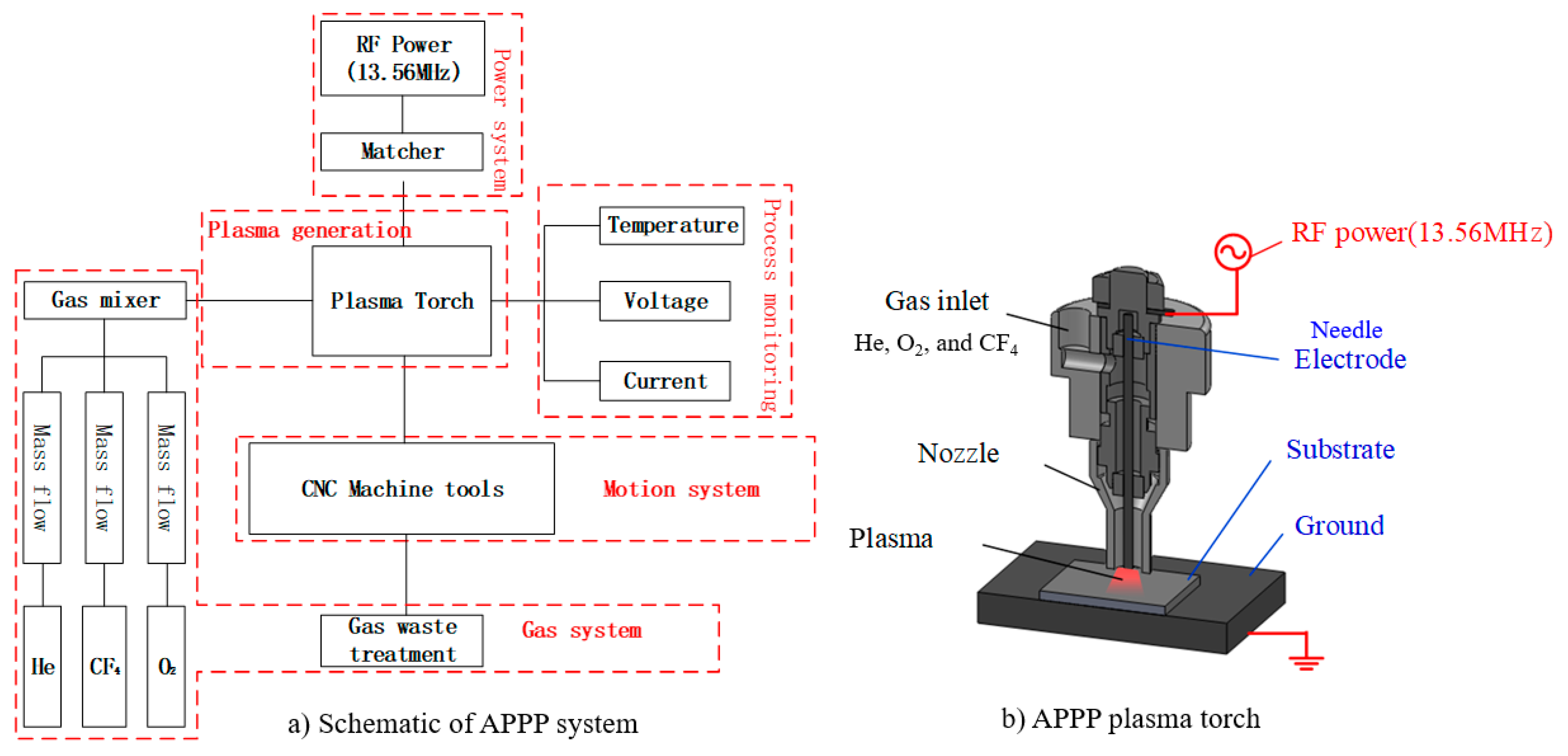
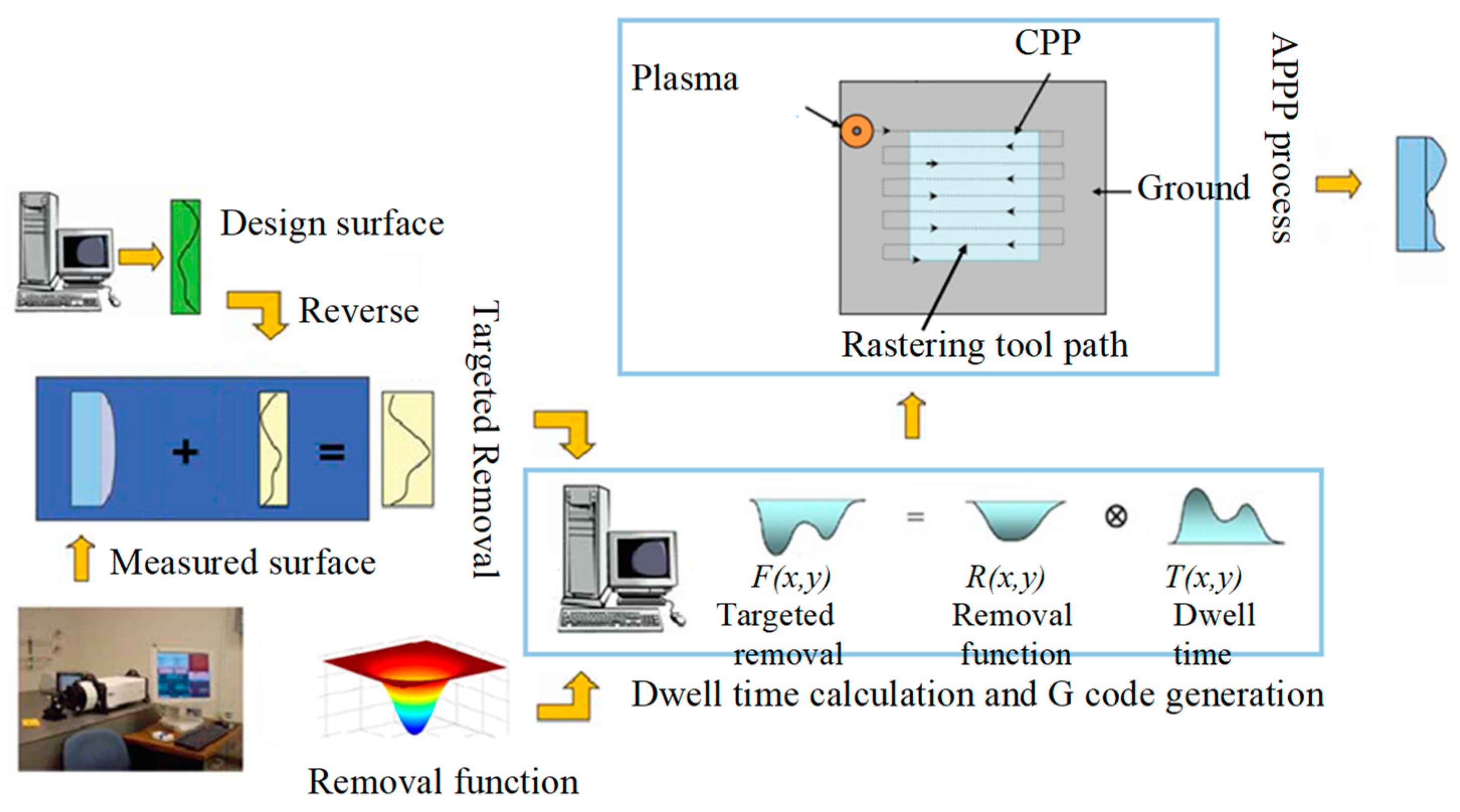
2. APPP System Configuration and Removal Investigation
2.1. System Configuration
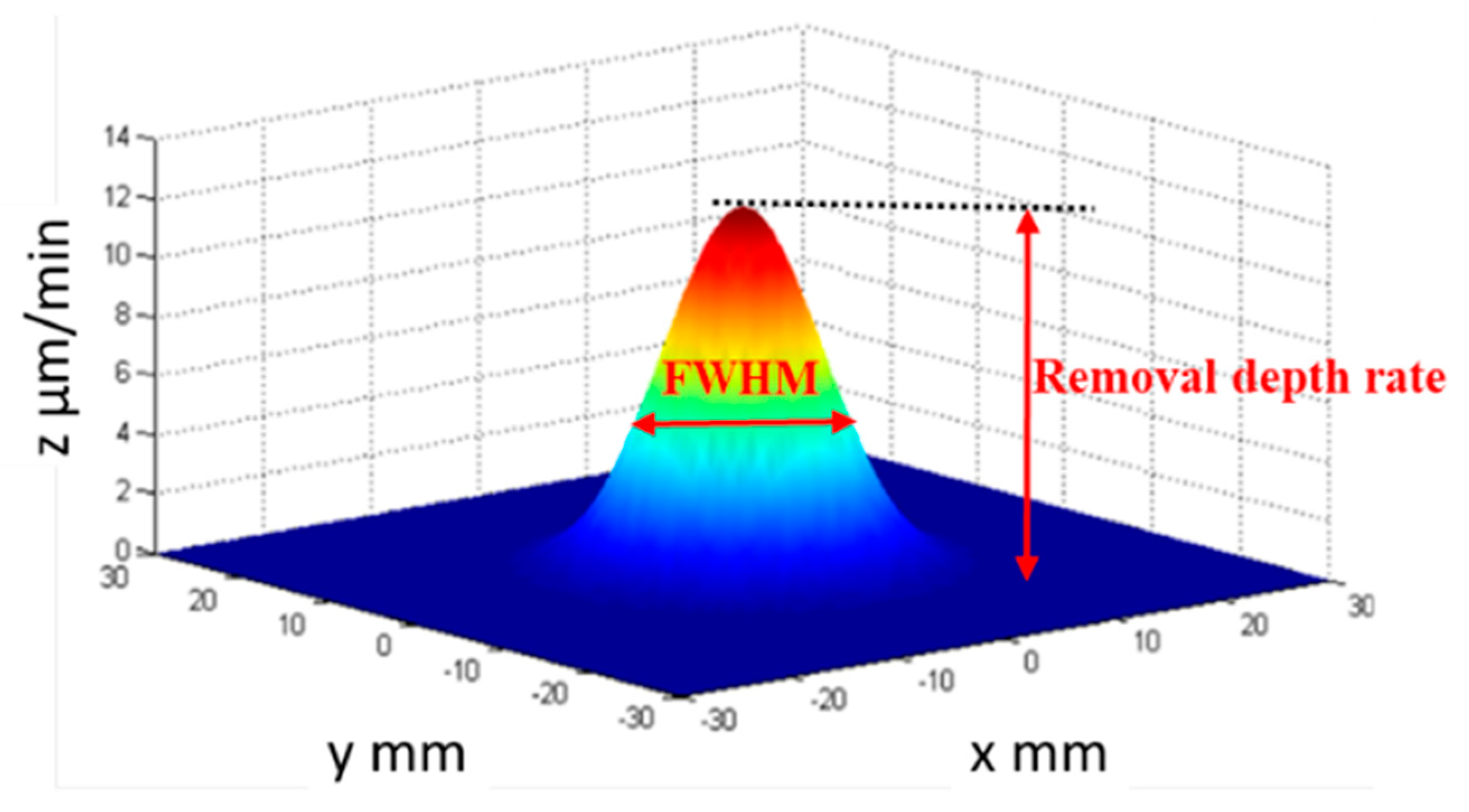
2.2. Removal Investigation
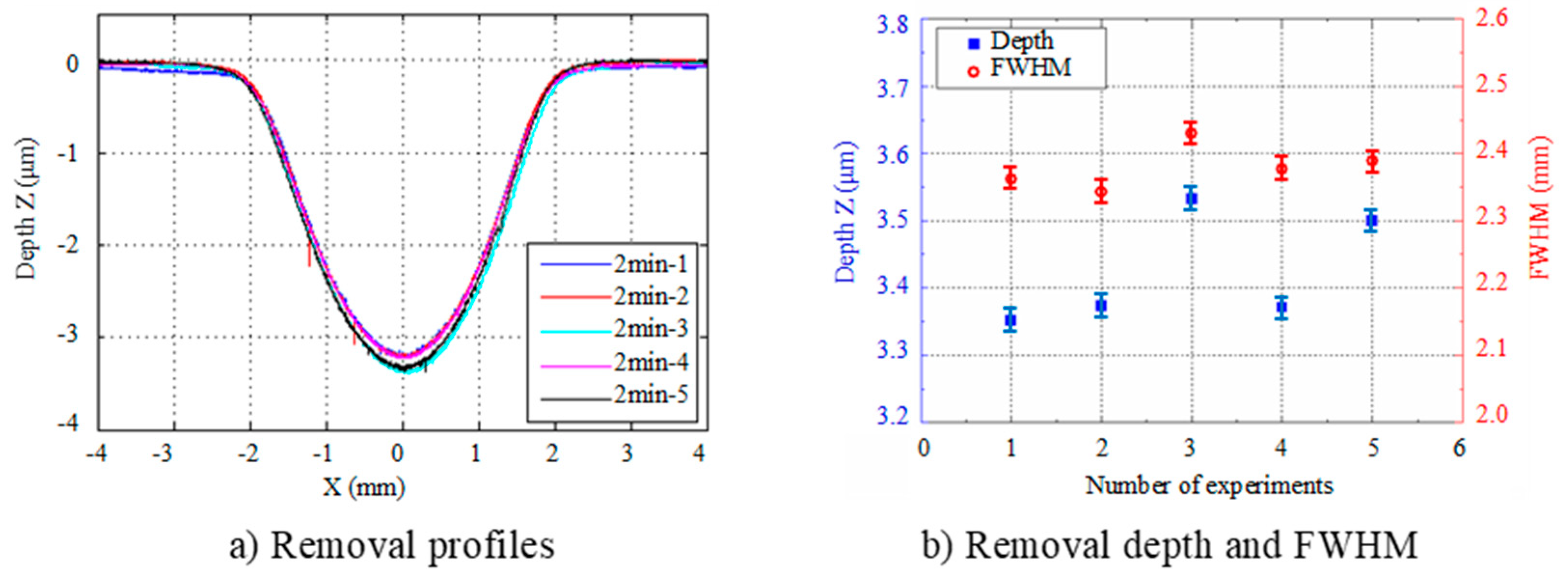
2.2.1. Repeatability of the Removal Function
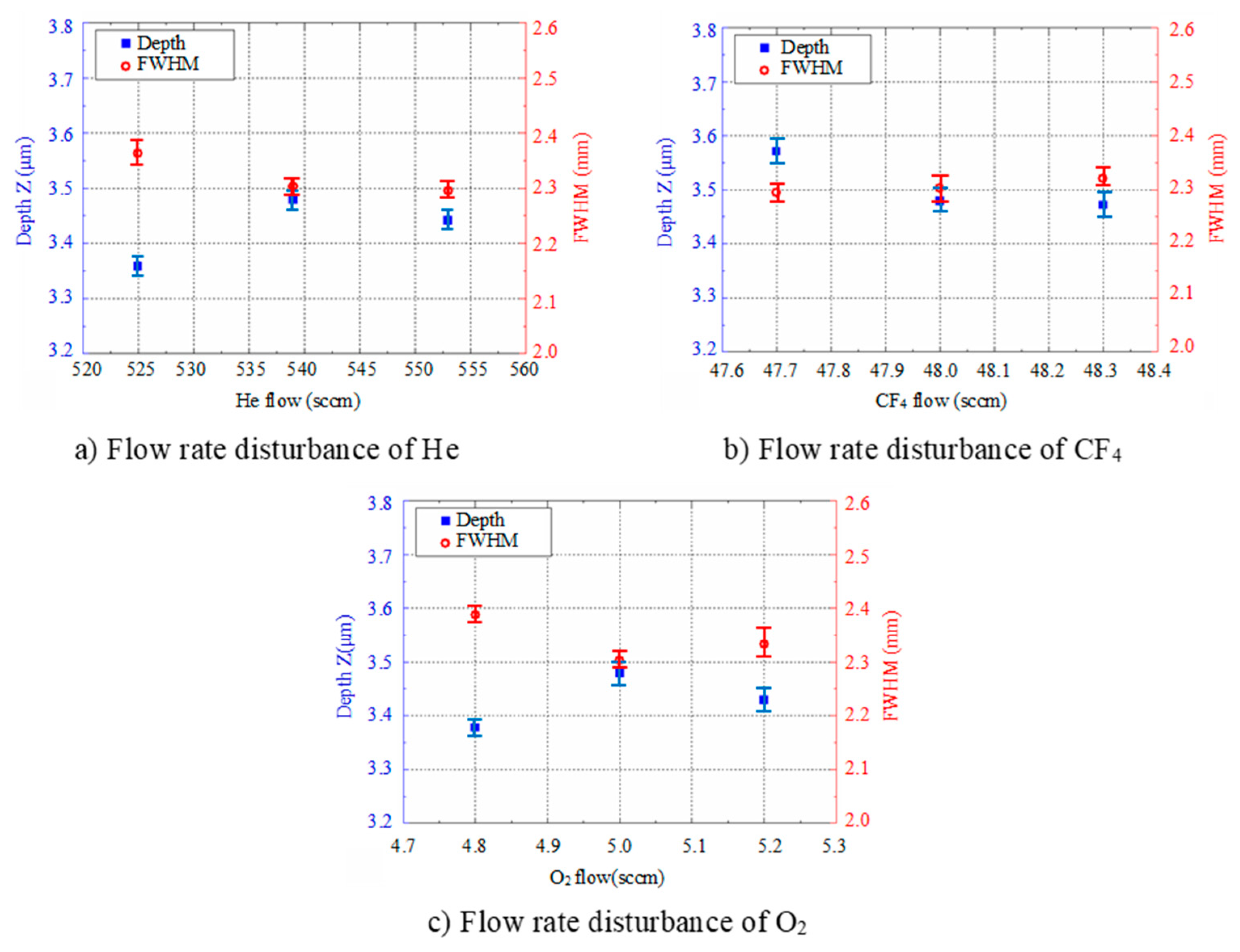
2.2.2. Robustness of the Removal Function to Gas Flow Disturbance
3. Multi-Aperture Structuring Principle and Analysis
3.1. Mathematical Model
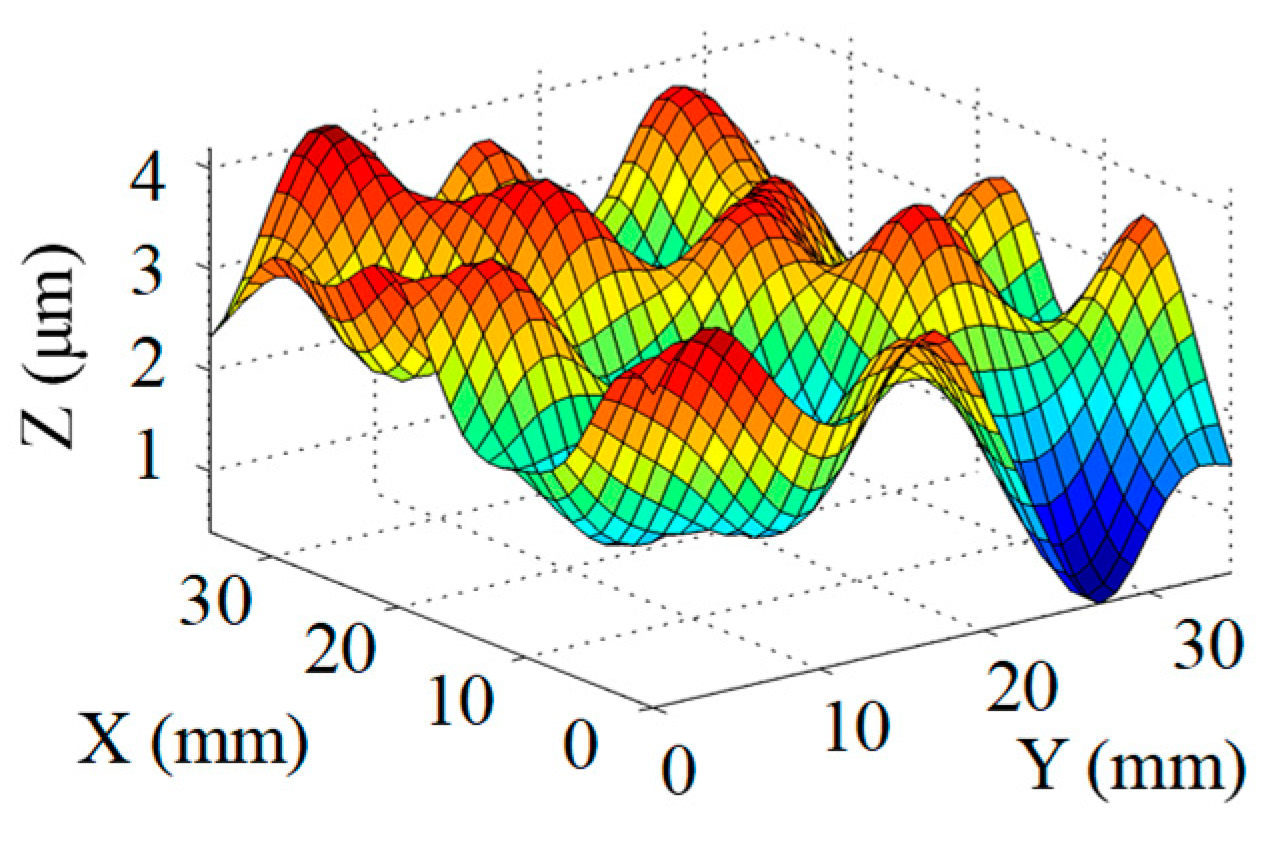
3.2. Simulation and Analysis
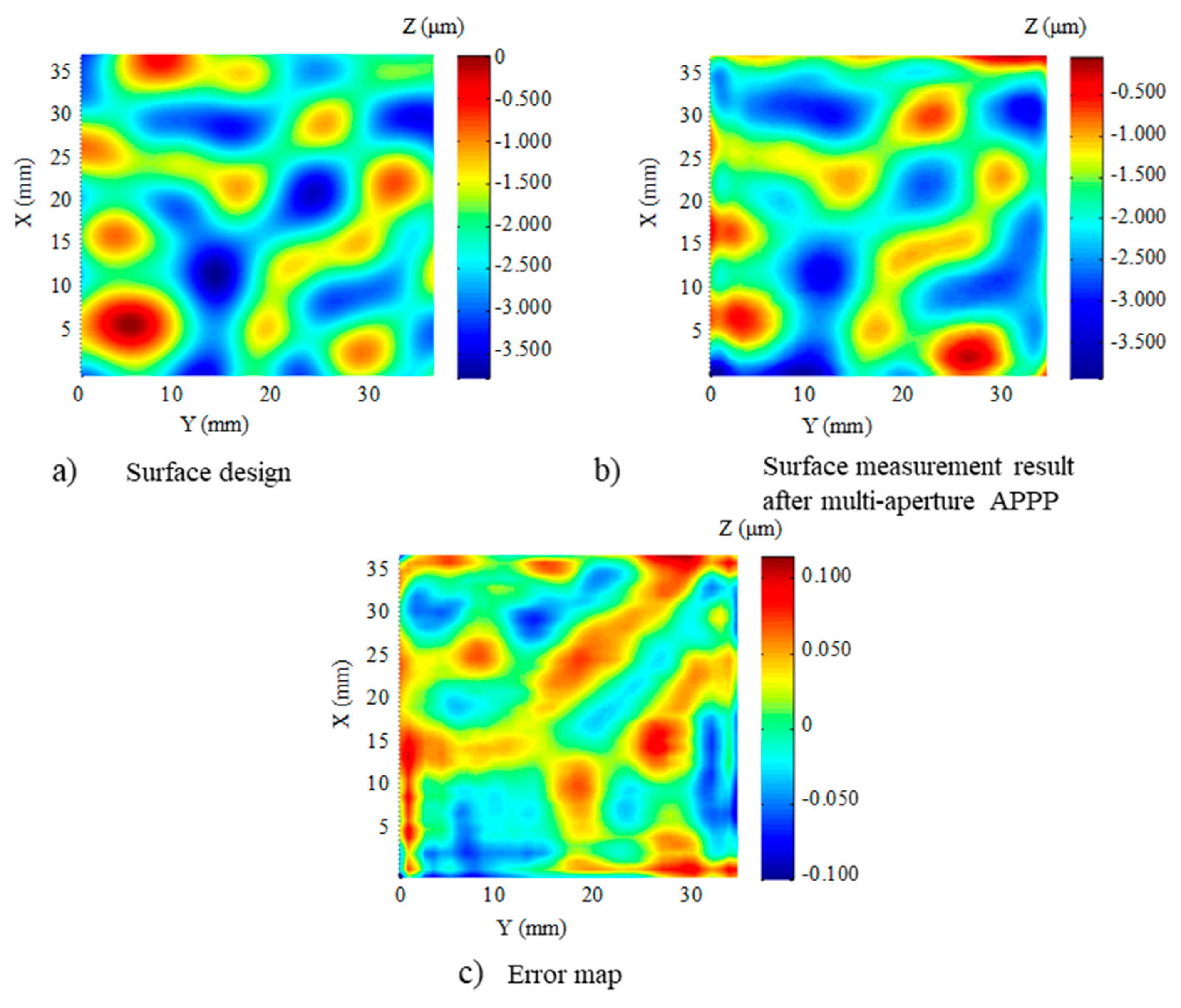
4. Experiments and Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Miller, G.H.; Moses, E.I.; Wuest, C.R. The national ignition facility. Opt. Eng. 2004, 43, 2841–2854. [Google Scholar] [CrossRef]
- Lion, C. The LMJ program: An overview. J. Phys. Conf. Ser. 2010, 244, 012003. [Google Scholar] [CrossRef]
- Zhu, Q.; Zheng, W.; Wei, X.; Jing, F.; Hu, D.; Zhou, W.; Feng, B.; Wang, J.; Peng, Z.; Liu, L. Research and construction progress of the SG-III laser facility. In Proceedings of the Pacific Rim Laser Damage 2013: Optical Materials for High Power Lasers, International Society for Optics and Photonics, Shanghai, China, 19–23 May 2013; p. 87861G. [Google Scholar]
- Neauport, J.; Ribeyre, X.; Daurios, J.; Valla, D.; Lavergne, M.; Beau, V.; Videau, L. Design and optical characterization of a large continuous phase plate for laser integration line and laser megajoule facilities. Appl. Opt. 2003, 42, 2377–2382. [Google Scholar] [CrossRef] [PubMed]
- Tricard, M.; Dumas, P.; Menapace, J. Continuous phase plate polishing using magnetorheological finishing. In Proceedings of the Laser Beam Shaping IX, International Society for Optics and Photonics, San Diego, CA, USA, 17 September 2008; p. 70620V. [Google Scholar]
- Xu, M.; Dai, Y.; Xie, X.; Zhou, L.; Peng, W. Fabrication of continuous phase plates with small structures based on recursive frequency filtered ion beam figuring. Opt. Express 2017, 25, 10765–10778. [Google Scholar] [CrossRef] [PubMed]
- Dimitrakellis, P.; Gogolides, E. Atmospheric plasma etching of polymers: A palette of applications in cleaning/ashing, pattern formation, nanotexturing and superhydrophobic surface fabrication. Microelectron. Eng. 2018, 194, 109–115. [Google Scholar] [CrossRef]
- Moravej, M.; Yang, X.; Hicks, R.F.; Penelon, J.; Babayan, S.E. A radio-frequency nonequilibrium atmospheric pressure plasma operating with argon and oxygen. J. Appl. Phys. 2006, 99, 93305. [Google Scholar] [CrossRef]
- Fricke, K.; Steffen, H.; Von Woedtke, T.; Schröder, K.; Weltmann, K.D. High rate etching of polymers by means of an atmospheric pressure plasma jet. Plasma Process. Polym. 2011, 8, 51–58. [Google Scholar] [CrossRef]
- Wang, L.; Ning, W.; Fu, M.; Wu, C.; Jia, S. An experimental study of photoresist material etching by an atmospheric-pressure plasma jet with Ar/air mixed gas. J. Plasma Phys. 2013, 79, 683–689. [Google Scholar] [CrossRef]
- Dimitrakellis, P.; Gogolides, E.; Zeniou, A.; Awsiuk, K.; Rysz, J.; Marzec, M.M. Transition between stable hydrophilization and fast etching/hydrophilization of poly (methyl) methacrylate polymer using a novel atmospheric pressure dielectric barrier discharge source. J. Vac. Sci. Technol. A Vac. Surf. Films 2017, 35, 41303. [Google Scholar] [CrossRef]
- Dufour, T.; Hubert, J.; Viville, P.; Duluard, C.Y.; Desbief, S.; Lazzaroni, R.; Reniers, F. PTFE surface etching in the post-discharge of a scanning RF plasma torch: Evidence of ejected fluorinated species. Plasma Process. Polym. 2012, 9, 820–829. [Google Scholar] [CrossRef]
- Knoll, A.J.; Luan, P.; Bartis, E.A.J.; Hart, C.; Raitses, Y.; Oehrlein, G. Real time characterization of polymer surface modifications by an atmospheric-pressure plasma jet: Electrically coupled versus remote mode. Appl. Phys. Lett. 2014, 105, 171601. [Google Scholar] [CrossRef]
- Jourdain, R.; Castelli, M.; Shore, P.; Sommer, P.; Proscia, D. Reactive atom plasma (RAP) figuring machine for meter class optical surfaces. Prod. Eng. 2013, 7, 665–673. [Google Scholar] [CrossRef][Green Version]
- Dai, Z.; Xie, X.; Chen, H.; Zhou, L. Non-linear compensated dwell time for efficient fused silica surface figuring using inductively coupled plasma. Plasma Chem. Plasma Process. 2018, 38, 443–459. [Google Scholar] [CrossRef]
- Meister, J.; Arnold, T. New process simulation procedure for high-rate plasma jet machining. Plasma Chem. Plasma Process. 2011, 31, 91–107. [Google Scholar] [CrossRef]
- Sun, R.; Yang, X.; Ohkubo, Y.; Endo, K.; Yamamura, K. Optimization of gas composition used in plasma chemical vaporization machining for figuring of reaction-sintered silicon carbide with low surface roughness. Sci. Rep. 2018, 8, 2376. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Endo, K.; Yamamura, K. Damage-free finishing of CVD-SiC by a combination of dry plasma etching and plasma-assisted polishing. Int. J. Mach. Tools Manuf. 2017, 115, 38–46. [Google Scholar] [CrossRef]
- Li, D.; Li, N.; Su, X.; Liu, K.; Ji, P.; Wang, B. Modelling of removal characteristics and surface morphology formation in capacitively coupled atmospheric pressure plasma processing of fused silica optics. Opt. Mater. Express 2019, 9, 1893–1906. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, B.; Wang, J.; Jin, H.; Zhang, Y.; Dong, S. Chemical machining of Zerodur material with atmospheric pressure plasma jet. CIRP Ann. 2010, 59, 337–340. [Google Scholar] [CrossRef]
- Jiao, C.; Li, S.; Xie, X. Algorithm for ion beam figuring of low-gradient mirrors. Appl. Opt. 2009, 48, 4090–4096. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.A. Optimization of computer controlled polishing. Appl. Opt. 1977, 16, 218–224. [Google Scholar] [CrossRef] [PubMed]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Siam: Philadelphia, PA, USA, 1995. [Google Scholar]

| He Flow (sccm) | CF4 Flow (sccm) | O2 Flow (sccm) | Distance (mm) | Power (W) |
|---|---|---|---|---|
| 539 | 48 | 5 | 3 | 48 |
| Parameters | Nominal Value | Disturbance Value |
|---|---|---|
| He flow (sccm) | 539 | 525, 539, 553 |
| CF4 flow (sccm) | 48 | 47.7, 48, 48.3 |
| O2 flow (sccm) | 5 | 4.8, 5, 5.2 |
| Machining Mode | Dwell Time Distribution | Residue Error Distribution |
|---|---|---|
| Single Removal Function ① | 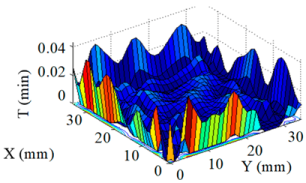 | 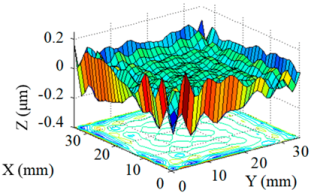 |
| Single Removal Function ② | 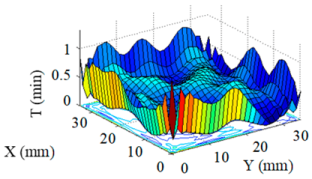 | 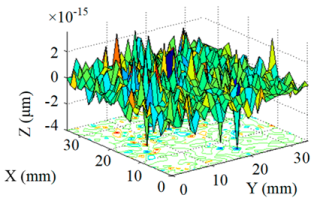 |
| Combined Removal Functions ① and ② |  |  |
| Machining Mode | Dwell Time (min) | Residue Error | |
|---|---|---|---|
| PV (μm) | RMS (μm) | ||
| Single Removal Function ① | 5.61 | 0.46 | 0.055 |
| Single Removal Function ② | 340.94 | 7.55 × 10−15 | 8.05 × 10−16 |
| Combined Removal Functions ① and ② | 57.24 (①/②: 4.64/52.6) | 1.49 × 10−5 | 1.11 × 10−6 |
| Electrode Diameter (mm) | He flow (sccm) | CF4 Flow (sccm) | O2 Flow (sccm) | Discharge Distance (mm) | Power (W) | Removal Rate (μm/min) | FWHM (mm) |
|---|---|---|---|---|---|---|---|
| 3 | 539 | 48 | 5 | 3 | 106 | 20.8 | 5.7 |
| Electrode Diameter (mm) | He flow (sccm) | CF4 Flow (sccm) | O2 Flow (sccm) | Discharge Distance (mm) | Power (W) | Removal Rate (μm/min) | FWHM (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 539 | 48 | 5 | 3 | 48 | 1.65 | 2.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Li, N.; Su, X.; Liu, K.; Ji, P.; Wang, B. Continuous Phase Plate Structuring by Multi-Aperture Atmospheric Pressure Plasma Processing. Micromachines 2019, 10, 260. https://doi.org/10.3390/mi10040260
Li D, Li N, Su X, Liu K, Ji P, Wang B. Continuous Phase Plate Structuring by Multi-Aperture Atmospheric Pressure Plasma Processing. Micromachines. 2019; 10(4):260. https://doi.org/10.3390/mi10040260
Chicago/Turabian StyleLi, Duo, Na Li, Xing Su, Kan Liu, Peng Ji, and Bo Wang. 2019. "Continuous Phase Plate Structuring by Multi-Aperture Atmospheric Pressure Plasma Processing" Micromachines 10, no. 4: 260. https://doi.org/10.3390/mi10040260
APA StyleLi, D., Li, N., Su, X., Liu, K., Ji, P., & Wang, B. (2019). Continuous Phase Plate Structuring by Multi-Aperture Atmospheric Pressure Plasma Processing. Micromachines, 10(4), 260. https://doi.org/10.3390/mi10040260





