Dynamic Modeling of the Multiring Disk Resonator Gyroscope
Abstract
1. Introduction
2. Materials and Methods
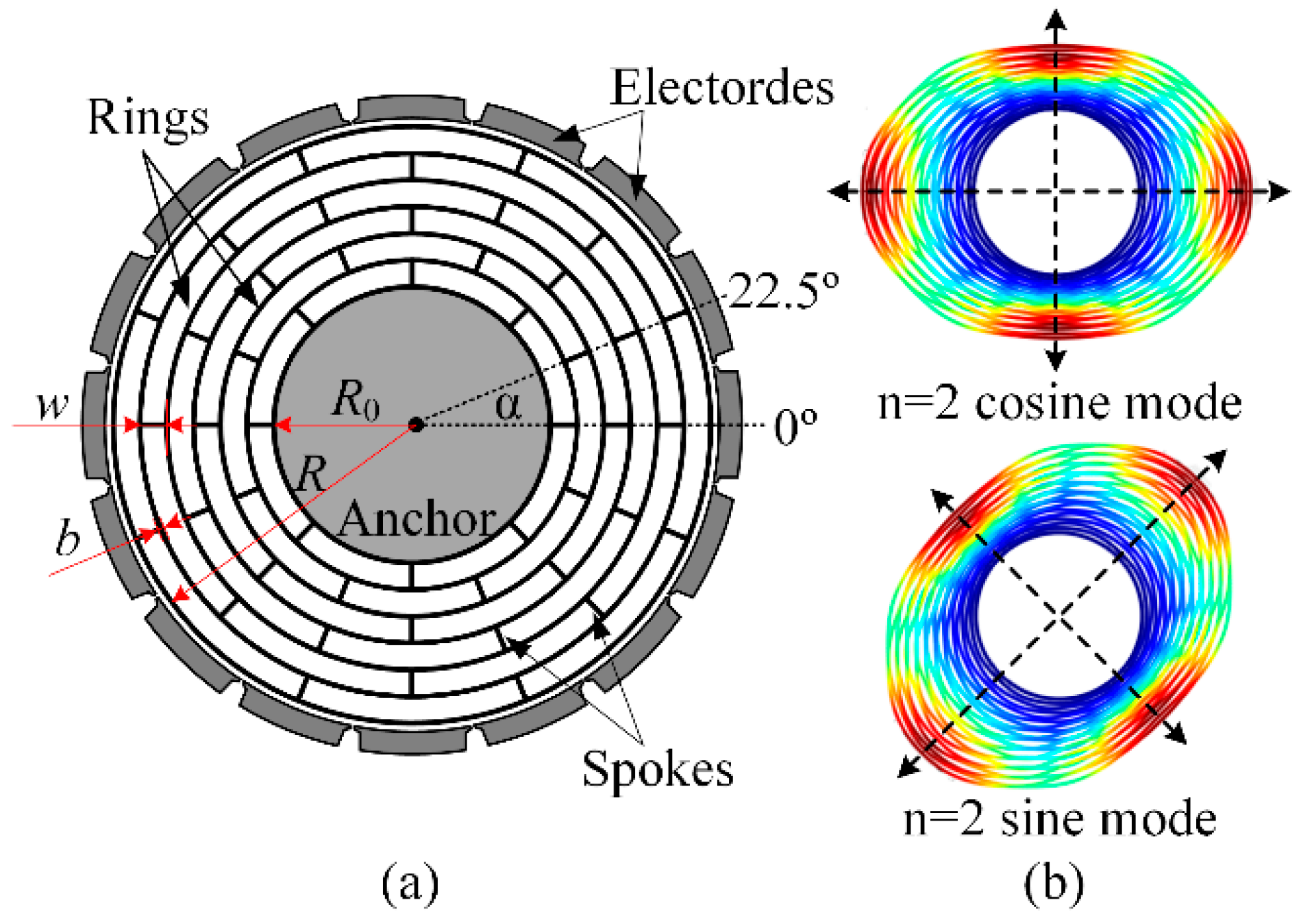
2.1. Design Model and Working Principle of the DRG
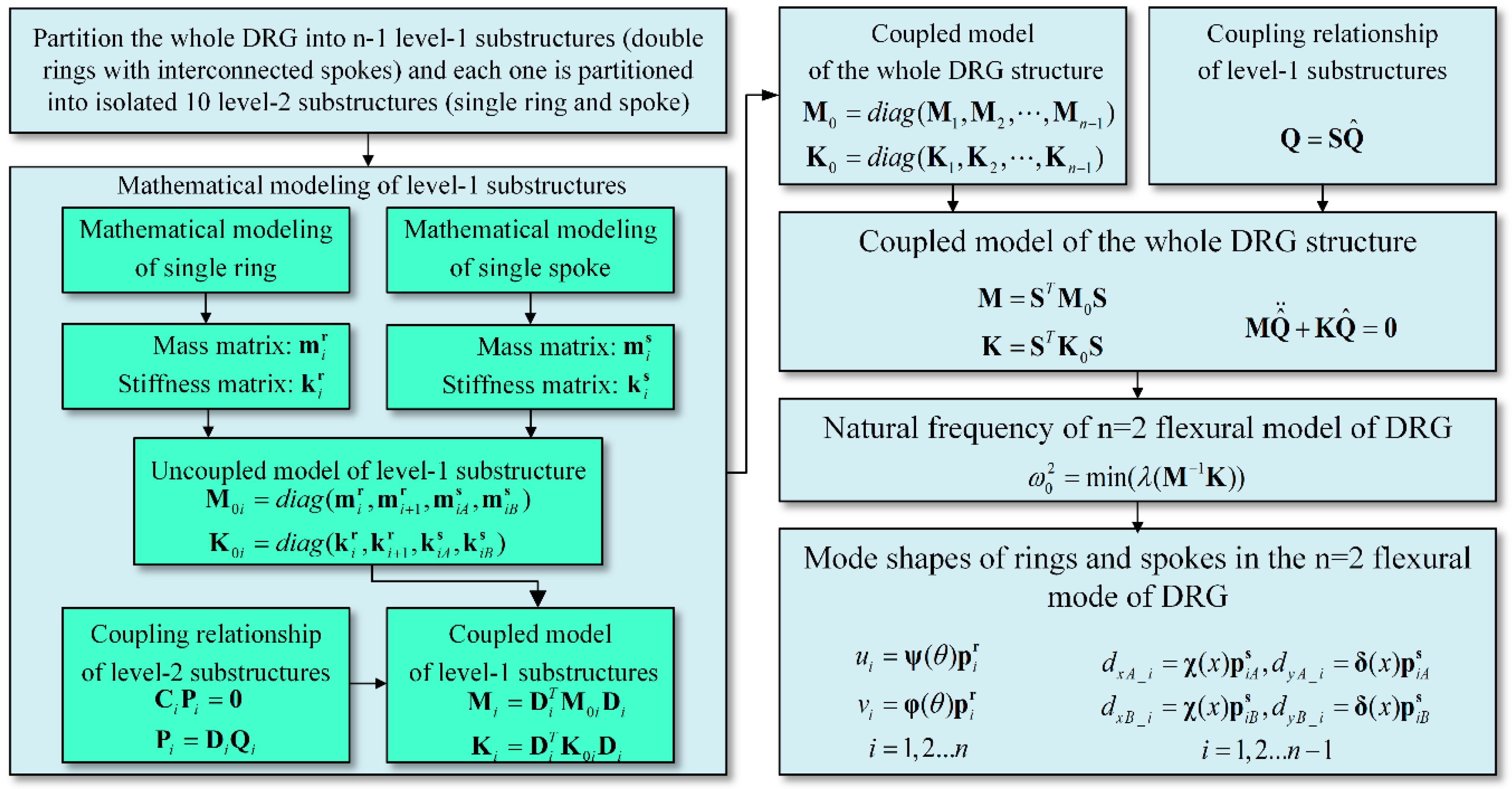
2.2. Component Mode Synthesis Technique
2.3. Mathematical Modeling of Free Vibrating DRGs
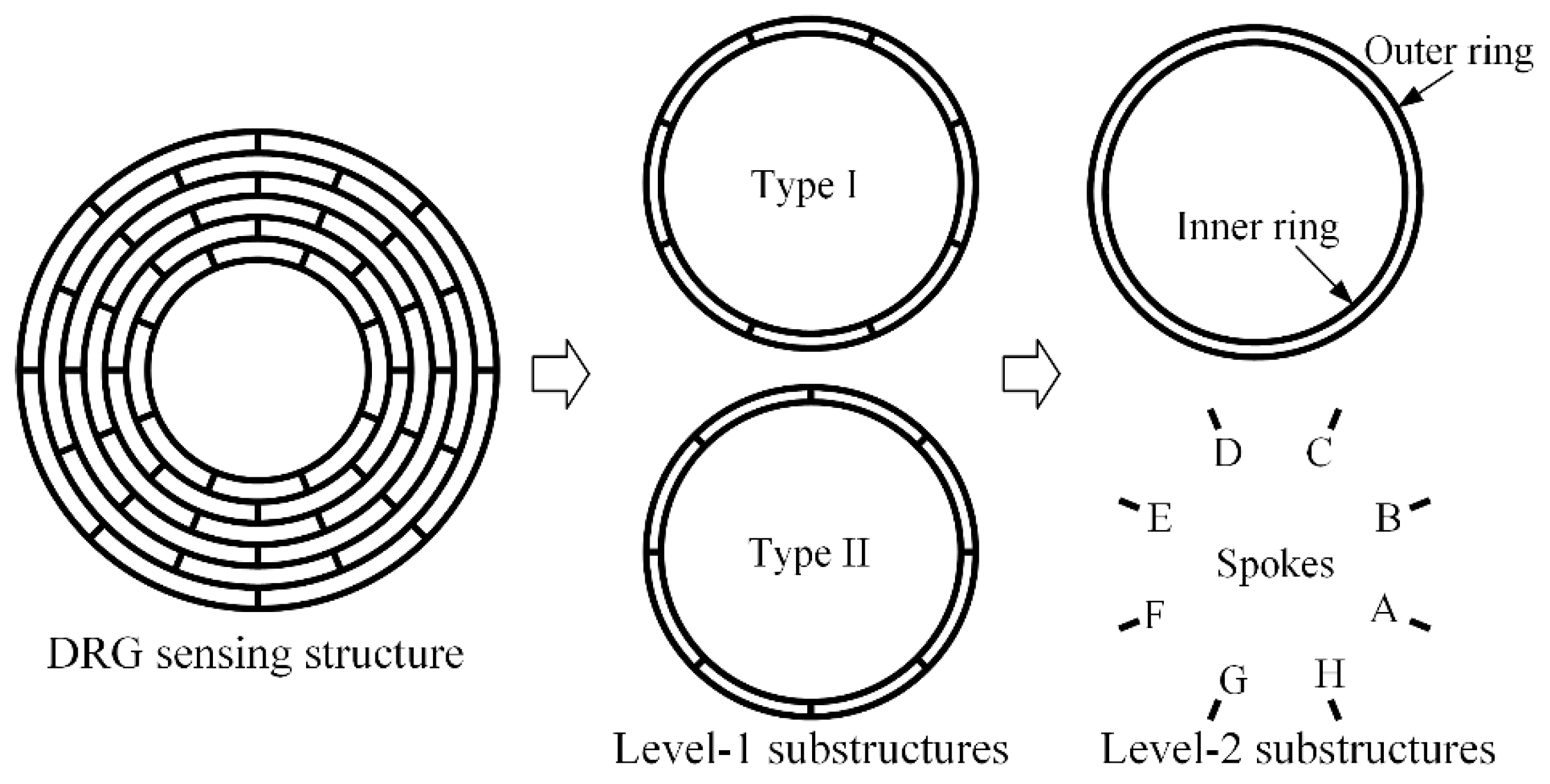
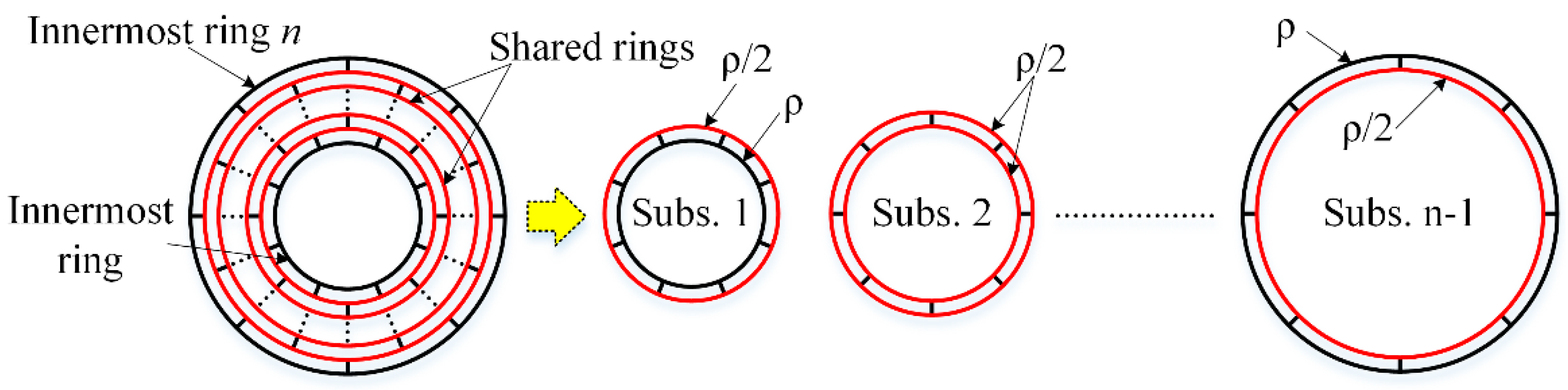
2.3.1. Substructures Partition
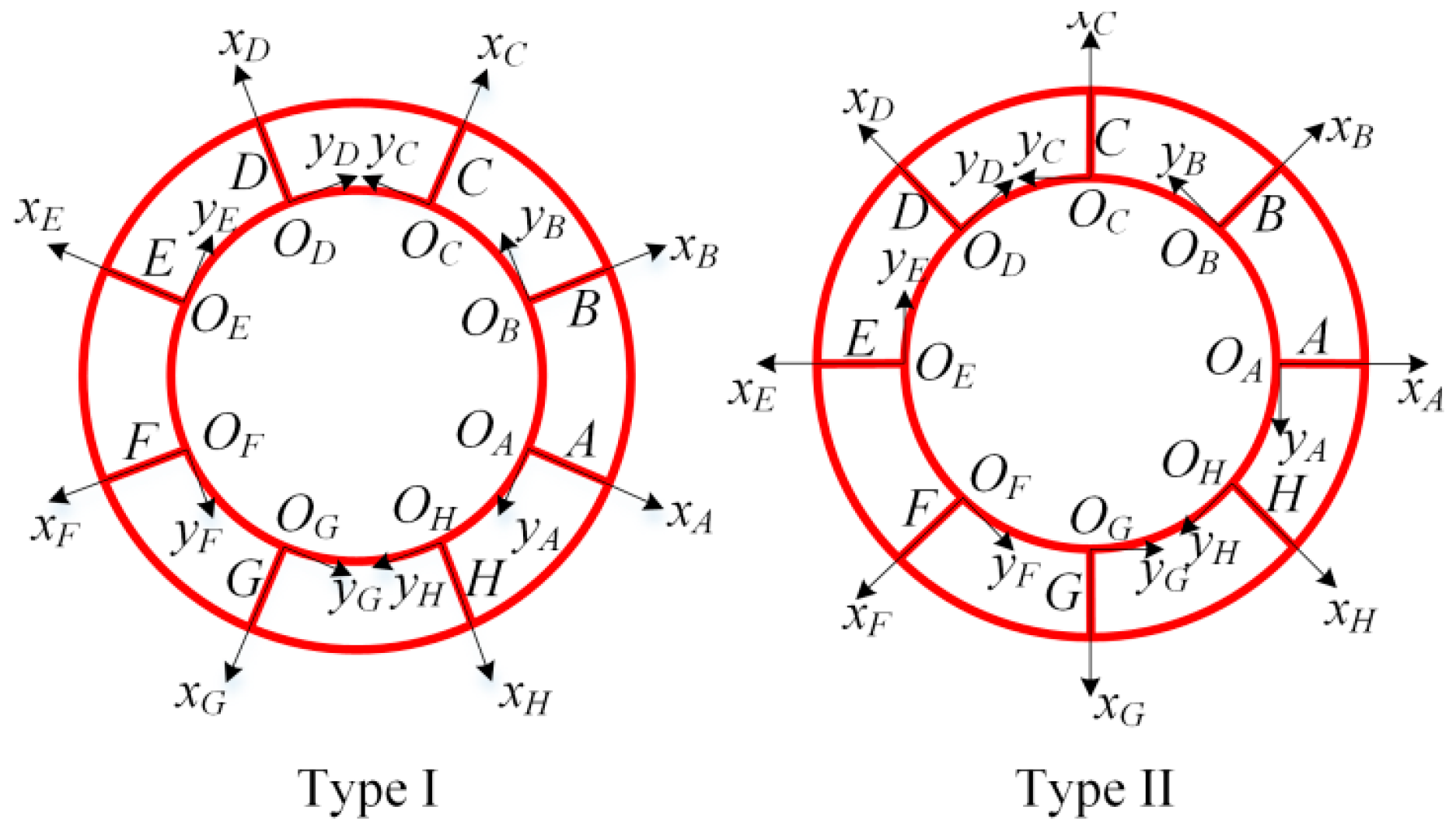
2.3.2. Mathematical Modeling of the Level-2 Substructures
2.3.3. Mathematical Modeling of the Level-1 Substructures
2.3.4. Mathematical Modeling of the Whole Sensing Structure
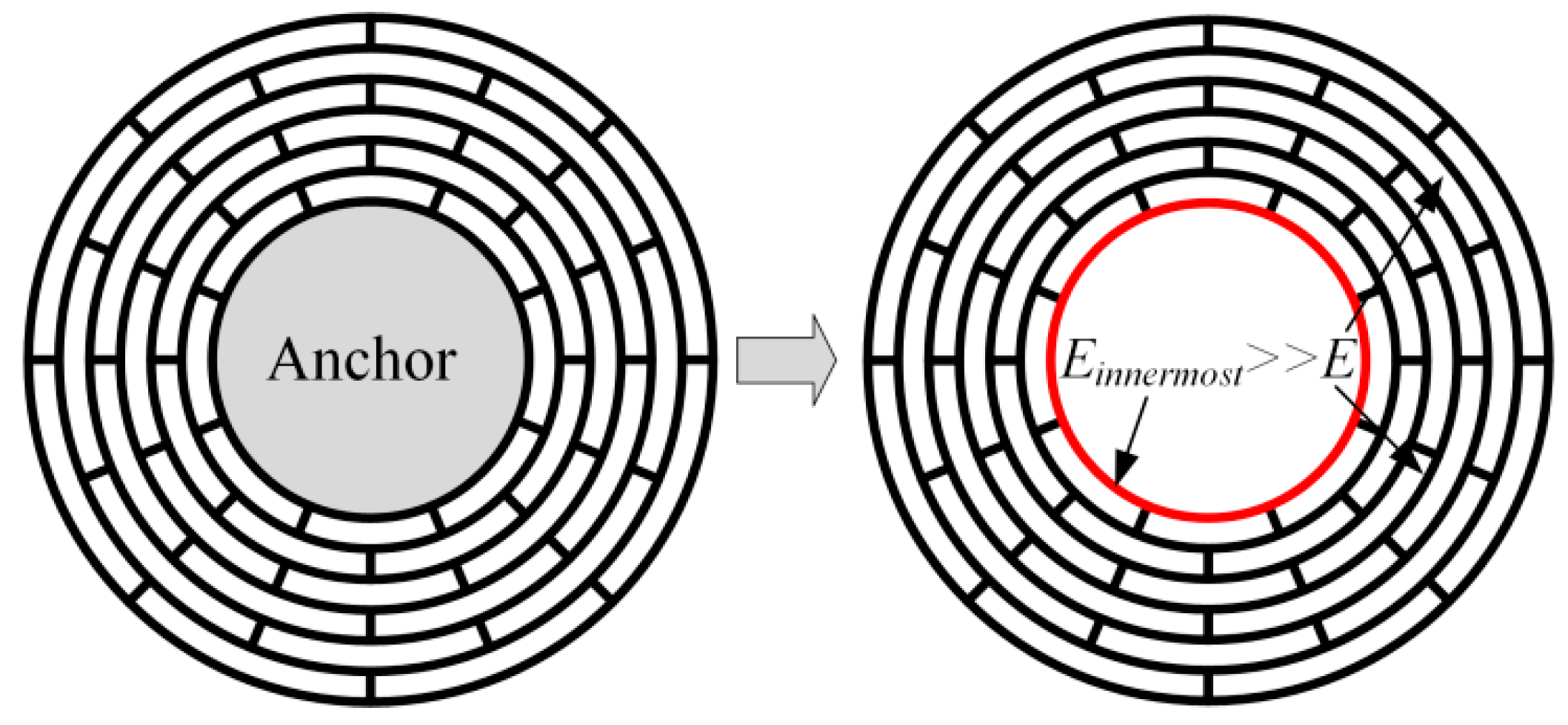
2.4. Mathematical Modeling of the Central-supported DRG
3. Results
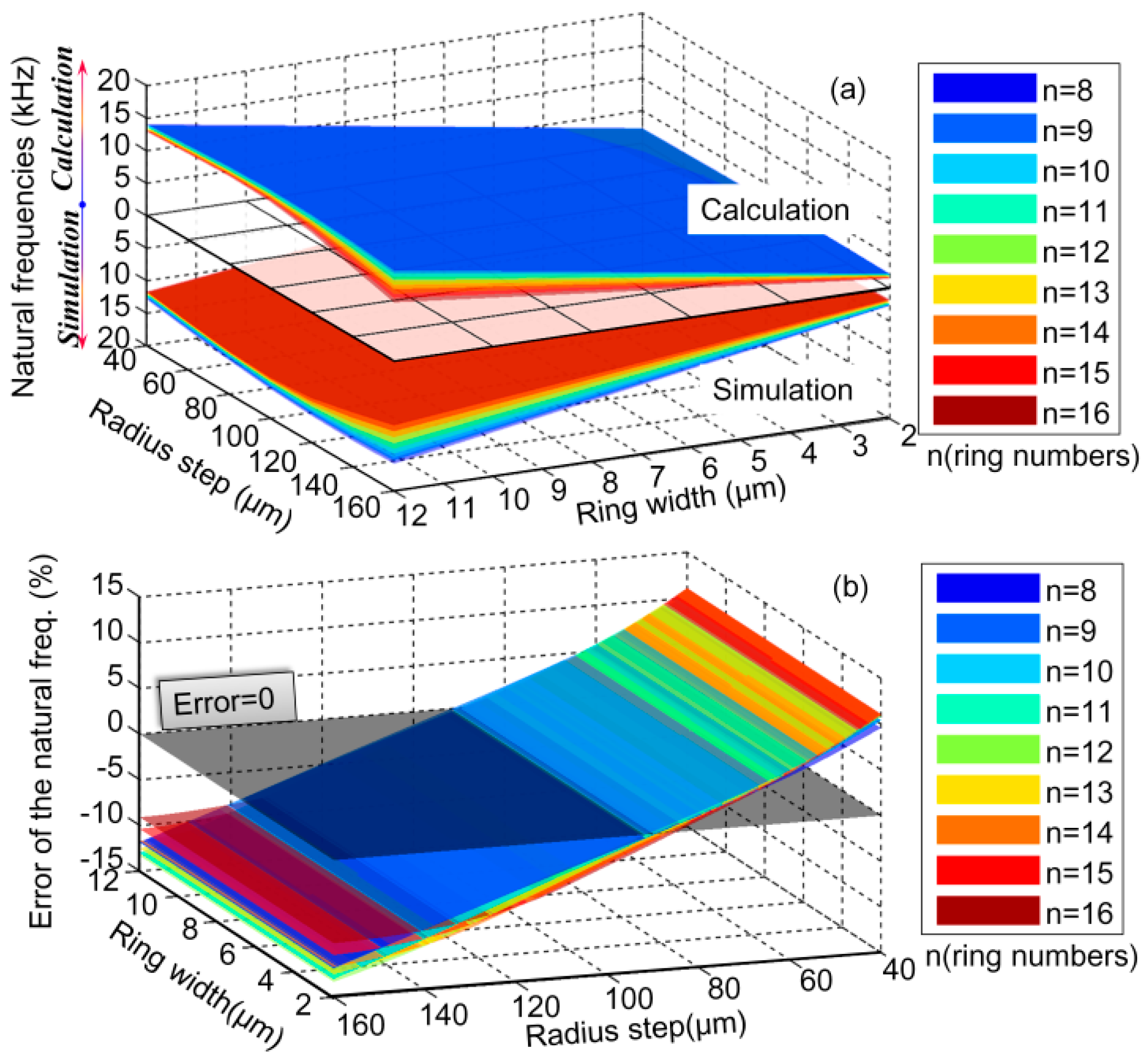
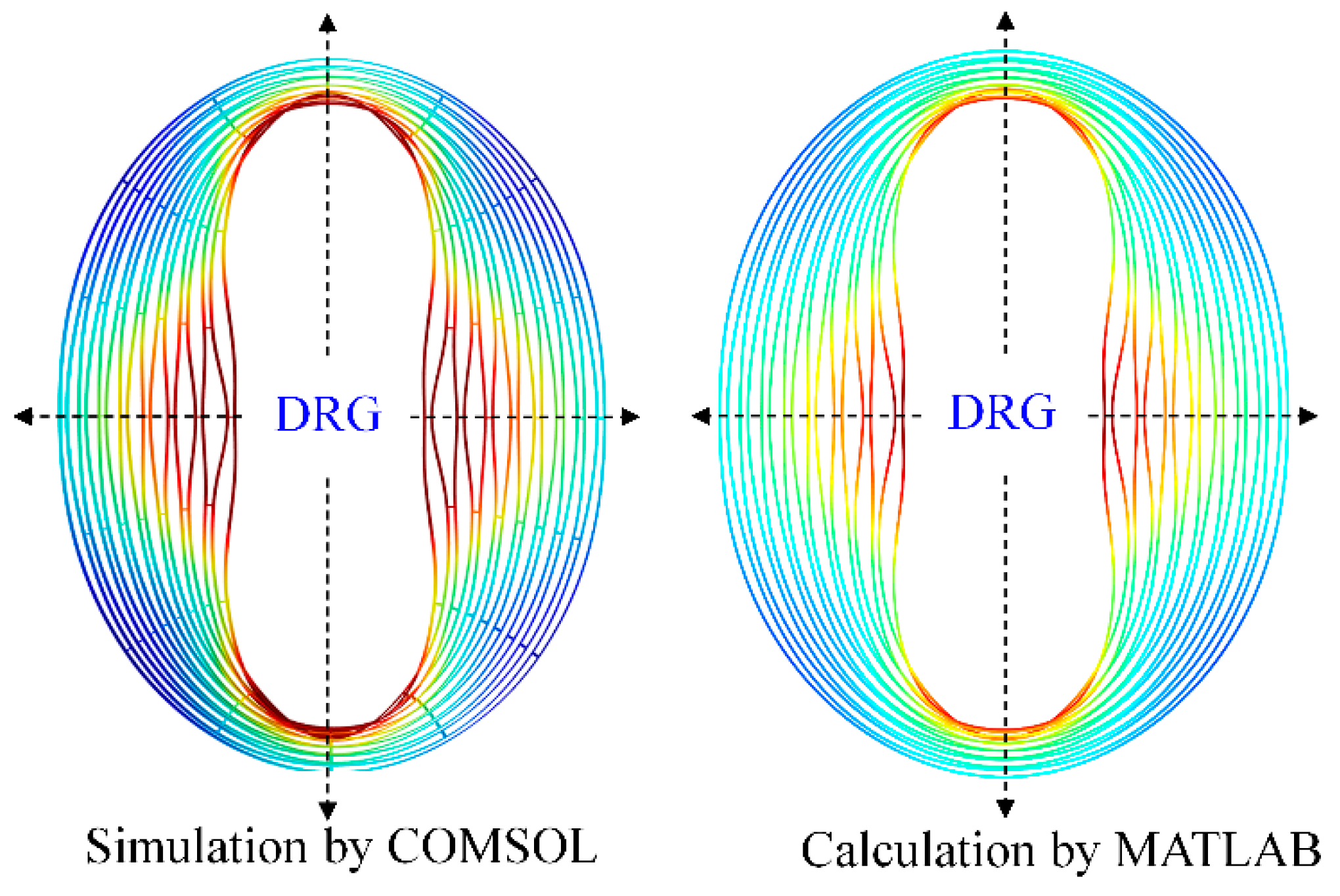
3.1. Validation by Finite Element Analysis (FEA)
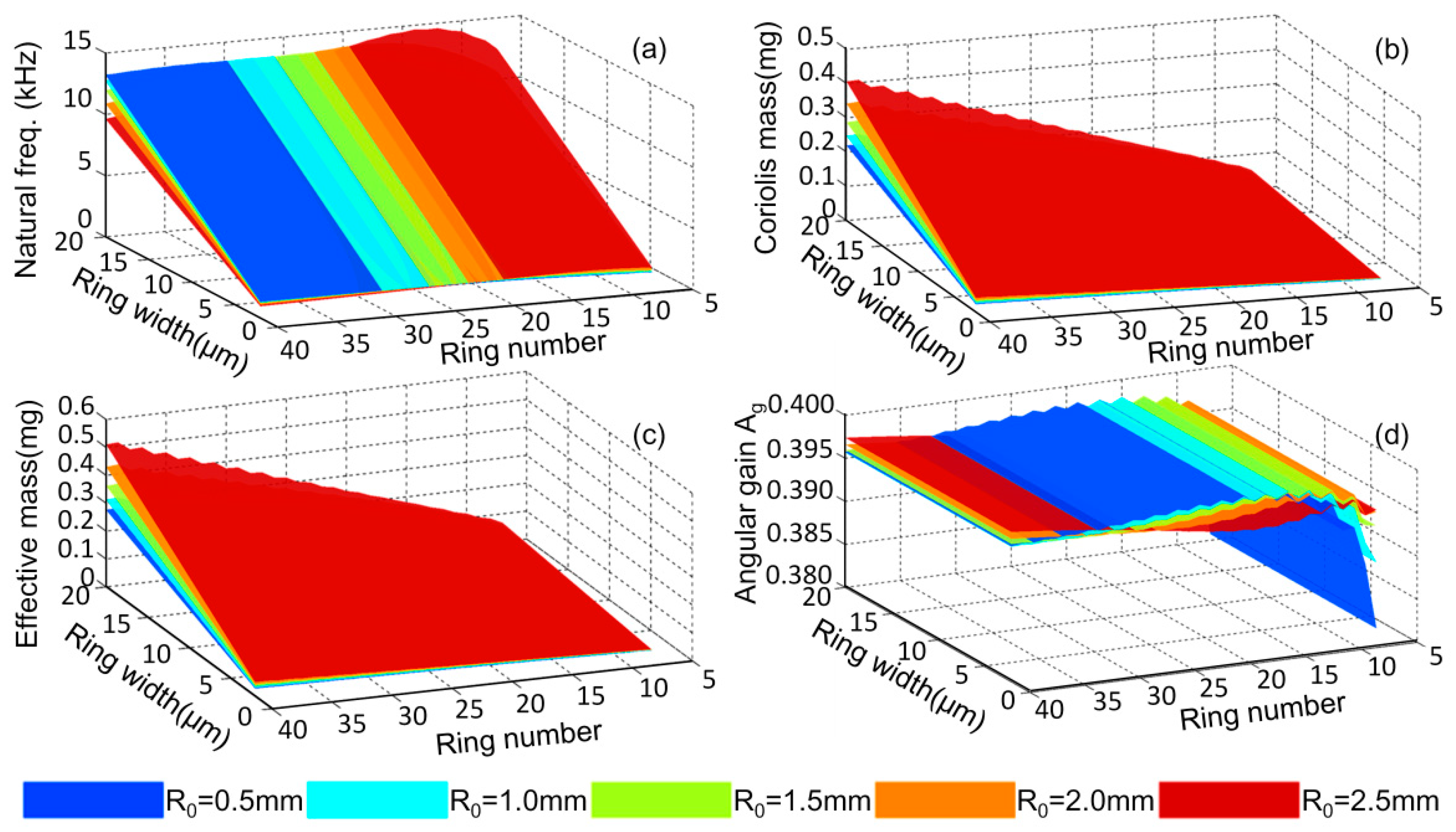
3.2. Derivation and Investigation of the Lumped Mass-Spring Model of DRG
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yazdi, N.; Ayazi, F.; Najafi, K. Micromachined inertial sensors. Proc. IEEE 1998, 86, 1640–1659. [Google Scholar] [CrossRef]
- Xia, D.; Yu, C.; Kong, L. The Development of Micromachined Gyroscope Structure and Circuitry Technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed]
- Shkel, A.M. Type I and Type II Micromachined Vibratory Gyroscopes. In Proceedings of the 2006 IEEE/Ion Position, Location and Navigation Symposium, Coronado, CA, USA, 25–27 April 2006; pp. 586–593. [Google Scholar]
- Abdul-Wahed, A.M.; Mahmoud, M.A.E. A novel multiple-shell vibratory ring gyroscope. In Proceedings of the 2015 Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS (DTIP), Montpellier, France, 27–30 April 2015; pp. 1–4. [Google Scholar]
- Su, T.H.; Nitzan, S.H.; Taheri-Tehrani, P.; Kline, M.H.; Boser, B.E.; Horsley, D.A. Silicon MEMS Disk Resonator Gyroscope with an Integrated CMOS Analog Front-End. IEEE Sens. J. 2014, 14, 3426–3432. [Google Scholar] [CrossRef]
- Ahn, C.H.; Nitzan, S.; Ng, E.J.; Hong, V.A.; Yang, Y.; Kimbrell, T.; Horsley, D.A.; Kenny, T.W. Encapsulated high frequency (235 kHz), high-Q (100 k) disk resonator gyroscope with electrostatic parametric pump. Appl. Phys. Lett. 2014, 105, 243504. [Google Scholar] [CrossRef]
- Taheri-Tehrani, P.; Izyumin, O.; Izyumin, I.; Ahn, C.H.; Ng, E.J.; Hong, V.A.; Yang, Y.; Kenny, T.W.; Boser, B.E.; Horsley, D.A. Disk resonator gyroscope with whole-angle mode operation. In Proceedings of the International Symposium on Inertial Sensors and Systems (ISISS), Hapuna Beach, HI, USA, 23–26 March 2015; pp. 1–4. [Google Scholar]
- Ahn, C.H.; Ng, E.J.; Hong, V.A.; Yang, Y.; Lee, B.J.; Ward, M.W.; Kenny, T.W. Geometric compensation of (100) single crystal silicon disk resonating gyroscope for mode-matching. In Proceedings of the 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 1723–1726. [Google Scholar]
- Zhou, X.; Li, Q.; Xiao, D.; Hou, Z.; Chen, Z.; Wu, Y.; Wu, X. The mechanical sensitivity optimization of a disk resonator gyroscope with mutative ring thickness. In Proceedings of the International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 22–25 February 2016; pp. 54–57. [Google Scholar]
- Challoner, A.D.; Ge, H.H.; Liu, J.Y. Boeing Disc Resonator Gyroscope. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 5–8 May 2014; pp. 504–514. [Google Scholar]
- Cho, J.Y. High-Performance Micromachined Vibratory Rate- and Rate-Integrating Gyroscopes. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2012. [Google Scholar]
- Putty, M.W. A Micromachined Vibrating Ring Gyroscope. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1995. [Google Scholar]
- Zhou, X.; Wu, Y.; Xiao, D.; Hou, Z.; Li, Q.; Yu, D.; Wu, X. An investigation on the ring thickness distribution of disk resonator gyroscope with high mechanical sensitivity. Int. J. Mech. Sci. 2016, 117, 174–181. [Google Scholar] [CrossRef]
- Zhou, X.; Xiao, D.; Hou, Z.; Li, Q.; Wu, Y.; Wu, X. Influence of the Structure Parameters on Sensitivity and Brownian Noise of the Disk Resonator Gyroscope. J. Microeletromech. Syst. 2017, 26, 519–527. [Google Scholar] [CrossRef]
- Eley, R.; Fox, C.H.J.; McWilliam, S. Anisotropy Effects on the Vibration of Cirlular Rings Made from Crystalline Silicon. J. Sound Vib. 1999, 228, 11–35. [Google Scholar] [CrossRef]
- Chang, C.-O.; Chang, G.-E.; Chou, C.-S.; Chien, W.-T.C.; Chen, P.-C. In-plane free vibration of a single-crystal silicon ring. Int. J. Solids Struct. 2008, 45, 6114–6132. [Google Scholar] [CrossRef]
- Chang, C.O.; Chang, G.E.; Chou, C.S.; Shieh, F.H. Single-crystal silicon micro-ring gyros copes-attitude sensors. In Proceedings of the 3rd International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 14–16 June 2007; pp. 608–613. [Google Scholar]
- Sheng, W.; Wei, X.M. A new calculation of potential energy of supporting springs and the application in design of vibrating ring gyroscope. Aerosp. Sci. Technol. 2011, 15, 409–415. [Google Scholar] [CrossRef]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration sensitivity analysis of MEMS vibratory ring gyroscopes. Sens. Actuators A Phys. 2011, 171, 163–177. [Google Scholar] [CrossRef]
- Hurty, W.C. Dynamic analysis of structural systems using component modes. AIAA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- MacNeal, R.H. Special Issue on Structural Dynamics A hybrid method of component mode synthesis. Comput. Struct. 1971, 1, 581–601. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Papadioti, D.-C. Component mode synthesis techniques for finite element model updating. Comput. Struct. 2013, 126, 15–28. [Google Scholar] [CrossRef]
- Hinke, L.; Dohnal, F.; Mace, B.R.; Waters, T.P.; Ferguson, N.S. Component mode synthesis as a framework for uncertainty analysis. J. Sound Vib. 2009, 324, 161–178. [Google Scholar] [CrossRef]
- Bampton, M.C.C.; Craig, J.R.R. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- Bathe, K.-J.; Dong, J. Component mode synthesis with subspace iterations for controlled accuracy of frequency and mode shape solutions. Comput. Struct. 2014, 139, 28–32. [Google Scholar] [CrossRef]
- Seshu, P. Substructuring and Component Mode Synthesis. Shock Vib. 1997, 4, 199–210. [Google Scholar] [CrossRef]
- Xiao, D.; Zhou, X.; Li, Q.; Hou, Z.; Xi, X.; Wu, Y.; Wu, X. Design of a Disk Resonator Gyroscope with High Mechanical Sensitivity by Optimizing the Ring Thickness Distribution. J. Microelectromech. Syst. 2016, 25, 606–616. [Google Scholar] [CrossRef]
- Ahn, C.H.; Ng, E.J.; Hong, V.A.; Yang, Y.; Lee, B.J.; Flader, I.; Kenny, T.W. Mode-Matching of Wineglass Mode Disk Resonator Gyroscope in (100) Single Crystal Silicon, Microelectromechanical Systems. J. Microelectromech. Syst. 2015, 24, 343–350. [Google Scholar] [CrossRef]
- Ahn, C.H.; Ng, E.J.; Hong, V.A.; Huynh, J.; Wang, S.; Kenny, T.W. Characterization of Oxide-Coated Polysilicon Disk Resonator Gyroscope Within a Wafer-Scale Encapsulation Process. J. Microelectromech. Syst. 2015, 24, 1687–1694. [Google Scholar] [CrossRef]
- Craig, R.; Chang, C.J. Free-interface methods of substructure coupling for dynamic analysis. AIAA J. 1976, 14, 1633–1635. [Google Scholar] [CrossRef]
- Ohayon, R.; Soize, C. Clarification about component mode synthesis methods for substructures with physical flexible interfaces. Int. J. Aeronaut. Space Sci. 2014, 15, 113–122. [Google Scholar] [CrossRef]
- Kim, W.; Chung, J. Free Non-linear Vibration of a Rotating Thin Ring with the In-plane and Out-of-plane Motions. J. Sound Vib. 2002, 258, 167–178. [Google Scholar] [CrossRef]
- Bashmal, S.; Bhat, R.; Rakheja, S. In-plane free vibration of circular annular disks. J. Sound Vib. 2009, 322, 216–226. [Google Scholar] [CrossRef]
- Chidamparam, P.; Leissa, A.W. Vibrations of Planar Curved Beams, Rings, and Arches. Appl. Mech. Rev. 1993, 46, 467–483. [Google Scholar] [CrossRef]
- Yang, J.; Ono, T.; Esashi, M. Energy dissipation in submicrometer thick single-crystal silicon cantilevers. J. Microelectromech. Syst. 2002, 11, 775–783. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Xiao, D.; Zhou, X.; Hou, Z.; Zhuo, M.; Xu, Y.; Wu, X. Dynamic Modeling of the Multiring Disk Resonator Gyroscope. Micromachines 2019, 10, 181. https://doi.org/10.3390/mi10030181
Li Q, Xiao D, Zhou X, Hou Z, Zhuo M, Xu Y, Wu X. Dynamic Modeling of the Multiring Disk Resonator Gyroscope. Micromachines. 2019; 10(3):181. https://doi.org/10.3390/mi10030181
Chicago/Turabian StyleLi, Qingsong, Dingbang Xiao, Xin Zhou, Zhanqiang Hou, Ming Zhuo, Yi Xu, and Xuezhong Wu. 2019. "Dynamic Modeling of the Multiring Disk Resonator Gyroscope" Micromachines 10, no. 3: 181. https://doi.org/10.3390/mi10030181
APA StyleLi, Q., Xiao, D., Zhou, X., Hou, Z., Zhuo, M., Xu, Y., & Wu, X. (2019). Dynamic Modeling of the Multiring Disk Resonator Gyroscope. Micromachines, 10(3), 181. https://doi.org/10.3390/mi10030181




