Swimming of Spermatozoa in a Maxwell Fluid
Abstract
1. Introduction
2. Governing Equations and Numerical Methods
2.1. Green’s Function for a Linear Maxwell Fluid
2.2. Boundary Integral Equation
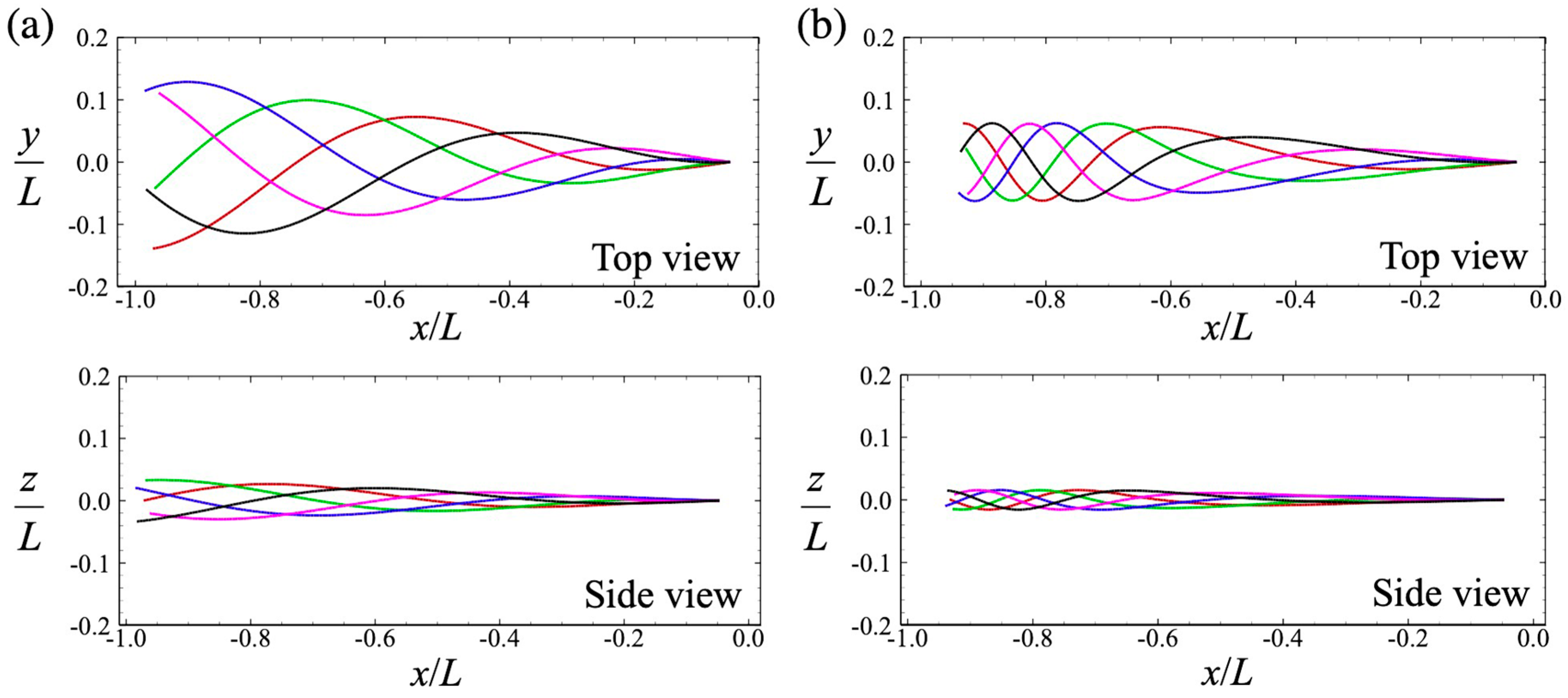
2.3. Flagellar Waveform and Head Geometry
2.4. Numerical Procedure
3. Results and Discussion
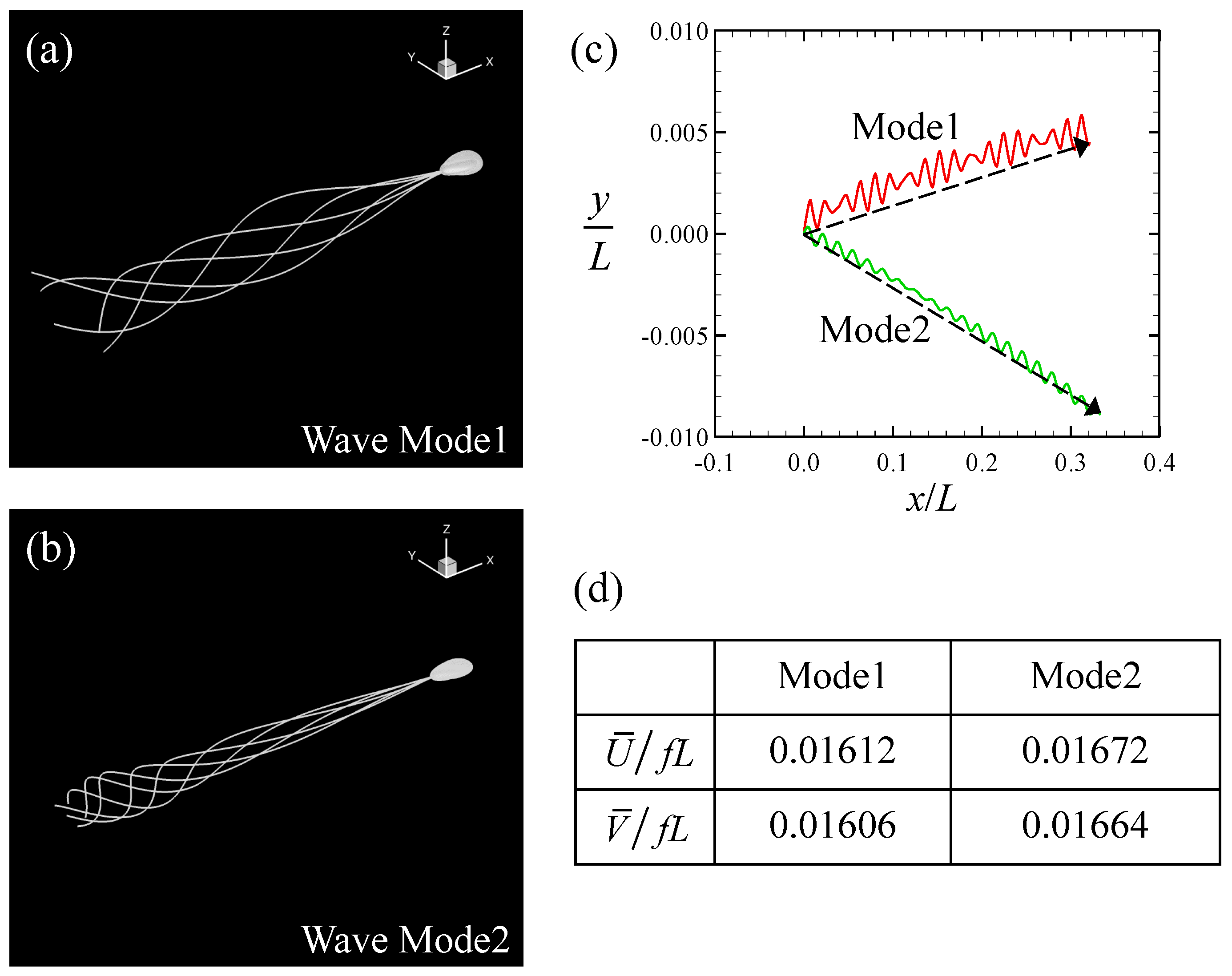
3.1. Swimming Motion of a Sperm Cell in a Newtonian Fluid
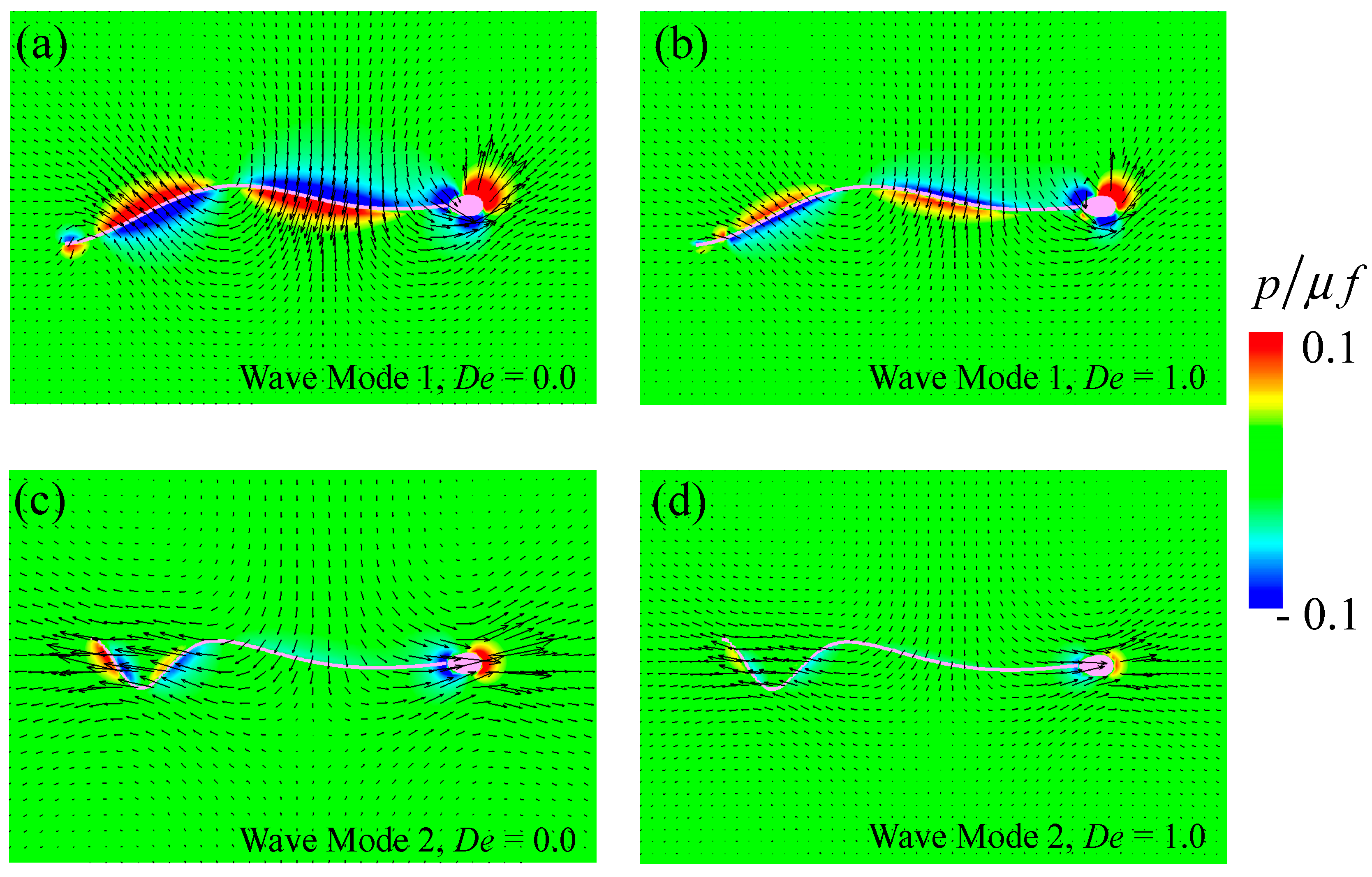
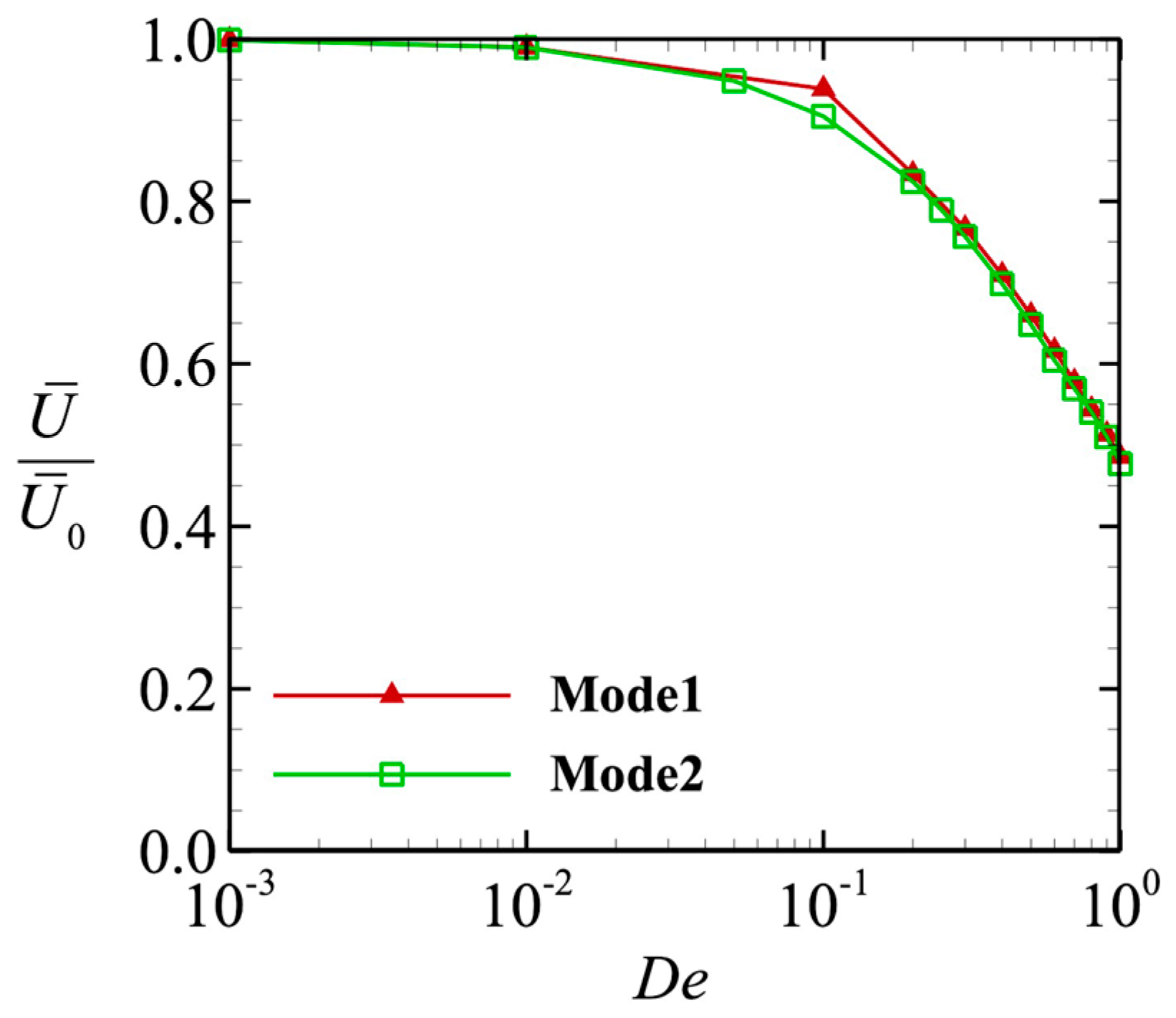
3.2. Swimming Motion of a Sperm Cell in a Maxwell Fluid
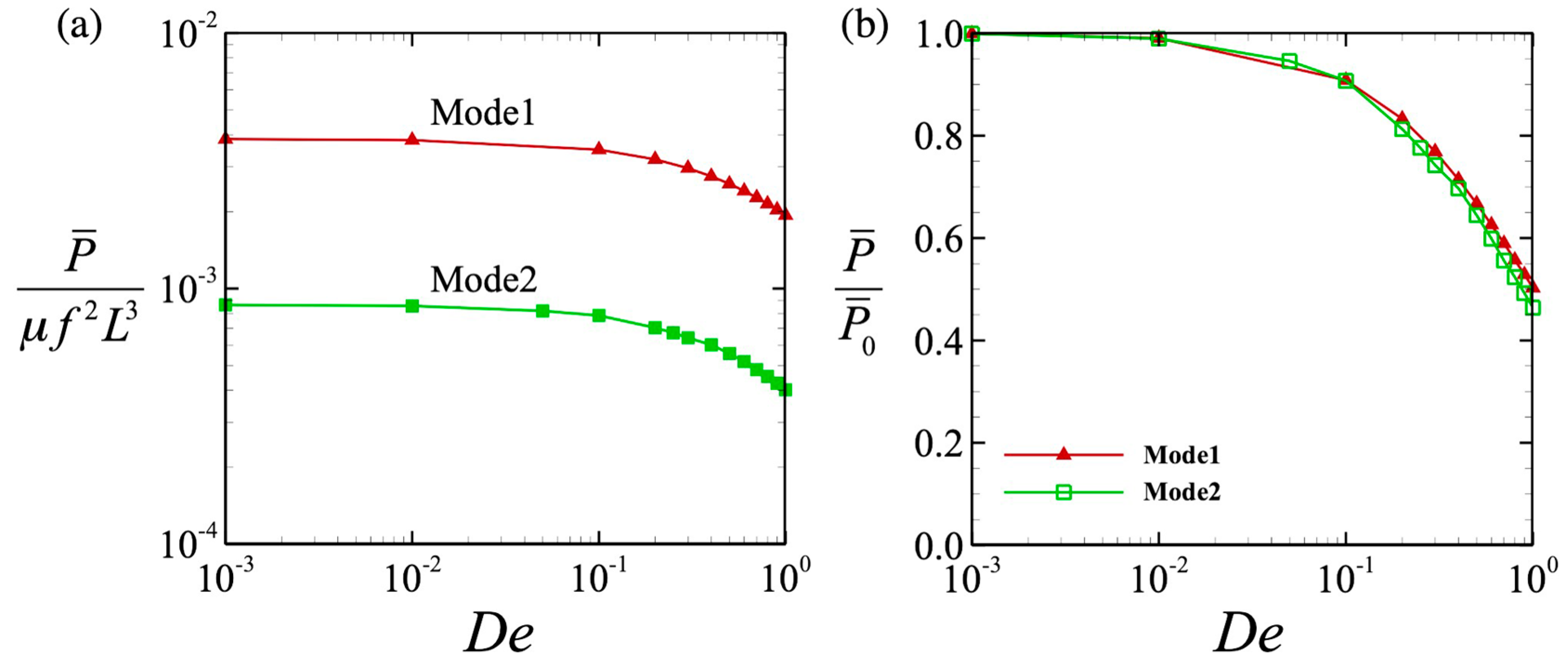
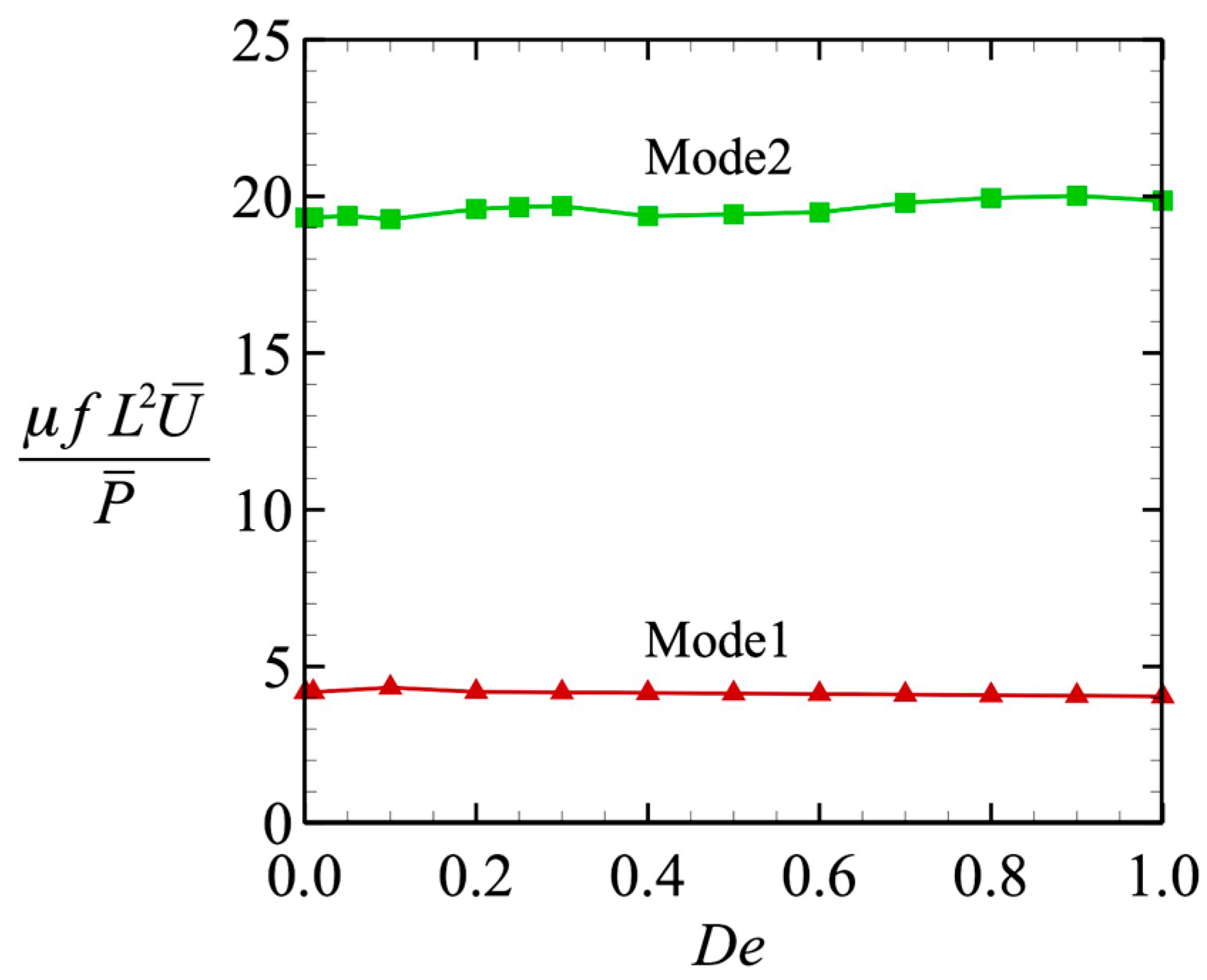
3.3. Power and Swimming Efficiency
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gaffney, E.A.; Gadêlha, H.; Smith, D.J.; Blake, J.R.; Kirkman-Brown, J.C. Mammalian sperm motility: Observation and theory. Annu. Rev. Fluid Mech. 2011, 43, 501–528. [Google Scholar] [CrossRef]
- Hyakutake, T.; Suzuki, H.; Yamamoto, S. Effect of non-Newtonian fluid properties on bovine sperm motility. J. Biomech. 2015, 48, 2941–2947. [Google Scholar] [CrossRef] [PubMed]
- Khalil, I.S.M.; Dijkslag, H.C.; Abelmann, L.; Misra, S. MagnetoSperm: A microrobot that navigates using weak magnetic fields. Appl. Phys. Lett. 2014, 104, 223701. [Google Scholar] [CrossRef]
- Kaynak, M.; Ozcelik, A.; Nourhani, A.; Lammert, P.E.; Crespi, V.H.; Huang, T.J. Acoustic actuation of bioinspired microswimmers. Lab Chip 2017, 17, 395–400. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.J.; Gaffney, E.A.; Blake, J.R.; Kirkman-Brown, J.C. Human sperm accumulation near surfaces: A simulation study. J. Fluid Mech. 2009, 621, 289–320. [Google Scholar] [CrossRef]
- Ishimoto, K.; Gaffney, E.A. A study of spermatozoan swimming stability near a surface. J. Theor. Biol. 2014, 360, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Gadêlha, H.; Gaffney, E.A.; Smith, D.J.; Kirkman-Brown, J.C. Nonlinear instability in flagellar dynamics: A novel modulation mechanics in sperm migration? J. R. Soc. Interface 2010, 7, 1689–1697. [Google Scholar] [CrossRef] [PubMed]
- Kantsler, V.; Dunkel, J.; Blayney, M.; Goldstein, R.E. Rheotaxis facilitates upstream navigation of mammalian sperm cells. eLife 2014, 3, e02403. [Google Scholar] [CrossRef] [PubMed]
- Ishimoto, K.; Gaffney, E.A. Fluid flow and sperm guidance: A simulation study of hydrodynamic sperm rheotaxis. J. R. Soc. Interface 2015, 12, 20150172. [Google Scholar] [CrossRef] [PubMed]
- Omori, T.; Ishikawa, T. Upward swimming of a sperm cell in shear flow. Phys. Rev. E 2016, 93, 032402. [Google Scholar] [CrossRef] [PubMed]
- Elgeti, J.; Winkler, R.G.; Gompper, G. Physics of microswimmers—Single particle motion and collective behavior. Rep. Prog. Phys. 2015, 78, 056601. [Google Scholar] [CrossRef] [PubMed]
- Ishimoto, K.; Gadêlha, H.; Gaffney, E.A.; Smith, D.J.; Kirkman-Brown, J.C. Human sperm swimming in a high viscosity mucus analogue. J. Theor. Biol. 2018, 446, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wróbel, J.K.; Lynch, S.; Barrett, A.; Fauci, L.; Cortez, R. Enhanced flagellar swimming through a compliant viscoelastic network in Stokes flow. J. Fluid Mech. 2016, 792, 775–797. [Google Scholar] [CrossRef]
- Ishimoto, K.; Gaffney, E.A. Boundary element methods for particles and microswimmers in a linear viscoelastic fluid. J. Fluid Mech. 2017, 831, 228–251. [Google Scholar] [CrossRef]
- Smith, D.J.; Gaffney, E.A.; Blake, J.R. Mathematical modelling of cilia-driven transport of biological fluids. Proc. R. Soc. A 2009, 465, 2417–2439. [Google Scholar] [CrossRef]
- Tornberg, A.-K.; Shelly, M.J. Simulating the dynamics and interactions of flexible fibers in Stokes flows. J. Comput. Phys. 2004, 196, 8–40. [Google Scholar] [CrossRef]
- Dresdner, R.D.; Katz, D.F. Relationships of mammalian sperm motility and morphology to hydrodynamic aspects of cell function. Biol. Reprod. 1981, 25, 920–930. [Google Scholar] [CrossRef] [PubMed]
- Ishijima, S.; Hamaguchi, M.S.; Naruse, M.; Ishijima, A.; Hamaguchi, Y. Rotational movement of a spermatozoon around its long axis. J. Exp. Biol. 1992, 163, 15–31. [Google Scholar] [PubMed]
- Friedrich, B.M.; Riedel-Kruse, I.H.; Howard, J.; Julicher, F. High-precision tracking of sperm swimming fine structure provides strong test of resistive force theory. J. Exp. Biol. 2010, 213, 1226–1234. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omori, T.; Ishikawa, T. Swimming of Spermatozoa in a Maxwell Fluid. Micromachines 2019, 10, 78. https://doi.org/10.3390/mi10020078
Omori T, Ishikawa T. Swimming of Spermatozoa in a Maxwell Fluid. Micromachines. 2019; 10(2):78. https://doi.org/10.3390/mi10020078
Chicago/Turabian StyleOmori, Toshihiro, and Takuji Ishikawa. 2019. "Swimming of Spermatozoa in a Maxwell Fluid" Micromachines 10, no. 2: 78. https://doi.org/10.3390/mi10020078
APA StyleOmori, T., & Ishikawa, T. (2019). Swimming of Spermatozoa in a Maxwell Fluid. Micromachines, 10(2), 78. https://doi.org/10.3390/mi10020078





