µ-PIV Measurements of Flows Generated by Photolithography-Fabricated Achiral Microswimmers
Abstract
1. Introduction
2. Materials and Methods
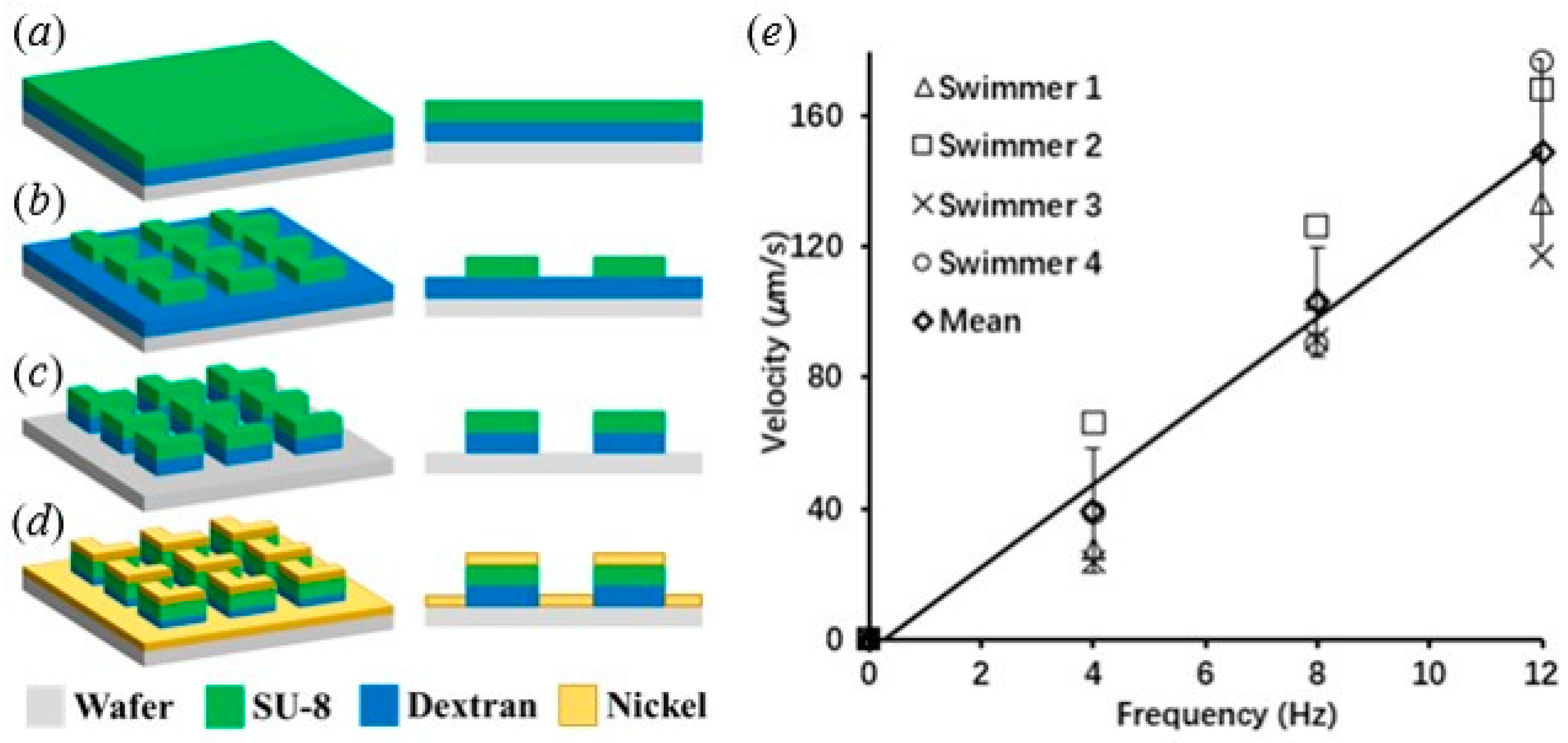
2.1. Microswimmer Fabrication
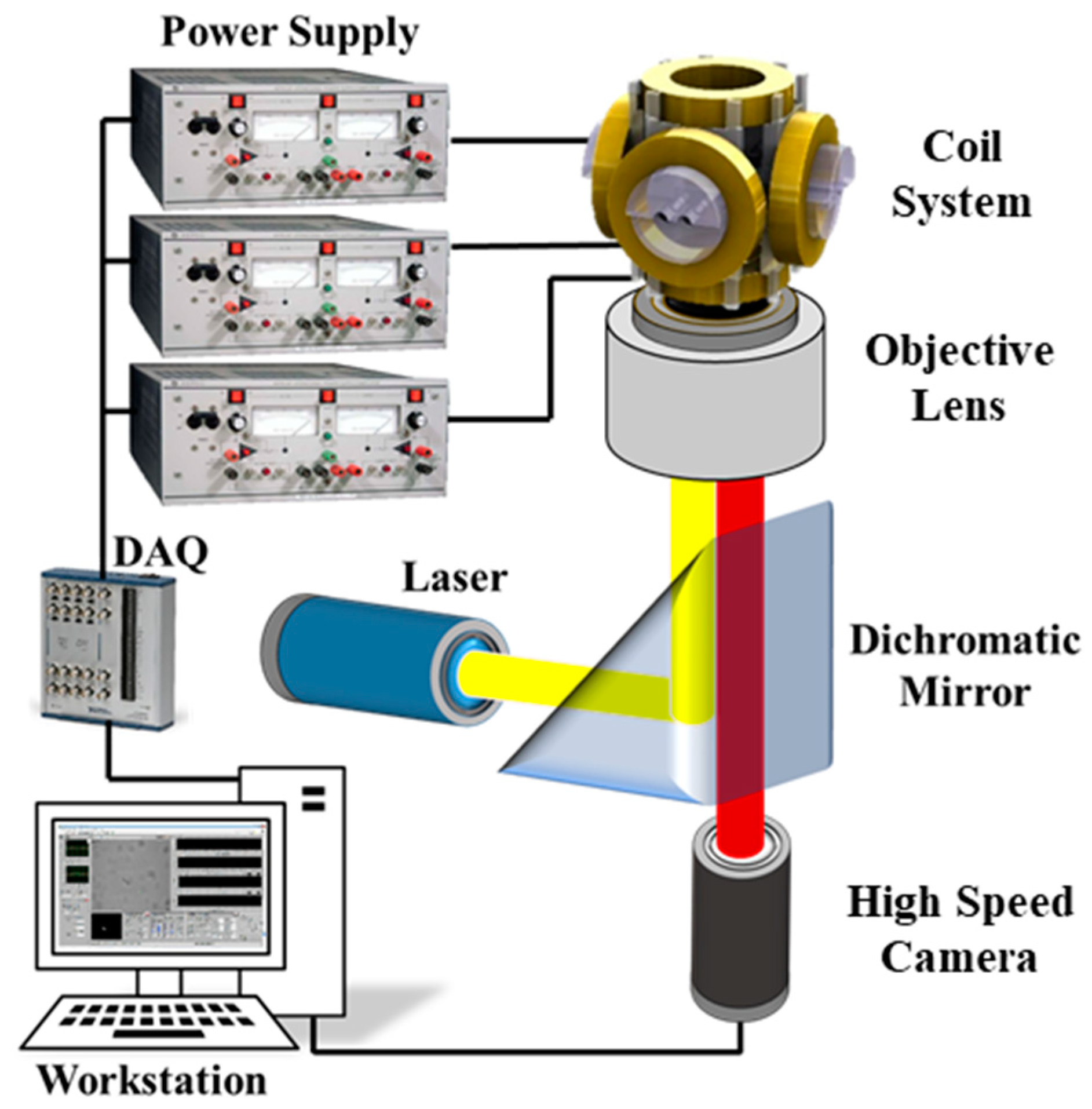
2.2. Magnetic Actuation and µ-PIV
3. Results and Discussion
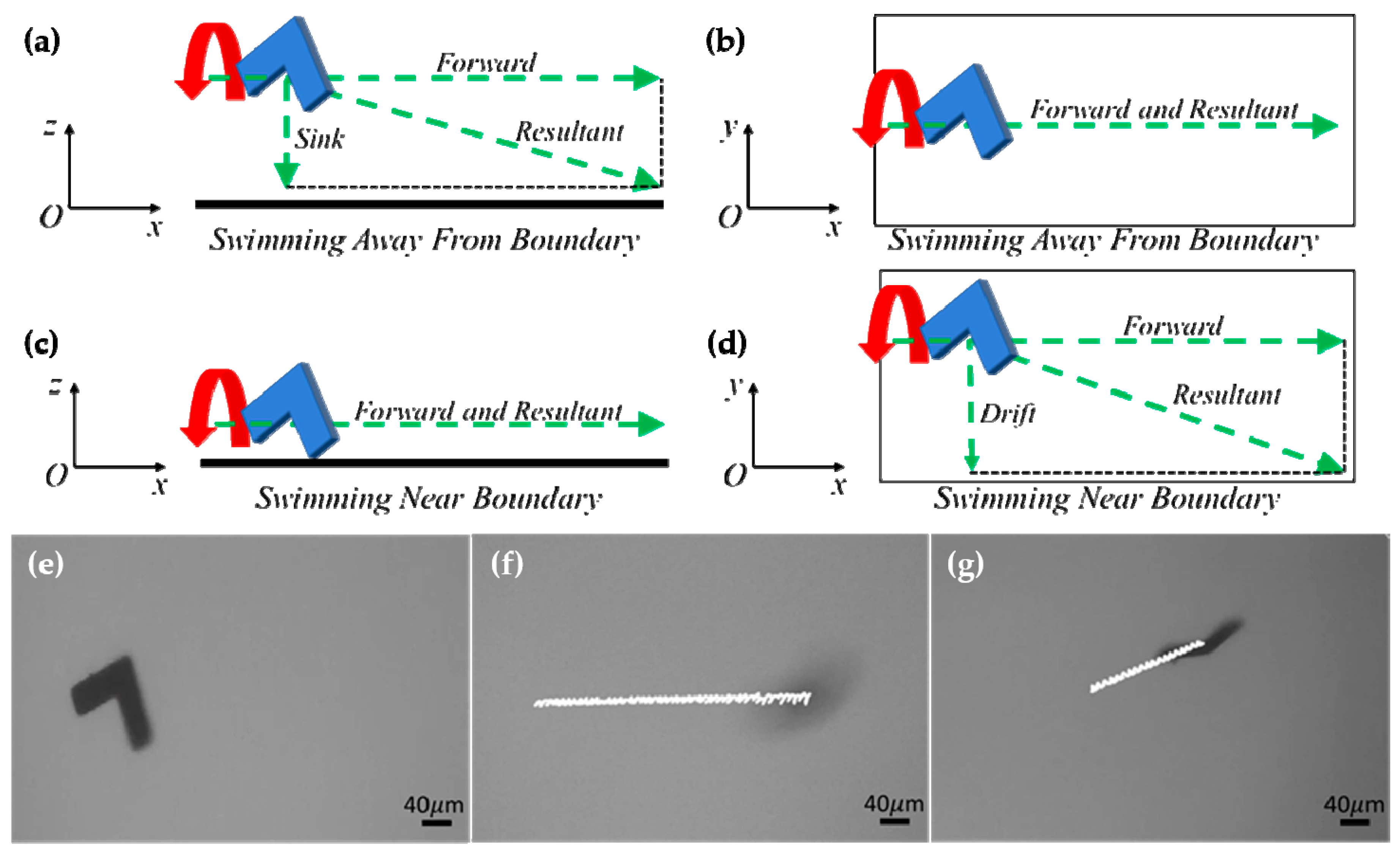
3.1. Swimming Profile
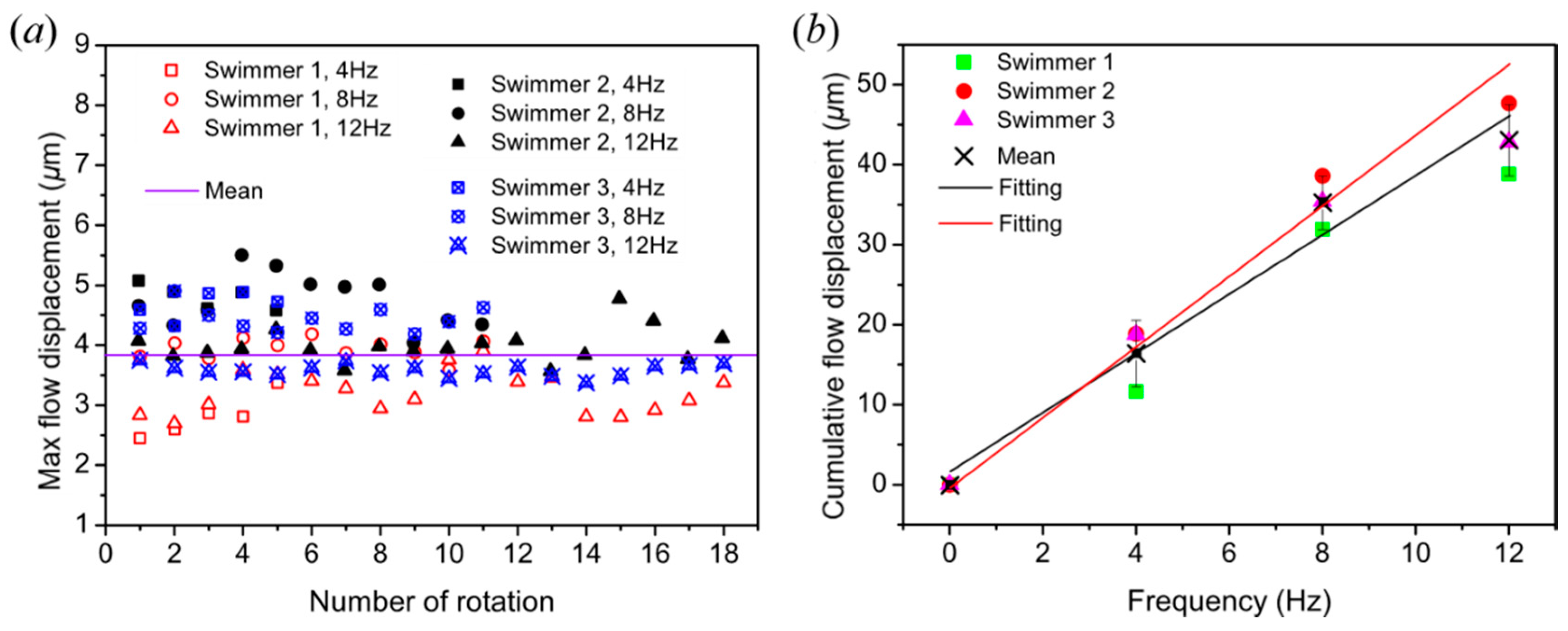
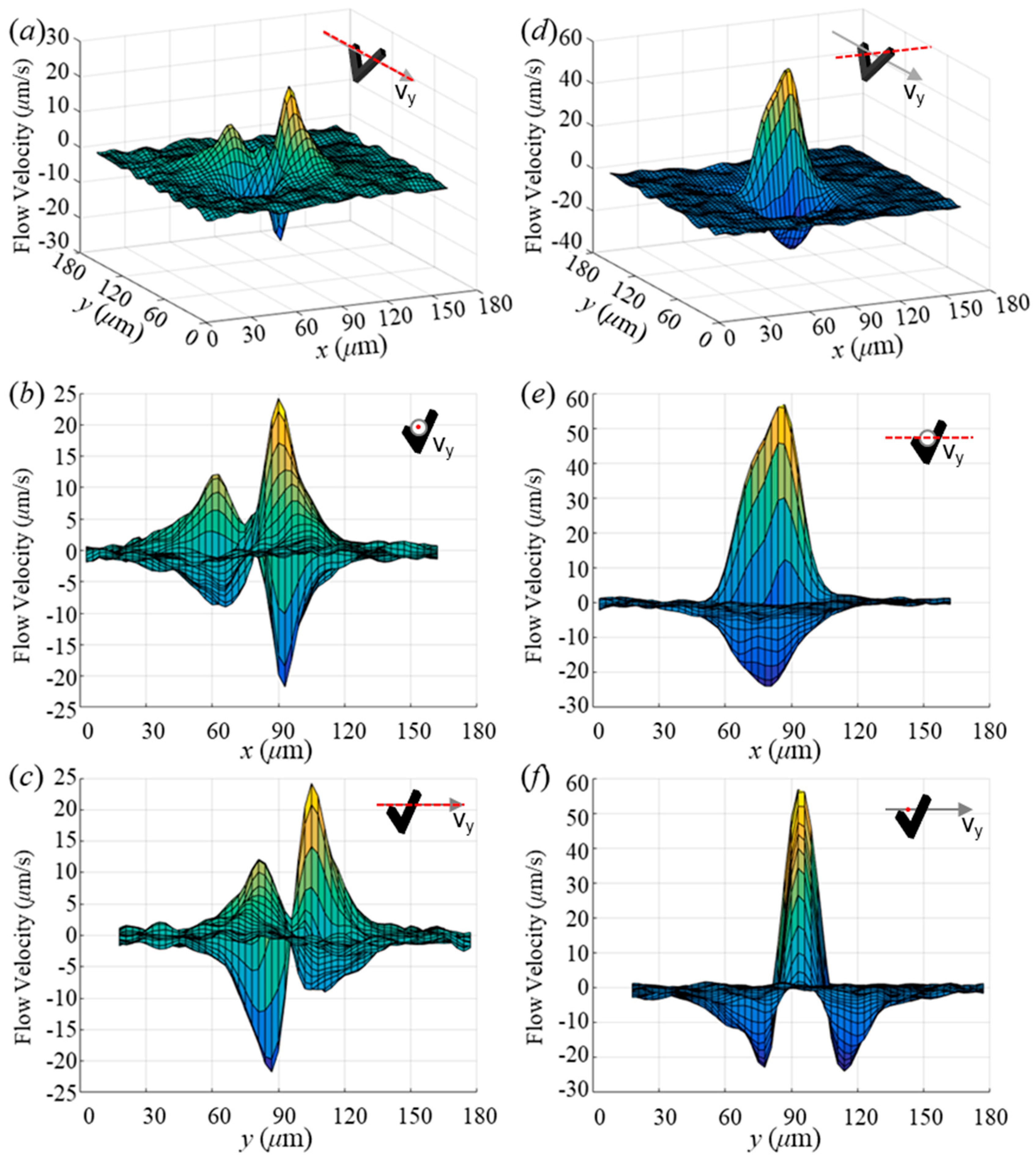
3.2. Near-Swimmer Flow Displacement
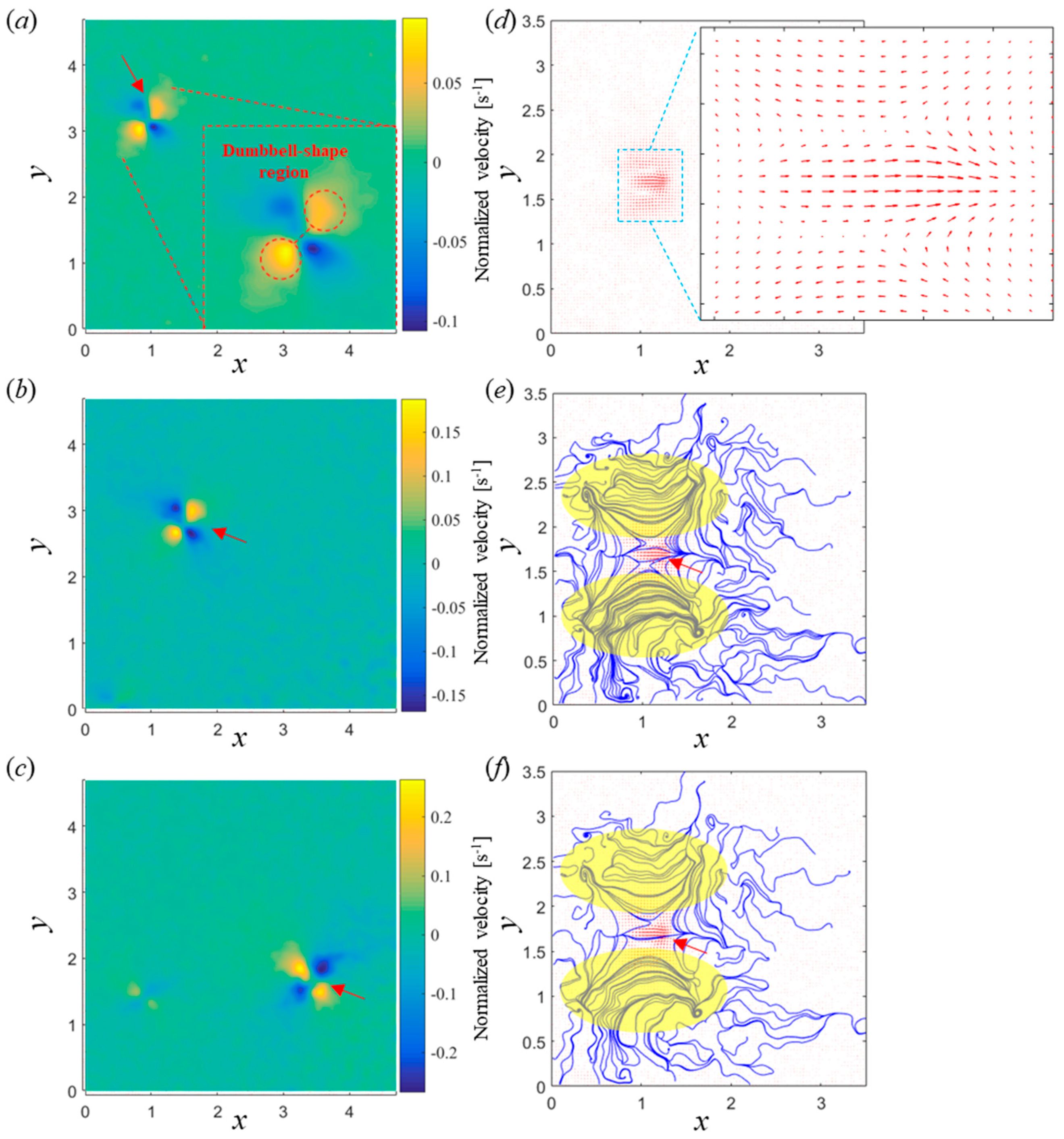
3.3. Flow Field Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dogangil, G.; Ergeneman, O.; Abbott, J.J.; Pane, S.; Hall, H.; Muntwyler, S.; Nelson, B.J. Toward targeted retinal drug delivery with wireless magnetic microrobots. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 1921–1926. [Google Scholar]
- Fusco, S.; Chatzipirpiridis, G.; Sivaraman, K.M.; Ergeneman, O.; Nelson, B.J.; Pané, S. Chitosan Electrodeposition for Microrobotic Drug Delivery. Adv. Healthcare Mater. 2013, 2, 1037–1044. [Google Scholar] [CrossRef] [PubMed]
- Torelli, E.; Manzano, M.; Srivastava, S.K.; Marks, R.S. DNA origami nanorobot fiber optic genosensor to TMV. Biosens. Bioelectron. 2018, 99, 209–215. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, S.; Kagan, D.; Jack Hu, C.-M.; Campuzano, S.; Lobo-Castañon, M.J.; Lim, N.; Kang, D.Y.; Zimmerman, M.; Zhang, L.; Wang, J. Micromachine-Enabled Capture and Isolation of Cancer Cells in Complex Media. Angew. Chem. Int. Ed. 2011, 50, 4161–4164. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Hutmacher, D.W.; Chollet, F.; Poo, A.N.; Burdet, E. Microrobotics and MEMS-Based Fabrication Techniques for Scaffold-Based Tissue Engineering. Macromol. Biosci. 2005, 5, 477–489. [Google Scholar] [CrossRef]
- Kim, S.; Qiu, F.; Kim, S.; Ghanbari, A.; Moon, C.; Zhang, L.; Nelson, B.J.; Choi, H. Fabrication and Characterization of Magnetic Microrobots for Three-Dimensional Cell Culture and Targeted Transportation. Adv. Mater. 2013, 25, 5863–5868. [Google Scholar] [CrossRef]
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef]
- Zhang, L.; Abbott, J.J.; Dong, L.; Kratochvil, B.E.; Bell, D.; Nelson, B.J. Artificial bacterial flagella: Fabrication and magnetic control. Appl. Phys. Lett. 2009, 94, 064107. [Google Scholar] [CrossRef]
- Tottori, S.; Zhang, L.; Peyer, K.E.; Nelson, B.J. Assembly, Disassembly, and Anomalous Propulsion of Microscopic Helices. Nano Lett. 2013, 13, 4263–4268. [Google Scholar] [CrossRef]
- Maier, A.M.; Weig, C.; Oswald, P.; Frey, E.; Fischer, P.; Liedl, T. Magnetic Propulsion of Microswimmers with DNA-Based Flagellar Bundles. Nano Lett. 2016, 16, 906–910. [Google Scholar] [CrossRef]
- Dreyfus, R.; Baudry, J.; Roper, M.L.; Fermigier, M.; Stone, H.A.; Bibette, J. Microscopic artificial swimmers. Nature 2005, 437, 862–865. [Google Scholar] [CrossRef]
- Ali, J.; Cheang, U.K.; Darvish, A.; Kim, H.; Kim, M.J. Biotemplated flagellar nanoswimmers. APL Mater. 2017, 5, 116106. [Google Scholar] [CrossRef]
- Li, T.; Chang, X.; Wu, Z.; Li, J.; Shao, G.; Deng, X.; Qiu, J.; Guo, B.; Zhang, G.; He, Q.; et al. Autonomous Collision-Free Navigation of Microvehicles in Complex and Dynamically Changing Environments. ACS Nano 2017, 11, 9268–9275. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.; Zhang, Q.; Gao, W.; Pei, A.; Ren, B. Highly Efficient Light-Driven TiO2–Au Janus Micromotors. ACS Nano 2016, 10, 839–844. [Google Scholar] [CrossRef] [PubMed]
- Esteban-Fernández de Ávila, B.; Angell, C.; Soto, F.; Lopez-Ramirez, M.A.; Báez, D.F.; Xie, S.; Wang, J.; Chen, Y. Acoustically Propelled Nanomotors for Intracellular siRNA Delivery. ACS Nano 2016, 10, 4997–5005. [Google Scholar] [CrossRef] [PubMed]
- Palacci, J.; Sacanna, S.; Steinberg, A.P.; Pine, D.J.; Chaikin, P.M. Living Crystals of Light-Activated Colloidal Surfers. Science 2013, 339, 936–940. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-F.; Huang, Y.-F.; Tsai, S.-C.; Lai, H.-Y.; Lee, E. Electrophoretic and Electroosmotic Motion of a Charged Spherical Particle within a Cylindrical Pore Filled with Debye–Bueche–Brinkman Polymeric Solution. Langmuir 2016, 32, 13106–13115. [Google Scholar] [CrossRef]
- Cheang, U.K.; Meshkati, F.; Kim, D.; Kim, M.J.; Fu, H.C. Minimal geometric requirements for micropropulsion via magnetic rotation. Phys. Rev. E 2014, 90, 033007. [Google Scholar] [CrossRef]
- Cheang, U.K.; Kim, M.J. Fabrication and control of simple low Reynolds number microswimmers. Appl. Phys. Lett. 2016, 109, 034101. [Google Scholar] [CrossRef]
- Tottori, S.; Nelson, B.J. Controlled Propulsion of Two-Dimensional Microswimmers in a Precessing Magnetic Field. Small 2018, 14, 1800722. [Google Scholar] [CrossRef]
- Mirzae, Y.; Dubrovski, O.; Kenneth, O.; Morozov, K.I.; Leshansky, A.M. Geometric constraints and optimization in externally driven propulsion. Sci. Rob. 2018, 3, eaas8713. [Google Scholar] [CrossRef]
- Kümmel, F.; ten Hagen, B.; Wittkowski, R.; Buttinoni, I.; Eichhorn, R.; Volpe, G.; Löwen, H.; Bechinger, C. Circular motion of asymmetric self-propelling particles. Phys. Rev. Lett. 2013, 110, 198302. [Google Scholar] [CrossRef] [PubMed]
- ten Hagen, B.; Kümmel, F.; Wittkowski, R.; Takagi, D.; Löwen, H.; Bechinger, C. Gravitaxis of asymmetric self-propelled colloidal particles. Nat. Commun. 2014, 5, 4829. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Petit, T.; Choi, H.; Nelson, B.J.; Zhang, L. Dumbbell Fluidic Tweezers for Dynamical Trapping and Selective Transport of Microobjects. Adv. Funct. Mater. 2017, 27, 1604571. [Google Scholar] [CrossRef]
- Petit, T.; Zhang, L.; Peyer, K.E.; Kratochvil, B.E.; Nelson, B.J. Selective Trapping and Manipulation of Microscale Objects Using Mobile Microvortices. Nano Lett. 2012, 12, 156–160. [Google Scholar] [CrossRef]
- Ali, J.; Cheang, U.K.; Liu, Y.; Kim, H.; Rogowski, L.; Sheckman, S.; Patel, P.; Sun, W.; Kim, M.J. Fabrication and magnetic control of alginate-based rolling microrobots. AIP Adv. 2016, 6, 125205. [Google Scholar] [CrossRef]
- Meshkati, F.; Fu, H.C. Modeling rigid magnetically rotated microswimmers: Rotation axes, bistability, and controllability. Phys. Rev. E 2014, 90, 063006. [Google Scholar] [CrossRef]
- Morozov, K.I.; Mirzae, Y.; Kenneth, O.; Leshansky, A.M. Dynamics of arbitrary shaped propellers driven by a rotating magnetic field. Phys. Rev. Fluids 2017, 2, 044202. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, L.; Yu, J.; Zhang, L. Characterizing dynamic behaviors of three-particle paramagnetic microswimmer near a solid surface. Robot. Biomim. 2017, 4, 20. [Google Scholar] [CrossRef]
- Kim, J.; Jang, Y.; Byun, D.; Kim, M.; Nam, S.-W.; Park, S. Quantitative measurement of dynamic flow induced by Tetrahymena pyriformis (T. pyriformis) using micro-particle image velocimetry. J. Vis. 2011, 14, 361–370. [Google Scholar] [CrossRef]
- Drescher, K.; Dunkel, J.; Cisneros, L.H.; Ganguly, S.; Goldstein, R.E. Fluid dynamics and noise in bacterial cell–cell and cell–surface scattering. PNAS 2011, 108, 10940–10945. [Google Scholar] [CrossRef]
- Drescher, K.; Goldstein, R.E.; Michel, N.; Polin, M.; Tuval, I. Direct Measurement of the Flow Field around Swimming Microorganisms. Phys. Rev. Lett. 2010, 105, 168101. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Cheang, U.K.; Kim, D.; Ali, J.; Kim, M.J. Hydrodynamics of a self-actuated bacterial carpet using microscale particle image velocimetry. Biomicrofluidics 2015, 9, 024121. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-Y.; Pekkan, K. High-speed three-dimensional characterization of fluid flows induced by micro-objects in deep microchannels. Biochip J. 2013, 7, 95–103. [Google Scholar] [CrossRef]
- Zhong, S.; Moored, K.W.; Pinedo, V.; Garcia-Gonzalez, J.; Smits, A.J. The flow field and axial thrust generated by a rotating rigid helix at low Reynolds numbers. Exp. Therm Fluid Sci. 2013, 46, 1–7. [Google Scholar] [CrossRef]
- Jeon, H.; Kim, Y.-C.; Yim, D.; Yoo, J.Y.; Jin, S. Flow Visualization and Performance Measurements of a Flagellar Propeller. J. Bionic Eng. 2012, 9, 322–329. [Google Scholar] [CrossRef]
- Martínez-Aranda, S.; Galindo-Rosales, F.J.; Campo-Deaño, L. Complex flow dynamics around 3D microbot prototypes. Soft Matter 2016, 12, 2334–2347. [Google Scholar] [CrossRef] [PubMed]
- Ali, J.; Kim, H.; Cheang, U.K.; Kim, M.J. Micro-PIV measurements of flows induced by rotating microparticles near a boundary. Microfluid. Nanofluid. 2016, 20, 131. [Google Scholar] [CrossRef]
- Sachs, J.; Morozov, K.I.; Kenneth, O.; Qiu, T.; Segreto, N.; Fischer, P.; Leshansky, A.M. Role of symmetry in driven propulsion at low Reynolds number. Phys. Rev. E 2018, 98, 063105. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, L.; Ali, J.; Cheang, U.K.; Shi, X.; Kim, D.; Kim, M.J. µ-PIV Measurements of Flows Generated by Photolithography-Fabricated Achiral Microswimmers. Micromachines 2019, 10, 865. https://doi.org/10.3390/mi10120865
Tan L, Ali J, Cheang UK, Shi X, Kim D, Kim MJ. µ-PIV Measurements of Flows Generated by Photolithography-Fabricated Achiral Microswimmers. Micromachines. 2019; 10(12):865. https://doi.org/10.3390/mi10120865
Chicago/Turabian StyleTan, Liyuan, Jamel Ali, U Kei Cheang, Xiangcheng Shi, Dalhyung Kim, and Min Jun Kim. 2019. "µ-PIV Measurements of Flows Generated by Photolithography-Fabricated Achiral Microswimmers" Micromachines 10, no. 12: 865. https://doi.org/10.3390/mi10120865
APA StyleTan, L., Ali, J., Cheang, U. K., Shi, X., Kim, D., & Kim, M. J. (2019). µ-PIV Measurements of Flows Generated by Photolithography-Fabricated Achiral Microswimmers. Micromachines, 10(12), 865. https://doi.org/10.3390/mi10120865








