A Liquid-Metal-Based Dielectrophoretic Microdroplet Generator
Abstract
1. Introduction
2. Experiments and Methods
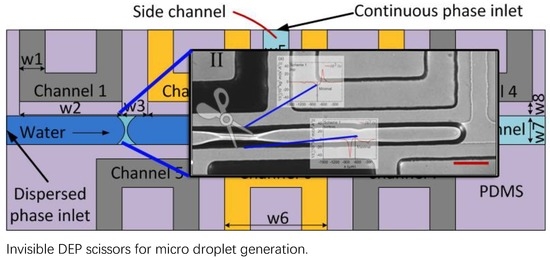
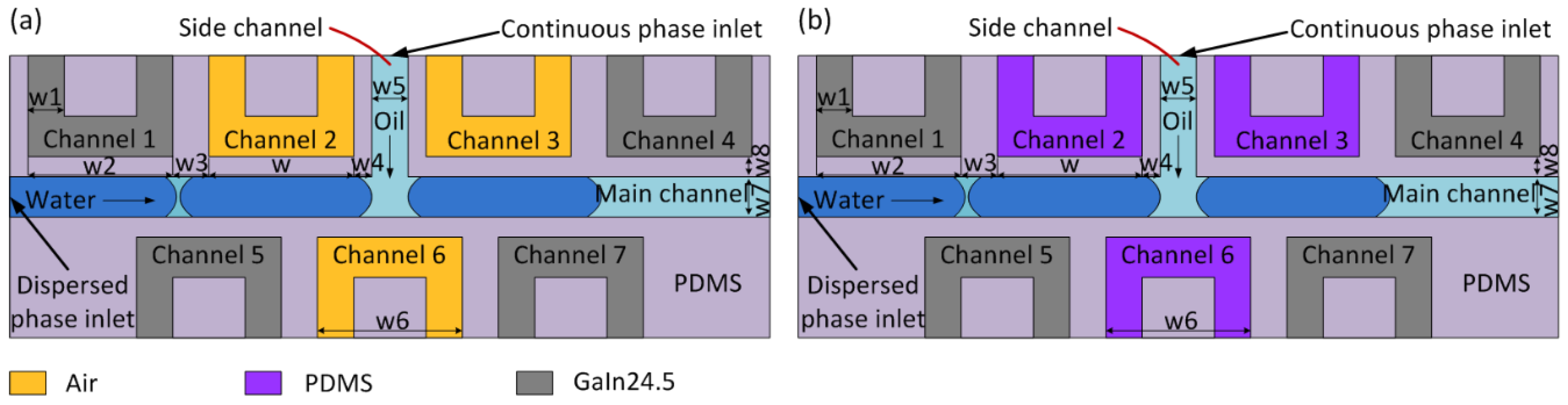
2.1. Dielectrophoresis Droplet Generator
2.2. Droplet Generation System
3. Results and Discussion
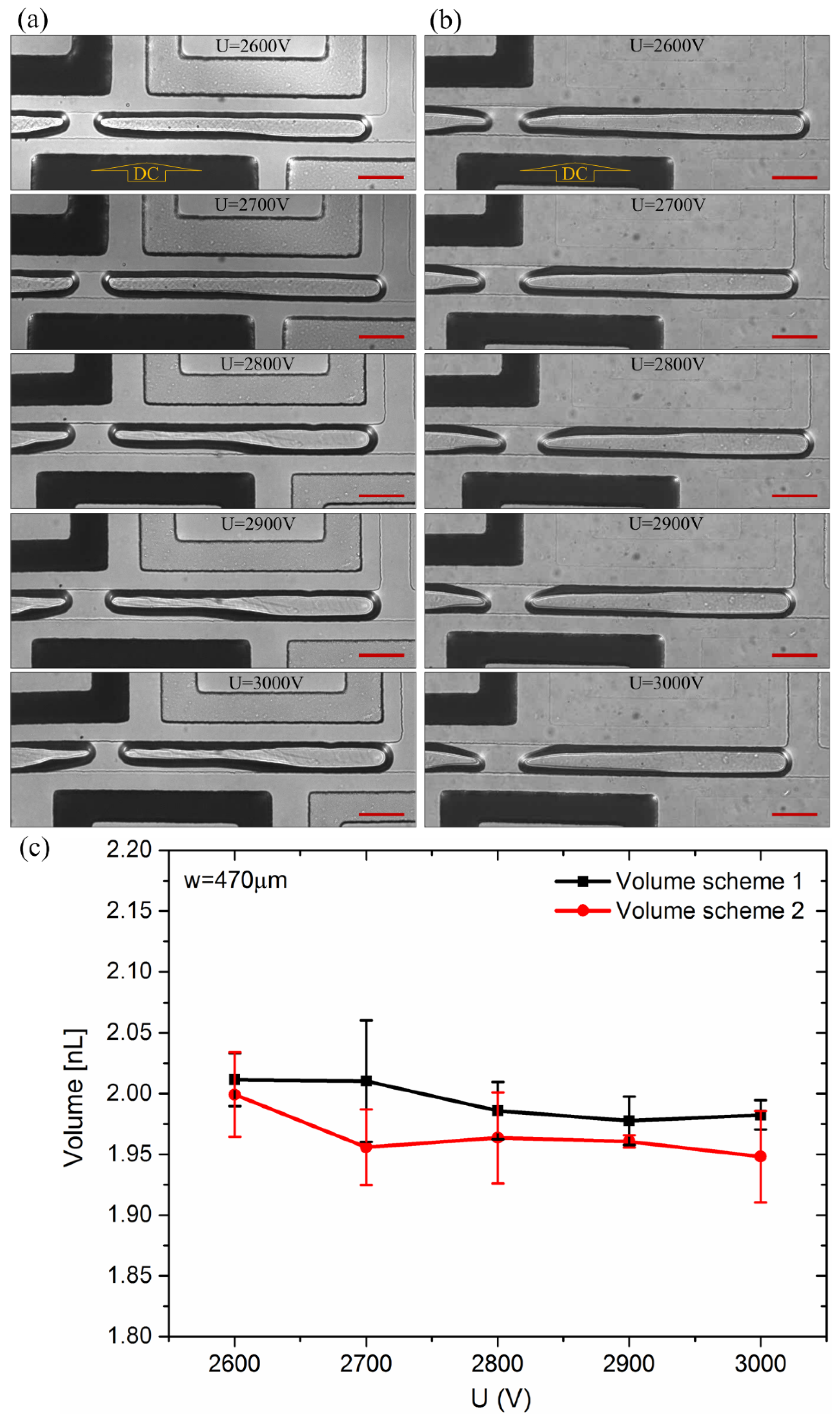
3.1. Droplet Generation
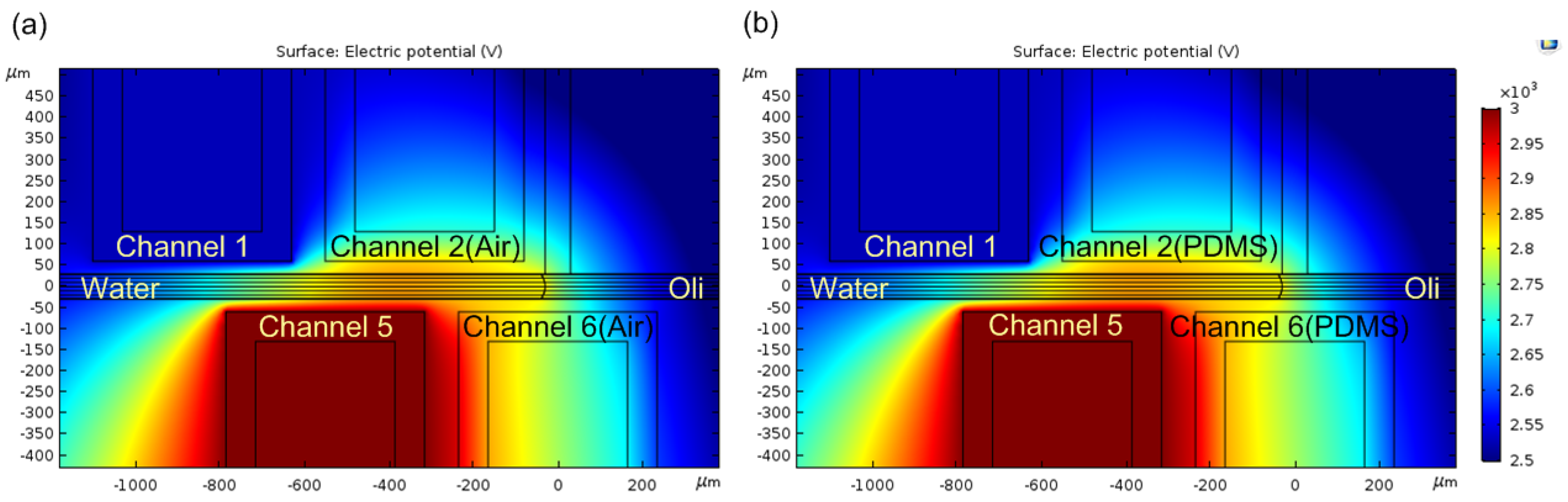
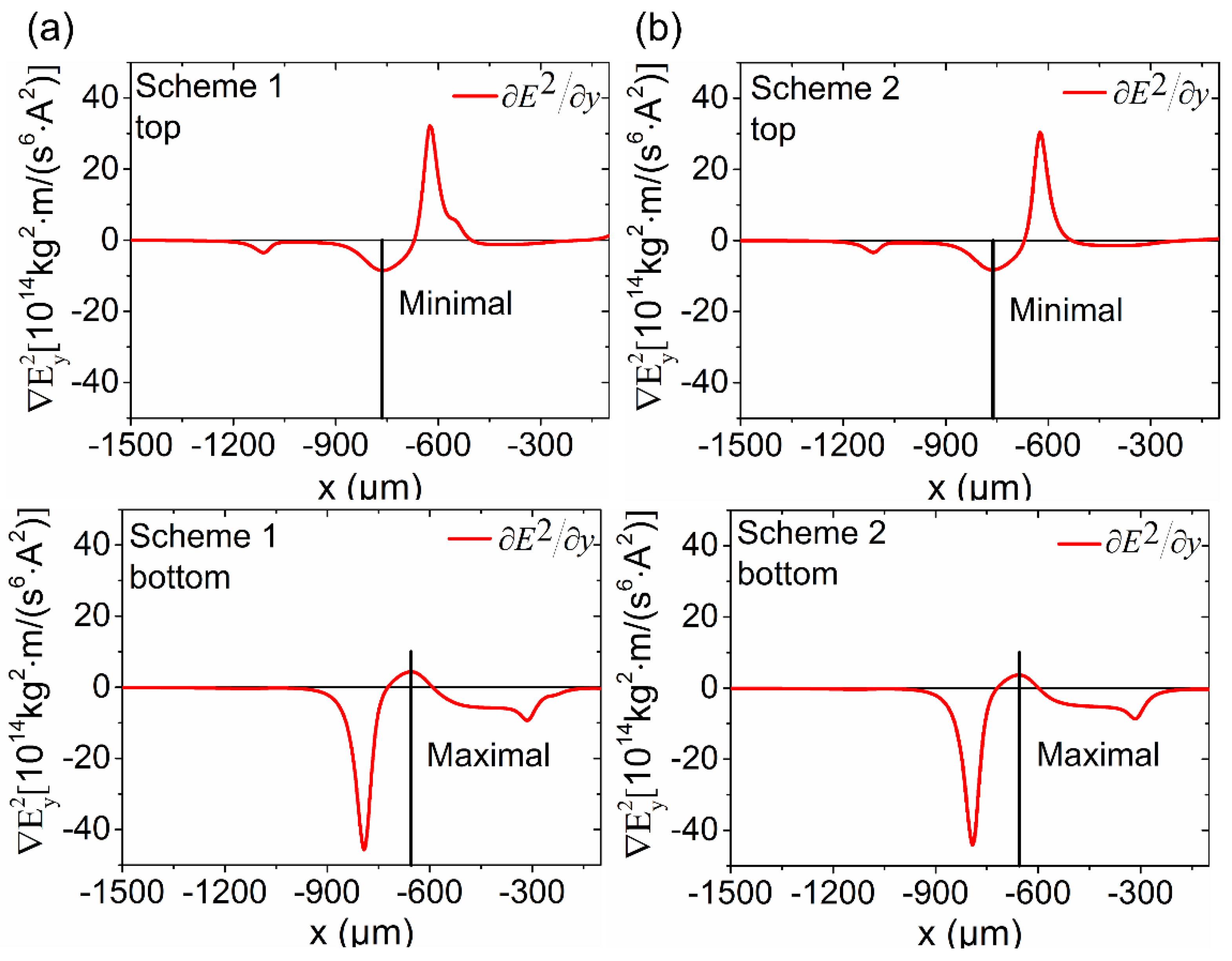
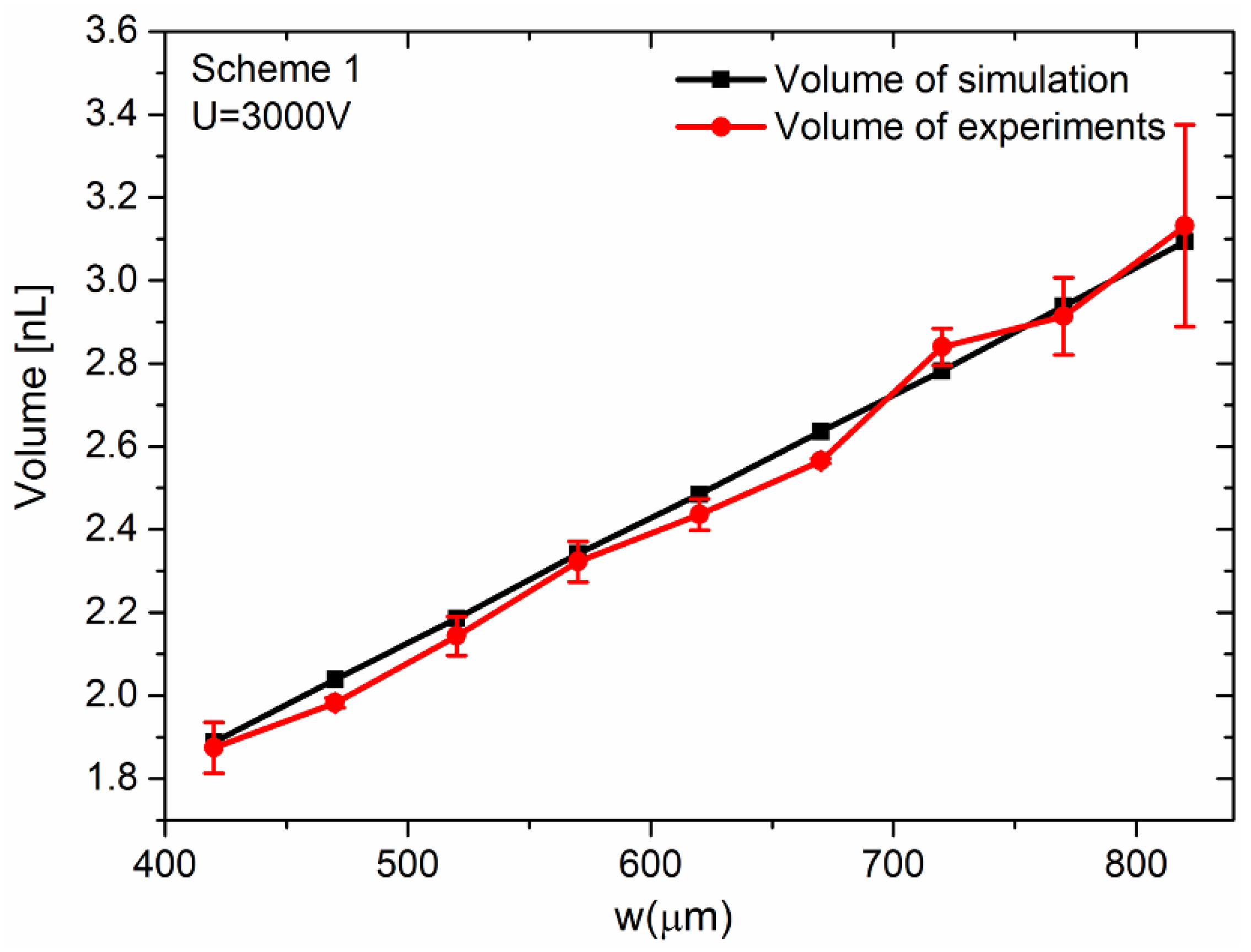
3.2. Simulation and Parametric Study
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roach, L.S.; Song, H.; Ismagilov, R.F. Controlling nonspecific protein adsorption in a plug-based microfluidic system by controlling interfacial chemistry using fluorous-phase surfactants. Anal. Chem. 2005, 77, 785–796. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, P.S.; Jahnz, M.; Schwille, P. A new embedded process for compartmentalized cell-free protein expression and on-line detection in microfluidic devices. ChemBioChem 2005, 6, 811–814. [Google Scholar] [CrossRef] [PubMed]
- Huebner, A.; Srisa-Art, M.; Holt, D.; Abell, C.; Hollfelder, F.; Demello, A.J.; Edel, J.B. Quantitative detection of protein expression in single cells using droplet microfluidics. Chem. Commun. 2007, 12, 1218–1220. [Google Scholar] [CrossRef] [PubMed]
- Hung, L.H.; Choi, K.M.; Tseng, W.Y.; Tan, Y.C.; Shea, K.J.; Lee, A.P. Alternating droplet generation and controlled dynamic droplet fusion in microfluidic device for CdS nanoparticle synthesis. Lab Chip 2006, 6, 174–178. [Google Scholar] [CrossRef] [PubMed]
- Hatakeyama, T.; Chen, D.L.; Ismagilov, R.F. Microgram-scale testing of reaction conditions in solution using nanoliter plugs in microfluidics with detection by MALDI-MS. J. Am. Chem. Soc. 2006, 128, 2518–2519. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Tice, J.D.; Roach, L.S.; Ismagilov, R.F. A droplet-based, composite PDMS/glass capillary microfluidic system for evaluating protein crystallization conditions by microbatch and vapor-diffusion methods with on-chip X-ray diffraction. Angew. Chem. Int. Ed. 2004, 43, 2508–2511. [Google Scholar] [CrossRef] [PubMed]
- Sesen, M.; Alan, T.; Neild, A. Microfluidic plug steering using surface acoustic waves. Lab Chip 2015, 15, 3030–3038. [Google Scholar] [CrossRef]
- Sesen, M.; Alan, T.; Neild, A. Microfluidic on-demand droplet merging using surface acoustic waves. Lab Chip 2014, 14, 3325–3333. [Google Scholar] [CrossRef]
- Jin, H.J.; Lee, K.H.; Destgeer, G.; Kang, S.L.; Cho, H.; Ha, B.H.; Sung, H.J. In situ seriate droplet coalescence under an optical force. Microfluid. Nanofluid. 2015, 18, 1247–1254. [Google Scholar]
- Mazutis, L.; Griffiths, A.D. Selective droplet coalescence using microfluidic systems. Lab Chip 2012, 12, 1800–1806. [Google Scholar] [CrossRef]
- Skelley, A.M.; Kirak, O.; Suh, H.; Jaenisch, R.; Voldman, J. Microfluidic control of cell pairing and fusion. Nat. Methods 2009, 6, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Thorsen, T.; Roberts, R.W.; Arnold, F.H.; Quake, S.R. Dynamic pattern formation in a vesicle-generating microfluidic device. Phys. Rev. Lett. 2001, 86, 4163–4166. [Google Scholar] [CrossRef] [PubMed]
- Garstecki, P.; Fuerstman, M.J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction—Scaling and mechanism of break-up. Lab Chip 2006, 6, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.H.; Nguyen, N.T.; Yobas, L.; Kang, T.G. Formation and manipulation of ferrofluid droplets at a microfluidic T-junction. J. Micromech. Microeng. 2010, 20, 045004. [Google Scholar] [CrossRef]
- Ganan-Calvo, A.M. Generation of steady liquid microthreads and micron-sized monodisperse sprays in gas streams. Phys. Rev. Lett. 1998, 80, 285–288. [Google Scholar] [CrossRef]
- Anna, S.L.; Bontoux, N.; Stone, H.A. Formation of dispersions using “flow focusing” in microchannels. Appl. Phys. Lett. 2003, 82, 364–366. [Google Scholar] [CrossRef]
- Garstecki, P.; Gitlin, I.; DiLuzio, W.; Whitesides, G.M.; Kumacheva, E.; Stone, H.A. Formation of monodisperse bubbles in a microfluidic flow-focusing device. Appl. Phys. Lett. 2004, 85, 2649–2651. [Google Scholar] [CrossRef]
- Takeuchi, S.; Garstecki, P.; Weibel, D.B.; Whitesides, G.M. An axisymmetric flow-focusing microfluidic device. Adv. Mater. 2005, 17, 1067–1072. [Google Scholar] [CrossRef]
- Utada, A.S.; Lorenceau, E.; Link, D.R.; Kaplan, P.D.; Stone, H.A.; Weitz, D.A. Monodisperse double emulsions generated from a microcapillary device. Science 2005, 308, 537–541. [Google Scholar] [CrossRef]
- Ganan-Calvo, A.M.; Gonzalez-Prieto, R.; Riesco-Chueca, P.; Herrada, M.A.; Flores-Mosquera, M. Focusing capillary jets close to the continuum limit. Nat. Phys. 2007, 3, 737–742. [Google Scholar] [CrossRef]
- Herrada, M.A.; Ganan-Calvo, A.M.; Ojeda-Monge, A.; Bluth, B.; Riesco-Chueca, P. Liquid flow focused by a gas: Jetting, dripping, and recirculation. Phys. Rev. E 2008, 78, 036323. [Google Scholar] [CrossRef] [PubMed]
- Ward, T.; Faivre, M.; Abkarian, M.; Stone, H.A. Microfluidic flow focusing: Drop size and scaling in pressure versus flow-rate-driven pumping. Electrophoresis 2005, 26, 3716–3724. [Google Scholar] [CrossRef] [PubMed]
- Abate, A.R.; Romanowsky, M.B.; Agresti, J.J.; Weitz, D.A. Valve-based flow focusing for drop formation. Appl. Phys. Lett. 2009, 94, 023503. [Google Scholar] [CrossRef]
- Link, D.R.; Grasland-Mongrain, E.; Duri, A.; Sarrazin, F.; Cheng, Z.D.; Cristobal, G.; Marquez, M.; Weitz, D.A. Electric control of droplets in microfluidic devices. Angew. Chem. Int. Ed. 2006, 45, 2556–2560. [Google Scholar] [CrossRef] [PubMed]
- Barbier, V.; Willaime, H.; Tabeling, P.; Jousse, F. Producing droplets in parallel microfluidic systems. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 046306. [Google Scholar] [CrossRef] [PubMed]
- Jeffries, G.D.M.; Kuo, J.S.; Chiu, D.T. Dynamic modulation of chemical concentration in an aqueous droplet. Angew. Chem. Int. Ed. 2007, 46, 1326–1328. [Google Scholar] [CrossRef]
- Baroud, C.N.; de Saint Vincent, M.R.; Delville, J.P. An optical toolbox for total control of droplet microfluidics. Lab Chip 2007, 7, 1029–1033. [Google Scholar] [CrossRef]
- Psaltis, D.; Quake, S.R.; Yang, C.H. Developing optofluidic technology through the fusion of microfluidics and optics. Nature 2006, 442, 381–386. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Ting, T.H.; Yap, Y.F.; Wong, T.N.; Chai, J.C.K.; Ong, W.L.; Zhou, J.; Tan, S.H.; Yobas, L. Thermally mediated droplet formation in microchannels. Appl. Phys. Lett. 2007, 91, 084102. [Google Scholar] [CrossRef]
- Yap, Y.F.; Tan, S.H.; Nguyen, N.T.; Murshed, S.M.S.; Wong, T.N.; Yobas, L. Thermally mediated control of liquid microdroplets at a bifurcation. J. Phys. D Appl. Phys. 2009, 42, 065503. [Google Scholar] [CrossRef]
- Willaime, H.; Barbier, V.; Kloul, L.; Maine, S.; Tabeling, P. Arnold tongues in a microfluidic drop emitter. Phys. Rev. Lett. 2006, 96, 054501. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.T.; Lee, G.B. Formation of microdroplets in liquids utilizing active pneumatic choppers on a microfluidic chip. J. Microelectromech. Syst. 2006, 15, 1492–1498. [Google Scholar] [CrossRef]
- Schmid, L.; Franke, T. SAW-controlled drop size for flow focusing. Lab Chip 2013, 13, 1691–1694. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.Y.; Li, P.; Lin, S.C.S.; Stratton, Z.S.; Nama, N.; Guo, F.; Slotcavage, D.; Mao, X.L.; Shi, J.J.; Costanzo, F.; et al. Surface acoustic wave microfluidics. Lab Chip 2013, 13, 3626–3649. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.H.; Destgeer, G.; Ha, B.; Park, J.; Sung, H.J. On-demand droplet splitting using surface acoustic waves. Lab Chip 2016, 16, 3235–3243. [Google Scholar] [CrossRef] [PubMed]
- Chong, Z.Z.; Tan, S.H.; Ganan-Calvo, A.M.; Tor, S.B.; Loh, N.H.; Nguyen, N.T. Active droplet generation in microfluidics. Lab Chip 2016, 16, 35–58. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Tan, S.H.; Yap, Y.F.; Ng, M.Y.; Nguyen, N.T. Numerical and experimental investigations of the formation process of ferrofluid droplets. Microfluid. Nanofluid. 2011, 11, 177–187. [Google Scholar] [CrossRef]
- Carreras, P.; Mohr, S.; Fielden, P.; Goddard, N. Electrokinetic Diluting and Sorting of Droplets in a Microfluidic Platform; Japan Society Applied Physics: Tokyo, Japan, 2007; pp. 328–329. [Google Scholar]
- Pollack, M.G.; Shenderov, A.D.; Fair, R.B. Electrowetting-based actuation of droplets for integrated microfluidics. Lab Chip 2002, 2, 96–101. [Google Scholar] [CrossRef]
- Cho, S.K.; Moon, H.J.; Kim, C.J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. J. Microelectromech. Syst. 2003, 12, 70–80. [Google Scholar] [CrossRef]
- Paik, P.; Pamula, V.K.; Pollack, M.G.; Fair, R.B. Electrowetting-based droplet mixers for microfluidic systems. Lab Chip 2003, 3, 28–33. [Google Scholar] [CrossRef]
- Paik, P.; Pamula, V.K.; Fair, R.B. Rapid droplet mixers for digital microfluidic systems. Lab Chip 2003, 3, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, T.; Torii, T.; Higuchi, T. Chemical reactions in microdroplets by electrostatic manipulation of droplets in liquid media. Lab Chip 2002, 2, 19–23. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Moon, H.; Fowler, J.; Schoellhammer, T.; Kim, C.J. Electrowetting and electrowetting-on-dielectric for microscale liquid handling. Sens. Actuators A Phys. 2002, 95, 259–268. [Google Scholar] [CrossRef]
- Schwartz, J.A.; Vykoukal, J.V.; Gascoyne, P.R.C. Droplet-based chemistry on a programmable micro-chip. Lab Chip 2004, 4, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Ganan-Calvo, A.M.; Lopez-Herrera, J.M.; Riesco-Chueca, P. The combination of electrospray and flow focusing. J. Fluid Mech. 2006, 566, 421–445. [Google Scholar] [CrossRef]
- Kim, H.; Luo, D.W.; Link, D.; Weitz, D.A.; Marquez, M.; Cheng, Z.D. Controlled production of emulsion drops using an electric field in a flow-focusing microfluidic device. Appl. Phys. Lett. 2007, 91, 133106. [Google Scholar] [CrossRef]
- Tan, S.H.; Semin, B.; Baret, J.C. Microfluidic flow-focusing in ac electric fields. Lab Chip 2014, 14, 1099–1106. [Google Scholar] [CrossRef]
- He, P.; Kim, H.; Luo, D.W.; Marquez, M.; Cheng, Z.D. Low-frequency ac electro-flow-focusing microfluidic emulsification. Appl. Phys. Lett. 2010, 96, 174103. [Google Scholar] [CrossRef]
- Colgate, E.; Matsumoto, H. An investigation of electrowetting-based microactuation. J. Vac. Sci. Technol. A Vac. Surf. Films 1990, 8, 3625–3633. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J.C. Electrowetting: From basics to applications. J. Phys. Condens. Matter 2005, 17, R705–R774. [Google Scholar] [CrossRef]
- Quilliet, C.; Berge, B. Electrowetting: A recent outbreak. Curr. Opin. Colloid Interface Sci. 2001, 6, 34–39. [Google Scholar] [CrossRef]
- Li, F.; Mugele, F. How to make sticky surfaces slippery: Contact angle hysteresis in electrowetting with alternating voltage. Appl. Phys. Lett. 2008, 92, 244108. [Google Scholar] [CrossRef]
- Malloggi, F.; Gu, H.; Banpurkar, A.G.; Vanapalli, S.A.; Mugele, F. Electrowetting—A versatile tool for controlling microdrop generation. Eur. Phys. J. E 2008, 26, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Murade, C.U.; Duits, M.H.G.; Mugele, F. A microfluidic platform for on-demand formation and merging of microdroplets using electric control. Biomicrofluidics 2011, 5, 011101. [Google Scholar] [CrossRef] [PubMed]
- Malloggi, F.; Vanapalli, S.A.; Gu, H.; van den Ende, D.; Mugele, F. Electrowetting-controlled droplet generation in a microfluidic flow-focusing device. J. Phys. Condens. Matter 2007, 19, 462101. [Google Scholar] [CrossRef]
- Gu, H.; Malloggi, F.; Vanapalli, S.A.; Mugele, F. Electrowetting-enhanced microfluidic device for drop generation. Appl. Phys. Lett. 2008, 93, 183507. [Google Scholar] [CrossRef]
- Anna, S.L.; Mayer, H.C. Microscale tipstreaming in a microfluidic flow focusing device. Phys. Fluids 2006, 18, 121512. [Google Scholar] [CrossRef]
- Gu, H.; Duits, M.H.G.; Mugele, F. A hybrid microfluidic chip with electrowetting functionality using ultraviolet (UV)-curable polymer. Lab Chip 2010, 10, 1550–1556. [Google Scholar] [CrossRef]
- Castro-Hernandez, E.; Garcia-Sanchez, P.; Tan, S.H.; Ganan-Calvo, A.M.; Baret, J.C.; Ramos, A. Breakup length of AC electrified jets in a microfluidic flow-focusing junction. Microfluid. Nanofluid. 2015, 19, 787–794. [Google Scholar] [CrossRef]
- Siegel, A.C.; Shevkoplyas, S.S.; Weibel, D.B.; Bruzewicz, D.A.; Martinez, A.W.; Whitesides, G.M. Cofabrication of electromagnets and microfluidic systems in poly(dimethylsiloxane). Angew. Chem. Int. Ed. 2006, 45, 6877–6882. [Google Scholar] [CrossRef]
- Tan, S.H.; Maes, F.; Semin, B.; Vrignon, J.; Baret, J.C. The Microfluidic Jukebox. Sci. Rep. 2014, 4, 4787. [Google Scholar] [CrossRef] [PubMed]
- Jones, T.B.; Gunji, M.; Washizu, M.; Feldman, M.J. Dielectrophoretic liquid actuation and nanodroplet formation. J. Appl. Phys. 2001, 89, 1441–1448. [Google Scholar] [CrossRef]
- Jones, T.B. Liquid dielectrophoresis on the microscale. J. Electrost. 2001, 51, 290–299. [Google Scholar] [CrossRef]
- Prakash, R.; Paul, R.; Kaler, K. Liquid DEP actuation and precision dispensing of variable volume droplets. Lab Chip 2010, 10, 3094–3102. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.N.; Whitesides, G.M. Soft lithography. Annu. Rev. Mater. Sci. 1998, 28, 153–184. [Google Scholar] [CrossRef]
- Pohl, H.A. Dielectrophoresis: The behavior of Neutral Matter in Nonuniform Electric Fields (Cambridge Monographs on Physics); Cambridge University Press: Cambridge, UK; New York, NY, USA, 1978. [Google Scholar]
- Mauro, A. Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields. Q. Rev. Biol. 1980, 55, 68–69. [Google Scholar] [CrossRef]
- Ahn, K.; Kerbage, C.; Hunt, T.P.; Westervelt, R.M.; Link, D.R.; Weitz, D.A. Dielectrophoretic manipulation of drops for high-speed microfluidic sorting devices. Appl. Phys. Lett. 2006, 88, 024104. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Zhang, L.; Gao, M.; Wang, Q.; Deng, Z.; Gui, L. A Liquid-Metal-Based Dielectrophoretic Microdroplet Generator. Micromachines 2019, 10, 769. https://doi.org/10.3390/mi10110769
Wang R, Zhang L, Gao M, Wang Q, Deng Z, Gui L. A Liquid-Metal-Based Dielectrophoretic Microdroplet Generator. Micromachines. 2019; 10(11):769. https://doi.org/10.3390/mi10110769
Chicago/Turabian StyleWang, Ronghang, Lunjia Zhang, Meng Gao, Qifu Wang, Zhongshan Deng, and Lin Gui. 2019. "A Liquid-Metal-Based Dielectrophoretic Microdroplet Generator" Micromachines 10, no. 11: 769. https://doi.org/10.3390/mi10110769
APA StyleWang, R., Zhang, L., Gao, M., Wang, Q., Deng, Z., & Gui, L. (2019). A Liquid-Metal-Based Dielectrophoretic Microdroplet Generator. Micromachines, 10(11), 769. https://doi.org/10.3390/mi10110769