Squeezing Dynamic Mechanism of High-Viscosity Droplet and its Application for Adhesive Dispensing in Sub-Nanoliter Resolution
Abstract
1. Introduction
2. Principles and Modeling
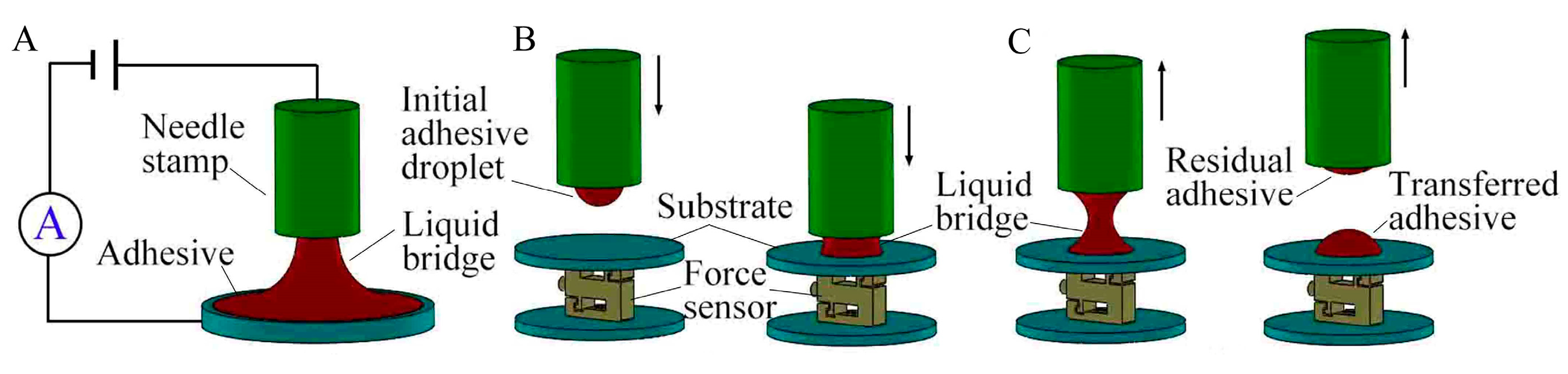
2.1. Transfer Printing Principle
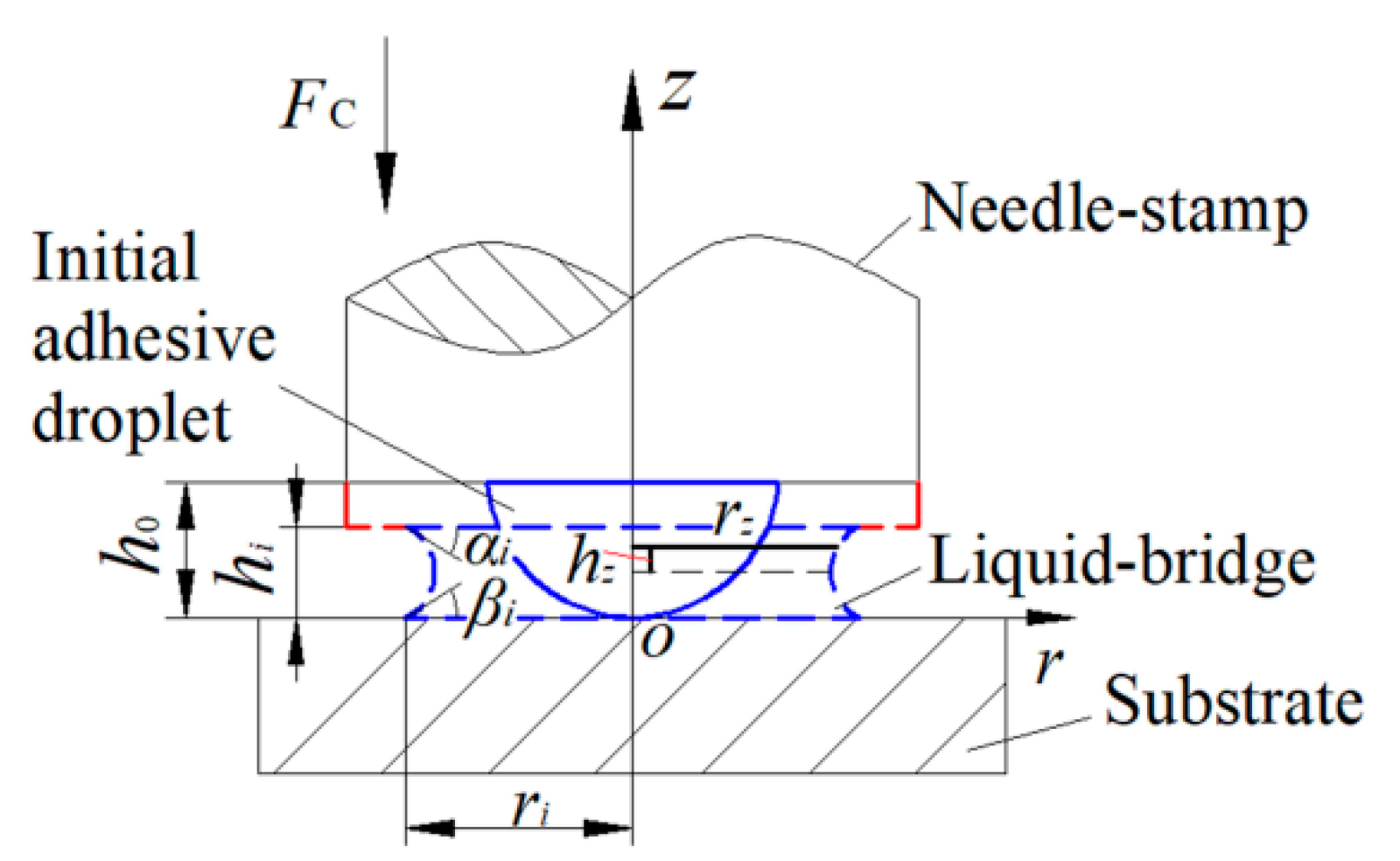
2.2. Modeling of Squeezing-and-Deforming of Initial Droplet
- The liquid-bridge is axisymmetric and incompressible with low Reynolds number Re ().
- The wettability of the stamp is similar to that of the substrate, thus the contact angle αi on the needle-stamp is approximately equal to the contact angle βi on the substrate, and the meniscus of the liquid-bridge is assumed to be the concave surface of the spherical cap, shown in Figure 2.
- The height of the liquid-bridge hi is much smaller than the contact radius ri between the liquid-bridge and the substrate. Then the slit between stamp and substrate is formed, and the pitch of slit is equal to hi () [21].
- The gravity in sub-nanoliter level can be ignored under low Bond number Bo (). Thus, the dominating terms are those considering the pressure gradients and the shear stress derivatives in the z-direction. Equation (1) can therefore be simplified to Equation (2).
3. Materials and Methods
3.1. Materials and Instruments
3.2. Experimental Process
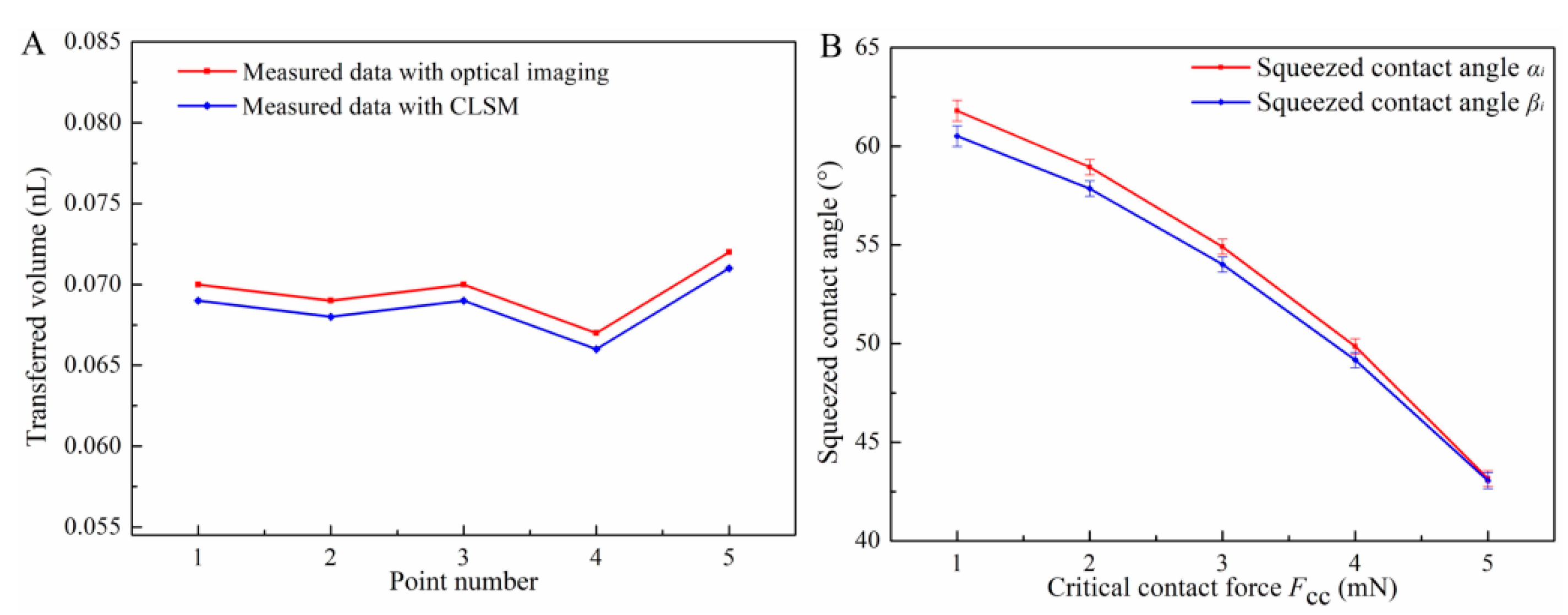
3.3. Calculation of Adhesive Volume
4. Results and Discussions
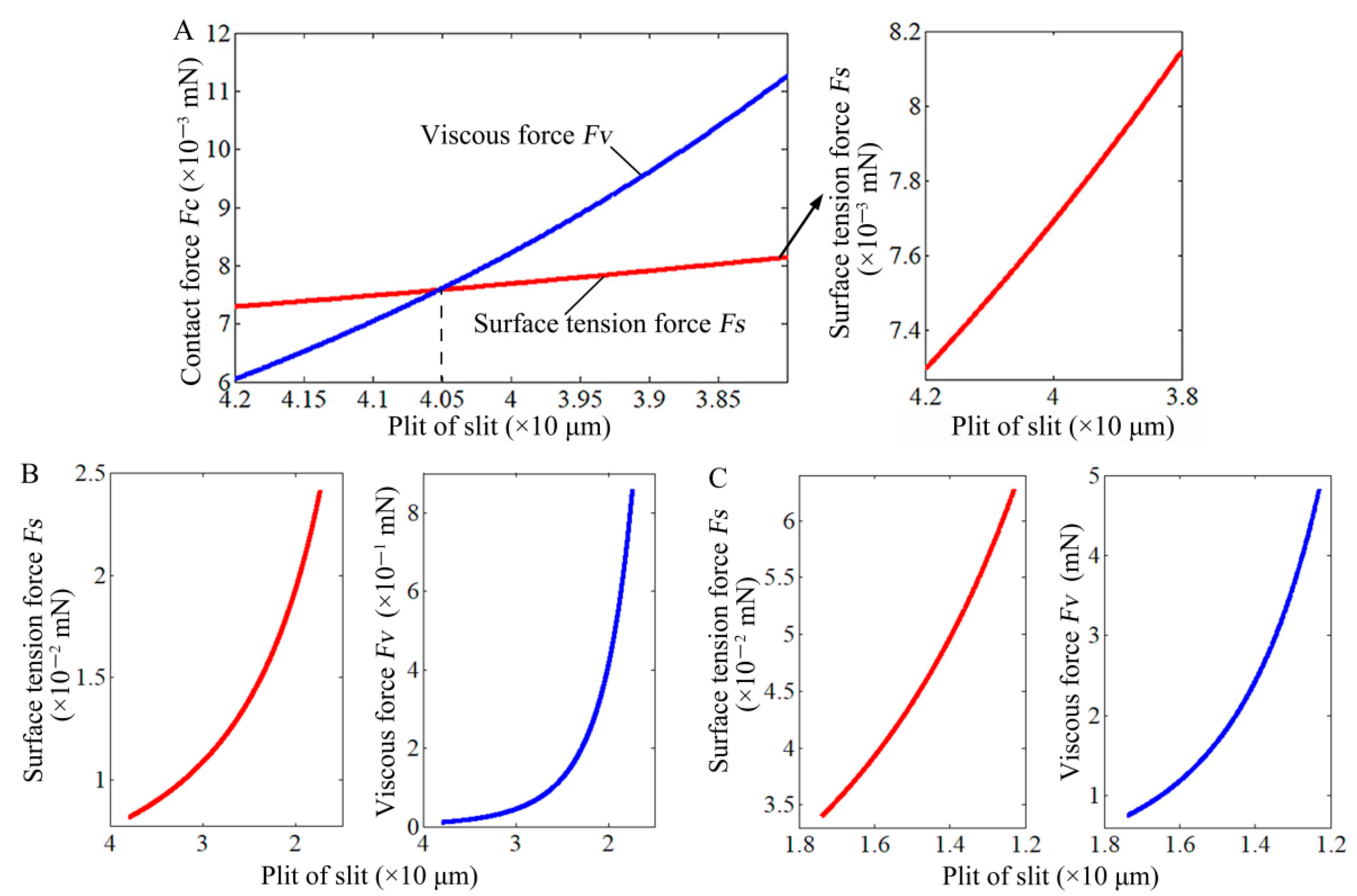
4.1. Analysis of the Squeezing-and-Deforming Process of a Droplet
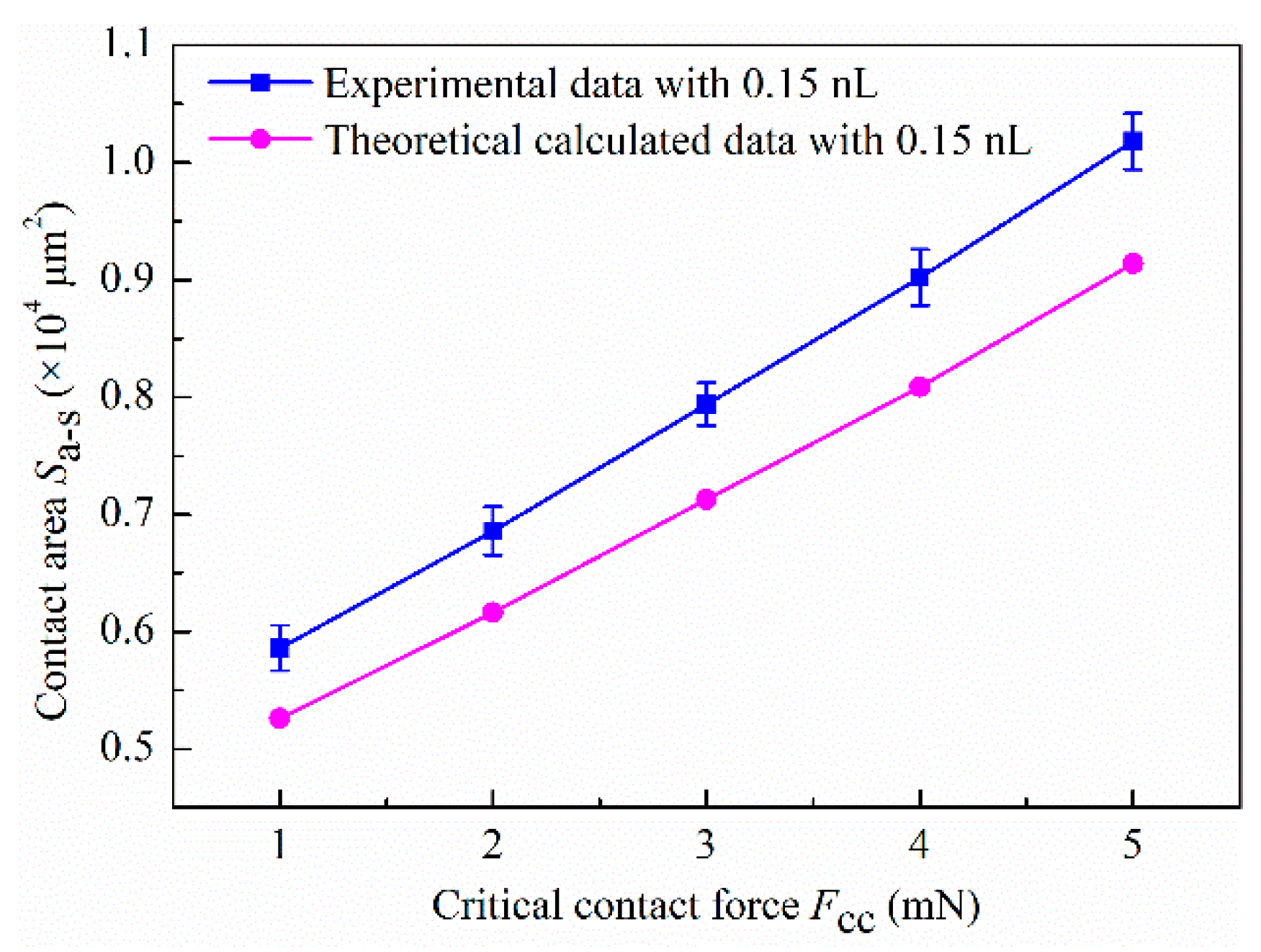
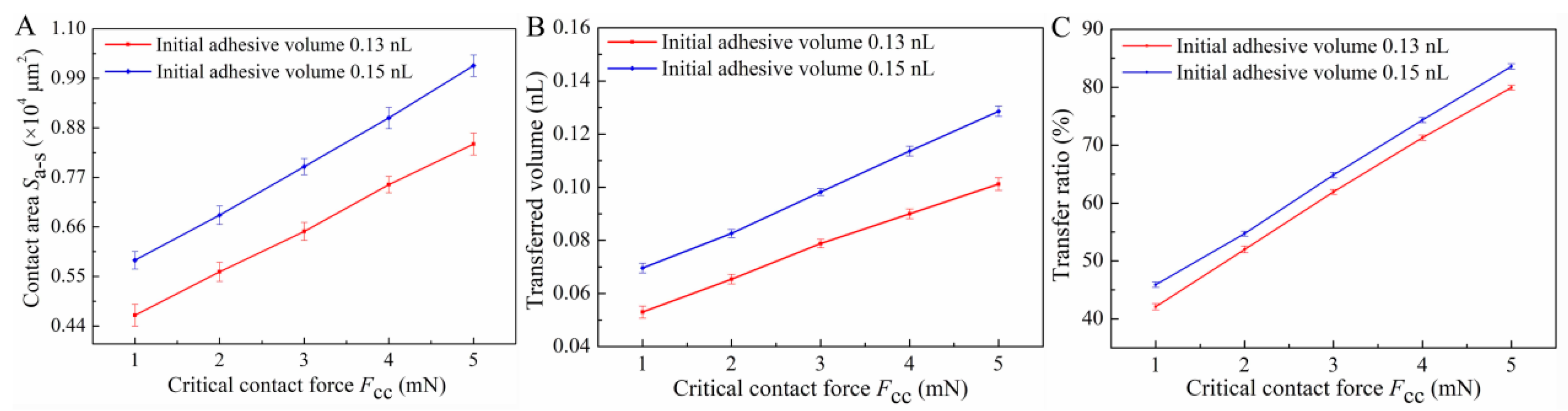
4.2. Discussion of Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, X.; Elmer, J.; DebRoy, T. Heat transfer and fluid flow in laser microwelding. J. Appl. Phys. 2005, 97, 084909. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, G.; Guo, Y.; Tian, Y. Study of PMMA thermal bonding. Microsyst. Technol. 2007, 13, 403–407. [Google Scholar] [CrossRef]
- Cozma, A.; Puers, B. Characterization of the electrostatic bonding of silicon and Pyrex glass. J. Micromech. Microeng. 1995, 5, 98–102. [Google Scholar] [CrossRef]
- Yang, L.; King, C.K.; Bernstein, J.B. Liquid dispensing encapsulation in semiconductor packaging. Microelectron. Int. 2003, 20, 29–35. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.; Kim, J.; Lee, S.; Cho, D.-I. Surface/bulk micromachined single-crystalline-silicon micro-gyroscope. J. Microelectromech. Syst. 2000, 9, 557–567. [Google Scholar]
- Adams, R.D.; Davies, R. Strength of joints involving composites. J. Adhes. 1996, 59, 171–182. [Google Scholar] [CrossRef]
- Heidarpour, F.; Farahani, M.; Ghabezi, P. Experimental investigation of the effects of adhesive defects on the single lap joint strength. Int. J. Adhes. Adhes. 2018, 80, 128–132. [Google Scholar] [CrossRef]
- Rispler, A.R.; Tong, L.; Steven, G.P.; Wisnom, M.R. Shape optimisation of adhesive fillets. Int. J. Adhes. Adhes. 2000, 20, 221–231. [Google Scholar] [CrossRef]
- Zhao, Y.-X.; Li, H.-X.; Ding, H.; Xiong, Y.-L. Integrated modelling of a time-pressure fluid dispensing system for electronics manufacturing. Int. J. Adv. Manuf. Technol. 2005, 26, 1–9. [Google Scholar] [CrossRef]
- Nguyen, Q.-H.; Choi, M.-K.; Choi, S.-B. A new type of piezostack-driven jetting dispenser for semiconductor electronic packaging: Modeling and control. Smart Mater. Struct. 2008, 17, 015033. [Google Scholar] [CrossRef]
- Mecozzi, L.; Gennari, O.; Coppola, S.; Olivieri, F.; Rega, R.; Mandracchia, B.; Vespini, V.; Bramanti, A.; Ferraro, P.; Grilli, S. Easy Printing of High Viscous Microdots by Spontaneous Breakup of Thin Fibers. ACS Appl. Mater. Interfaces 2018, 10, 2122–2129. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Braunschweig, A.B.; Zheng, Z.; Mirkin, C.A. Force- and time-dependent feature size and shape control in molecular printing via polymer-pen lithography. Small 2010, 6, 1082–1086. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Braunschweig, A.B.; Mirkin, C.A. “Force-feedback” leveling of massively parallel arrays in polymer pen lithography. Nano Lett. 2010, 10, 1335–1340. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kumar, S. Liquid transfer in printing processes: Liquid bridges with moving contact lines. Annu. Rev. Fluid Mech. 2015, 47, 67–94. [Google Scholar] [CrossRef]
- Zhang, X.; Padgett, R.; Basaran, O. Nonlinear deformation and breakup of stretching liquid bridges. J. Fluid Mech. 1996, 329, 207–245. [Google Scholar] [CrossRef]
- Chen, H.; Tang, T.; Amirfazli, A. Fast liquid transfer between surfaces: Breakup of stretched liquid bridges. Langmuir 2015, 31, 11470–11476. [Google Scholar] [CrossRef]
- Huang, C.-H.; Carvalho, M.S.; Kumar, S. Stretching liquid bridges with moving contact lines: Comparison of liquid-transfer predictions and experiments. Soft Matter 2016, 12, 7457–7469. [Google Scholar] [CrossRef]
- Collins, R.T.; Jones, J.J.; Harris, M.T.; Basaran, O.A. Electrohydrodynamic tip streaming and emission of charged drops from liquid cones. Nat. Phys. 2007, 4, 149–154. [Google Scholar] [CrossRef]
- Marginean, I.; Parvin, L.; Heffernan, L.; Vertes, A. Flexing the electrified meniscus: The birth of a jet in electrosprays. Anal. Chem. 2004, 76, 4202–4207. [Google Scholar] [CrossRef]
- SchaÈffer, E.; Thurn-Albrecht, T.; Russell, T.P.; Steiner, U. Electrically induced structure formation and pattern transfer. Nature 2000, 403, 874. [Google Scholar] [CrossRef]
- Müller, M.; Tong, Y.; Fricke, H.; Vallée, T. An efficient numerical model for the evaluation of compression flow of high-viscosity adhesives. Int. J. Adhes. Adhes. 2018, 85, 251–262. [Google Scholar] [CrossRef]
- Engmann, J.; Servais, C.; Burbidge, A.S. Squeeze flow theory and applications to rheometry: A review. J. Non-Newton. Fluid 2005, 132, 1–27. [Google Scholar] [CrossRef]
- Jackson, J. A study of squeezing flow. Appl. Sci. Res. 1963, 11, 148–152. [Google Scholar] [CrossRef]
- Chen, H.; Amirfazli, A.; Tang, T. Modeling liquid bridge between surfaces with contact angle hysteresis. Langmuir 2013, 29, 3310–3319. [Google Scholar] [CrossRef]
- Cai, S.; Bhushan, B. Meniscus and viscous forces during normal separation of liquid-mediated contacts. Nanotechnology 2007, 18, 465704. [Google Scholar] [CrossRef]
- Cai, S.; Bhushan, B. Meniscus and viscous forces during separation of hydrophilic and hydrophobic surfaces with liquid-mediated contacts. Mater. Sci. Eng. R Rep. 2008, 61, 78–106. [Google Scholar] [CrossRef]



| Surface Tension γ (mN/m) | Density ρ (g/cm3) | Contact Angle α0 on Steel (°) | Contact Angle β0 on Silicon Wafer (°) | Viscosity µ (Pa·s) |
|---|---|---|---|---|
| 36.96 | 1.84 | 74 | 71 | 93.93 |
| Experiment Condition | Descent Velocity of Stamp U (mm/min) | Lifting Velocity of Stamp (mm/min) | Defined Contact Force FCC (mN) | Initial Average Volume (nL) | Initial Average Height h0 (μm) | Pitch of Slit hi with 1–5 mN (μm) |
|---|---|---|---|---|---|---|
| I | 0.09 | 60 | 1~5 | 0.13 | 39.0 | 15.9~11.3 |
| II | 0.09 | 60 | 1~5 | 0.15 | 42.0 | 17.4~12.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Xu, Z.; Xu, X.; Wang, D.; Wang, X.; Yan, Y.; Wang, L. Squeezing Dynamic Mechanism of High-Viscosity Droplet and its Application for Adhesive Dispensing in Sub-Nanoliter Resolution. Micromachines 2019, 10, 728. https://doi.org/10.3390/mi10110728
Zhu P, Xu Z, Xu X, Wang D, Wang X, Yan Y, Wang L. Squeezing Dynamic Mechanism of High-Viscosity Droplet and its Application for Adhesive Dispensing in Sub-Nanoliter Resolution. Micromachines. 2019; 10(11):728. https://doi.org/10.3390/mi10110728
Chicago/Turabian StyleZhu, Ping, Zheng Xu, Xiaoyu Xu, Dazhi Wang, Xiaodong Wang, Ying Yan, and Liding Wang. 2019. "Squeezing Dynamic Mechanism of High-Viscosity Droplet and its Application for Adhesive Dispensing in Sub-Nanoliter Resolution" Micromachines 10, no. 11: 728. https://doi.org/10.3390/mi10110728
APA StyleZhu, P., Xu, Z., Xu, X., Wang, D., Wang, X., Yan, Y., & Wang, L. (2019). Squeezing Dynamic Mechanism of High-Viscosity Droplet and its Application for Adhesive Dispensing in Sub-Nanoliter Resolution. Micromachines, 10(11), 728. https://doi.org/10.3390/mi10110728






