Acoustophoretic Control of Microparticle Transport Using Dual-Wavelength Surface Acoustic Wave Devices
Abstract
1. Introduction
2. Methods
2.1. Acoustofluidic Theory and Numerical Models
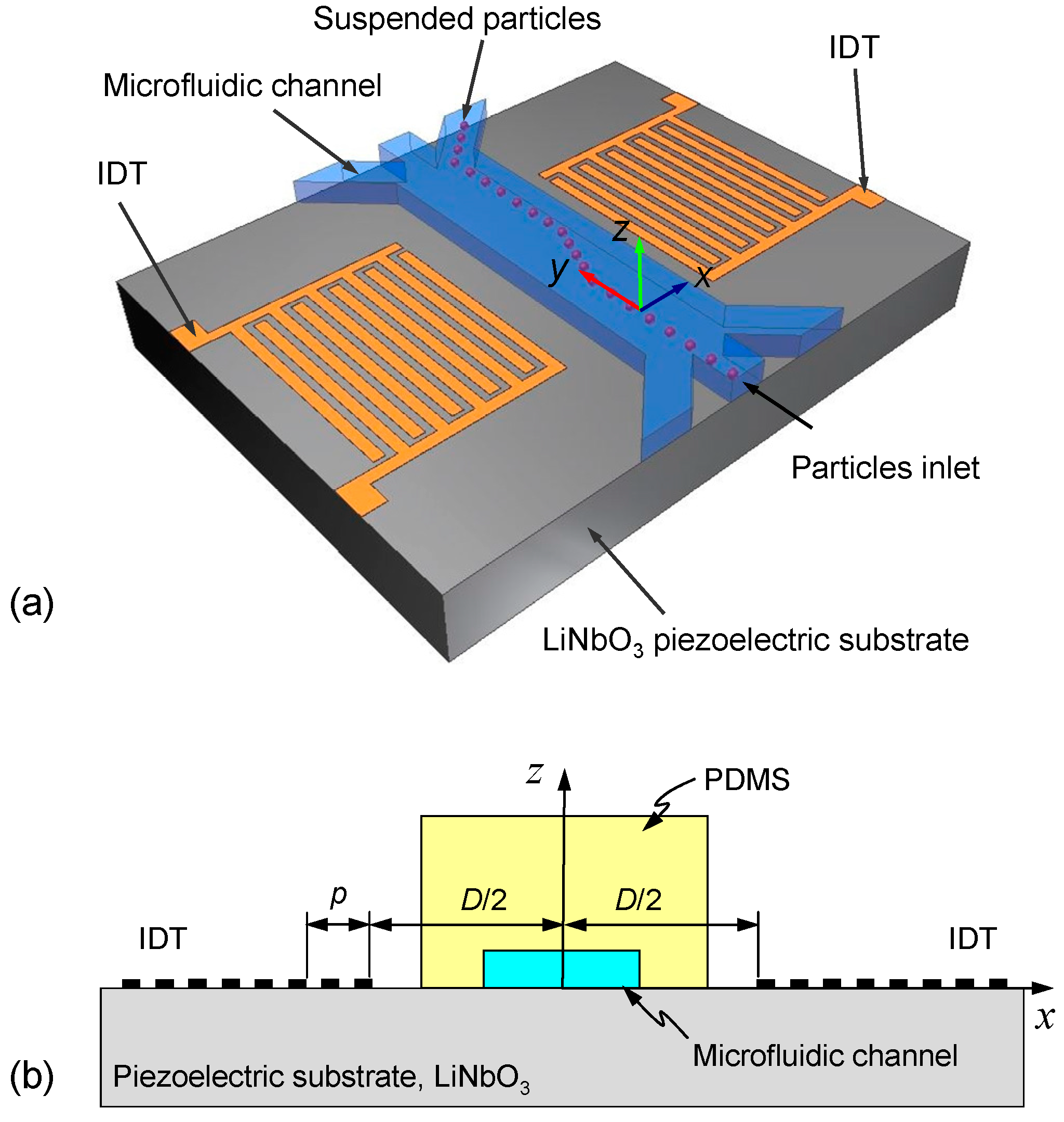
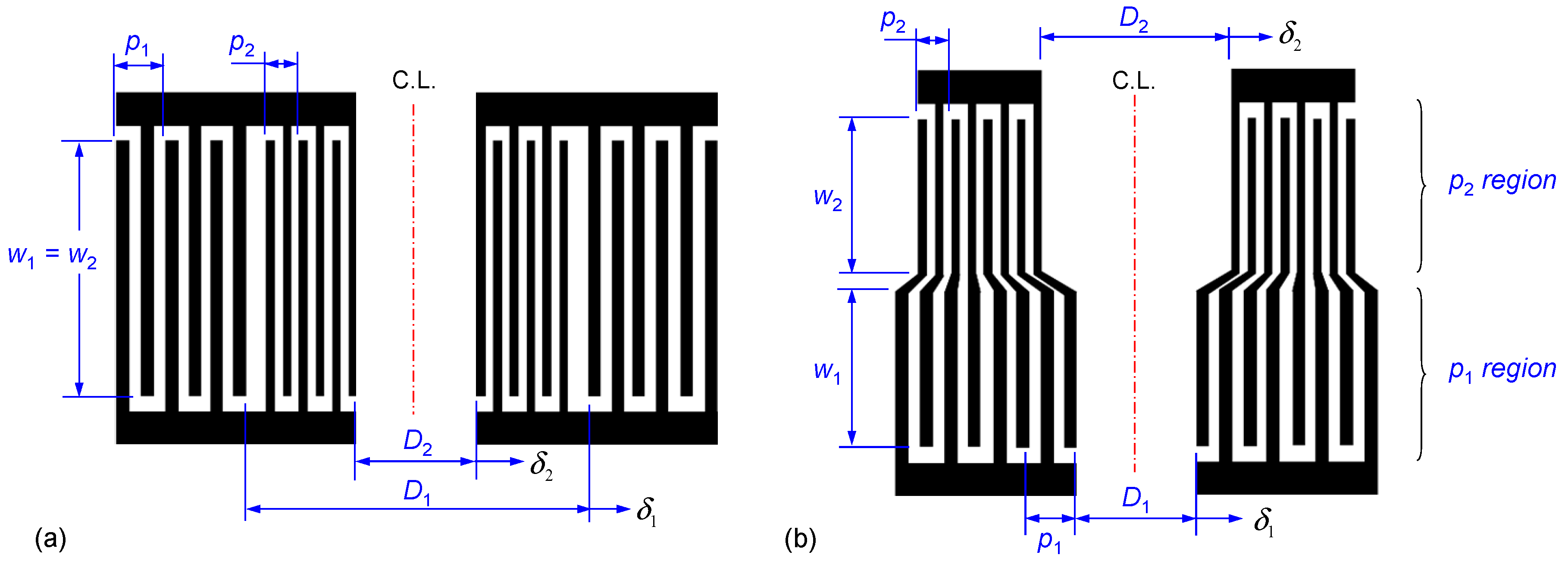
2.2. Device Design Approach
2.3. Device Fabrication and Experimental Setup
3. Results and Discussion
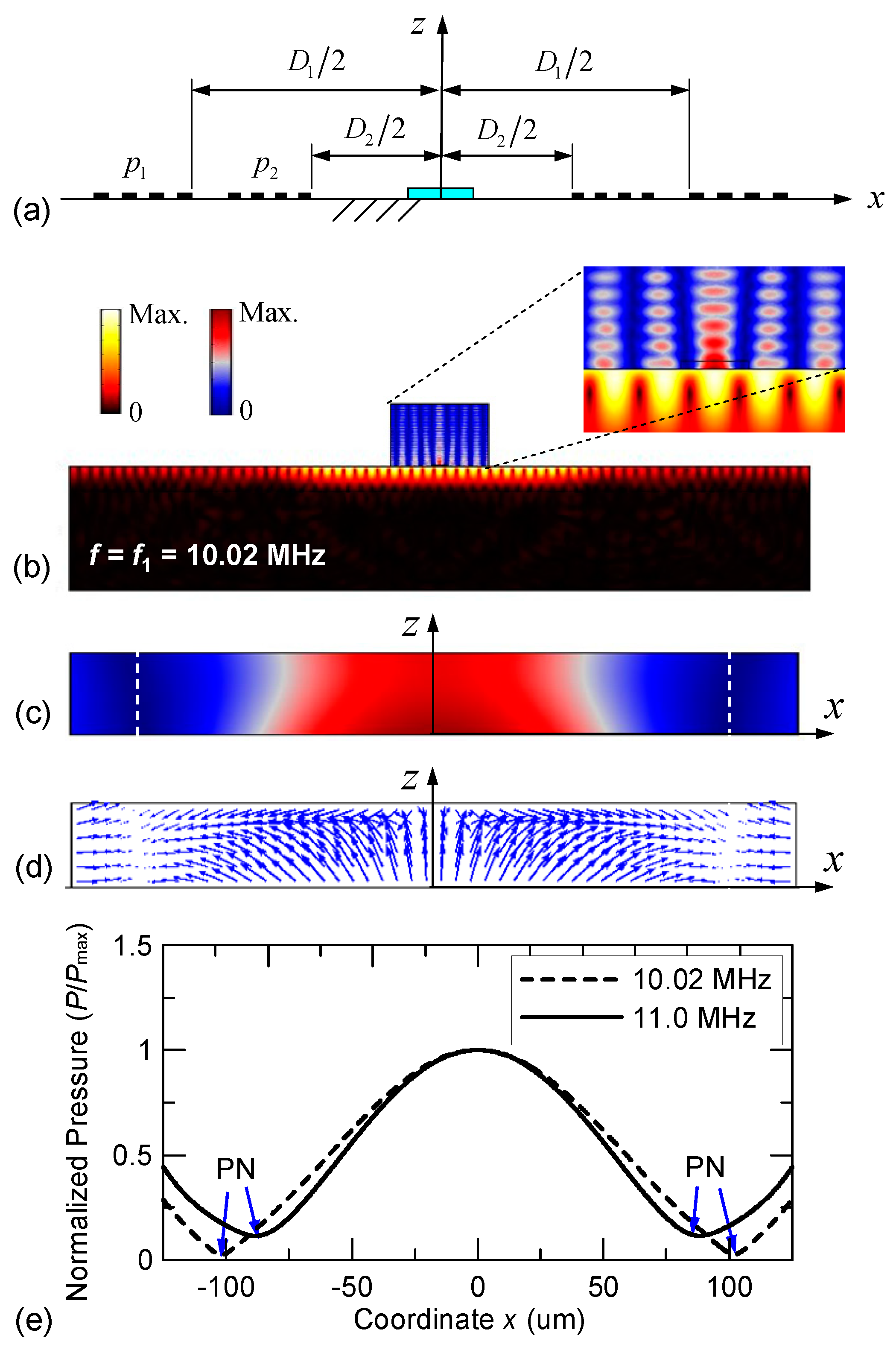
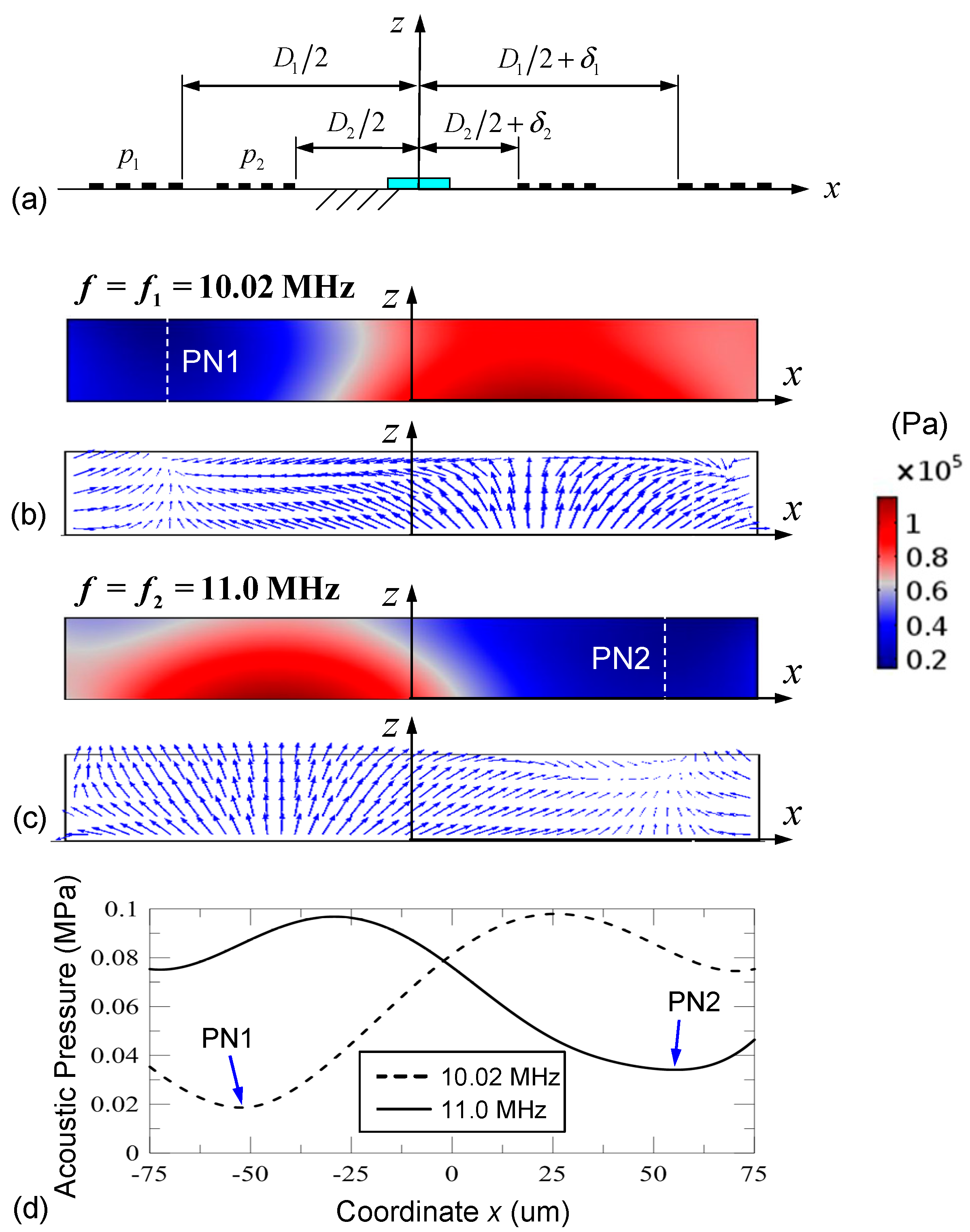
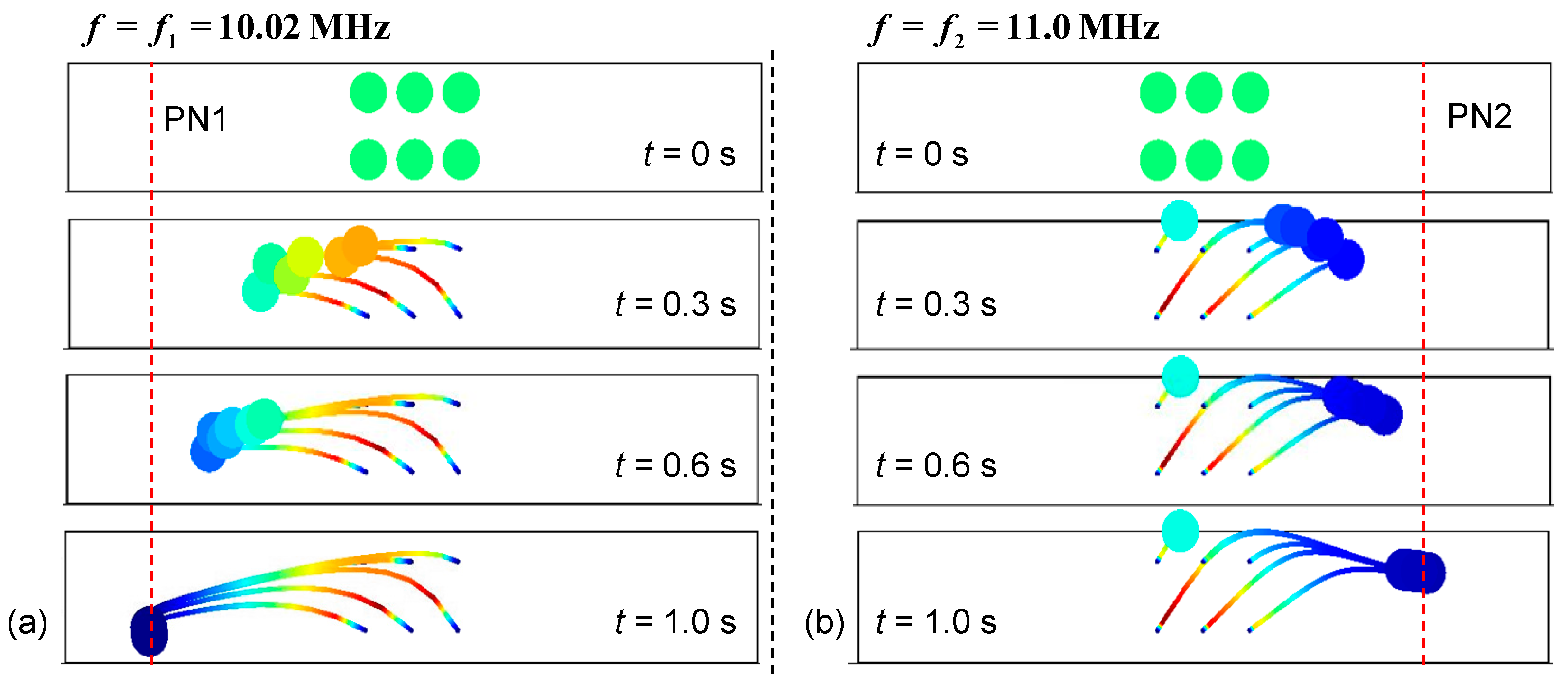
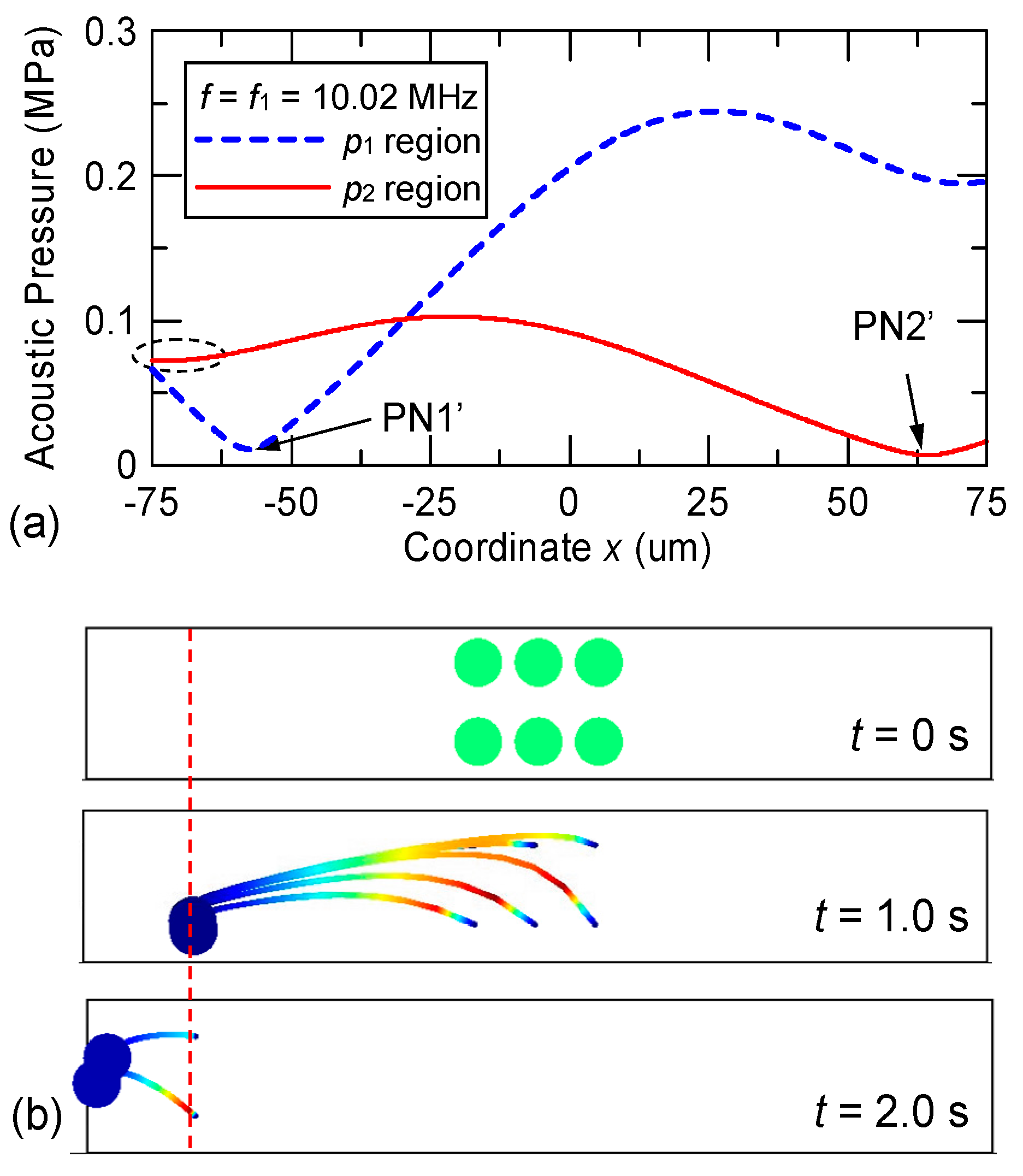
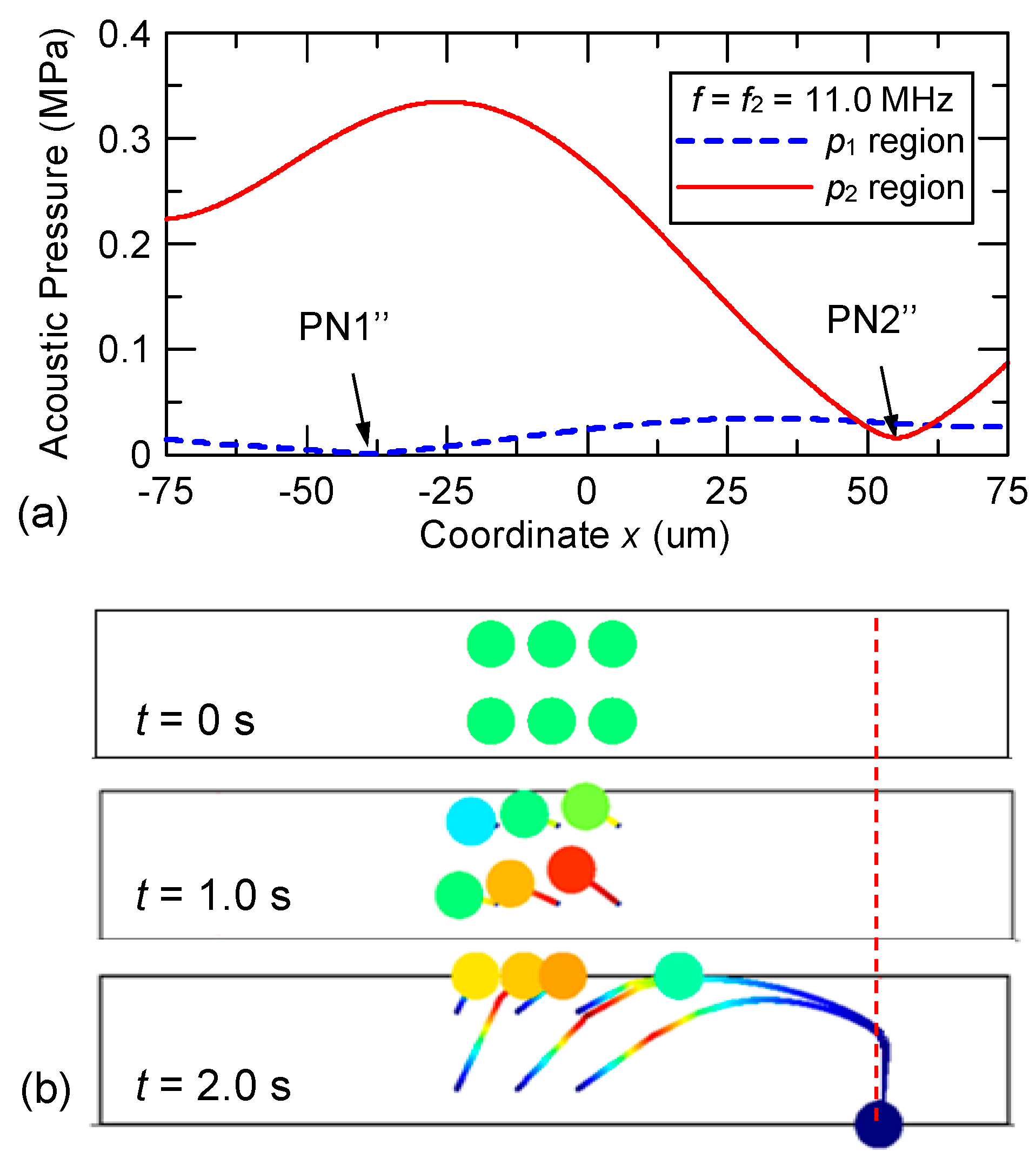
3.1. Design Details, Simulation Results and Discussion
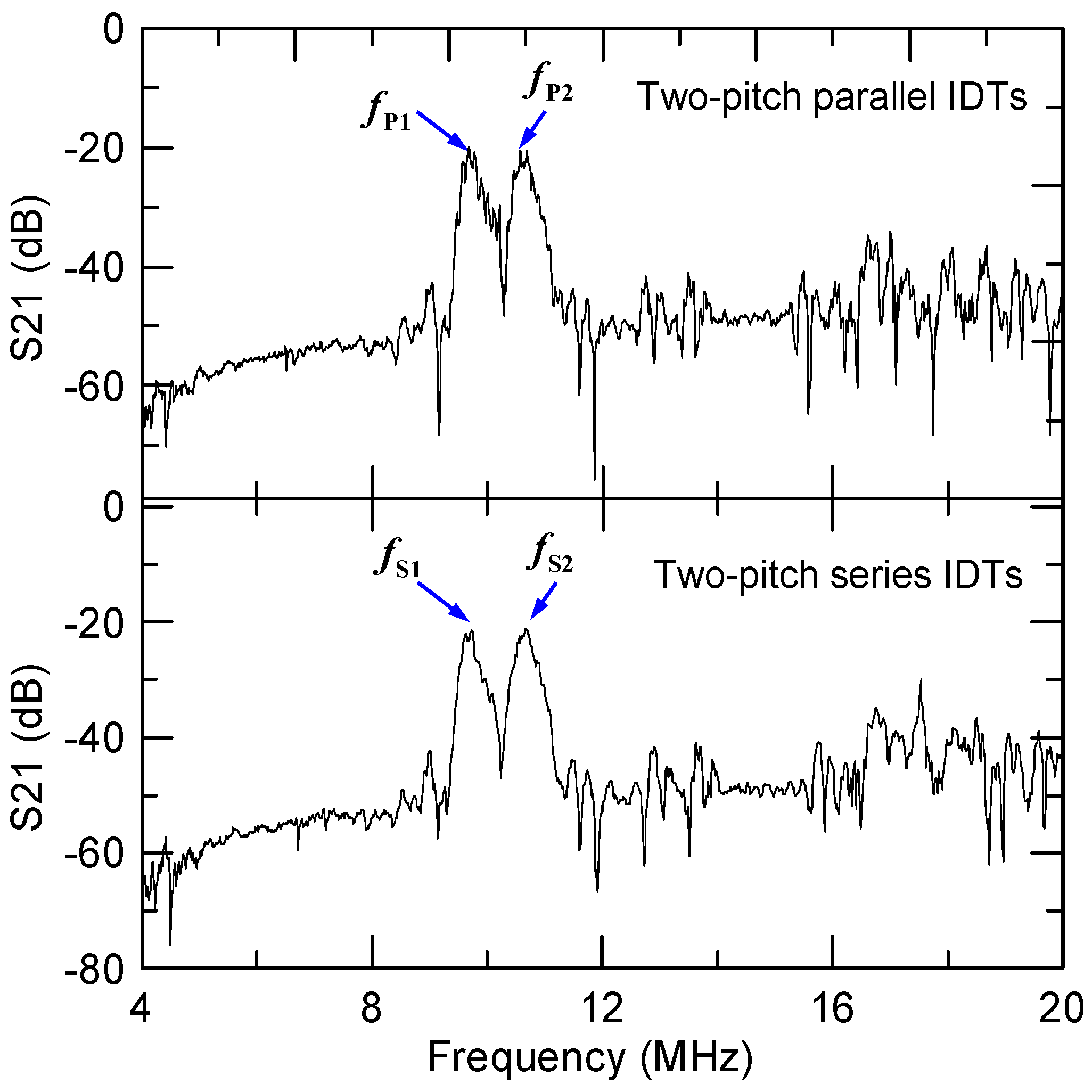
3.2. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Laurell, T.; Petersson, F.; Nilsson, A. Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 2007, 36, 492–506. [Google Scholar] [CrossRef] [PubMed]
- Destgeer, G.; Hyung, J.S. Recent advances in microfluidic actuation and micro-object manipulation via surface acoustic waves. Lab Chip 2015, 15, 2722–2738. [Google Scholar] [CrossRef] [PubMed]
- Friend, J.R.; Yeo, L.Y. Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 2011, 83, 647. [Google Scholar] [CrossRef]
- Endo, A.; Yanagimoto, M.; Asami, T.; Miura, H. Noncontact atomization of droplets using an aerial ultrasonic source with two vibrating plates. Jpn. J. Appl. Phys. 2015, 54, 07HE13. [Google Scholar] [CrossRef]
- Glass, N.R.; Shilton, R.J.; Chan, P.P.; Friend, J.R.; Yeo, L.Y. Miniaturized Lab-on-a-Disc (miniLOAD). Small 2012, 8, 1881–1888. [Google Scholar] [CrossRef] [PubMed]
- Reboud, J.; Auchinvole, C.; Syme, C.D.; Wilson, R.; Cooper, J.M. Acoustically controlled enhancement of molecular sensing to assess oxidative stress in cells. Chem. Commun. 2013, 49, 2918–2920. [Google Scholar] [CrossRef] [PubMed]
- Burguillos, M.A.; Magnusson, C.; Nordin, M.; Lenshof, A.; Augustsson, P.; Hansson, M.J.; Elmér, E.; Lilja, H.; Brundin, P.; Laurell, T.; et al. Microchannel acoustophoresis does not impact survival or function of microglia, leukocytes or tumor cells. PLoS ONE 2013, 8, e64233. [Google Scholar] [CrossRef]
- Tolt, T.L.; Feke, D.L. Separation of dispersed phases from liquids in acoustically driven chambers. Chem. Eng. Sci. 1993, 48, 527–540. [Google Scholar] [CrossRef]
- Mandralis, Z.; Feke, D.L.; Bolek, W.; Burger, W.; Benes, E. Enhanced synchronized ultrasonic and flow-field fractionation of suspensions. Ultrasonics 1994, 32, 113–122. [Google Scholar] [CrossRef]
- Gupta, S.; Feke, D.L.; Manas-Zloczower, I. Fractionation of mixed particulate solids according to compressibility using ultrasonic standing wave fields. Chem. Eng. Sci. 1995, 50, 3275–3284. [Google Scholar] [CrossRef]
- Jung, B.; Fisher, K.; Ness, K.D.; Rose, K.A.; Mariella, R.P., Jr. Acoustic particle filter with adjustable effective pore size for automated sample preparation. Anal. Chem. 2008, 80, 8447–8452. [Google Scholar] [CrossRef] [PubMed]
- Mazzoccoli, J.P.; Feke, D.L.; Baskaran, H.; Pintauro, P.N. Development of multilayered cell-hydrogel composites using an acoustic focusing technique. Biotechnol. Prog. 2010, 26, 600–605. [Google Scholar] [CrossRef] [PubMed]
- Raeymaekers, B.; Pantea, C.; Sinha, D.N. Manipulation of diamond nanoparticles using bulk acoustic waves. J. Appl. Phys. 2011, 109, 014317. [Google Scholar] [CrossRef]
- Greenhall, J.; Guevara Vasquez, F.; Raeymaekers, B. Continuous and unconstrained manipulation of micro-particles using phase-control of bulk acoustic waves. Appl. Phys. Lett. 2013, 103, 074103. [Google Scholar] [CrossRef]
- Greenhall, J.; Guevara Vasquez, F.; Raeymaekers, B. Ultrasound directed self-assembly of user-specified patterns of nanoparticles dispersed in a fluid medium. Appl. Phys. Lett. 2016, 108, 103103. [Google Scholar] [CrossRef]
- Johansson, L.; Evander, M.; Lilliehorn, T.; Almqvist, M.; Nilsson, J.; Laurell, T.; Johansson, S. Temperature and trapping characterization of an acoustic trap with miniaturized integrated transducers—Towards in-trap temperature regulation. Ultrasonics 2013, 53, 1020–1032. [Google Scholar] [CrossRef] [PubMed]
- Nayak, P.P.; Kar, D.P.; Bhuyan, S. Droplets merging through wireless ultrasonic actuation. Ultrasonics 2016, 64, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.H.J.; Soh, H.T. Acoustophoretic sorting of viable mammalian cells in a microfluidic device. Anal. Chem. 2012, 84, 10756–10762. [Google Scholar] [CrossRef] [PubMed]
- Collino, R.R.; Ray, T.R.; Fleming, R.C.; Sasaki, C.H.; Haj-Hariri, H.; Begley, M.R. Acoustic field controlled patterning and assembly of anisotropic particles. Extreme Mech. Lett. 2015, 5, 37–46. [Google Scholar] [CrossRef]
- Leibacher, I.; Reichert, P.; Dual, J. Microfluidic droplet handling by bulk acoustic wave (BAW) acoustophoresis. Lab Chip 2015, 15, 2896–2905. [Google Scholar] [CrossRef]
- Glynne-Jones, P.; Boltryk, R.J.; Harris, N.R.; Cranny, A.W.; Hill, M. Mode-switching: A new technique for electronically varying the agglomeration position in an acoustic particle manipulator. Ultrasonics 2010, 50, 68–75. [Google Scholar] [CrossRef] [PubMed]
- Ito, M.; Sugimoto, S.; Matsui, Y.; Kondoh, J. Study of surface acoustic wave streaming phenomenon based on temperature measurement and observation of streaming in liquids. Jpn. J. Appl. Phys. 2007, 46, 4718. [Google Scholar] [CrossRef]
- Collins, D.J.; Devendran, C.; Ma, Z.; Ng, J.W.; Neild, A.; Ai, Y. Acoustic tweezers via sub–time-of-flight regime surface acoustic waves. Sci. Adv. 2016, 2, e1600089. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.-T.; Chen, Y.-Y. Exact analysis of dispersive SAW devices on ZnO/diamond/Si-layered structures. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 142–149. [Google Scholar] [PubMed]
- Destgeer, G.; Im, S.; Ha, B.H.; Jung, J.H.; Ansari, M.A.; Sung, H.J. Adjustable, rapidly switching microfluidic gradient generation using focused travelling surface acoustic waves. Appl. Phys. Lett. 2014, 104, 023506. [Google Scholar] [CrossRef]
- Shilton, R.J.; Langelier, S.M.; Friend, J.R.; Yeo, L.Y. Surface acoustic wave solid-state rotational micromotor. Appl. Phys. Lett. 2012, 100, 033503. [Google Scholar] [CrossRef]
- Wu, T.-T.; Chang, I.-H. Actuating and detecting of microdroplet using slanted finger interdigital transducers. J. Appl. Phys. 2005, 98, 024903. [Google Scholar] [CrossRef]
- Alzuaga, S.; Ballandras, S.; Bastien, F.; Daniau, W.; Gauthier-Manuel, B.; Manceau, J.F.; Cretin, B.; Vairac, P.; Laude, V.; Khelif, A.; et al. A large scale XY positioning and localisation system of liquid droplet using SAW on LiNbO3. In Proceedings of the IEEE Symposium on Ultrasonics, Honolulu, HI, USA, 5–8 October 2003; Volume 2, p. 1790. [Google Scholar]
- Fukaya, T.; Kondoh, J. Experimental consideration of droplet manipulation mechanism using surface acoustic wave. Jpn. J. Appl. Phys. 2015, 54, 07HE06. [Google Scholar] [CrossRef]
- Oseev, A.; Lucklum, R.; Zubtsov, M.; Schmidt, M.P.; Hirsch, S. SAW based phononic crystal liquid sensor-Periodic microfluidic channels approach. In Proceedings of the IEEE International Symposium on Ultrasonics, Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar]
- Wu, C.H.; Yang, C.-H. Guided waves propagating in a bi-layer system consisting of a piezoelectric plate and a dielectric fluid layer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1612–1618. [Google Scholar]
- Wang, T.; Ke, M.; Qiu, C.; Liu, Z. Particle trapping and transport achieved via an adjustable acoustic field above a phononic crystal plate. J. Appl. Phys. 2016, 119, 214502. [Google Scholar] [CrossRef]
- Destgeer, G.; Ha, B.; Park, J.; Sung, H.J. Lamb wave-based acoustic radiation force-driven particle ring formation inside a sessile droplet. Anal. Chem. 2016, 88, 3976–3981. [Google Scholar] [CrossRef] [PubMed]
- Muller, P.B.; Barnkob, R.; Jensen, M.J.H.; Bruus, H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab Chip 2012, 12, 4617–4627. [Google Scholar] [CrossRef] [PubMed]
- Wiklund, M.; Green, R.; Ohlin, M. Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices. Lab Chip 2012, 12, 2438–2451. [Google Scholar] [CrossRef] [PubMed]
- Nama, N.; Barnkob, R.; Mao, Z.; Kähler, C.J.; Costanzo, F.; Huang, T.J. Numerical study of acoustophoretic motion of particles in a PDMS microchannel driven by surface acoustic waves. Lab Chip 2015, 15, 2700–2709. [Google Scholar] [CrossRef] [PubMed]
- Devendran, C.; Albrecht, T.; Brenker, J.; Alan, T.; Neild, A. The importance of travelling wave components in standing surface acoustic wave (SSAW) systems. Lab Chip 2016, 16, 3756–3766. [Google Scholar] [CrossRef] [PubMed]
- Franke, T.; Abate, A.R.; Weitz, D.A.; Wixforth, A. Surface acoustic wave (SAW) directed droplet flow in microfluidics for PDMS devices. Lab Chip 2009, 9, 2625–2627. [Google Scholar] [CrossRef]
- Laurell, T.; Lenshof, A. Microscale Acoustofluidics; The Royal Society of Chemistry: Cambridge, UK, 2015. [Google Scholar]
- Shi, J.; Ahmed, D.; Mao, X.; Lin, S.C.S.; Lawit, A.; Huang, T.J. Acoustic tweezers: Patterning cells and microparticles using standing surface acoustic waves (SSAW). Lab Chip 2009, 9, 2890–2895. [Google Scholar] [CrossRef] [PubMed]
- Collins, D.J.; Alan, T.; Helmerson, K.; Neild, A. Surface acoustic waves for on-demand production of picoliter droplets and particle encapsulation. Lab Chip 2013, 13, 3225–3231. [Google Scholar] [CrossRef]
- Destgeer, G.; Ha, B.H.; Park, J.; Jung, J.H.; Alazzam, A.; Sung, H.J. Microchannel anechoic corner for size-selective separation and medium exchange via traveling surface acoustic waves. Anal. Chem. 2015, 87, 4627–4632. [Google Scholar] [CrossRef]
- Skowronek, V.; Rambach, R.W.; Schmid, L.; Haase, K.; Franke, T. Particle deflection in a poly (dimethylsiloxane) microchannel using a propagating surface acoustic wave: Size and frequency dependence. Anal. Chem. 2013, 88, 9955–9959. [Google Scholar] [CrossRef]
- Ding, X.; Peng, Z.; Lin, S.C.S.; Geri, M.; Li, S.; Li, P.; Chen, Y.; Dao, M.; Suresh, S.; Huang, T.J. Cell separation using tilted-angle standing surface acoustic waves. Proc. Natl. Acad. Sci. USA 2014, 111, 12992–12997. [Google Scholar] [CrossRef]
- Ren, L.; Chen, Y.; Li, P.; Mao, Z.; Huang, P.H.; Rufo, J.; Gao, F.; Wang, L.; McCoy, J.P.; Levin, S.J.; et al. A high-throughput acoustic cell sorter. Lab Chip 2015, 15, 3870–3879. [Google Scholar] [CrossRef] [PubMed]
- Collins, D.J.; Morahan, B.; Garcia-Bustos, J.; Doerig, C.; Plebanski, M.; Neild, A. Two-dimensional single-cell patterning with one cell per well driven by surface acoustic waves. Nat. Commun. 2015, 6, 8686. [Google Scholar] [CrossRef] [PubMed]
- Orloff, N.D.; Dennis, J.R.; Cecchini, M.; Schonbrun, E.; Rocas, E.; Wang, Y.; Novotny, D.; Simmonds, R.W.; Moreland, J.; Takeuchi, I.; et al. Manipulating particle trajectories with phase-control in surface acoustic wave microfluidics. Biomicrofluidics 2011, 5, 044107. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Huang, Y.-W.; Hsu, C.-H. Transportation control of microfluidic particles using mode switching between surface acoustic waves and plate waves. Jpn. J. Appl. Phys. 2017, 56, 07JD05. [Google Scholar] [CrossRef]
- Ding, X.; Lin, S.C.S.; Lapsley, M.I.; Li, S.; Guo, X.; Chan, C.Y.; Chiang, I.-K.; Wang, L.; McCoy, J.P.; Huang, T.J. Standing surface acoustic wave (SSAW) based multichannel cell sorting. Lab Chip 2012, 12, 4228–4231. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Ding, X.; Guo, F.; Chen, Y.; Lapsley, M.I.; Lin, S.C.S.; Wang, L.; McCoy, J.P.; Cameron, C.E.; Huang, T.J. An on-chip, multichannel droplet sorter using standing surface acoustic waves. Anal. Chem. 2013, 85, 5468–5474. [Google Scholar] [CrossRef] [PubMed]
- Bourquin, Y.; Reboud, J.; Wilson, R.; Cooper, J.M. Tuneable surface acoustic waves for fluid and particle manipulations on disposable chips. Lab Chip 2010, 10, 1898–1901. [Google Scholar] [CrossRef] [PubMed]
- Royer, D.; Dieulesaint, E. Elastic Waves in Soilds; Springer: Berlin, Germany, 2000. [Google Scholar]
- Hsu, J.-C. Switchable frequency gaps in piezoelectric phononic crystal slabs. Jpn. J. Appl. Phys. 2012, 51, 07GA04. [Google Scholar] [CrossRef]
- Guo, J.; Kang, Y.; Ai, Y. Radiation dominated acoustophoresis driven by surface acoustic waves. J. Colloid Interface Sci. 2015, 455, 203–211. [Google Scholar] [CrossRef]
- Liu, W.Y.; Fu, X.T.; Zhang, X.Q. The attenuation of poly(dimethylsiloxane) film to surface acoustic wave on a piezoelectric substrate. Ferroelectrics 2016, 493, 62–68. [Google Scholar] [CrossRef]
- Hahn, P.; Leibacher, I.; Baasch, T.; Dual, J. Numerical simulation of acoustofluidic manipulation by radiation forces and acoustic streaming for complex particles. Lab Chip 2015, 15, 4302–4313. [Google Scholar] [CrossRef] [PubMed]
- Gor’kov, L.P. On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys. Doklady 1962, 6, 773. [Google Scholar]
- Settnes, M.; Bruus, H. Forces acting on a small particle in an acoustical field in a viscous fluid. Phys. Rev. E 2012, 85, 016327. [Google Scholar] [CrossRef] [PubMed]
- Barnkob, R.; Nama, N.; Ren, L.; Huang, T.J.; Costanzo, F.; Kähler, C.J. Acoustically driven fluid and particle motion in confined and leaky systems. Phys. Rev. Appl. 2018, 9, 014027. [Google Scholar] [CrossRef]
- Koklu, M.; Sabuncu, A.C.; Beskok, A. Acoustophoresis in shallow microchannels. J. Colloid Interface Sci. 2010, 351, 407–414. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Multiphysics. Available online: www.comsol.com (accessed on 13 January 2019).
- Winkler, A.; Brünig, R.; Faust, C.; Weser, R.; Schmidt, H. Towards efficient surface acoustic wave (SAW)-based microfluidic actuators. Sens. Actuators A Phys. 2016, 247, 259–268. [Google Scholar] [CrossRef]
- Ng, J.W.; Devendran, C.; Neild, A. Acoustic tweezing of particles using decaying opposing travelling surface acoustic waves (DOTSAW). Lab Chip 2017, 17, 3489–3497. [Google Scholar] [CrossRef]
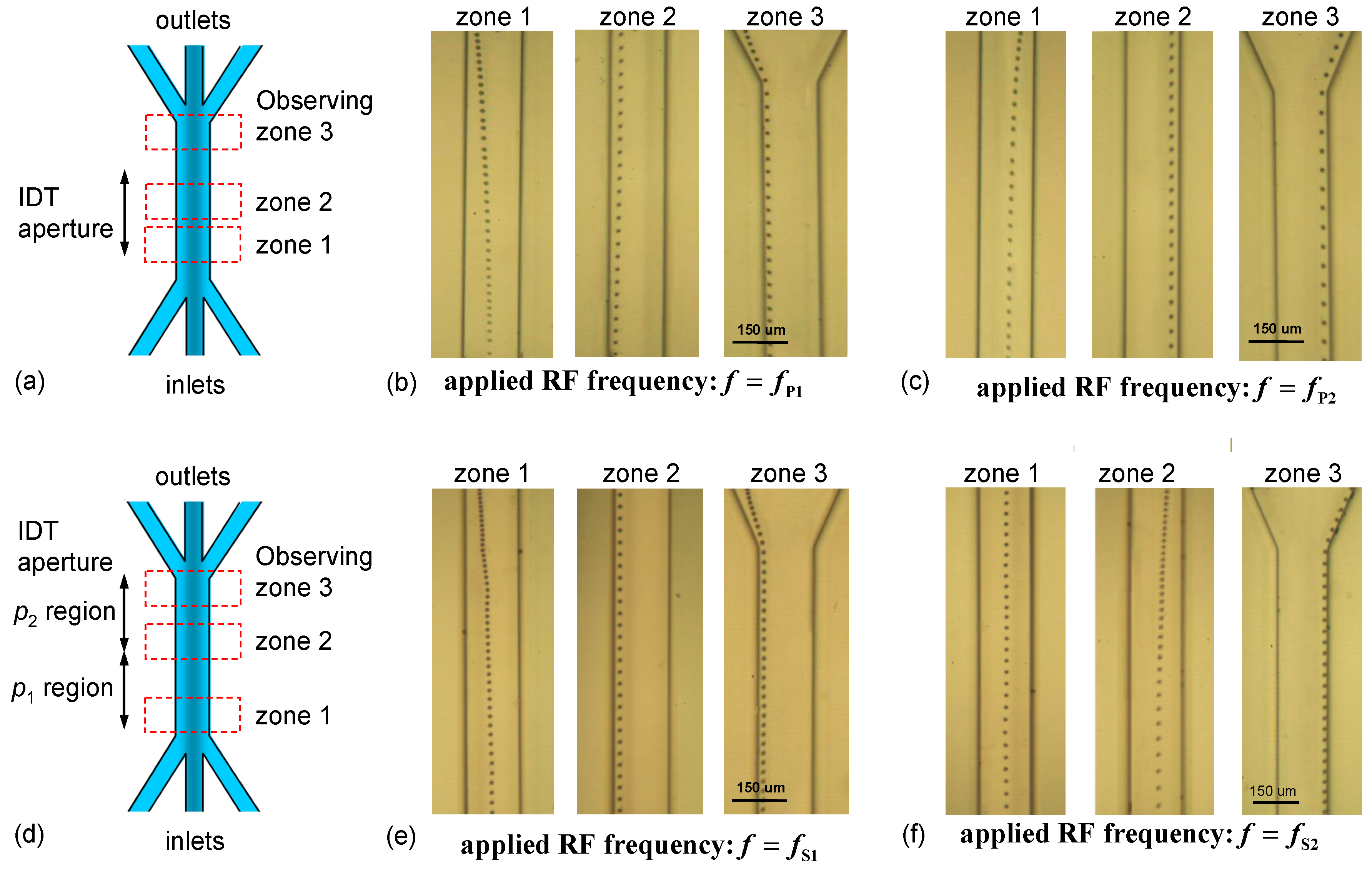
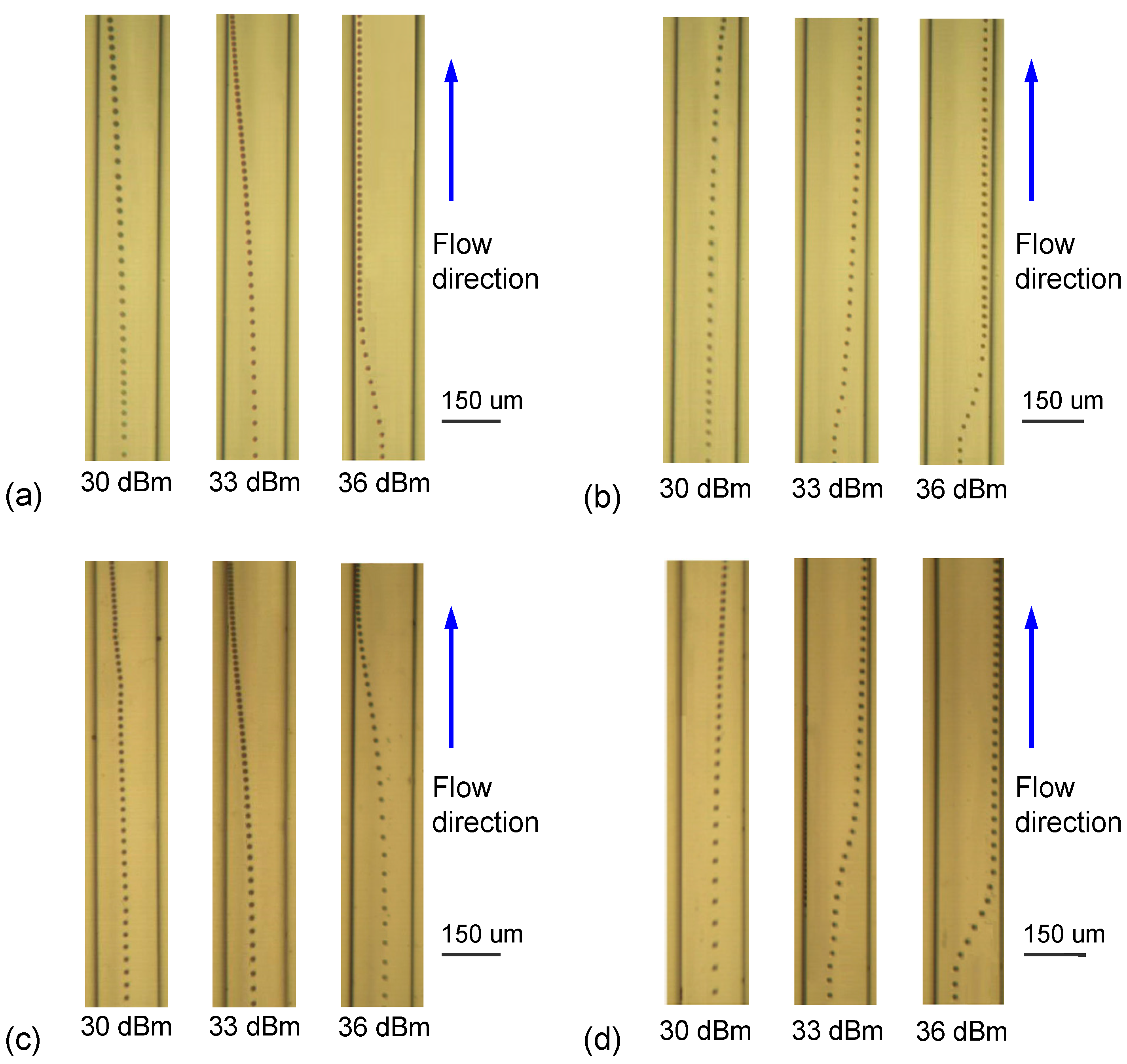
| IDT Design | Parallel | Series | |
|---|---|---|---|
| Pitch (μm) | p1 | 398 | 398 |
| p2 | 363 | 363 | |
| Aperture (μm) | w1 | 2000 | 2000 |
| w2 | 2000 | 2000 | |
| Number of Pairs (p1 and p2) | 20 + 20 | 20 + 20 | |
| Delay Length (μm) | D1 + δ1 | 18,010 | 2886 |
| D2 + δ2 | 3357 | 3357 | |
| Right-Side IDT Translation (μm) | δ1 | 25 | 25 |
| δ2 | –29 | –29 |
| LiNbO3 [52] | Value | Unit | |
|---|---|---|---|
| Elastic Constants | 20.3 | 1010 N/m2 | |
| 5.3 | |||
| 7.5 | |||
| 24.5 | |||
| 6.0 | |||
| 0.9 | |||
| Piezoelectric Constants | e15 | 3.7 | C/m2 |
| e22 | 2.5 | ||
| e31 | 0.2 | ||
| e33 | 1.3 | ||
| Permittivity | 38.9 | 10−11 F/m | |
| 25.7 | |||
| Mass Density | ρLN | 4700 | kg/m3 |
| PDMS [54] | |||
| Speed of Sound | cPDMS | 1000 | m/s |
| Mass Density | ρPDMS | 970 | kg/m3 |
| Attenuation Coefficient | αPDMS | 947 | Np/m |
| Water [34] | |||
| Speed of Sound | cf | 1495 | m/s |
| Mass Density | ρf | 998 | kg/m3 |
| Attenuation Coefficient | αf | 4.22 | Np/m |
| Dynamic Viscosity | η | 0.893 | mPa·s |
| Polystyrene [34] | |||
| Speed of Sound | cp | 2350 | m/s |
| Mass Density | ρp | 1050 | kg/m3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, J.-C.; Hsu, C.-H.; Huang, Y.-W. Acoustophoretic Control of Microparticle Transport Using Dual-Wavelength Surface Acoustic Wave Devices. Micromachines 2019, 10, 52. https://doi.org/10.3390/mi10010052
Hsu J-C, Hsu C-H, Huang Y-W. Acoustophoretic Control of Microparticle Transport Using Dual-Wavelength Surface Acoustic Wave Devices. Micromachines. 2019; 10(1):52. https://doi.org/10.3390/mi10010052
Chicago/Turabian StyleHsu, Jin-Chen, Chih-Hsun Hsu, and Yeo-Wei Huang. 2019. "Acoustophoretic Control of Microparticle Transport Using Dual-Wavelength Surface Acoustic Wave Devices" Micromachines 10, no. 1: 52. https://doi.org/10.3390/mi10010052
APA StyleHsu, J.-C., Hsu, C.-H., & Huang, Y.-W. (2019). Acoustophoretic Control of Microparticle Transport Using Dual-Wavelength Surface Acoustic Wave Devices. Micromachines, 10(1), 52. https://doi.org/10.3390/mi10010052






