1. Introduction
Approximately 10% of the global population is affected by end-stage kidney disease (ESKD). Unfortunately, worldwide, only 2.5 million people annually will receive renal replacement therapy [
1,
2], such as hemodialysis, to clear uremic toxins in the blood. According to the European Union Toxin (EUTox) database, a uremic toxin is a food and drug organic metabolite in the bloodstream that needs to be removed from the blood circulation. However, if these uremic toxins remain in the bloodstream, the patient will suffer from a number of complications, including, but not limited to, cardiovascular disease, anemia, and progressive kidney failure [
3,
4,
5]. Uremic toxins are subdivided into three main categories according to their size and binding ability: (1) water-soluble (and non-protein bound; MW < 500 Da); (2) middle molecule (MW > 500 Da); (3) protein-bound uremic toxins (PBUTs) (MW < 500 Da). Hemodialysis falls short as a treatment since it only reproduces the glomerulus’ filtration function in removing water-soluble, some middle molecules, and not yet bound uremic toxins. The latter are not effectively cleared since they are too big to be removed via ultrafiltration once bound to albumin (MW > 65 kDa). Indeed, in normal physiological conditions, PBUTs are removed by active transport in the proximal tubule (PT). Therefore, to improve the effectiveness of hemodialysis, the functionality of the proximal tubule also needs to be mimicked.
Significant experimental strides have been made toward fabricating a bioartificial kidney (BAK) using hemodialysis hollow fibers populated with PT cells, e.g., genetically modified conditional immortalized proximal tubule cells expressing organic anionic transporter-1 (ciPTECs-OAT1) [
6,
7]. More specifically, PT cells create a solute barrier via the formation of tight junctions between adjacent cells. PT cells are well coordinated to be uniformly polarized along their basolateral (blood capillary side) and apical (urine/PT luminal side) membranes. In addition, both membrane surfaces have specific transporters to move unwanted solutes against the concentration gradient. These transporters include anti-porters, co-transporters, efflux pumps, and exchangers [
8]. Considering the multitude of transporters and solute interactions and non-obvious kinetic influences on toxin clearance, computational models can support the research and design improvements to BAKs by providing a quantitative framework to model the combinatorial solute–transporter interactions. Moreover, the research performed to optimize BAKs can be accelerated at a reduced experimental cost by coupling experimental and computational models.
Computational models have been used throughout organ-on-chip and pharmacokinetic research and applied to understand physiological nephron function, including the influence of osmosis-driven and gradient-driven water reabsorption in the proximal tubule [
9]; the effect of tubuloglomerular feedback dynamics on solute clearance by coupling a single nephron model [
10]; and the effect of apical flow on water-soluble transport in single and coupled nephrons [
10]. Other computational models have focused on replicating the transporter membrane interactions that influence the clearance of uremic toxins and solutes. For example, Layton used the available parameters from rat renal physiological models and made appropriate scaling-up assumptions for the transporter numbers in human models to investigate the effect of flow on transporter density [
11]. Refoyo et al. developed a computational model to replicate an experimental model of the function of ciPTECs-OAT1cultured on a dialysis hollow fiber with constant indoxyl sulfate perfusion [
12]. They were able to validate their model by matching their clearance rates with experiments [
6]. However, all the models mentioned above lumped the transporter function and the transporter density together into a general inward flux. This assumption leads to a reduction in information on the influence and importance of the transporters on uremic toxin clearance and limits the use of models to investigate the combinatorial solute–transporter interactions.
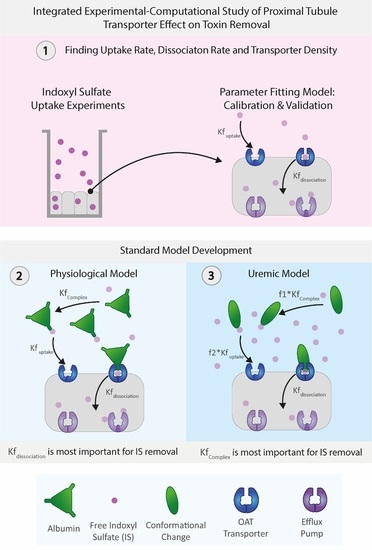
Building on these modeling works, in this integrated experimental–computational study, we developed a proximal tubule computational model focusing on the organic anionic transporter 1 (OAT1) transporting indoxyl sulfate (IS, an anionic protein-bound uremic toxin), capturing in detail the transporter density along the basolateral cell membrane as well as the activity of the transporter. The model’s unknown parameters (i.e., the transporter density, transporter uptake, and dissociation rates) were determined through dedicated experiments of indoxyl sulfate uptake of ciPTECs-OAT1 monolayers in tissue culture well plates. A more physiologically relevant model was developed by including albumin interaction with IS in both healthy and uremic conditions (including and excluding albumin conformational changes). As such, the proposed computational model provides an exciting avenue to help understand the toxin–transporter intricacies in the PT and make better-informed decisions on BAK designs.
3. Discussion
It is a non-trivial task to design an effective renal replacement therapy with functional PT cell cultures. However, understanding the intricate transporter–toxin interactions, quantifying the functional transport density, and replicating the conformational changes of carrier proteins, such as albumin in the system, can guide researchers as to the essential parameters that can increase toxin removal from a uremic patient. In this study, we developed a computational model that defines the basolateral cell membrane of the PT as an inward boundary flux that incorporates the transporter density, transporter uptake, and dissociation rate as main parameters for indoxyl sulfate (IS) removal. The computational model was fitted and validated with reliable experimental time-series data of IS uptake in a well plate.
We found that the computational model can accurately replicate the OAT1 function and IS transport by modeling the IS uptake boundary condition as mass action kinetics using
as a constant, where case 1 was the most reliable function of the uptake boundary condition, which was followed closely by modeling
as the Michalis–Menten function (case 3). The model parameters operated at the saturation level, which can be seen in
Figure 2c–f, where increasing the parameters has minimal effect on the IS removal. The transporter density is higher than what was reported for other cell lines [
15], but this is a reasonable value, since the model represents uptake by the genetically modified cell line that overexpresses OAT1 [
16].
The advantage of implementing the boundary condition that decouples the OAT1 density and function (
,
) was that we could investigate the transporter parameters’ sensitivities on the removal of IS in various conditions. It was seen that the standard model is influenced mainly by the uptake rate of IS from the transporter. It was evident that the standard model operates in excess albumin from
Figure 3c, where there was 0% sensitivity and no effects on IS removal with a significant change in the albumin concentration. These results suggest there was sufficient albumin in a healthy and uremic patient, such that the albumin concentration (without conformational changes) was not a limiting factor for IS removal.
When investigating the physiological and uremic conditions, it was evident that they operate in excess albumin and transporter density. The albumin concentration and binding were similar in the physiological condition (2.5 µM) and uremic concentration (180 µM). The models were functioning at transporter density saturation, and increasing the transporter density beyond 1.15 × 107 transporters µm−2 had a minimal effect on IS removal. The notable difference between the physiological and uremic concentrations was the time taken to remove IS entirely from the system (17.5 and 35 h, respectively). The uptake rate and transporter density equally limit the removal of IS in the physiological condition. In contrast, the transporter density and dissociation rate dominated the uremic condition without conformational changes, while the transporter density, uptake rate, and albumin binding rate dominated the uremic condition with conformational changes.
Research has shown that albumin undergoes conformational changes, mainly glycation, which altered the IS binding characteristics [
7,
17,
18,
19] and reduced its removal from the system by 85% [
7]. The Uremic model captured these conformational changes using a reduction factor on the association function of IS to albumin (
) and the IS uptake rate (
. Transporter density appeared to be the least sensitive parameter, and research efforts should not be put toward increasing the transporter density if there were more than 1.15 × 10
7 transporters µm
−2 present along the cell membrane. To understand the best approach in optimizing IS removal in uremic patients, the above results implied that experimentalists should focus on (1) investigating the role of albumin in toxin removal during dialysis sessions; (2) investigating physical, electrical, or chemical stimuli for increasing IS dissociation rate from the OAT1 [
20]; and (3) quantifying the functional transporter density of the basolateral epithelial membrane.
Although the model was calibrated using experimental data, there were a few notable limitations of the model. First, the experiments were performed with a genetically modified cell line (ciPTECs-OAT1). Future experiments should include isolated proximal tubule cells to investigate transporter density variability among donor patients. Second, the model only replicates the interaction with IS and OAT1, which was a grand oversimplification of the in vitro and in vivo situation where there are over 400 genetically identified epithelial transporters and more than 130 uremic toxins [
8]. However, the computational model safely assumed that the OAT1 was responsible for most IS transport on the basolateral membrane since the previous laboratory experiments measured a 7–10-fold decrease in IS binding affinity to other transporters such as OAT3 [
7]. As such, the model does not account for toxin–toxin interactions or their competition for the same transporter and binding site. Third, the model also focused on the small-scale kinetics occurring in well plate volumes and excluded reacting species (albumin, IS, or OAT1) production and degradation. In order to upscale the model to replicate the BAK, the complexity of the model’s geometry would need to increase, including the flow and potential effects thereof on the transporter density, IS uptake, and dissociation rates. Finally, the laboratory experiments were performed in the absence of albumin, although there was evidence that albumin increases the clearance of IS in the bioartificial kidney (BAK) [
6,
7].
Additionally, the half-maximal inhibitory concentration (IC50) value of IS binding to OAT1 was reported in the presence of fluorescein and should be conducted with an incremental increase of IS to 500 µM. The uremic milieu and the large medication load that CKD patients were prescribed may lead to drug–toxin and toxin–toxin interactions, further complicating modeling the transporter functioning [
21]. Therefore, the performance of the BAK, which relies on the excretory capacity of ciPTECs-OAT1, could be compromised in vivo. Understanding the drug–toxin and toxin–toxin interactions and the alterations in drug pharmacokinetics would be a step forward toward adequate polypharmacy adjustment in CKD patients. With these limitations in mind, we suggest that future work should focus on obtaining time-series experimental data of the uptake of IS in the presence of albumin, basolateral flow, and uremic plasma to extend the model proposed in this study.
4. Conclusions
To conclude, we have developed a computational model with an inward flux boundary condition that models the individual effects of (OAT1) transporter density, toxin (IS) uptake, and dissociation rate in the basolateral cell membrane that was fitted accurately and validated with the experimental results of IS uptake by a ciPTECs-OAT1 monolayer. The standard model allows investigation of the individual influences of the IS uptake rate (, the dissociation rate of IS into the cell monolayer and the initial density of OAT1 on the basolateral cell membrane (). The standard model results suggested that IS removal was influenced mainly by the transporter density and IS uptake rate by the OAT1 and not by the initial albumin concentration as the model operated with excess albumin (1 mM). Additionally, the model was expanded to include albumin-binding effects in physiological and uremic conditions by altering the binding affinities of IS to albumin, resulting in the development of a uremic patient model including albumin conformational changes. In this scenario, the transporter density, IS uptake rate, and albumin binding became the most influential parameters on IS removal. By coupling computational and experimental data, the models developed within this study can be confidently considered to be a good representation of the IS transport processes in the proximal tubule by OAT1, within the limitations specified. Thus, the results of this study provide an exciting avenue to help understand the toxin–transporter intricacies in the PT and make better-informed decisions on BAK designs.
5. Materials and Methods
The computational models, i.e., a parameter-fitting model and the standard model, were developed in combination with the experimental setup described below. OAT1 was selected as the transporter of interest, considering the availability of a stable cell line that expresses the transporter in culture [
16]. Indoxyl sulfate was selected as the uremic toxin of interest, since it is a protein-bound uremic toxin commonly transported by
and has detrimental effects in uremic patients [
3,
6,
22]. The parameter-fitting model was a two-compartment model that was used to fit the unknown parameters of IS uptake rate by OAT1 from the well plate (
the dissociation rate of IS into the cell monolayer
, and the initial concentration of OAT1 on the basolateral cell membrane (
), based on the IS experimental data (see
Table 2). All parameter values and geometries used in the model are displayed in
Table 2.
All computational modeling work was performed in the Virtual Cell Alpha 7.2.0 open-source systems biology platform developed at the University of Connecticut, Farmington, Connecticut [
22].
5.1. Parameter-Fitting Model of Indoxyl Sulfate (IS) Transport
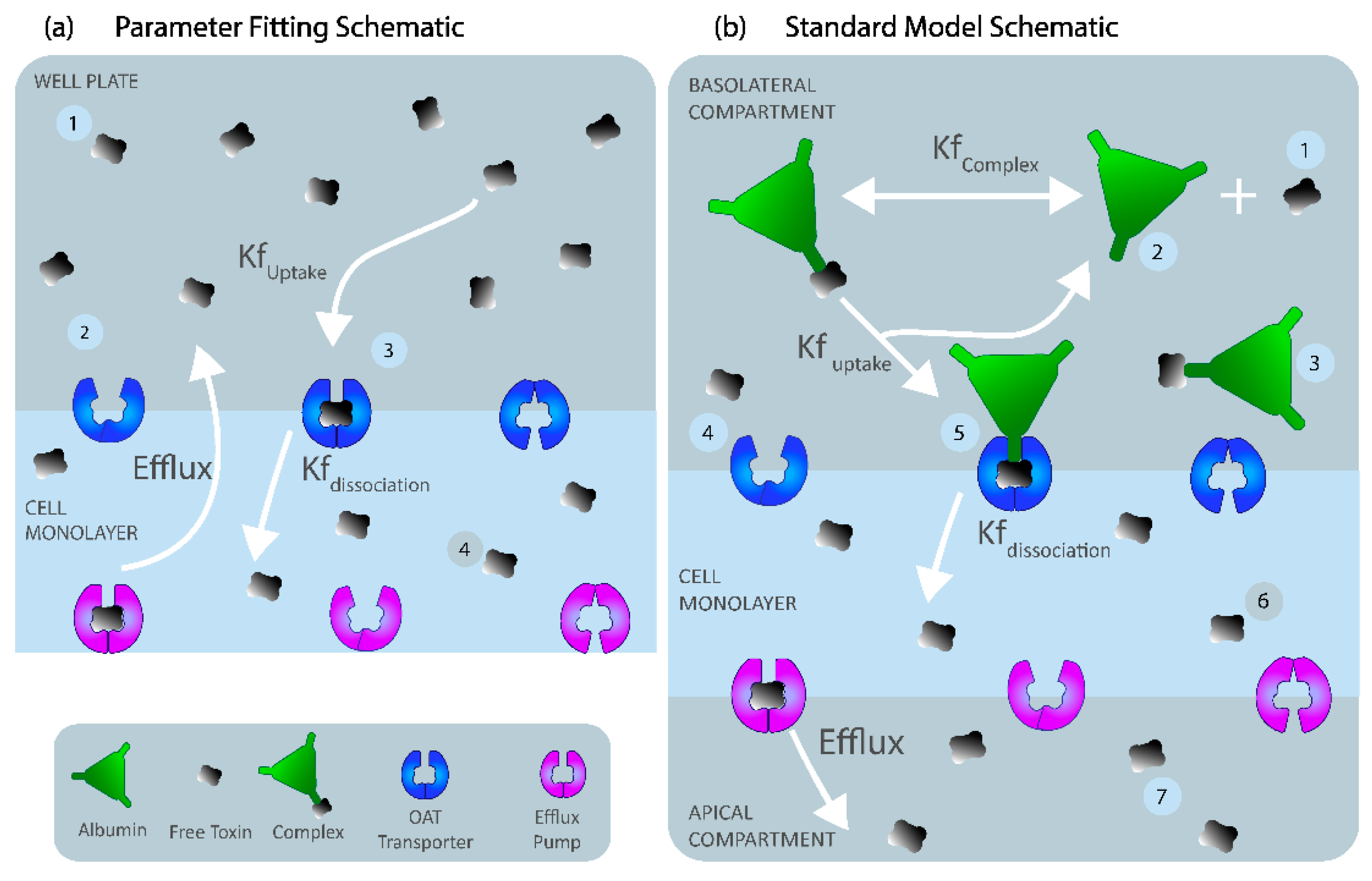
The parameter-fitting model of IS was developed to reflect the experimental time-series experiments of IS uptake in well plates (described in 5.7.
Experimental Work below). The ‘well-mixed’ (uniform distribution of species) two-compartment model was developed with the basolateral cell membrane separating the well plate volume and cell cytoplasm (
Figure 6a). The compartments were modeled with a volume of 100 µL (size blood) and a monolayer compartment volume of 3.2 × 10
8 µm
3 (size basolateral) with a cell membrane surface area of 0.32 cm
2 (size membrane), corresponding to a standard 96-well plate setting (see
Table 2 for parameter values). OAT1 was modeled using two-step mass action binding kinetics within the basolateral membrane to replicate IS uptake rate by the transporter (
and the intracellular dissociation rate of IS
(
Figure 6a). These mass action binding kinetics resulted in the best fit of the experimental data (see Section “Selecting the
function” below). The Breast Cancer Resistance Protein transporter (BCRP) efflux function was modeled as a Michaelis–Menten reaction within the apical membrane. BCRP is a known IS efflux transporter expressed on the apical membrane of the ciPTECs-OAT1 cell line [
25,
26]. We assume that the total amount of transporters and indoxyl sulfate was constant throughout the experiment (closed system). Moreover, since there was no albumin in the medium experimentally, we ignore the influence of albumin-IS binding in the parameter-fitting model to have a closer resemblance to the experimental setup. Equations (1)–(4) represent the system of ODEs describing the IS parameter-fitting model. The code of the IS parameter-fitting model can be found in the Virtual Cell database as “0D_IS_only”. The models were simulated to match the experimental sampling every 0.5 s within a timeframe of 45 min using Virtual Cell’s Combined Stiff Solver (IDA/CVODE) with a tolerance of 1 × 10
−9.
where
u represents the conversion factor of the membrane reacting species to relate the cytosolic (volumetric) concentrations to the membrane concentrations:
conversion factor ,
with Avogadro’ s constant .
The unknown parameters in the system of equations (
and
and the total OAT1 transporter density
) were fitted in the mathematical model using the experimental LC-MS/MS time-series data of intracellular concentration (
) when
= 25 µM measured at 1, 2, 5, 10, 15, 20, 25, 30, and 45 min (
n = 6). The model was subsequently validated by the 25, 50, 100, and 500 µM LC-MS/MS data points at 1, 2, 5, 10, 15, 20, 25, 30, and 45 min (
n = 6). The RMSE was used to quantify and compare how good the fit was for each function. In particular, the parameter-fitting model was solved for different values of
and
and the total OAT1 transporter density
to minimize the difference between the predicted and measured IS concentration inside the cell monolayer at seven different time points. For this, we used the
Evolutionary Programming solver supported by COPASI (Virginia Tech, Blacksburg, VA, USA,
http://copasi.org/, accessed on 18 September 2021). Evolutionary programming is a method to find the parameter values that result in the best fit of the experimental data and was inspired by the evolutionary theory of reproduction and selection. The first fitted values for the selected parameters (individual) asexually reproduce with one of the replicates undergoing a
mutation or a slight alteration (competitor). The individual and the competitor compete, and the algorithm counts the number of times the individual outperforms the competitor. The individual results were ranked based on the number of wins, and the worst-fitted results were discarded, leaving the best fit/solution. The settings selected for COPASI are in
Table 3, including the upper and lower limits of the fitting model. The parameter-fitting model was fitted three times with an increased number of runs to ensure the fitted parameter values (
and
and
OAT1) had an error smaller than 1 × 10
−6.
5.2. Selecting the Function
Importantly, not only were the toxin transport parameters (
and
) and the total OAT1 transporter density (
) unknown, it was also unclear which type of kinetics describes the toxin transport best. In order to investigate this, we fitted the IS uptake rate by OAT1 (
) for various types of kinetics with increased complexity. More specifically, the parameter-fitting model was adjusted to have four cases of IS uptake (
: (1)
was a constant; (2) total membrane flux was lumped as Michaelis–Menten equations (3); and (4) there were two variations of the Michaelis–Menten equation. The COPASI parameter-fitting settings are specified in
Table S2 in the Supplementary Materials.
The best was selected based on the lowest root mean square error when compared among the four cases described in Equations (5)–(8) with = 4.181 × 10−4 s−1 and = 1.15 × 107 molecules µm−2.
5.3. Root Mean Square Error (RMSE)
The root mean square error was calculated, as shown in Equation (9), to evaluate the intracellular indoxyl sulfate (IS) best-fit curve with the experimental data. The RMSE was evaluated at 25, 50, 100, and 500 µM of IS’s initial concentration in the well plate at times 1, 2, 5, 10, 15, 20, 25, 30, and 45 min.
where
concentration of IS at time i of the in vitro experiment,
concentration of IS at time i of the simulation,
= total number of data points,
= data point corresponding to the time of measurement
5.4. Standard Model
For the standard model, we assumed similar kinetics as the parameter-fitting model with albumin. IS must initially bind to albumin to form a complex to interact with the transporter (OAT1). Once the IS–albumin complex binds to OAT1, albumin was returned to the blood compartment, and IS was transported into the cell (illustrated in
Figure 6b). The standard model was considered to be a closed system with no generation of IS or OAT1. OAT1 was assumed to be evenly distributed along the membrane length. The standard model was simplified to an ODE system with seven reacting species to simulate a boundary influx with a two-step IS binding with the OAT1 transporter at the basolateral cell membrane and a Michaelis–Menten efflux boundary condition on the apical cell membrane to represent IS transport by the BCRP into the apical compartment (see
Figure 6b). The initial conditions and parameter settings, determined from the literature and the parameter fitting model, are represented in
Table 2. The model was simulated using Equations (10)–(16).
Similar to the experimental and fitting setup, the standard model has the same compartment geometries and thus volumes as the fitting model to reduce size effects on the simulation, resulting in three compartments: blood (100 µL), cell monolayer (3.2 × 108 µm3), and dialysate (100 µL). Both basolateral and apical membranes (0.32 cm2) were modeled as interfaces between the blood and cell compartments and the cell and dialysate compartments, respectively.
The standard model was simulated until there was complete removal of indoxyl sulfate (17.5 h) using a Virtual Cell’s Combined Stiff Solver (IDA/CVODE) with a tolerance of 1 × 10
−9, sampling every 50 s. The standard model used the fitted parameters,
and
and OAT1 from the IS parameter fitting model. The standard model code can be found in the Virtual Cell database as “0D_Full_3Compartment_ IS” (University of Connecticut, Farmington, Connecticut [
22]).
Note that we modeled various albumin conditions ranging from scenarios with 1 mM albumin (standard model—
Section 5.4, physiological condition and uremic condition—
Section 5.6) or without albumin (for the parameter-fitting model, since the experiments were performed in the absence of albumin—
Section 5.1).
where,
5.5. Sensitivity Analysis
A sensitivity analysis was performed on the standard model where the individual parameter values were altered to investigate which parameter was most influential on the IS concentration in the dialysate (
). The sensitivity analysis was performed for the transporter density (
), uptake (
) and dissociation rate (
), albumin concentration (
,) and albumin-binding rate (
) to IS using Equation (17). A total of 17.5 h was chosen as the end time point for the standard and uremic models as it was the time taken for the complete removal of IS in the standard model.
where
= IS in the dialysate using the standard model at 17.5 h
IS in the dialysate at + or − 20% of the standard model parameter values at 17.5 h
varied parameter
standard model parameter value
5.6. Developing a Uremic Model
The standard model was adapted to account for physiological (
) and uremic (
concentrations. The effect of albumin conformational changes was included in the uremic condition model to investigate the uremic patient condition further. The binding coefficients of IS to albumin (
and uptake rate (
were multiplied by a reducing factor f1 and f2, respectively, to mimic these albumin conformational changes in uremic conditions. A parameter scan was performed to find the best parameter set of f1 and f2 to result in an 85% reduction of IS [
7] removal when compared to the model with no conformational changes at 17.5 h.
5.7. Experimental Work
5.7.1. Cell Culture of CiPTECs-OAT1
Conditionally immortalized proximal tubule epithelial cells obtained from urine samples of healthy volunteers and overexpressing the organic anion transporter 1 (ciPTECs-OAT1) were cultured as described by Nieskens et al. [
25]. Cells were seeded at a density of 63,000 cells/cm
2, cultured at 33 °C to allow expansion, then cultured for 7 days at 37 °C for differentiation and maturation. Cells were cultured using Dulbecco’s modified eagle medium (DMEM HAM’s F12, Life Technologies, Paisly, UK), 5 μg/mL insulin, 5 μg/mL transferrin, 5 μg/mL selenium, 35 ng/mL hydrocortisone, 10 ng/mL epidermal growth factor (EGF), 40 pg/mL tri-iodothyronine (Sigma-Aldrich, Zwijndrecht, The Netherlands), and 10% fetal calf serum (FCS, Greiner Bio One, Kremsmuenster, Austria).
5.7.2. Exposure to IS
To determine the time-dependent OAT1-mediated intracellular uptake of IS, mature monolayers of ciPTECs-OAT1 were incubated with IS (25, 50, 100, and 500 μM prepared in Krebs–Henseleit buffer (Sigma-Aldrich, Zwijndrecht, The Netherlands) supplemented with HEPES (10 mM, Sigma-Aldrich, Zwijndrecht, The Netherlands, pH 7.4) for variable periods of time. Uptake was stopped by washing one time with ice-cold HBSS (Life Technologies Europe BV, Roskilde, Denmark), and then, the cells were lysed by 100 µL 0.1M NaOH for 10 min at room temperature and under mild shaking. The intracellular IS concentration was determined in the cell lysate by LC-MS/MS, as described below.
5.7.3. Intracellular Detection of IS
Reagents
IS potassium salt and isotope-labeled IS potassium salt (13C6, 99%) as internal standard were purchased from Sigma-Aldrich (Zwijndrecht, The Netherlands) and Cambridge Isotope Laboratory (Tewksbury, Massachusetts, USA), respectively. Water (U°LC-MS grade), acetonitrile (HPLC-S grade), and methanol (HPLC grade) were purchased from Biosolve (Valkenswaard, The Netherlands). Formic acid (analytical grade) was obtained from Merck (Darmstadt, Germany). Ultrapure water was produced by a Milli-Q® Advantage A10 Water Purification Systems (Merck, Amsterdam, The Netherlands).
Equipment
The LC-MS/MS system consisted of a DGU-14A degasser, a CTO-10Avp column oven, a Sil-HTc autosampler, and two LC10-ADvp- pumps (Shimadzu, Kyoto, Japan) and a Finnigan TSQ Quantum Discovery Max triple quadrupole mass spectrometer with electrospray ionization (Thermo Electron, Waltham, MA, USA). The Xcalibur software (version 1.4, Thermo Electron) was used to record and process the data.
Sample Pre-Treatment
The cell lysate underwent the protein precipitation procedure. About 20 μL of cell lysate was crushed by 80 μL of protein precipitant containing 0.5 µg/mL of internal standard, which was followed by vortexing for 2 min and centrifuging for 2 min at 1000 rpm. After that, 64 µL of supernatant was collected in 1 mL round-bottom wells of a polypropylene 96-deep well plate and diluted with 200 µL of ultrapure water. Finally, the plate was gently shaken before placing it in the autosampler for LC-MS/MS analysis.