Interactions between Triterpenes and a P-I Type Snake Venom Metalloproteinase: Molecular Simulations and Experiments
Abstract
:1. Introduction
2. Results and Discussion
2.1. Inhibition of Batx-I Activity
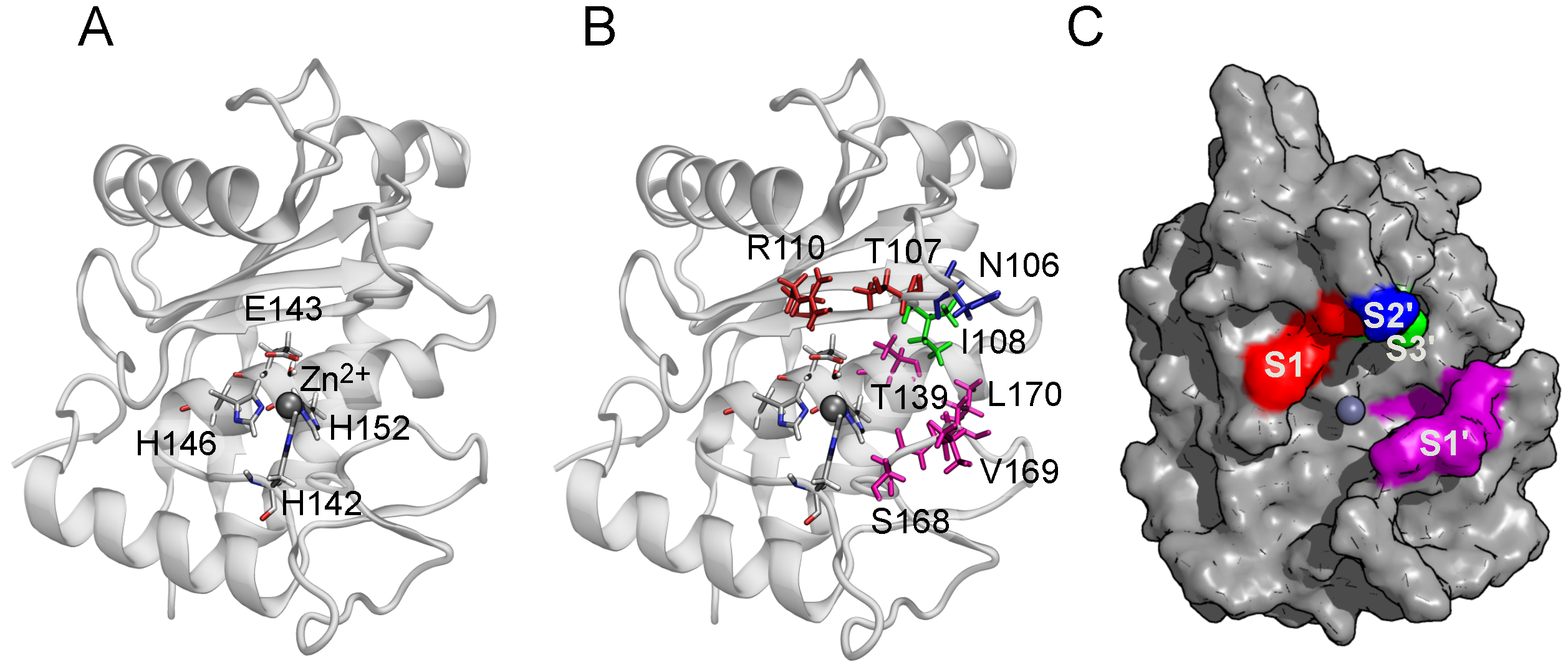
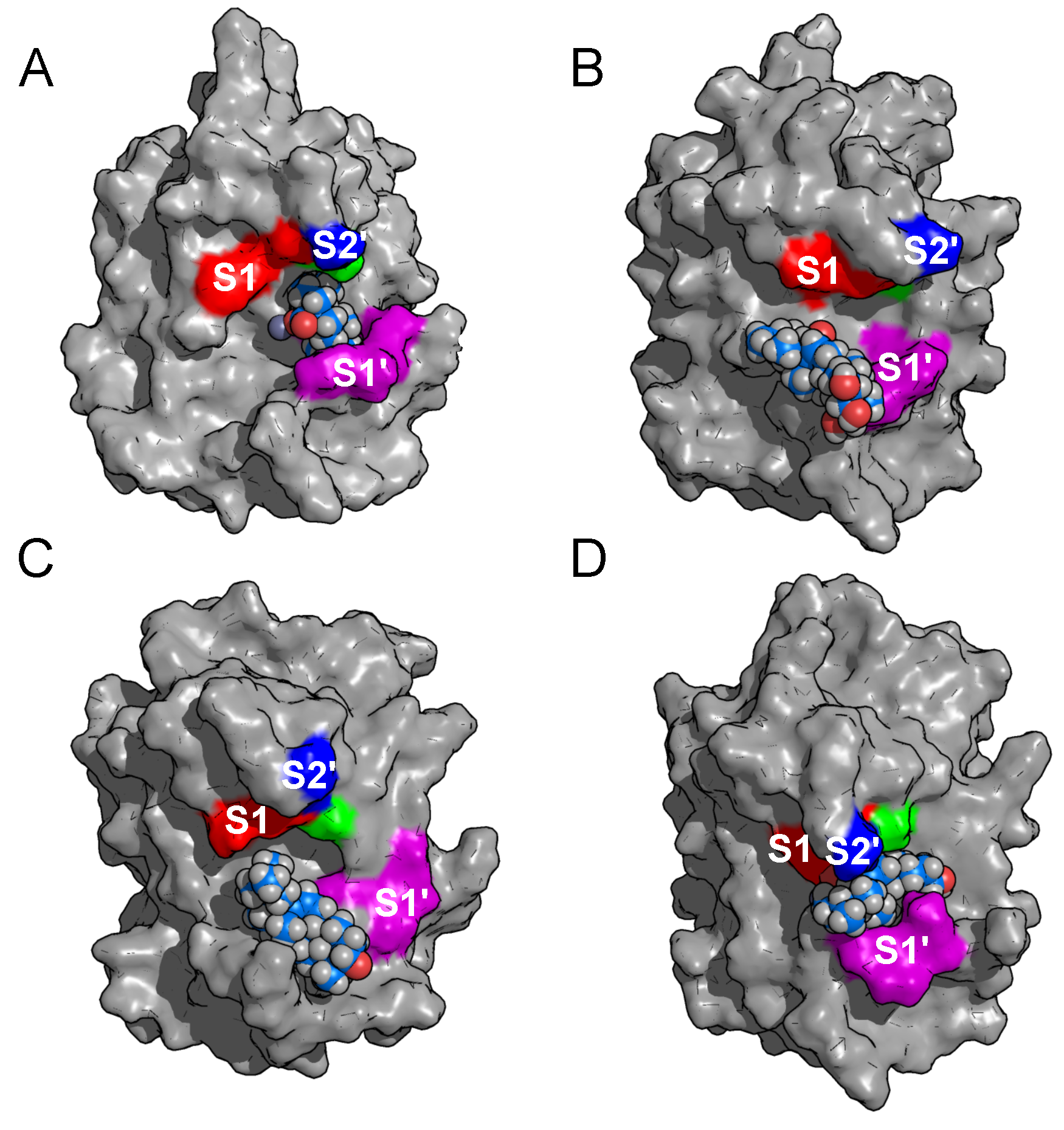
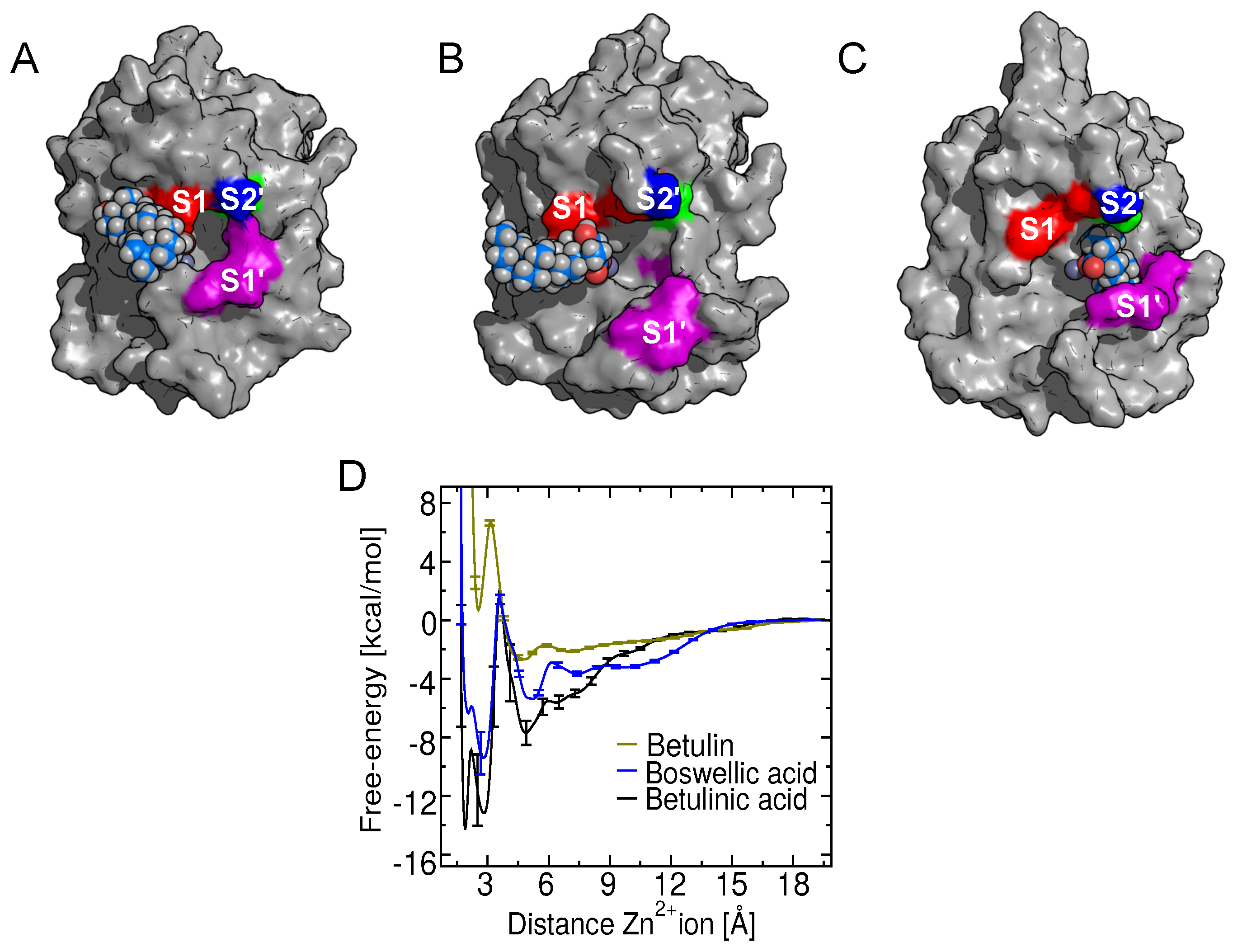
2.2. Binding Modes in Unbiased Simulations
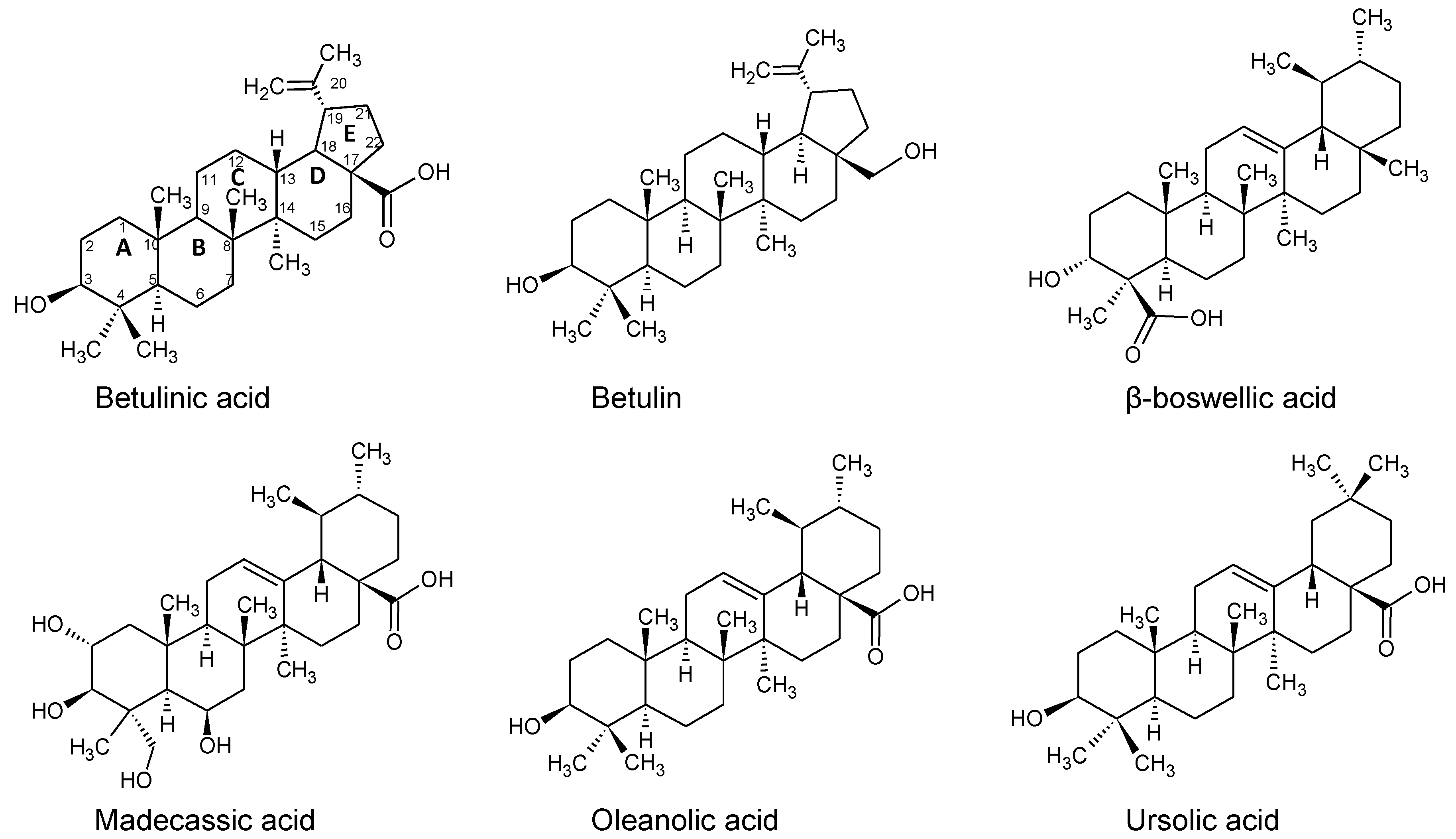
2.3. Binding of Triterpenes with Carboxylates at Position C-17
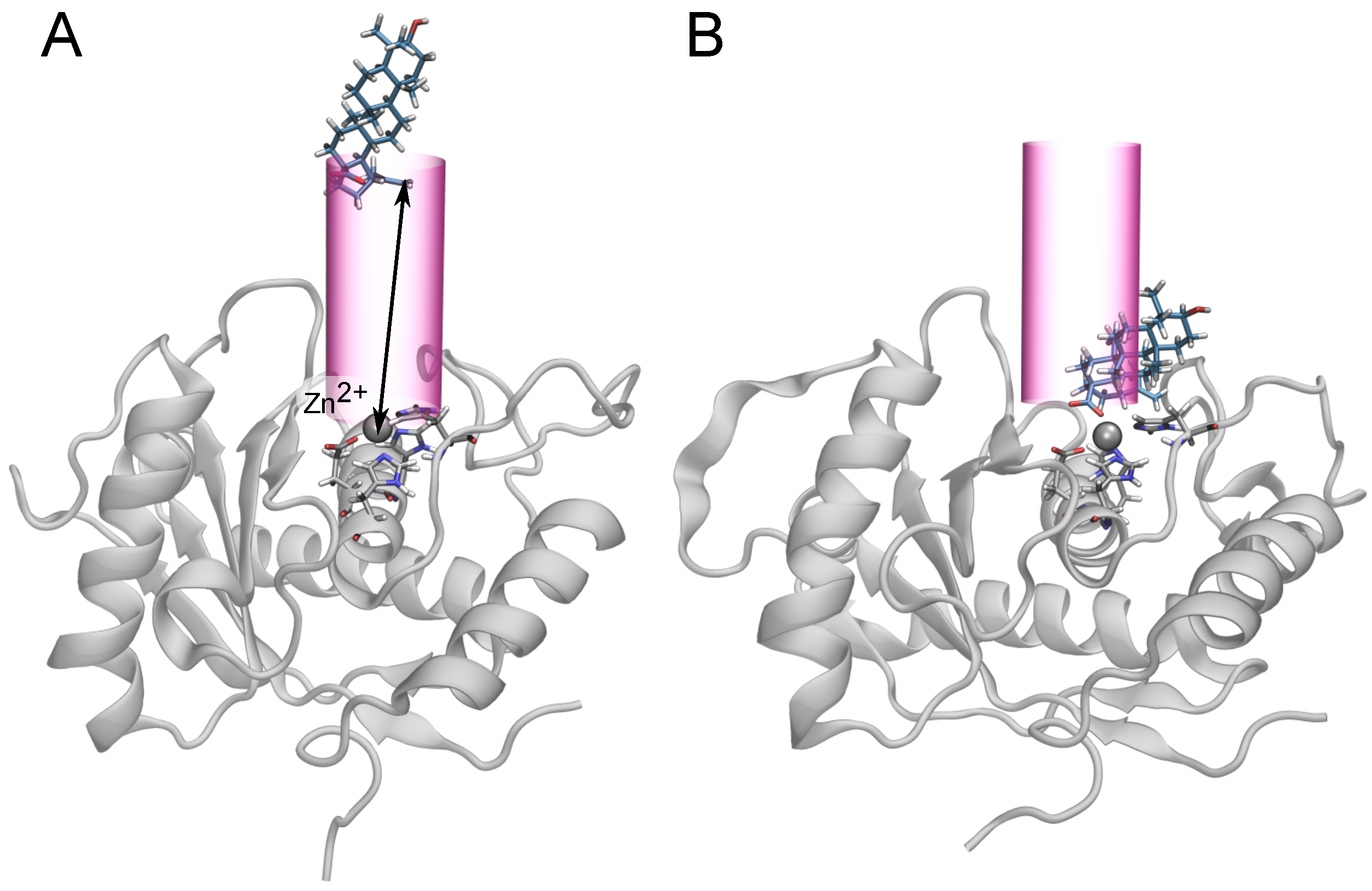
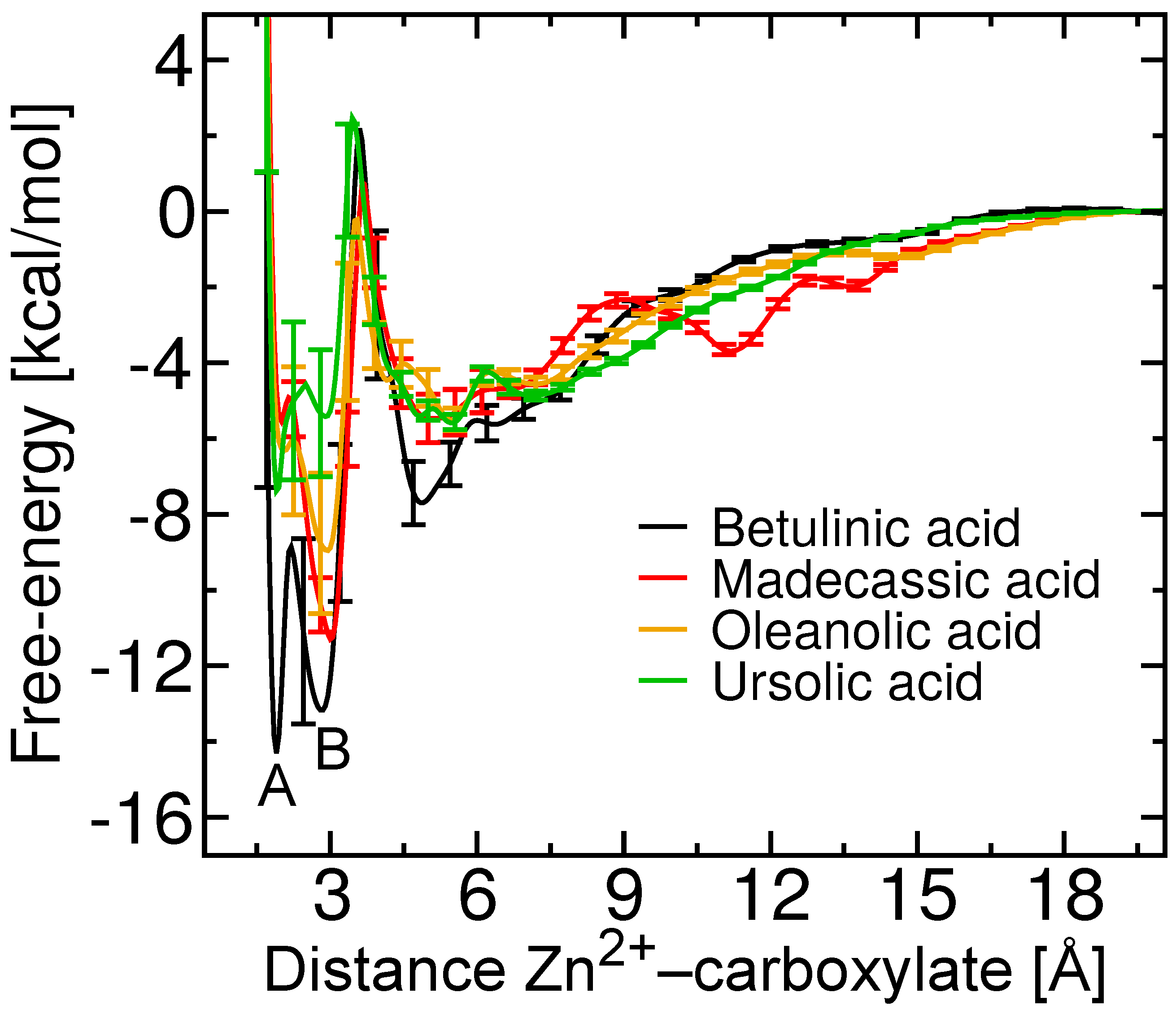
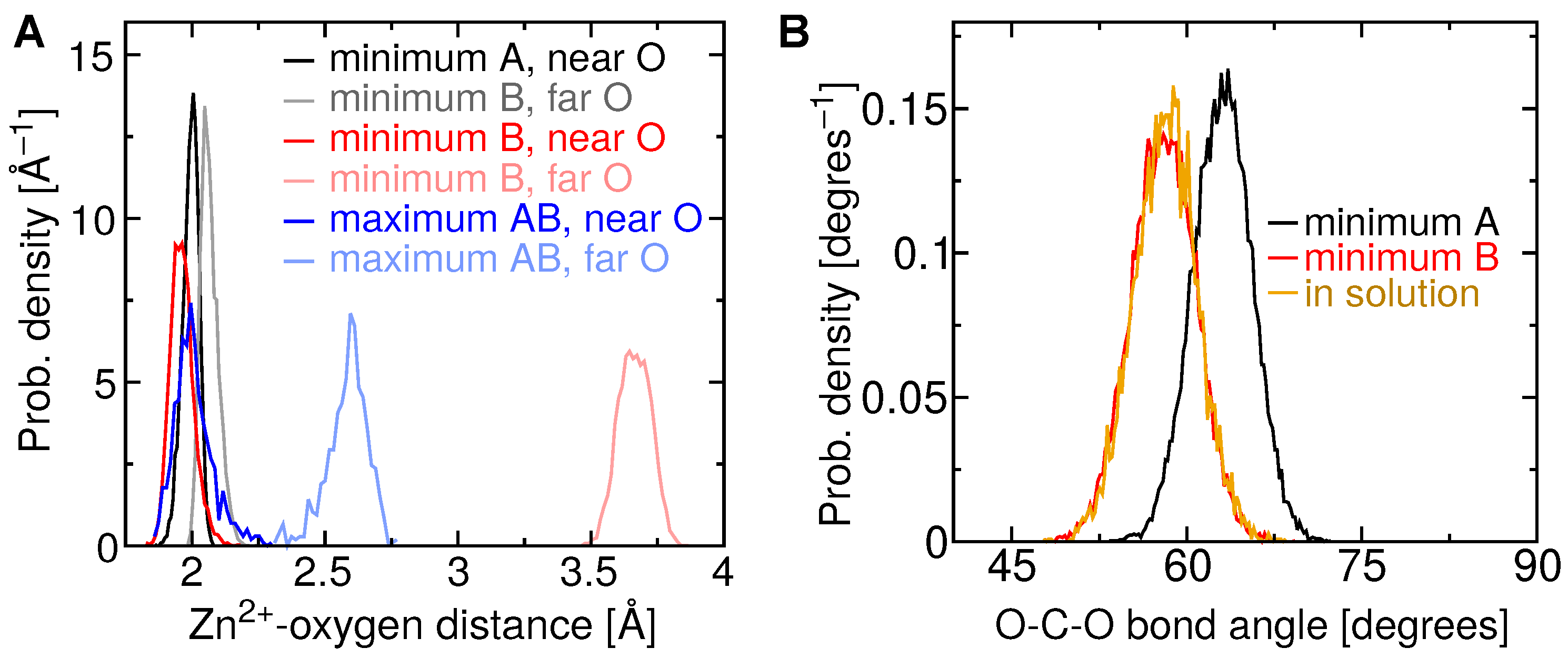
2.4. Two Binding Modes of Carboxylate–Zn
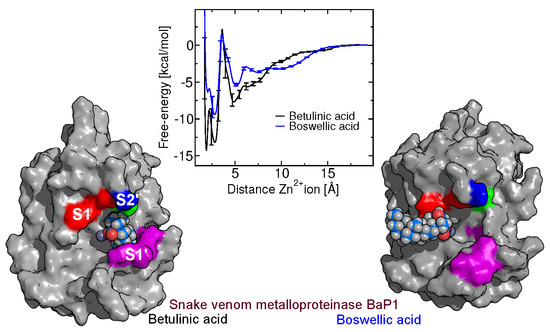
2.5. Free-Energy Barriers
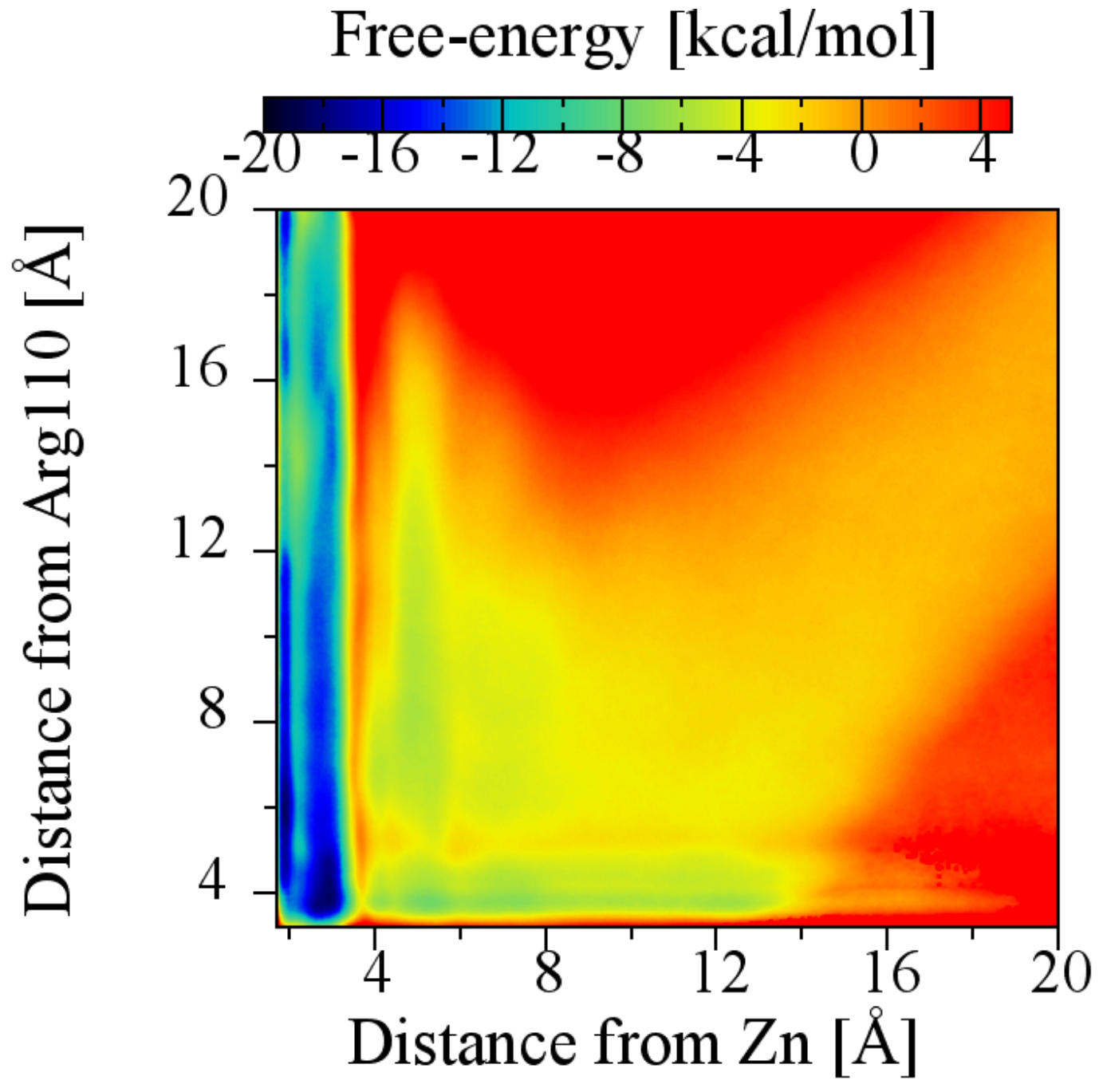
2.6. The Role of Arg110
2.7. Thermodynamic Decomposition of Binding Free Energy
2.8. Binding of Betulin and -Boswellic Acid
3. Conclusions
4. Materials and Methods
4.1. Chemicals and Reagents
4.2. Purification of the Metalloproteinase Batx-I
4.3. Inhibition of Proteolytic Activity
4.4. Molecular Docking Methods
4.5. Molecular Dynamics Methods
4.6. Free Energy Calculations
4.7. Determination of Binding Enthalpy and Entropy
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ABF | Adaptive biasing force |
| COLVARS | Colective variables |
| EDTA | Ethylenediamine-tetraacetic acid |
| FES | Free energy surface |
| DTPA | Diethylene triamine pentaacetic acid |
| MM-PBSA | Molecular-mechanics Poisson–Boltzmann surface area |
| MM-GBSA | Molecular-mechanics Generalized Born surface area |
| PMF | Potential of mean force |
| RP-HPLC | Reverse phase-High-performance liquid chromatography |
| SDS-PAGE | Sodium dodecyl sulfate polyacrylamide gel electrophoresis |
| SVMPs | Snake venom metalloproteinases |
| TPEN | N, N, N’, N’-Tetrakis (2-pyridylmethyl) ethane-1,2-diamine |
| TTD | Tetraethylthiuram disulfide |
References
- Tasoulis, T.; Isbister, G.K. A review and database of snake venom proteomes. Toxins 2017, 9, 290. [Google Scholar] [CrossRef] [PubMed]
- Markland, F.S., Jr.; Swenson, S. Snake venom metalloproteinases. Toxicon 2013, 62, 3–18. [Google Scholar] [CrossRef] [PubMed]
- Kini, R.M.; Koh, C.Y. Metalloproteases affecting blood coagulation, fibrinolysis and platelet aggregation from snake venoms: Definition and nomenclature of interaction sites. Toxins 2016, 8, 284. [Google Scholar] [CrossRef] [PubMed]
- Fox, J.W.; Serrano, S.M. Insights into and speculations about snake venom metalloproteinase (SVMP) synthesis, folding and disulfide bond formation and their contribution to venom complexity. FEBS J. 2008, 275, 3016–3030. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gutiérrez, J.M.; Rucavado, A.; Escalante, T.; Díaz, C. Hemorrhage induced by snake venom metalloproteinases: biochemical and biophysical mechanisms involved in microvessel damage. Toxicon 2005, 45, 997–1011. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, J.M.; Escalante, T.; Rucavado, A.; Herrera, C.; Fox, J.W. A comprehensive view of the structural and functional alterations of extracellular matrix by snake venom metalloproteinases (SVMPs): Novel perspectives on the pathophysiology of envenoming. Toxins 2016, 8, 304. [Google Scholar] [CrossRef] [PubMed]
- Baldo, C.; Jamora, C.; Yamanouye, N.; Zorn, T.M.; Moura-da Silva, A.M. Mechanisms of vascular damage by hemorrhagic snake venom metalloproteinases: Tissue distribution and in situ hydrolysis. PLoS Negl. Trop. Dis. 2010, 4, e727. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, C.D.F.P.; Fernandes, C.M.; Zuliani, J.P.; Zamuner, S.F. Inflammatory effects of snake venom metalloproteinases. Mem. Inst. Oswaldo Cruz 2005, 100, 181–184. [Google Scholar] [CrossRef]
- Hsu, C.C.; Huang, T.F. Biological activities of snake venom metalloproteinases on platelets, neutrophils, endothelial cells, and extracellular matrices. In Toxins and Hemostasis; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Gutiérrez, J.M.; Rucavado, A. Snake venom metalloproteinases: Their role in the pathogenesis of local tissue damage. Biochimie 2000, 82, 841–850. [Google Scholar] [CrossRef]
- Rojas, G.; Espinoza, M.; Lomonte, B.; Gutiérrez, J. Effect of storage temperature on the stability of the liquid polyvalent antivenom produced in Costa Rica. Toxicon 1990, 28, 101–105. [Google Scholar] [CrossRef]
- Segura, Á.; Herrera, M.; González, E.; Vargas, M.; Solano, G.; Gutiérrez, J.M.; León, G. Stability of equine IgG antivenoms obtained by caprylic acid precipitation: Towards a liquid formulation stable at tropical room temperature. Toxicon 2009, 53, 609–615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gutiérrez, J.M.; León, G.; Rojas, G.; Lomonte, B.; Rucavado, A.; Chaves, F. Neutralization of local tissue damage induced by Bothrops asper (terciopelo) snake venom. Toxicon 1998, 36, 1529–1538. [Google Scholar] [CrossRef]
- Knudsen, C.; Laustsen, A.H. Recent Advances in Next Generation Snakebite Antivenoms. Trop. Med. Infect. Dis. 2018, 3, 42. [Google Scholar] [CrossRef]
- Peng, W.J.; Yan, J.W.; Wan, Y.N.; Wang, B.X.; Tao, J.H.; Yang, G.J.; Pan, H.F.; Wang, J. Matrix metalloproteinases: A review of their structure and role in systemic sclerosis. J. Clin. Immunol. 2012, 32, 1409–1414. [Google Scholar] [CrossRef] [PubMed]
- Escalante, T.; Franceschi, A.; Rucavado, A.; Gutiérrez, J.M. Effectiveness of batimastat, a synthetic inhibitor of matrix metalloproteinases, in neutralizing local tissue damage induced by BaP1, a hemorrhagic metalloproteinase from the venom of the snake Bothrops asper. Biochem. Pharmacol. 2000, 60, 269–274. [Google Scholar] [CrossRef]
- Howes, J.M.; Theakston, R.D.G.; Laing, G. Neutralization of the haemorrhagic activities of viperine snake venoms and venom metalloproteinases using synthetic peptide inhibitors and chelators. Toxicon 2007, 49, 734–739. [Google Scholar] [CrossRef] [PubMed]
- Urs, A.N.N.; Yariswamy, M.; Ramakrishnan, C.; Joshi, V.; Suvilesh, K.N.; Savitha, M.N.; Velmurugan, D.; Vishwanath, B.S. Inhibitory potential of three zinc chelating agents against the proteolytic, hemorrhagic, and myotoxic activities of Echis carinatus venom. Toxicon 2015, 93, 68–78. [Google Scholar]
- Baraldi, P.T.; Magro, A.J.; Matioli, F.F.; Marcussi, S.; Lemke, N.; Calderon, L.A.; Stábeli, R.G.; Soares, A.M.; Correa, A.G.; Fontes, M.R. A novel synthetic quinolinone inhibitor presents proteolytic and hemorrhagic inhibitory activities against snake venom metalloproteases. Biochimie 2016, 121, 179–188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferreira, F.B.; Pereira, T.M.; Souza, D.L.; Lopes, D.S.; Freitas, V.; Ávila, V.M.; Kümmerle, A.E.; Sant’Anna, C.M.R. Structure-Based Discovery of Thiosemicarbazone Metalloproteinase Inhibitors for Hemorrhage Treatment in Snakebites. ACS Med. Chem. Lett. 2017, 8, 1136–1141. [Google Scholar] [CrossRef] [PubMed]
- Aung, H.T.; Nikai, T.; Komori, Y.; Nonogaki, T.; Niwa, M.; Takaya, Y. Biological and pathological studies of rosmarinic acid as an inhibitor of hemorrhagic Trimeresurus flavoviridis (habu) venom. Toxins 2010, 2, 2478–2489. [Google Scholar] [CrossRef] [PubMed]
- Vale, H.F.; Mendes, M.M.; Fernandes, R.S.; Costa, T.R.; S Hage-Melim, L.I.; A Sousa, M.; Hamaguchi, A.; Homsi-Brandeburgo, M.I.; Franca, S.C.; Silva, C.H.; et al. Protective effect of Schizolobium parahyba flavonoids against snake venoms and isolated toxins. Curr. Top. Med. Chem. 2011, 11, 2566–2577. [Google Scholar] [CrossRef]
- Januário, A.H.; Santos, S.L.; Marcussi, S.; Mazzi, M.V.; Pietro, R.C.; Sato, D.N.; Ellena, J.; Sampaio, S.V.; França, S.C.; Soares, A.M. Neo-clerodane diterpenoid, a new metalloprotease snake venom inhibitor from Baccharis trimera (Asteraceae): Anti-proteolytic and anti-hemorrhagic properties. Chem. Biol. Interact. 2004, 150, 243–251. [Google Scholar] [CrossRef] [PubMed]
- Preciado, L.M.; Rey-Suárez, P.; Henao, I.C.; Pereañez, J.A. Betulinic, oleanolic and ursolic acids inhibit the enzymatic and biological effects induced by a PI snake venom metalloproteinase. Chem. Biol. Interact. 2018, 279, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Villalta-Romero, F.; Gortat, A.; Herrera, A.E.; Arguedas, R.; Quesada, J.; de Melo, R.L.; Calvete, J.J.; Montero, M.; Murillo, R.; Rucavado, A.; et al. Identification of new snake venom metalloproteinase inhibitors using compound screening and rational peptide design. ACS Med. Chem. Lett. 2012, 3, 540–543. [Google Scholar] [CrossRef] [PubMed]
- Sunitha, K.; Hemshekhar, M.; Gaonkar, S.L.; Sebastin Santhosh, M.; Suresh Kumar, M.; Priya, B.S.; Kemparaju, K.; Rangappa, K.S.; Nanjunda Swamy, S.; Girish, K.S.; et al. Neutralization of Haemorrhagic Activity of Viper Venoms by 1-(3-Dimethylaminopropyl)-1-(4-Fluorophenyl)-3-Oxo-1, 3-Dihydroisobenzofuran- 5-Carbonitrile. Basic. Clin. Pharmacol. Toxicol. 2011, 109, 292–299. [Google Scholar] [CrossRef] [PubMed]
- Srinivasa, V.; Sundaram, M.S.; Anusha, S.; Hemshekhar, M.; Nayaka, S.C.; Kemparaju, K.; Girish, K.S.; Rangappa, K.S. Novel apigenin based small molecule that targets snake venom metalloproteases. PLoS ONE 2014, 9, e106364. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, H.; Cai, W.; Hénin, J.; Roux, B.; Chipot, C. New Coarse Variables for the Accurate Determination of Standard Binding Free Energies. J. Chem. Theory Comput. 2017, 13, 5173–5178. [Google Scholar] [CrossRef] [PubMed]
- Limongelli, V.; Bonomi, M.; Parrinello, M. Funnel metadynamics as accurate binding free-energy method. Proc. Natl. Acad. Sci. USA 2013, 110, 6358–6363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeller, F.; Zacharias, M. Evaluation of generalized Born model accuracy for absolute binding free energy calculations. J. Phys. Chem. B 2014, 118, 7467–7474. [Google Scholar] [CrossRef] [PubMed]
- Lingott, T.; Merfort, I.; Steinbrecher, T. Free energy calculations on snake venom metalloproteinase BaP1. Chem. Biol. Drug Des. 2012, 79, 990–1000. [Google Scholar] [CrossRef] [PubMed]
- Chinnasamy, S.; Chinnasamy, S.; Nagamani, S.; Muthusamy, K. Identification of potent inhibitors against snake venom metalloproteinase (SVMP) using molecular docking and molecular dynamics studies. J. Biomol. Struct. Dyn. 2015, 33, 1516–1527. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Greene, D.; Xiao, L.; Qi, R.; Luo, R. Recent developments and applications of the MMPBSA method. Front. Mol. Biosci. 2018, 4, 87. [Google Scholar] [CrossRef] [PubMed]
- Woo, H.J.; Roux, B. Calculation of Absolute Protein–ligand Binding Free Energy from Computer Simulations. Proc. Natl. Acad. Sci. USA 2005, 102, 6825–6830. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Roux, B. Free Energy Perturbation Hamiltonian Replica-exchange Molecular Dynamics (FEP/H-REMD) for Absolute Ligand Binding Free Energy Calculations. J. Chem. Theory Comput. 2010, 6, 2559–2565. [Google Scholar] [CrossRef] [PubMed]
- Darve, E.; Pohorille, A. Calculating Free Energies Using Average Force. J. Chem. Phys. 2001, 115, 9169–9183. [Google Scholar] [CrossRef]
- Comer, J.; Gumbart, J.C.; Hènin, J.; Lelièvre, T.; Pohorille, A.; Chipot, C. The Adaptive Biasing Force Method: Everything You Always Wanted to Know But Were Afraid to Ask. J. Phys. Chem. B 2015, 119, 1129–1151. [Google Scholar] [CrossRef] [PubMed]
- Lingott, T.; Schleberger, C.; Gutierrez, J.M.; Merfort, I. High-resolution crystal structure of the snake venom metalloproteinase BaP1 complexed with a peptidomimetic: Insight into inhibitor binding. Biochemistry 2009, 48, 6166–6174. [Google Scholar] [CrossRef] [PubMed]
- Patiño, A.C.; Pereañez, J.A.; Núñez, V.; Benjumea, D.M.; Fernandez, M.; Rucavado, A.; Sanz, L.; Calvete, J.J. Isolation and biological characterization of Batx-I, a weak hemorrhagic and fibrinogenolytic PI metalloproteinase from Colombian Bothrops atrox venom. Toxicon 2010, 56, 936–943. [Google Scholar] [CrossRef] [PubMed]
- Mors, W.B.; Do Nascimento, M.C.; Pereira, B.M.R.; Pereira, N.A. Plant natural products active against snake bite—The molecular approach. Phytochemistry. 2000, 55, 627–642. [Google Scholar] [CrossRef]
- Cheng, Y.-C.; Prusoff, W.H. Relationship between the inhibition constant (Ki) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem. Pharmacol. 1973, 22, 3099–3108. [Google Scholar]
- Recht, M.I.; Nienaber, V.; Torres, F.E. Fragment-based screening for enzyme inhibitors using calorimetry. In Methods in Enzymology; Elsevier: New York, NY, USA, 2016; Volume 567, pp. 47–69. [Google Scholar]
- Jacobsen, J.A.; Jourden, J.L.M.; Miller, M.T.; Cohen, S.M. To bind zinc or not to bind zinc: An examination of innovative approaches to improved metalloproteinase inhibition. Biochim. Biophys. Acta 2010, 1803, 72–94. [Google Scholar] [CrossRef] [PubMed]
- Leme, A.F.P.; Escalante, T.; Pereira, J.G.; Oliveira, A.K.; Sanchez, E.F.; Gutiérrez, J.M.; Serrano, S.M.; Fox, J.W. High resolution analysis of snake venom metalloproteinase (SVMP) peptide bond cleavage specificity using proteome based peptide libraries and mass spectrometry. J. Proteom. 2011, 74, 401–410. [Google Scholar] [CrossRef] [PubMed]
- Skiles, J.W.; Gonnella, N.C.; Jeng, A.Y. The design, structure, and therapeutic application of matrix metalloproteinase inhibitors. Curr. Med. Chem. 2001, 8, 425–474. [Google Scholar] [CrossRef] [PubMed]
- Takeda, S.; Takeya, H.; Iwanaga, S. Snake venom metalloproteinases: Structure, function and relevance to the mammalian ADAM/ADAMTS family proteins. BBA-Proteins Proteom. 2012, 1824, 164–176. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.E.; Haymet, A. Free Energy, Entropy, and Internal Energy of Hydrophobic Interactions: Computer Simulations. J. Chem. Phys. 1993, 98, 6445–6454. [Google Scholar] [CrossRef]
- Wan, S.; Stote, R.H.; Karplus, M. Calculation of the aqueous solvation energy and entropy, as well as free energy, of simple polar solutes. J. Chem. Phys. 2004, 121, 9539–9548. [Google Scholar] [CrossRef] [PubMed]
- Hulme, E.C.; Trevethick, M.A. Ligand binding assays at equilibrium: Validation and interpretation. Br. J. Pharmacol. 2010, 161, 1219–1237. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; MacKerell, A. CHARMM Additive and Polarizable Force Fields for Biophysics and Computer-aided Drug Design. BBA-Gen. Subj. 2015, 1850, 861–871. [Google Scholar] [CrossRef] [PubMed]
- Laemmli, U.K. Cleavage of structural proteins during the assembly of the head of bacteriophage T4. Nature 1970, 227, 680–685. [Google Scholar] [CrossRef] [PubMed]
- Vandooren, J.; Geurts, N.; Martens, E.; Van den Steen, P.E.; De Jonghe, S.; Herdewijn, P.; Opdenakker, G. Gelatin degradation assay reveals MMP-9 inhibitors and function of O-glycosylated domain. World J. Biol. Chem. 2011, 2, 14. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) I: Bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell Jr, A.D. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of bonded parameters and partial atomic charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; MacKerell, A.D., Jr. Optimization of the Additive CHARMM All-atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.; Grubmüller, H.; MacKerell, A., Jr. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.; Cheng, X.; Swails, J.M.; Yeom, M.S.; Eastman, P.K.; Lemkul, J.A.; Wei, S.; Buckner, J.; Jeong, J.C.; Qi, Y.; et al. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2015, 12, 405–413. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Hopkins, C.W.; Le Grand, S.; Walker, R.C.; Roitberg, A.E. Long-time-step molecular dynamics through hydrogen mass repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Fiorin, G.; Klein, M.L.; Hènin, J. Using collective variables to drive molecular dynamics simulations. Math. Probl. Eng. 2013, 111, 3345–3362. [Google Scholar] [CrossRef]


| Terpene | (M) | Experimental (kcal/mol) | Theoretical (kcal/mol) |
|---|---|---|---|
| Betulinic acid | |||
| Ursolic acid | |||
| Oleanolic acid | |||
| Madecassic acid | ND | ||
| Betulin | ND | ||
| -Boswellic acid | ND | ND |
| Free-Energy Minimum | (kcal/mol) | (kcal/mol) | (kcal/mol) | (kcal/mol) |
|---|---|---|---|---|
| A | ||||
| B |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Preciado, L.M.; Pereañez, J.A.; Azhagiya Singam, E.R.; Comer, J. Interactions between Triterpenes and a P-I Type Snake Venom Metalloproteinase: Molecular Simulations and Experiments. Toxins 2018, 10, 397. https://doi.org/10.3390/toxins10100397
Preciado LM, Pereañez JA, Azhagiya Singam ER, Comer J. Interactions between Triterpenes and a P-I Type Snake Venom Metalloproteinase: Molecular Simulations and Experiments. Toxins. 2018; 10(10):397. https://doi.org/10.3390/toxins10100397
Chicago/Turabian StylePreciado, Lina María, Jaime Andrés Pereañez, Ettayapuram Ramaprasad Azhagiya Singam, and Jeffrey Comer. 2018. "Interactions between Triterpenes and a P-I Type Snake Venom Metalloproteinase: Molecular Simulations and Experiments" Toxins 10, no. 10: 397. https://doi.org/10.3390/toxins10100397
APA StylePreciado, L. M., Pereañez, J. A., Azhagiya Singam, E. R., & Comer, J. (2018). Interactions between Triterpenes and a P-I Type Snake Venom Metalloproteinase: Molecular Simulations and Experiments. Toxins, 10(10), 397. https://doi.org/10.3390/toxins10100397