Anatomical Distribution of Diarrhetic Shellfish Toxins (DSTs) in the Japanese Scallop Patinopecten yessoensis and Individual Variability in Scallops and Mytilus edulis Mussels: Statistical Considerations
Abstract
:1. Introduction
2. Results
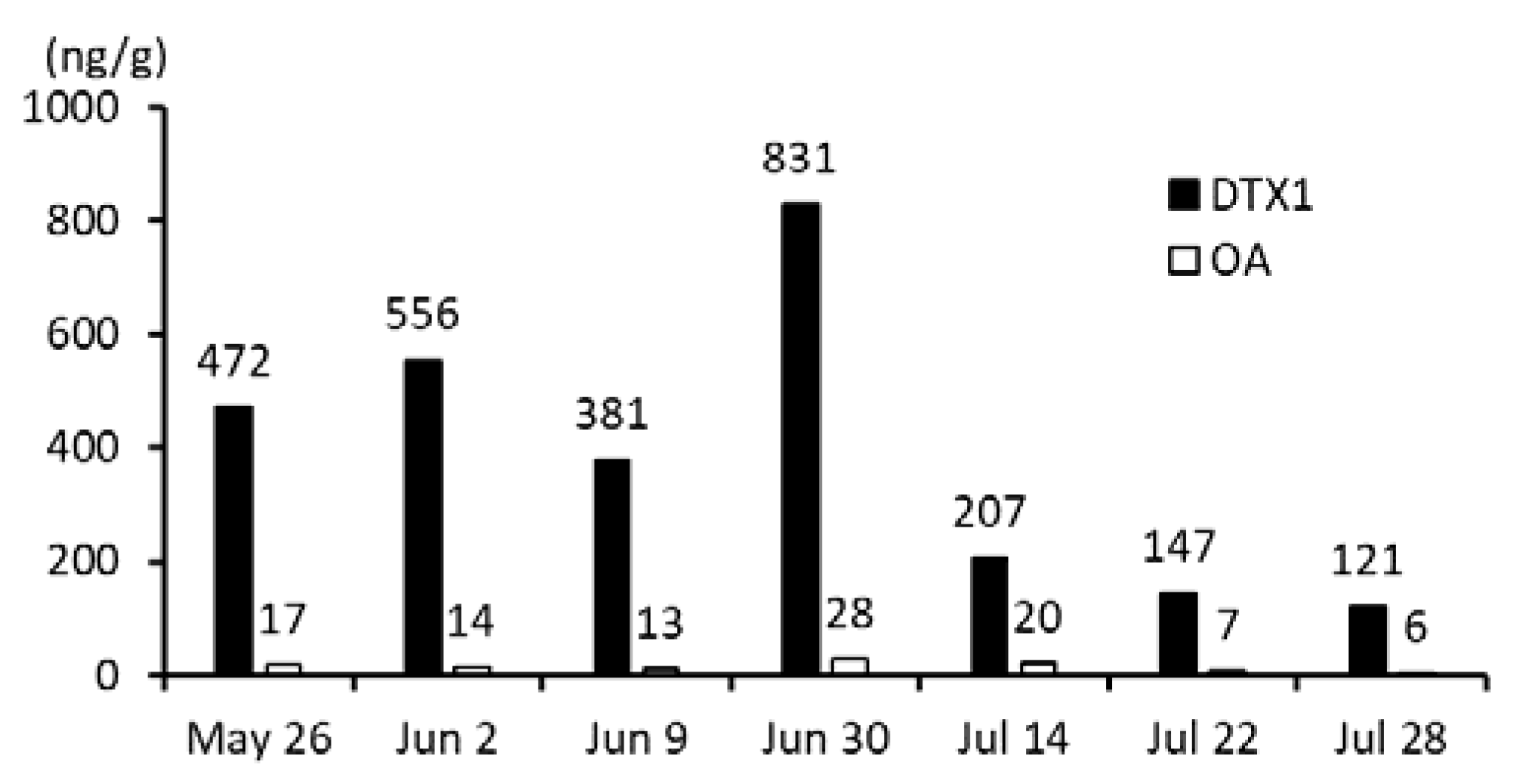
2.1. Concentrations and Distribution of DSTs
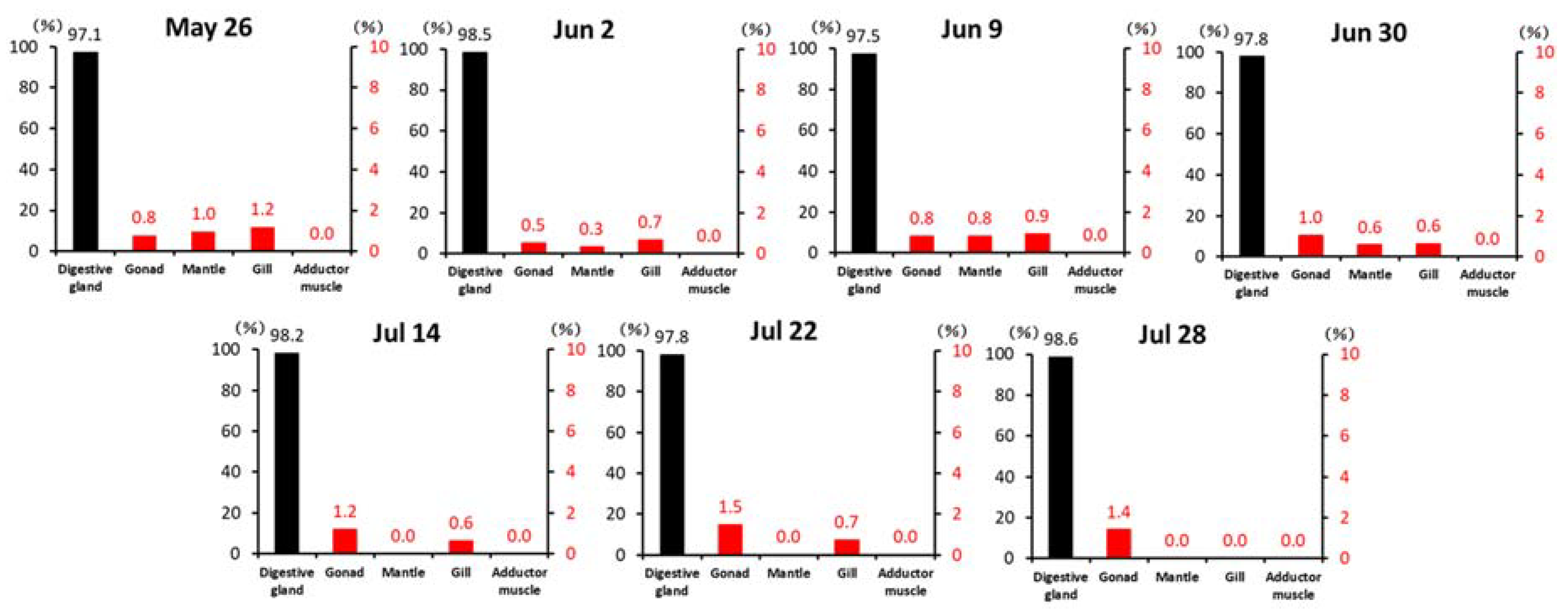
2.1.1. Anatomical Compartmentalization of DST in Scallops
2.1.2. DST Analysis of 30 Individual Scallops and Mussels
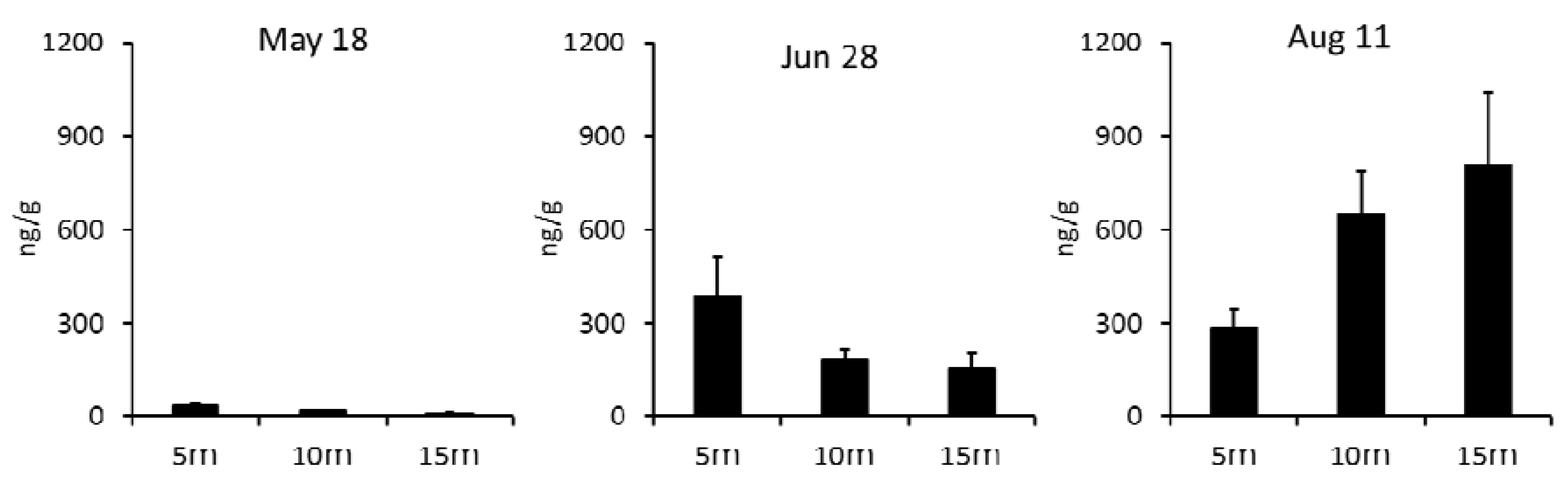
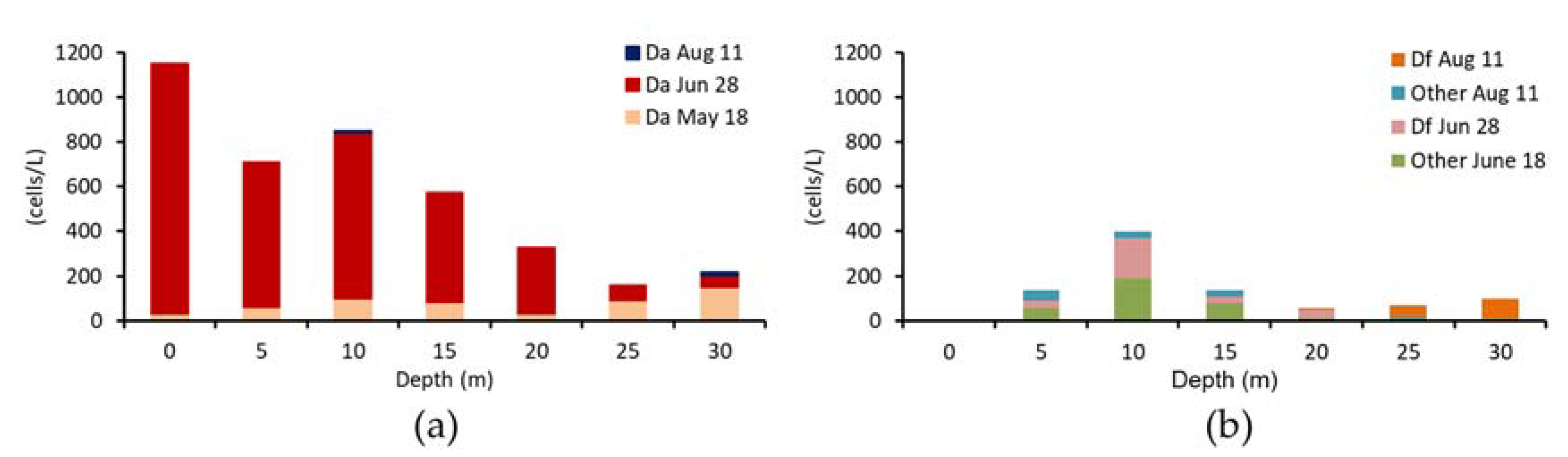
2.1.3. Analysis of DST Concentration in Scallop Samples from Different Water Depths
2.2. Statistical Analysis
2.2.1. Statistical Resampling Analysis of DSTs in Scallops and Mussels
2.2.2. Estimating the Mean Concentration of the Population (Cultured Scallops) When the Individual Concentration of a Sample Is Defined
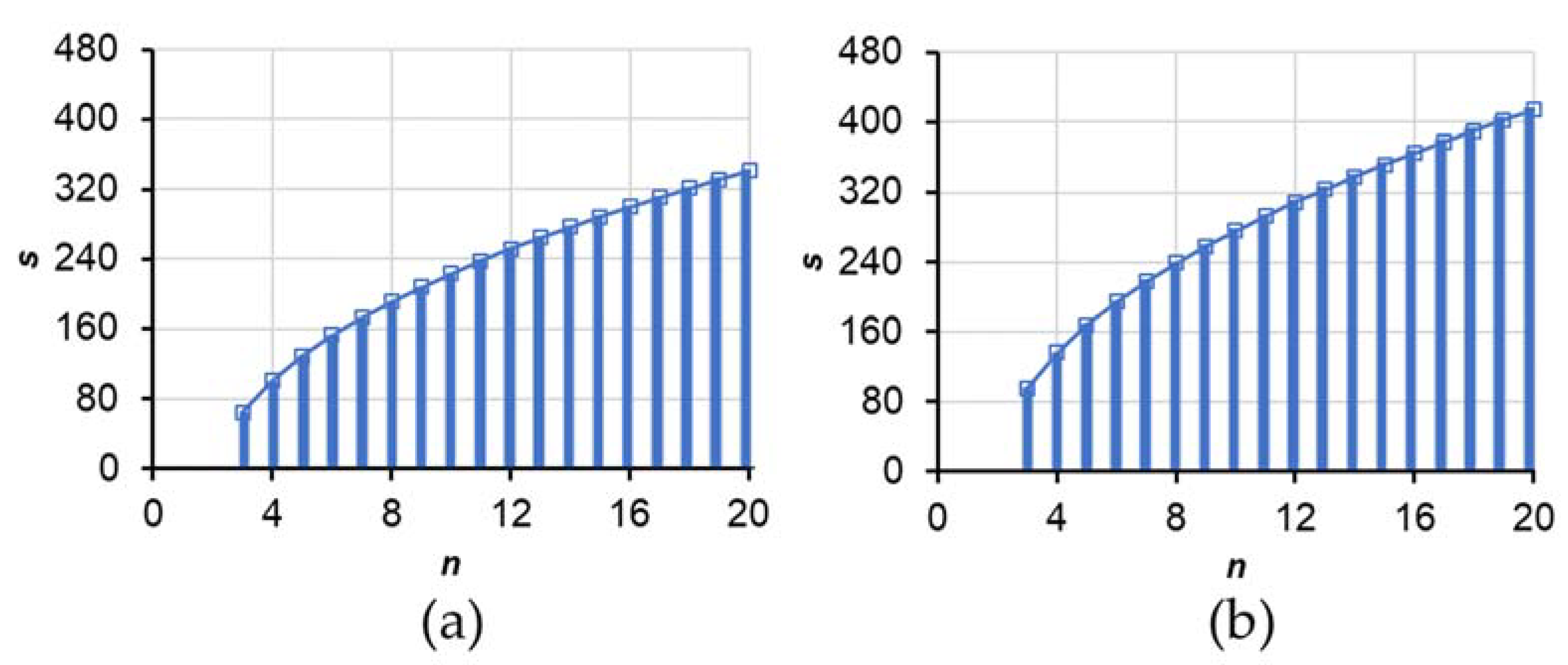
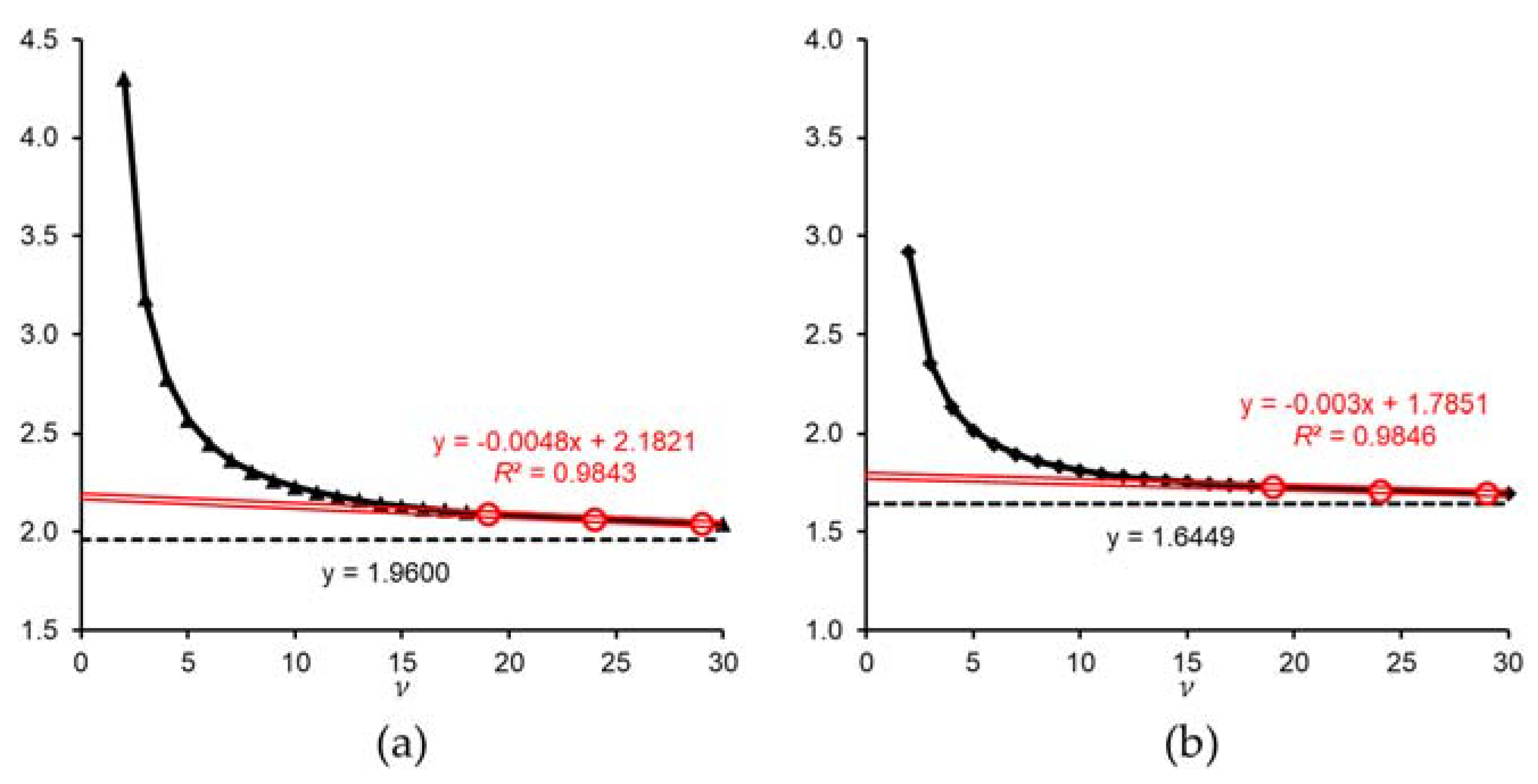
2.2.3. Adequacy of Sample Size Based on the t-Value and Confidence Interval
3. Discussion
4. Materials and Methods
4.1. Plankton Monitoring
4.2. Scallops and Mussels
4.3. Extraction of DSTs and Hydrolysis of Esterified DSTs
4.4. Standard Toxins
4.5. LC/MS/MS Analysis of DSTs
4.6. Statistical Analyses
- N = number of individuals in the population.
- n = number of individuals in the sample.
- Two-tailed significance level (α) = 0.05 or 0.10.
- Confidence level = 1 − α.
- Confidence interval (CI) = 100 (1 − α)%.
- Statistical degrees of freedom = n − 1 = Greek letter nu (ν).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yasumoto, T.; Oshima, Y.; Yamaguchi, M. Occurrence of a new type of shellfish poisoning in the Tohoku. Bull. Jpn. Soc. Sci. Fish. 1978, 44, 1249–1255. [Google Scholar] [CrossRef]
- Yasumoto, T.; Murata, M.; Oshima, Y.; Sano, M.; Matsumoto, G.K.; Clardy, J. Diarrhetic shellfish toxins. Tetrahedron 1985, 41, 1019–1025. [Google Scholar] [CrossRef]
- Yasumoto, T.; Murata, M. Marine toxins. Chem. Rev. 1993, 93, 1897–1909. [Google Scholar] [CrossRef]
- Bialojan, C.; Takagi, A. Inhibitory effect of a marine-sponge toxin, okadaic acid, on protein phosphatases. Specificity and kinetics. Biochem. J. 1988, 256, 283–290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Terao, K.; Ito, E.; Yanagi, T.; Yasumoto, T. Histopathological studies on experimental marine toxin poisoning. I. Ultrastructural changes in the small intestine and liver of suckling mice induced by dinophysistoxin-1 and pectenotoxin-1. Toxicon 1986, 24, 1145–1151. [Google Scholar] [CrossRef]
- Fujiki, H.; Suganuma, M.; Suguri, H.; Yoshizawa, S.; Takagi, K.; Uda, N.; Wakamatsu, K.; Yamada, K.; Murata, M.; Yasumoto, T.; et al. Diarrhetic shellfish toxin, dinophysistoxin-1, is a potent tumor promoter on mouse skin. Jpn. J. Cancer Res. 1988, 79, 1089–1093. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Ota, H.; Yamasaki, M. Direct evidence of transformation of dinophysistoxin-1 to 7-O-acyl-dinophysistoxin-1 (dinophysistoxin-3) in the scallop Patinopecten yessoensis. Toxicon 1999, 37, 187–198. [Google Scholar] [CrossRef]
- Guidelines for Risk Management of Shellfish Toxins in Bivalves. Available online: http://www.maff.go.jp/j/syouan/tikusui/gyokai/g_kenko/busitu/pdf/150306_kaidoku_guide.pdf (accessed on 25 September 2018).
- Standard for Liver and Raw Bivalve Molluscs (CODEX STAN 292-2008). Available online: http://www.fao.org/fao-who-codexalimentarius/sh-proxy/es/?lnk=1&url=https%253A%252F%252Fworkspace.fao.org%252Fsites%252Fcodex%252FStandards%252FCODEX%2BSTAN%2B292-2008%252FCXS_292e_2015.pdf (accessed on 25 September 2018).
- Sandra, E.S.; Parson, J.G. Scallops: Biology, Ecology, Aquaculture, and Fisheries, 3rd ed.; Elsevier Science: Amsterdam, The Netherlands, 2016; Volume 40, pp. 891–936. ISBN 978-0-444-62710-0. [Google Scholar]
- Matsushima, R.; Uchida, H.; Nagai, S.; Watanabe, R.; Kamio, M.; Nagai, H.; Kaneniwa, M.; Suzuki, T. Assimilation, accumulation and metabolism of dinophysistoxins (DTXs) and pectenotoxins (PTXs) in the Japanese scallop Patinopecten yessoensis. Toxins 2015, 7, 5141–5154. [Google Scholar] [CrossRef] [PubMed]
- Matsushima, R.; Uchida, H.; Watanabe, R.; Oikawa, H.; Kosaka, Y.; Tanabe, T.; Suzuki, T. Distribution of Diarrhetic Shellfish Toxins in Mussels, Scallops, and Ascidian. Food Saf. 2018, 6, 101–106. [Google Scholar] [CrossRef]
- Lemeshow, S.; Hosmer, D.W.; Klar, J.; Lwango, S.K. World Health Organization. Adequacy of Sample Size in Health Studies; John Wiley & Sons Ltd.: West Sussex, UK, 1990; pp. 36–62. ISBN 0471925179. [Google Scholar]
- Student. The probable error of a mean. Biometrika 1908, 6, 1–25. [Google Scholar] [CrossRef]
- Fisher, R.A. Applications of “tudent’s” distribution. Metron 1925, 5, 90–104. [Google Scholar]
- Suzuki, T.; Miyazono, A.; Baba, K.; Sugawara, R.; Kamiyama, T. LC–MS/MS analysis of okadaic acid analogues and other lipophilic toxins in single-cell isolates of several Dinophysis species collected in Hokkaido, Japan. Harmful Algae 2009, 8, 233–238. [Google Scholar] [CrossRef]
- Sampling Plans for Aflatoxin Analysis in Peanuts and Corn; Report for FAO Technical Consultation; FAO: Rome, Italy, May 1993.
- Suzuki, T.; Jin, T.; Shirota, Y.; Mitsuya, T.; Okumura, Y.; Kamiyama, T. Quantification of lipophilic toxins associated with diarrhetic shellfish poisoning in Japanese bivalves by liquid chromatography-mass spectrometry and comparison with mouse bioassay. Fish. Sci. 2005, 71, 1370–1378. [Google Scholar] [CrossRef]
- EU-Harmonised Standard Operating Procedure for Determination of Lipophilic Marine Biotoxins in Molluscs by LCMS/MS Version 5. Available online: http://www.aecosan.msssi.gob.es/AECOSAN/docs/documentos/laboratorios/LNRBM/ARCHIVO2EU-Harmonised-SOP-LIPO-LCMSMS_Version5.pdf (accessed on 25 September 2018).
- NMIJ CRM Catalog 2016–2017, National Institute of Advanced Industrial Science and Technology (AIST), National Metrology Institute of Japan (NMIJ). Available online: https://www.nmij.jp/english/service/C/CRM_Catalog_(JE)160901.pdf (accessed on 25 September 2018).
- R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 25 September 2018).



| 2014 | 26 May | 2 June | 9 June | 30 June | 14 July | 22 July | 28 July |
|---|---|---|---|---|---|---|---|
| Number of Individuals | 16 | 18 | 17 | 18 | 15 | 20 | 14 |
| Digestive gland | 72.90 | 72.87 | 72.97 | 70.80 | 60.80 | 75.16 | 58.56 |
| Gonad | 42.39 | 39.99 | 40.79 | 44.22 | 48.05 | 54.46 | 39.83 |
| Mantle | 155.01 | 151.37 | 163.48 | 175.80 | 163.66 | 213.96 | 169.30 |
| Gill | 95.31 | 93.43 | 106.28 | 92.20 | 87.08 | 116.42 | 85.49 |
| Adductor muscle | 301.69 | 315.19 | 311.42 | 355.14 | 318.80 | 434.35 | 340.26 |
| 2014 | 26 May | 2 June | 9 June | 16 June | 7 July | 8 August |
|---|---|---|---|---|---|---|
| Scallop (Digestive gland/Whole meat %) | 3.87 ± 1.07 (10.14%) | 3.62 ± 0.81 (10.56%) | 3.70 ± 0.98 (8.78%) | 3.81 ± 0.72 (9.18%) | - | - |
| Mussel (Digestive gland/Whole meat %) | - | 1.69 ± 0.45 (14.72%) | - | - | 1.40 ± 0.46 (14.89%) | 1.51 ± 0.45 (12.90%) |
| 2016 | 18 May | 28 June | 11 August |
|---|---|---|---|
| Number of Individuals | 10 | 15 | 15 |
| 5 m | 6.45 ± 1.24 | 4.77 ± 0.82 | 1.40 ± 0.36 |
| 10 m | 6.16 ± 0.91 | 5.18 ± 1.33 | 1.38 ± 0.26 |
| 15 m | 5.30 ± 0.45 | 4.22 ± 0.75 | 1.46 ± 0.42 |
| Transparency (m) | Date (2016) | Depth (m) | Water Temperature (°C) | Salinity (psu) | D. fortii (Cells/L) | D. acuminate (Cells/L) | Other Dinophysis (Cells/L) | |
|---|---|---|---|---|---|---|---|---|
| 18 May | 0 | 11.2 | 30.84 | 0 | 30 | 0 | ||
| 5 | 9.7 | 31.98 | 0 | 60 | 0 | |||
| 5.0 | 10 | 9.2 | 32.03 | 0 | 100 | 0 | ||
| 15 | 8.1 | 32.32 | 0 | 80 | 0 | |||
| 20 | 7.8 | 32.59 | 0 | 30 | 0 | |||
| 25 | 7.4 | 32.67 | 0 | 90 | 0 | |||
| 30 | 7.3 | 32.70 | 0 | 150 | 0 | |||
| 28 June | 0 | 16.6 | 29.58 | 0 | 1120 | 0 | ||
| 5 | 14.8 | 31.15 | 30 | 650 | 60 | Dt60 | ||
| 4.0 | 10 | 13.7 | 31.94 | 180 | 740 | 190 | Dn150, Dt40 | |
| 15 | 13.4 | 32.09 | 30 | 490 | 80 | Dn60, Dr20 | ||
| 20 | 13.0 | 32.18 | 40 | 300 | 10 | Dr10 | ||
| 25 | 12.8 | 32.22 | 0 | 70 | 10 | Dn10 | ||
| 30 | 12.3 | 32.33 | 0 | 50 | 10 | Dn10 | ||
| 11 August | 0 | 22.6 | 31.14 | 0 | 0 | 0 | ||
| 5 | 20.7 | 31.67 | 0 | 0 | 50 | Dt50 | ||
| 10.5 | 10 | 16.9 | 32.37 | 0 | 10 | 30 | Dt30 | |
| 15 | 12.7 | 32.64 | 0 | 0 | 30 | Dt20, Dr10 | ||
| 20 | 10.8 | 32.95 | 10 | 0 | 0 | |||
| 25 | 8.6 | 32.95 | 50 | 0 | 10 | Dt10 | ||
| 30 | 7.9 | 33.02 | 90 | 20 | 0 | |||
| Scallop | Mussel | Scallop | Mussel | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 5 | 95 | 99 | 1 | 5 | 95 | 99 | n | 1 | 5 | 95 | 99 | 1 | 5 | 95 | 99 |
| 5 | 75.6 | 82.1 | 119.0 | 126.3 | 49.5 | 60.4 | 144.4 | 163.7 | 5 | 72.5 | 80.7 | 120.7 | 130.3 | 44.3 | 58.2 | 149.8 | 172.0 |
| 6 | 77.7 | 84.0 | 117.0 | 123.7 | 52.0 | 63.9 | 139.4 | 155.8 | 6 | 75.6 | 82.3 | 118.8 | 127.2 | 48.8 | 61.3 | 144.6 | 164.2 |
| 7 | 80.0 | 85.4 | 114.9 | 120.4 | 56.2 | 66.9 | 134.8 | 148.8 | 7 | 76.6 | 83.5 | 116.8 | 124.4 | 51.3 | 63.8 | 139.8 | 157.2 |
| 8 | 81.1 | 86.5 | 113.9 | 119.0 | 58.5 | 69.5 | 132.6 | 144.4 | 8 | 78.4 | 84.7 | 115.7 | 122.9 | 54.9 | 66.5 | 137.3 | 154.3 |
| 9 | 82.9 | 87.6 | 112.9 | 117.6 | 61.9 | 71.8 | 129.8 | 140.3 | 9 | 79.2 | 85.5 | 114.3 | 121.1 | 56.5 | 67.8 | 133.9 | 150.0 |
| 10 | 84.4 | 88.5 | 111.6 | 116.0 | 64.1 | 73.7 | 126.9 | 138.6 | 10 | 80.7 | 86.3 | 114.0 | 120.1 | 59.4 | 69.8 | 132.6 | 147.9 |
| 11 | 85.5 | 89.3 | 111.0 | 114.7 | 67.0 | 75.9 | 124.8 | 135.4 | 11 | 81.4 | 86.8 | 113.3 | 119.1 | 60.6 | 70.4 | 131.4 | 145.4 |
| 12 | 86.1 | 89.8 | 110.4 | 114.1 | 69.4 | 77.4 | 123.7 | 132.1 | 12 | 82.4 | 87.4 | 112.9 | 118.8 | 62.5 | 72.0 | 130.7 | 144.1 |
| 13 | 87.4 | 90.7 | 109.4 | 112.9 | 70.6 | 78.5 | 121.6 | 129.7 | 13 | 82.9 | 87.9 | 112.2 | 117.6 | 63.5 | 73.0 | 128.8 | 140.9 |
| 14 | 87.8 | 91.2 | 108.6 | 112.1 | 72.5 | 79.7 | 119.9 | 127.7 | 14 | 83.6 | 88.5 | 112.1 | 117.4 | 65.3 | 74.2 | 128.7 | 140.8 |
| 15 | 88.7 | 91.7 | 108.0 | 111.1 | 74.2 | 81.2 | 118.9 | 126.3 | 15 | 84.5 | 88.9 | 111.6 | 116.3 | 65.6 | 75.1 | 126.8 | 137.8 |
| 16 | 89.7 | 92.5 | 107.6 | 110.3 | 75.0 | 82.2 | 117.5 | 124.2 | 16 | 84.6 | 89.2 | 111.0 | 115.6 | 66.8 | 75.9 | 126.0 | 136.9 |
| 17 | 90.0 | 92.8 | 107.1 | 109.7 | 77.6 | 83.7 | 116.5 | 122.4 | 17 | 85.1 | 89.5 | 110.7 | 115.1 | 67.2 | 76.6 | 124.9 | 136.2 |
| 18 | 90.8 | 93.2 | 106.5 | 109.1 | 78.5 | 84.8 | 115.1 | 120.4 | 18 | 85.8 | 89.8 | 110.6 | 115.2 | 68.9 | 77.2 | 124.3 | 135.3 |
| 19 | 91.4 | 93.6 | 106.2 | 108.4 | 80.0 | 85.6 | 113.8 | 119.2 | 19 | 86.0 | 90.0 | 110.2 | 114.7 | 69.9 | 77.5 | 123.9 | 134.4 |
| 20 | 92.0 | 94.0 | 105.8 | 107.8 | 81.1 | 86.7 | 112.9 | 117.3 | 20 | 85.8 | 90.2 | 109.9 | 114.0 | 69.5 | 78.0 | 123.2 | 133.6 |
| 21 | 92.6 | 94.5 | 105.2 | 107.2 | 82.2 | 87.4 | 111.9 | 116.0 | 21 | 86.8 | 90.6 | 109.6 | 113.9 | 70.5 | 78.8 | 122.6 | 132.3 |
| 22 | 93.1 | 94.9 | 104.9 | 106.6 | 83.7 | 88.4 | 110.8 | 114.5 | 22 | 87.1 | 90.8 | 109.4 | 113.6 | 71.0 | 79.2 | 122.0 | 132.7 |
| 23 | 93.5 | 95.2 | 104.5 | 106.3 | 84.7 | 89.2 | 110.1 | 113.5 | 23 | 87.2 | 91.0 | 109.3 | 113.2 | 72.0 | 79.8 | 121.6 | 131.1 |
| 24 | 94.1 | 95.7 | 104.0 | 105.5 | 86.1 | 90.2 | 108.8 | 111.7 | 24 | 87.4 | 91.0 | 109.2 | 113.0 | 72.3 | 79.9 | 121.3 | 130.5 |
| 25 | 94.6 | 96.1 | 103.6 | 105.0 | 87.3 | 91.1 | 107.9 | 110.3 | 25 | 88.0 | 91.3 | 109.1 | 113.1 | 73.3 | 80.5 | 121.1 | 130.4 |
| ν | Two-Tailed Probability | |
|---|---|---|
| 0.10 | 0.05 | |
| 2 | 2.9200 | 4.3027 |
| 3 | 2.3534 | 3.1824 |
| 4 | 2.1318 | 2.7764 |
| 5 | 2.0150 | 2.5706 |
| 6 | 1.9432 | 2.4469 |
| 7 | 1.8946 | 2.3646 |
| 8 | 1.8595 | 2.3060 |
| 9 | 1.8331 | 2.2622 |
| 10 | 1.8125 | 2.2281 |
| 11 | 1.7959 | 2.2010 |
| 12 | 1.7823 | 2.1788 |
| 13 | 1.7709 | 2.1604 |
| 14 | 1.7613 | 2.1448 |
| 15 | 1.7531 | 2.1314 |
| 16 | 1.7459 | 2.1199 |
| 17 | 1.7396 | 2.1098 |
| 18 | 1.7341 | 2.1009 |
| 19 | 1.7291 | 2.0930 |
| 20 | 1.7247 | 2.0860 |
| 21 | 1.7207 | 2.0796 |
| 22 | 1.7171 | 2.0739 |
| 23 | 1.7139 | 2.0687 |
| 24 | 1.7109 | 2.0639 |
| 25 | 1.7081 | 2.0595 |
| 26 | 1.7056 | 2.0555 |
| 27 | 1.7033 | 2.0518 |
| 28 | 1.7011 | 2.0484 |
| 29 | 1.6991 | 2.0452 |
| 30 | 1.6973 | 2.0423 |
| 50 | 1.6759 | 2.0086 |
| 100 | 1.6602 | 1.9840 |
| ∞ | 1.6449 | 1.9600 |
| n | t (α = 0.05) | Sample Standard Deviation (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 550 | 600 | 650 | ||
| 3 | 4.3027 | 248.4 | 372.6 | 496.8 | 621.0 | 745.2 | 869.5 | 993.7 | 1117.9 | 1242.1 | 1366.3 | 1490.5 | 1614.7 |
| 4 | 3.1825 | 159.1 | 238.7 | 318.3 | 397.8 | 477.4 | 556.9 | 636.5 | 716.1 | 795.6 | 875.2 | 954.8 | 1034.3 |
| 5 | 2.7764 | 124.2 | 186.2 | 248.3 | 310.4 | 372.5 | 434.6 | 496.7 | 558.7 | 620.8 | 682.9 | 745.0 | 807.1 |
| 6 | 2.5706 | 104.9 | 157.4 | 209.9 | 262.4 | 314.8 | 367.3 | 419.8 | 472.2 | 524.7 | 577.2 | 629.7 | 682.1 |
| 7 | 2.4469 | 92.5 | 138.7 | 185.0 | 231.2 | 277.5 | 323.7 | 369.9 | 416.2 | 462.4 | 508.7 | 554.9 | 601.1 |
| 8 | 2.3646 | 83.6 | 125.4 | 167.2 | 209.0 | 250.8 | 292.6 | 334.4 | 376.2 | 418.0 | 459.8 | 501.6 | 543.4 |
| 9 | 2.3060 | 76.9 | 115.3 | 153.7 | 192.2 | 230.6 | 269.0 | 307.5 | 345.9 | 384.3 | 422.8 | 461.2 | 499.6 |
| 10 | 2.2622 | 71.5 | 107.3 | 143.1 | 178.8 | 214.6 | 250.4 | 286.1 | 321.9 | 357.7 | 393.5 | 429.2 | 465.0 |
| 11 | 2.2281 | 67.2 | 100.8 | 134.4 | 167.9 | 201.5 | 235.1 | 268.7 | 302.3 | 335.9 | 369.5 | 403.1 | 436.7 |
| 12 | 2.2010 | 63.5 | 95.3 | 127.1 | 158.8 | 190.6 | 222.4 | 254.1 | 285.9 | 317.7 | 349.5 | 381.2 | 413.0 |
| 13 | 2.1788 | 60.4 | 90.6 | 120.9 | 151.1 | 181.3 | 211.5 | 241.7 | 271.9 | 302.1 | 332.4 | 362.6 | 392.8 |
| 14 | 2.1604 | 57.7 | 86.6 | 115.5 | 144.3 | 173.2 | 202.1 | 231.0 | 259.8 | 288.7 | 317.6 | 346.4 | 375.3 |
| 15 | 2.1448 | 55.4 | 83.1 | 110.8 | 138.4 | 166.1 | 193.8 | 221.5 | 249.2 | 276.9 | 304.6 | 332.3 | 360.0 |
| 16 | 2.1315 | 53.3 | 79.9 | 106.6 | 133.2 | 159.9 | 186.5 | 213.2 | 239.8 | 266.4 | 293.1 | 319.7 | 346.4 |
| 17 | 2.1199 | 51.4 | 77.1 | 102.8 | 128.5 | 154.2 | 180.0 | 205.7 | 231.4 | 257.1 | 282.8 | 308.5 | 334.2 |
| 18 | 2.1098 | 49.7 | 74.6 | 99.5 | 124.3 | 149.2 | 174.0 | 198.9 | 223.8 | 248.6 | 273.5 | 298.4 | 323.2 |
| 19 | 2.1009 | 48.2 | 72.3 | 96.4 | 120.5 | 144.6 | 168.7 | 192.8 | 216.9 | 241.0 | 265.1 | 289.2 | 313.3 |
| 20 | 2.0930 | 46.8 | 70.2 | 93.6 | 117.0 | 140.4 | 163.8 | 187.2 | 210.6 | 234.0 | 257.4 | 280.8 | 304.2 |
| n | t (α = 0.10) | Sample Standard Deviation (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 550 | 600 | 650 | ||
| 3 | 2.9200 | 168.6 | 252.9 | 337.2 | 421.5 | 505.8 | 590.1 | 674.3 | 758.6 | 842.9 | 927.2 | 1011.5 | 1095.8 |
| 4 | 2.3534 | 117.7 | 176.5 | 235.3 | 294.2 | 353.0 | 411.8 | 470.7 | 529.5 | 588.4 | 647.2 | 706.0 | 764.9 |
| 5 | 2.1318 | 95.3 | 143.0 | 190.7 | 238.3 | 286.0 | 333.7 | 381.3 | 429.0 | 476.7 | 524.4 | 572.0 | 619.7 |
| 6 | 2.0150 | 82.3 | 123.4 | 164.5 | 205.7 | 246.8 | 287.9 | 329.0 | 370.2 | 411.3 | 452.4 | 493.6 | 534.7 |
| 7 | 1.9432 | 73.4 | 110.2 | 146.9 | 183.6 | 220.3 | 257.1 | 293.8 | 330.5 | 367.2 | 404.0 | 440.7 | 477.4 |
| 8 | 1.8946 | 67.0 | 100.5 | 134.0 | 167.5 | 201.0 | 234.4 | 267.9 | 301.4 | 334.9 | 368.4 | 401.9 | 435.4 |
| 9 | 1.8595 | 62.0 | 93.0 | 124.0 | 155.0 | 186.0 | 216.9 | 247.9 | 278.9 | 309.9 | 340.9 | 371.9 | 402.9 |
| 10 | 1.8331 | 58.0 | 87.0 | 115.9 | 144.9 | 173.9 | 202.9 | 231.9 | 260.9 | 289.8 | 318.8 | 347.8 | 376.8 |
| 11 | 1.8125 | 54.6 | 82.0 | 109.3 | 136.6 | 163.9 | 191.3 | 218.6 | 245.9 | 273.2 | 300.6 | 327.9 | 355.2 |
| 12 | 1.7959 | 51.8 | 77.8 | 103.7 | 129.6 | 155.5 | 181.5 | 207.4 | 233.3 | 259.2 | 285.1 | 311.1 | 337.0 |
| 13 | 1.7823 | 49.4 | 74.1 | 98.9 | 123.6 | 148.3 | 173.0 | 197.7 | 222.4 | 247.2 | 271.9 | 296.6 | 321.3 |
| 14 | 1.7709 | 47.3 | 71.0 | 94.7 | 118.3 | 142.0 | 165.7 | 189.3 | 213.0 | 236.6 | 260.3 | 284.0 | 307.6 |
| 15 | 1.7613 | 45.5 | 68.2 | 91.0 | 113.7 | 136.4 | 159.2 | 181.9 | 204.6 | 227.4 | 250.1 | 272.9 | 295.6 |
| 16 | 1.7530 | 43.8 | 65.7 | 87.7 | 109.6 | 131.5 | 153.4 | 175.3 | 197.2 | 219.1 | 241.0 | 263.0 | 284.9 |
| 17 | 1.7459 | 42.3 | 63.5 | 84.7 | 105.9 | 127.0 | 148.2 | 169.4 | 190.5 | 211.7 | 232.9 | 254.1 | 275.2 |
| 18 | 1.7396 | 41.0 | 61.5 | 82.0 | 102.5 | 123.0 | 143.5 | 164.0 | 184.5 | 205.0 | 225.5 | 246.0 | 266.5 |
| 19 | 1.7341 | 39.8 | 59.7 | 79.6 | 99.5 | 119.3 | 139.2 | 159.1 | 179.0 | 198.9 | 218.8 | 238.7 | 258.6 |
| 20 | 1.7291 | 38.7 | 58.0 | 77.3 | 96.7 | 116.0 | 135.3 | 154.7 | 174.0 | 193.3 | 212.7 | 232.0 | 251.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsushima, R.; Uchida, H.; Watanabe, R.; Oikawa, H.; Oogida, I.; Kosaka, Y.; Kanamori, M.; Akamine, T.; Suzuki, T. Anatomical Distribution of Diarrhetic Shellfish Toxins (DSTs) in the Japanese Scallop Patinopecten yessoensis and Individual Variability in Scallops and Mytilus edulis Mussels: Statistical Considerations. Toxins 2018, 10, 395. https://doi.org/10.3390/toxins10100395
Matsushima R, Uchida H, Watanabe R, Oikawa H, Oogida I, Kosaka Y, Kanamori M, Akamine T, Suzuki T. Anatomical Distribution of Diarrhetic Shellfish Toxins (DSTs) in the Japanese Scallop Patinopecten yessoensis and Individual Variability in Scallops and Mytilus edulis Mussels: Statistical Considerations. Toxins. 2018; 10(10):395. https://doi.org/10.3390/toxins10100395
Chicago/Turabian StyleMatsushima, Ryoji, Hajime Uchida, Ryuichi Watanabe, Hiroshi Oikawa, Izumi Oogida, Yuki Kosaka, Makoto Kanamori, Tatsuro Akamine, and Toshiyuki Suzuki. 2018. "Anatomical Distribution of Diarrhetic Shellfish Toxins (DSTs) in the Japanese Scallop Patinopecten yessoensis and Individual Variability in Scallops and Mytilus edulis Mussels: Statistical Considerations" Toxins 10, no. 10: 395. https://doi.org/10.3390/toxins10100395
APA StyleMatsushima, R., Uchida, H., Watanabe, R., Oikawa, H., Oogida, I., Kosaka, Y., Kanamori, M., Akamine, T., & Suzuki, T. (2018). Anatomical Distribution of Diarrhetic Shellfish Toxins (DSTs) in the Japanese Scallop Patinopecten yessoensis and Individual Variability in Scallops and Mytilus edulis Mussels: Statistical Considerations. Toxins, 10(10), 395. https://doi.org/10.3390/toxins10100395





