Comparison of the ISU, NCI, MSM, and SPADE Methods for Estimating Usual Intake: A Simulation Study of Nutrients Consumed Daily
Abstract
:1. Introduction
2. Materials and Methods
- The ratio of the shifted, power-transformed observed intakes is adjusted to take into account nuisance effects, such as day of the week and interview mode (telephone or in-person). Construct smoothed daily intakes by undoing the initial power transformation and shifting for the adjusted observations.
- A grafted polynomial function is fit to the normal probability plot of the smoothed intakes using least-squares. The inverse of the fitted function is used to transform the smoothed intakes to normality.
- Moment estimates of variance components are computed for the transformed intakes, and an estimate of the normal-scale usual intake distribution is obtained,
- A grafted cubic and a 9-point approximation to use to transform the normal-scale usual intake distribution to original scale.
- The observed intakes are transformed to improve normality by means of a one-parameter Box-Cox transformation, indicated by λ in this paper.
- A linear mixed effects model on the transformed intake data is fit to estimate the mean and the within- and between-person variances.
- (value to be set) pseudo-person intakes from a normal distribution is simulated with mean equal to the estimated mean and variance equal to the between-person variance.
- The simulated values by a 9-point approximation is back-transformed, which involves the estimated Box-Cox parameter and the within-person variation.
- A linear regression model is applied to the data and the residuals are used for the shrinkage part of the MSM method.
- The fitted model residuals are transformed to normality by means of a two-parameter Box-Cox transformation, with λ restricted to .
- The within- and between-person variances are estimated by means of the transformed residuals.
- The back-transformation is defined by a closed formula, involving the estimated λ and the within-person variance.
- The distribution is estimated by the inverse regression model after the back-transformation to the original scale of the residuals.
- The observed intakes are transformed by means of a one-parameter Box-Cox transformation.
- A linear mixed effects model on the transformed scale is used to estimate the mean and within-person and between-person variances.
- The mean on the transformed scale is directly back-transformed by Gaussian Quadrature, using the total variance of the model and the Box-Cox transformation parameter λ.
- The percentiles on the transformed scale correspond exactly with the percentiles on the original scale, and their back-transformation by Gaussian Quadrature involves the within-person variance and λ [19]. The distribution is calculated directly in the back-transformation step.
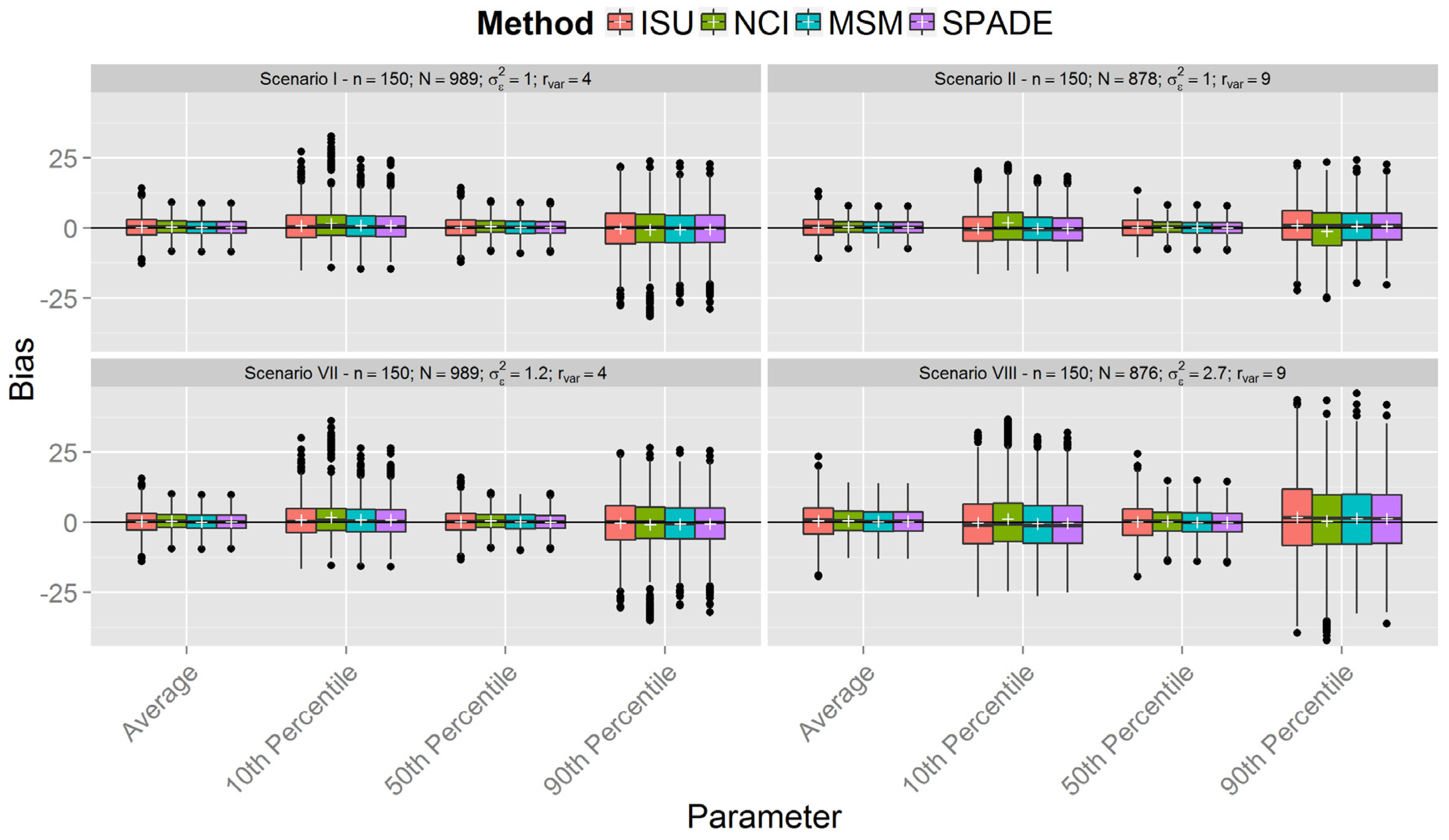
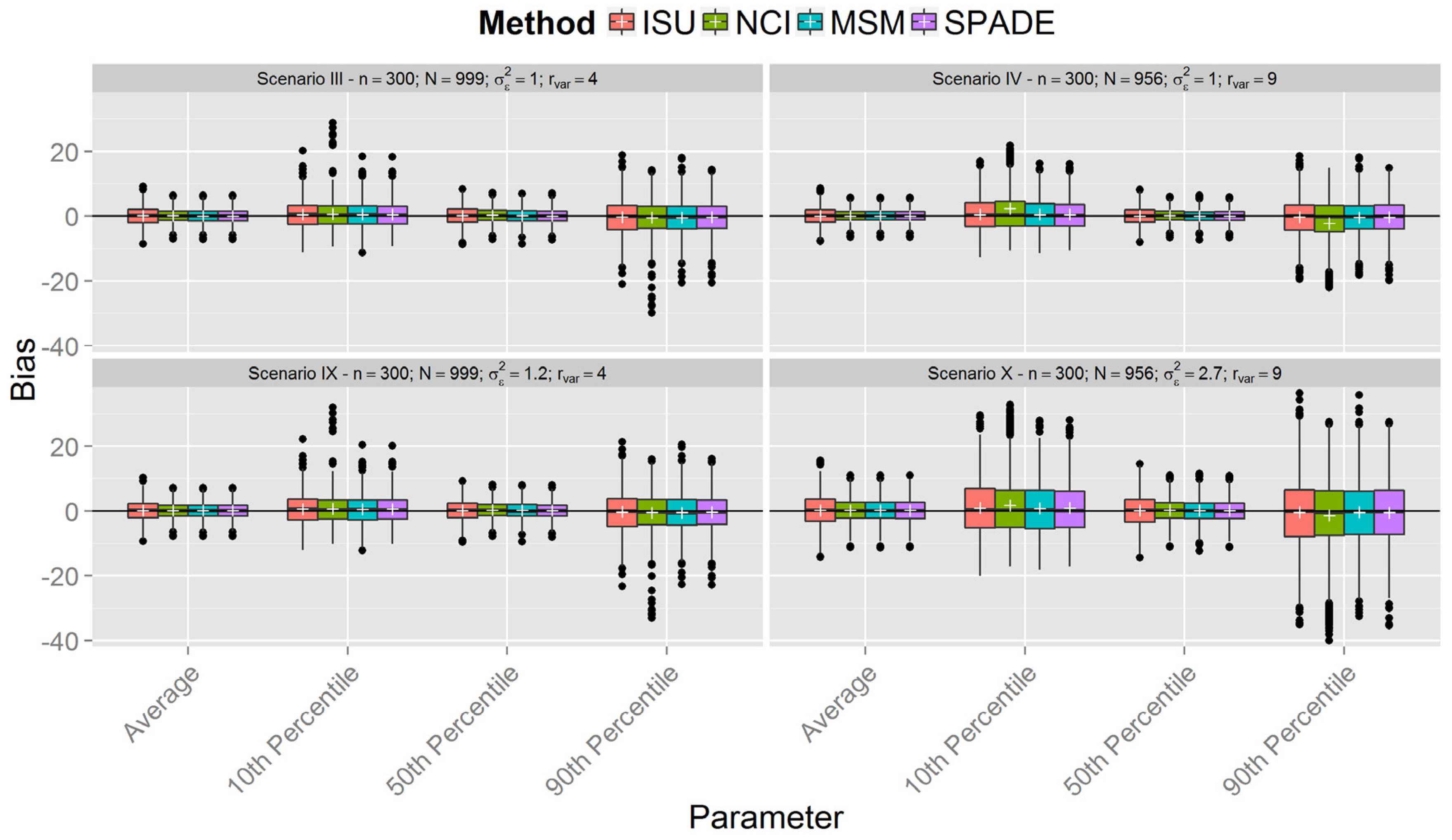
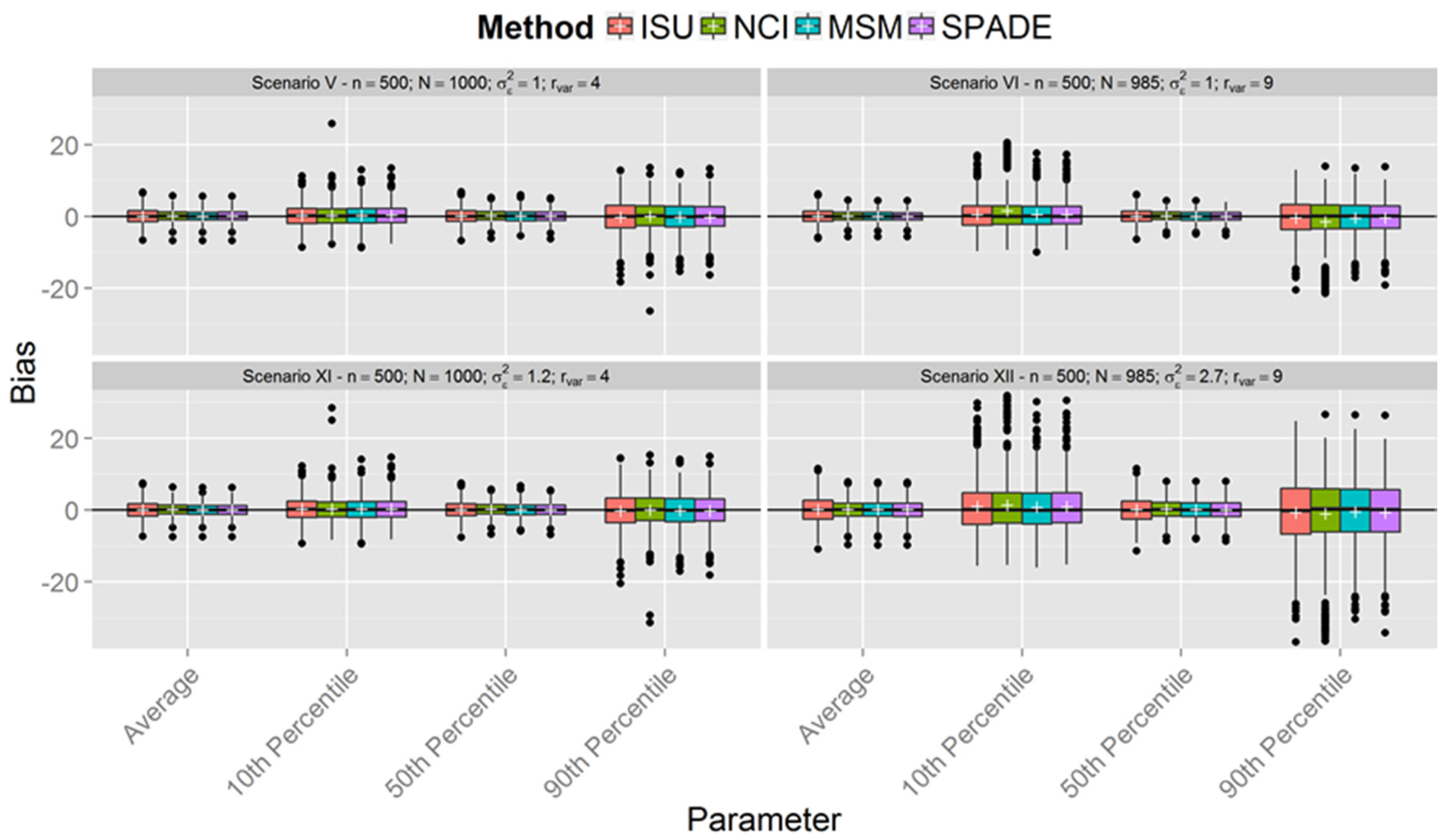
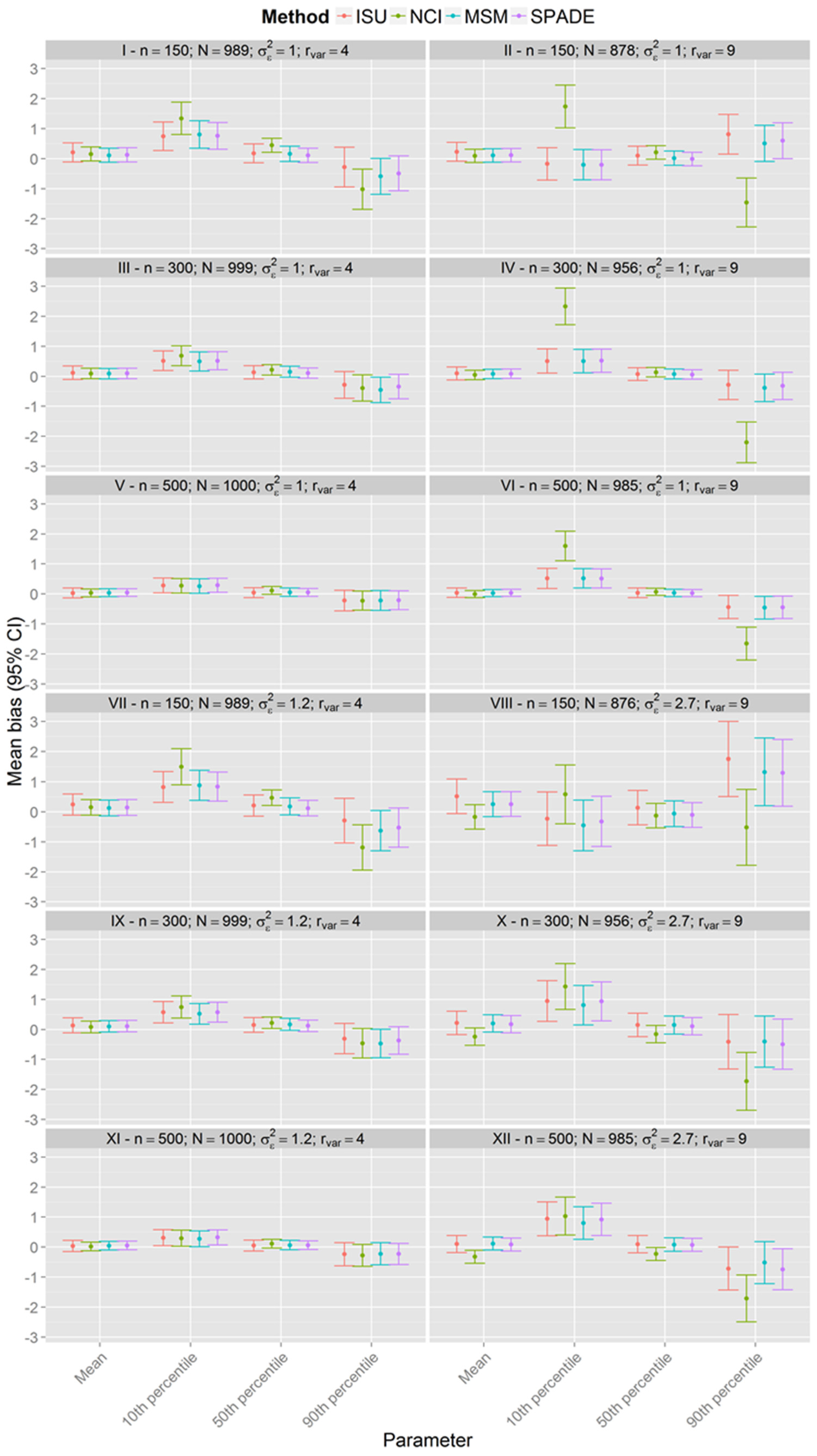
Simulations
| Scenario | n | Within-Person Variance | Between-Person Variance | Variance Ratio |
| I | 150 | 1 | 0.25 | 4 |
| II | 0.11 | 9 | ||
| III | 300 | 0.25 | 4 | |
| IV | 0.11 | 9 | ||
| V | 500 | 0.25 | 4 | |
| VI | 0.11 | 9 | ||
| VII | 150 | 1.2 | 0.3 | 4 |
| VIII | 2.7 | 9 | ||
| IX | 300 | 1.2 | 4 | |
| X | 2.7 | 9 | ||
| XI | 500 | 1.2 | 4 | |
| XII | 2.7 | 9 |
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Willett, W. Nutritional Epidemiology, Monographs in Epidemiology and Biostatistics, 3rd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2013. [Google Scholar]
- Slob, W. Modeling long-term exposure of the whole population to chemicals in food. Risk Anal. Off. Publ. Soc. Risk Anal. 1993, 13, 525–530. [Google Scholar] [CrossRef]
- Gay, C. Estimation of population distributions of habitual nutrient intake based on a short-run weighed food diary. Br. J. Nutr. 2000, 83, 287–293. [Google Scholar] [PubMed]
- Wallace, L.A.; Duan, N.; Ziegenfus, R. Can Long-Term Exposure Distributions Be Predicted from Short-Term Measurements? Risk Anal. 1994, 14, 75–85. [Google Scholar] [CrossRef] [PubMed]
- Buck, R.J.; Hammerstrom, K.A.; Ryan, P.B. Estimating long-term exposures from short-term measurements. J. Expo. Anal. Environ. Epidemiol. 1995, 5, 359–373. [Google Scholar] [PubMed]
- Nusser, S.M.; Carriquiry, A.L.; Dodd, K.W.; Fuller, W.A. A Semiparametric Transformation Approach to Estimating Usual Daily Intake Distributions. J. Am. Stat. Assoc. 1996, 91, 1440–1449. [Google Scholar] [CrossRef]
- Guenther, P.M.; Kott, P.S.; Carriquiry, A.L. Development of an approach for estimating usual nutrient intake distributions at the population level. J. Nutr. 1997, 127, 1106–1112. [Google Scholar] [PubMed]
- Chang, H.-Y.; Suchindran, C.M.; Pan, W.-H. Using the overdispersed exponential family to estimate the distribution of usual daily intakes of people aged between 18 and 28 in Taiwan. Stat. Med. 2001, 20, 2337–2350. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, K.; Boeing, H.; Dufour, A.; Volatier, J.L.; Telman, J.; Virtanen, M.; Becker, W.; De Henauw, S.; EFCOSUM Group. Estimating the distribution of usual dietary intake by short-term measurements. Eur. J. Clin. Nutr. 2002, 56 (Suppl. 2), S53–S62. [Google Scholar] [CrossRef] [PubMed]
- Tooze, J.A.; Grunwald, G.K.; Jones, R.H. Analysis of repeated measures data with clumping at zero. Stat. Methods Med. Res. 2002, 11, 341–355. [Google Scholar] [CrossRef] [PubMed]
- Tooze, J.A.; Midthune, D.; Dodd, K.W.; Freedman, L.S.; Krebs-Smith, S.M.; Subar, A.F.; Guenther, P.M.; Carroll, R.J.; Kipnis, V. A new statistical method for estimating the usual intake of episodically consumed foods with application to their distribution. J. Am. Diet. Assoc. 2006, 106, 1575–1587. [Google Scholar] [CrossRef] [PubMed]
- Slob, W. Probabilistic dietary exposure assessment taking into account variability in both amount and frequency of consumption. Food Chem. Toxicol. Int. J. Publ. Br. Ind. Biol. Res. Assoc. 2006, 44, 933–951. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Waijers, P.M.C.M.; Dekkers, A.L.M.; Boer, J.M.A.; Boshuizen, H.C.; van Rossum, C.T.M. The potential of AGE MODE, an age-dependent model, to estimate usual intakes and prevalences of inadequate intakes in a population. J. Nutr. 2006, 136, 2916–2920. [Google Scholar] [PubMed]
- Staudenmayer, J.; Ruppert, D.; Buonaccorsi, J.P. Density Estimation in the Presence of Heteroscedastic Measurement Error. J. Am. Stat. Assoc. 2008, 103, 726–736. [Google Scholar] [CrossRef]
- Kipnis, V.; Midthune, D.; Buckman, D.W.; Dodd, K.W.; Guenther, P.M.; Krebs-Smith, S.M.; Subar, A.F.; Tooze, J.A.; Carroll, R.J.; Freedman, L.S. Modeling data with excess zeros and measurement error: application to evaluating relationships between episodically consumed foods and health outcomes. Biometrics 2009, 65, 1003–1010. [Google Scholar] [CrossRef] [PubMed]
- Tooze, J.A.; Kipnis, V.; Buckman, D.W.; Carroll, R.J.; Freedman, L.S.; Guenther, P.M.; Krebs-Smith, S.M.; Subar, A.F.; Dodd, K.W. A mixed-effects model approach for estimating the distribution of usual intake of nutrients: The NCI method. Stat. Med. 2010, 29, 2857–2868. [Google Scholar] [CrossRef] [PubMed]
- Haubrock, J.; Nöthlings, U.; Volatier, J.-L.; Dekkers, A.; Ocké, M.; Harttig, U.; Illner, A.-K.; Knüppel, S.; Andersen, L.F.; Boeing, H. European Food Consumption Validation Consortium Estimating usual food intake distributions by using the multiple source method in the EPIC-Potsdam Calibration Study. J. Nutr. 2011, 141, 914–920. [Google Scholar] [CrossRef] [PubMed]
- Nusser, S.M.; Fuller, W.A.; Guenther, P.M. Estimating Usual Dietary Intake Distributions: Adjusting for Measurement Error and Nonnormality in 24-Hour Food Intake Data. In Survey Measurement and Process Quality; Lyberg, L., Biemer, P., Collins, M., De Leeuw, E., Dippo, C., Schwarz, N., Trewin, D., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 689–709. [Google Scholar]
- Dekkers, A.L.M.; Slob, W. Gaussian Quadrature is an efficient method for the back-transformation in estimating the usual intake distribution when assessing dietary exposure. Food Chem. Toxicol. 2012, 50, 3853–3861. [Google Scholar] [CrossRef] [PubMed]
- Goedhart, P.W.; Voet, H.; Knüppel, S.; Dekkers, A.L.M.; Dodd, K.W.; Boeing, H.; Klaveren, J. A Comparison by Simulation of Different Methods to Estimate the Usual Intake Distribution for Episodically Consumed Foods; European Food Safety Authority: Parma, Italy, 2012. [Google Scholar]
- Dekkers, A.L.; Verkaik-Kloosterman, J.; van Rossum, C.T.; Ocke, M.C. SPADE, a New Statistical Program to Estimate Habitual Dietary Intake from Multiple Food Sources and Dietary Supplements. J. Nutr. 2014, 144, 2083–2091. [Google Scholar] [CrossRef] [PubMed]
- Souverein, O.W.; Dekkers, A.L.; Geelen, A.; Haubrock, J.; de Vries, J.H.; Ocké, M.C.; Harttig, U.; Boeing, H.; van’t Veer, P.; EFCOVAL Consortium. Comparing four methods to estimate usual intake distributions. Eur. J. Clin. Nutr. 2011, 65 (Suppl. 1), S92–S101. [Google Scholar] [CrossRef] [PubMed]
- Freedman, L.S.; Midthune, D.; Carroll, R.J.; Krebs-Smith, S.; Subar, A.F.; Troiano, R.P.; Dodd, K.; Schatzkin, A.; Bingham, S.A.; Ferrari, P.; et al. Adjustments to improve the estimation of usual dietary intake distributions in the population. J. Nutr. 2004, 134, 1836–1843. [Google Scholar] [PubMed]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. B Methodol. 1964, 26, 211–252. [Google Scholar]
- SAS|Business Analytics and Business Intelligence Software. Available online: http://www.sas.com/ (accessed on 9 March 2016).
- Iowa State University. Available online: http://www.side.stat.iastate.edu/pc-side.php/ (accessed on 9 March 2016).
- National Cancer Institute. Available online: http://www.riskfactor.cancer.gov/diet/usualintakes/ (accessed on 9 March 2016).
- Harttig, U.; Haubrock, J.; Knüppel, S.; Boeing, H. EFCOVAL Consortium the MSM program: Web-based statistics package for estimating usual dietary intake using the Multiple Source Method. Eur. J. Clin. Nutr. 2011, 65 (Suppl. 1), S87–S91. [Google Scholar] [CrossRef] [PubMed]
- The Multiple Source Method (MSM). Available online: https://msm.dife.de (accessed on 9 March 2016).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- National Institute for Public Health and the Environment. Available online: https://rivm.nl/en/Topics/SPADE (accessed on 9 March 2016).
- McAvay, G.; Rodin, J. Interindividual and intraindividual variation in repeated measures of 24-hour dietary recall in the elderly. Appetite 1988, 11, 97–110. [Google Scholar] [CrossRef]
- AutoHotkey. Available online: http://www.autohotkey.com/ (accessed on 9 March 2016).
- National Research Council (U.S.). Nutrient Adequacy: Assessment Using Food Consumption Surveys; National Academy Press: Washington, DC, USA, 1986. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laureano, G.H.C.; Torman, V.B.L.; Crispim, S.P.; Dekkers, A.L.M.; Camey, S.A. Comparison of the ISU, NCI, MSM, and SPADE Methods for Estimating Usual Intake: A Simulation Study of Nutrients Consumed Daily. Nutrients 2016, 8, 166. https://doi.org/10.3390/nu8030166
Laureano GHC, Torman VBL, Crispim SP, Dekkers ALM, Camey SA. Comparison of the ISU, NCI, MSM, and SPADE Methods for Estimating Usual Intake: A Simulation Study of Nutrients Consumed Daily. Nutrients. 2016; 8(3):166. https://doi.org/10.3390/nu8030166
Chicago/Turabian StyleLaureano, Greice H. C., Vanessa B. L. Torman, Sandra P. Crispim, Arnold L. M. Dekkers, and Suzi A. Camey. 2016. "Comparison of the ISU, NCI, MSM, and SPADE Methods for Estimating Usual Intake: A Simulation Study of Nutrients Consumed Daily" Nutrients 8, no. 3: 166. https://doi.org/10.3390/nu8030166
APA StyleLaureano, G. H. C., Torman, V. B. L., Crispim, S. P., Dekkers, A. L. M., & Camey, S. A. (2016). Comparison of the ISU, NCI, MSM, and SPADE Methods for Estimating Usual Intake: A Simulation Study of Nutrients Consumed Daily. Nutrients, 8(3), 166. https://doi.org/10.3390/nu8030166




