Energy Expenditure Estimation in Children, Adolescents and Adults by Using a Respiratory Magnetometer Plethysmography System and a Deep Learning Model
Abstract
1. Introduction
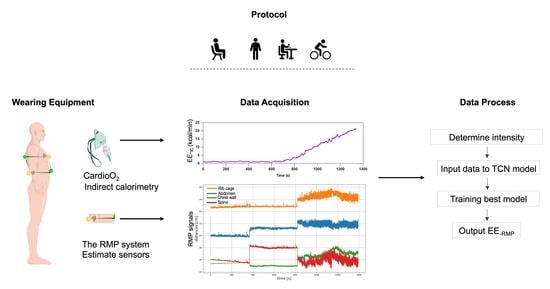
2. Materials and Methods
2.1. Ethical Approval and Subjects
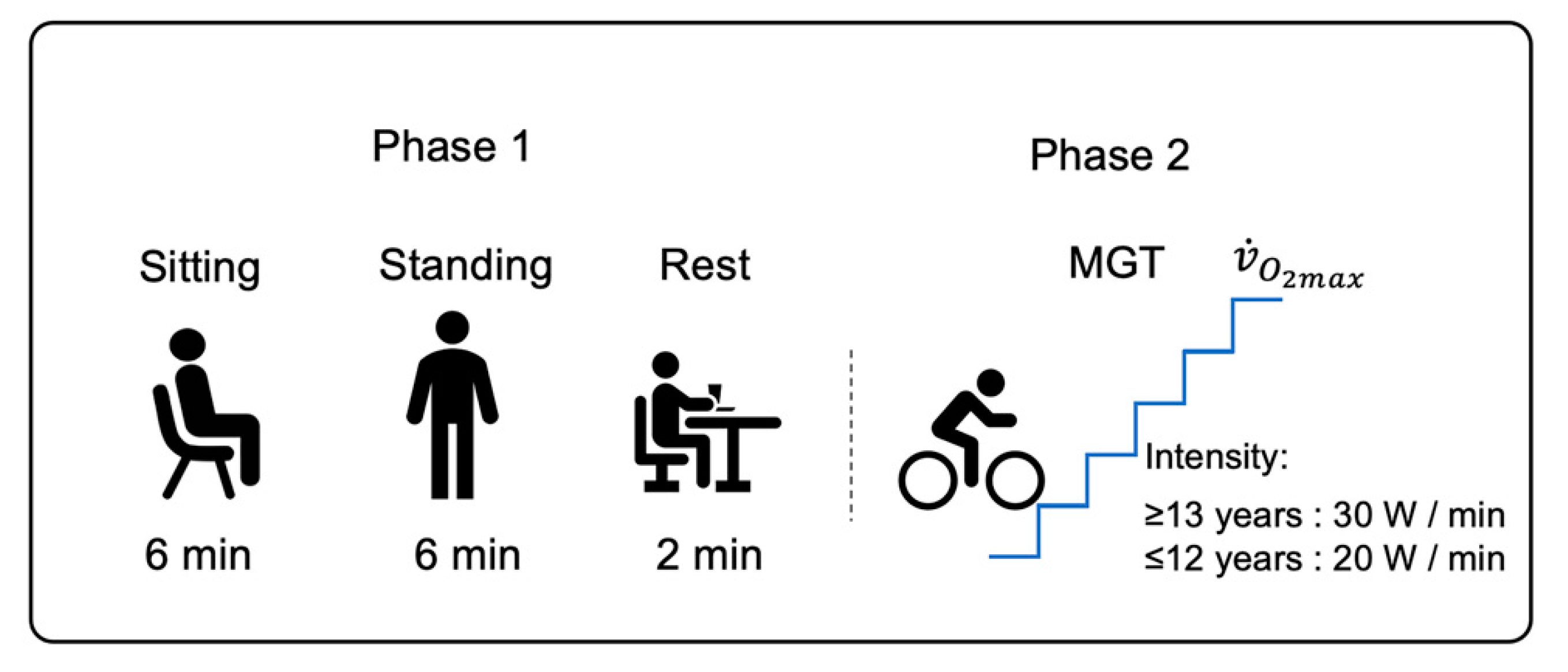
2.2. Protocol
2.2.1. Study Design
2.2.2. Maximal Graded Test
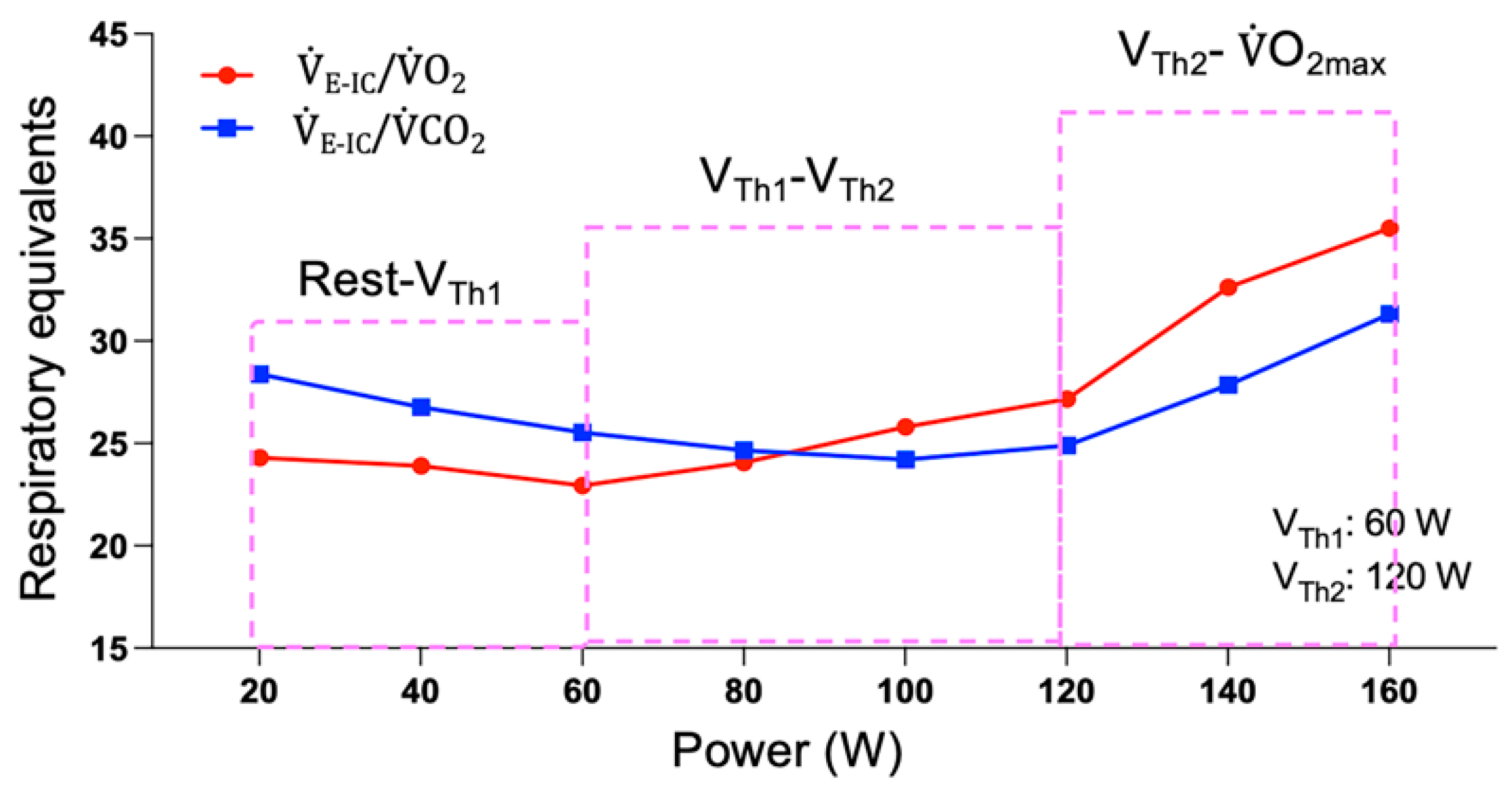
2.2.3. Ventilatory Thresholds
2.2.4. Stage of Development
2.2.5. Anthropometric Characteristics
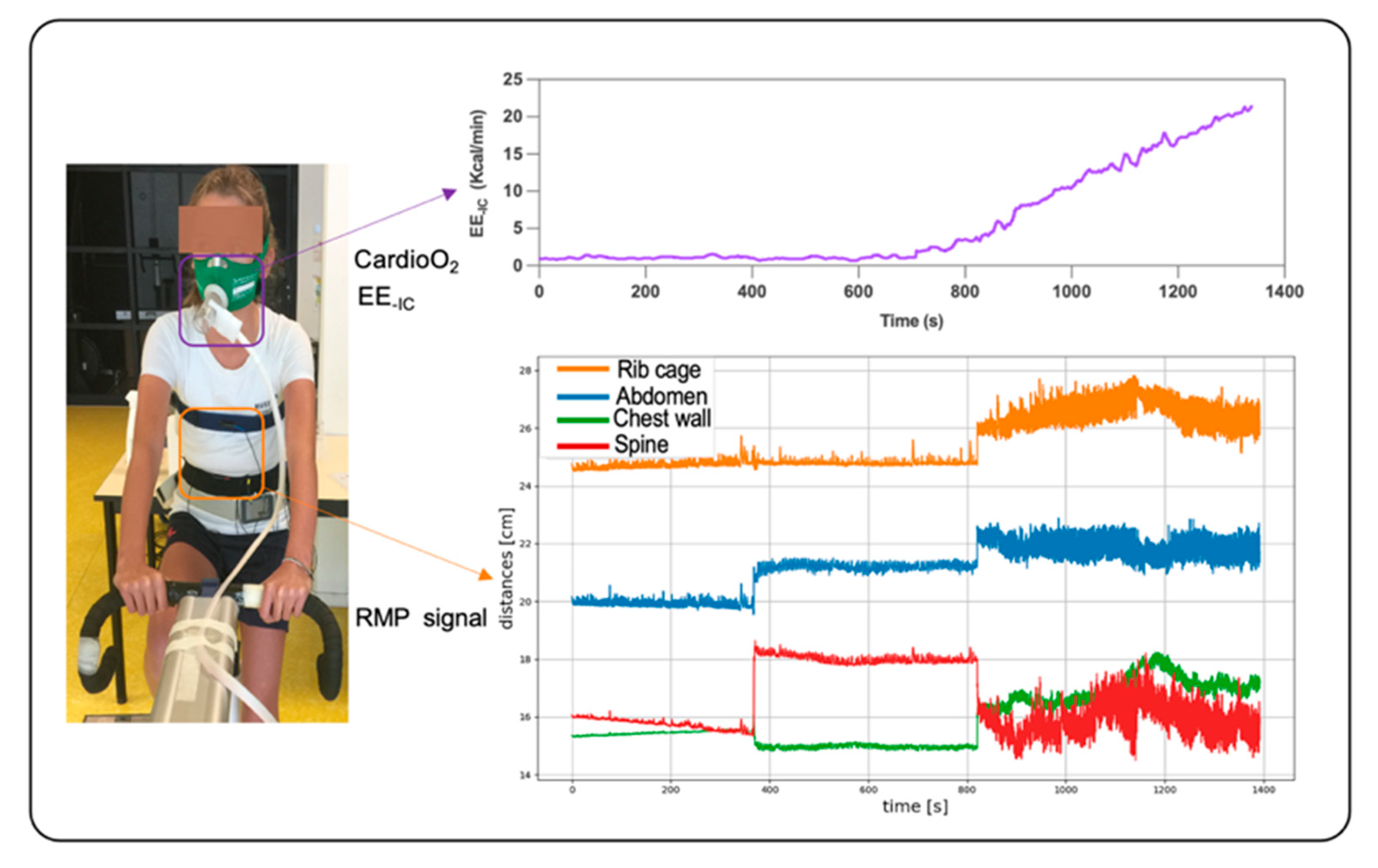
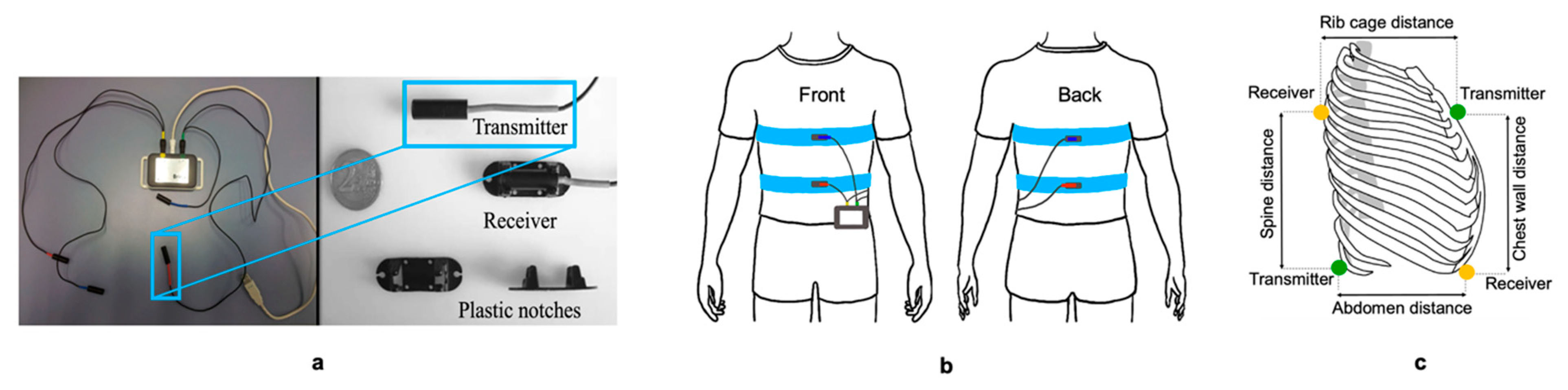
2.3. Measurement Systems
2.3.1. Respiratory Gas Exchange and Heart Rate Measurements
2.3.2. RMP System
2.4. Data Processing
2.4.1. Method for Determining Three Levels of Intensity during the Maximal Graded Test
2.4.2. Window Segmentation and Feature Extraction
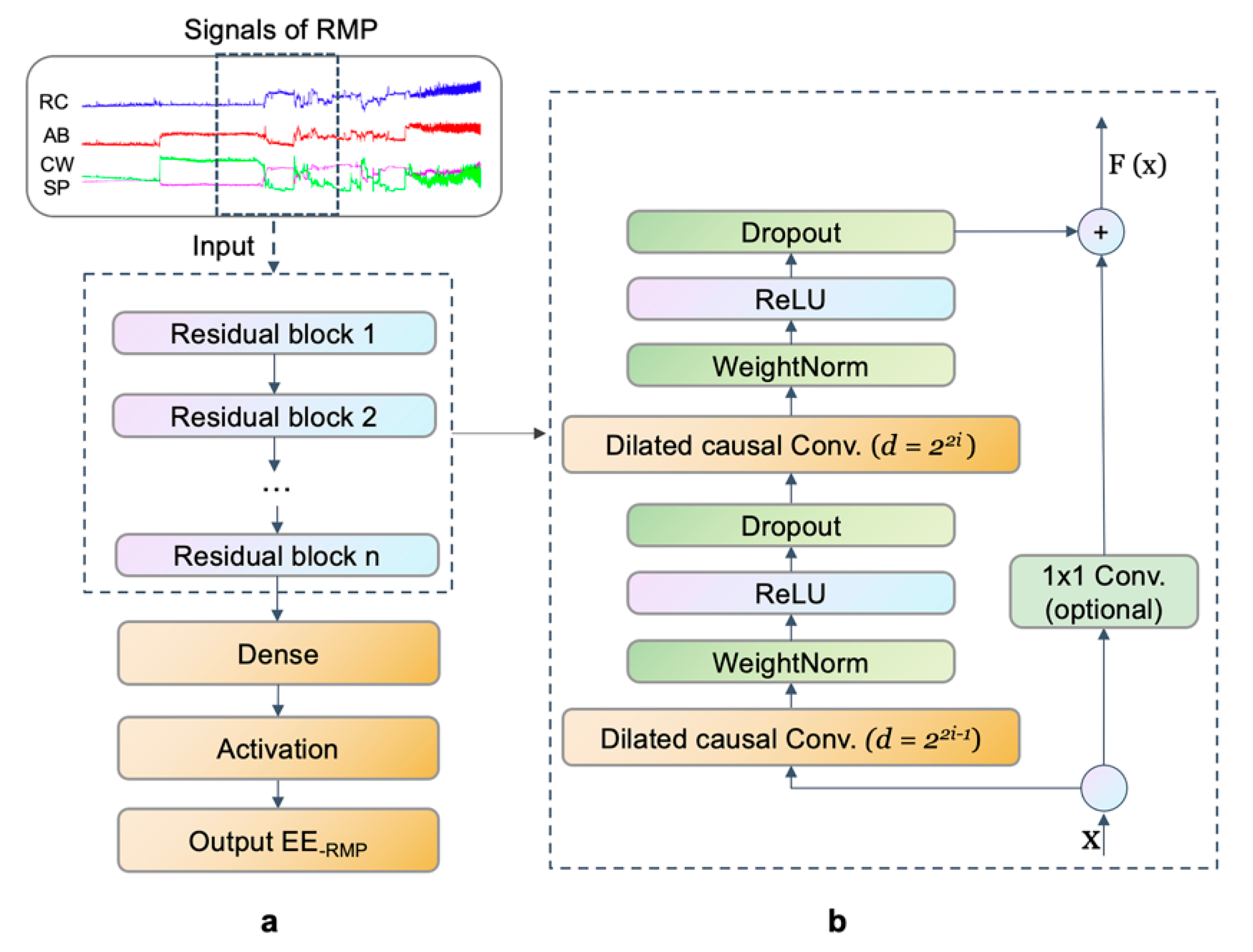
2.4.3. Network Architecture and Training Model
Network Architecture
Training Model
2.5. Statistical Analyses
3. Results
3.1. Model Performance
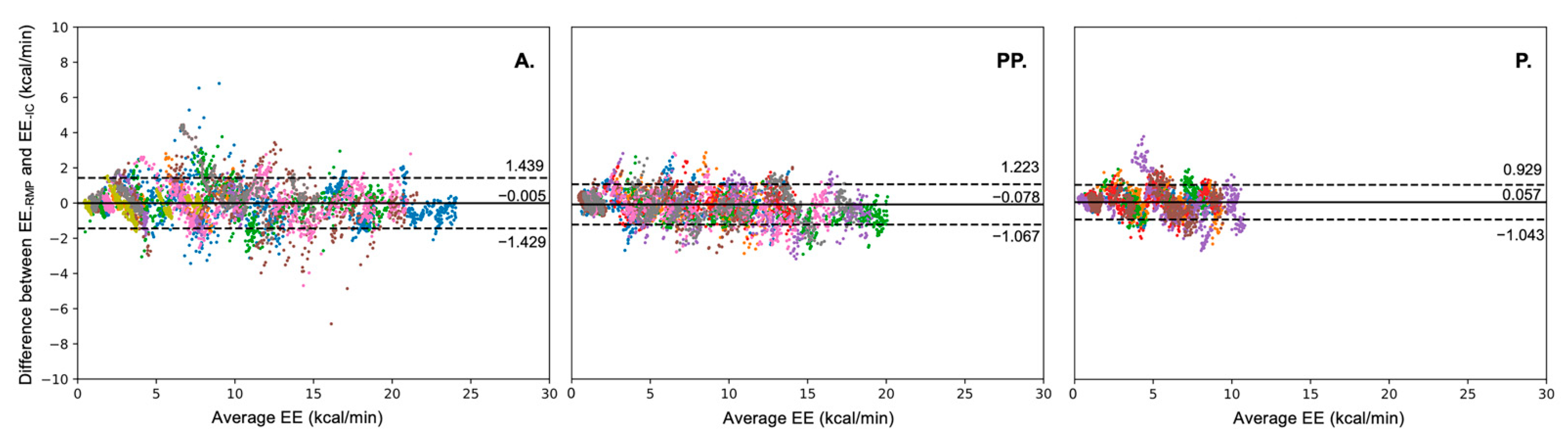
3.2. Comparison of EE-IC and EE-RMP at Different Intensity Levels
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hills, A.P.; Mokhtar, N.; Byrne, N.M. Assessment of physical activity and energy expenditure: An overview of objective measures. Front. Nutr. 2014, 1, 5. [Google Scholar] [CrossRef] [PubMed]
- Knowler, W.C.; Barrett-Connor, E.; Fowler, S.E.; Hamman, R.F.; Lachin, J.M.; Walker, E.A.; Nathan, D.M.; Diabetes Prevention Program Research Group. Reduction in the incidence of type 2 diabetes with lifestyle intervention or metformin. N. Engl. J. Med. 2002, 346, 393–403. [Google Scholar] [CrossRef] [PubMed]
- Manini, T.M.; Everhart, J.E.; Patel, K.V.; Schoeller, D.A.; Colbert, L.H.; Visser, M.; Tylavsky, F.; Bauer, D.C.; Goodpaster, B.H.; Harris, T.B. Daily activity energy expenditure and mortality among older adults. JAMA 2006, 296, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Tuomilehto, J.; Lindström, J.; Eriksson, J.G.; Valle, T.T.; Hämäläinen, H.; Ilanne-Parikka, P.; Keinänen-Kiukaanniemi, S.; Laakso, M.; Louheranta, A.; Rastas, M. Prevention of type 2 diabetes mellitus by changes in lifestyle among subjects with impaired glucose tolerance. N. Engl. J. Med. 2001, 344, 1343–1350. [Google Scholar] [CrossRef] [PubMed]
- Sigal, R.J.; Kenny, G.P.; Wasserman, D.H.; Castaneda-Sceppa, C. Physical activity/exercise and type 2 diabetes. Diabetes Care 2004, 27, 2518–2539. [Google Scholar] [CrossRef]
- Montoye, H.J.; Washburn, R.; Servais, S.; Ertl, A.; Webster, J.G.; Nagle, F.J. Estimation of energy expenditure by a portable accelerometer. Med. Sci. Sport. Exerc. 1983, 15, 403–407. [Google Scholar] [CrossRef]
- Chen, C.; Jafari, R.; Kehtarnavaz, N. Improving human action recognition using fusion of depth camera and inertial sensors. IEEE Trans. Hum.-Mach. Syst. 2014, 45, 51–61. [Google Scholar] [CrossRef]
- Bassett, D.R.; Ainsworth, B.E.; Swartz, A.M.; Strath, S.J.; O’Brien, W.L.; King, G.A. Validity of four motion sensors in measuring moderate intensity physical activity. Med. Sci. Sport. Exerc. 2000, 32, S471–S480. [Google Scholar] [CrossRef] [PubMed]
- Brage, S.; Brage, N.; Franks, P.W.; Ekelund, U.; Wareham, N.J. Reliability and validity of the combined heart rate and movement sensor Actiheart. Eur. J. Clin. Nutr. 2005, 59, 561–570. [Google Scholar] [CrossRef] [PubMed]
- Juul, A.; Jeukendrup, A. Heart rate monitoring: Applications and limitations. Sports Med. 2003, 33, 517–538. [Google Scholar]
- Durnin, J.; Edwards, R. Pulmonary ventilation as an index of energy expenditure. Q. J. Exp. Physiol. Cogn. Med. Sci. 1955, 40, 370–377. [Google Scholar] [CrossRef] [PubMed]
- Ford, A.B.; Hellerstein, H.K. Estimation of energy expenditure from pulmonary ventilation. J. Appl. Physiol. 1959, 14, 891–893. [Google Scholar] [CrossRef] [PubMed]
- Gastinger, S.; Sefati, H.; Nicolas, G.; Sorel, A.; Gratas-Delamarche, A.; Prioux, J. A new method to estimate energy expenditure from abdominal and rib cage distances. Eur. J. Appl. Physiol. 2011, 111, 2823–2835. [Google Scholar] [CrossRef]
- Houssein, A.; Ge, D.; Gastinger, S.; Dumond, R.; Prioux, J. Estimation of respiratory variables from thoracoabdominal breathing distance: A review of different techniques and calibration methods. Physiol. Meas. 2019, 40, 03TR01. [Google Scholar] [CrossRef] [PubMed]
- Gastinger, S.; Sefati, H.; Nicolas, G.; Sorel, A.; Gratas-Delamarche, A.; Prioux, J. Estimates of ventilation from measurements of rib cage and abdominal distances: A portable device. Eur. J. Appl. Physiol. 2010, 109, 1179–1189. [Google Scholar] [CrossRef] [PubMed]
- Dumond, R.; Gastinger, S.; Rahman, H.A.; Le Faucheur, A.; Quinton, P.; Kang, H.; Prioux, J. Estimation of respiratory volume from thoracoabdominal breathing distances: Comparison of two models of machine learning. Eur. J. Appl. Physiol. 2017, 117, 1533–1555. [Google Scholar] [CrossRef] [PubMed]
- Houssein, A.; Ge, D.; Gastinger, S.; Dumond, R.; Prioux, J. A novel algorithm for minute ventilation estimation in remote health monitoring with magnetometer plethysmography. Comput. Biol. Med. 2021, 130, 104189. [Google Scholar] [CrossRef]
- Rosenthal, M.; Bain, S.; Cramer, D.; Helms, P.; Denison, D.; Bush, A.; Warner, J. Lung function in white children aged 4 to 19 years: I—Spirometry. Thorax 1993, 48, 794–802. [Google Scholar] [CrossRef]
- Malhotra, P.; Singh, P.P.; Singh, S.; Sidhu, L. Physical growth of high altitude Spitian boys. J. Hum. Ecol. 2006, 20, 147–151. [Google Scholar] [CrossRef][Green Version]
- Sharipova, O. The features of the physical development, calcium-phosphorus metabolism and mineral density of the bones in children with chronic lung diseases. Med. Health Sci. J. 2011, 5, 76–82. [Google Scholar] [CrossRef]
- Patil, S.S.; Patil, S.R.; Durgawale, P.M. Physical growth pattern among adolescents from Satara District: Using sitting height, leg length, and other anthropometric measurements. J. Datta Meghe Inst. Med. Sci. Univ. 2018, 13, 143. [Google Scholar] [CrossRef]
- Matecki, S.; Prioux, J.; Jaber, S.; Hayot, M.; Prefaut, C.; Ramonatxo, M. Respiratory pressures in boys from 11–17 years old: A semilongitudinal study. Pediatr. Pulmonol. 2003, 35, 368–374. [Google Scholar] [CrossRef] [PubMed]
- Wysocki, M.; Fiamma, M.-N.; Straus, C.; Poon, C.-S.; Similowski, T. Chaotic dynamics of resting ventilatory flow in humans assessed through noise titration. Respir. Physiol. Neurobiol. 2006, 153, 54–65. [Google Scholar] [CrossRef] [PubMed]
- Yeragani, V.K.; Radhakrishna, R.K.; Tancer, M.; Uhde, T. Nonlinear measures of respiration: Respiratory irregularity and increased chaos of respiration in patients with panic disorder. Neuropsychobiology 2002, 46, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Fiamma, M.-N.; Samara, Z.; Baconnier, P.; Similowski, T.; Straus, C. Respiratory inductive plethysmography to assess respiratory variability and complexity in humans. Respir. Physiol. Neurobiol. 2007, 156, 234–239. [Google Scholar] [CrossRef] [PubMed]
- Small, M.; Judd, K.; Lowe, M.; Stick, S. Is breathing in infants chaotic? Dimension estimates for respiratory patterns during quiet sleep. J. Appl. Physiol. 1999, 86, 359–376. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Pande, A.; Mohapatra, P.; Han, J.J. Using deep learning for energy expenditure estimation with wearable sensors. In Proceedings of the 2015 17th International Conference on E-health Networking, Application & Services (HealthCom), Boston, MA, USA, 14–17 October 2015; pp. 501–506. [Google Scholar] [CrossRef]
- Lanningham-Foster, L.; Levine, J.A. Energy Expenditure in Children: The Role of NEAT (Non-exercise Activity Thermogenesis). In Pediatric Obesity; Springer: Berlin/Heidelberg, Germany, 2018; pp. 305–319. [Google Scholar]
- Zhou, F.; Yin, X.; Phillipe, K.; Houssein, A.; Gastinger, S.; Prioux, J. Ventilatory responses at submaximal exercise intensities in healthy children and adolescents during the growth spurt period: A semi-longitudinal study. Eur. J. Appl. Physiol. 2021, 121, 3211–3223. [Google Scholar] [CrossRef]
- De Prado, D.M.L.; Braga, A.M.F.W.; Rondon, M.U.P.; Azevedo, L.F.; Matos, L.D.; Negrão, C.E.; Trombetta, I.C. Cardiorespiratory responses during progressive maximal exercise test in healthy children. Arq. Bras. Cardiol. 2010, 94, 493–499. [Google Scholar] [CrossRef]
- Wasserman, K.; Whipp, B.J.; Koyl, S.; Beaver, W.L. Anaerobic threshold and respiratory gas exchange during exercise. J. Appl. Physiol. 1973, 35, 236–243. [Google Scholar] [CrossRef]
- Tanner, J.M. Growth at Adolescence; Blackwell: Oxford, UK, 1962. [Google Scholar]
- Weiner, J.S.; Lourie, J.A. Practical Human Biology; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Alam, R.; Peden, D.B.; Gong, J.; Lach, J. Non-invasive inference of minute ventilation using wearable ECG and Gaussian process regression. In Proceedings of the 2019 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Chicago, IL, USA, 19–22 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar] [CrossRef]
- Kenny, G.P.; Notley, S.R.; Gagnon, D. Direct calorimetry: A brief historical review of its use in the study of human metabolism and thermoregulation. Eur. J. Appl. Physiol. 2017, 117, 1765–1785. [Google Scholar] [CrossRef]
- Ainslie, P.N.; Reilly, T.; Westerterp, K.R. Estimating human energy expenditure. Sports Med. 2003, 33, 683–698. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Garcia, J.A.; Cvetković, B.; Luštrek, M. A survey on energy expenditure estimation using wearable devices. ACM Comput. Surv. 2020, 53, 1–35. [Google Scholar] [CrossRef]
- Kenny, G.P.; Webb, P.; Ducharme, M.B.; Reardon, F.D.; Jay, O. Calorimetric measurement of postexercise net heat loss and residual body heat storage. Med. Sci. Sport. Exerc. 2008, 40, 1629–1636. [Google Scholar] [CrossRef] [PubMed]
- Kenny, G.P.; Jay, O. Thermometry, calorimetry, and mean body temperature during heat stress. Compr. Physiol. 2011, 3, 1689–1719. [Google Scholar] [CrossRef]
- Westerterp, K.R. Pattern and intensity of physical activity. Nature 2001, 410, 539. [Google Scholar] [CrossRef]
- Chowdhury, E.A.; Western, M.J.; Nightingale, T.E.; Peacock, O.J.; Thompson, D. Assessment of laboratory and daily energy expenditure estimates from consumer multi-sensor physical activity monitors. PLoS ONE 2017, 12, e0171720. [Google Scholar] [CrossRef]
- Adamakis, M. Energy Expenditure of Adolescents During Overground Walking and Running. J. Sci. Sport Exerc. 2022, 1–9. [Google Scholar] [CrossRef]
- Steenbock, B.; Wright, M.N.; Wirsik, N.; Brandes, M. Accelerometry-based prediction of energy expenditure in preschoolers. J. Meas. Phys. Behav. 2019, 2, 94–102. [Google Scholar] [CrossRef]
- Lee, M.; Park, J.-H.; Seo, M.-W.; Kang, S.-K.; Lee, J.-M. A New Equation to Estimate Energy Expenditure Using Heart Rate in Children. Sustainability 2021, 13, 5092. [Google Scholar] [CrossRef]
- Lopez, G.A.; Brønd, J.C.; Andersen, L.B.; Dencker, M.; Arvidsson, D. Validation of SenseWear Armband in children, adolescents, and adults. Scand. J. Med. Sci. Sport. 2018, 28, 487–495. [Google Scholar] [CrossRef] [PubMed]
- Ekelund, U.; Yngve, A.; Brage, S.; Westerterp, K.; Sjöström, M. Body movement and physical activity energy expenditure in children and adolescents: How to adjust for differences in body size and age. Am. J. Clin. Nutr. 2004, 79, 851–856. [Google Scholar] [CrossRef] [PubMed]
- Bitar, A.; Vernet, J.; Coudert, J.; Vermorel, M. Longitudinal changes in body composition, physical capacities and energy expenditure in boys and girls during the onset of puberty. Eur. J. Nutr. 2000, 39, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Hoos, M.B.; Gerver, W.-J.M.; Kester, A.D.; Westerterp, K.R. Physical activity levels in children and adolescents. Int. J. Obes. 2003, 27, 605–609. [Google Scholar] [CrossRef]
- Waters, R.L.; Lunsford, B.R.; Perry, J.; Byrd, R. Energy-speed relationship of walking: Standard tables. J. Orthop. Res. 1988, 6, 215–222. [Google Scholar] [CrossRef]
- Konno, K.; Mead, J. Measurement of the separate volume changes of rib cage and abdomen during breathing. J. Appl. Physiol. 1967, 22, 407–422. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z.; Sun, F.; Wu, T.; Wang, T.; Li, Y. Deep multi-branch two-stage regression network for accurate energy expenditure estimation with ECG and IMU data. IEEE Trans. Biomed. Eng. 2022, 69, 3224–3233. [Google Scholar] [CrossRef]
- Farrahi, V.; Niemelä, M.; Kangas, M.; Korpelainen, R.; Jämsä, T. Calibration and validation of accelerometer-based activity monitors: A systematic review of machine-learning approaches. Gait Posture 2019, 68, 285–299. [Google Scholar] [CrossRef]
- Zhao, Z.; Gong, Z.; Niu, M.; Ma, J.; Wang, H.; Zhang, Z.; Li, Y. Automatic Respiratory Sound Classification Via Multi-Branch Temporal Convolutional Network. In Proceedings of the ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 9102–9106. [Google Scholar] [CrossRef]
- Chowdhury, A.K.; Tjondronegoro, D.; Zhang, J.; Hagenbuchner, M.; Cliff, D.; Trost, S.G. Deep learning for energy expenditure prediction in pre-school children. In Proceedings of the IEEE Conference on Biomedical and Health Informatics (BHI 2018), Las Vegas, NV, USA, 4–7 March 2018. [Google Scholar]
- Nweke, H.F.; Teh, Y.W.; Al-Garadi, M.A.; Alo, U.R. Deep learning algorithms for human activity recognition using mobile and wearable sensor networks: State of the art and research challenges. Expert Syst. Appl. 2018, 105, 233–261. [Google Scholar] [CrossRef]
- Amelard, R.; Hedge, E.T.; Hughson, R.L. Temporal convolutional networks predict dynamic oxygen uptake response from wearable sensors across exercise intensities. NPJ Digit. Med. 2021, 4, 156. [Google Scholar] [CrossRef] [PubMed]
- Prioux, J.; Ramonatxo, M.; Hayot, M.; Mucci, P.; Préfaut, C. Effect of ageing on the ventilatory response and lactate kinetics during incremental exercise in man. Eur. J. Appl. Physiol. 2000, 81, 100–107. [Google Scholar] [CrossRef] [PubMed]


| Groups | N | Pubertal Stages (I–V) | Age (years) | Height (cm) | BM (kg) | BMI (kg/m2) | O2max (l/min) |
|---|---|---|---|---|---|---|---|
| A. | 9 | 28.11 ± 2.93 | 175.67 ± 12.98 | 70.66 ± 18.51 | 22.48 ± 2.82 | 3.16 ± 1.21 | |
| PP. | 8 | IV & V | 14.75 ± 0.71 | 172.06 ± 7.79 | 56.61 ± 7.61 | 19.06 ± 1.12 | 3.29 ± 0.58 |
| P. | 6 | II & III | 11.67 ± 0.52 | 152.10 ± 4.29 | 41.65 ± 4.84 | 18.02 ± 2.29 | 1.99 ± 0.17 |
| EE | O2 | ||||
|---|---|---|---|---|---|
| Group | Samples | R2 | RMSE | R2 | RMSE |
| (Valid/Train) | (kcal/min) | (ml/min/kg) | |||
| A. | 1590/6360 | 0.98 | 0.74 | 0.98 | 2.09 |
| PP. | 1408/5636 | 0.98 | 0.61 | 0.98 | 2.04 |
| P. | 975/3900 | 0.97 | 0.49 | 0.97 | 2.24 |
| Group | Intensity | EE-IC ± SD | EE-RMP ± SD | Mean Differences | |
|---|---|---|---|---|---|
| Kcal/min | Kcal/min | (EE-RMP–EE-IC) ± SD | |||
| A. | Sitting | 1.19 ± 0.43 | 1.14 ± 0.44 | −0.05 ± 0.09 | NS |
| Standing | 1.15 ± 0.41 | 1.09 ± 0.40 | −0.06 ± 0.08 | * | |
| Rest-VTh1 | 4.44 ± 2.00 | 4.42 ± 2.00 | 0.06 ± 0.13 | NS | |
| VTh1-VTh2 | 10.22 ± 4.15 | 10.28 ± 4.07 | 0.14 ± 0.25 | NS | |
| O2max | 14.64 ± 5.85 | 14.76 ± 5.62 | 0.12 ± 0.35 | NS | |
| PP. | Sitting | 1.25 ± 0.20 | 1.25 ± 0.20 | −0.01 ± 0.04 | NS |
| Standing | 1.31 ± 0.28 | 1.35 ± 0.28 | 0.03 ± 0.04 | NS | |
| Rest-VTh1 | 4.53 ± 1.47 | 4.37 ± 1.42 | −0.17 ± 0.11 | ** | |
| VTh1-VTh2 | 10.30 ± 2.18 | 10.10 ± 1.96 | −0.19 ± 0.30 | NS | |
| O2max | 15.23 ± 2.62 | 15.03 ± 2.41 | −0.20 ± 0.40 | NS | |
| P. | Sitting | 0.96 ± 0.16 | 0.98 ± 0.18 | 0.02 ± 0.06 | NS |
| Standing | 0.99 ± 0.25 | 1.10 ± 0.25 | 0.11 ± 0.03 | *** | |
| Rest-VTh1 | 3.17 ± 0.66 | 3.18 ± 0.65 | 0.00 ± 0.09 | NS | |
| VTh1-VTh2 | 6.16 ± 0.41 | 6.22 ± 0.32 | 0.06 ± 0.16 | NS | |
| O2max | 8.77 ± 0.87 | 8.90 ± 0.67 | 0.13 ± 0.24 | NS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Yin, X.; Hu, R.; Houssein, A.; Gastinger, S.; Martin, B.; Li, S.; Prioux, J. Energy Expenditure Estimation in Children, Adolescents and Adults by Using a Respiratory Magnetometer Plethysmography System and a Deep Learning Model. Nutrients 2022, 14, 4190. https://doi.org/10.3390/nu14194190
Zhou F, Yin X, Hu R, Houssein A, Gastinger S, Martin B, Li S, Prioux J. Energy Expenditure Estimation in Children, Adolescents and Adults by Using a Respiratory Magnetometer Plethysmography System and a Deep Learning Model. Nutrients. 2022; 14(19):4190. https://doi.org/10.3390/nu14194190
Chicago/Turabian StyleZhou, Fenfen, Xiaojian Yin, Rui Hu, Aya Houssein, Steven Gastinger, Brice Martin, Shanshan Li, and Jacques Prioux. 2022. "Energy Expenditure Estimation in Children, Adolescents and Adults by Using a Respiratory Magnetometer Plethysmography System and a Deep Learning Model" Nutrients 14, no. 19: 4190. https://doi.org/10.3390/nu14194190
APA StyleZhou, F., Yin, X., Hu, R., Houssein, A., Gastinger, S., Martin, B., Li, S., & Prioux, J. (2022). Energy Expenditure Estimation in Children, Adolescents and Adults by Using a Respiratory Magnetometer Plethysmography System and a Deep Learning Model. Nutrients, 14(19), 4190. https://doi.org/10.3390/nu14194190