Optimising an FFQ Using a Machine Learning Pipeline to Teach an Efficient Nutrient Intake Predictive Model
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Design and Population
2.2. Data Preprocessing
2.3. Methods
- Regression problem: In regression problems we try to predict continuous values. In our case, we try to predict the values of the intake of nutrient selected per food group.
- Classification problem: In classification problems the predicted values are discrete. In our case, we try to predict the diet quality scores for chosen nutrients and food groups.
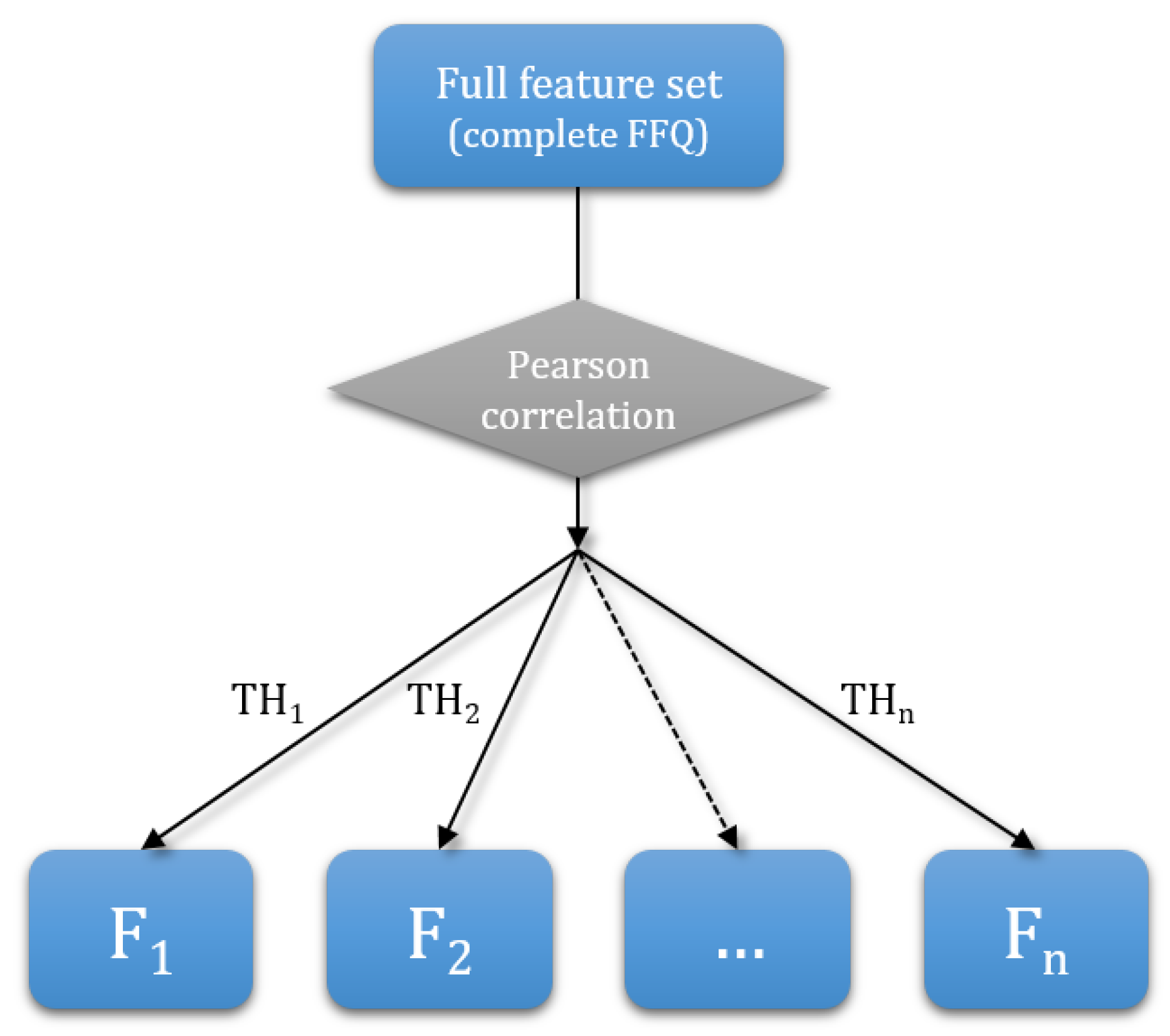
2.3.1. Dimensionality Reduction
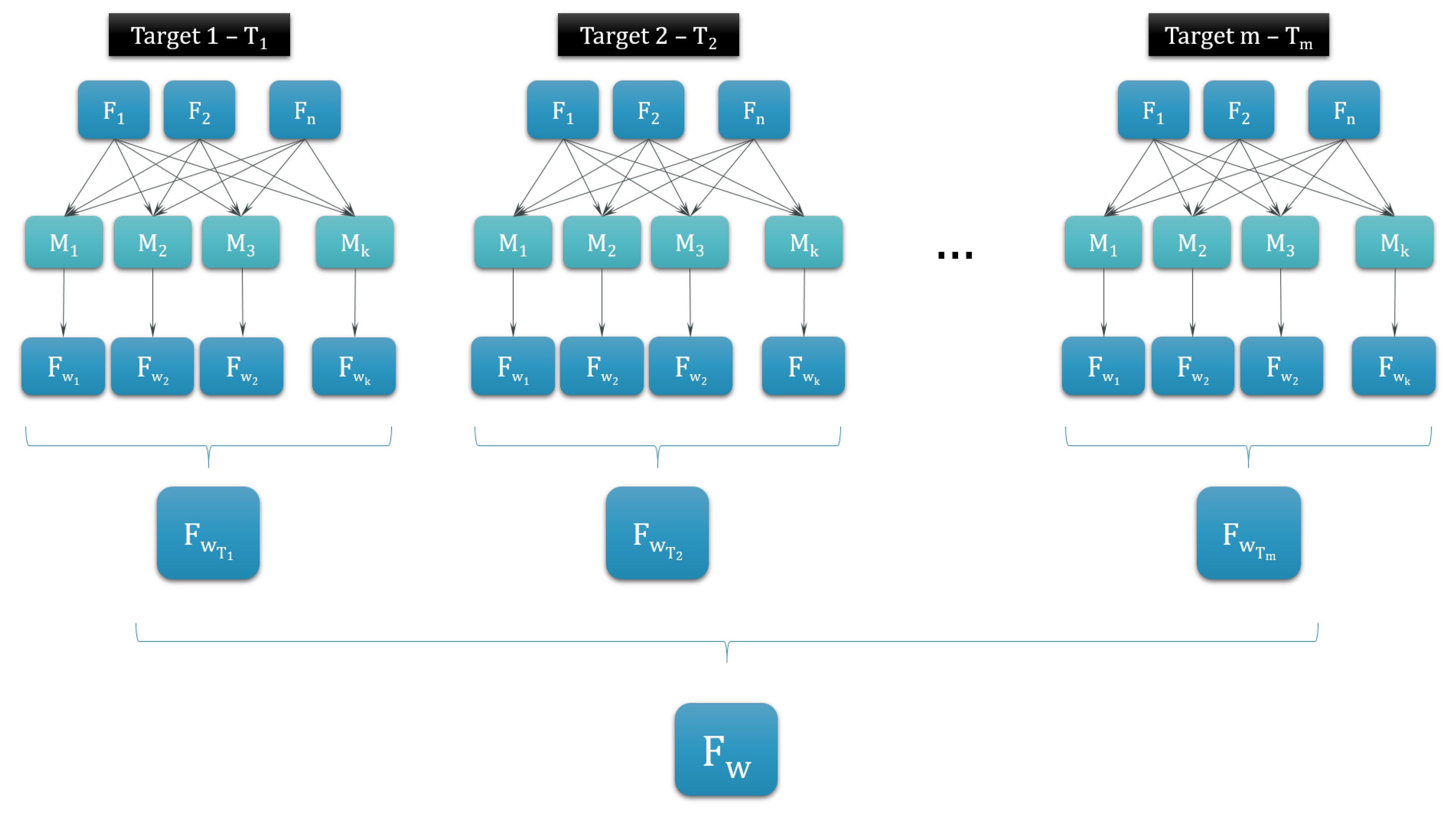
2.3.2. Machine-Learning Algorithms
2.3.3. Evaluation Method—PROMETHEE
- Rank methods—for each of the subsets of questions F0, F1, F2, F3, F4 and F5 we rank the methods by their performances on that subset;
- Ranked subsets of questions—for each of the models (machine-learning and statistical methods) we rank the subsets of questions by the performance of that model on them.
3. Results
3.1. Dimensionality Reduction
3.2. Evaluation—PROMETHEE
3.2.1. Fat Intake
3.2.2. Sugar Intake
3.2.3. Fiber Intake
3.2.4. Protein Intake
3.2.5. Salt Intake
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Question | Feature |
|---|---|
| How often do you eat fruit (tinned/fresh)? | fruit |
| How often do you drink juice (not cordial or squash)? | juice |
| How often do you eat salad (not garnish or added to sandwiches)? | salad |
| How often do you eat vegetables (tinned/frozen/fresh, but not potatoes)? | veg |
| How often do you eat chips/fried potatoes? | chips |
| How often do you eat beans or pulses (baked beans, chick peas, dahl…)? | beans |
| How often do you eat fiber-rich breakfast cereal (porridge, muesli…)? | fiber |
| How often do you eat wholemeal bread or chapattis? | wholebread |
| How often do you eat cheese/yogurt? | cheese |
| How often do you eat crisps/savoury snacks? | crisps |
| How often do you eat sweet biscuits, cakes, chocolate, sweets? | cakes |
| How often do you eat ice cream/Cream? | cream |
| How often do you drink non-alcoholic fizzy drinks/pop (not sugar free or diet? | pop |
| How often do you eat SALTED nuts, peanuts or seeds? | nuts_salted |
| How often do you eat UNSALTED nuts, peanuts or seeds? | nuts |
| How often do you eat grains (pasta, rice, couscous, bulgur…)? | grains |
| How often do you eat pre-prepared sauces, gravies, dry soup mixes? | pre-prepared |
| How often do you eat pizza, pasta/noodle dishes with cheese sauce? | pizza |
| How often do you eat bread, buns and other bread pastries (non-sweet)? | bread |
| How often do you eat potato (mashed, baked, cooked; not fried)? | potato |
| How often do you eat eggs (boiled, fried, scrambled,…)? | eggs |
| How often do you eat beef, lamb, pork, ham (steaks, roasts, joints, chops…)? | redmeat |
| How often do you eat chicken, turkey (steaks, roasts…- not in batter/breadcrumbs)? | whitemeat |
| How often do you eat sausages, bacon, corned beef, meat pies/pasties…? | sausage |
| How often do you eat chicken, turkey (nuggets/twizzlers, pies or in batter/breadcrumbs)? | nuggets |
| How often do you eat white fish in batter or breadcrumbs? | batterfish |
| How often do you eat white fish NOT in batter or breadcrumbs or oily fish (salmon, tuna)? | fish |
References
- Reščič, N.; Valenčič, E.; Mlinarič, E.; Seljak, B.K.; Luštrek, M. Mobile Nutrition Monitoring for Well-Being. In UbiComp/ISWC ’19 Adjunct, Proceedings of the 2019 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2019 ACM International Symposium on Wearable Computers; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1194–1197. [Google Scholar] [CrossRef]
- Cleghorn, C.L.; Harrison, R.A.; Ransley, J.K.; Wilkinson, S.; Thomas, J.; Cade, J.E. Can a dietary quality score derived from a short-form FFQ assess dietary quality in UK adult population surveys? Public Health Nutr. 2016, 19, 2915–2923. [Google Scholar] [CrossRef] [Green Version]
- Thompson, F.; Byers, T. Dietary Assessment Resource Manual. J. Nutr. 1994, 124, 2245S–2317S. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.; Oh, K.; Kim, H. Dietary assessment methods in epidemiologic studies. Epidemiol. Health 2014, 36. [Google Scholar] [CrossRef] [PubMed]
- Gerdessen, J.C.; Souverein, O.W.; van‘t Veer, P.; de Vries, J.H. Optimising the selection of food items for FFQs using Mixed Integer Linear Programming. Public Health Nutr. 2015, 18, 68–74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panaretos, D.; Koloverou, E.; Dimopoulos, A.C.; Kouli, G.M.; Vamvakari, M.; Tzavelas, G.; Pitsavos, C.; Panagiotakos, D.B. A comparison of statistical and machine-learning techniques in evaluating the association between dietary patterns and 10-year cardiometabolic risk (2002–2012): The ATTICA study. Br. J. Nutr. 2018, 120, 326–334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uemura, H.; Ghaibeh, A.; Katsuura-Kamano, S.; Yamaguchi, M.; Bahari, T.; Ishizu, M.; Moriguchi, H.; Arisawa, K. Systemic inflammation and family history in relation to the prevalence of type 2 diabetes based on an alternating decision tree. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gjoreski, M.; Kochev, S.; Reščič, N.; Gregorič, M.; Eftimov, T.; Seljak, B.K. Exploring Dietary Intake Data collected by FPQ using Unsupervised Learning. In Proceedings of the 2019 IEEE International Conference on Big Data, Los Angeles, CA, USA, 9–12 December 2019; pp. 5126–5130. [CrossRef]
- Chin, E.L.; Simmons, G.; Bouzid, Y.Y.; Kan, A.; Burnett, D.J.; Tagkopoulos, I.; Lemay, D.G. Nutrient Estimation from 24-Hour Food Recalls Using Machine Learning and Database Mapping: A Case Study with Lactose. Nutrients 2019, 11, 3045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gregorič, M.; Blaznik, U.; Delfar, N.; Zaletel, M.; Lavtar, D.; Koroušić-Seljak, B.; Golja, P.; Zdešar Kotnik, K.; Pravst, I.; Fidler Mis, N.; et al. Slovenian national food consumption survey in adolescents, adults and elderly: External scientific report. EFSA Support. Publ. 2019, 16, 1729E. [Google Scholar] [CrossRef] [Green Version]
- Zupanič, N.; Hristov, H.; Gregorič, M.; Blaznik, U.; Delfar, N.; Seljak, B.; Ding, E.; Fidler Mis, N.; Pravst, I. Total and Free Sugars Consumption in a Slovenian Population Representative Sample. Nutrients 2020, 12, 1729. [Google Scholar] [CrossRef] [PubMed]
- Sim, J.; Lee, J.; Kwon, O. Missing Values and Optimal Selection of an Imputation Method and Classification Algorithm to Improve the Accuracy of Ubiquitous Computing Applications. Math. Probl. Eng. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Azur, M.; Stuart, E.; Frangakis, C.; Leaf, P. Multiple Imputation by Chained Equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef] [PubMed]
- van Buuren, S. Multiple imputation of discrete and continuous data by fully conditional specification. Stat. Methods Med Res. 2007, 16, 219–242. [Google Scholar] [CrossRef] [PubMed]
- Muller, A.; Mufcller, A.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media: Newton, MA, USA, 2018. [Google Scholar]
- Eftimov, T.; Kocev, D. Performance Measures Fusion for Experimental Comparison of Methods for Multi-label Classification. In Proceedings of the AAAI Spring Symposium: Combining Machine Learning with Knowledge Engineering, Palo Alto, CA, USA, 25–27 March 2019. [Google Scholar]
- Brans, J.P.; Vincke, P. A Preference Ranking Organisation Method: (The PROMETHEE Method for Multiple Criteria Decision-Making). Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef] [Green Version]
- KAGGLE. Available online: https://github.com/dmlc/xgboost/blob/master/demo/README.md#usecases (accessed on 28 October 2020).
- Ichikawa, M.; Hosono, A.; Tamai, Y.; Watanabe, M.; Shibata, K.; Tsujimura, S.; Oka, K.; Fujita, H.; Okamoto, N.; Kamiya, M.; et al. Handling missing data in an FFQ: Multiple imputation and nutrient intake estimates. Public Health Nutr. 2019, 22, 1351–1360. [Google Scholar] [CrossRef] [PubMed]
- NHANES. Available online: http://www.cdc.gov/nchs/nhanes/index.htm (accessed on 28 October 2020).
| Answer_tag | Rarely or Never | Less than Once a Week | Once a Week | 2–3 Times a Week | 4–6 Times a Week | 1–2 Times a Day | 3–4 Times a Day | 5+ a Day |
|---|---|---|---|---|---|---|---|---|
| salad | 0.00 | 4.00 | 11.2 | 28.8 | 56.8 | 120 | 280 | 480 |
| vegetables | 0.00 | 4.00 | 11.2 | 28.8 | 56.8 | 120 | 280 | 480 |
| Score | 1 (Bad) | 2 (Medium) | 3 (Good) |
|---|---|---|---|
| Vegetables | less than 80 g | 80 g to 240 g | more than 240 g |
| Threshold | # of Features | Features | Feature Set Tag |
|---|---|---|---|
| 0.40 | 19 | fruit, juice, salad, vegetables, chips, beans, fiber, wholebread, cheese, cakes, cream, grains, pizza, nuts_salt, nuts, potato, readmeat, whitemeat, fish | F1 |
| 0.30 | 16 | fruit, juice, salad, vegetables, chips, beans, fiber, wholebread, cheese, cakes, grains, nuts, potato, readmeat, whitemeat, fish | F2 |
| 0.25 | 10 | fruit, juice, salad, beans, fiber, wholebread, grains, nuts, readmeat, whitemeat | F3 |
| 0.20 | 6 | fruit, juice, salad, fiber, wholebread, grains | F4 |
| 0.10 | 2 | fruit, juice | F5 |
| Classification | Regression | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | avg. | F0 | F1 | F2 | F3 | F4 | F5 | avg. | |
| Logistic/Linear Regression | 9.0 | 6.0 | 1.0 | 5.0 | 4.0 | 4.5 | 4.0 | 7.0 | 6.0 | 3.5 | 2.5 | 1.0 | 1.0 | 2.0 |
| K-Nearest Neighbors | 10.0 | 8.0 | 5.0 | 2.0 | 7.0 | 1.0 | 6.0 | 8.0 | 7.0 | 5.0 | 2.5 | 4.0 | 4.0 | 6.0 |
| Decision Tree | 8.0 | 9.0 | 9.0 | 7.0 | 8.0 | 3.0 | 9.0 | 9.0 | 8.0 | 9.0 | 8.0 | 8.0 | 7.5 | 9.0 |
| SVM | 4.0 | 3.0 | 3.0 | 1.0 | 6.0 | 2.0 | 1.0 | 10.0 | 9.0 | 7.0 | 4.0 | 2.0 | 1.0 | 6.0 |
| Bagging Clf./Reg. | 7.0 | 7.0 | 8.0 | 8.0 | 5.0 | 7.0 | 8.0 | 6.0 | 5.0 | 6.0 | 6.0 | 7.0 | 7.5 | 7.0 |
| Gradient Boosting Clf./Reg. | 5.0 | 5.0 | 2.0 | 4.0 | 2.5 | 4.5 | 3.0 | 3.0 | 1.0 | 3.5 | 7.0 | 5.5 | 5.5 | 3.5 |
| Random Forest | 6.0 | 2.0 | 6.0 | 6.0 | 2.5 | 8.0 | 5.0 | 4.0 | 3.5 | 2.0 | 5.0 | 5.5 | 5.5 | 3.5 |
| Voting Clf./Reg. | 3.0 | 4.0 | 4.0 | 3.0 | 1.0 | 6.0 | 2.0 | 5.0 | 3.5 | 1.0 | 1.0 | 3.0 | 1.0 | 1.0 |
| Zero imputation | 1.5 | 10.0 | 10.0 | 10.0 | 10.0 | 9.5 | 10.0 | 1.5 | 10.0 | 10.0 | 10.0 | 10.0 | 10.0 | 10.0 |
| Multiple imputation | 1.5 | 1.0 | 7.0 | 9.0 | 9.0 | 9.5 | 7.0 | 1.5 | 2.0 | 8.0 | 9.0 | 9.0 | 9.0 | 8.0 |
| Classification | Regression | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | F0 | F1 | F2 | F3 | F4 | F5 | |
| Logistic/Linear Regression | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 5.0 | 4.0 | 6.0 |
| K-Nearest Neighbors | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Decision Tree | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 4.0 | 5.0 | 6.0 | 3.0 |
| SVM | 1.0 | 2.0 | 4.0 | 3.0 | 5.0 | 6.0 | 2.0 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Bagging Classifier/Regressor | 1.0 | 2.0 | 3.0 | 5.0 | 4.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 5.0 |
| Gradient Boosting Classifier/Regressor | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Random Forest | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Voting Classifier/Regressor | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Zero imputation | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Multiple imputation | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Average rank | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Classification | Regression | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | avg. | F0 | F1 | F2 | F3 | F4 | F5 | avg. | |
| Logistic/Linear Reg. | 8.0 | 8.0 | 8.0 | 5.0 | 5.0 | 8.5 | 8.0 | 8.0 | 8.0 | 8.0 | 1.0 | 1.5 | 1.5 | 4.0 |
| K-Nearest Neighbors | 9.0 | 9.0 | 10.0 | 7.0 | 9.0 | 6.0 | 9.0 | 9.0 | 9.0 | 9.0 | 4.0 | 3.0 | 5.0 | 8.0 |
| Decision Tree | 6.0 | 7.0 | 7.0 | 8.0 | 6.0 | 1.0 | 6.0 | 7.0 | 7.0 | 7.0 | 9.0 | 9.0 | 8.0 | 9.0 |
| SVM | 10.0 | 10.0 | 9.0 | 9.0 | 8.0 | 8.5 | 10.0 | 10.0 | 10.0 | 10.0 | 6.0 | 7.0 | 5.0 | 10.0 |
| Bagging Clf./Reg. | 4.0 | 4.5 | 4.0 | 2.5 | 1.0 | 2.0 | 2.0 | 5.0 | 5.0 | 4.0 | 7.0 | 6.0 | 5.0 | 6.0 |
| Gradient Boost. Clf./Reg. | 3.0 | 3.0 | 2.0 | 1.0 | 3.0 | 4.0 | 1.0 | 3.0 | 3.0 | 2.0 | 3.0 | 4.5 | 5.0 | 1.0 |
| Random Forest | 7.0 | 4.5 | 3.0 | 2.5 | 4.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 5.0 | 4.5 | 5.0 | 3.0 |
| Voting Clf./Reg. | 5.0 | 6.0 | 5.0 | 4.0 | 2.0 | 3.0 | 3.5 | 6.0 | 6.0 | 6.0 | 2.0 | 1.5 | 1.5 | 2.0 |
| Zero imputation | 1.5 | 2.0 | 6.0 | 10.0 | 10.0 | 8.5 | 7.0 | 1.5 | 2.0 | 5.0 | 10.0 | 10.0 | 10.0 | 7.0 |
| Multiple imputation | 1.5 | 1.0 | 1.0 | 6.0 | 7.0 | 8.5 | 3.5 | 1.5 | 1.0 | 1.0 | 8.0 | 8.0 | 9.0 | 5.0 |
| Classification | Regression | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | F0 | F1 | F2 | F3 | F4 | F5 | |
| Logistic/Linear Regression | 3.0 | 1.0 | 2.0 | 5.0 | 4.0 | 6.0 | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 |
| K-Nearest Neighbors | 5.0 | 4.0 | 1.0 | 2.0 | 3.0 | 6.0 | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 |
| Decision Tree | 1.0 | 2.0 | 3.0 | 5.0 | 4.0 | 6.0 | 3.0 | 1.0 | 2.0 | 6.0 | 5.0 | 4.0 |
| SVM | 6.0 | 4.0 | 1.0 | 3.0 | 2.0 | 5.0 | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 |
| Bagging Classifier/Regressor | 1.0 | 2.0 | 3.0 | 5.0 | 4.0 | 6.0 | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 |
| Gradient Boosting Classifier/Regressor | 2.0 | 1.0 | 3.0 | 5.0 | 4.0 | 6.0 | 2.0 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Random Forest | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 |
| Voting Classifier/Regressor | 2.0 | 3.0 | 1.0 | 5.0 | 4.0 | 6.0 | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 |
| Zero imputation | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Multiple imputation | 1.0 | 2.0 | 3.0 | 5.0 | 4.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Average rank | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 | 3.0 | 2.0 | 1.0 | 5.0 | 4.0 | 6.0 |
| Classification | Regression | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | avg. | F0 | F1 | F2 | F3 | F4 | F5 | avg. | |
| Logistic/Linear Regression | 3.0 | 6.5 | 5.0 | 1.0 | 4.0 | 7.0 | 2.0 | 7.0 | 7.0 | 7.0 | 5.0 | 1.5 | 2.0 | 4.5 |
| K-Nearest Neighbors | 10.0 | 10.0 | 10.0 | 7.0 | 1.5 | 4.0 | 9.0 | 8.0 | 8.0 | 8.0 | 6.0 | 3.0 | 4.5 | 7.0 |
| Decision Tree | 6.0 | 9.0 | 9.0 | 9.0 | 8.0 | 3.0 | 10.0 | 10.0 | 10.0 | 10.0 | 9.0 | 8.0 | 8.0 | 10.0 |
| SVM | 9.0 | 8.0 | 7.0 | 2.0 | 1.5 | 10.0 | 8.0 | 9.0 | 9.0 | 9.0 | 7.0 | 4.5 | 1.0 | 8.5 |
| BaggingClf./Reg. | 7.0 | 6.5 | 4.0 | 6.0 | 7.0 | 1.0 | 6.0 | 5.0 | 6.0 | 5.0 | 4.0 | 7.0 | 6.5 | 6.0 |
| Gradient Boosting Clf./Reg. | 4.0 | 3.0 | 3.0 | 5.0 | 6.0 | 2.0 | 1.0 | 3.0 | 3.0 | 2.0 | 1.0 | 4.5 | 4.5 | 1.0 |
| Random Forest | 5.0 | 5.0 | 8.0 | 3.0 | 5.0 | 5.0 | 5.0 | 5.0 | 4.0 | 4.0 | 2.0 | 6.0 | 6.5 | 3.0 |
| Voting Clf./Reg. | 8.0 | 4.0 | 2.0 | 4.0 | 3.0 | 9.0 | 4.0 | 5.0 | 5.0 | 3.0 | 3.0 | 1.5 | 3.0 | 2.0 |
| Zero imputation | 1.5 | 2.0 | 6.0 | 10.0 | 10.0 | 7.0 | 7.0 | 1.5 | 2.0 | 6.0 | 10.0 | 10.0 | 10.0 | 8.5 |
| Multiple imputation | 1.5 | 1.0 | 1.0 | 8.0 | 9.0 | 7.0 | 3.0 | 1.5 | 1.0 | 1.0 | 8.0 | 9.0 | 9.0 | 4.5 |
| Classification | Regression | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | F0 | F1 | F2 | F3 | F4 | F5 | |
| Logistic/Linear Regression | 2.0 | 3.0 | 4.0 | 1.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| K-Nearest Neighbors | 3.0 | 5.0 | 4.0 | 2.0 | 1.0 | 6.0 | 2.0 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Decision Tree | 2.0 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 | 2.0 | 3.0 | 1.0 | 4.0 | 6.0 | 5.0 |
| SVM | 4.0 | 2.0 | 5.0 | 1.0 | 3.0 | 6.0 | 3.0 | 1.0 | 2.0 | 4.0 | 5.0 | 6.0 |
| Bagging Classifier/Regressor | 3.0 | 1.0 | 2.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Gradient Boosting Classifier/Regressor | 2.0 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Random Forest | 3.0 | 1.0 | 5.0 | 2.0 | 4.0 | 6.0 | 2.0 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Voting Classifier/Regressor | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Zero imputation | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Multiple imputation | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Average rank | 2.0 | 1.0 | 4.0 | 3.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Classification | Regression | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | avg. | F0 | F1 | F2 | F3 | F4 | F5 | avg. | |
| Logistic/Linear Regression | 3.0 | 1.0 | 1.0 | 1.0 | 2.0 | 7.5 | 1.0 | 4.0 | 3.0 | 2.0 | 3.0 | 3.5 | 1.0 | 2.0 |
| K-Nearest Neighbors | 5.0 | 4.0 | 3.0 | 2.0 | 1.0 | 4.0 | 2.0 | 8.0 | 7.0 | 7.0 | 6.0 | 3.5 | 7.0 | 7.0 |
| Decision Tree | 10.0 | 10.0 | 9.0 | 9.0 | 5.0 | 5.5 | 10.0 | 9.0 | 10.0 | 9.0 | 8.0 | 8.0 | 7.0 | 10.0 |
| SVM | 7.5 | 3.0 | 7.0 | 5.0 | 8.0 | 7.5 | 7.0 | 10.0 | 9.0 | 8.0 | 7.0 | 6.5 | 1.0 | 8.0 |
| Bagging Clf./Reg. | 9.0 | 6.0 | 5.5 | 7.0 | 6.0 | 5.5 | 8.0 | 7.0 | 6.0 | 6.0 | 5.0 | 6.5 | 4.5 | 6.0 |
| Gradient Boosting Clf./Reg. | 4.0 | 9.0 | 8.0 | 4.0 | 3.0 | 2.0 | 5.0 | 3.0 | 2.0 | 1.0 | 1.0 | 3.5 | 4.5 | 1.0 |
| Random Forest | 6.0 | 8.0 | 4.0 | 8.0 | 7.0 | 3.0 | 6.0 | 6.0 | 5.0 | 4.0 | 3.0 | 3.5 | 7.0 | 4.0 |
| Voting Clf./Reg. | 7.5 | 5.0 | 5.5 | 6.0 | 4.0 | 1.0 | 4.0 | 5.0 | 4.0 | 3.0 | 3.0 | 1.0 | 1.0 | 3.0 |
| Zero imputation | 1.5 | 7.0 | 10.0 | 10.0 | 10.0 | 9.0 | 9.0 | 1.5 | 8.0 | 10.0 | 10.0 | 10.0 | 10.0 | 9.0 |
| Multiple imputation | 1.5 | 2.0 | 2.0 | 3.0 | 9.0 | 10.0 | 3.0 | 1.5 | 1.0 | 5.0 | 9.0 | 9.0 | 9.0 | 5.0 |
| Classification | Regression | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | F0 | F1 | F2 | F3 | F4 | F5 | |
| Logistic/Linear Regression | 3.0 | 1.0 | 2.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| K-Nearest Neighbors | 3.0 | 1.0 | 2.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Decision Tree | 1.0 | 3.0 | 2.0 | 6.0 | 5.0 | 4.0 | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 5.0 |
| SVM | 3.0 | 1.0 | 2.0 | 4.0 | 6.0 | 5.0 | 3.0 | 2.0 | 1.0 | 4.0 | 5.0 | 6.0 |
| Bagging Classifier/Regressor | 2.0 | 3.0 | 1.0 | 4.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Gradient Boosting Classifier/Regressor | 1.0 | 4.0 | 2.0 | 3.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Random Forest | 2.0 | 3.0 | 1.0 | 5.0 | 6.0 | 4.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Voting Classifier/Regressor | 2.0 | 3.0 | 1.0 | 4.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Zero imputation | 1.0 | 2.0 | 3.0 | 4.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Multiple imputation | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Average rank | 2.0 | 3.0 | 1.0 | 4.0 | 6.0 | 5.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Classification | Regression | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | avg. | F0 | F1 | F2 | F3 | F4 | F5 | avg. | |
| Logistic/Linear Regression | 5.0 | 3.0 | 1.0 | 1.0 | 3.0 | 7.0 | 1.0 | 5.0 | 1.0 | 1.0 | 2.5 | 2.0 | 1.5 | 1.0 |
| K-Nearest Neighbors | 8.0 | 8.0 | 8.0 | 7.0 | 6.0 | 1.0 | 7.0 | 9.0 | 8.0 | 7.0 | 6.0 | 4.5 | 6.5 | 7.0 |
| Decision Tree | 10.0 | 9.0 | 9.0 | 5.5 | 7.0 | 3.0 | 9.0 | 10.0 | 9.0 | 9.0 | 8.0 | 8.0 | 6.5 | 9.0 |
| SVM | 3.0 | 1.0 | 2.0 | 3.0 | 8.0 | 8.0 | 3.0 | 6.5 | 6.0 | 6.0 | 6.0 | 6.5 | 1.5 | 5.0 |
| Bagging Clf./Reg. | 9.0 | 5.5 | 5.0 | 2.0 | 2.0 | 5.0 | 4.0 | 8.0 | 5.0 | 5.0 | 6.0 | 6.5 | 6.5 | 6.0 |
| Gradient Boosting Clf./Reg. | 6.0 | 3.0 | 6.0 | 5.5 | 5.0 | 4.0 | 5.0 | 3.0 | 2.5 | 3.0 | 2.5 | 2.0 | 4.0 | 3.0 |
| Random Forest | 7.0 | 5.5 | 4.0 | 4.0 | 4.0 | 6.0 | 6.0 | 6.5 | 4.0 | 4.0 | 2.5 | 4.5 | 6.5 | 4.0 |
| Voting Clf./Reg. | 4.0 | 3.0 | 3.0 | 8.0 | 1.0 | 2.0 | 2.0 | 4.0 | 2.5 | 2.0 | 2.5 | 2.0 | 3.0 | 2.0 |
| Zero imputation | 1.5 | 10.0 | 10.0 | 10.0 | 10.0 | 9.5 | 10.0 | 1.5 | 10.0 | 10.0 | 10.0 | 10.0 | 10.0 | 10.0 |
| Multiple imputation | 1.5 | 7.0 | 7.0 | 9.0 | 9.0 | 9.5 | 8.0 | 1.5 | 7.0 | 8.0 | 9.0 | 9.0 | 9.0 | 8.0 |
| Classification | Regression | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | F0 | F1 | F2 | F3 | F4 | F5 | |
| Logistic/Linear Regression | 1.0 | 3.0 | 2.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| K-Nearest Neighbors | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Decision Tree | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 3.0 | 2.0 | 5.0 | 6.0 | 4.0 |
| SVM | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Bagging Classifier/Regressor | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Gradient Boosting Classifier/Regressor | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Random Forest | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Voting Classifier/Regressor | 1.0 | 2.0 | 3.0 | 5.0 | 4.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Zero imputation | 1.0 | 2.0 | 3.0 | 6.0 | 5.0 | 4.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Multiple imputation | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Average rank | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Classification | Regression | |
|---|---|---|
| Average Rank | Average Rank | |
| Logistic/Linear Regression | 5.0 | 6.0 |
| K-Nearest Neighbors | 9.0 | 7.0 |
| Decision Tree | 7.0 | 9.0 |
| SVM | 8.0 | 8.0 |
| Bagging Classifier/Regressor | 1.0 | 4.0 |
| Gradient Boosting Classifier/Regressor | 3.0 | 1.0 |
| Random Forest | 6.0 | 3.0 |
| Voting Classifier/Regressor | 2.0 | 2.0 |
| Zero imputation | 10.0 | 10.0 |
| Multiple imputation | 4.0 | 6.0 |
| Classification | Regression | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | F4 | F5 | F0 | F1 | F2 | F3 | F4 | F5 | |
| Average rank | 2.0 | 1.0 | 3.0 | 4.0 | 5.0 | 6.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Classification | Regression | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Logistic/Linear Regression | 7.0 | 2.0 | 3.0 | 1.0 | 5.0 | 7.0 | 7.0 | 6.0 | 6.0 | 3.0 | 2.0 | 1.0 |
| K-Nearest Neighbors | 10.0 | 10.0 | 10.0 | 6.0 | 6.0 | 4.0 | 9.0 | 8.0 | 8.0 | 5.0 | 3.0 | 5.5 |
| cDecision Tree | 8.0 | 8.0 | 7.0 | 9.0 | 7.0 | 1.0 | 8.0 | 9.0 | 7.0 | 9.0 | 9.0 | 8.0 |
| SVM | 9.0 | 9.0 | 9.0 | 7.0 | 8.0 | 8.0 | 10.0 | 10.0 | 10.0 | 7.0 | 6.5 | 3.0 |
| Bagging Classifier/Regressor | 6.0 | 5.0 | 4.0 | 3.0 | 2.0 | 2.0 | 6.0 | 5.0 | 5.0 | 6.0 | 6.5 | 5.5 |
| Gradient Boosting Classifier/Regressor | 3.0 | 4.0 | 5.0 | 2.0 | 3.0 | 3.0 | 3.0 | 2.0 | 1.0 | 1.5 | 4.0 | 4.0 |
| Random Forest | 5.0 | 6.0 | 6.0 | 5.0 | 4.0 | 6.0 | 4.0 | 3.0 | 3.0 | 4.0 | 5.0 | 7.0 |
| Voting Classifier/Regressor | 4.0 | 3.0 | 2.0 | 4.0 | 1.0 | 5.0 | 5.0 | 4.0 | 4.0 | 1.5 | 1.0 | 2.0 |
| Zero imputation | 1.5 | 7.0 | 8.0 | 10.0 | 10.0 | 9.0 | 1.5 | 7.0 | 9.0 | 10.0 | 10.0 | 10.0 |
| Multiple imputation | 1.5 | 1.0 | 1.0 | 8.0 | 9.0 | 10.0 | 1.5 | 1.0 | 2.0 | 8.0 | 8.0 | 9.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reščič, N.; Eftimov, T.; Koroušić Seljak, B.; Luštrek, M. Optimising an FFQ Using a Machine Learning Pipeline to Teach an Efficient Nutrient Intake Predictive Model. Nutrients 2020, 12, 3789. https://doi.org/10.3390/nu12123789
Reščič N, Eftimov T, Koroušić Seljak B, Luštrek M. Optimising an FFQ Using a Machine Learning Pipeline to Teach an Efficient Nutrient Intake Predictive Model. Nutrients. 2020; 12(12):3789. https://doi.org/10.3390/nu12123789
Chicago/Turabian StyleReščič, Nina, Tome Eftimov, Barbara Koroušić Seljak, and Mitja Luštrek. 2020. "Optimising an FFQ Using a Machine Learning Pipeline to Teach an Efficient Nutrient Intake Predictive Model" Nutrients 12, no. 12: 3789. https://doi.org/10.3390/nu12123789
APA StyleReščič, N., Eftimov, T., Koroušić Seljak, B., & Luštrek, M. (2020). Optimising an FFQ Using a Machine Learning Pipeline to Teach an Efficient Nutrient Intake Predictive Model. Nutrients, 12(12), 3789. https://doi.org/10.3390/nu12123789








