1. Introduction
The appreciation of food involves all senses: sight, smell, taste, touch, and also hearing. While the sight of a cup of coffee may indicate its availability, it is typically its smell that makes it appealing and that triggers an appetite for most people. During consumption, the smell or aroma is perceived again retronasally and supported by its pleasant temperature and a bitter taste. These largely parallel sensations occur automatically and only raise awareness when one or more senses are disturbed. That said, the sense of smell has been shown to influence food choice and eating behavior [
1], and its impairment has even been associated with a higher risk for diet-related diseases like diabetes [
2]. Even more, olfactory stimuli can invoke emotional states, are linked to memory storage and retrieval, and as such also serve as important cues to rapid detection of potentially dangerous situations and threats (see e.g., [
3,
4]. Given that the estimated prevalence of smell impairment is 3.5% in the United States [
5], continuous efforts are made toward an efficient and precise assessment of olfactory function.
The Sniffin’ Sticks test suite (Burghart, Wedel, Germany; [
6]), is an established tool in the assessment of olfactory function. It consists of three tests involving sets of impregnated felt-tip pens: odor detection threshold (T), odor discrimination (D), and odor identification (I). Each test produces numbers in the range from 1 to 16 (T) or from 0 to 16 (D and I) as a performance measure. Overall olfactory function is assessed by summing all three test results, resulting in the
TDI score. Comparison of individual TDI scores to the comprehensive set of available normative data (e.g., [
7,
8]) facilitates the interpretation of test scores and allows to reliably diagnose olfactory impairment. Notably, threshold, discrimination, and identification measure different facets of olfactory function [
9]. The threshold, however, has been found to explain a larger portion of variability in TDI scores than the two other measures [
10]. Moreover, the discrimination and identification tests follow relatively simple test protocols in which all stimuli are presented only once and in a predefined order. The threshold, in comparison, is of a more complex nature, and the method, therefore provides the largest potential for possible improvements. It follows a so-called adaptive method, specifically, a “transformed” one-up/two-down staircase procedure [
11]. The procedure first assesses a starting concentration and then moves on to the “actual” threshold estimation, during which fixed step widths are used: for each incorrect answer, the stimulus concentration is increased by one step; and for two consecutive correct answers, the stimulus concentration is decreased by one step [
6].
Since the one-up/two-down staircase was first conceived, several new approaches to threshold estimation, including Bayesian methods, have been published. Bayesian methods estimate parameters of the psychometric function (e.g., threshold or slope) using Bayesian inference: based on prior assumptions about the true parameter value, the stimulus concentration to be presented next is selected such that the expected information gain (about the parameter) is maximized. The first published Bayesian adaptive psychometric method is the QUEST procedure [
12], which is still popular today. QUEST has two distinct properties that set it apart from the staircase described above. Firstly, it always considers the entire response history and is not solely based on the past one or two trials to select the optimal stimulus concentration to be presented next. Secondly, QUEST is not tied to a fixed step width, allowing it to traverse through a large range of concentrations more quickly.
In a clinical setting, at the otorhinolaryngologist’s (ear-nose-throat, ENT) practice or at the bedside in the hospital, shorter testing times are always beneficial, as they reduce strain on patients and free up time for other parts of diagnostics and treatment. But also when working with healthy participants, e.g., in a psychophysical lab or in large cohort studies, reduced testing time spares resources and allows for a larger number of measurements in a given time.
QUEST has been shown to converge reliably and quickly in gustatory threshold estimations [
13,
14]. Inspired by these results we set out to design and test a QUEST-based procedure for olfactory threshold estimation and to compare its performance with that of the established staircase method.
3. Results
3.1. Odor Discrimination and Identification
The average test score was 13.3 (SD = 1.5, range: 11–16;
) for odor discrimination, and 13.0 (SD = 1.6, range: 11–16;
) for odor identification. When summed with the staircase threshold estimates from the Test and Retest sessions, we observed TDI scores of 33.34 (SD = 3.8; range: 26.5–43) and 33.64 (SD = 3.8; range: 26.75–41.75), respectively. Individual as well as cumulative scores indicate a below-average ability to smell (roughly around the 25th percentile) in our sample compared to recent normative data from over 9000 subjects [
8].
3.2. Starting Concentrations
The average starting concentration was pen no. 9.9 (SD = 4.2, range: 1–16) for the Test and 9.6 (SD = 4.1, range: 1–16) for the Retest session of the staircase. The average difference in starting concentrations between sessions was 4.9 (SD = 4.0, range: 0–15). In comparison, we used a slightly higher, fixed starting concentration of pen no. 7 for QUEST.
3.3. Test Duration
The average number of trials needed to complete the staircase measurements was 23.6 (SD = 4.8, range: 13–41), which translates to approx. 11.5 min and is 2 minutes longer than for QUEST, which per our parameters always lasted 9.5 minutes (20 trials). Test duration varied slightly between staircase sessions and was 24.4 trials (SD = 4.2, range: 16–34) for the test and 22.9 trials (SD = 5.4, range: 13–41) for the retest session. Please note that the number of trials and the testing duration for the staircase are based on the time required to reach seven reversal points after the starting concentration had been determined, thereby deviating from the “standard” procedure, which treats the starting concentration as the first reversal.
3.4. Test-Retest Reliability
The mean Test thresholds did not differ from the mean Retest thresholds for the staircase (
,
;
,
;
,
). For QUEST, on the other hand, mean test and retest thresholds differed significantly, with slightly higher sensitivity (higher
T unit) in the Retest (
,
;
,
;
,
; see
Figure 1).
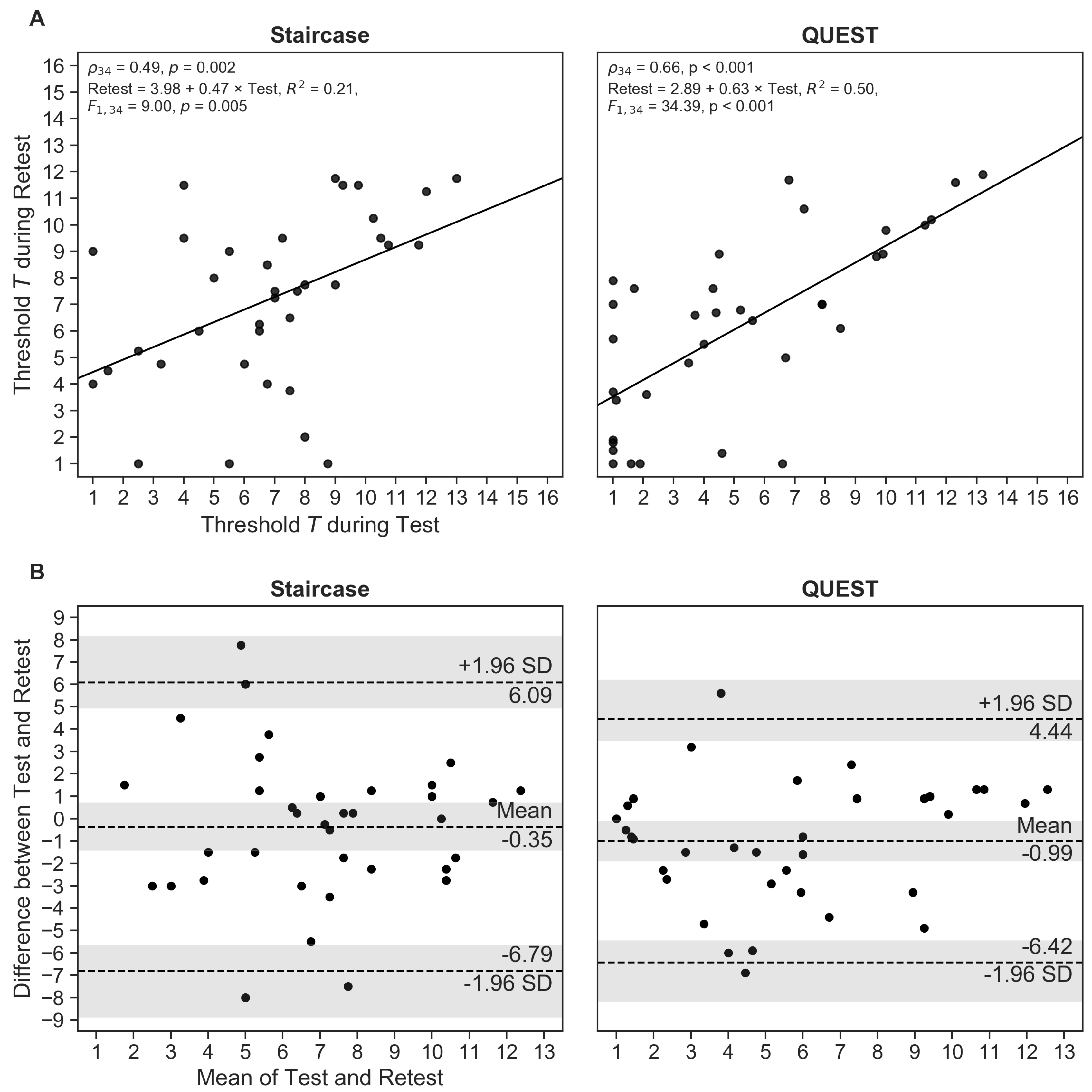
The test and retest thresholds correlated significantly for both procedures, with QUEST demonstrating a stronger relationship between measurements than the staircase (staircase:
,
; QUEST:
,
;
Figure 2A).
As already pointed out, correlation gives an indication of the strength of the monotonic relationship between values, but only provides limited information on their agreement. We therefore calculated the repeatability coefficient RC and created Bland–Altman plots to generate a better understanding of the measurement differences. The prediction of the RC is that two measurements (test and retest) will differ by the value of RC or less for 95% of participants. We found that RC was about 16% smaller for QUEST than for the staircase (
,
), suggesting a slightly better agreement between Test and Retest measurements for the QUEST procedure. Accordingly, the Bland–Altman plot (
Figure 2B) showed narrower limits of agreement for QUEST (staircase:
and
; QUEST:
and
; 95% CIs in brackets). The mean of the differences between measurements was relatively small and deviated less than 1
T unit from zero—the “ideal” difference—for both methods (
;
). This systematic negative shift indicates that participants, on average, reached higher
T units in the second session than in the first. The differences between Test and Retest measurements for three (staircase) and two participants (QUEST), respectively, fell outside their respective limits of agreement, which corresponds to the expected proportion of 5% of outliers (
;
), demonstrating the appropriateness of the estimated limits. Considering the confidence intervals of the limits of agreement, an equal number of measurement differences (four) fell outside the predicted range for both procedures.
To test whether the time between Test and Retest sessions might be linked to the observed differences between Test and Retest threshold estimates, we computed correlations between those measures. We found no relationship for either method (staircase: , ; QUEST: , ).
3.5. Comparison between Procedures
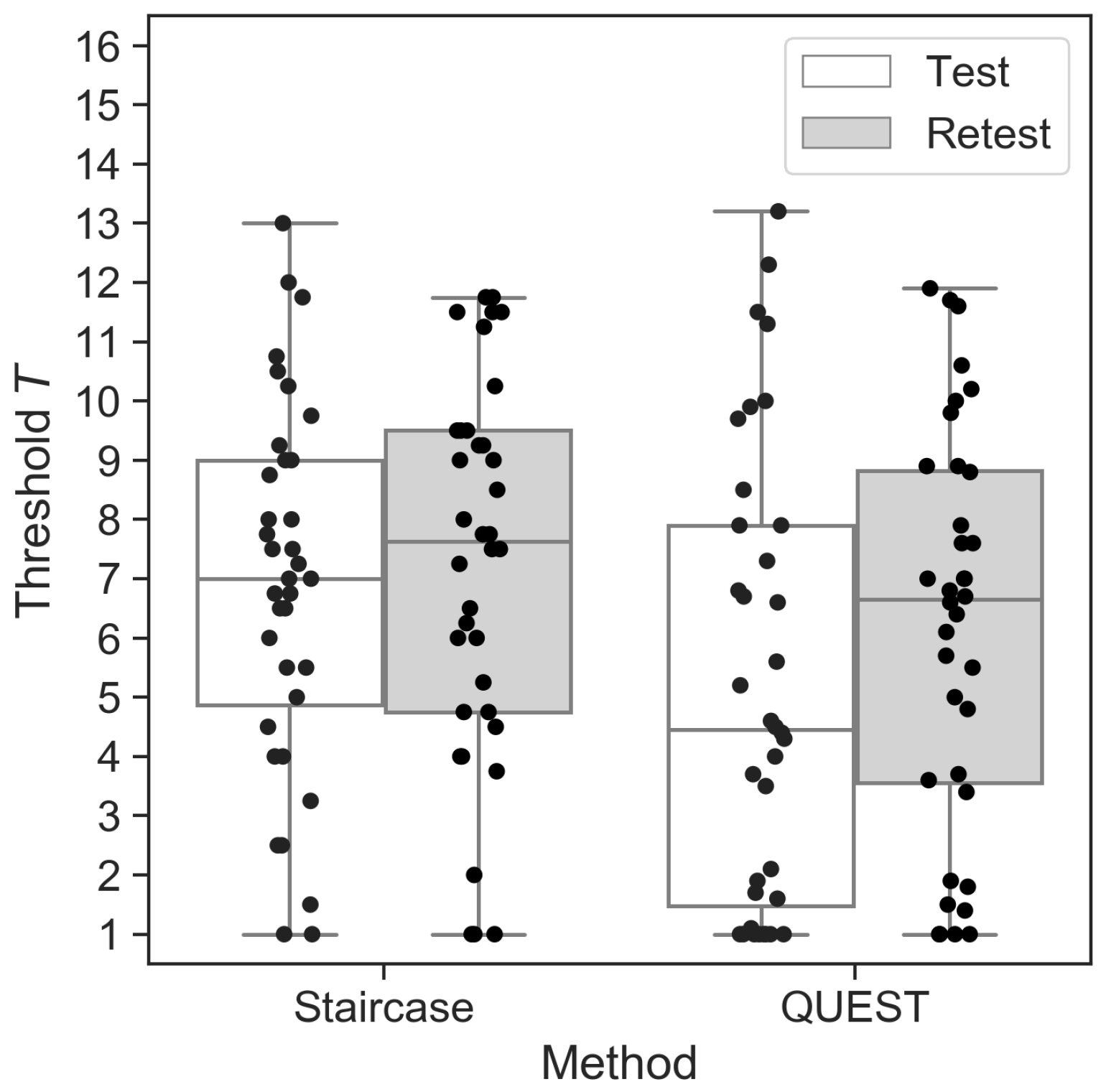
Although the threshold estimates, averaged across sessions, for the staircase were significantly higher than those for QUEST (
,
;
,
;
,
;
Figure 3A), we found a strong correlation between the procedures (
;
Figure 3B). The regression slope was close to 1, providing an indication of agreement across procedures. The Bland-Altman plot based on the session means (
Figure 3C) shows a systematic difference between both procedures; specifically, QUEST thresholds were, on average,
T units smaller than the staircase estimates (95% CIs in brackets). The limits of agreement reached from
to
, meaning the difference between the two procedures will fall into this range for 95% of measurements. Only for 1 participant the observed differences between staircase and QUEST fell outside the limits of agreement (
; when considering the CIs of the limits, 3 participants fell outside the expected range (
)
The corrected limits of agreement, taking into account individual measurements (as opposed to session means only), were and , which is substantially larger than the uncorrected limits. The large confidence intervals that expand even beyond the concentration range reflect the relatively large within-participant variability across sessions in both threshold procedures.
4. Discussion
In the presented study we used a QUEST-based algorithm to estimate olfactory detection thresholds for 2-phenylethanol with the aim to provide a reliable test result as it had recently been demonstrated for taste thresholds [
13] with reduced testing time. The results were compared to a slightly modified version of the widely-used testing protocol based on a one-up/two-down staircase procedure [
6,
7,
9,
15,
16].
Test–retest reliability was assessed using multiple approaches. Comparison of Test and Retest thresholds revealed a small yet significant mean difference for QUEST: threshold estimates during retest were higher than in the test, indicating an increase in participants’ sensitivity. A similar effect was reported in a previous study [
6]. However, with a mean difference of approx. 1
T unit or pen number, the practical relevance of this effect is debatable, even more so when considering the large variability of measurement results within individual participants.
Following common practice of establishing test-retest reliability of olfactory thresholds (see e.g., [
6,
9,
29]), we calculated correlations between Test and retest sessions. The correlation coefficient for QUEST (
) indicated solid, but not exceptionally great test–retest reliability. Reliability of the staircase procedure was only moderate (
) and lower than reported in previous studies for
n-butanol (
; [
6]) and 2-phenylethanol (
; [
9]) thresholds.
To acknowledge previous criticism of correlation analysis – which focuses on the agreement, but not on the differences between measurements [
18,
19,
20] – we calculated repeatability coefficients and generated Bland–Altman plots for the analysis of session differences. Repeatability was higher for QUEST than for the staircase; however, measurement results of both procedures varied considerably across sessions for many participants. This inter-session variability is further substantiated by the differences in starting concentrations assessed for the staircase, which varied up 15 pen numbers in the most extreme case. The effect was not universal: some participants performed better in the Test than in the Retest session, whereas for others performance dropped across sessions, and remained almost unchanged in others. Since both sessions had been scheduled within a relatively short time period and all measurements have been performed by the same experimenter, measurement variability can be mostly attributed to variability within participants themselves.
The comparison of the staircase and QUEST procedures via the session means of each participant showed that the staircase yielded slightly higher pen numbers (i.e., lower thresholds) than QUEST. This was expected as the procedures were assumed to converge at approx. 71% and 80% correct responses, respectively. We found a strong correlation between the session means of the procedures (), and regression analysis showed an almost perfect linear relationship, which some would interpret as a good agreement between QUEST and staircase results. The 95% limits of agreement, taking into account the within-participant variability, showed a large expected deviation between both procedures (range: QUEST thresholds almost 7 T units smaller or more than 4 T units greater than staircase results), with the corresponding CIs of those boundaries even exceeding the concentration range. This result is indicative of the large variability we found within participants in both procedure. The limits of agreement based on the within-participant session means were much narrower, as variability is greatly reduced through averaging.
A potential source of variability might be guessing. In fact, the probability of responding correctly merely by guessing is .
In a series of simulations, it could be shown that with an increasing number of trials the frequency of correct guesses might get unacceptably high, potentially leading increased variability in the threshold estimates [
30]. The author determined that, for a staircase procedure like the one in our study, the expected proportion of such false-positive responses exceeds 5% with the 23rd trial. For our staircase experiments, the average number of trials was 23.6; and the procedure finished after 23 or more trials for 24 of the 36 participants in the Test, and for 20 participants in the Retest session. Therefore, the large variability between Test and Retest threshold estimates in the staircase could, at least partially, be ascribed to correct guesses “contaminating” the procedure. However, QUEST—which always finished after 20 trials—only had slightly better test-retest reliability according the the repeatability coefficient, suggesting that the largest portion of test-retest variability in our investigations was probably not caused by (too) long trial sequences and related false-positive responses alone.
Surprisingly, a number of participants were unable to correctly identify pen no. 1 at least on one occasion, and this effect was more pronounced during QUEST compared to the staircase. It seems plausible that the variable step size used by QUEST made it possible to approach even the extreme concentration ranges quickly, whereas the staircase requires a longer sequence of incorrect responses to reach pen no. 1.
Despite careful selection of healthy participants who reported no smell impairment, olfactory performance was lower than recently reported in a sample comprising over 9000 participants [
8]. This coincidental finding highlights the need for a comprehensive smell screening before enrollment. To what extend olfactory function contributed to the present results and limits their generalizability remains to be explored.
All QUEST runs completed after 20 trials for all participants. The procedure could be further optimized by introducing a dynamic stopping rule. For example, [
13] set the algorithm to terminate once the threshold estimate had reached a certain degree of confidence. Such a rule can reduce testing time, as the run may finish in fewer than 20 trials, and should be considered in future studies. Although the reduction or omission of a minimum trial number bears potential to reduce the testing time further, it needs to be shown first that the algorithm performs well under these conditions and, most importantly, large-scale studies need to show whether such a reduced or faster protocol is appropriate to assess odor sensitivity in participants with odor abilities at the extremes (particularly insensitive/sensitive).
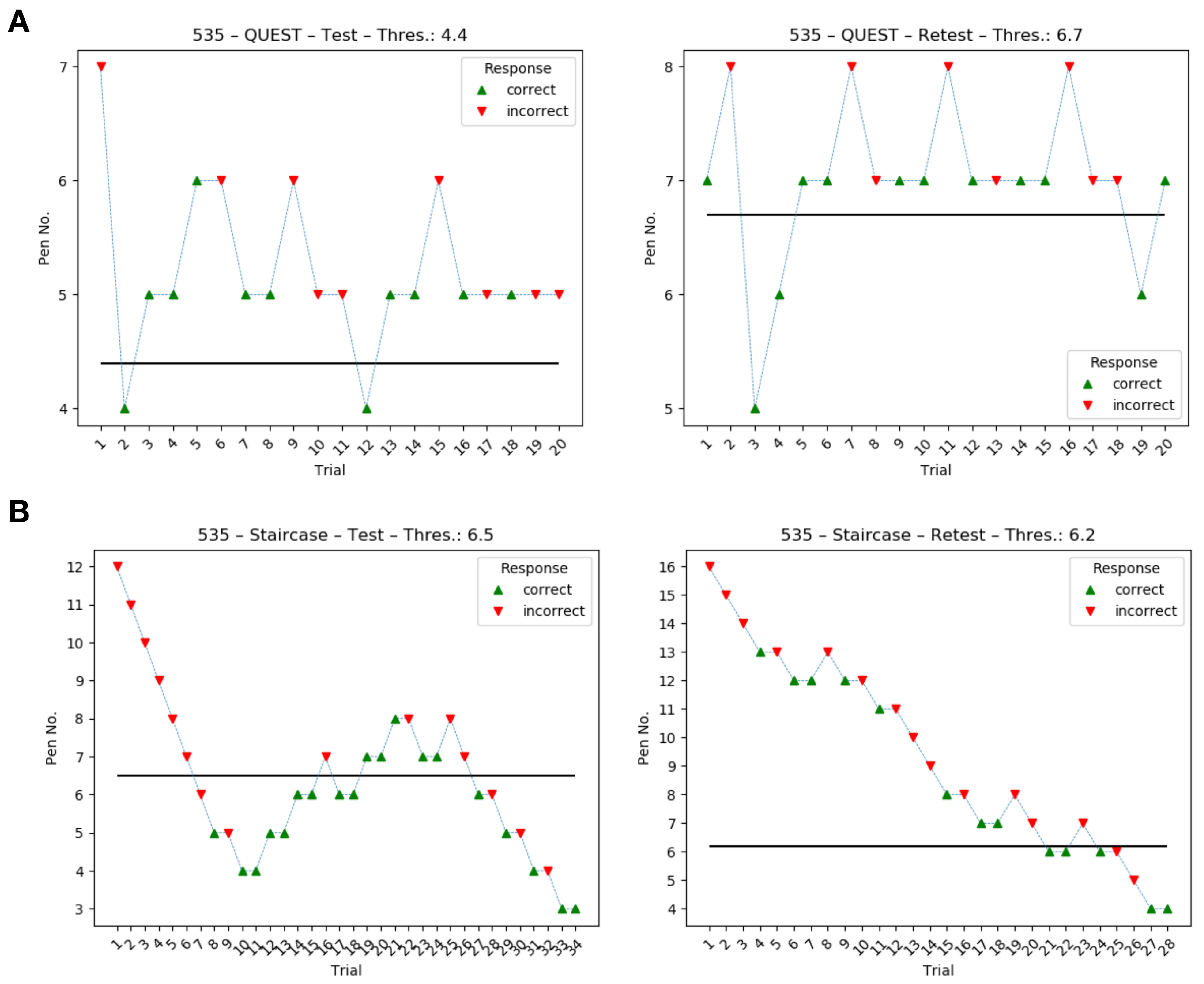
Inspection of the data showed that some staircase runs had not fully converged although seven reversal points were reached. In these cases, participants exhibited a somewhat “fluctuating” response behavior (or threshold) that caused the procedure to move in the direction of higher concentrations throughout the experiment (see
Figure A1 in the
appendix and supplementary data for an example). QUEST proved to behave more consistently, at least in some cases, by either converging to a threshold or by reaching pen no. 1, which would then sometimes not be identified correctly. These interesting differences between procedures require further investigation to fully understand their cause and influence on threshold estimates and, ultimately, diagnostics.