Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests
Abstract
:1. Introduction
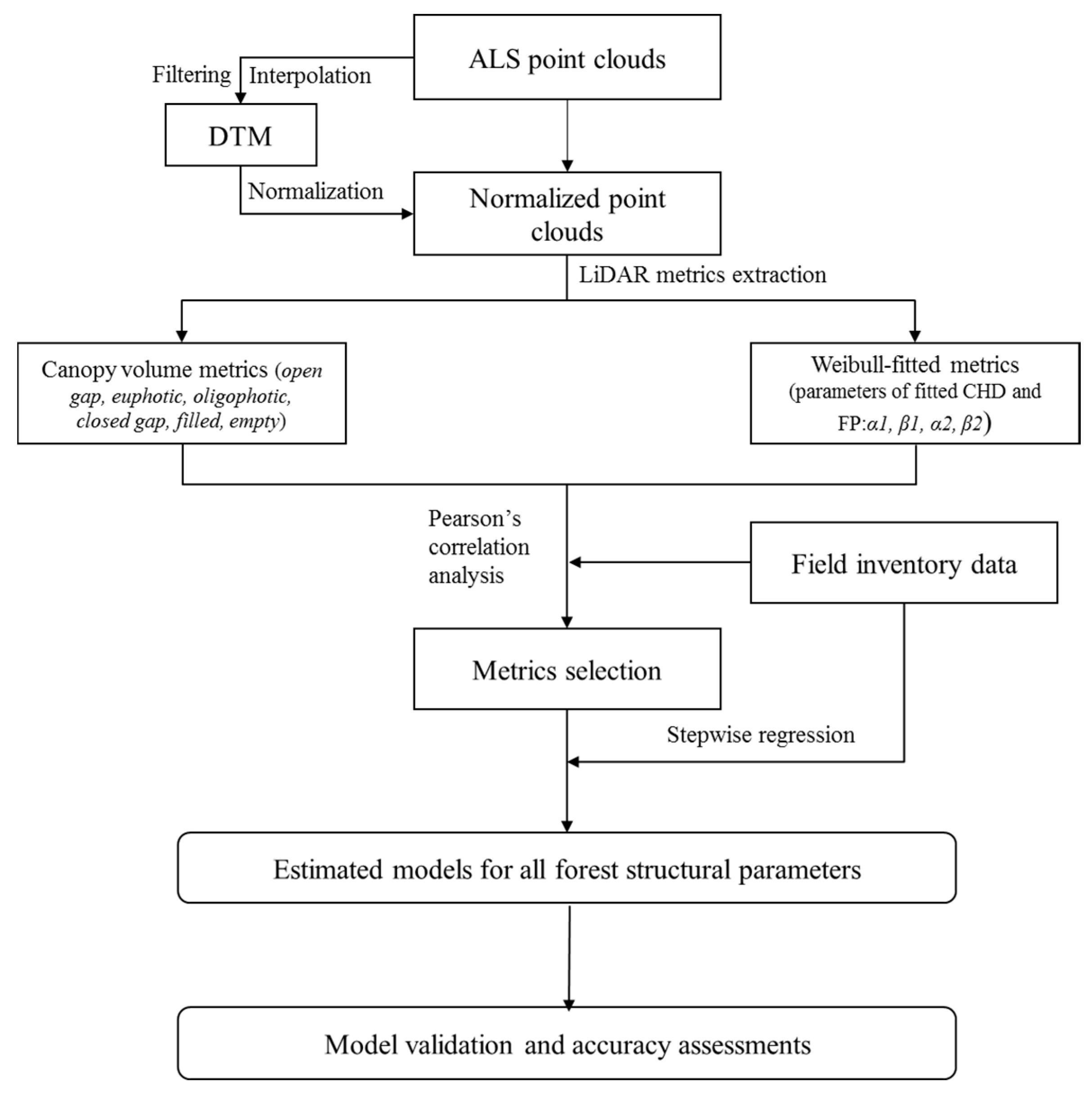
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition and Pre-Processing
2.2.1. LiDAR Data
2.2.2. Field Data
2.3. Derived Metrics
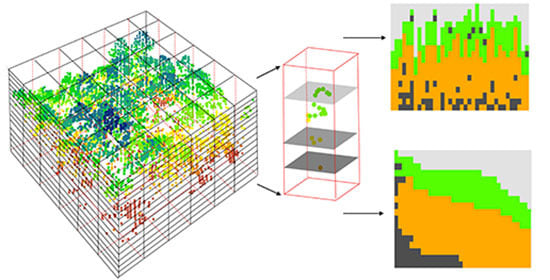
2.3.1. Canopy Volume Model Approach
2.3.2. Weibull Fitting Approach
2.4. Metrics Selection and Statistical Analysis
3. Results
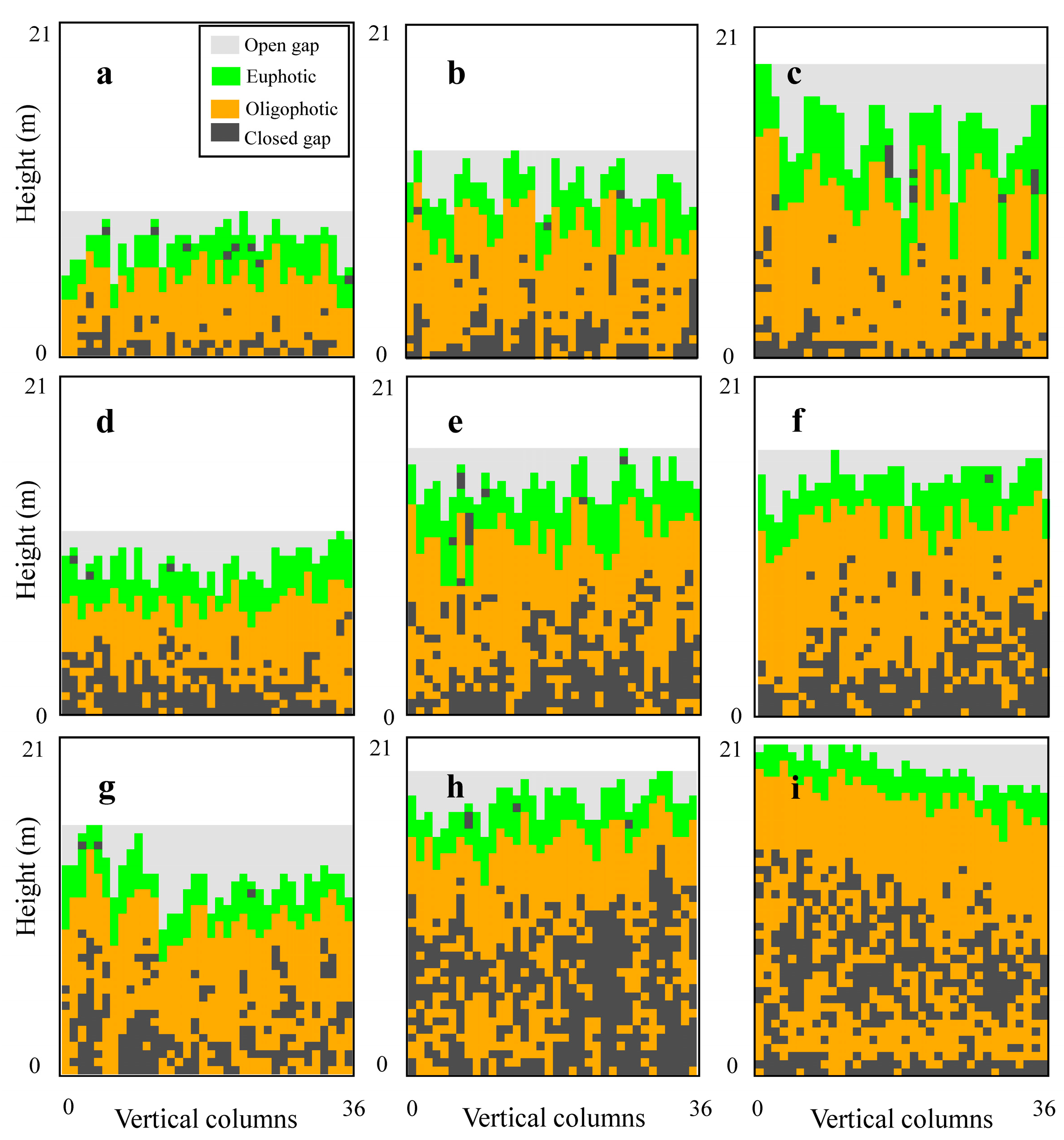
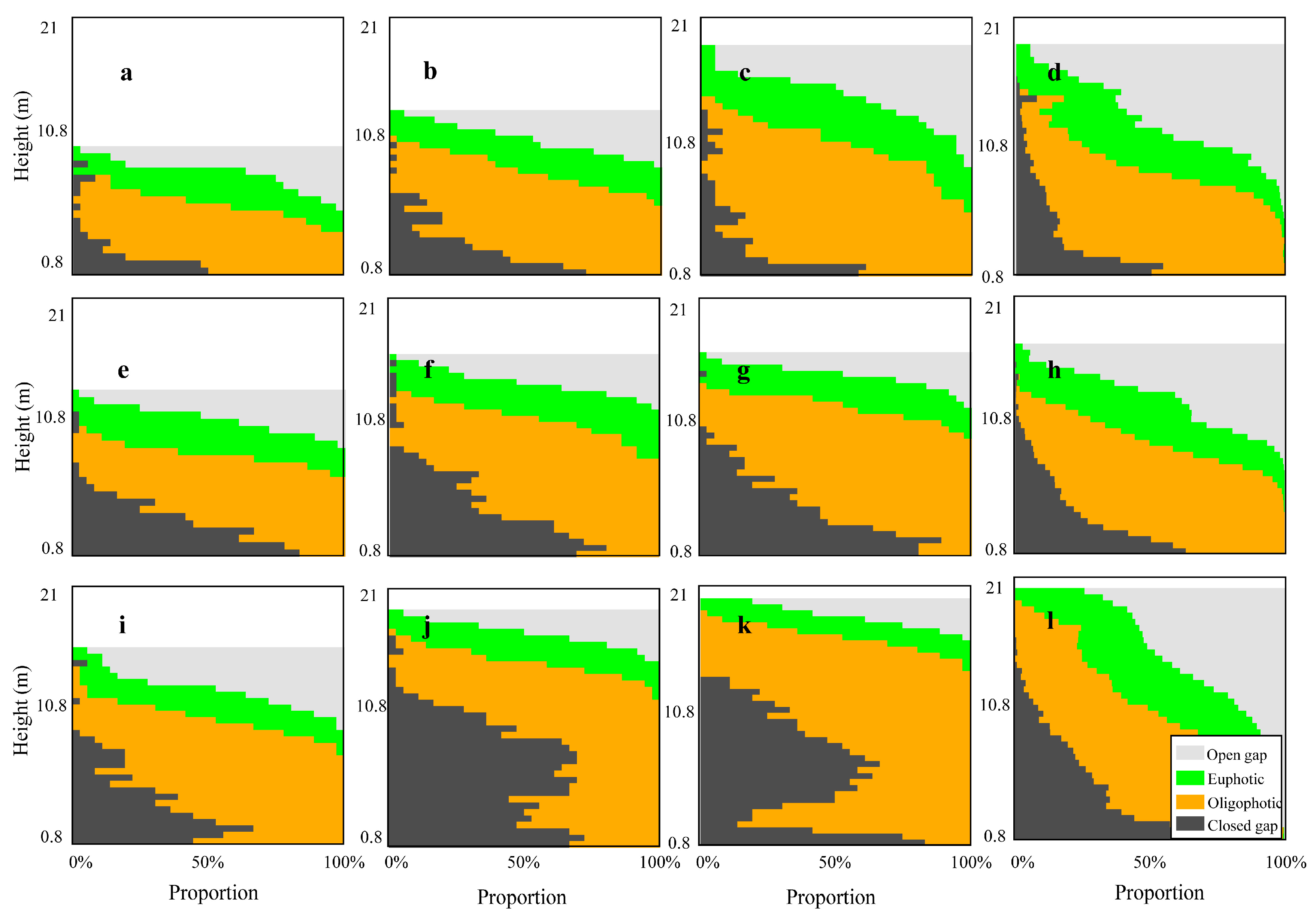
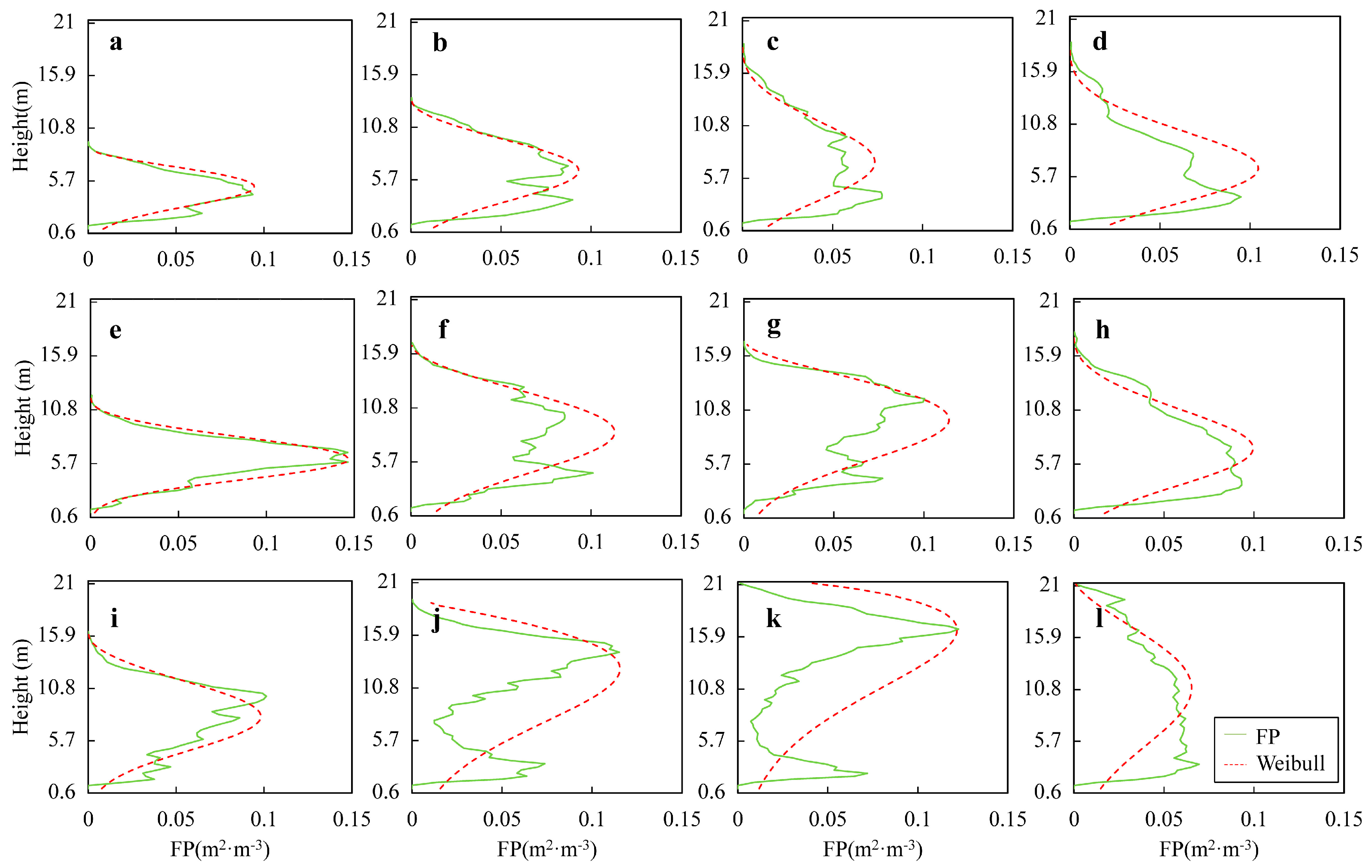
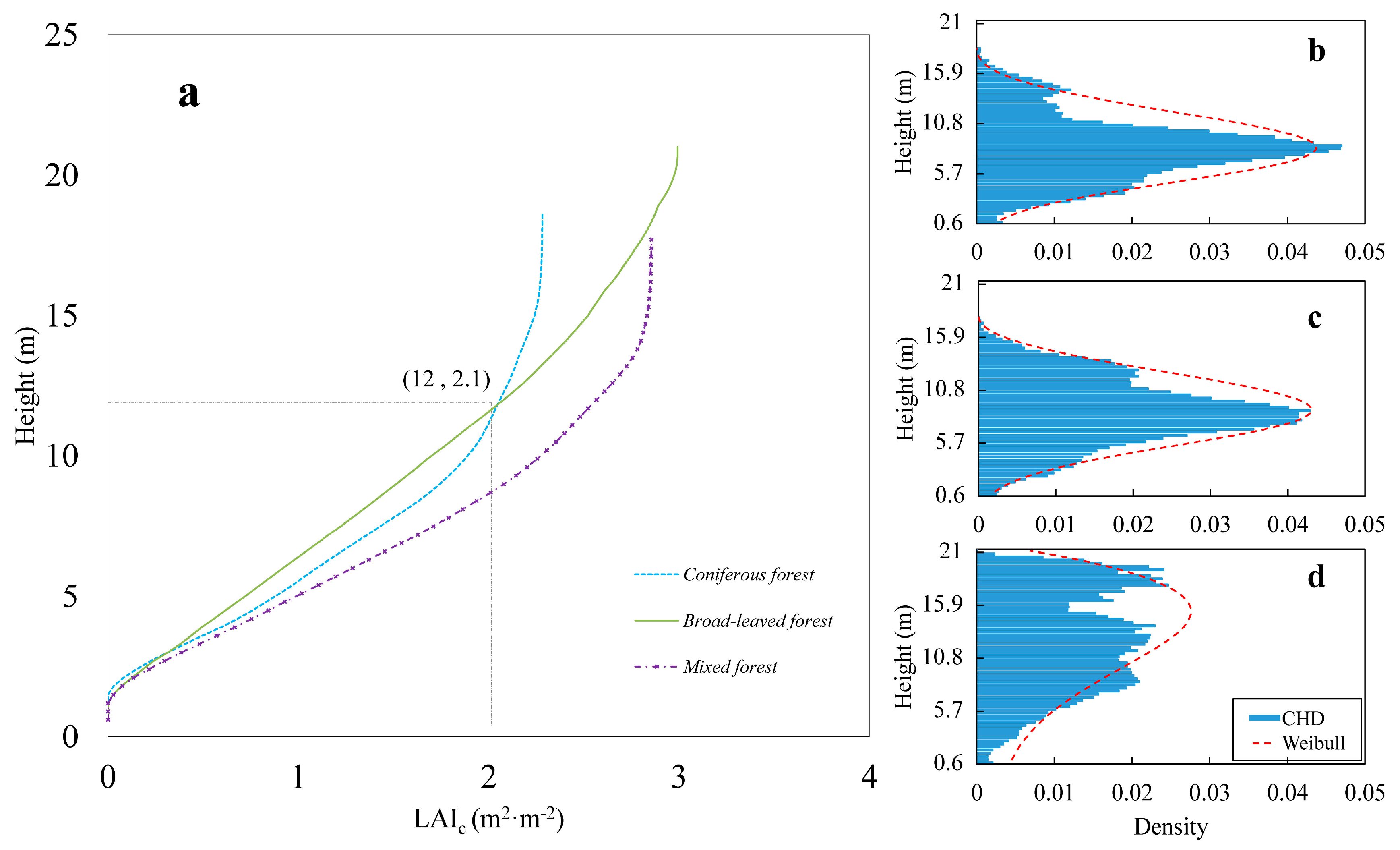
3.1. Profile Analysis
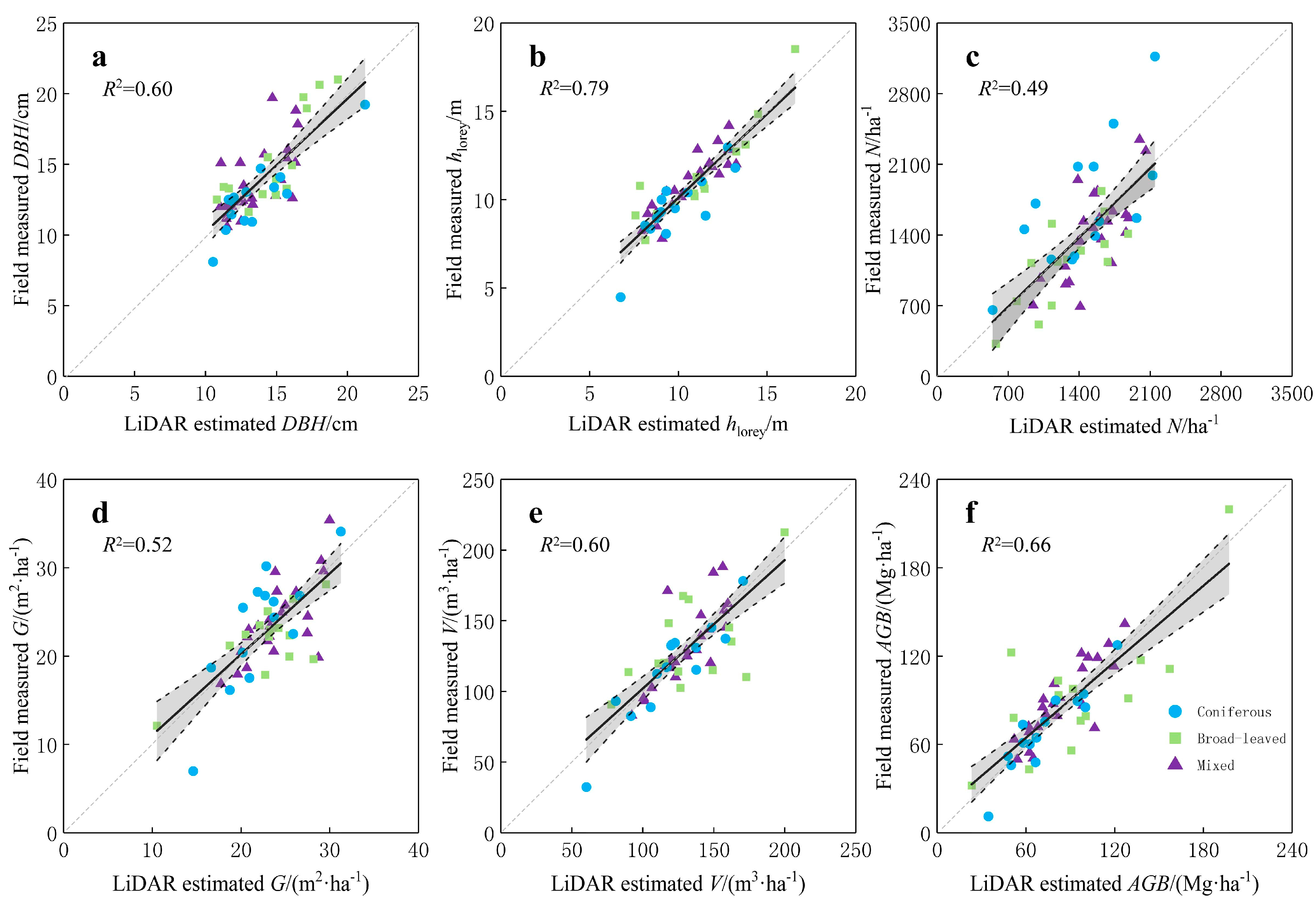
3.2. Accuracy Assessments
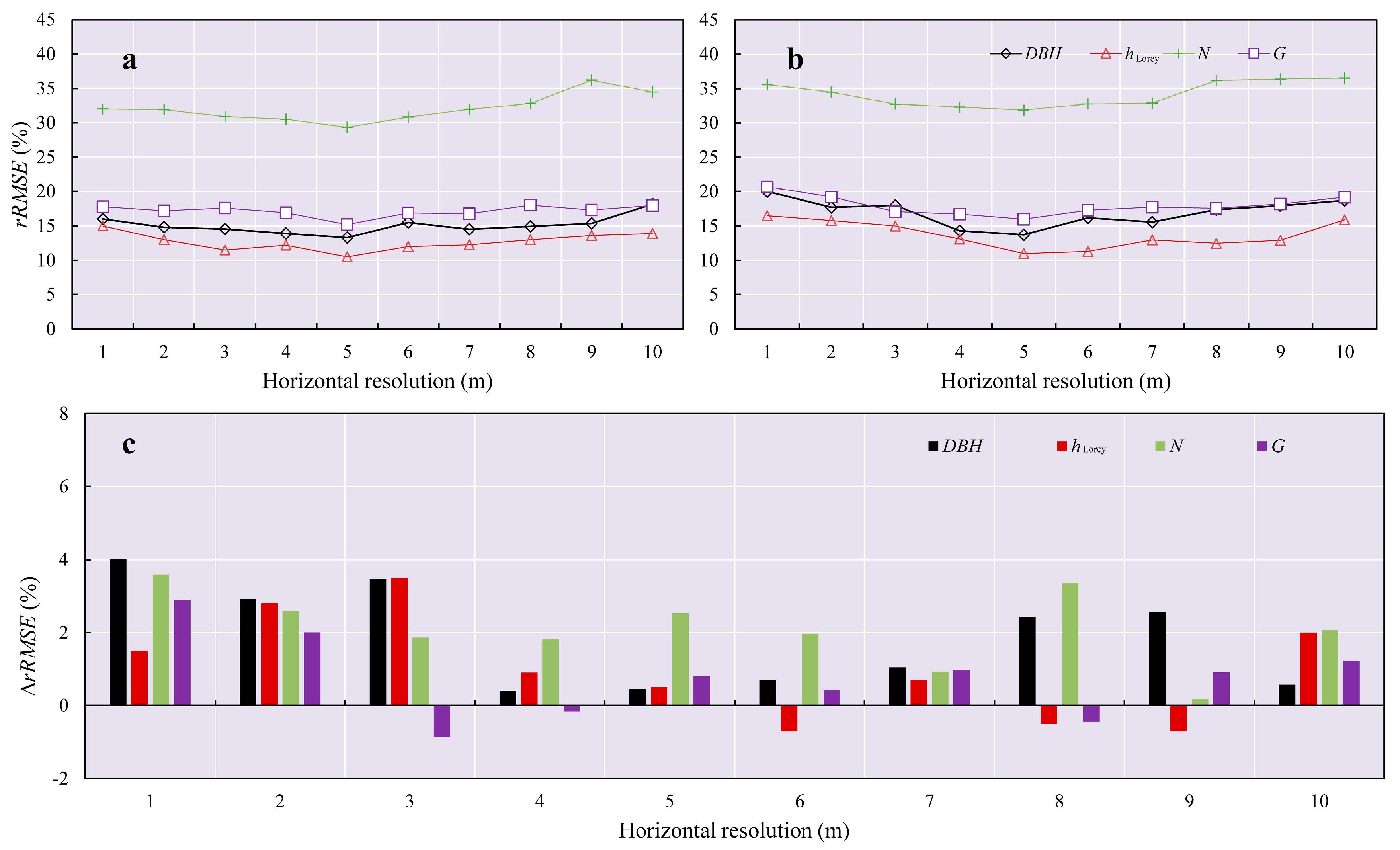
3.3. The Selection of Voxel Sizes
4. Discussion
4.1. Canopy Vertical Profiles
4.2. Predictive Models
4.3. The Selection of Voxel Sizes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Tree Species | Component | a | b | R2 | References |
|---|---|---|---|---|---|
| Masson pine | Stem wood (Ws) | 0.141 | 1.092 | 0.9970 | Jiang et al. (1992) [42] |
| Live branches (Wb) | 0.065 | 0.991 | 0.9871 | ||
| Foliage (Wf) | 0.132 | 0.745 | 0.9827 | ||
| Chinese fir | Stem wood (Ws) | 0.124 | 0.680 | 0.9704 | Ye and Jiang (1983) [43] |
| Live branches (Wb) | 0.203 | 0.385 | 0.7223 | ||
| Foliage (Wf) | 0.850 | 0.189 | 0.6567 | ||
| Slash pine | Stem wood (Ws) | 0.235 | 0.900 | 0.9523 | Wang and Shi (1990) [44] |
| Live branches (Wb) | 0.080 | 1.064 | 0.8520 | ||
| Foliage (Wf) | 0.456 | 0.610 | 0.8802 | ||
| Sawtooth oak | Stem wood (Ws) | 0.018 | 1.034 | 0.9864 | Xu et al. (2011) [46] |
| Live branches (Wb) | 0.00008 | 1.468 | 0.9745 | ||
| Foliage (Wf) | 0.004 | 0.769 | 0.8662 | ||
| Sweet gum | Stem wood (Ws) | 0.093 | 0.801 | 0.9310 | Qian (2000) [45] |
| Live branches (Wb) | 0.083 | 0.649 | 0.9890 | ||
| Foliage (Wf) | 1.084 | 0.217 | 0.6940 | ||
| Other broadleaves a | Stem wood (Ws) | 0.023 | 0.985 | 0.9903 | Sun et al. (1992) [47] |
| Live branches (Wb) | 0.00004 | 3.785 | 0.9623 | ||
| Foliage (Wf) | 0.00003 | 1.378 | 0.9456 |
| Variables | Predictive Models | Adj-R2 | RMSE | rRMSE % |
|---|---|---|---|---|
| All plots | ||||
| DBH/cm | 0.60 *** | 1.72 | 12.33 | |
| hLorey/m | 0.75 *** | 0.97 | 9.15 | |
| N/(ha−1) | 0.42 *** | 423.75 | 29.86 | |
| G/(m2·ha−1) | 0.44 *** | 3.99 | 17.23 | |
| V/(m3·ha−1) | 0.46 *** | 22.34 | 17.46 | |
| AGB/(Mg·ha−1) | 0.64 *** | 19.17 | 22.47 | |
| Coniferous forests | ||||
| DBH/cm | 0.67 ** | 1.20 | 9.50 | |
| hLorey/m | 0.66 | 1.09 | 11.47 | |
| N/(ha−1) | 0.60 | 315.78 | 18.68 | |
| G/(m2·ha−1) | 0.62 ** | 4.53 | 19.63 | |
| V/(m3·ha−1) | 0.69 ** | 22.40 | 19.22 | |
| AGB/(Mg·ha−1) | 0.72 ** | 16.86 | 24.17 | |
| Broad-leaved forests | ||||
| DBH/cm | 0.61 ** | 1.70 | 11.12 | |
| hLorey/m | 0.84 *** | 0.78 | 6.91 | |
| N/(ha−1) | 0.60 | 298.99 | 26.55 | |
| G/(m2·ha−1) | 0.54 | 2.62 | 11.96 | |
| V/(m3·ha−1) | 0.56 | 19.49 | 14.68 | |
| AGB/(Mg·ha−1) | 0.57 | 26.80 | 28.42 | |
| Mixed forests | ||||
| DBH/cm | 0.48 ** | 1.66 | 11.94 | |
| hLorey/m | 0.81 *** | 0.60 | 5.60 | |
| N/(ha−1) | 0.48 ** | 336.73 | 28.52 | |
| G/(m2·ha−1) | 0.45 ** | 3.08 | 12.86 | |
| V/(m3·ha−1) | 0.60 *** | 16.76 | 12.70 | |
| AGB/(Mg·ha−1) | 0.64 *** | 13.20 | 14.77 | |
| Variables | Predictive Models | Adj-R2 | RMSE | rRMSE % |
|---|---|---|---|---|
| All plots | ||||
| DBH/cm | 0.50 *** | 1.86 | 13.31 | |
| hLorey/m | 0.61 *** | 1.18 | 11.13 | |
| N/(ha−1) | 0.39 *** | 415.17 | 29.26 | |
| G/(m2·ha−1) | 0.41 *** | 3.67 | 15.82 | |
| V/(m3·ha−1) | 0.42 *** | 22.36 | 17.48 | |
| AGB/(Mg·ha−1) | 0.54 *** | 19.84 | 23.25 | |
| Coniferous forests | ||||
| DBH/cm | 0.54 | 1.40 | 11.09 | |
| hLorey/m | 0.64 | 1.21 | 12.79 | |
| N/(ha−1) | 0.58 | 431.65 | 25.53 | |
| G/(m2·ha−1) | 0.55 | 4.73 | 20.48 | |
| V/(m3·ha−1) | 0.72 ** | 18.32 | 15.72 | |
| AGB/(Mg·ha−1) | 0.74 ** | 18.51 | 26.55 | |
| Broad-leaved forests | ||||
| DBH/cm | 0.51 | 1.81 | 11.79 | |
| hLorey/m | 0.83 *** | 0.88 | 7.72 | |
| N/(ha−1) | 0.52 | 299.82 | 26.63 | |
| G/(m2·ha−1) | 0.50 | 2.74 | 12.48 | |
| V/(m3·ha−1) | 0.58 | 18.97 | 14.28 | |
| AGB/(Mg·ha−1) | 0.60 | 26.45 | 28.05 | |
| Mixed forests | ||||
| DBH/cm | 0.48 | 1.78 | 12.79 | |
| hLorey/m | 0.75 *** | 0.75 | 6.94 | |
| N/(ha−1) | 0.44 | 324.73 | 22.68 | |
| G/(m2·ha−1) | 0.45 *** | 3.12 | 13.01 | |
| V/(m3·ha−1) | 0.65 *** | 16.31 | 12.36 | |
| AGB/(Mg·ha−1) | 0.71 *** | 13.00 | 14.55 | |
| Variables | Predictive Models | Adj-R2 | RMSE | rRMSE % |
|---|---|---|---|---|
| All forests | ||||
| DBH/cm | 0.61 *** | 1.67 | 11.97 | |
| hLorey/m | 0.77 *** | 0.90 | 8.54 | |
| N/(ha−1) | 0.45 *** | 410.02 | 28.90 | |
| G/(m2·ha−1) | 0.50 *** | 3.47 | 14.96 | |
| V/(m3·ha−1) | 0.58 *** | 21.07 | 16.47 | |
| AGB/(Mg·ha−1) | 0.65 *** | 18.25 | 21.39 | |
| Coniferous forests | ||||
| DBH/cm | 0.74 ** | 1.08 | 8.59 | |
| hLorey/m | 0.77** | 0.99 | 10.43 | |
| N/(ha−1) | 0.64 | 339.29 | 20.07 | |
| G/(m2·ha−1) | 0.69 ** | 4.23 | 18.32 | |
| V/(m3·ha−1) | 0.78 ** | 18.21 | 15.63 | |
| AGB/(Mg·ha−1) | 0.81 ** | 14.53 | 20.83 | |
| Broad-leaved forests | ||||
| DBH/cm | 0.68 | 1.54 | 10.06 | |
| hLorey/m | 0.88 *** | 0.72 | 6.39 | |
| N/(ha−1) | 0.62 | 273.49 | 24.29 | |
| G/(m2·ha−1) | 0.63 | 2.49 | 11.34 | |
| V/( m3·ha−1) | 0.67 | 16.65 | 12.54 | |
| AGB/(Mg·ha−1) | 0.66 | 26.67 | 28.29 | |
| Mixed forests | ||||
| DBH/cm | 0.55 ** | 1.58 | 11.34 | |
| hLorey/m | 0.84 *** | 0.55 | 5.13 | |
| N/(ha−1) | 0.50 *** | 319.05 | 22.28 | |
| G/(m2·ha−1) | 0.56 ** | 2.77 | 11.56 | |
| V/(m3·ha−1) | 0.71 *** | 15.87 | 12.02 | |
| AGB/(Mg·ha−1) | 0.79 *** | 10.89 | 12.19 | |
References
- Pan, Y.; Birdsey, R.A.; Phillips, O.L.; Jackson, R.B. The Structure, Distribution, and Biomass of the World’s Forests. Ann. Rev. Ecol. Evol. Syst. 2013, 44, 593–622. [Google Scholar] [CrossRef]
- Hill, S.; Lati, H.; Heurich, M.; Müller, J. Individual-tree-and stand-based development following natural disturbance in a heterogeneously structured forest: A LiDAR-based approach. Ecol. Inform. 2017, 38, 12–25. [Google Scholar] [CrossRef]
- Franklin, J.F.; Spies, T.A.; Pelt, R.V.; Carey, A.B.; Thornburgh, D.A.; Rae, D.; Lindenmayer, D.B.; Harmon, M.E.; Keeton, W.S.; Shaw, D.C.; et al. Disturbances and structural development of nsatural forest ecosystems with silvicultural implications, using Douglas-fir forests as an example. For. Ecol. Manag. 2002, 155, 399–423. [Google Scholar] [CrossRef]
- Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return lidar data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and woodland stand structural complexity: Its definition and measurement. For. Ecol. Manag. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Spies, T.A. Forest Structure: A Key to the Ecosystem. Northwest Sci. 1998, 72, 34–39. [Google Scholar]
- Zimble, D.A.; Evans, D.L.; Carlson, G.C.; Parker, R.C.; Grado, S.C.; Gerard, P.D. Characterizing vertical forest structure using small-footprint airborne LiDAR. Remote Sens. Environ. 2003, 87, 171–182. [Google Scholar] [CrossRef]
- Miura, N.; Jones, S.D. Characterizing forest ecological structure using pulse types and heights of airborne laser scanning. Remote Sens. Environ. J. 2010, 114, 1069–1076. [Google Scholar] [CrossRef]
- Pasher, J.; King, D.J. Multivariate forest structure modelling and mapping using high resolution airborne imagery and topographic information. Remote Sens. Environ. 2010, 114, 1718–1732. [Google Scholar] [CrossRef]
- Corlett, R.T. Where are the Subtropics? Biotropica 2013, 45, 273–275. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Cristiano, P.M.; Zhang, Y.F.; Campanello, P.I.; Tan, Z.H.; Zhang, Y.P.; Goldstein, G.; Cao, K.F. Carbon Economy of Subtropical Forests. Trop. Tree Physiol. 2016, 6, 337–355. [Google Scholar]
- Global Forest Resources Assessment 2015. Available online: http://www.fao.org/3/a-i4808e.pdf (accessed on 14 June 2017).
- Ouyang, S.; Xiang, W.; Wang, X.; Zeng, Y.; Lei, P.; Deng, X.; Peng, C. Significant effects of biodiversity on forest biomass during the succession of subtropical forest in south China. For. Ecol. Manag. 2016, 372, 291–302. [Google Scholar] [CrossRef]
- Bouvier, M.; De, M.; Renaud, J. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P.; White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; et al. Remote Sensing Technologies for Enhancing Forest Inventories: A Review Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Mcroberts, R.E.; Tomppo, E.O. Remote sensing support for national forest inventories. Remote Sens. Environ. 2007, 110, 412–419. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Wulder, M. Optical remote-sensing techniques for the assessment of forest inventory and biophysical parameters. Prog. Phys. Geogr. 1998, 22, 449–476. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Niemann, K.O.; Wulder, M.A. Integration of GLAS and Landsat TM data for aboveground biomass estimation. Carbon 2010, 36, 129–141. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Laurin, G.V.; Saah, D. Aboveground Forest Biomass Estimation with Landsat and LiDAR Data and Uncertainty Analysis of the Estimates. Int. J. For. Res. 2012, 2012. [Google Scholar] [CrossRef]
- Rosenqvist, Å.; Milne, A.; Lucas, R.; Imhoff, M.; Dobson, C. A review of remote sensing technology in support of the Kyoto Protocol. Environ. Sci. Policy 2003, 6, 441–455. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, X.; Fan, W. Estimates of forest structure parameters from GLAS data and multi-angle imaging spectrometer data. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 65–71. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D.; Wu, M.; Zhao, W. Remote estimation of canopy height and aboveground biomass of maize using high-resolution stereo images from a low-cost unmanned aerial vehicle system. Ecol. Indic. 2016, 67, 637–648. [Google Scholar] [CrossRef]
- Véga, C.; Renaud, J.; Durrieu, S.; Bouvier, M. On the interest of penetration depth, canopy area and volume metrics to improve Lidar-based models of forest parameters. Remote Sens. Environ. 2016, 175, 32–42. [Google Scholar] [CrossRef]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Abstract, C.J.H. Predicting Forest Stand Characteristics with Airborne Scanning Lidar. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
- Silva, C.A.; Klauberg, C.; Hudak, A.T.; Vierling, L.A.; Liesenberg, V.; Carvalho, S.P.C.E.; Rodriguez, L.C.E. A principal component approach for predicting the stem volume in Eucalyptus plantations in Brazil using airborne LiDAR data. Forestry 2016, 89, 422–433. [Google Scholar] [CrossRef]
- Tesfamichael, S.G.; Beech, C. Combining Akaike’s Information Criterion and discrete return LiDAR data to estimate structural attributes of savanna woody vegetation. J. Arid Environ. 2016, 129, 25–34. [Google Scholar] [CrossRef]
- Sabol, J.; Procházka, D.; Patočka, Z. Development of models for forest variable estimation from airborne laser scanning data using an area-based approach at a plot level. J. For. Sci. 2016, 62, 137–142. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. J. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Montealegre, A.L.; Riva, J.D.; García-martín, A. Use of low point density ALS data to estimate stand-level structural variables in Mediterranean Aleppo pine forest. Forestry 2016, 1–10. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Magnussen, S.; Næsset, E.; Gobakken, T. Reliability of LiDAR derived predictors of forest inventory attributes: A case study with Norway spruce. Remote Sens. Environ. 2010, 114, 700–712. [Google Scholar] [CrossRef]
- Magnussen, S.; Næsset, E.; Gobakken, T. Prediction of tree-size distributions and inventory variables from cumulants of canopy height distributions. Forestry 2013, 86, 583–595. [Google Scholar] [CrossRef]
- MacArthur, R.; MacArthur, J.W. On bird species diversity. Ecology 1961, 42, 594–598. [Google Scholar]
- Aber, J.D. A method for estimating foliage-height profiles in broad-leaved forests. Ecology 1979, 67, 35–40. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G. Lidar Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 361, 339–361. [Google Scholar] [CrossRef]
- Lovell, J.L.; Jupp, D.L.B.; Culvenor, D.S.; Coops, N.C.; Les, R. Using airborne and ground-based ranging lidar to measure canopy structure in Australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating canopy structure of Douglas-fir forest stands from discrete-return LiDAR. Trees 2007, 21, 295–310. [Google Scholar] [CrossRef]
- Hilker, T.; Leeuwen, M.V.; Coops, N.C. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees 2010, 24, 819–832. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Song, Y.B.; Ding, Y.P. The development and latest progress of JSCORS. Bull. Surv. Mapp. 2009, 2, 73–74. [Google Scholar]
- Jiang, B.; Yuan, W.; Zhu, G. A preliminary study on the plantation biomass and produce structure of Pinus massoniana, Pinus elliottii and Pinus taeda. J. Zhejiang For. Sci. Technol. 1992, 12, 1–9. [Google Scholar]
- Ye, J.; Yang, Z. Biomass structure of planted Chinese fir in Southern Jiangsu province, China. Acta Ecol. Sin. 1983, 3, 7–14. [Google Scholar]
- Wang, Q.; Shi, Y. A preliminary study on the biomass and production of slash pine plantation in Jiangsu province. Acta Phytoecol. Geobot. Sin. 1990, 14, 2–12. [Google Scholar]
- Xu, J.; Wang, M.; Huang, Q.; Gong, S. Study on aboveground biomass model of natural individual trees of Quercus acutissima. Anhui For. Sci. Technol. 2011, 37, 3–6. [Google Scholar]
- Qian, G. Studies on the dynamic change of the net production quantity of liquidambar formosana plantation. Acta Agric. Univ. Jiangxiensis 2000, 22, 399–404. [Google Scholar]
- Sun, D.; Ruan, H.; Ye, J. Biomass Structure of Oak-Dominated Secondary Forest in Kongqingshan. Available online: http://refhub.elsevier.com/S0034-4257(16)30106-7/rf0260 (accessed on 14 June 2017).
- Zhao, K.; Popescu, S.; Nelson, R. Lidar remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Weishampel, J.F.; Drake, J.B.; Cooper, A.; Blair, J.B.; Hofton, M. Forest canopy recovery from the 1938 hurricane and subsequent salvage damage measured with airborne LiDAR. Remote Sens. Environ. 2007, 109, 142–153. [Google Scholar] [CrossRef]
- Bailey, R.; Dell, T. Quantifying diameter distributions with the Weibull function. For. Sci. 1973, 19, 97–104. [Google Scholar]
- Penner, M.; Woods, M.; Pitt, D.G. A comparison of airborne laser scanning and image point cloud derived tree size class distribution models in Boreal Ontario. Forests 2015, 6, 4034–4054. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Wulder, M.A. Enriching ALS-derived area-based estimates of volume through tree-level downscaling. Forests 2015, 6, 2608–2630. [Google Scholar] [CrossRef]
- Zhao, J.; LI, J.; Liu, Q. Review of forest vertical structure parameter inversion based on remote sensing technology. J. Remote Sens. 2013, 17, 697. [Google Scholar]
- Jupp, D.L.B.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating forest LAI profiles and structural parameters using a ground-based laser called ‘Echidna®. Tree Physiol. 2008, 29, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Hilker, T.; Coops, N.C.; Newnham, G.J.; Leeuwen, M.V.; Wulder, M.A.; Stewart, J.; Culvenor, D.S. Comparison of Terrestrial and Airborne LiDAR in Describing Stand Structure of a Thinned Lodgepole Pine Forest. J. For. 2012, 10, 97–104. [Google Scholar]
- Sprugel, D. Correcting for Bias in Log-Transformed Allometric Equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T. Comparing regression methods in estimation of biophysical properties of forest stands from two different inventories using laser scanner data. Remote Sens. Environ. 2005, 94, 541–553. [Google Scholar] [CrossRef]
- García-gutiérrez, J.; Martínez-Álvarez, F.; Troncoso, A.; Riquelme, J.C. A comparison of machine learning regression techniques for LiDAR-derived estimation of forest variables. Neurocomputing 2015, 167, 24–31. [Google Scholar] [CrossRef]
- Naesset, E.; Okland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kutner, M.; Nachtsheim, C.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill/Irwin: New York, NY, USA, 2004. [Google Scholar]
- Bengio, Y. No Unbiased Estimator of the Variance of K-Fold Cross-Validation. J. Mach. Learn. Res. 2004, 5, 1089–1105. [Google Scholar]
- Parker, G.G. Structure and Microclimate of Forest Canopies. In Forest Canopies; Lowman, M.D., Nadkarni, N.M., Eds.; Academic Press: San Diego, CA, USA, 1995; pp. 73–106. [Google Scholar]
- Wilkes, P.; Suarez, L.; Andrew, H.; Andrew, M.; William, W.; Mariela, S.-B.; Skidmore, A.K. Using discrete-return ALS to quantify number of canopy strata across diverse forest types Using discrete-return airborne laser scanning to quantify number of canopy strata across diverse forest types. Methods Ecol. Evol. 2015, 1–13. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface Lidar Remote Sensing of Basal Area and Biomass in Deciduous Forests of Eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Leiterer, R.; Torabzadeh, H.; Furrer, R.; Schaepman, M.E.; Morsdorf, F. Towards Automated Characterization of Canopy Layering in Mixed Temperate Forests Using Airborne Laser Scanning. Forests 2015, 6, 4146–4167. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Ishii, H. The role of crown architecture, leaf phenology and photosynthetic activity in promoting complementary use of light among coexisting species in temperate forests. Ecol. Res. 2010, 25, 715–722. [Google Scholar] [CrossRef]
- He, J.; Zhu, S. The Preliminary Study on the Law of the Crown Structure of Massons Pine in Mid-Subtropical Region. J. Mt. Agric. Biol. 1990, 9, 61–72. [Google Scholar]
- Liang, X.; Ye, W. Advances in Study of Forest Gaps. J. Trop. Subtrop. Bot. 2001, 9, 355–364. [Google Scholar]
- Kneeshaw, D.D.; Bergeron, Y. Canopy Gap Characteristics and Tree Replacement in the Southeastern Boreal Forest. Ecology 1998, 79, 783–794. [Google Scholar] [CrossRef]
- An, S.; Zhao, R. Analysis of Characteristics of Secondary Forest Vegetation in the North Subtropical Zone of China. J. Nanjing Univ. Sci. 1991, 27, 324–331. [Google Scholar]
- Spies, T.A.; Frankli, J.F. Gap Characteristics and Vegetation Response in Coniferous Forests of the Pacific Northwest. Ecology 1989, 70, 543–545. [Google Scholar] [CrossRef]
- Yang, J.; Liu, X.; Yang, X. Forest canopy structure, light environment and their effects on the vegetation pattern and growth of understory in forests. J. Sci. Teach. Univ. 2015, 35, 57–62. [Google Scholar]
- Montgomery, R.A.; Chazdon, R.L. Forest structure, canopy architectura, and light transmittance in old-growth and second-growth tropical rain forests. Ecology 2001, 82, 2707–2718. [Google Scholar] [CrossRef]
- Zhu, S.; He, J. The Preliminary Study on the Law of the Crown Structure of Masson’s pine in South-subtropcial. J. Mt. Agric. Biol. 1993, 12, 36–44. [Google Scholar]
- Messier, C.; Sylvain, P.; Bergeron, Y. Effects of Overstory and Understory Vegetation on the Understory Light Environment in Mixed Boreal Forests. J. Veg. Sci. 1998, 9, 511–520. [Google Scholar] [CrossRef]
- Parent, S.; Messier, C. A simple and efficient method to estimate microsite light availability under a forest canopy. Can. J. For. Res. 1996, 26, 151–154. [Google Scholar] [CrossRef]
- Zhao, F.; Yang, X.; Schull, M.A.; Román-colón, M.O.; Yao, T.; Wang, Z.; Zhang, Q.; Jupp, D.L.B.; Lovell, J.L.; Culvenor, D.S.; et al. Measuring effective leaf area index, foliage profile, and stand height in New England forest stands using a full-waveform ground-based lidar. Remote Sens. Environ. 2011, 115, 2954–2964. [Google Scholar] [CrossRef]
- Tang, H.; Dubayah, R.; Brolly, M.; Ganguly, S.; Zhang, G. Large-scale retrieval of leaf area index and vertical foliage profile from the spaceborne waveform lidar (GLAS/ICESat). Remote Sens. Environ. 2014, 154, 8–18. [Google Scholar] [CrossRef]
- Fu, T.; Pang, Y.; Huang, Q.F.; Liu, Q.W.; Xu, G.C. Prediction of Subtropical Forest Parameters Using Airborne Laser Scanner. J. Remote Sens. 2011, 15, 1092–1104. [Google Scholar]
- Xu, Z.; Cao, L.; Ruan, H.; Li, W.; Jiang, S. Inversion of subtropical forest stand characteristics by integrating very high resolution imagery acquired from UAV and LiDAR point-cloud. Chin. J. Plant Ecol. 2015, 39, 849–856. [Google Scholar]
- Wilkes, P.; Jones, S.; Suarez, L.; Haywood, A.; Mellora, A.; Soto-Berelov, M.; Woodgate, W. MAUP and LiDAR derived canopy structure. Int. Geosci. Remote Sens. Symp. 2013, 173–175. [Google Scholar]
- Maltamo, M.; Bollandsås, O.M.; Næsset, E.; Gobakken, T.; Packalén, P. Different plot selection strategies for field training data in ALS-assisted forest inventory. Forestry 2011, 84, 23–31. [Google Scholar] [CrossRef]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Mereu, S.; Muys, B.; Coppin, P. 3D modeling of light interception in heterogeneous forest canopies using ground-based LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 792–800. [Google Scholar] [CrossRef]
- Stoker, J. Volumetric Visualization of multiple-return Lidar Data: Using Voxels. Photogramm. Eng. Remote Sens. 2009, 75, 109–112. [Google Scholar]
- Zheng, G.; Moskal, L.M. Computational-Geometry-Based Retrieval of Computational-Geometry-Based Retrieval of Effective Leaf Area Index Using Terrestrial Laser Scanning. IEEE Geosci. Remote Sens. Soc. 2015, 50, 3958–3969. [Google Scholar] [CrossRef]
- Grau, E.; Durrieu, S.; Fournier, R.; Gastellu-etchegorry, J.; Yin, T. Estimation of 3D vegetation density with Terrestrial Laser Scanning data using voxels. A sensitivity analysis of influencing parameters. Remote Sens. Environ. 2017, 191, 373–388. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Noland, T.L. Classification of tree species based on structural features derived from high density LiDAR data. Agric. For. Meteorol. 2013, 171–172, 104–114. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Leiterer, R.; Schaepman, M.E.; Morsdorf, F. Quantification of hidden canopy volume of airborne laser scanning data using a voxel traversal algorithm. Remote Sens. Environ. 2017, 194, 424–436. [Google Scholar] [CrossRef]
- Oshio, H.; Asawa, T.; Hoyano, A.; Miyasaka, S. Estimation of the leaf area density distribution of individual trees using high-resolution and multi-return airborne LiDAR data. Remote Sens. Environ. 2015, 166, 116–125. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.; Fournier, R.A. A model for deriving voxel-level tree leaf area density estimates from ground-based LiDAR. Environ. Model. Softw. 2014, 51, 184–189. [Google Scholar] [CrossRef]



| Parameters | Coniferous Forest (n = 14) | Broad-Leaved Forest (n = 14) | Mixed Forest (n = 23) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Range | Mean | SD | Range | Mean | SD | Range | Mean | SD | |
| DBH/cm | 8.08–19.22 | 12.62 | 2.53 | 11.63–20.99 | 15.32 | 3.29 | 10.58–19.69 | 13.90 | 2.51 |
| hLorey/m | 4.47–12.97 | 9.50 | 2.00 | 7.70–18.52 | 11.35 | 2.75 | 7.79–14.18 | 10.79 | 1.71 |
| N/(ha−1) | 656–3167 | 1690.64 | 643.15 | 322.00–1833.00 | 1126.00 | 428.55 | 689.00–2344.00 | 1431.78 | 438.40 |
| G/(m2·ha−1) | 6.97–34.07 | 23.08 | 6.79 | 12.11–28.10 | 21.92 | 3.89 | 16.84–35.37 | 23.98 | 4.46 |
| V/(m3·ha−1) | 32.19–178.08 | 116.53 | 34.75 | 90.62–212.45 | 132.77 | 32.30 | 82.78–187.91 | 131.98 | 28.67 |
| AGB/(Mg·ha−1) | 11.02–127.39 | 69.74 | 27.76 | 32.03–219.67 | 94.28 | 44.93 | 49.65–141.73 | 89.36 | 25.95 |
| LiDAR Metrics | Description | |
|---|---|---|
| Standard metrics | ||
| Height-based | Percentile heights (h25, h50, h75 and h95) | The percentiles of the canopy height distributions (25th, 50th, 75th and 95th) of first returns. |
| Mean height (hmean) | Mean height above ground of all first returns. | |
| Coefficient of variation of heights (hcv) | Coefficient of variation of heights of all first returns. | |
| Skewness and Kurtosis of heights (i.e., hskewness and hkurtosis) | The skewness and kurtosis of the heights of all points. | |
| Density-based | Canopy return density (d1, d3, d5, d7 and d9) | The proportion of points above the quantiles (10th, 30th, 50th, 70th and 80th) to total number of points. |
| Canopy cover above 2 m (CC2m) | Percentages of first returns above 2 m. | |
| Canopy metrics | ||
| Canopy volume | Filled and Empty zones of CVM (i.e., Filled and Empty) | The voxels contained point clouds and voxels contained no point clouds within canopy spaces. |
| Open and Closed gap zones of CVM (i.e., Open gap (OG) and Closed gap (CG)) | The empty voxels located above and below the canopy respectively. | |
| Euphotic and Oligophotic zones of CVM (i.e., Euphotic (Eu) and Oligophotic (Oligo)) | The voxels located within an uppermost percentile (65%) of all filled grid cells of that column, and voxels located below the point in the profile | |
| Weibull-fitted | α1 and β1 parameter of Weibull distribution | The scale parameter α and shape parameter β of the Weibull density distribution fitted to CHD. |
| α2 and β2 parameter of Weibull distribution | The scale parameter α and shape parameter β of the Weibull density distribution fitted to FP. | |
| Forest Types | Parameters | SM Models | CM Models | Combination Models | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard Metrics | Adj-R2 | RMSE | rRMSE % | Canopy Metrics | Adj-R2 | RMSE | rRMSE % | All Metrics | Adj-R2 | RMSE | rRMSE % | ||
| All plots | DBH/cm | h95, d1, d7 | 0.60 *** | 1.72 | 12.33 | OG, Oligo, Empty, β2 | 0.50 *** | 1.86 | 13.31 | hcv, h75, d1, Oligo | 0.61 *** | 1.67 | 11.97 |
| hLorey/m | hcv, h95, d7, d9 | 0.75 *** | 0.97 | 9.15 | Oligo, Filled, Empty, α1 | 0.61 *** | 1.18 | 11.13 | h50, d1, Empty, β1 | 0.77 *** | 0.90 | 8.54 | |
| N/(ha−1) | hcv, d1, d7, d9 | 0.42 *** | 423.75 | 29.86 | OG, Eu, Oligo, β1 | 0.39 *** | 415.17 | 29.26 | d1, Oligo, α1, β1 | 0.45 *** | 410.02 | 28.90 | |
| G/(m2·ha−1) | h95, d3, d7 | 0.44 *** | 3.99 | 17.23 | Oligo, Empty, α2 | 0.41 *** | 3.67 | 15.82 | hkurtosis, h25, h95, Empty | 0.50 *** | 3.47 | 14.96 | |
| V/(m3·ha−1) | hcv, h25, h50, d3 | 0.46 *** | 22.34 | 17.46 | OG, Eu, Oligo, α1 | 0.42 *** | 22.36 | 17.48 | h75, Oligo, Empty, β1 | 0.58 *** | 21.07 | 16.47 | |
| AGB/(Mg·ha−1) | hkurtosis, h95, d3, d9 | 0.64 *** | 19.17 | 22.47 | OG, Oligo, CG, Empty | 0.54 *** | 19.84 | 23.25 | h95, d3, CC2m, Oligo | 0.66 *** | 18.25 | 21.39 | |
| Coniferous forest | DBH/cm | h95, d1, d7 | 0.67 ** | 1.20 | 9.50 | OG, Oligo, Empty, β2 | 0.54 | 1.40 | 11.09 | hcv, h75, d1, Oligo | 0.74 ** | 1.08 | 8.59 |
| hLorey/m | hcv, h95, d7, d9 | 0.66 | 1.09 | 11.47 | Oligo, Filled, Empty, α1 | 0.64 | 1.21 | 12.79 | h50, d1, Empty, β1 | 0.77 ** | 0.99 | 10.43 | |
| N/(ha−1) | hcv, d1, d7, d9 | 0.60 | 315.78 | 18.68 | OG, Eu, Oligo, β1 | 0.58 | 431.65 | 25.53 | d1, Oligo, α1, β1 | 0.64 | 339.29 | 20.07 | |
| G/(m2·ha−1) | h95, d3, d7 | 0.62 ** | 4.53 | 19.63 | Oligo, Empty, α2 | 0.55 | 4.73 | 20.48 | hkurtosis, h25, h95, Empty | 0.69 ** | 4.23 | 18.32 | |
| V/(m3·ha−1) | hcv, h25, h50, d3 | 0.69 ** | 22.40 | 19.22 | OG, Eu, Oligo, α1 | 0.72 ** | 18.32 | 15.72 | h75, Oligo, Empty, β1 | 0.78 ** | 18.21 | 15.63 | |
| AGB/(Mg·ha−1) | hkurtosis, h95, d3, d9 | 0.72 ** | 16.86 | 24.17 | OG, Oligo, CG, Empty | 0.74 ** | 18.51 | 26.55 | h95, d3, CC2m, Oligo | 0.81 ** | 14.53 | 20.83 | |
| Broad-leaved forest | DBH/cm | h95, d1, d7 | 0.61 ** | 1.70 | 11.12 | OG, Oligo, Empty, β2 | 0.51 | 1.81 | 11.79 | hcv, h75, d1, Oligo | 0.68 | 1.54 | 10.06 |
| hLorey/m | hcv, h95, d7, d9 | 0.84 *** | 0.78 | 6.91 | Oligo, Filled, Empty, α1 | 0.83 *** | 0.88 | 7.72 | h50, d1, Empty, β1 | 0.88 *** | 0.72 | 6.39 | |
| N/(ha−1) | hcv, d1, d7, d9 | 0.60 | 298.99 | 26.55 | OG, Eu, Oligo, β1 | 0.52 | 299.82 | 26.63 | d1, Oligo, α1, β1 | 0.62 | 273.49 | 24.29 | |
| G/(m2·ha−1) | h95, d3, d7 | 0.54 | 2.62 | 11.96 | Oligo, Empty, α2 | 0.50 | 2.74 | 12.48 | hkurtosis, h25, h95, Empty | 0.63 | 2.49 | 11.34 | |
| V/(m3·ha−1) | hcv, h25, h50, d3 | 0.56 | 19.49 | 14.68 | OG, Eu, Oligo, α1 | 0.58 | 18.97 | 14.28 | h75, Oligo, Empty, β1 | 0.67 | 16.65 | 12.54 | |
| AGB/(Mg·ha−1) | hkurtosis, h95, d3, d9 | 0.57 | 26.80 | 28.42 | OG, Oligo, CG, Empty | 0.60 | 26.45 | 28.05 | h95, d3, CC2m, Oligo | 0.66 | 26.67 | 28.29 | |
| Mixed forest | DBH/cm | h95, d1, d7 | 0.48 ** | 1.66 | 11.94 | OG, Oligo, Empty, β2 | 0.48 | 1.78 | 12.79 | hcv, h75, d1, Oligo | 0.55 ** | 1.58 | 11.34 |
| hLorey/m | hcv, h95, d7, d9 | 0.81 *** | 0.60 | 5.60 | Oligo, Filled, Empty, α1 | 0.75 *** | 0.75 | 6.94 | h50, d1, Empty, β1 | 0.84 *** | 0.55 | 5.13 | |
| N/(ha−1) | hcv, d1, d7, d9 | 0.48 ** | 336.73 | 28.52 | OG, Eu, Oligo, β1 | 0.44 | 324.73 | 22.68 | d1, Oligo, α1, β1 | 0.50 *** | 319.05 | 22.28 | |
| G/(m2·ha−1) | h95, d3, d7 | 0.45 ** | 3.08 | 12.86 | Oligo, Empty, α2 | 0.45 *** | 3.12 | 13.01 | hkurtosis, h25, h95, Empty | 0.56 ** | 2.77 | 11.56 | |
| V/(m3·ha−1) | hcv, h25, h50, d3 | 0.60 *** | 16.76 | 12.70 | OG, Eu, Oligo, α1 | 0.65 *** | 16.31 | 12.36 | h75, Oligo, Empty, β1 | 0.71 *** | 15.87 | 12.02 | |
| AGB/(Mg·ha−1) | hkurtosis, h95, d3, d9 | 0.64 *** | 13.20 | 14.77 | OG, Oligo, CG, Empty | 0.71 *** | 13.00 | 14.55 | h95, d3, CC2m, Oligo | 0.79 *** | 10.89 | 12.19 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Cao, L.; She, G. Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests. Remote Sens. 2017, 9, 940. https://doi.org/10.3390/rs9090940
Zhang Z, Cao L, She G. Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests. Remote Sensing. 2017; 9(9):940. https://doi.org/10.3390/rs9090940
Chicago/Turabian StyleZhang, Zhengnan, Lin Cao, and Guanghui She. 2017. "Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests" Remote Sensing 9, no. 9: 940. https://doi.org/10.3390/rs9090940
APA StyleZhang, Z., Cao, L., & She, G. (2017). Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests. Remote Sensing, 9(9), 940. https://doi.org/10.3390/rs9090940