Next Article in Journal
A Global Analysis of Sentinel-2A, Sentinel-2B and Landsat-8 Data Revisit Intervals and Implications for Terrestrial Monitoring
Previous Article in Journal
Evaluation of Sentinel-2A Satellite Imagery for Mapping Cotton Root Rot
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 9
Issue 9
10.3390/rs9090903
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Lidar Aboveground Vegetation Biomass Estimates in Shrublands: Prediction, Uncertainties and Application to Coarser Scales

by
Aihua Li
1,
Shital Dhakal
1,
Nancy F. Glenn
1,*,
Lucas P. Spaete
1,
Douglas J. Shinneman
2,
David S. Pilliod
2,
Robert S. Arkle
2 and
Susan K. McIlroy
2
1
The Department of Geosciences, Boise State University, 1910 University Drive, Boise, ID 83725, USA
2
U.S. Geological Survey, Forest and Rangeland Ecosystem Science Center, 970 Lusk Street Boise, Boise, ID 83706, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2017, 9(9), 903; https://doi.org/10.3390/rs9090903
Submission received: 4 June 2017 / Revised: 11 August 2017 / Accepted: 29 August 2017 / Published: 31 August 2017
(This article belongs to the Section Remote Sensing in Agriculture and Vegetation)
Browse Figures
Versions Notes

Abstract

:
Our study objectives were to model the aboveground biomass in a xeric shrub-steppe landscape with airborne light detection and ranging (Lidar) and explore the uncertainty associated with the models we created. We incorporated vegetation vertical structure information obtained from Lidar with ground-measured biomass data, allowing us to scale shrub biomass from small field sites (1 m subplots and 1 ha plots) to a larger landscape. A series of airborne Lidar-derived vegetation metrics were trained and linked with the field-measured biomass in Random Forests (RF) regression models. A Stepwise Multiple Regression (SMR) model was also explored as a comparison. Our results demonstrated that the important predictors from Lidar-derived metrics had a strong correlation with field-measured biomass in the RF regression models with a pseudo R2 of 0.76 and RMSE of 125 g/m2 for shrub biomass and a pseudo R2 of 0.74 and RMSE of 141 g/m2 for total biomass, and a weak correlation with field-measured herbaceous biomass. The SMR results were similar but slightly better than RF, explaining 77–79% of the variance, with RMSE ranging from 120 to 129 g/m2 for shrub and total biomass, respectively. We further explored the computational efficiency and relative accuracies of using point cloud and raster Lidar metrics at different resolutions (1 m to 1 ha). Metrics derived from the Lidar point cloud processing led to improved biomass estimates at nearly all resolutions in comparison to raster-derived Lidar metrics. Only at 1 m were the results from the point cloud and raster products nearly equivalent. The best Lidar prediction models of biomass at the plot-level (1 ha) were achieved when Lidar metrics were derived from an average of fine resolution (1 m) metrics to minimize boundary effects and to smooth variability. Overall, both RF and SMR methods explained more than 74% of the variance in biomass, with the most important Lidar variables being associated with vegetation structure and statistical measures of this structure (e.g., standard deviation of height was a strong predictor of biomass). Using our model results, we developed spatially-explicit Lidar estimates of total and shrub biomass across our study site in the Great Basin, U.S.A., for monitoring and planning in this imperiled ecosystem.

Graphical Abstract

1. Introduction

Aboveground biomass (‘AGB’ or ‘biomass’ hereafter) is a strong indicator of ecosystem structure, function, and productivity. In dryland ecosystems, AGB is important for estimating fuel loads, measuring carbon storage, assessing habitat quality, and monitoring changes in native species [1,2,3]. Although AGB per unit area in drylands is relatively low compared to other ecosystems, drylands cover one fifth of the earth’s land area and thus play a significant role as a carbon sink and provider of essential ecosystem services [4,5].
In western North America, semiarid sagebrush communities once extended across >500,000 km2, but the ecosystem is now one of the most imperiled on the continent [6,7]. An increase in invasive species, fire frequency, and other disturbances has resulted in a decrease in the extent of native shrub-steppe communities [7,8,9,10]. Indeed, the risk of permanent habitat loss from fire is so great, especially in the Great Basin, that in 2015, the secretary of the U.S. Department of Interior (DOI) released a secretarial order (SO3336; https://www.forestsandrangelands.gov/rangeland/index.shtml) that directed wildland fire prevention, suppression, and restoration in sagebrush-steppe ecosystems to protect the greater sage-grouse and other sagebrush-associated species. However, one limitation to the effective implementation of SO3336 is a lack of accurate and timely estimates of the distribution of AGB in sagebrush-steppe ecosystems, information that is critical for fuel management and fire risk planning at regional to landscape scales [11].
Various direct and indirect methods are available for in-situ measurements of AGB of shrubs and herbaceous (forb and grass) species [12,13,14]. Some of the most common methods include harvesting [12]), clip-and-weigh [14], visual estimations [15], and point-intercept sampling [13]. These methods are labor intensive [13,14], which limits their scale of application. Although these field-based methods perform reasonably well (i.e., acceptable accuracy, precision, and reproducibility) at small spatial extents, at larger extents, such as landscapes greater than about 1 ha, performance declines because of the natural heterogeneity of dryland soils and vegetation. Hence, field-based measurements may misrepresent actual AGB values (as well as vegetation structure and composition) and are certainly inefficient and expensive when applied across entire landscapes. Techniques to improve the accuracy, precision, repeatability, and efficiency of AGB estimates over large areas (10 s of km) are needed, particularly in sagebrush-steppe and similar ecosystems that are experiencing landscape-level changes associated with invasive species, fire, and climate change.
Remote sensing has the potential to meet this need by providing multi-scale contiguous estimates of AGB, which are ideally suited for modeling over broad spatial [16,17] and temporal scales [18]. For more than a decade, light detection and ranging (Lidar) has been successfully used to measure forest volume, height and AGB [19,20,21,22,23], and the vegetation characteristics of shrubs (e.g., shrub height, canopy cover, leaf area index) in rangelands [24,25,26]. In some shrub species, there is a strong link between shrub height and other biophysical characteristics (e.g., cover, AGB, canopy volume [27]), thus making Lidar advantageous for vegetation structure measurements.
Metrics derived from Lidar (e.g., mean height, variance of height, canopy relief ratio) can be correlated with biophysical vegetation characteristics in the field using statistical methods such as Classical Multiple Linear Regression (CMLR) [28], Partial Least Square Regression [29], Hierarchical Bayesian [30], Random Forests [31], and Artificial Neural Networks [32]. The machine learning algorithm Random Forests (RF) assembles the analysis of Classification and Regression Trees (CART) by bootstrapping samples to iteratively construct a large number of decision trees, each grown with a randomized subset of predictors [33]. RF has been widely used in non-linear relational models and high dimensional data sets [34,35]. Recently, RF has gained attention in the field of remote sensing due to the classification and computational accuracy, the potential to capture complex and non-linear relationships between predictors, the ability to support small sizes of training data relative to a large number of predictors, and because it provides a measure of variable importance [36,37]. RF has been demonstrated to be more accurate than simple regression techniques for forest biomass estimations [18,38] and a number of studies have demonstrated that RF provides low prediction variance and bias, and strong model performance, e.g., [39,40,41].
Statistical and machine learning methods for Lidar remote sensing studies are typically implemented on raster-based datasets instead of point cloud data. Raster-based models of Lidar data are relatively easy to process and store in comparison to point clouds [42]. A raster dataset is created by the aggregation of irregularly distributed points, typically starting with the upper-left points of the grid cell. Interpolation is performed for cells that contain no points. Therefore, vegetation metrics derived from rasterized imagery over a specific plot will differ from those calculated directly from the point cloud due to the likely mismatch between the field plot and grid cell boundaries. As an example of these effects. El-Ashmawy and Shaker [43] found that the overall accuracy of land cover classification in British Columbia was slightly higher using point clouds than raster-based classifications.
The research objectives of this study were to model AGB in the sagebrush-steppe by linking field-measured biomass with 35 airborne Lidar-derived vegetation metrics using RF and Stepwise Multiple Regression (SMR), explore the uncertainty associated with Lidar-derived metrics and the models tested, and ultimately develop a spatially-explicit estimate of biomass across the xeric study site in the Great Basin. To accomplish these objectives, we compared the vegetation metrics from both Lidar point clouds and rasterized Lidar images as a proxy for the estimation of AGB to determine which processing method introduced a lower uncertainty and produced better results. We also compared different Lidar-derived metrics at a range of spatial scales to identify the best model for biomass prediction across a regional area. In addition, the RF and SMR models were compared to explore their relative strengths for predicting total and shrub biomass. All our analyses were performed to estimate biomass at the 1-ha plot scale since the in-situ biomass was measured across 1-ha plots.

2. Study Area and Data

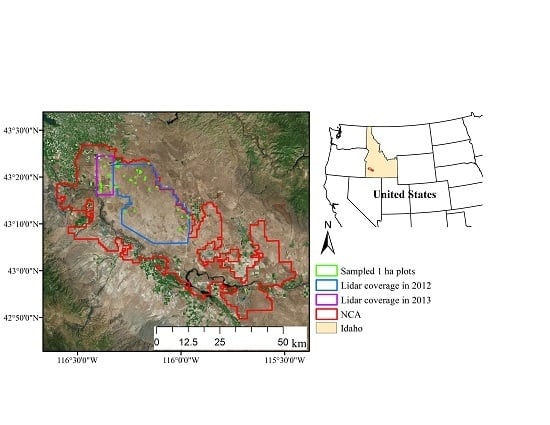
2.1. Study Area

The 75,164 ha study area is located within the 243,000 ha U.S. DOI Morley Nelson Snake River Birds of Prey National Conservation Area (NCA) in the Snake River Plain ecoregion of southwestern Idaho, USA (Figure 1). The NCA receives approximately 20 cm of precipitation annually, and has an average annual maximum and minimum temperature of 20 °C and 6 °C, respectively [44]. Native vegetation is generally composed of an open canopy of shrubs dominated by big sagebrush (A. tridentata) of up to 1.5 m tall [45], with a generally sparse cover of native bunchgrass (e.g., P. secunda, Festuca idahoensis) and forbs. Other native shrub species include shadscale (Altriplex confertifolia), winterfat (Ceratoides lanata), budsage (Artemisia spinescen), and rabbitbrush (Chrysothamnus visciflorus). Since 1980, about half of the NCA has burned, resulting in a mosaic of plant communities, with compositions spanning a gradient between intact native shrublands, shrublands degraded by biological invasion and wildfire, and grasslands where native perennial plants have been fully replaced by nonnative annuals, including cheatgrass (Bromus tectorum), medusahead (Taeniatherum caput-medusae), and various forbs (e.g., tall tumblemustard, Sisymbrium altissimum). Nonnative annuals have likely increased the amount of litter, fine fuel loads, and fuel continuity on the NCA compared with historical conditions. Likewise, the amount of bare mineral soil and biological soil crusts have likely diminished. Currently 37% or less of the NCA retains an intact native shrubland community; the remainder is predominantly a mixture of nonnative annual grasslands (i.e., Bromus tectorum) or a mosaic of native perennial (i.e., Poa secunda) and nonnative annual grasslands with occasional forbs and shrubs [46].

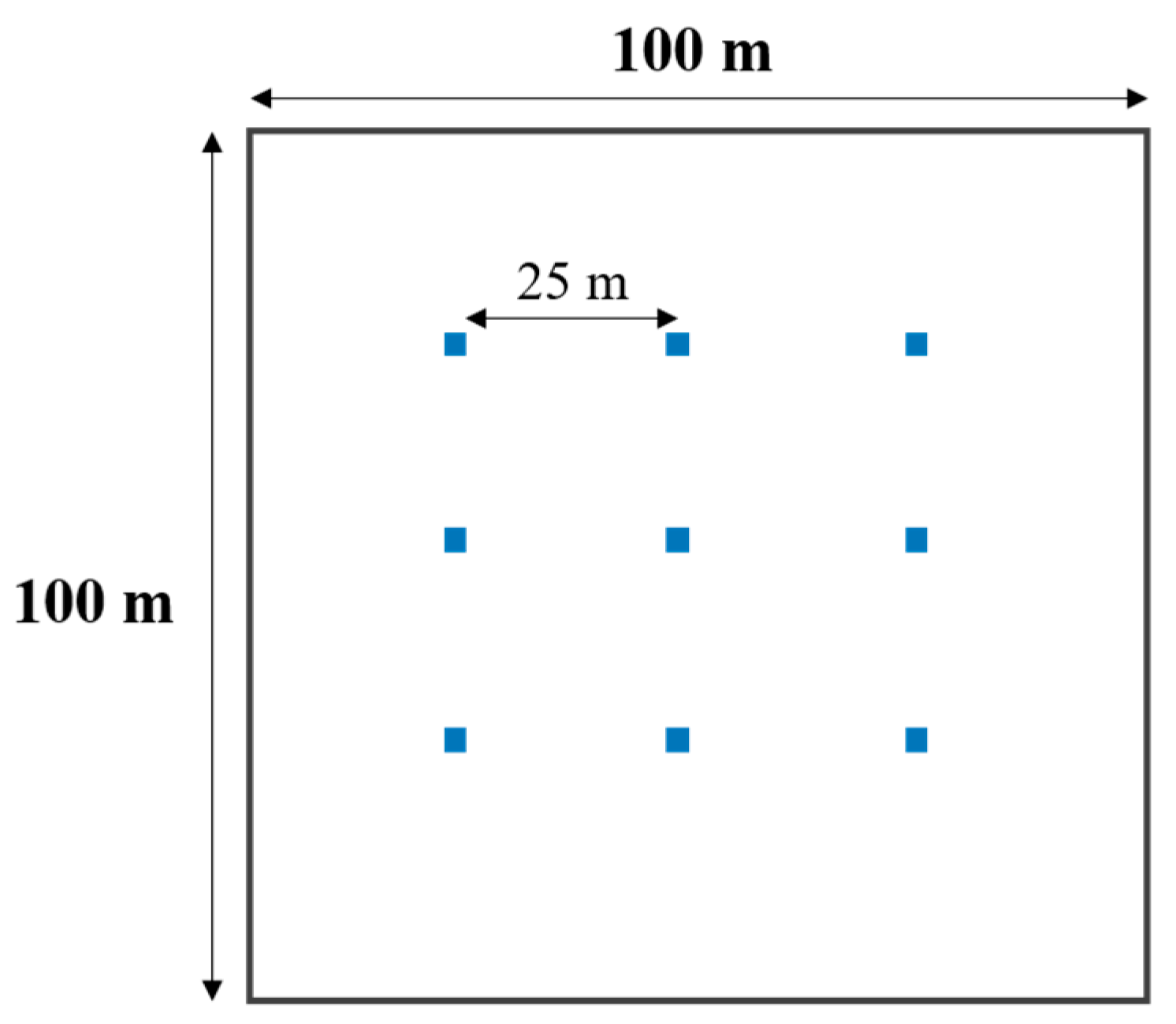
2.2. Field Sampling

In the summers of 2012 and 2013, we established forty-six (n = 46) 100-m by 100-m (1 ha) field plots at locations throughout the northwestern NCA. We used a stratified random sampling approach within unburned, burned-treated, and burned-untreated areas over the Lidar coverage to capture invasion and successional gradients as part of a related study [47]. We located the corners of each plot using a survey-grade GNSS (Global Navigation Satellite System). We tested a point-quarter sampling design and deemed it suitable to quantify the cover of sparse plants such as shrubs in early successional habitats [48]. Each 1-ha plot included a three by three grid of nine subplots of 1 m2 each, with 25 m spacing between subplots (Figure 2). The subplots were sampled to represent the 1-ha plot. Vegetation within each subplot was classified as either herbaceous or shrub, then clipped at ground level, bagged, and labeled. We oven-dried and weighed the harvested vegetation. If shrubs were too large to be harvested, a portion was collected for reference and the number of equivalent portions remaining in the quadrat was estimated. We calculated the biomass across each 1-ha plot as the average of the nine subplots for the herbaceous and shrub classes. We combined the data collected in 2012 and 2013 into one dataset (n = 46 plots) to compare with Lidar collected in the same years. We assumed negligible differences in shrub biomass between years due to the slow growth of shrubs in our study area (e.g., [16]). We estimated the herbaceous and shrub cover and biomass across the 46 field plots. Herbaceous and shrub cover ranged from 0 to 100% and 0 to 87%, respectively. The herbaceous class had a mean biomass of ~144 g/m2 and the shrub class had a mean biomass of ~208 g/m2 (Table 1).

2.3. Airborne Lidar Data Acquisitions

The Lidar data were collected over 65,194 ha in 2012 and 9970 ha in 2013, with an ALS60 system (Leica Geosystems, Heerbrugg, Switzerland) operated by Watershed Sciences (Corvallis/Portland, Oregon), with a small-footprint Lidar of an 18 cm diameter at nadir and a point density of approximately eight points per m2. The Lidar system was ≥148 kHz and was flown at 1500 m above ground level, with a scan angle of 48° (±12°) from nadir (field of view). An opposing flight line side-lap of ≥50% (i.e., 100% overlap) was maintained to increase the point density. The absolute vertical accuracy was ~0.03 m and the relative accuracy was ~0.024 m. The vertical accuracy was primarily assessed from ground check points on open, bare earth surfaces with level slope (<20°) by the vendor.

3. Methodology

3.1. Data Processing

We buffered and height filtered the Lidar point cloud data using the BCAL Lidar Tools developed for vegetation analysis (http://bcal.boisestate.edu/tools/Lidar; [24]). The height filtering classifies Lidar points into ground and vegetation points. The height filtering was performed using a 5-m canopy spacing, which has previously been shown to perform well in the semi-arid sagebrush-steppe environment [24], a 5-cm ground threshold, nearest neighbor interpolation, and 40 iterations. Two groups of metrics were calculated from resulting Lidar vegetation points: metrics based on numerical values (e.g., canopy height) and metrics based on the density of points (e.g., canopy density). We calculated 35 metrics using the BCAL Lidar Tools (Table 2). We conducted two separate analyses of the 35 metrics to explore the effect of rasterization of the point cloud on the ability of the vegetation metrics to predict biomass. The first averaged the metrics derived from the rasterized vegetation products (created at a range of scales) of the plot and the second averaged the metrics directly from the point cloud of the same plot, with no rasterization. We used 1-m, 7-m, 30-m, and 1-ha resolutions to test the appropriate scale to represent biomass and to explore the differences between deriving metrics with the Lidar point cloud and rasterized data. The 1-m and 1-ha resolutions were chosen as they matched the field subplot and plot sizes, respectively. The 7-m resolution was chosen because a related study used RapidEye 7-m resolution data [49] and the 30-m resolution was chosen as a potential to compare and fuse with Landsat imagery in future studies (also see [50]). In addition, testing the input metrics at coarser scales (e.g., 7 m, 30 m, and 100 m spatial resolutions) for the biomass modeling will provide a possible strategy for using several of NASA’s previous and future space-based Lidar missions with large footprint sizes. For example, ICESAT-1’s GLAS had a footprint size of ~70 m; whereas ICESAT-2’s ATLAS and GEDI will have ~12 and ~25 m footprint sizes, respectively. While our study does not simulate the full waveform or photon counting lasers of these instruments, we can provide a measure of the uncertainty of vegetation biomass estimates at these coarser scales. In addition, earth system models are now beginning to use Lidar data, but at coarser scales (e.g., the iSNOBAL snow model used with airborne Lidar data from NASA’s Airborne Snow Observatory uses 50 m grid cells of Lidar derived information [51]).
In the point cloud processing approach, the metrics were derived from the point cloud data at 1 m, 7 m, 30 m, and 100 m. We then used the average of these metrics at the different scales to represent the 1-ha plots (e.g., an average of the 1-m metrics across the 1-ha plot). In the raster processing approach, the Lidar point cloud data were rasterized at the same resolutions (1 m, 7 m, 30 m, and 100 m) and we then averaged the rasterized metrics to represent the 1-ha plot. The resulting 1-ha scale metrics, derived from different scales using either the point cloud or rasterization approach, were then compared to the field-based biomass average at the 1-ha plot level.

3.2. Moldeing Plot-Scale Biomass

3.2.1. RF Regression Model

The non-parametric machine learning approach, Random Forests (RF), was used to assess the relationship between field-level biomass with vegetation metrics developed from Lidar. We used SPM Suite (Salford Predictive Modeler Software Suite version 7, Salford Systems, San Diego, CA, USA) for the implementation of the RF algorithm. Each RF regression run generated 2000 trees and the maximum number of variables considered per node was kept equal to the square root of the number of variables for the run [33]. All 35 predictor variables (Table 2) were used to perform the initial RF run and ranked based on their predictive power. The predictive power of the variable or variable ranking was performed by a ‘Standard Method’: testing the variable stepwise and retaining it only if the error gain exceeds a certain threshold. This means that if a variable substituted with incorrect values can predict the target accurately, then the variable has no relevance for predicting the outcome and hence is assigned a low score (SPM user guide, 2013). For the best variable selection, we used the backward feature elimination method where the lowest performing variables were iteratively removed until the best model was obtained. The best models for total AGB, shrub AGB, and herbaceous AGB were determined based on the highest coefficient of determination (R2) (referred to as pseudo R2 in RF) and lowest root-mean-square error (RMSE) estimated using “out-of-bag” (OOB) testing. The OOB error provided an internal leave-one-out cross-validation using the ‘boot’ package in R statistical software (R Development Core Team 2013) and has previously been used as an unbiased estimate of error [39,52,53]. The number of predictor variables in the models was kept as low as possible to maintain model parsimony. The variable selection was performed to reduce the number of predictor variables and to understand which predictor variables are most suitable to estimate biomass [54]. The analyses were performed for all four resolutions (i.e., 1 m, 7 m, 30 m, 100 m) for both raster and point cloud derived metrics.

3.2.2. SMR Model

In stepwise regression, predictor variables are entered into the regression equation one at a time based on given statistical criteria. At each step in the analysis, the predictor variable with the highest correlation to the dependent variable is entered into the regression equation first [55]. When the additional variables do not statistically improve the regression equation and increase R2, the process ends. Based on results from the RF, the SMR model was used to model the relationship between the 35 Lidar derived metrics at a 1 m raster resolution and field AGB at the plot level (1 ha). A common problem with linear regression and its use in biomass estimation is multicollinearity between the independent variables, possibly leading to the violation of basic assumptions [55]. Hence, we used the SMR approach adopted by Lefsky et al. [56], which selects the two most important independent variables that were not collinear using the Pearson’s correlation coefficient.

3.3. Imputation of Regional Biomass and Uncertainty

A Nearest Neighbor (NN) imputation technique developed in the R statistical computing environment (R Development Core Team 2013) was used to apply the optimal RF model to scale biomass estimates to the larger study area. In the NN imputation, the best predictor variables selected by the optimal RF model form an attribution space. Missing data are then computed using biomass estimates produced as weighted averages of the neighbors, which are determined by the similarity (distance) [35,57]. Nearest Neighbor imputation methods can use different distance metrics to determine the similarity between target and reference records, including Euclidean, Mahalanobis, Minkowski, and fuzzy in the attribution space [58]. We used the R imputation package, yaimpute, with the available Lidar coverage to obtain a contiguous map of predicted biomass. The yaimpute package has a built-in function to calculate NN distances based on the RF proximity matrix [31,59]. A detailed explanation of imputation, its types, and its fundamental difference with interpolation can be found in Hudak et al. [31]. Our RF biomass model was trained and developed at the 1-ha plot scale, hence a spatially-explicit plot-scale average biomass map was developed at this scale. We also developed a spatially-explicit map of the coefficient of variation (CV, equal to the value of the standard deviation divided by the mean) for shrub and total AGB estimates in RF [17]. The imputed AGB for a given pixel was estimated by averaging all estimates produced by all regression trees for that pixel and the standard deviation of each pixel estimate across all trees was calculated by retaining the individual pixel estimates from all trees.

4. Results

4.1. Plot-Scale Biomass from Raster-Derived Vegetation Metrics

Lidar-derived metrics using rasterization were found to have a strong relationship with total AGB and shrub biomass using RF regression models. Lidar metrics, including HAAD and Hstd from the 1-m raster image, predicted total biomass with an R2 of 0.74 and RMSE of 141 g/m2, whereas shrub biomass was predicted with an R2 of 0.76 and RMSE of 152 g/m2 (Table 3).
As the raster resolution decreased, the prediction capability of the Lidar metrics also decreased with an R2 of 0.70, 0.58, and 0.52 at 7 m, 30 m, and 100 m, respectively, for total AGB. Similarly, the RMSE increased as the resolution decreased. We observed a similar trend for the shrub biomass.

4.2. Plot-Scale Biomass from Point Cloud-Derived Vegetation Metrics

Unlike the raster processing, the coarsening of the pixel size had a smaller effect on the total and shrub AGB prediction capability of the point cloud-derived metrics. Whereas the AGB estimation ability of the RF model from point clouds was not statistically different from raster processing at the 1-m resolution, the predictions at 7-m, 30-m, and 100-m resolutions improved using the point cloud data (Table 4). Notably, the RMSE of the shrub AGB estimates was lower in the point cloud processing at the 7-m, 30-m, and 100-m scales in comparison to the raster processing.
In contrast to shrub and total biomass, herbaceous biomass was poorly predicted by Lidar metrics. This result fitted our expectations as herbaceous vegetation types are short in stature and differentiating ground from herbaceous returns in Lidar is difficult. The results were consistent across all scales and all processing approaches and hence only the results from the 1-m raster and point cloud datasets are listed in Table 5.

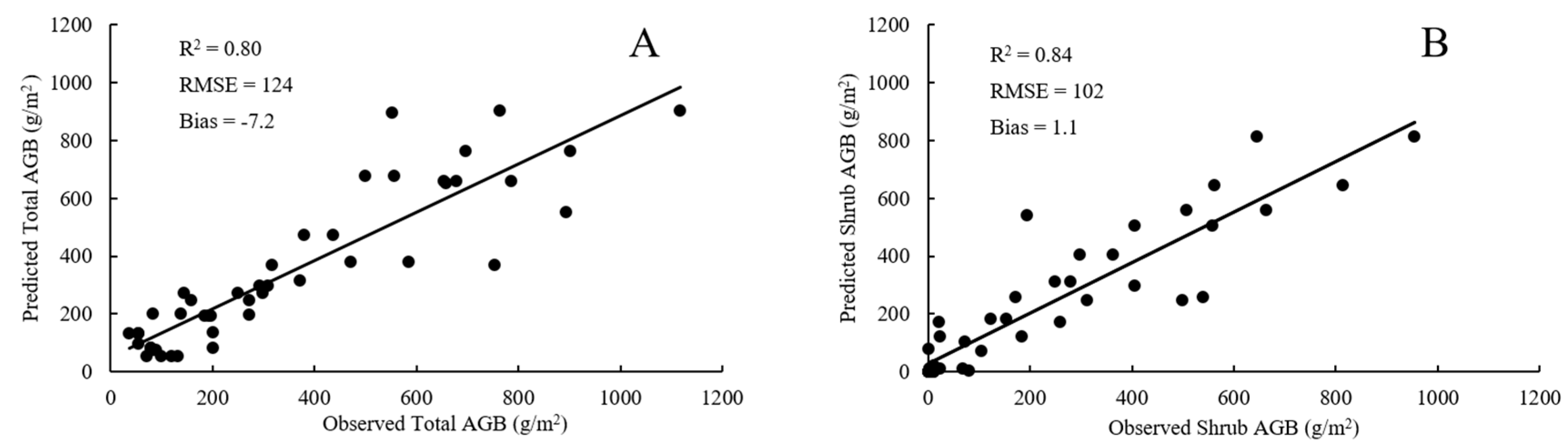
4.3. Comparison of RF Model and SMR Model

The Pearson’s correlation analysis identified the metric Hstd as the variable with the highest correlation with total AGB (Pearson’s correlation r = 0.85) and shrub biomass (Pearson’s correlation r = 0.84). A regression analysis of total AGB with Hstd provided us with the following equation, with an R2 of 0.72 and p-values < 0.001.
Total AGB = 12,374.67 × Hstd − 142.058
An analysis of the residuals obtained from the above equation was correlated with the remaining 34 metrics and Hskew was found to have the highest correlation (Pearson’s correlation r = 0.39). Hence Hskew was added to the equation, resulting in an R2 of 0.79, RMSE of 129 g/m2, and p-value < 0.001 (Figure 3).
Total AGB = 10,230 × Hstd + 386 × Hskew − 226.416
Applying the same methodology to the shrub biomass, provided the following model with an R2 of 0.77, RMSE of 120 g/m2, and p-value < 0.001 (Figure 3).
Shrub AGB = 25,655.23 × Hstd − 19,052.4 × HMAD − 169.62627
Comparing the pseudo R2 using OOB testing with the R2 from the linear regression model, we found the RF results to be slightly worse than the SMR models for both total and shrub AGB. We then used the optimal RF model (1 m raster scale) to estimate the predicted biomass for each observed (field) biomass. This resulted in the RF predicted total AGB of R2 = 0.80 and shrub AGB of R2 = 0.84 with RMSE values of 124 g/m2 and 102 g/m2, respectively (Figure 4).

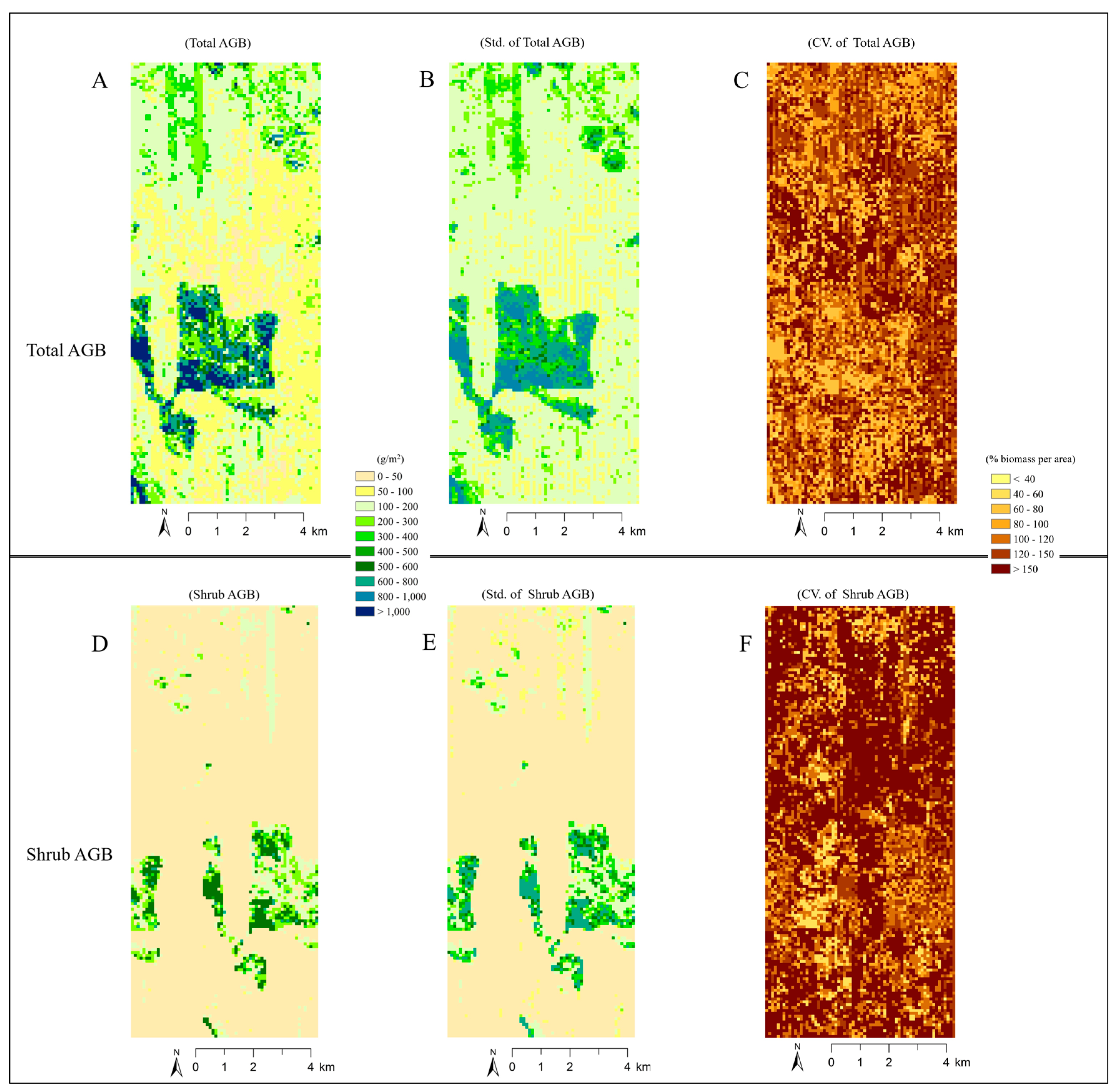
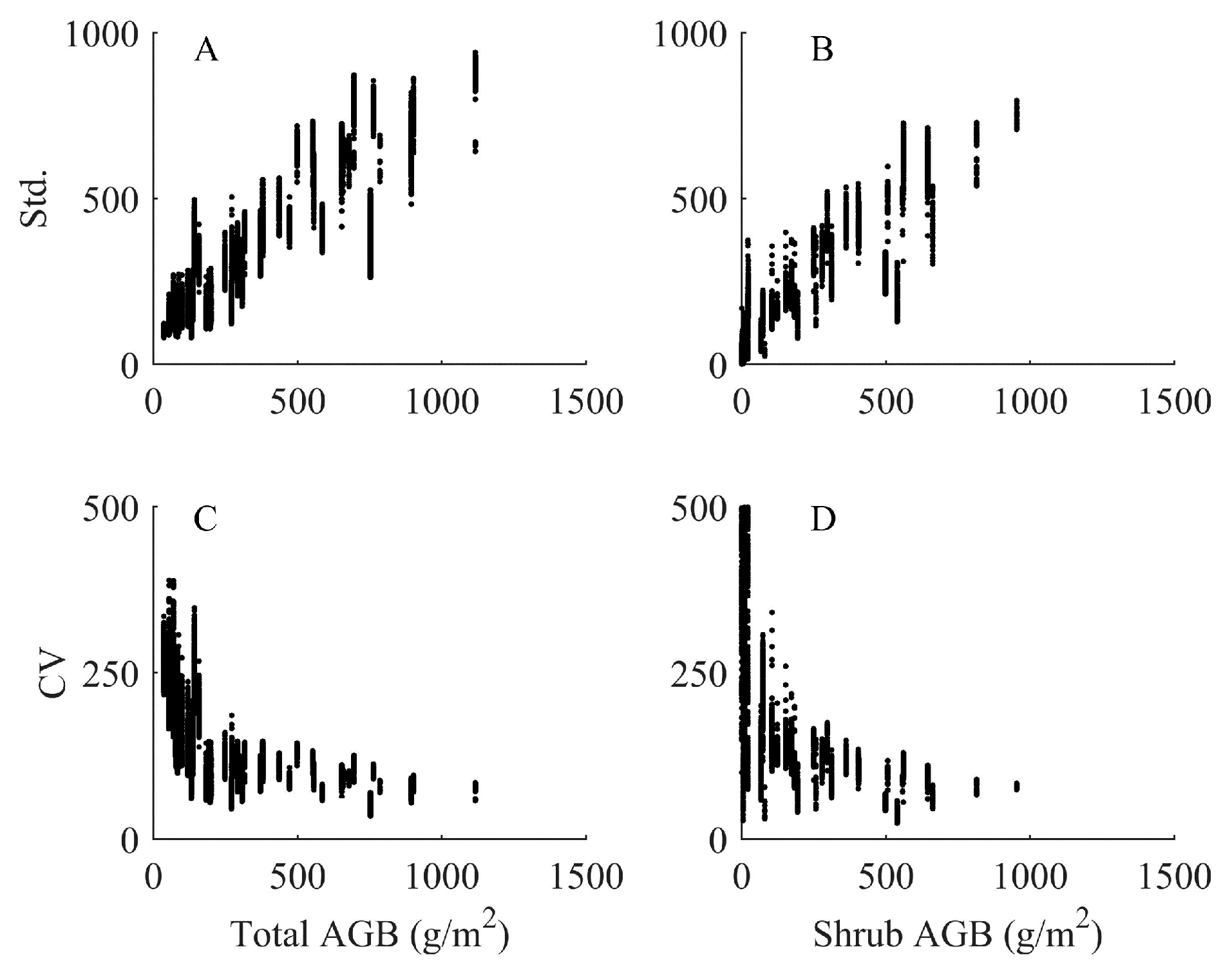
4.4. Analysis of Imputed Regional Biomass

Using RF, total and shrub biomass were best modeled with 1-m Lidar-derived metrics (Table 3 and Table 4). For total AGB, raster processing and point cloud processing had an R2/RMSE of 0.74/141 g/m2 and 0.71/147 g/m2, respectively. For shrub AGB, raster processing and point cloud processing had an R2/RMSE of 0.76/125 g/m2 and 0.73/129 g/m2, respectively. There was no significant difference between the two data processing methods used (raster or point cloud). Based on these results and because raster processing is computationally more efficient, spatially-explicit, contiguous total and shrub aboveground biomass maps over the Lidar coverages were produced by imputation using predictors associated with the 1-m raster-derived metrics. Figure 5A,B and Figure 6A,B show that the shrub-dominant regions had higher biomass values in comparison to the sparse shrub and grass dominant areas. Note the crops depicted in the northeast corner of the 2013 Lidar were not masked as they had a small influence on the overall mean biomass values calculated for the study area. In this study area, the mean shrub biomass is 50–60 g/m2 and the mean total biomass is 210–263 g/m2 (Table 6). There are wide expanses of no shrub cover across the NCA (more discussion below) and in fact, the shrub biomass imputation represents large regions of 0–50 g/m2 of biomass. These areas are likely representative of regions where the herbaceous class was present; this is confirmed by the total biomass imputations where biomass pixels in the ~0–200 g/m2 are more abundant. The CV maps (Figure 5C,F and Figure 6C,F) illustrate the variation of the model estimates, represented as a percentage of the estimated biomass in each pixel. Larger biomass estimates had a higher standard deviation and lower CV (Figure 5, Figure 6 and Figure 7). Given the poor modeling results of the herbaceous cover class, and considering that the total biomass model includes both herbaceous and shrub components, the uncertainty in the total biomass imputation is higher than the shrub biomass imputation.

5. Discussion

5.1. RF Biomass Regression Model

5.1.1. Uncertainty

Processing of the point cloud data significantly improved the estimation of total and shrub AGB using coarser scales (7 m, 30 m and 100 m) in comparison to the raster image processing (based on R2 and RMSE, Table 3 and Table 4). However, 1-m scale point cloud and raster image processing provided nearly equivalent estimates of 1-ha plot average biomass. At the 1-m scale, the rasterization approach incorporates fewer points outside of the pixel boundary (and in close proximity). Furthermore, rasterization at 1 m had a greater probability of aligning with field plots and was less influenced by values from adjoining pixels in comparison to coarser pixel sizes. The similar RF regression model results indicate that the rasterization method preserves most of the 3D point cloud vegetation characteristics and thus is essentially equivalent to using point cloud data at the 1-m scale. At coarser raster scales, we attribute the declining results to boundary effects and alignment with field plots.
In contrast, the pixel size in which point cloud processing was performed had negligible effects on the total and shrub AGB estimation. There is almost no loss of detail while extracting or averaging information from the original point cloud. Furthermore, the point cloud processing significantly reduced the RMSE at all scales in comparison to the rasterized approach. However, based on the R2 alone, at a 1-m resolution, the point cloud processing was not significantly different to raster data processing. The coarse-scale raster results may be more representative of expected results from large footprint Lidar than the point cloud analyses. This is because a large footprint Lidar is an integrated waveform (or photons in the case of ICESAT-2) of the canopy profile over the entire footprint.
The bias in in-situ data also introduces uncertainty into the biomass models. As shown in Figure 2, averaging the biomass from the subplots to obtain the in-situ plot level biomass takes into account areas of no sampling in the outer 30-m buffer of the subplots. Because the predictors will adapt to the attribution space of the training samples [60], the RF imputation includes similar uncertainties as those in the training samples. This is likely the reason behind the appearance of the long linear features of a relatively high biomass in the resulting imputation map (Figure 5 and Figure 6). Although the average biomass over the nine 1-m subplots may represent herbaceous and small shrubs across a 1-ha plot (e.g., [48]), error in the field data may have been introduced because of relatively larger shrubs close to the subplot edge which were not fully accounted for in the field sampling. Moreover, estimating the biomass from Lidar without corresponding species level classification can be a disadvantage when different species have similar structural arrangements but substantially different AGB (e.g., in this landscape, low-AGB nonnative forbs, such as tumble mustard, can be incorrectly quantified as shrub, [39]).

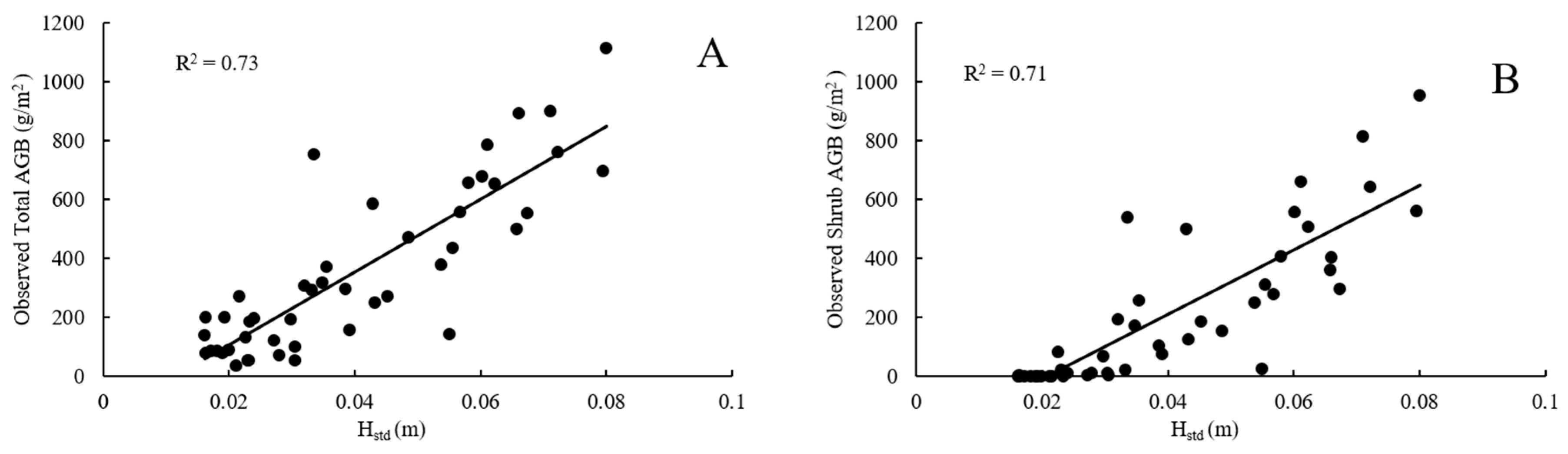
5.1.2. RF Regression Model Variables

Previous research in similar ecosystems has shown volume (e.g., [61,62,63]) or the approximation of volume (the product of basal area and height or the product of percent vegetation cover and height) (e.g., [16,64]) to be a strong proxy of shrub biomass. A related study by Li et al. [16] compared percent cover and height, but did not account for height variability metrics in their linear regression model to estimate biomass. Their results showed that the percent cover of shrubs was the best predictor for biomass. Yet in our sparse vegetation area, height variability-related metrics (including Hstd, HAAD, and HMAD) scored higher than other predictors for both total and shrub biomass in all RF models, with high R2 and low RMSE values. Considering the Lidar acquisition parameters in this study as equal to those in Li’s study [16], a higher number of Lidar returns from the vegetation canopy will occur in denser and larger shrubs (represented in the study in [16]) compared to the sparse canopies with smaller shrubs in our study. Vegetation Lidar returns are also more likely to be mixed with those of annual grasses, perennial bunchgrasses, litter, or bare ground in our study area. Hence, shrub height underestimation is likely more pronounced in this study due to constraints related to the laser pulse length [24,26,65,66]. Yet the variability of height may still be sufficiently captured by the Lidar to represent the spatial pattern of biomass with smaller shrub canopies in our study site.
In this study, five predictors (Hstd, HAAD, HCV, Hrange, and FHDall) at the 1-m scale explained roughly 76% of the variability in shrub AGB (Table 3) in the optimal RF regression model. For the RF model for shrub biomass, the remaining 24% error may be credited to uncertainties associated with sparse vegetation distribution, the misclassification of canopy as ground, and the underestimation of the vegetation height [24,67]. Similar results were found by Estornell et al. [68] in a Mediterranean shrubland ecosystem. In their research, the median height, standard deviation of height, and percentile of height derived from airborne Lidar were the best predictors, explaining up to 78% and 84% of variability for biomass and volume, respectively. Greaves et al. [17] also reported a similar finding in an arctic shrubland, in which Lidar volume and canopy metrics coupled with vegetation indices from optical data explained roughly 71% of the variability of shrub biomass.
Given the prominence of Hstd in the SMR and RF models, we further tested the ability of Hstd alone to estimate AGB biomass. Using univariate linear regression, we found that Hstd explained 73% and 71% of the variance of total and shrub AGB, respectively (Figure 8). While this relationship is likely oversimplified and the model fit is erroneous at low shrub biomass estimates, it is interesting to conceptualize that a vegetation roughness measure may coarsely approximate biomass. Notably, previous studies in this ecosystem have found vegetation roughness to be a proxy for classifying sagebrush [69] and sagebrush heights [24].
In sum, most of the shrub biomass models were based on variables associated with vegetation structure (e.g., height and cover) and related metrics (e.g., standard deviation of height and percentile of height). In this study, the complexity of the RF model made interpreting the model challenging, but demonstrated the non-linearity of the relationship between biomass and its related driving variables, while also providing a variable importance to better understand the nature of the relationships.

5.2. Model Performances of RF and SMR

Both RF and SMR have been widely used in ecology [70,71] and remote sensing [40,50]. As a non-parametric machine learning method, RF has no formal distributional assumptions. It approaches the issue of non-linearity by using numerous trees and the “small observations large predictors” problem. However, when the trees become larger (e.g., due to a larger number of input variables), the resulting models are more difficult to interpret, resulting in a dynamic predictor set when the training data change a little. As shown in Table 3 and Table 4, the best RF model with metrics using point cloud processing has different important predictors from the best RF model with metrics using raster processing, even at a fine resolution. On the other hand, there are also limitations associated with SMR [70]. For example, SMR assumes a normal distribution of the error between observed and predicted values (i.e., the residuals of the regression) and that there is no multicollinearity in the predictor variables. Also, in linear regression, the constant value of predictor(s) will result in constant biomass values; yet different shrubs may have the same biomass but different 3D structures [17]. In addition, a common assumption is that a large number of predictors will require a large number of observations, otherwise the linear regression may fit the randomness that is inherent in most datasets. Interestingly, the best SMR model was more parsimonious (two predictors) than the best RF models (e.g., five predictors for shrub biomass) and had high model R2; and the two predictors in the best SMR model were included in the five important predictors in the best RF model. Yet, a high variable importance of an input variable (HAAD) in RF was not included in the SMR. This result may indicate that this variable represents interactions that are too complex to be captured by parametric regression models or simply because of correlation between the variables. If the former is true, RF’s non-linear model fit for biomass may be more appropriate as biomass is not controlled simply with one or two driving variables but a complex environment. Moreover, the RF model constrains predicted biomass within the range of the observed biomass (in comparison, SMR may represent invalid biomass values when the value of predictors is beyond the model range). Based on the results of this study, and understanding that advantages and disadvantages exist with most statistical representations, we recommend exploring a number of statistical approaches that may shed light on the behavior of the response variable, as well as the relative importance of predictor variables.

5.3. Broader Application of the Imputed Shrub Biomass

Our imputation models estimated mean shrub biomass values of 51 ± 126 g/m2 and 60 ± 149 g/m2 with 2013 Lidar and 2012 Lidar, respectively. While there are not many studies in similar xeric sagebrush-steppe ecosystems to compare these results to, our estimates are similar to those by Uresk et al. [72]. They estimated the total phytomass of big sagebrush in Eastern Washington to be 69 g/m2 when they converted the individual sagebrush biomass to area based on density. As a comparison, Brown [73] estimated much higher shrub biomass values in Montana and Idaho, ranging from ~55 to 1490 g/m2, but their numbers are based on intact big sagebrush sites that included relatively mesic locations with mountain big sagebrush (A. t. vaseyana). Cleary et al. [74] estimated shrub biomass in Wyoming to be ~655 g/m2, also in mountain big sagebrush. They also converted their individual biomass estimates to mass per area based on density. It is important to note that our shrub biomass estimates (in a consistently arid landscape) included scattered shrub species other than big sagebrush.
All things considered, there is a significant gap in baseline data on aboveground biomass across a range of growing conditions in sagebrush ecosystems, that can be used for fuel management and restoration. Our imputations provide the first spatially-explicit Lidar estimates of biomass across rangelands in the Great Basin and in more xeric conditions, in general. Considering that the areas of Lidar acquisition in this study are representative of the larger NCA, our estimates of shrub biomass of 51–60 g/m2 may be used as a baseline for the larger NCA. However, additional field and Lidar data are necessary to develop models across larger areas representing more diverse growing conditions.
Biomass estimates of the herbaceous cover class were not well predicted at any scale in this study. The low predictive power was likely caused by the lack of signal (returns) in the Lidar from the short herbaceous community. Due to the complexity of the 3D structure in shrub-grass mixed compositions, Lidar-derived metrics may have more variability or even the same biomass values that were observed for some field plots. In the RF attribution space, the variability of metrics led to more variations of biomass predictions among the RF trees and led to more uncertainties (higher CV). A previous study in a similar environment demonstrated that spectral information can represent herbaceous communities well [41]. Therefore, the synergistic use of multispectral and hyperspectral data is likely to fill the deficiencies of herbaceous biomass estimates with Lidar data [50]. In addition, the total biomass estimates, which include the herbaceous class, are likely skewed by the high performance of the shrub biomass. Thus, to develop a strong model of total biomass, challenges associated with estimating herbaceous biomass will need to be overcome.

6. Conclusions

Lidar coupled with field training data explained more than 74% of the variance in shrub biomass in this shrub-steppe ecosystem. Further, the use of point cloud processing reduced uncertainties between 5% and 15% of the mean biomass at scales coarser than 1 m. Whereas rasterization is much easier to perform, we warn that it should only be used when the Lidar data can support fine scale pixel sizes (e.g., 1 m in studies similar to ours). Further development of analysis tools for Lidar point cloud processing, including efficient data processing (e.g., [42]), will encourage the use of point cloud processing over raster processing.
Our results are sufficiently robust to support the contiguous mapping of biomass at the regional scale using Lidar-derived vegetation metrics coupled with machine learning RF. Further validation of the imputation maps can be conducted with additional data captured manually or with TLS (terrestrial Lidar) or UAS (unmanned aerial systems). As Lidar becomes more readily available through programs such as USGS 3DEP and from GEDI and ICESAT-2, future studies in the Great Basin and similar dryland ecosystems can implement our approach to estimate biomass. The use of height variability/roughness or percent vegetation cover in the RF models could be selected on the basis of the shrub structure (e.g., cover, height, density) observed in field plots. Lidar can also be used to map biomass in areas of pinyon-juniper (e.g., [75]), aspen (e.g., [76]), and coniferous communities (e.g., [35]), thus collectively providing biomass estimates across common community types in the Great Basin. These Lidar-derived biomass maps coupled with biomass estimates of herbaceous cover from optical data (e.g., [50]) will provide the necessary level of detail and accuracy to make effective management decisions relevant to SO 3336 and other directives. Quantification of biomass in this and similar rangelands can be applied to modeling vegetation dynamics, estimating pre-fire and post-fire fuel loads, measuring carbon storage, assessing habitat quality, and quantifying changes in native species. The next steps for this important region are to integrate multi-source and scale data (airborne Lidar, imaging spectroscopy, time-series multispectral imagery) to extend the biomass estimates across the wider Great Basin.

Acknowledgments

This study was supported by NSF EAR 1226145, Joint Fire Science Program (Project ID: 11-1-2-30), and NASA TE NNX14AD81G. We thank Charles Baun, Idaho Army National Guard for use of the 2012 Lidar data. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Author Contributions

The article is a result of collaboration with all listed co-authors. The overarching project idea was formulated by Glenn, Shinneman, Pilliod, and Arkle. Li, Dhakal, Glenn, and Spaete designed the remote sensing analysis; Li and Dhakal analyzed the data and led the writing; Shinneman, Pilliod, Arkle, and McIlroy provided field data and writing contributions and contributed valuable advice and comments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Angell, R.F.; Svejcar, T.; Bates, J.; Saliendra, N.Z.; Johnson, D.A. Bowen ratio and closed chamber carbon dioxide flux measurements over sagebrush steppe vegetation. Agric. For. Meteorol. 2001, 108, 153–161. [Google Scholar] [CrossRef]
  2. Shrestha, G.; Stahl, P.D. Carbon accumulation and storage in semi-arid sagebrush steppe: Effects of long-term grazing exclusion. Agric. Ecosyst. Environ. 2008, 125, 173–181. [Google Scholar] [CrossRef]
  3. Rengsirikul, K.; Kanjanakuha, A.; Ishii, Y.; Kangvansaichol, K.; Sripichitt, P.; Punsuvon, V.; Vaithanomsat, P.; Nakamanee, G.; Tudsri, S. Potential forage and biomass production of newly introduced varieties of leucaena (Leucaena leucocephala (Lam.) de Wit.) in Thailand. Grassl. Sci. 2011, 57, 94–100. [Google Scholar] [CrossRef]
  4. Perez-Quezada, J.F.; Delpiano, C.A.; Snyder, K.A.; Johnson, D.A.; Franck, N. Carbon pools in an arid shrubland in Chile under natural and afforested conditions. J. Arid Environ. 2011, 75, 29–37. [Google Scholar] [CrossRef]
  5. Zandler, H.; Brenning, A.; Samimi, C. Quantifying dwarf shrub biomass in an arid environment: Comparing empirical methods in a high dimensional setting. Remote Sens. Environ. 2015, 158, 140–155. [Google Scholar] [CrossRef]
  6. Barbour, M.G.; Billings, W.D. North American Terrestrial Vegetation; Cambridge University Press: Cambridge, UK, 2000; ISBN 0-521-55027-0. [Google Scholar]
  7. Miller, R.F.; Knick, S.T.; Pyke, D.A.; Meinke, C.W.; Hanser, S.E.; Wisdom, M.J.; Hild, A.L. Characteristics of sagebrush habitats and limitations to long-term conservation. Greater sage-grouse: Ecology and conservation of a landscape species and its habitats. Stud. Avian Biol. 2011, 38, 145–184. [Google Scholar]
  8. Anderson, J.E.; Inouye, R.S. Landscape-scale changes in plant species abundance and biodiversity of a sagebrush steppe over 45 years. Ecol. Monogr. 2011, 71, 531–556. [Google Scholar] [CrossRef]
  9. Creutzburg, M.K.; Halofsky, J.E.; Halofsky, J.S.; Christopher, T.A. Climate change and land management in the rangelands of central Oregon. Environ. Manag. 2015, 55, 43–55. [Google Scholar] [CrossRef] [PubMed]
  10. Pyke, D.A.; Chambers, J.C.; Beck, J.L.; Brooks, M.L.; Mealor, B.A. Land uses, fire, and invasion: Exotic annual Bromus and human dimensions. In Exotic Brome-Grasses in Arid and Semiarid Ecosystems of the Western US: Causes, Consequences, and Management Implications; Germino, M.J., Chambers, J.C., Brown, C.S., Eds.; Springer International Publishing: Basel, Switzerland, 2016; pp. 307–336. ISBN 978-3-319-24928-5. [Google Scholar]
  11. Integrated Rangeland Fire Management Strategy Actionable Science Plan Team. The Integrated Rangeland Fire Management Strategy Actionable Science Plan; U.S. Department of the Interior: Washington, DC, USA, 2016; p. 128. Available online: https://www.fs.fed.us/rm/pubs_journals/2016/rmrs_2016_berg_k001.pdf (accessed on 29 August 2017).
  12. Sala, O.E.; Lauenroth, W.K. Small rainfall events: An ecological role in semiarid regions. Oecologia 1982, 53, 301–304. [Google Scholar] [CrossRef] [PubMed]
  13. Clark, P.E.; Hardegree, S.P.; Moffet, C.A.; Pierson, F.B. Point sampling to stratify biomass variability in sagebrush steppe vegetation. Rangel. Ecol. Manag. 2008, 61, 614–622. [Google Scholar] [CrossRef]
  14. Bonham, C.D. Measurements for Terrestrial Vegetation; John Wiley & Sons: Chichester, UK, 2013; ISBN 978-0-4709-7258-8. [Google Scholar]
  15. Waite, R.B. The application of visual estimation procedures for monitoring pasture yield and composition in exclosures and small plots. Trop. Grassl. 1994, 28, 38–42. [Google Scholar]
  16. Li, A.; Glenn, N.F.; Olsoy, P.J.; Mitchell, J.J.; Shrestha, R. Aboveground biomass estimates of sagebrush using terrestrial and airborne Lidar data in a dryland ecosystem. Agric. For. Meteorol. 2015, 213, 138–147. [Google Scholar] [CrossRef]
  17. Greaves, H.E.; Vierling, L.A.; Eitel, J.U.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. High-resolution mapping of aboveground shrub biomass in Arctic tundra using airborne Lidar and imagery. Remote Sens. Environ. 2016, 184, 361–373. [Google Scholar] [CrossRef]
  18. Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
  19. Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
  20. Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return Lidar: An example from low density, fire prone ponderosa pine forests. For. Ecol. Manag. 2005, 208, 189–209. [Google Scholar] [CrossRef]
  21. Ku, N.W.; Popescu, S.C.; Ansley, R.J.; Perotto-Baldivieso, H.L.; Filippi, A.M. Assessment of available rangeland woody plant biomass with a terrestrial LIDAR system. Photogramm. Eng. Remote Sens. 2012, 78, 349–361. [Google Scholar] [CrossRef]
  22. Lin, Y.; Hyyppä, J.; Kukko, A.; Jaakkola, A.; Kaartinen, H. Tree height growth measurement with single-scan airborne, static terrestrial and mobile laser scanning. Sensors 2012, 12, 12798–12813. [Google Scholar] [CrossRef] [PubMed]
  23. Zheng, G.; Moskal, L.M.; Kim, S.H. Retrieval of effective leaf area index in heterogeneous forests with terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 777–786. [Google Scholar] [CrossRef]
  24. Streutker, D.R.; Glenn, N.F. Lidar measurement of sagebrush steppe vegetation heights. Remote Sens. Environ. 2006, 102, 135–145. [Google Scholar] [CrossRef]
  25. Su, J.G.; Bork, E.W. Characterization of diverse plant communities in Aspen Parkland rangeland using Lidar data. Appl. Veg. Sci. 2007, 10, 407–416. [Google Scholar] [CrossRef]
  26. Glenn, N.F.; Spaete, L.P.; Sankey, T.T.; Derryberry, D.R.; Hardegree, S.P.; Mitchell, J.J. Errors in Lidar-derived shrub height and crown area on sloped terrain. J. Arid Environ. 2011, 75, 377–382. [Google Scholar] [CrossRef]
  27. Bork, E.W.; Su, J.G. Integrating LIDAR data and multispectral imagery for enhanced classification of rangeland vegetation: A meta analysis. Remote Sens. Environ. 2007, 111, 11–24. [Google Scholar] [CrossRef]
  28. García-Gutiérrez, J.; González-Ferreiro, E.; Mateos-García, D.; Riquelme-Santos, J.C.; Miranda, D. A comparative study between two regression methods on Lidar data: A case Study. In Hybrid Artificial Intelligent Systems HAIS 2011, Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, Wrocław, Poland, 23–25 May 2011; Corchado, E., Kurzyński, M., Woźniak, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6679. [Google Scholar]
  29. Laurin, G.V.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Del Frate, F.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with Lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
  30. Wilson, A.M.; Silander, J.A.; Gelfand, A.; Glenn, J.H. Scaling up: Linking field data and remote sensing with a hierarchical model. Int. J. Geogr. Inf. Sci. 2011, 25, 509–521. [Google Scholar] [CrossRef]
  31. Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from Lidar data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef]
  32. Debouk, H.; Riera-Tatché, R.; Vega-García, C. Assessing post-fire regeneration in a Mediterranean mixed forest using Lidar data and artificial neural networks. Photogramm. Eng. Remote Sens. 2013, 79, 1121–1130. [Google Scholar] [CrossRef]
  33. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  34. Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
  35. Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ. 2010, 114, 1263–1276. [Google Scholar] [CrossRef]
  36. Guan, H.; Yu, J.; Li, J.; Luo, L. Random Forests-Based Feature Selection for Land-Use Classification Using LIDAR Data and Orthoimagery. International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2012, 39, B7. [Google Scholar]
  37. Mitchell, J.J.; Shrestha, R.; Moore-Ellison, C.A.; Glenn, N.F. Single and multi-date Landsat classifications of basalt to support soil survey efforts. Remote Sens. 2013, 5, 4857–4876. [Google Scholar] [CrossRef]
  38. Gleason, C.J.; Im, J. Forest biomass estimation from airborne Lidar data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
  39. Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
  40. Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
  41. Mitchell, J.J.; Shrestha, R.; Spaete, L.P.; Glenn, N.F. Combining airborne hyperspectral and Lidar data across local sites for upscaling shrubland structural information: Lessons for HyspIRI. Remote Sens. Environ. 2015, 167, 98–110. [Google Scholar] [CrossRef]
  42. Passalacqua, P.; Belmont, P.; Staley, D.M.; Simley, J.D.; Arrowsmith, J.R.; Bode, C.A.; Crosby, C.; DeLong, S.B.; Glenn, N.F.; Kelly, S.A.; et al. Analyzing high resolution topography for advancing the understanding of mass and energy transfer through landscapes: A review. Earth Sci. Rev. 2015, 148, 174–193. [Google Scholar] [CrossRef] [Green Version]
  43. El-Ashmawy, N.; Shaker, A. Raster vs. Point Cloud Lidar Data Classification. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 79. [Google Scholar] [CrossRef]
  44. Western Region Climate Center (WRCC). Swan Falls Power House, Idaho, Period of Record General Climate Summary. 2012. Available online: http://www.wrcc.dri.edu/cgi-bin/cliMAIN.pl?id8928 (accessed on 1 June 2017).
  45. Anderson, K. Vegetation Measurement in Sagebrush Steppe Using Terrestrial Laser Scanning. Master’s Thesis, Idaho State University, Pocatello, ID, USA, 2014. [Google Scholar]
  46. U.S. Department of the Interior; Bureau of Land Management; Boise District Office. Snake River Birds of Prey National Conservation Area Proposed Resource Management Plan and Final Environmental Impact Statement. 2008. Available online: https://eplanning.blm.gov/epl-front-office/projects/lup/35553/41909/44409/SRBOPA_NCA_FEIS_V2_Appendices_508.pdf (accessed on 1 June 2017).
  47. Shinneman, D.J.; Arkle, R.; Pilliod, D.; Glenn, N.F. Quantifying and Predicting Fuels and the Effects of Reduction Treatments along Successional and Invasion Gradients in Sagebrush Habitats. Final Report to the Joint Fire Science Program; 2015; pp. 1–44. Available online: https://www.firescience.gov/projects/11-1-2-30/project/11-1-2-30_final_report.pdf (accessed on 1 June 2017).
  48. Pilliod, D.S.; Arkle, R.S. Performance of quantitative sampling methods across gradients of cover in Great Basin plant communities. Rangel. Ecol. Manag. 2013, 66, 634–647. [Google Scholar] [CrossRef]
  49. Spaete, L.P.; Glenn, N.F.; Baun, C.W. 2013 Morley Nelson Snake River Birds of Prey National Conservation Area RapidEye 7 m Landcover Classification; Boise State University: Boise, ID, USA, 2016; Available online: http://dx.doi.org/10.18122/B21592 (accessed on 1 June 2017).
  50. Glenn, N.F.; Neuenschwander, A.; Vierling, L.A.; Spaete, L.; Li, A.; Shinneman, D.J.; McIlroy, S.K. Landsat 8 and ICESat-2: Performance and potential synergies for quantifying dryland ecosystem vegetation cover and biomass. Remote Sens. Environ. 2016, 185, 233–242. [Google Scholar] [CrossRef]
  51. Painter, T.H.; Berisford, D.F.; Boardman, J.W.; Bormann, K.J.; Deems, J.S.; Gehrke, F.; Hedrick, A.; Joyce, M.; Laidlaw, R.; Marks, D.; et al. The Airborne Snow Observatory: Fusion of scanning Lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 2016, 184, 139–152. [Google Scholar] [CrossRef]
  52. Naidoo, L.; Cho, M.A.; Mathieu, R.; Asner, G. Classification of savanna tree species, in the Greater Kruger National Park region, by integrating hyperspectral and Lidar data in a Random Forest data mining environment. ISPRS J. Photogramm. Remote Sens. 2012, 69, 167–179. [Google Scholar] [CrossRef]
  53. Prinzie, A.; Van den Poel, D. Random forests for multiclass classification: Random multinomial logit. Expert Syst. Appl. 2008, 34, 1721–1732. [Google Scholar] [CrossRef]
  54. Ismail, R.; Mutanga, O.; Kumar, L. Modeling the potential distribution of pine forests susceptible to sirex noctilio infestations in Mpumalanga, South Africa. Trans. GIS 2010, 14, 709–726. [Google Scholar] [CrossRef]
  55. Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 978-0-470-54281-1. [Google Scholar]
  56. Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef]
  57. Hudak, A.; Evans, J.S.; Crookstone, N.L.; Falkowski, M.J.; Steigers, B.K.; Taylor, R.; Hemingway, H. Aggregating pixel-level basal area predictions derived from Lidar data to industrial forest stands in North-Central Idaho. In Proceedings of the Third Forest Vegetation Simulator Conference, Fort Collins, CO, USA, 13–15 February 2007; pp. 133–145. [Google Scholar]
  58. Eskelson, B.N.; Temesgen, H.; Lemay, V.; Barrett, T.M.; Crookston, N.L.; Hudak, A.T. The roles of nearest neighbor methods in imputing missing data in forest inventory and monitoring databases. Scand. J. For. Res. 2009, 24, 235–246. [Google Scholar] [CrossRef]
  59. Crookston, N.L.; Finley, A.O. yaImpute: An R Package for kNN Imputation. J. Stat. Softw. 2008, 23, 1–16. [Google Scholar] [CrossRef]
  60. Strobl, C.; Malley, J.; Tutz, G. An introduction to recursive partitioning: Rationale, application, and characteristics of classification and regression trees, bagging, and random forests. Psychol. Methods 2009, 14, 323–348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  61. Olsoy, P.J.; Glenn, N.F.; Clark, P.E.; Derryberry, D.R. Aboveground total and green biomass of dryland shrub derived from terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2014, 88, 166–173. [Google Scholar] [CrossRef]
  62. Olsoy, P.J.; Glenn, N.F.; Clark, P.E. Estimating sagebrush biomass using terrestrial laser scanning. Rangel. Ecol. Manag. 2014, 67, 224–228. [Google Scholar] [CrossRef]
  63. Greaves, H.E.; Vierling, L.A.; Eitel, J.U.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. Estimating aboveground biomass and leaf area of low-stature Arctic shrubs with terrestrial Lidar. Remote Sens. Environ. 2015, 164, 26–35. [Google Scholar] [CrossRef]
  64. Ni-Meister, W.; Lee, S.; Strahler, A.H.; Woodcock, C.E.; Schaaf, C.; Yao, T.; Ranson, K.J.; Sun, G.; Blair, J.B. Assessing general relationships between aboveground biomass and vegetation structure parameters for improved carbon estimate from Lidar remote sensing. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
  65. Spaete, L.P.; Glenn, N.F.; Derryberry, D.R.; Sankey, T.T.; Mitchell, J.J.; Hardegree, S.P. Vegetation and slope effects on accuracy of a Lidar-derived DEM in the sagebrush steppe. Remote Sens. Lett. 2011, 2, 317–326. [Google Scholar] [CrossRef]
  66. Mitchell, J.J.; Glenn, N.F.; Sankey, T.T.; Derryberry, D.R.; Anderson, M.O.; Hruska, R.C. Small-footprint Lidar estimations of sagebrush canopy characteristics. Photogramm. Eng. Remote Sens. 2011, 77, 521–530. [Google Scholar] [CrossRef]
  67. Riaño, D.; Chuvieco, E.; Ustin, S.L.; Salas, J.; Rodríguez-Pérez, J.R.; Ribeiro, L.M.; Viegas, D.X.; Moreno, J.M.; Fernández, H. Estimation of shrub height for fuel-type mapping combining airborne Lidar and simultaneous color infrared ortho imaging. Int. J. Wildland Fire 2007, 16, 341–348. [Google Scholar] [CrossRef]
  68. Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; Hermosilla, T. Estimation of biomass and volume of shrub vegetation using Lidar and spectral data in a Mediterranean environment. Biomass Bioenergy 2012, 46, 710–721. [Google Scholar] [CrossRef]
  69. Mundt, J.T.; Streutker, D.R.; Glenn, N.F. Mapping sagebrush distribution using fusion of hyperspectral and Lidar classifications. Photogramm. Eng. Remote Sens. 2006, 72, 47–54. [Google Scholar] [CrossRef]
  70. Whittingham, M.J.; Stephens, P.A.; Bradbury, R.B.; Freckleton, R.P. Why do we still use stepwise modelling in ecology and behaviour? J. Anim. Ecol. 2006, 75, 1182–1189. [Google Scholar] [CrossRef] [PubMed]
  71. Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
  72. Uresk, D.W.; Gilbert, R.O.; Rickard, W.H. Sampling big sagebrush for phytomass. J. Range Manag. 1977, 30, 311–314. [Google Scholar] [CrossRef]
  73. Brown, J.K. Fuel and Fire Behavior Prediction in Big Sagebrush. USDA Forest Service Research Paper INT (USA). 1982. Available online: https://www.fs.fed.us/rm/pubs_int/int_rp290.pdf (accessed on 1 June 2017).
  74. Cleary, M.B.; Pendall, E.; Ewers, B.E. Testing sagebrush allometric relationships across three fire chronosequences in Wyoming, USA. J. Arid Environ. 2008, 72, 285–301. [Google Scholar] [CrossRef]
  75. Sankey, T.; Shrestha, R.; Sankey, J.B.; Hardegree, S.P.; Strand, E. Lidar-derived estimate and uncertainty of carbon sink in successional phases of woody encroachment. J. Geophys. Res. Biogeosci. 2013, 118, 1144–1155. [Google Scholar] [CrossRef]
  76. Margolis, H.A.; Nelson, R.F.; Montesano, P.M.; Beaudoin, A.; Sun, G.; Andersen, H.E.; Wulder, M.A. Combining satellite Lidar, airborne Lidar, and ground plots to estimate the amount and distribution of aboveground biomass in the boreal forest of North America. Can. J. For. Res. 2015, 45, 838–855. [Google Scholar] [CrossRef]
Remotesensing 09 00903 g001 550
Figure 1. The Morley Nelson Snake River Birds of Prey National Conservation Area (NCA), located in southwestern Idaho, USA. This study area is located in the northwestern portion of the NCA where the 2012 and 2013 Lidar data were obtained.
Figure 1. The Morley Nelson Snake River Birds of Prey National Conservation Area (NCA), located in southwestern Idaho, USA. This study area is located in the northwestern portion of the NCA where the 2012 and 2013 Lidar data were obtained.
Remotesensing 09 00903 g001
Remotesensing 09 00903 g002 550
Figure 2. Schematic of the field sampling procedure. The nine squares represent the 1 m2 subplots distributed in the 1 ha plots.
Figure 2. Schematic of the field sampling procedure. The nine squares represent the 1 m2 subplots distributed in the 1 ha plots.
Remotesensing 09 00903 g002
Remotesensing 09 00903 g003 550
Figure 3. Scatterplots between the observed AGB (field-measured biomass) and the AGB with Equations (2) and (3) for total (A) and shrub (B) biomass.
Figure 3. Scatterplots between the observed AGB (field-measured biomass) and the AGB with Equations (2) and (3) for total (A) and shrub (B) biomass.
Remotesensing 09 00903 g003
Remotesensing 09 00903 g004 550
Figure 4. Scatterplots between the observed AGB (field-measured biomass) and the predicted AGB with the RF regression model for total (A) and shrub (B) biomass.
Figure 4. Scatterplots between the observed AGB (field-measured biomass) and the predicted AGB with the RF regression model for total (A) and shrub (B) biomass.
Remotesensing 09 00903 g004
Remotesensing 09 00903 g005 550
Figure 5. Imputed total AGB (A), standard deviation of the imputed total AGB (B) and coefficient of variation (CV) of the imputed total AGB (C) and imputed shrub AGB (D), standard deviation of the imputed shrub AGB (E) and coefficient of variation (CV) of the imputed shrub AGB (F), across a sub-area (middle portion) of the 2012 Lidar.
Figure 5. Imputed total AGB (A), standard deviation of the imputed total AGB (B) and coefficient of variation (CV) of the imputed total AGB (C) and imputed shrub AGB (D), standard deviation of the imputed shrub AGB (E) and coefficient of variation (CV) of the imputed shrub AGB (F), across a sub-area (middle portion) of the 2012 Lidar.
Remotesensing 09 00903 g005
Remotesensing 09 00903 g006 550
Figure 6. Imputed total AGB (A), standard deviation of the imputed total AGB (B) and coefficient of variation (CV) of the imputed total AGB (C) and imputed shrub AGB (D), standard deviation of the imputed shrub AGB (E) and coefficient of variation (CV) of the imputed shrub AGB (F), across the coverage of the 2013 Lidar.
Figure 6. Imputed total AGB (A), standard deviation of the imputed total AGB (B) and coefficient of variation (CV) of the imputed total AGB (C) and imputed shrub AGB (D), standard deviation of the imputed shrub AGB (E) and coefficient of variation (CV) of the imputed shrub AGB (F), across the coverage of the 2013 Lidar.
Remotesensing 09 00903 g006
Remotesensing 09 00903 g007 550
Figure 7. Scatterplots of the imputed biomass values and the standard deviation for total AGB (A) and for shrub AGB (B) and scatterplots of the imputed biomass values and the coefficient of variation for total AGB (C) and for shrub AGB (D).
Figure 7. Scatterplots of the imputed biomass values and the standard deviation for total AGB (A) and for shrub AGB (B) and scatterplots of the imputed biomass values and the coefficient of variation for total AGB (C) and for shrub AGB (D).
Remotesensing 09 00903 g007
Remotesensing 09 00903 g008 550
Figure 8. Linear regression of observed total AGB (A) and shrub AGB (B) with standard deviation of heights (Hstd).
Figure 8. Linear regression of observed total AGB (A) and shrub AGB (B) with standard deviation of heights (Hstd).
Remotesensing 09 00903 g008
Table
Table 1. Statistics of vegetation cover and biomass from the field sites, n = 46 (1-ha plots).
Table 1. Statistics of vegetation cover and biomass from the field sites, n = 46 (1-ha plots).
Herbaceous Cover (%)Shrub Cover (%)Herbaceous AGB (g/m2)Shrub AGB (g/m2)Total AGB (g/m2)
Minimum23.4031.1036.8
Maximum98.646.9489.4954.41116.8
Mean ± Std.65 ± 2012 ± 13144 ± 87208 ± 253352 ± 281
Table
Table 2. Lidar metrics (n = 35) and their descriptions.
Table 2. Lidar metrics (n = 35) and their descriptions.
Lidar MetricDescription
HminThe minimum of all height points within each pixel
HmaxThe maximum of all height points within each pixel
HrangeThe difference of maximum and minimum of all height points within each pixel
HmeanThe average of all height points within each pixel
HMADThe Median Absolute Deviation from Median Height value (HMAD) of all height points within each pixel, where HMAD = 1.4826 × median (|height − median height|)
HAADThe Mean Absolute Deviation from Mean Height (HAAD) value of all height points within each pixel, where HAAD = mean (|height − mean height|)
HvarThe variance of all height points within each pixel
HstdThe standard deviation of all height points within each pixel
HskewThe skewness of all height points within each pixel
HkurtThe kurtosis of all height points within each pixel
HIQRThe Interquartile Range (HIQR) of all height points within each pixel, where HIQR = Q75 − Q25, where Qx is xth percentile
HCVThe coefficient of variation of all height points within each pixel
H5, H10 etc.The 5th, 10th, 25th, 50th, 75th, 90th, and 95th percentiles of all height points within each pixel
nAllThe total number of all points within each pixel
nVThe total number of all the points within each pixel that are above the specified Crown Threshold value (CT)
nGThe total number of all the points within each pixel that are below the specified Ground Threshold value (GT)
Veg_densityThe percent ratio of vegetation returns and ground returns within each pixel
Veg_covThe percent ratio of vegetation returns and total returns within each pixel
pGPercent of points within each pixel that are below the specified Ground Threshold
pH1, pH2.5 etc.Percent of vegetation in height ranges 0–1 m, 1–2.5 m, 2.5–10 m, 10–20 m, 20–30 m, and >30 m within each pixel
CRRCanopy relief ratio of points within each pixel, where CRR = ((Hmean − Hmin))/((Hmax − Hmin))
HtextTexture of height of points within each pixel, where Htext = St. Dev. (Height > GT and Height < CT)
FHDallFoliage arrangement in the vertical direction (Foliage Height Diversity), where FHDall = −∑pi *lnpi where pi is the proportion of horizontal foliage coverage in the i-th layer to the sum of the foliage coverage of all the layers
FHDGTFHD calculated only from the points above GT
Table
Table 3. Results of the RF regression using raster data processing for total and shrub biomass at different resolutions representing 1-ha plots.
Table 3. Results of the RF regression using raster data processing for total and shrub biomass at different resolutions representing 1-ha plots.
Scale (m)Pseudo R2RMSE (g/m2)Predictors
Total AGB10.74141Hstd, HAAD, H90, HSkew, Hvar, Htext
70.70152Htext, FHDGT, H95, HAAD
300.58180FHDGT, nV, HAAD, H5
1000.52188FHDGT, nV, H16, HAAD
Shrub AGB10.76125Hstd, HAAD, HCV, Hrange, FHDall
70.67143Htext, FHDGT, HAAD
300.50176FHDGT, HAAD, HCV
1000.40184Htext, H50, pG, nG
Table
Table 4. Results of the RF regression using point cloud processing for total and shrub biomass at different resolutions representing 1-ha plots.
Table 4. Results of the RF regression using point cloud processing for total and shrub biomass at different resolutions representing 1-ha plots.
Scale (m)Pseudo R2RMSE (g/m2)Predictors
Total AGB10.71147HMAD, HSkew, HIQR, HAAD, Hstd, Hkurt, H90, HCV
70.71148Htext, HIQR
300.70151HAAD, H95, HIQR, pH1, pG
1000.67160H90, H95, Htext, Veg_density
Shrub AGB10.73129HIQR, Hstd, HMAD, HCV
70.72132Htext, H90, HIQR, HCV
300.65146H90, HIQR, Htext, pH1
1000.64151H95, Htext, pH1, GIQR, FHDGT
Table
Table 5. Results of the RF regression for herbaceous biomass representing 1-ha plots.
Table 5. Results of the RF regression for herbaceous biomass representing 1-ha plots.
Scale (m)SourcePseudo R2RMSE (g/m2)Predictors
Herbaceous AGB1Raster0.206.86HSkew, Htext
1Point Cloud0.197.54HCV, Htext, HSkew
Table
Table 6. Statistics of total and shrub imputed AGB and associated CV at 1-ha
Table 6. Statistics of total and shrub imputed AGB and associated CV at 1-ha
2012 Lidar2013 Lidar
Total AGBShrub AGBTotal AGBShrub AGB
Biomass (g/m2)Minimum36.8036.80
Maximum1116.8954.41116.8662.5
Mean ± Std.263 ± 20460 ± 149210 ± 23851 ± 126
CV (% biomass per area)Minimum34.923.946.031.4
Maximum389.2499.9347.9495.0
Mean ± Std.121 ± 48148 ± 102136 ± 58190 ± 90

Share and Cite

MDPI and ACS Style

Li, A.; Dhakal, S.; Glenn, N.F.; Spaete, L.P.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K. Lidar Aboveground Vegetation Biomass Estimates in Shrublands: Prediction, Uncertainties and Application to Coarser Scales. Remote Sens. 2017, 9, 903. https://doi.org/10.3390/rs9090903

AMA Style

Li A, Dhakal S, Glenn NF, Spaete LP, Shinneman DJ, Pilliod DS, Arkle RS, McIlroy SK. Lidar Aboveground Vegetation Biomass Estimates in Shrublands: Prediction, Uncertainties and Application to Coarser Scales. Remote Sensing. 2017; 9(9):903. https://doi.org/10.3390/rs9090903

Chicago/Turabian Style

Li, Aihua, Shital Dhakal, Nancy F. Glenn, Lucas P. Spaete, Douglas J. Shinneman, David S. Pilliod, Robert S. Arkle, and Susan K. McIlroy. 2017. "Lidar Aboveground Vegetation Biomass Estimates in Shrublands: Prediction, Uncertainties and Application to Coarser Scales" Remote Sensing 9, no. 9: 903. https://doi.org/10.3390/rs9090903

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop