Abstract
Accurate three-dimensional (3D) data from indoor spaces are of high importance for various applications in construction, indoor navigation and real estate management. Mobile scanning techniques are offering an efficient way to produce point clouds, but with a lower accuracy than the traditional terrestrial laser scanning (TLS). In this paper, we first tackle the problem of how the quality of a point cloud should be rigorously evaluated. Previous evaluations typically operate on some point cloud subset, using a manually-given length scale, which would perhaps describe the ranging precision or the properties of the environment. Instead, the metrics that we propose perform the quality evaluation to the full point cloud and over all of the length scales, revealing the method precision along with some possible problems related to the point clouds, such as outliers, over-completeness and misregistration. The proposed methods are used to evaluate the end product point clouds of some of the latest methods. In detail, point clouds are obtained from five commercial indoor mapping systems, Matterport, NavVis, Zebedee, Stencil and Leica Pegasus: Backpack, and three research prototypes, Aalto VILMA , FGI Slammer and the Würzburg backpack. These are compared against survey-grade TLS point clouds captured from three distinct test sites that each have different properties. Based on the presented experimental findings, we discuss the properties of the proposed metrics and the strengths and weaknesses of the above mapping systems and then suggest directions for future research.
Keywords:
point cloud; indoor; mobile laser scanning; MLS; metric; 3D scanning; mobile mapping; SLAM; review; comparison 1. Introduction
Demand for digital 3D models of building indoor spaces has been growing as the cost of producing one has reduced [1,2,3]. The use of these models can be characterized as two-fold, schematics and visualization. On the one hand, schematic model applications include creating as-built models for the planning and monitoring of construction processes and building conditions. On the other hand, visually-appealing virtual models of cultural and historical sites enable people to experience them remotely, being advantageous for those sites that are too fragile for normal tourism. Virtual models also have marketing and other applications. The schematic and virtual properties of digital 3D models can also be combined. Indoor models of public buildings, e.g., airports and shopping malls, can be used to assist indoor navigation and location-based services. Decision making on city planning can be facilitated, and construction permit processes speed up with digitization.
The raw material of a digital 3D model is more and more often a point cloud that is obtained either from laser scanning or imagery [1]. On the one hand, terrestrial laser scanners (TLS) provide good quality point clouds, but data collection requires careful planning and is time consuming. This is especially true in indoor spaces where visibility is restricted by walls and other clutter that raise the number of needed scanning locations up to a large number. On the other hand, mobile laser scanning (MLS) offers the possibility to quickly cover large and complex areas, with less problems from occlusions as data are measured continuously. However, to guarantee a certain level of accuracy of the final 3D point cloud, the trajectory of the MLS platform must be known with an according level of accuracy. While outdoors, reference coordinates from a global navigation satellite system (GNSS) can be used in conjunction with an inertial measurement unit (IMU) for localization [4], indoors, the absence of the GNSS signal must be compensated with other methods. These methods rely on data overlap, i.e., on simultaneous localization and mapping (SLAM) [5,6,7,8,9]. With imagery, bundle adjustment (BA) is used (see, e.g., [10,11]).
The evaluation of point clouds can be roughly divided into three approaches. First, the control point approach consists of (manually) choosing two control points to mark spots (or objects) inside a single point cloud A, calculating a Euclidean distance between these points, then doing the same for point clouds, say, B, C, D, and finally, comparing the distances obtained from these different point clouds (A, B, C, D). With three points, this leads to (semi-manual) triangulation. Collecting dozens of control points with a traditional total station, Jung et al. [12] evaluate Euclidean errors between these with respect to building information model (BIM) standards. Control points may, in principle, be obtained in an automated way. Such points are often referred to as features. However, the automated mining of features is based on an assumption that the point cloud is properly registered internally so that the local geometry of points is well defined (as in [13]). In a case like ours, where the internal registration may contain error misshaping the cloud, or where the point cloud may lack some points or may contain some extra points, the local geometry may also be changed, also changing the composition of the features. Such changes would render the extracted features unreliable for the purpose of automated point cloud evaluation.
Second, the subset approach consists of (manually) extracting a subset of points from the point cloud A and then performing an analysis based on that. In general, object deformation research in geodesy that used to be based on a few control points is headed in this direction [14]. An example related to indoor scanning can be found in [15], where normal vector angles of points were used to segment walls in Zeb1 and Leica point clouds, and the so-obtained subsets were then compared against each other. Also in our case, the subset may represent an indoor surface that is then used to calculate, for example, a root mean square error (RMSE) using nearest neighbor distances. All nearest neighbors reside in another point cloud B, which is assumed to be more accurate and is used to evaluate the properties of A. Now, as the measure is based on multiple points that span a subspace of a three-dimensional space, it is likely to be more robust than a measure based on a few control points. Specifically, where the control point approach binds only one degree of freedom in a rotation-translation mapping between A and B, i.e., the distance between two points, a subset of points may bind multiple degrees of freedom. After an appropriately done registration for the point clouds A and B, there is little difference in how the details of Euclidean distance measurements are chosen between the nearest points [16]. Subset extraction may be automated if enough a priori knowledge is available. In the robotics community, the evaluation of the point registration quality is done by benchmarking the results of simultaneous localization and mapping (SLAM) algorithms. For example, this takes place in the context of RoboCup, which is a challenge where mobile robots have to perform certain tasks competitively in an unknown test site, or unknown for the robot at least. Initially, Schwertfeger et al. [17] used reference blocks, so-called fiducials to evaluate maps created in a RoboCup Rescue mission. Later on, map structures were scored based on their topological rigority [18]. Finally, in [19], the authors used an independently available, accurate environment map of an urban area and a Monte Carlo localization (MCL) technique that matches sensor data against the reference map in combination with manual quality control.
Third, the full point cloud approach takes two point clouds as given and performs a computation with a chosen metric. In contrast to the subset and control point approaches, even more robustness is gained, if the whole point cloud spans a larger subspace of the three-dimensional space than any of its subsets. This approach is especially employed in change detection, for point clouds obtained from TLS measurements [20]. In these cases, the frequency of scans is high compared to the rate of change in the sense that the changes are so slow that displacement fields can be calculated for deformation monitoring. In this work, however, point cloud alterations are more sudden and complex. They may follow either from a physical source, e.g., a moved chair, or from a computational source, e.g., an incomplete registration caused by an SLAM algorithm. The literature on the latter is especially scarce. Research has modeled systematic errors, automated some parts of TLS registration and point cloud segmentation, but less attention has been put on designing data acquisition and quality assessment [21]. This has left the quantification of the quality of a point cloud mostly as an open question. Previously, Gelfand et al. [22] have proposed a measure for the estimation of pose uncertainty for an automatically done iterative closest point (ICP) registration. However, this measure relies on externally-provided surface normals, if no connectivity information among the points is available, as is the case for some of the methods that we evaluate. Hence, for universality, the point clouds are taken to contain point coordinates only.
In this paper, we focus on the third, the full point cloud, approach. Specifically, using a mobile mapping method, we first obtain a full point cloud A, which perhaps contains some internal geometrical misalignment. Then, that cloud A is brought to the same coordinates as an internally properly aligned TLS point cloud B, using remote sensing best practices. Finally, we concentrate on measuring the internal quality of the point cloud A by performing a comparison against the cloud B. In other words, our focus is on evaluating the qualities of the indoor 3D point cloud A, from a schematic point of view. We present a theoretical argument on what is the right metric to do such an evaluation and that has potential also for an automated approach. Hence, the contribution of this paper is two-fold. First, the comparison of the state-of-the-art mobile methods is valuable as itself, and second, the proposition for an automatable full-point cloud metric sheds understanding on an issue that will increase in importance in the future, namely the quality assurance of point clouds.
The rest of the paper is organized as follows. The background on the metrics for our method is presented in Section 2. Point clouds are obtained using selected state-of-the-art methods presented in Section 3, namely five commercial systems, Matterport [23], Zebedee [7], NavVis [24], Leica Pegasus: Backpack [25] (here ’Pegasus’) and Kaarta Stencil [26], and three research prototypes, Aalto VILMA [6,27], FGI Slammer [28] and the Würzburg backpack [5]. Survey-grade TLS point clouds obtained with Leica and Faro scanners are used as the reference. In Section 4, our three distinct indoor test sites that each have different properties are introduced. Results are presented in Section 5, with an elaborate discussion in Section 6. Section 7 concludes the paper.
2. Theory on Point Cloud Quality
Point cloud to point cloud (p2p) comparisons have been previously employed in change detection [29], deformation measurements [30], comparison studies [31] and reconstruction method evaluation [32] as well as in the study of objects, concerning their isometry invariances [33] and shape similarity [34,35]. p2p comparison is one form of a shape similarity problem. Given two point clouds, the problem is to determine how similar or dissimilar the two are from each other. For this, we need a metric.
2.1. On Metrics
Quantitatively, a metric expresses a distance between two point clouds. The Hausdorff distances and -norms, including the root means squared (RMS, ) distance, are the most common, as they are employed inside the iterative closest point (ICP) algorithm [36], but Gromov–Hausdorff [34] and Gromov–Wasserstein [35] distances are also used. Of these, the most commonly-used Hausdorff and -norms are dependent on the object rigidness or the explicit similarity of the two point clouds. The latter two on the other hand rely on the “wholeness” of the point cloud, i.e., that the object manifold is covered by the point cloud. Bronstein et al. [34] state that they model a non-rigid shape employing a “two-dimensional smooth, compact, connected and complete Riemannian surface (possibly with boundary) embedded into .” The point clouds taken from indoor environments, however, cannot be guaranteed to: (1) be implicitly or explicitly similar, since due to the measurement geometry, some surfaces may be left out for some methods that in contrast can be captured with other methods; (2) be outlier free, e.g., due to reflecting surfaces such as windows and glass surfaces; nor (3) have a similar level of noise, since the noise is partially a product of the measurement method, and the level of noise cannot be assumed to be the same when comparing two point clouds taken with different methods. Particularly, for the Gromov–Hausdorff and Gromov–Wasserstein metrics, there is no guarantee that the detection of deformations can be separated from the effects of (1–3). Moreover, useful algorithmics such as finding coverings with farthest point sampling [34] are prone to become dysfunctional from (1–3). See Figure 1 for an outline of the discussed metrics. The properties (1–3) lead to the following problems, which we then attempt to overcome by proposing novel metrics.
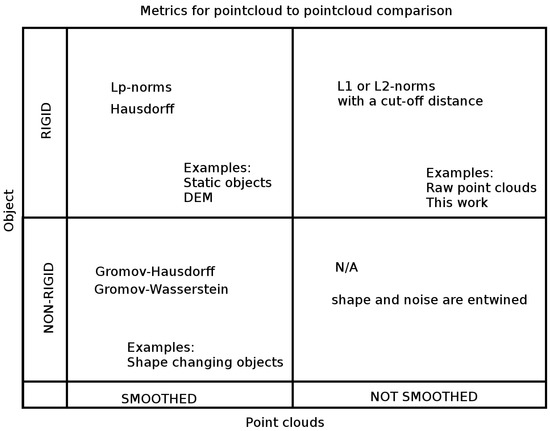
Figure 1.
Metrics for point cloud to point cloud comparison. In this work, the focus is on the comparison of as-is point clouds captured from rigid environments. DEM stands for digital elevation models. See the text in Section 2.3 for the details.
2.2. Formulating the Problems with the Indoor Point Clouds
First, we state that a 3D point cloud S consists of points , where each belongs to . The set thus consists of unordered points (cf. Appendix A). Second, each point cloud is a representation of an object or an (indoor) environment, and since these are constituted mainly of continuous surfaces, adjacent points are assumed to be connected (vegetation offers counter-examples for this assumption when, e.g., LIDAR beams penetrate it; indoor vegetation is thus considered negligible). These connections can be treated as links between the points, which are then nodes in a graph. Another approach is to assume that the points lie on or, due to noise, are close to a continuous two-dimensional surface. Either way, nearest neighbor algorithms can be used, but three major problems are encountered.
- Completeness problem: p2p comparison should be plausible even when the other point cloud is somewhat incomplete (or over-complete), e.g., if the measurement route chosen by the operator leads to missing (or extra) surfaces in the resulting point cloud. Incompleteness may also follow from visual obstructions.
- Outliers are produced by windows, reflecting surfaces or method properties that may be regarded as artifacts. p2p comparison should detect these.
- Multi-scale problem: In human-built indoor environments, all details exist for a purpose and accordingly have defined semantics, i.e., names. The noise level of the scanning method should be sufficiently low to successfully capture the smallest named details. However, in addition to containing these small details, indoor spaces span large distances. Capturing a model spanning large distances with high spatial resolution is data intensive and threatens computational tractability.
The incompleteness problem means that (large areas of) missing points in indoor point clouds are impossible to compensate by using implicit surface assumptions, in contrast to simple objects. Missing surfaces may lead to a point cloud consisting of a union of disjoint sets of measured points that fails to capture a complex indoor topology. For example, the “inside” of connected walls that span the entire building is much complex entity than the “inside” of an object that has an (almost) convex hull. The overcompleteness also easily causes confusion on how to interpret automated p2p comparison results. If the point cloud A, which covers a larger area, is compared against the point cloud B, it is hard to determine computationally if the large distances between the nearest neighbors follow from A containing outliers, A being deformed due to a mapping method, or from A covering a larger area than B. Outliers also prevent the use of surface reconstruction based on implicit surface assumptions.
Considering the multi-scale problem, the characteristic length of features L varies from the scale of millimeters to the one of dozens of meters being a property of the environment; see Figure 2. The noise in point locations (or the spatial resolution), on the other hand, is a specific property of a given method. For convenience, let us characterize this noise with a single standard deviation . In other words, we focus on the ranging precision and ignore the ranging error (or accuracy) for now. Considering the characteristic length of features L, the following applies:
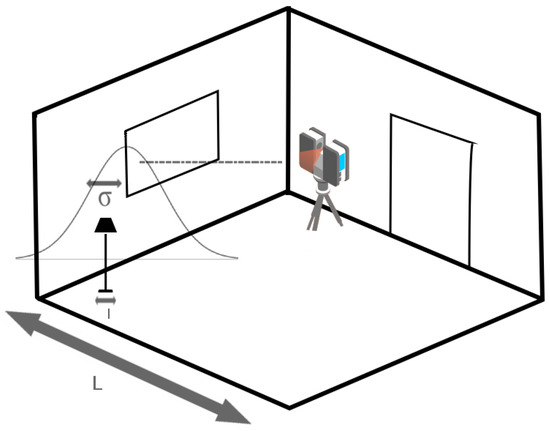
Figure 2.
Depiction of the multi-scale problem. Indoor spaces and objects within have vastly different length scales, e.g., the width of foot of the lamp is a lot shorter than the width of the room, . Problems arise when the standard deviation of the scanning error is of the same length scale as some of these length scales, . The deviation is exaggerated for illustration purposes.
- When the characteristic length of features , accuracy and precision can be separated, and the correct object shape is recovered.
- When or less, however, problems occur:
- (a)
- Features cannot be properly captured, making object shapes unrecoverable.
- (b)
- Accuracy and precision cannot be reliably separated.
In other words, the precision of the scanning method dictates whether all features of the chosen environment can be properly captured. Furthermore, if a feature of some small length scale is not separable from its surroundings, it becomes an indistinguishable part of one of the larger features. Hence, if the method precision is reduced, not only small features become indistinguishable, but also the shapes of the large distinguishable features change. See the thought experiment illustration in Figure 2.
2.3. The Proposed Metric
To deal with the previous problems, we must first make some assumptions; see Figure 1. First, we consider that indoor environments are rigid, so that any method originated deformation can be detected, with the caveat that some objects may have moved during the time when different measurements were taken. Second, to compensate for the multi-scale problem, we do not attempt to smooth the point clouds, but treat them as they are provided by the selected methods. This is to say, we do not make any external assumptions on the shape or the geometry of the data. Third, we introduce a cut-off radius for metrics to compensate for the problem with completeness, as follows.
Consider two point clouds S and R. Point , and its nearest point in R is . If the distance of these two points, , is greater than the threshold, , those two points do not affect the overall measure E. Formally, the p2p error metric:
where we use the norms or and the weight factor:
Introducing is a trade-off. It makes the measure more robust to the completeness problem, reducing the effects of missing or extra surfaces, but simultaneously makes the metric forgive all outliers. In principle, the cut-off radius should be chosen carefully so that it does not entirely forgive shortcomings in method precision, but that the completeness problem is avoided. In practice, this is impossible. Regardless, picking manually some is a common way of conducting a successful registration, employed, e.g., in geo-industry professional software. The reason why picking a value for works is because the point clouds are manually pre-aligned with a sufficient precision and visually approved after it. Otherwise, the practical use of a manually chosen is very limited because of the explained paradox.
The novelty of our approach is based on avoiding this loophole. Instead of trying to find the ‘correct’ , we examine the behavior of E of Equation (1) as a function of . This way, the three major problems introduced in Section 2.2 can be detected, not only by human intervention, but automatically. We shall return to this in the Results section.
3. Methods and Materials
The reference data collected from the three test sites and the eight studied methods are introduced in this section. For details on the test sites, FGI hallway, Innopoli 3 car park and Startup Sauna, see Section 4.
3.1. Reference Data
Reference data at FGI was collected using a Leica ScanStation P40 laser scanner having 3D position accuracy of 3 mm at a 50-m range. The data were acquired with resolution settings providing a point spacing of 1.6 mm and 3.1 mm at a 10-m distance from the scanner (angular resolution 0.009 and 0.018). Twelve scans in total were conducted covering the second floor corridor and the major part of the FGI library. The distance between scan positions varied from 5–14 m. The scans were matched together using 13 spherical targets (radius 0.099 m) and the cloud-to-cloud method in the Leica Cyclone 9.0 software. The RMS error for registration was 2 mm.
Reference data at Innopoli 3 car park were collected using the same laser scanner as at FGI. The data were acquired with resolution settings providing a point spacing of 3.1 mm and 6.3 mm at a 10-m distance from the scanner (angular resolution 0.018 and 0.036 ). Twenty three scans in total were conducted covering two floors and a ramp in a car park. The distance between scan positions varied from 10–20 m. The scans were matched together using visual alignment and the cloud-to-cloud method in the Leica Cyclone 9.0 software. The RMS error for registration was 5.7 mm. The same registration method was employed to transfer the compared point clouds into the same coordinates.
Reference data at the Startup Sauna test site were collected with the Faro Focus 3D laser scanner with a total of 28 scans, using multiple spherical scan targets. The distance between scan positions was from 3–8 m, with scans taken at different heights, due to the complex indoor space topology. The total point cloud size of 800 million points was reduced to 1:10 with Faro software.
3.2. Matterport
Matterport is motorized, tripod-mounted 3D camera that uses PrimeSense chips. Their accuracy has been evaluated in [37]. 2D and 3D sensors capture high-dynamic-range (HDR) images and depth image data; see Figure 3.

Figure 3.
Matterport.
The camera system spins in place and transfers the data to the 3D Capture app on an iPad in 30 s. 3D Capture app is also used to visualize scanning progress and edit scans on the fly. The distance between neighboring stations is within 1–3 m, and the 3D Capture app stitches transferred scans together automatically. Captured projects can be uploaded to to Matterport’s cloud servers for more complete and detailed post-processing. The Matterport Cloud creates a 3D model that combines HDR-quality imagery with dimensional geometry. Polygonal meshes can be streamed to the Matterport 3D Showcase media player. Furthermore, users can view the 3D models through their web browsers using the Unity multimedia plug-in. It is possible to move through the interior and then zoom out to a dollhouse or floor plan view of the model. The virtual reality (VR) 3D scene can be experienced by using VR platforms like the Samsung Gear VR headset. As an alternative to the VR, 3D files (.obj) of the scanned scene are downloadable. These 3D files can be transferred to point clouds, as we have done.
3.3. NavVis
The NavVis 3D Mapping Trolley was first released in 2014 [24]. NavVis consists of six 16 Megapixel cameras and three laser scanners with a 30-m range installed on a trolley chassis; see Figure 4. The total weight of the trolley is about 40 kg. One scanner on top of the system is positioned horizontally and is used for SLAM positioning, while two tilted scanners are installed on the trolley arm for point cloud acquisition. A touch screen is used for the operation, and NavVis has real-time processing and viewing of collected point cloud data. Post-processing is carried out by automated software by NavVis. The post-processing has two main steps: point cloud processing and web processing. In the point cloud processing, the raw data are processed into the point cloud, and images from individual cameras are stitched into panoramas. Individual datasets (for example, different floors) are combined manually using NavVis software. In the web processing, the material is optimized for a walkable model in the web browser. Sticker markers that are automatically detected in the data can be used for automatic registration of the datasets and also for georeferencing if the location of these markers is available. User interaction with respect to data processing is limited to the selection of the point cloud density. The default is m, with optional m or m.

Figure 4.
Data acquisition using NavVis.
3.4. Zebedee
Zebedee [7] is a hand-held 3D mapping system, which consists of a lightweight laser scanner with a 15–30-m maximum range (dependent on surface reflectivity and environmental conditions) and an industrial-grade IMU mounted on a simple spring mechanism. As an operator holding the device moves through the environment, in Figure 5, the scanner loosely oscillates about the spring, thereby producing rotational motion that converts the laser’s inherent 2D scanning plane into a local 3D field of view. With the use of proprietary software, the six degree of freedom sensor trajectory can be calculated from the laser and inertial measurements in real time, and the range measurements can be projected into a common coordinate frame to generate a 3D point cloud. There is also a newer version of the device on the market.

Figure 5.
Data acquisition using Zebedee.
3.5. Kaarta Stencil
Stencil is a stand-alone, light weight and low-cost system delivering the integrated power of mapping and real-time position estimation; see Figure 6. Stencil is based on scientific work [38] and depends on LIDAR and IMU data for localization. The processing architecture is based on ROS (Robot Operating System). The system uses Velodyne VLP-16 connected to a low-cost MEMS IMU and a processing computer for real-time six DoF mapping and localization, depending on the licensing. A 10-Hz scan frequency is used for the data capture, and the “strongest” echo mode of the scanner is used to create the point observations from the LIDAR signal. VLP-16 has a field of view with a 30 azimuthal opening using 16 scan lines. The stencil tilt angle is recommended to be within the envelope. The progress of the mapping can be monitored on-line via an external monitor attached with a USB cable.

Figure 6.
Data acquisition using Kaarta Stencil.
3.6. Leica Pegasus: Backpack
Leica Pegasus: Backpack is a commercial mapping system for indoor documentation, see Figure 7. The system incorporates two Velodyne VLP-16 scanners: one mounted horizontally for localization in GNSS-denied environments and one to perform vertical scanning for 3D reconstruction. The system uses NovAtel IGM-S1 for GNSS-IMU positioning when available. The scanners operate at a 10-Hz frequency, and as they cast 16 profiles simultaneously at a field of view, the scene is covered with 160 scan lines per second each with an angular resolution of mrad. Beam divergence of the scanner is about 3 mrad, and the ranging accuracy is 30 mm. The system is also fitted with five cameras for 2-Hz image data capture covering a field of view. According to the manufacturer, the absolute position accuracy for an indoor scene (SLAM based without control points) is 5 cm–50 cm after 10 min of walking, with a requirement of a minimum of three loop closures or double pass conditions. A variety of factors are listed, which may negatively influence the accuracy of trajectory. These include small rooms or hallways, the need to pivot while walking, stairs and uneven pavement, extremely smooth or blank surfaces, surfaces too far from the scanners and fast vertical movement.

Figure 7.
Mapping the hallway test site with Leica Pegasus: Backpack.
3.7. Würzburg Backpack
The backpack features a horizontally-mounted SICK LMS100 profiler; see Figure 8. In addition, it comes with a low-end IMU, the Phidget IMU Precision 3/3/3. The 2D profiler and the IMU are used to build a 2D grid map of the environment using the state-of-the-art in 2D SLAM, HectorSLAM [39]. It represents the environment as a 2D occupancy grid, which is a very well-known representation for maps in robotics. The 2D laser scanner performs six DoF motion while the backpack is carried. First, the scan is transformed into a local stabilized coordinate frame using the IMU-estimated attitude of the LIDAR system. Then, in a scan-matching process, the acquired stabilized scan is matched with the existing map, which is updated. The information of the 2D SLAM solution is exchanged with the navigation filter, which is an EKF (extended Kalman filter) in a bi-directional fashion, and thus, fused with the values of the Phidget IMU to produce six DoF pose estimates. The 2D mapping and the navigation module are not synchronized, and the EKF usually runs at a higher update rate. HectorSLAM uses this EKF for the pose estimation, and the EKF values are projected onto the xy-plane and are used as the start estimate for the optimization process of the 2D scan matcher. In the opposite direction, covariance intersection is used to fuse the SLAM pose with the full belief state of the navigation system.

Figure 8.
The Würzburg backpack consisting of a SICK LMS100 profiler, a low-end IMU and spinning RIEGL VZ400.
The central sensor of the backpack system is the 3D laser scanner RIEGL VZ400. The VZ400 is able to freely rotate around its vertical axis to acquire 3D scans. Due to the setup, however, there is an occlusion of about due to the backside of the backpack and the human carrier. The VZ400 is programmed to scan back and forth to avoid this blind spot. The data of the VZ400 are initially registered using the HectorSLAM trajectory. Then, it is split into segments and introduced to a semi-rigid six DoF SLAM [40]. The resulting continuous-time SLAM algorithm and a more precise description of the backpack are given in [5] and the references therein.
3.8. Aalto VILMA
VILMA is an experimental 3D scanning platform designed at Aalto University [6,27,41], see Figure 9. It relies on intrinsic localization that allows the pose recovery of a mobile 2D laser scanner without any external sensors such as the global navigation satellite systems (GNSS) or an inertial measurement unit (IMU). First, the position of the scanner is determined with respect to the trajectory length yielding a solution in 1D. This allows the use of an essential boundary condition, that the trajectory length is fixed, when horizontal turns (2D) and vertical turns (3D) are introduced using a curve-piece estimate described in [6]. Finally, the trajectory is optimized with six DoF semi-rigid SLAM [40] to recover the full six degrees of freedom. The VILMA method is operational on a 2D surface embedded in a 3D space, i.e., ground, and applicable for wheeled vehicles. The curve-piece estimate offers insights also for wearable scanner localization.

Figure 9.
Data acquisition using VILMA.
3.9. FGI Slammer
The FGI Slammer [28] is a research platform combining survey-grade sensors with the state-of-the-art 2D SLAM algorithms, the Karto Open library [42] and Hector SLAM [39]. Slammer consists of a NovAtel SPAN Flexpak6 GNSS receiver with a tactical-grade IMU (UIMU-LCI) and two Faro Focus 3D (120S and X330) high precision laser scanners mounted on a wheeled cart; see Figure 10. One scanner is mounted horizontally to collect data for SLAM, and another scanner is mounted vertically for 3D point cloud generation. A tablet computer is used for IMU and timing data recording. The ROS framework is used for data processing [43].

Figure 10.
FGI Slammer.
4. Test Sites
We have selected three test sites based on their distinct properties. First, the FGI building corridor and library represent a space that is narrow and crowded with elements. Second, the Innopoli 3 car park represents a wide space with a regular structure, but has a sloped floor connecting two floors. Third, the Startup Sauna is a space remodeled from an old industrial hall, filled with furniture elements of different sizes, from large truck containers, to normal tables and chairs, to small details, including handrails.
The data captured for this work and the approximate data capture times are shown in Table 1. Smooth walking speed (marked with w) stands for data capture doable in minutes or dozens of minutes, depending on the area size and the planned travel path. There were no essential differences with capture times, except that the capture times with TLS and Matterport are longer. The commercialized products offer the fastest data post-processing times, especially Stencil, which does most of the processing on-line and requires only a few minutes after scanning for automatic post-processing. All post-processing is doable within the time frame that it takes to register the TLS data. Regarding the Table 1 markings, the Slammer system that utilizes 2D SLAM unsuccessfully attempted to capture the car park (w-), and the NavVis system was operated only from below and above the ramp, the obtained point clouds being joined manually afterwards (w*).

Table 1.
Data capture numerics for this study from the three test sites. Gathering was planned to yield sufficiently different data to study the metrics. Abbreviation w stands for mobile methods that are used at smooth walking speed, roughly 2 min for the hallway, 10 min for the car park and 4 min for the Startup Sauna. See the text for w* and w-.
4.1. Hallway
The FGI second floor hallway is a test site containing a narrow 80 m-long hallway with a 100 turn in the middle; see Figure 11. The turn enables the study of the point cloud rigidness with respect to long indoor distances. Regarding outliers, the hallway runs through enlarged spaces containing many glass surfaces and windows. The test site has a flat floor.

Figure 11.
The hallway test site visualized from the turn point. The hallway continues to the left and to the right.
4.2. Car Park
The car park test site is located under the Innopoli 3 office building in Otaniemi, Finland. It has a sloped floor with water drains, presenting a challenge for 2D SLAM-based methods. Furthermore, it contains a ramp connecting two floors; see Figure 12. The ramp may be automatically modeled only with methods using 3D trajectories. Regarding outliers, there are no windows, and most of the surface material is concrete, which is close to a Lambertian surface.

Figure 12.
The car park ramp visualized using VILMA data. Two operators are walking up beside the platform. These dynamic effects do not hamper the SLAM-based registration, even if they remain in the final point cloud.
4.3. Startup Sauna
The Startup Sauna test site at Aalto University, Finland, is an old industry hall that has been decorated as a co-working space for startups; see Figure 13. The test site contains objects of multiple different scales, from cargo containers to small objects on tables, and power cords and rails. Windows and glass surfaces are present. Furthermore, the 3D capabilities of the methods may be tested here with stairs that provide access to working spaces residing on top of the cargo containers.

Figure 13.
Snapshot of TLS point cloud from Startup Sauna.
5. Results
We first compute the full point cloud results with the proposed metric, interpret these and then perform some more traditional rigidness and height elevation benchmarks based on point subsets to shed further understanding on the first interpretations.
5.1. Proposed Metrics on Full Point Clouds
The comparison metric E of Equation (1) is plotted as a function of the cut-off radius in Figure 14, Figure 15, Figure 16 and Figure 17, for the hallway, car park and Startup Sauna test sites, respectively.
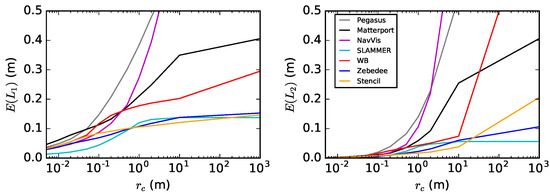
Figure 14.
Hallway test site. The error metric E, using L1 (left) and L2 (right) norms, as a function of the nearest point cut-off distance . The plot color legend is shown also in Table 1.
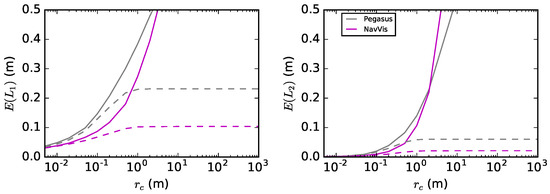
Figure 15.
Hallway test site. The full point cloud results (solid lines) compared against those reduced by a manual removal of extra points (dashed lines). The error metric E, using L1 (left) and L2 (right) norms, as a function of the nearest point cut-off distance . Differences are visible at length scales m.
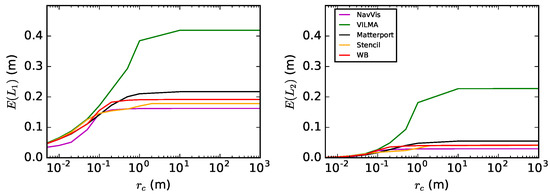
Figure 16.
The error metric E, using L1 (left) and L2 (right) norms, as a function of the nearest point cut-off distance , car park test site. For VILMA (green line), E saturates a bit later than for Matterport (black line), the Wurzburg backpack (red line), Stencil (orange line) and NavVis (magenta line). No outliers are present, so the metrics describe the accuracy and precision of the point cloud.
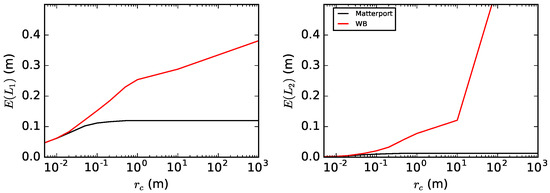
Figure 17.
Startup Sauna test site. The error metric E, using L1 (left) and L2 (right) norms, as a function of the nearest point cut-off distance . For the Würzburg backpack (red line), in contrast to Matterport (black line), E rises as an effect of outliers.
The metric E rises as a function of the cut-off distance when is small, which is expected. This behavior is due to the ranging precision noise in the point cloud and continues until grows larger than the standard deviation of the noise, . Methods may be ranked by their precision at this small length scale; see Table 2. Other than the noise, E contains the error from any missing or moved objects, but the total impact of these should be small. After the noise-originated effect is saturated, E remains constant unless the point cloud A that is compared against the point cloud B covers a larger scanned area or outliers or is otherwise substantially deformed. The results from the hallway test site in Figure 14 show that this is the case. Leica Pegasus: Backpack was used to map also the outskirts of the FGI building. This is why E keeps growing also on longer length scales in Figure 14 (grey line). A similar effect applies also to NavVis (magenta line) and Matterport (black line). This is not to be confused with the existence of outliers, which the Würzburg backpack method (red) produces. Note that the two first are commercial products, while the latter is an experimental setup where outlier removal is not implemented. Slammer (light blue) produces a significantly lower error E at length scales lower than m than the other methods, visible in Figure 14 for L1, but poorly visible for L2. This behavior is also represented in Table 2, showing numerical values for m. Stencil (orange) and Zebedee (blue) perform almost identically well, yielding a small E for all length scales .

Table 2.
Suggestive method ranking based on precision at length scales equaling to and under m, using the proposed metric results of Figure 11. Furthermore, numerical results for E using one value of are shown.
In order to test the convergence hypothesis for the proposed metric of Equation (1), Pegasus and NavVis point clouds are taken under a closer inspection. Both of these are separately considered as the point cloud A. We manually cut away selected areas so that the point cloud A would not cover a larger area than the reference point cloud B. This has a significant impact on the metric when is large; see Figure 15. Convergence is reached, and hence, the hypothesis is shown to be true.
Note that the total error cumulation is halted for all methods in the car park (see Figure 16), in contrast to the Startup Sauna where E for the Würzburg backpack increases as a function of the cut-off length (see Figure 17). The increase is again due to the abundant outliers left in the point cloud, see the visualization in Figure 18. As the Würzburg backpack method is experimental, it does not include an outlier filter, and E in this case quantifies the properties of the test sites. Depending on the test site, the amount of outliers differs.

Figure 18.
Startup Sauna test site, point cloud visualization. The registered Würzburg backpack and TLS point clouds are shown. Coloring is based on height. An abundance of outliers (marked with red circles for visualization purposes) that is present outside of the image is only partly shown.
The magnitude of the value of with which the saturation of total error E is reached is shown in Table 3. It is determined from the car park test site data, which is taken to be without outlier or completeness issues, as outliers produced by methods are negligible, visual obstructions are rare and the reference data covers a larger area than the methods do. The metric E saturates around m for NavVis, the Würzburg backpack and Stencil, although the latter has another saturation around 2 m, in Figure 16. Surprisingly, Stencil registration produces a double-floor artifact, when the data are captured by walking both ways in the open space. Namely, two separate parallel point planes represent the floor with a separation distance of about 10 cm in the direction of the plane normal. We will return to this in the Discussion section. The Würzburg backpack data were manually cropped so that a turn made before the ramp was left out. It was apparently incorrectly registered in SLAM. For VILMA, E saturation is around 2 m, which is the approximate height of the two operators walking beside the platform representing the source of the dynamic noise; see Figure 12. This observation offers a further token of validity for the proposed approach. Otherwise, the behavior of E at smaller is quite similar to other methods tested in the car park, except NavVis, which has a clearly better precision; see the L1 plot in Figure 16.

Table 3.
Magnitude of on which the saturation of total error E is reached without outliers or completeness issues. Best result first. See the text.
Summing up, the rise of E as a function of is always alarming and can be used to detect problems. It may be caused by three different factors: outliers in the point cloud A, A covering a larger area than B or/and internal registration errors in A, as in Figure 19. Naturally, the point cloud B needs to be outlier-free to detect outliers in A. Note that in Figure 19, the two cars that exist in A, but not in B also present a source of outliers when A is compared to B. These are not so easily removed with standard outlier filters.

Figure 19.
Snapshot of mutually-registered NavVis (blue) and TLS (other colors, by height) point clouds from the car park. The ramp up is shown at the bottom of the image. The second floor ceiling has been cut off for visual purposes. Red outliers are from the TLS cloud; these include two cars that have left the scene and are marked with white arrows.
5.2. Rigidness of Point Clouds Using a Floor Subset
When data are captured and processed, accumulating registration errors with SLAM may deform the resulting point cloud. Especially, long and dimensionally-constrained spaces are prone to enhance this behavior, which is why we examine the rigidness of the captured point clouds in the hallway test site, using the physically flat floor. This is a conventional semi-manual subset method. In principle, the study of the floor should reveal deviations caused by rotation or translation in four of the total six degrees of freedom, which is less than what the proposed full-point-cloud method is capable of.
A subset of points is extracted from each registered point cloud, using the same manually-designed geometric extraction shape so that the floor is conserved. Comparison is done against reference data in the height direction. The standard deviations of the floor elevation from the reference are shown in Table 4. These are in line with the previous results obtained with the proposed metrics in Figure 14 and Figure 15.

Table 4.
The standard deviations (STD) of the floor elevation from the reference. Best result first.
Floor subset data are visualized in Figure 20 and Figure 21, showing the four first listed methods and the latter three, respectively. Slammer, NavVis, Stencil and Zebedee perform well. The Pegasus point cloud contains some errors that apparently originate from registration issues. The Matterport point cloud is notably curved so that the hallway ends (red color) are at a higher elevation than where the cross-section lies. The Würzburg backpack produces duplicate surfaces, which cause up to a -m error. This is visible also from the error metric; see the red plot rise before m in Figure 14. Additionally, a 4 m-long end of one corridor is missing due to, apparently, a SLAM registration issue. In other words, the resulting Würzburg backpack point cloud in Figure 21 is affected so that the end part of the hallway is warped several meters and looks shorter than it should.
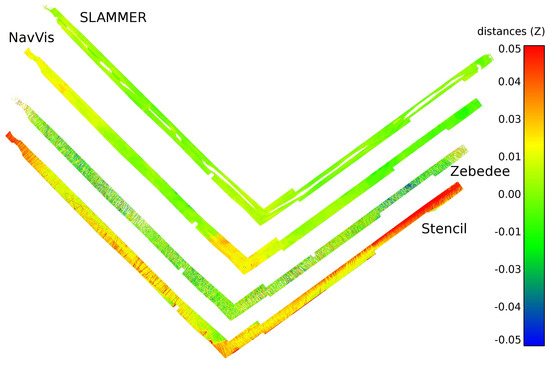
Figure 20.
Floor elevation deviations from the reference with a color scale from m– m.
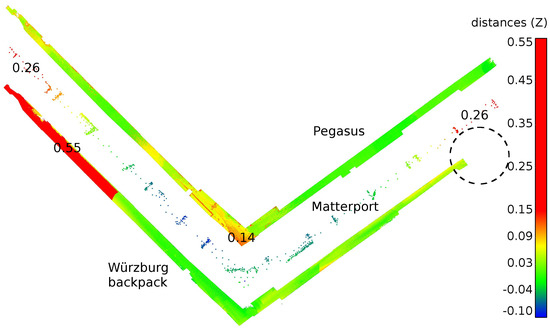
Figure 21.
Floor elevation deviations from the reference with the color scale from m– m. Deviations over m are shown in red. Note that the color scale is different than in the previous figure due to a different level of Z variation of the results. The dotted circle displays the location of some missing data. Numbers on the plot indicate maximum deviations in meters.
5.3. Benchmarking the 3D Capabilities of the Mapping Systems Using a Floor Subset
The capabilities of mapping systems in dealing with height differences are evaluated with the car park test site data. There are two distinct vertical length scales at the test site: first, the floors are mildly sloped to guide the water to the sewers, and then, there is a steep slope, the ramp between the two floors. As each mobile mapped point cloud is registered to the same coordinates, we use the same manually-designed geometrical shape to extract a subset from each point cloud. Then, we compare the point subset against the reference data using height and Euclidean distance measures between closest neighbors. Specifically, we extract a volume that contains some floor from both stories and the ramp itself. Hence, this is a similar semi-manual subset method as the one used in Section 5.2, and we use it to elaborate on and further the discussion on the results obtained with the proposed full point cloud method in Section 5.1.
The car park test site results are shown in Figure 22. NavVis is not operable in the slope, so measurements had to be done from below and above the ramp, manually combining the data afterwards. Regardless of this operation, the slope is still not fully covered. Matterport performs well, which can be determined from its point cloud, as the height rise between two floors is correctly captured. VILMA captures the slope quite well, though this is an experimental result as described in detail in [6]. Output contains much noise, with a cut-off saturation at 2 m, which follows from the approximate height of the operators, i.e., the properties of this dynamic noise. Stencil output contains the smallest errors. Stencil registration however produces a double-floor with planes 10 cm apart. The Würzburg backpack data look visually intact, although as previously explained, it was manually cropped so that a part of the trajectory containing one incorrectly registered turn was left out. Quantitative analysis of the backpack data in Figure 22e reveal that the rise between the two floors is left short. The points of the upper story floor are registered to the elevation level of the lower story ceiling that resides some 40 cm below the upper story floor. This and the previous incorrect registrations follow from issues with the SLAM scheme of this method.
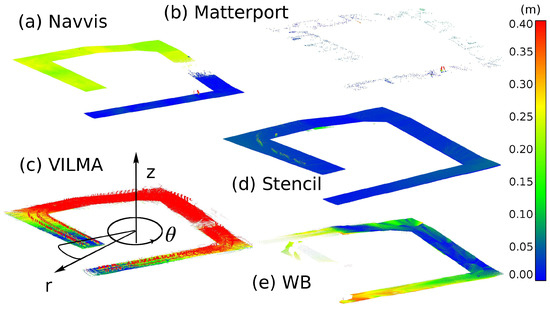
Figure 22.
(a–e) Height error colored point clouds from the car park test site. The height error is calculated between nearest neighbors. The color scale is from 0 (deep blue) to (deep red). The cylindrical coordinate system is spanned as shown in (c), with starting from the lower floor and increasing towards the higher floor. The scheme for spatial discretization as a function of for Figure 23 is also shown. See the text for details on missing data in (e).
We want to compare the differences of the floor subsets with a single quantity. For this purpose, the four-dimensional results visualized in Figure 22 are projected in a two-dimensional form; see Figure 23. Here, the position along the ramp is the single quantity, expressed with the angle , and is the height error with respect to the reference. In detail, a cylindrical coordinate system is spanned as shown in Figure 22c, with starting from the lower floor and increasing towards the higher floor. The height error averages are computed in volumetric blocks as a function of , using an angular discretization step length of .
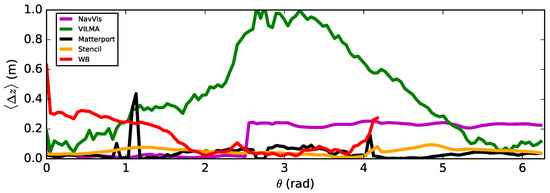
Figure 23.
Average height difference as a function of the location on the ramp . is the local average of measured point-to-point distances between a method and the reference point cloud. See the text for details.
In Figure 23, for VILMA (green line) rises due to the operators showing in the point cloud. For Matterport (black), the sharp spikes are similarly caused by dynamic operator-originated effects. The previously-discussed manual joining of point clouds with NavVis (magenta) shows as a step function behavior. Stencil (orange) reconstructs a double floor, which results in a small, but continuous error. For the Würzburg backpack (red), the plot shows a hint of the registration error prior to the manually-selected ramp data slice. The plot ends on the high end of the ramp, because as noted previously, the method data overlap the ceiling of the lower floor when compared against the TLS point cloud.
6. Discussion
With a full point cloud approach, we have identified three problems inherent to mobile indoor point cloud generation. One involves the different level of completeness of two point clouds being compared, one the outliers produced by the method and the last one the fact that there are features of various length scales present in indoor environments. The impacts of these three are quantified and made visible (in an inverse order) by the behavior of the proposed error metric E of Equation (1) as a function of , a cut-off distance. First, by observing the low end values of , the overall precision of the mapping methods can be estimated without the manual work of extracting point cloud subsets to study surfaces. Naturally, a sufficiently large sample of nearest neighbors must be obtained. The better the precision of the mobile mapping method, the smaller is the size of geometrical features that can be recovered. Second, it is important to see how fast the metric accumulates and, third, whether it converges to a constant value.
If the error metric E accumulates linearly or faster than linearly as a function of the length scale or if it does not converge, there may be something amiss. Its behavior cannot however be unambiguously interpreted. In terms of the metric, outliers are indistinguishable from the over-completeness of data if two point clouds covering areas of different sizes are compared. An experimental method, namely the Würzburg backpack, that lacks final polishing steps for the data was used to show this. To remove the outliers and distinguish between these effects, the means of other mapping methods, a pre-registration outlier filter [27] or a priori knowledge can be used. Changes created with respect to the point cloud by dynamic objects may still persist, and these are visible in the metric as a higher saturation plateau, as shown with the experimental method VILMA.
After the outlier removal, the over-completeness of data can still be indistinguishable from registration errors, i.e., interior point cloud deformation, within the metric. Switching the point clouds so that the smaller is compared to the larger may help if there are no drastic differences in the point densities between the clouds. In rare cases, if there are some (unknown) algorithmic artifacts, such as the double surfaces created by Stencil (see Appendix B), visual inspection is the only way to detect these.
All methods in this study were treated equally as black box systems, as commercial methods typically are like that. The results from three distinct test sites reveal strengths and weaknesses for the tested methods and are summarized in Table 5. Here, the word experimental denotes a platform built for scientific work.

Table 5.
Summarized strengths and weaknesses for each studied method.
The 3D capabilities of the methods were tested at different test sites. The car park ramp was scalable with various, but not all, mobile methods. The large elevation change breaks down any 2D assumptions, making approaches relying on horizontal SLAM fail. Narrow staircases were not included in this study, but commercial material claims that these should be scannable by Zebedee, Stencil and Matterport. Note that Matterport is not similarly mobile as the other methods, but was nevertheless included in this study, as it is a more light-weight solution than TLS. Even while the Startup Sauna test site contains stairs that break down 2D SLAM-based approaches, the Würzburg backpack method showed that an all-basin trajectory can still be used for a rather good outcome. The Würzburg backpack method has shortcomings with the six DoF semi-rigid SLAM that relies on an ICP-based algorithm (iterative closest point), which is unable to move past a local minimum. This issue can reportedly be dealt with, for example, by constructing an initial estimate for the trajectory that encompasses also the vertical dimension [6].
The three studied experimental systems have some similarities. VILMA employs the same six DoF semi-rigid SLAM as the Würzburg backpack method. However, VILMA relies on a curve-piece estimate for the trajectory, while the Würzburg backpack method employs HectorSLAM [39], which is a 2D SLAM, to provide for an initial trajectory. Concurrently, Slammer also uses HectorSLAM, but is capable only of 2D trajectories.
The proposed error metric E measures a total error that comes from different sources, including internal ranging errors of the scanner, the platform geometry, the way the scanning platform is operated and, finally, changes in all of these due to the environment. The metric may be useful in automated 3D quality assertion of point clouds. Applications exist in construction and renovation where point clouds are used as raw material to produce schematics, e.g., 3D BIM plans.
For future work considerations, it is noted that the proposed metric E is intended to evaluate non-smoothed point clouds captured from rigid objects. Additional data overlap would allow extending it to detect dynamic content and to distinguish external and internal similarities of objects. Furthermore, determining automatically the minimum detail size that is accurately captured, as a property of the method, or concurrently, the minimum detail size that is present, as a property of the multi-scale environment, is one goal worthwhile pursuing. Automatic distinguishing between the relative impact of different error sources is also one potential research direction.
7. Conclusions
We have conducted a comparison of the selected state-of-the-art methods in mobile indoor 3D scanning, by studying the properties of 3D point clouds provided by these mapping methods with a full-point cloud approach. The full-point cloud approach takes all data into account, facilitating automated processing and offering, in some regards, more perspective on the properties of the data than single control points or subsets derived (manually) from the full point clouds. Inherent to indoor point clouds, three encountered problems were identified. These have been dealt with by proposing novel metrics that do not operate on a manually-given length scale, which would perhaps describe the ranging precision of the mobile mapping method or some specific property of the environment. Instead, the metrics perform the quality evaluation over all of the length scales, revealing the method precision along with possible problems related to the point clouds, such as outliers, over-completeness and misregistration. Quantitative evaluation results, complemented with visual illustrations and qualitative analysis, have been presented. Point clouds with most precision were provided by the experimental Slammer and the commercial NavVis, but these two are wheeled platforms that are restricted to mainly flat surfaces. Mobile platforms capable of functioning with more complex trajectories differ in terms of operation and point cloud quality. Regarding the future, we suggest some research directions and that the proposed metrics may be useful in automated 3D quality assertion of point clouds.
Acknowledgments
This study was made possible by financial aid from the Finnish Academy projects “Centre of Excellence in Laser Scanning Research (CoE-LaSR) (272195)” and “Competence Based Growth Through Integrated Disruptive Technologies of 3D Digitalization, Robotics, Geospatial Information and Image Processing/Computing Point Cloud Ecosystem (293389)”. The authors wish to thank Jan Biström for helping with the Zebedee data.
Author Contributions
The coordination of the work was done jointly by Ville Lehtola and Harri Kaartinen. Ville Lehtola wrote the first draft of the paper, originated the idea on presented metrics, developed the theoretical arguments of Section 2, selected the test sites, ran the respective results in Section 3 and analyzed them. Andreas Nüchter provided the Würzburg backpack data and contributed to the discussion. Harri Kaartinen, Matti Vaaja, Aimad el Issaoui, Juho-Pekka Virtanen and Matti Kurkela provided the TLS data. Risto Kaijaluoto and Antero Kukko provided the Slammer data. Antero Kukko participated also in the Zebedee data collection. Risto Kaijaluoto and Ville Lehtola provided the Stencil data. Ville Lehtola provided the VILMA data. Tomi Rosnell and Eija Honkavaara provided the NavVis data. Lingli Zhu, Paula Litkey, Juha-Pekka Virtanen and Matti Kurkela provided the Matterport data. The article was improved by the contributions of all of the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Points might have also other properties than coordinates, e.g., as defined in the LAS (LASer) file format of the American Society for Photogrammetry and Remote Sensing (ASPRS). However, these other properties are not considered in this work.
Appendix B
Kaarta Stencil produced some double surfaces as mentioned in the Results section. Based on an email exchange with Kaarta’s CEO, “The double registration problem ... does not often occur except in tight indoor environments.”
References
- Musialski, P.; Wonka, P.; Aliaga, D.G.; Wimmer, M.; van Gool, L.; Purgathofer, W. A Survey of Urban Reconstruction. Comput. Graph. Forum 2013, 32, 146–177. [Google Scholar] [CrossRef]
- Tang, P.; Huber, D.; Akinci, B.; Lipman, R.; Lytle, A. Automatic reconstruction of as-built building information models from laser-scanned point clouds: A review of related techniques. Autom. Constr. 2010, 19, 829–843. [Google Scholar] [CrossRef]
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for existing buildings—Literature review and future needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Vastaranta, M.; Kukko, A.; Jaakkola, A.; Yu, X.; Pyörälä, J.; Liang, X.; Liu, J.; Wang, Y.; et al. Accuracy of Kinematic Positioning Using Global Satellite Navigation Systems under Forest Canopies. For. Trees Livelihoods 2015, 6, 3218–3236. [Google Scholar] [CrossRef]
- Lauterbach, H.; Borrmann, D.; Heß, R.; Eck, D.; Schilling, K.; Nüchter, A. Evaluation of a Backpack-Mounted 3D Mobile Scanning System. Remote Sens. 2015, 7, 13753–13781. [Google Scholar] [CrossRef]
- Lehtola, V.V.; Virtanen, J.P.; Vaaja, M.T.; Hyyppä, H.; Nüchter, A. Localization of a mobile laser scanner via dimensional reduction. ISPRS J. Photogramm. Remote Sens. 2016, 121, 48–59. [Google Scholar] [CrossRef]
- Bosse, M.; Zlot, R.; Flick, P. Zebedee: Design of a Spring-Mounted 3-D Range Sensor with Application to Mobile Mapping. IEEE Trans. Robot. 2012, 28, 1104–1119. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar odometry and mapping in real-time. In Proceedings of the Robotics: Science and Systems Conference (RSS), Berkeley, CA, USA, 14–16 July 2014; pp. 109–111. [Google Scholar]
- Liu, T.; Carlberg, M.; Chen, G.; Chen, J.; Kua, J.; Zakhor, A. Indoor localization and visualization using a human-operated backpack system. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010; pp. 1–10. [Google Scholar]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Reconstructing building interiors from images. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 80–87. [Google Scholar]
- Lehtola, V.V.; Kurkela, M.; Hyyppä, H. Automated image-based reconstruction of building interiors—A case study. Photogramm. J. Finl. 2014, 24. [Google Scholar] [CrossRef]
- Jung, J.; Yoon, S.; Ju, S.; Heo, J. Development of kinematic 3D laser scanning system for indoor mapping and as-built BIM using constrained SLAM. Sensors 2015, 15, 26430–26456. [Google Scholar] [CrossRef] [PubMed]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Holst, C.; Kuhlmann, H. Challenges and present fields of action at laser scanner based deformation analyses. J. Appl. Geod. 2016, 10, 17–25. [Google Scholar] [CrossRef]
- Sirmacek, B.; Shen, Y.; Lindenbergh, R.; Diakite, A.; Zlatanova, S. Comparison of Zeb1 and Leica C10 indoor laser scanning point clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 143–149. [Google Scholar] [CrossRef]
- Tsakiri, M.; Anagnostopoulos, V. Change Detection in Terrestrial Laser Scanner Data Via Point Cloud Correspondence. Int. J. Eng. Innov. Res. 2015, 4, 476–486. [Google Scholar]
- Schwertfeger, S.; Jacoff, A.S.; Scrapper, C.; Pellenz, J.; Kleiner, A. Evaluation of Maps using Fixed Shapes: The Fiducial Map Metric. In Proceedings of the 2010 Performance Metrics for Intelligent Systems (PerMIS ’10) Workshop, Baltimore, MD, USA, 28–30 September 2011. [Google Scholar]
- Schwertfeger, S.; Birk, A. Evaluation of Map Quality by Matching and Scoring High-Level, Topological Map Structures. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA ’13), Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Wulf, O.; Nüchter, A.; Hertzberg, J.; Wagner, B. Benchmarking Urban 6D SLAM. J. Field Rob. (JFR) 2008, 25, 148–163. [Google Scholar] [CrossRef]
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A review of the use of terrestrial laser scanning application for change detection and deformation monitoring of structures. Surv. Rev. 2017, 49, 99–116. [Google Scholar] [CrossRef]
- Scaioni, M. On the estimation of rigid-body transformation for tls registration. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B5, 601–606. [Google Scholar] [CrossRef]
- Gelfand, N.; Ikemoto, L.; Rusinkiewicz, S.; Levoy, M. Geometrically stable sampling for the ICP algorithm. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling, Banff, AL, Canada, 6–10 October 2003; pp. 260–267. [Google Scholar]
- Immersive 3D Spaces for real-world applications, Matterport. Available online: https://matterport.com/ (accessed on 21 October 2016).
- Navvis. Digitizing indoors—NavVis. Available online: http://www.navvis.com (accessed on 20 October 2016).
- Leica Geosystems. Leica Pegasus: Backpack. Available online: http://www.leica-geosystems.com (accessed on 1 Feburary 2017).
- Kaarta. Stencil. Available online: http://www.kaarta.com (accessed on 1 Feburary 2017).
- Lehtola, V.V.; Virtanen, J.P.; Kukko, A.; Kaartinen, H.; Hyyppä, H. Localization of mobile laser scanner using classical mechanics. ISPRS J. Photogramm. Remote Sens. 2015, 99, 25–29. [Google Scholar] [CrossRef]
- Kaijaluoto, R.; Kukko, A.; Hyyppä, J. Precise indoor localization for mobile laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-4/W5, 1–6. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change detection on points cloud data acquired with a ground laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, W19. [Google Scholar]
- Monserrat, O.; Crosetto, M. Deformation measurement using terrestrial laser scanning data and least squares 3D surface matching. ISPRS J. Photogramm. Remote Sens. 2008, 63, 142–154. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Oesau, S.; Lafarge, F.; Alliez, P. Indoor scene reconstruction using feature sensitive primitive extraction and graph-cut. ISPRS J. Photogramm. Remote Sens. 2014, 90, 68–82. [Google Scholar] [CrossRef]
- Mémoli, F.; Sapiro, G. A Theoretical and Computational Framework for Isometry Invariant Recognition of Point Cloud Data. Found. Comput. Math. 2005, 5, 313–347. [Google Scholar] [CrossRef]
- Bronstein, A.M.; Bronstein, M.M.; Kimmel, R.; Mahmoudi, M.; Sapiro, G. A Gromov-Hausdorff Framework with Diffusion Geometry for Topologically-Robust Non-rigid Shape Matching. Int. J. Comput. Vis. 2009, 89, 266–286. [Google Scholar] [CrossRef]
- Mémoli, F. Gromov—Wasserstein Distances and the Metric Approach to Object Matching. Found. Comput. Math. 2011, 11, 417–487. [Google Scholar] [CrossRef]
- Ezra, E.; Sharir, M.; Efrat, A. On the performance of the ICP algorithm. Comput. Geom. 2008, 41, 77–93. [Google Scholar] [CrossRef]
- Khoshelham, K.; Elberink, S.O. Accuracy and resolution of kinect depth data for indoor mapping applications. Sensors 2012, 12, 1437–1454. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2016, 41, 1–16. [Google Scholar] [CrossRef]
- Kohlbrecher, S.; Von Stryk, O.; Meyer, J.; Klingauf, U. A flexible and scalable slam system with full 3D motion estimation. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 155–160. [Google Scholar]
- Borrmann, D.; Elseberg, J.; Lingemann, K.; Nüchter, A.; Hertzberg, J. Globally consistent 3D mapping with scan matching. Robot. Auton. Syst. 2008, 56, 130–142. [Google Scholar] [CrossRef]
- Lehtola, V.V.; Virtanen, J.P.; Rönnholm, P.; Nüchter, A. Localization corrections for mobile laser scanner using local support-based outlier filtering. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-4, 81–88. [Google Scholar] [CrossRef]
- Karto Robotics. Available online: http://www.kartorobotics.com (accessed on 20 October 2016).
- ROS.org | Powering the world’s robots. Available online: http://www.ros.org (accessed on 20 October 2016).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).