Hybrid Spectral Unmixing: Using Artificial Neural Networks for Linear/Non-Linear Switching
Abstract
1. Introduction
2. Methodology
2.1. Research Design
2.1.1. Vertex Component Analysis (VCA)
2.1.2. Fully Constrained Least Square Method (FCLS)
2.1.3. Polynomial Post Nonlinear Mixture (PPNM)
2.1.4. Generalized Bilinear Mixing Model
2.2. Vicinity Parameters
2.2.1. Spectral Angular Distance (SAD)
2.2.2. Covariance Matrix
2.2.3. Nonlinearity Parameter
2.3. Learning
- The training set is used to fit the parameters of the classifier.
- Validation set is used to minimize over-fitting (i.e., verifying the accuracy of the training data) over some untrained data by the networks, while
- testing sets are used to test the final solution in order to confirm the actual predictive power of the network [65].
3. Experimental Setup and Results
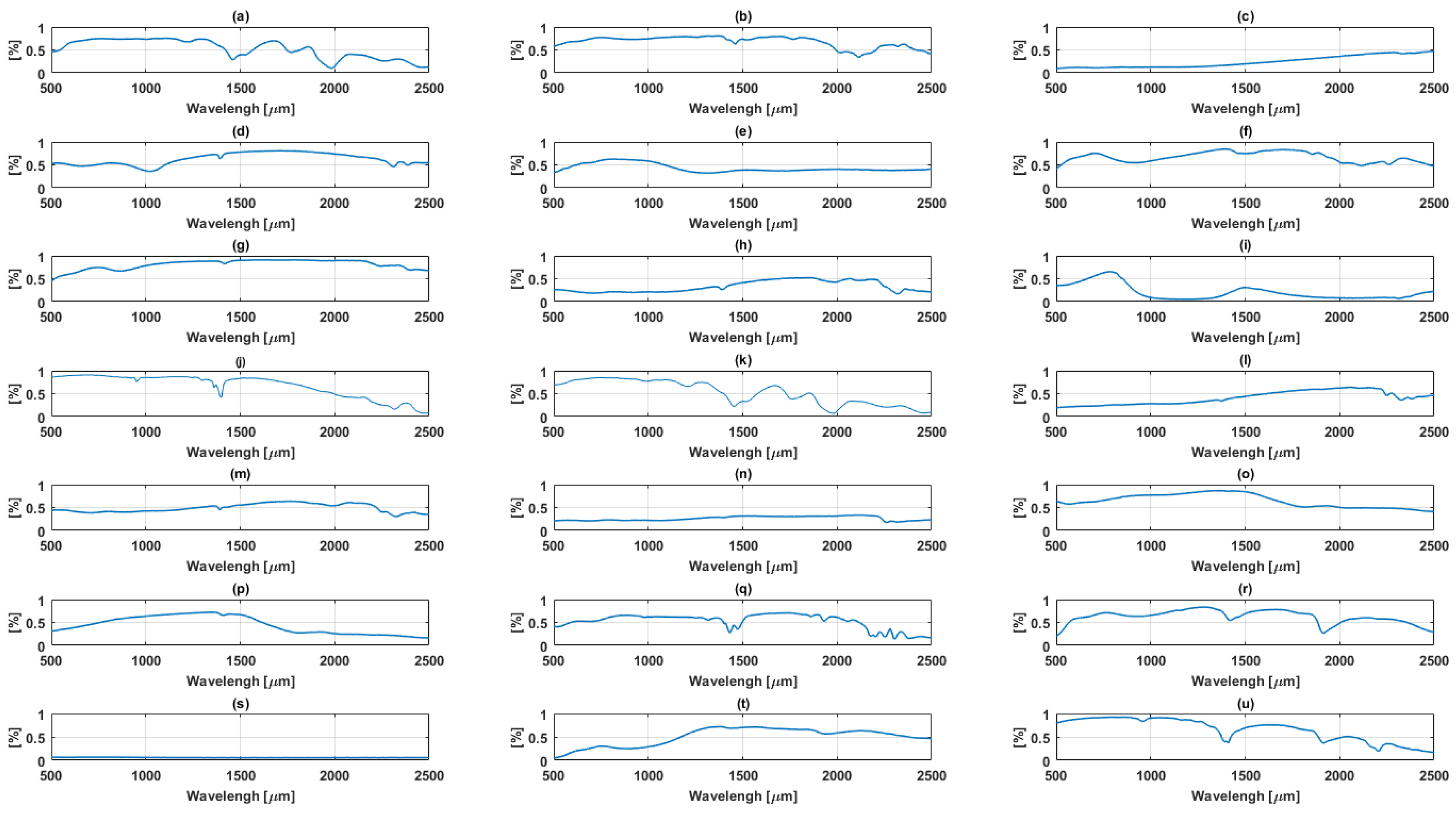
3.1. Data Description
3.1.1. Simulated Data
3.1.2. Real data
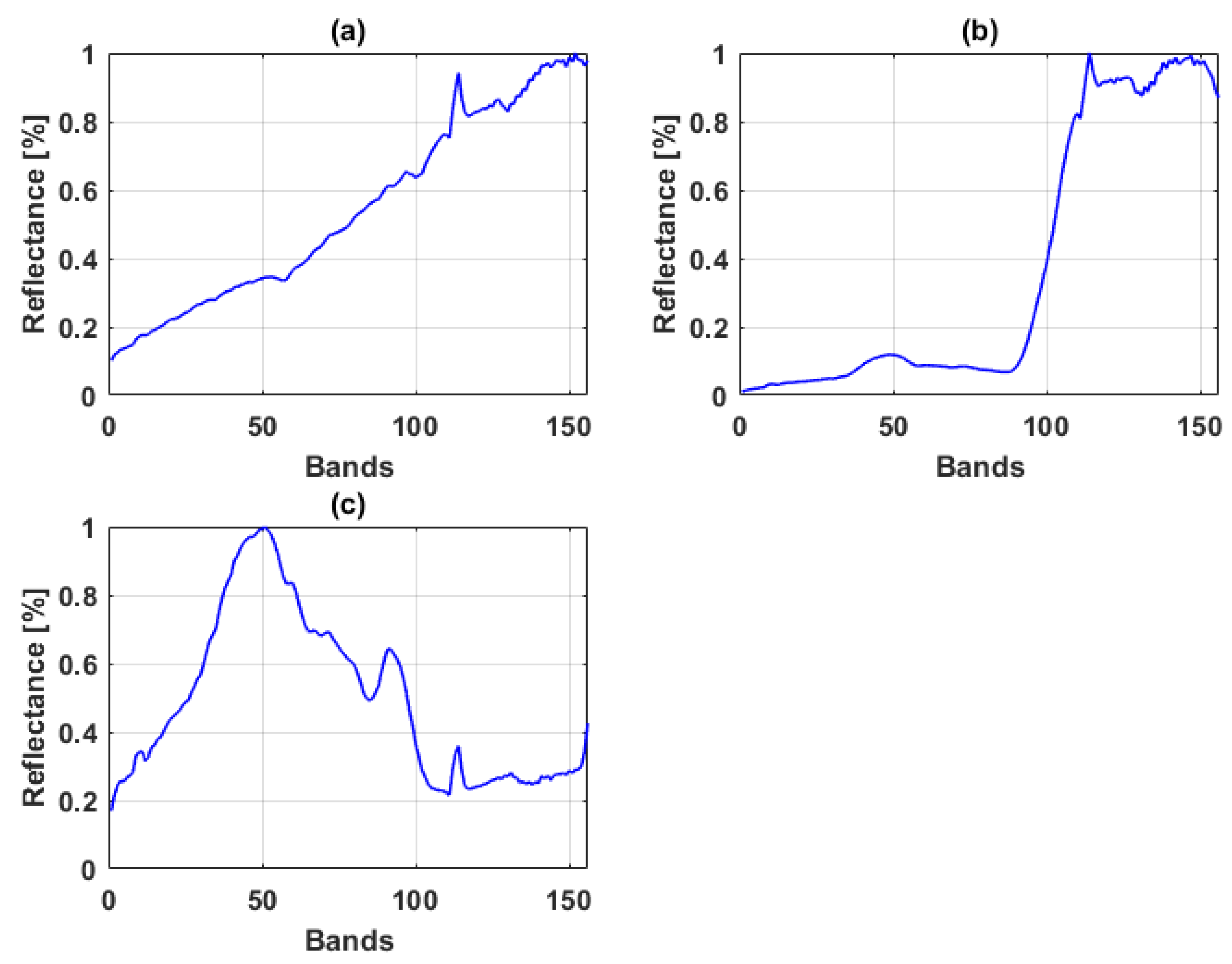
Samson Data
Jasper Ridge
3.2. Experiments with Synthetic Data
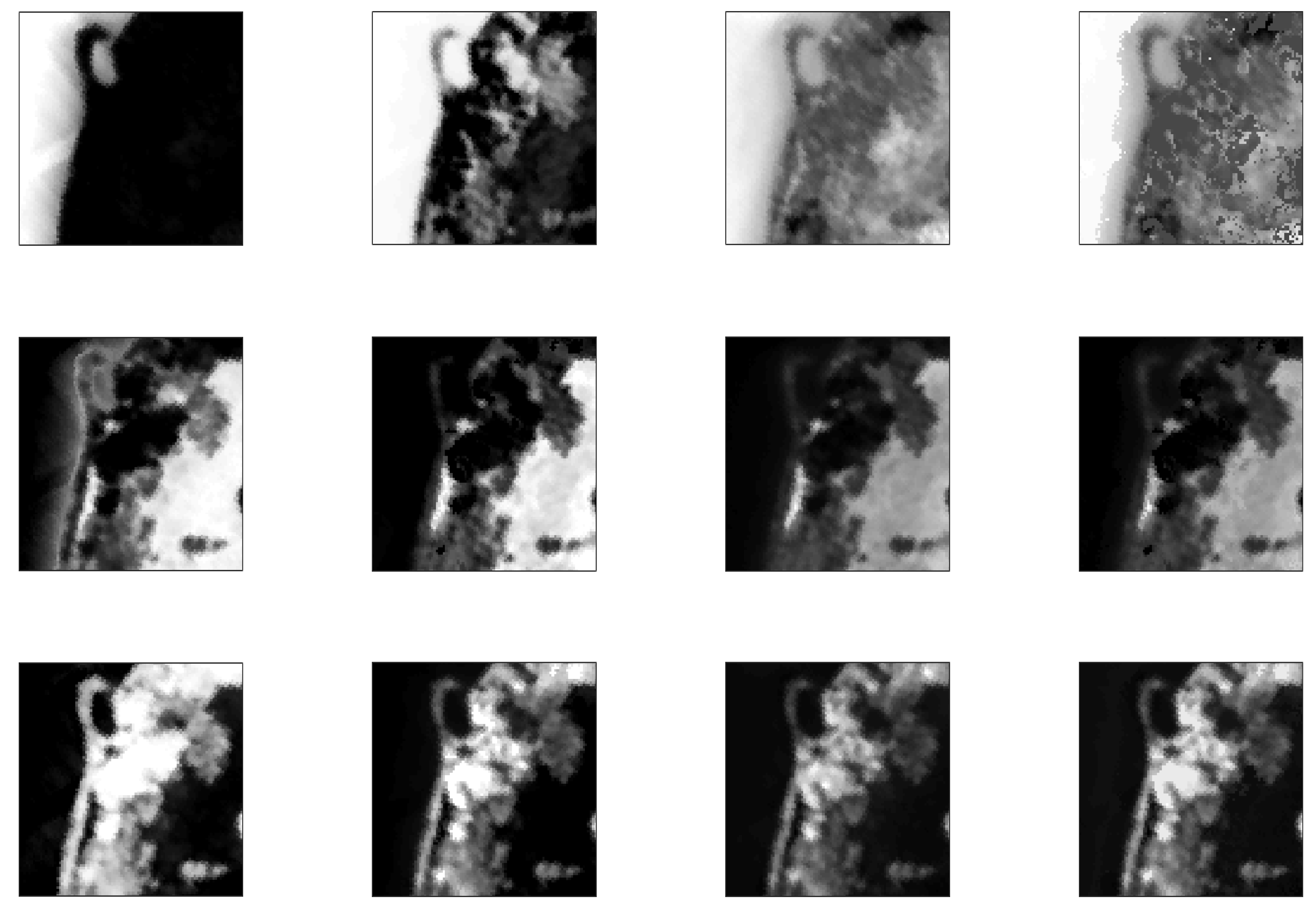
3.3. Experiment with Real Data
4. Discussion
4.1. Results
4.2. Advantages and Limitations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, L.; Du, B.; Zhang, L.; Fan, Y.; Song, D. A Mutation Operator Accelerated Quantum-Behaved Particle Swarm Optimization Algorithm for Hyperspectral Endmember Extraction. Remote Sens. 2017, 9, 197. [Google Scholar] [CrossRef]
- Uezato, T.; Murphy, R.J.; Melkumyan, A.; Chlingaryan, A. A novel spectral unmixing method incorporating spectral variability within endmember classes. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2812–2831. [Google Scholar] [CrossRef]
- Weeks, A.R. Fundamentals of Electronic Image Processing; SPIE Optical Engineering Press: Bellingham, WA, USA, 1996. [Google Scholar]
- Drumetz, L.; Tochon, G.; Chanussot, J.; Jutten, C. Estimating the number of endmembers to use in spectral unmixing of hyperspectral data with collaborative sparsity. In Proceedings of the the 13th International Conference on Latent Variable Analysis and Signal Separation (LVA-ICA), Grenoble, France, 21–23 February 2017; pp. 1–10. [Google Scholar]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y.; Richard, C.; Bermudez, J.; McLaughlin, S.; Hero, A.O. Nonlinear unmixing of hyperspectral images: Models and algorithms. IEEE Signal Process. Mag. 2014, 31, 82–94. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; Buller, G.S.; McLaughlin, S.; Oxford, W.; Clarke, D.; Piper, J. Robust unmixing algorithms for hyperspectral imagery. In Proceedings of the Sensor Signal Processing for Defence (SSPD), Edinburgh, UK, 22–23 September 2016; pp. 1–5. [Google Scholar]
- Chang, C.I. Adaptive Linear Spectral Mixture Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1240–1253. [Google Scholar]
- Shi, Z.; Tang, W.; Duren, Z.; Jiang, Z. Subspace matching pursuit for sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3256–3274. [Google Scholar]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse unmixing of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral unmixing with robust collaborative sparse regression. Remote Sens. 2016, 8, 588. [Google Scholar]
- Thouvenin, P.A.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral unmixing with spectral variability using a perturbed linear mixing model. IEEE Trans. Signal Process. 2016, 64, 525–538. [Google Scholar]
- Foody, G.M.; Cox, D. Subpixel Land Cover Composition Estimation Using Linear Mixture Model and Fuzzy Membership Functions. Int. J. Remote Sens. 1994, 15, 619–631. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Dias, J.M.B. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Bioucas-Dias, J.M. Nonlinear mixture model for hyperspectral unmixing. In Proceedings of the SPIE Europe Remote Sensing. International Society for Optics and Photonics, Berlin, Germany, 31 August 2009; p. 74770I. [Google Scholar]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Liu, C.; Ma, J. GBM-based unmixing of hyperspectral data using bound projected optimal gradient method. IEEE Geosci. Remote Sens. Lett. 2016, 13, 952–956. [Google Scholar] [CrossRef]
- Chen, J.; Richard, C.; Honeine, P. Nonlinear unmixing of hyperspectral data based on a linear-mixture/nonlinear-fluctuation model. IEEE Trans. Signal Process. 2013, 61, 480–492. [Google Scholar] [CrossRef]
- Marinoni, A.; Gamba, P. Accurate detection of anthropogenic settlements in hyperspectral images by higher order nonlinear unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1792–1801. [Google Scholar] [CrossRef]
- Altmann, Y. Nonlinear Spectral Unmixing of Hyperspectral Images. Ph.D. Thesis, l’Institut National Polytechnique de Toulouse (INP Toulouse), Toulouse, France, 2013. [Google Scholar]
- Altmann, Y.; Halimi, A.; Dobigeon, N.; Tourneret, J.Y. Supervised nonlinear spectral unmixing using a postnonlinear mixing model for hyperspectral imagery. IEEE Trans. Image Process. 2012, 21, 3017–3025. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, J.M.; Bioucas-Dias, J.M. Unmixing hyperspectral intimate mixtures. In Proceedings of the Remote Sensing. International Society for Optics and Photonics, Toulouse, France, 20 September 2010; p. 78300C. [Google Scholar]
- Sun, L.; Wu, Z.; Liu, J.; Xiao, L.; Wei, Z. Supervised spectral–spatial hyperspectral image classification with weighted Markov random fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1490–1503. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Li, J.; Li, S.S.; Zhang, B.; Benediktsson, J.A. Spectral-spatial hyperspectral image classification using subspace-based support vector machines and adaptive markov random fields. Remote Sens. 2016, 8, 355. [Google Scholar] [CrossRef]
- Ni, L.; Gao, L.; Li, S.; Li, J.; Zhang, B. Edge-constrained Markov random field classification by integrating hyperspectral image with LiDAR data over urban areas. J. Appl. Remote Sens. 2014, 8, 085089. [Google Scholar] [CrossRef]
- Zhang, B.; Li, S.; Jia, X.; Gao, L.; Peng, M. Adaptive Markov random field approach for classification of hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 973–977. [Google Scholar] [CrossRef]
- Jimenez, L.O.; Landgrebe, D.A. Supervised classification in high-dimensional space: Geometrical, statistical, and asymptotical properties of multivariate data. IEEE Trans. Syst. Man Cybern. Part C 1998, 28, 39–54. [Google Scholar] [CrossRef]
- Martínez, P.; Gualtieri, J.; Aguilar, P.; Pérez, R.; Linaje, M.; Preciado, J.; Plaza, A. Hyperspectral Image Classification Using a Self-organizing Map. Available online: http://www.umbc.edu/rssipl/people/aplaza/Papers/Conferences/2001.AVIRIS.SOM.pdf (accessed on 1 June 2017).
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in spectral-spatial classification of hyperspectral images. Proc. IEEE 2013, 101, 652–675. [Google Scholar] [CrossRef]
- Raith, S.; Vogel, E.P.; Anees, N.; Keul, C.; Güth, J.F.; Edelhoff, D.; Fischer, H. Artificial Neural Networks as a powerful numerical tool to classify specific features of a tooth based on 3D scan data. Comput. Biol. Med. 2017, 80, 65–76. [Google Scholar] [CrossRef] [PubMed]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2017. [Google Scholar] [CrossRef]
- Pal, S.K.; Mitra, S. Multilayer perceptron, fuzzy sets, and classification. IEEE Trans. Neural Netw. 1992, 3, 683–697. [Google Scholar] [CrossRef] [PubMed]
- Duran, O.; Althoefer, K.; Seneviratne, L.D. Automated pipe defect detection and categorization using camera/laser-based profiler and artificial neural network. IEEE Trans. Autom. Sci. Eng. 2007, 4, 118–126. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Duran, O.; Petrou, M. A time-efficient clustering method for pure class selection. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium (IGARSS’05), Seoul, Korea, 29 July 2005; Volume 1. [Google Scholar] [CrossRef]
- Pérez-Hoyos, A.; Martínez, B.; García-Haro, F.J.; Moreno, Á.; Gilabert, M.A. Identification of ecosystem functional types from coarse resolution imagery using a self-organizing map approach: A case study for Spain. Remote Sens. 2014, 6, 11391–11419. [Google Scholar] [CrossRef]
- Penn, B.S. Using self-organizing maps to visualize high-dimensional data. Comput. Geosci. 2005, 31, 531–544. [Google Scholar] [CrossRef]
- Wei, Y.; Qiu, J.; Shi, P.; Lam, H.K. A new design of H-infinity piecewise filtering for discrete-time nonlinear time-varying delay systems via TS fuzzy affine models. IEEE Trans. Syst. Man Cybern. 2017. [Google Scholar] [CrossRef]
- Wei, Y.; Qiu, J.; Lam, H.K.; Wu, L. Approaches to TS fuzzy-affine-model-based reliable output feedback control for nonlinear Itô stochastic systems. IEEE Trans. Fuzzy Syst. 2016. [Google Scholar] [CrossRef]
- Lam, H.K.; Li, H.; Liu, H. Stability analysis and control synthesis for fuzzy-observer-based controller of nonlinear systems: A fuzzy-model-based control approach. IET Control Theory Appl. 2013, 7, 663–672. [Google Scholar] [CrossRef]
- Wei, Y.; Qiu, J.; Karimi, H.R.; Wang, M. Model reduction for continuous-time Markovian jump systems with incomplete statistics of mode information. Int. J. Syst. Sci. 2014, 45, 1496–1507. [Google Scholar] [CrossRef]
- Wang, H.; Shi, P.; Agarwal, R.K. Network-based event-triggered filtering for Markovian jump systems. Int. J. Control 2016, 89, 1096–1110. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Audebert, N.; Saux, B.L.; Lefèvre, S. Segment-before-Detect: Vehicle Detection and Classification through Semantic Segmentation of Aerial Images. Remote Sens. 2017, 9, 368. [Google Scholar] [CrossRef]
- Ammour, N.; Alhichri, H.; Bazi, Y.; Benjdira, B.; Alajlan, N.; Zuair, M. Deep Learning Approach for Car Detection in UAV Imagery. Remote Sens. 2017, 9, 312. [Google Scholar] [CrossRef]
- Bejiga, M.B.; Zeggada, A.; Nouffidj, A.; Melgani, F. A convolutional neural network approach for assisting avalanche search and rescue operations with uav imagery. Remote Sens. 2017, 9, 100. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L. Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2015), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Giorgio, L.; Frate, F.D. A Neural Network Approach for Pixel Unmixing in Hyperspectral Data; Earth Observation Laboratory- Tor Vergata University Via del Politecnico: Rome, Italy.
- Kumar, U.; Raja, K.S.; Mukhopadhyay, C.; Ramachandra, T.V. A Neural Network Based Hybrid Mixture Model to Extract Information from Nonlinear Mixed Pixels. Information 2012, 3, 420–441. [Google Scholar] [CrossRef]
- Giorgio, A.L.; Frate, F.D. Pixel Unmixing in Hyperspectral Data by Means of Neural Networks. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4163–4172. [Google Scholar]
- Wu, H.; Prasad, S. Convolutional Recurrent Neural Networks forHyperspectral Data Classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Cutler, M.E.J.; Lewis, H. Mapping Sub-Pixel Proportional Land Cover With AVHRR Imagery. Int. J. Remote Sens. 1997, 18, 917–935. [Google Scholar] [CrossRef]
- Somers, B.; Asner, G.P.; Tits, L.; Coppin, P. Endmember variability in spectral mixture analysis: A review. Remote Sens. Environ. 2011, 115, 1603–1616. [Google Scholar] [CrossRef]
- Somers, B.; Cools, K.; Delalieux, S.; Stuckens, J.; Van der Zande, D.; Verstraeten, W.W.; Coppin, P. Nonlinear hyperspectral mixture analysis for tree cover estimates in orchards. Remote Sens. Environ. 2009, 113, 1183–1193. [Google Scholar] [CrossRef]
- Heinz, D.C.; Chang, C.-I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Bilinear models for nonlinear unmixing of hyperspectral images. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Nascimento, J.M.; Dias, J.M.B. Does independent component analysis play a role in unmixing hyperspectral data? IEEE Trans. Geosci. Remote Sens. 2005, 43, 175–187. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Nonlinear unmixing of hyperspectral images using a generalized bilinear model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4153–4162. [Google Scholar] [CrossRef]
- Altmann, Y.; Pereyra, M.; McLaughlin, S. Bayesian nonlinear hyperspectral unmixing with spatial residual component analysis. IEEE Trans. Comput. Imaging 2015, 1, 174–185. [Google Scholar] [CrossRef]
- Sohn, Y.; McCoy, R.M. Mapping desert shrub rangeland using spectral unmixing and modeling spectral mixtures with TM data. Photogramm. Eng. Remote Sens. 1997, 63, 707–716. [Google Scholar]
- Tuzel, O.; Porikli, F.; Meer, P. Region covariance: A fast descriptor for detection and classification. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 589–600. [Google Scholar]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Charalambous, C. Conjugate gradient algorithm for efficient training of artificial neural networks. IEEE Proc. G 1992, 139, 301–310. [Google Scholar] [CrossRef]
- Saini, L.M.; Soni, M.K. Artificial neural network-based peak load forecasting using conjugate gradient methods. IEEE Trans. Power Syst. 2002, 17, 907–912. [Google Scholar] [CrossRef]
- Nabipour, M.; Keshavarz, P. Modeling surface tension of pure refrigerants using feed-forward back-propagation neural networks. Int. J. Refrig. 2017, 75, 217–227. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Yuan, Y. Deep-Learning-Based Classification for DTM Extraction from ALS Point Cloud. Remote Sens. 2016, 8, 730. [Google Scholar] [CrossRef]
- Zhu, F.; Wang, Y.; Fan, B.; Xiang, S.; Meng, G.; Pan, C. Spectral unmixing via data-guided sparsity. IEEE Trans. Image Process. 2014, 23, 5412–5427. [Google Scholar] [CrossRef] [PubMed]
- Duran, O.; Petrou, M. A time-efficient method for anomaly detection in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3894–3904. [Google Scholar] [CrossRef]




| SNR (dB) = 50 | ||||
|---|---|---|---|---|
| INDIVIDUAL METHODS | ||||
| PPNMM | 0.0206 | 0.0307 | 0.0371 | 0.0486 |
| GBM | 0.0207 | 0.0303 | 0.0346 | 0.0449 |
| VCA | 0.0521 | 0.0696 | 0.0777 | 0.0778 |
| FCLS | 0.0714 | 0.0916 | 0.0922 | 0.0924 |
| HYBRID METHODS | ||||
| VCA – PPNMM | 0.0117 | 0.0201 | 0.0143 | 0.0373 |
| VCA – GBM | 0.0189 | 0.0201 | 0.0158 | 0.0353 |
| FCLS – PPNMM | 0.0177 | 0.0179 | 0.0177 | 0.0340 |
| FCLS – GBM | 0.0193 | 0.0196 | 0.0199 | 0.0174 |
| SNR (dB) = 30 | ||||
| INDIVIDUAL METHODS | ||||
| PPNMM | 0.0696 | 0.0951 | 0.0914 | 0.0886 |
| GBM | 0.0965 | 0.1193 | 0.1405 | 0.1285 |
| VCA | 0.0597 | 0.0662 | 0.0886 | 0.0945 |
| FCLS | 0.0684 | 0.0747 | 0.0894 | 0.0911 |
| HYBRID METHODS | ||||
| VCA – PPNMM | 0.0390 | 0.0317 | 0.0421 | 0.0556 |
| VCA – GBM | 0.0591 | 0.0412 | 0.0579 | 0.0662 |
| FCLS – PPNMM | 0.0396 | 0.0320 | 0.0539 | 0.0645 |
| FCLS – GBM | 0.0866 | 0.0926 | 0.0990 | 0.1081 |
| SNR (dB) = 10 | ||||
| INDIVIDUAL METHODS | ||||
| PPNMM | 0.0907 | 0.1510 | 0.1640 | 0.1733 |
| GBM | 0.1106 | 0.1222 | 0.1334 | 0.1740 |
| VCA | 0.1289 | 0.1514 | 0.1257 | 0.1988 |
| FCLS | 0.1169 | 0.1702 | 0.1791 | 0.1763 |
| HYBRID METHODS | ||||
| VCA – PPNMM | 0.0401 | 0.0421 | 0.0736 | 0.0775 |
| VCA – GBM | 0.0704 | 0.0911 | 0.0813 | 0.0915 |
| FCLS – PPNMM | 0.0440 | 0.0508 | 0.0813 | 0.0814 |
| FCLS – GBM | 0.0917 | 0.0959 | 0.1099 | 0.1112 |
| WITHOUT SAD MIN. | SNR (dB) = 10 | SNR (dB) = 30 | SNR (dB) = 50 |
|---|---|---|---|
| INDIVIDUAL METHODS | |||
| PPNMM | 0.1503 | 0.0537 | 0.0179 |
| GBM | 0.1220 | 0.1274 | 0.0168 |
| VCA | 0.1090 | 0.1000 | 0.0952 |
| FCLS | 0.1670 | 0.1370 | 0.0997 |
| HYBRID METHODS | |||
| VCA – PPNMM | 0.0433 | 0.0392 | 0.0150 |
| VCA – GBM | 0.0854 | 0.0784 | 0.0163 |
| FCLS – PPNMM | 0.0434 | 0.0402 | 0.0143 |
| FCLS – GBM | 0.1180 | 0.1080 | 0.0161 |
| WITHOUT SAD MAX. | SNR (dB) = 10 | SNR (dB) = 30 | SNR (dB) = 50 |
| INDIVIDUAL METHODS | |||
| PPNMM | 0.0969 | 0.0876 | 0.0878 |
| GBM | 0.1002 | 0.0920 | 0.0741 |
| VCA | 0.1216 | 0.0791 | 0.0451 |
| FCLS | 0.2726 | 0.1073 | 0.0560 |
| HYBRID METHODS | |||
| VCA – PPNMM | 0.0584 | 0.0467 | 0.0251 |
| VCA – GBM | 0.0885 | 0.0731 | 0.0525 |
| FCLS – PPNMM | 0.0521 | 0.0467 | 0.0251 |
| FCLS – GBM | 0.1689 | 0.1000 | 0.0772 |
| WITHOUT COVARIANCE DISTANCE | SNR (dB) = 10 | SNR (dB) = 30 | SNR (dB) = 50 |
| INDIVIDUAL METHODS | |||
| PPNMM | 0.0940 | 0.0518 | 0.0173 |
| GBM | 0.1243 | 0.0921 | 0.0166 |
| VCA | 1.0488 | 0.0824 | 0.0590 |
| FCLS | 1.1673 | 0.0966 | 0.0680 |
| HYBRID METHODS | |||
| VCA – PPNMM | 0.0506 | 0.0340 | 0.0145 |
| VCA – GBM | 0.0902 | 0.0588 | 0.0163 |
| FCLS – PPNMM | 0.0506 | 0.0336 | 0.0145 |
| FCLS – GBM | 0.1231 | 0.0916 | 0.0161 |
| WITHOUT NONLINEARITY PARAMETER | SNR (dB) = 10 | SNR (dB) = 30 | SNR (dB) = 50 |
| INDIVIDUAL METHODS | |||
| PPNMM | 0.1447 | 0.0532 | 0.0183 |
| GBM | 0.1100 | 0.1039 | 0.0185 |
| VCA | 0.1251 | 0.0982 | 0.0865 |
| FCLS | 0.1852 | 0.1167 | 0.0927 |
| HYBRID METHODS | |||
| VCA – PPNMM | 0.0448 | 0.0432 | 0.0173 |
| VCA – GBM | 0.0856 | 0.0789 | 0.0178 |
| FCLS – PPNMM | 0.0448 | 0.0431 | 0.0171 |
| FCLS – GBM | 0.1236 | 0.1096 | 0.0137 |
| SNR (dB) = 50 | ||||
|---|---|---|---|---|
| INDIVIDUAL METHODS | ||||
| PPNMM | 0.0253 | 0.0276 | 0.0378 | 0.0418 |
| GBM | 0.0253 | 0.0276 | 0.0347 | 0.0383 |
| VCA | 0.0775 | 0.0612 | 0.0717 | 0.0719 |
| FCLS | 0.0891 | 0.0663 | 0.0877 | 0.0612 |
| HYBRID METHODS | ||||
| VCA – PPNMM | 0.0125 | 0.0127 | 0.0230 | 0.0285 |
| VCA – GBM | 0.0457 | 0.0164 | 0.0269 | 0.0317 |
| FCLS – PPNMM | 0.0217 | 0.0214 | 0.0236 | 0.0316 |
| FCLS – GBM | 0.0513 | 0.0627 | 0.0850 | 0.0981 |
| SNR (dB) = 30 | ||||
| INDIVIDUAL METHODS | ||||
| PPNMM | 0.1520 | 0.1759 | 0.1464 | 0.1353 |
| GBM | 0.1568 | 0.1442 | 0.1473 | 0.1337 |
| VCA | 0.1007 | 0.1195 | 0.0313 | 0.2767 |
| FCLS | 0.1072 | 0.1713 | 0.1344 | 0.1819 |
| HYBRID METHODS | ||||
| VCA – PPNMM | 0.0231 | 0.0223 | 0.0219 | 0.0268 |
| VCA – GBM | 0.0317 | 0.0360 | 0.0364 | 0.0370 |
| FCLS – PPNMM | 0.0308 | 0.0358 | 0.0458 | 0.0654 |
| FCLS – GBM | 0.0437 | 0.0787 | 0.0901 | 0.0956 |
| SNR (dB) = 10 | ||||
| INDIVIDUAL METHODS | ||||
| PPNMM | 0.1809 | 0.1816 | 0.1856 | 0.1883 |
| GBM | 0.1517 | 0.1506 | 0.1440 | 0.1481 |
| VCA | 0.1196 | 0.0612 | 0.0717 | 0.0717 |
| FCLS | 0.1072 | 0.0663 | 0.0877 | 0.0612 |
| HYBRID METHODS | ||||
| VCA – PPNMM | 0.0548 | 0.0564 | 0.0570 | 0.0584 |
| VCA – GBM | 0.0751 | 0.0940 | 0.0962 | 0.0961 |
| FCLS – PPNMM | 0.0714 | 0.0739 | 0.0740 | 0.0763 |
| FCLS – GBM | 0.0974 | 0.0981 | 0.0990 | 0.1170 |
| Raw Data | 7000 | 3000 | 1000 | 300 |
|---|---|---|---|---|
| VCA – PPNMM | 0.1417 | 0.1478 | 0.1405 | 0.1994 |
| VCA – GBM | 0.2079 | 0.2049 | 0.3087 | 0.3897 |
| FCLS – PPNMM | 0.1402 | 0.1402 | 0.1590 | 0.1663 |
| FCLS – GBM | 0.1399 | 0.1397 | 0.1483 | 0.1495 |
| WINDOW | ||||
| VCA – PPNMM | 0.1697 | 0.1607 | 0.1781 | 0.1763 |
| VCA – GBM | 0.2595 | 0.2454 | 0.2932 | 0.3350 |
| FCLS – PPNMM | 0.1765 | 0.1624 | 0.1783 | 0.1790 |
| FCLS – GBM | 0.2448 | 0.2448 | 0.3442 | 0.3642 |
| WINDOW | ||||
| VCA – PPNMM | 0.1712 | 0.1640 | 0.1736 | 0.1704 |
| VCA – GBM | 0.2488 | 0.2250 | 0.3117 | 0.3460 |
| FCLS – PPNMM | 0.1632 | 0.1659 | 0.1705 | 0.1722 |
| FCLS – GBM | 0.2647 | 0.2459 | 0.2488 | 0.2732 |
| Raw Data | 6317 | 3158 | 1000 | 300 |
|---|---|---|---|---|
| VCA – PPNMM | 0.0839 | 0.0841 | 0.0871 | 0.0979 |
| VCA – GBM | 0.0841 | 0.0846 | 0.0879 | 0.0939 |
| FCLS – PPNMM | 0.1229 | 0.1230 | 0.1258 | 0.1308 |
| FCLS – GBM | 0.1614 | 0.1615 | 0.1674 | 0.1696 |
| WINDOW | ||||
| VCA – PPNMM | 0.0888 | 0.0885 | 0.0902 | 0.0973 |
| VCA – GBM | 0.0975 | 0.1040 | 0.1079 | 0.1112 |
| FCLS – PPNMM | 0.1148 | 0.1151 | 0.1197 | 0.1292 |
| FCLS – GBM | 0.1615 | 0.1617 | 0.1657 | 0.1710 |
| WINDOW | ||||
| VCA – PPNMM | 0.0904 | 0.0905 | 0.0949 | 0.0994 |
| VCA – GBM | 0.0945 | 0.0945 | 0.1061 | 0.1106 |
| FCLS – PPNMM | 0.1154 | 0.1197 | 0.1216 | 0.1245 |
| FCLS – GBM | 0.1616 | 0.1616 | 0.1636 | 0.1658 |
| 7000 Samples | 3000 Samples | |||||||
|---|---|---|---|---|---|---|---|---|
| Raw Data | VCA–PPNMM | VCA–GBM | FCLS–PPNMM | FCLS—GBM | VCA–PPNMM | VCA–GBM | FCLS–PPNMM | FCLS—GBM |
| TRAIN | 0.0905 | 0.1025 | 0.1184 | 0.1084 | 0.0953 | 0.0859 | 0.1085 | 0.1200 |
| VALIDATION | 0.0777 | 0.0780 | 0.1008 | 0.0980 | 0.0809 | 0.0866 | 0.1006 | 0.0995 |
| TEST | 0.0751 | 0.0797 | 0.1012 | 0.1000 | 0.0811 | 0.0832 | 0.1013 | 0.0906 |
| Window | ||||||||
| TRAIN | 0.0967 | 0.1054 | 0.0981 | 0.1268 | 0.0473 | 0.0533 | 0.0991 | 0.1229 |
| VALIDATION | 0.0524 | 0.0505 | 0.1274 | 0.1138 | 0.0465 | 0.0549 | 0.0923 | 0.1125 |
| TEST | 0.0486 | 0.0614 | 0.1276 | 0.1147 | 0.0454 | 0.0506 | 0.0914 | 0.1135 |
| Window | ||||||||
| TRAIN | 0.0906 | 0.1523 | 0.0941 | 0.1171 | 0.0393 | 0.1531 | 0.0997 | 0.1146 |
| VALIDATION | 0.1696 | 0.0704 | 0.0911 | 0.0954 | 0.0351 | 0.0530 | 0.0918 | 0.1117 |
| TEST | 0.1608 | 0.0382 | 0.0938 | 0.0944 | 0.0354 | 0.0445 | 0.0920 | 0.1121 |
| 6317 Samples | 3158 Samples | |||||||
|---|---|---|---|---|---|---|---|---|
| Raw Data | VCA–PPNMM | VCA–GBM | FCLS–PPNMM | FCLS—GBM | VCA–PPNMM | VCA–GBM | FCLS–PPNMM | FCLS—GBM |
| TRAIN | 0.0255 | 0.0741 | 0.1058 | 0.1585 | 0.0280 | 0.0732 | 0.1182 | 0.1167 |
| VALIDATION | 0.0466 | 0.0101 | 0.0792 | 0.0098 | 0.0553 | 0.1026 | 0.0733 | 0.1311 |
| TEST | 0.0494 | 0.0105 | 0.0762 | 0.0098 | 0.0569 | 0.1053 | 0.0719 | 0.1311 |
| Window | ||||||||
| TRAIN | 0.0726 | 0.0842 | 0.1046 | 0.1581 | 0.0722 | 0.0897 | 0.1021 | 0.1161 |
| VALIDATION | 0.0530 | 0.0100 | 0.0748 | 0.0098 | 0.0588 | 0.0692 | 0.0703 | 0.1309 |
| TEST | 0.0533 | 0.0100 | 0.0740 | 0.0098 | 0.0594 | 0.0696 | 0.0706 | 0.1309 |
| Window | ||||||||
| TRAIN | 0.0836 | 0.0842 | 0.1046 | 0.1581 | 0.0822 | 0.0843 | 0.1007 | 0.1160 |
| VALIDATION | 0.0536 | 0.0100 | 0.0748 | 0.0098 | 0.0569 | 0.0654 | 0.0710 | 0.1308 |
| TEST | 0.0545 | 0.0100 | 0.0740 | 0.0098 | 0.0569 | 0.0640 | 0.0712 | 0.1308 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.M.; Duran, O.; Zweiri, Y.; Smith, M. Hybrid Spectral Unmixing: Using Artificial Neural Networks for Linear/Non-Linear Switching. Remote Sens. 2017, 9, 775. https://doi.org/10.3390/rs9080775
Ahmed AM, Duran O, Zweiri Y, Smith M. Hybrid Spectral Unmixing: Using Artificial Neural Networks for Linear/Non-Linear Switching. Remote Sensing. 2017; 9(8):775. https://doi.org/10.3390/rs9080775
Chicago/Turabian StyleAhmed, Asmau M., Olga Duran, Yahya Zweiri, and Mike Smith. 2017. "Hybrid Spectral Unmixing: Using Artificial Neural Networks for Linear/Non-Linear Switching" Remote Sensing 9, no. 8: 775. https://doi.org/10.3390/rs9080775
APA StyleAhmed, A. M., Duran, O., Zweiri, Y., & Smith, M. (2017). Hybrid Spectral Unmixing: Using Artificial Neural Networks for Linear/Non-Linear Switching. Remote Sensing, 9(8), 775. https://doi.org/10.3390/rs9080775






