Modelling Shadow Using 3D Tree Models in High Spatial and Temporal Resolution
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Scanned Tree and Its Location
2.2. Input Data
2.3. Pre-Calculations
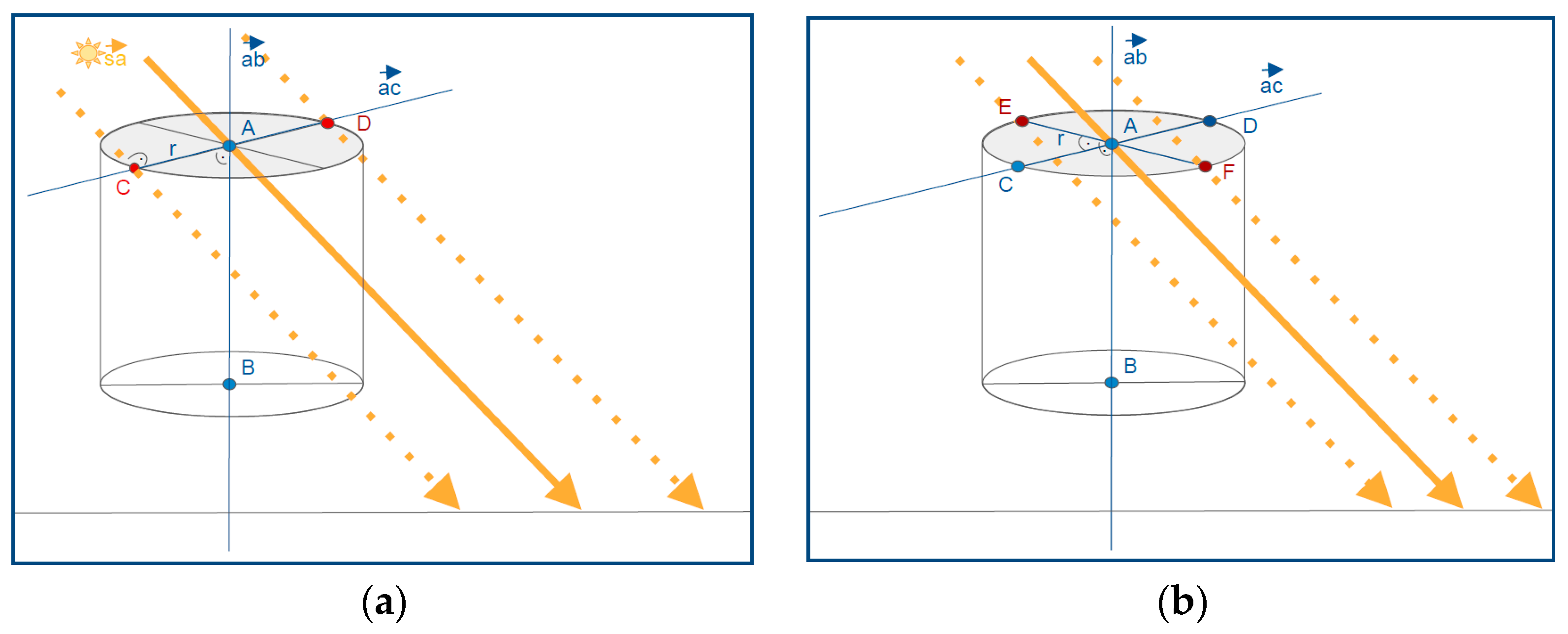
2.4. Computing Vertices of Cylinders as a Base for Tree Shadow Projections
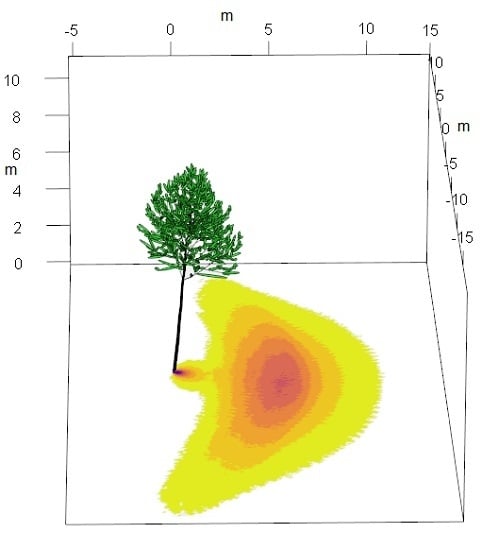
2.5. Projecting the Cylinder Shadow onto the Ground and Calculating Energy Loss Due to Shading
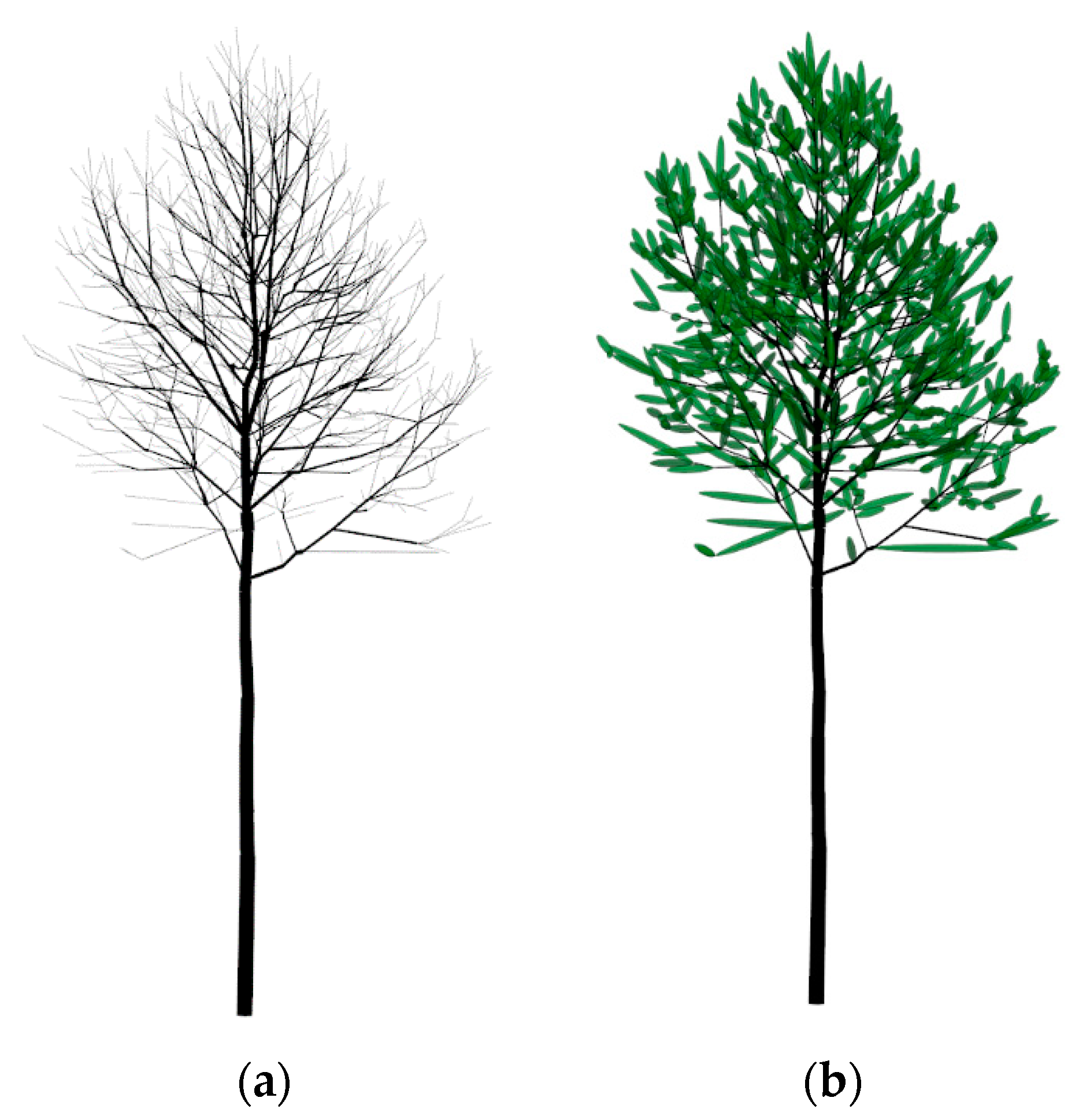
2.6. Computing Ellipsoids to Simulate Leaves
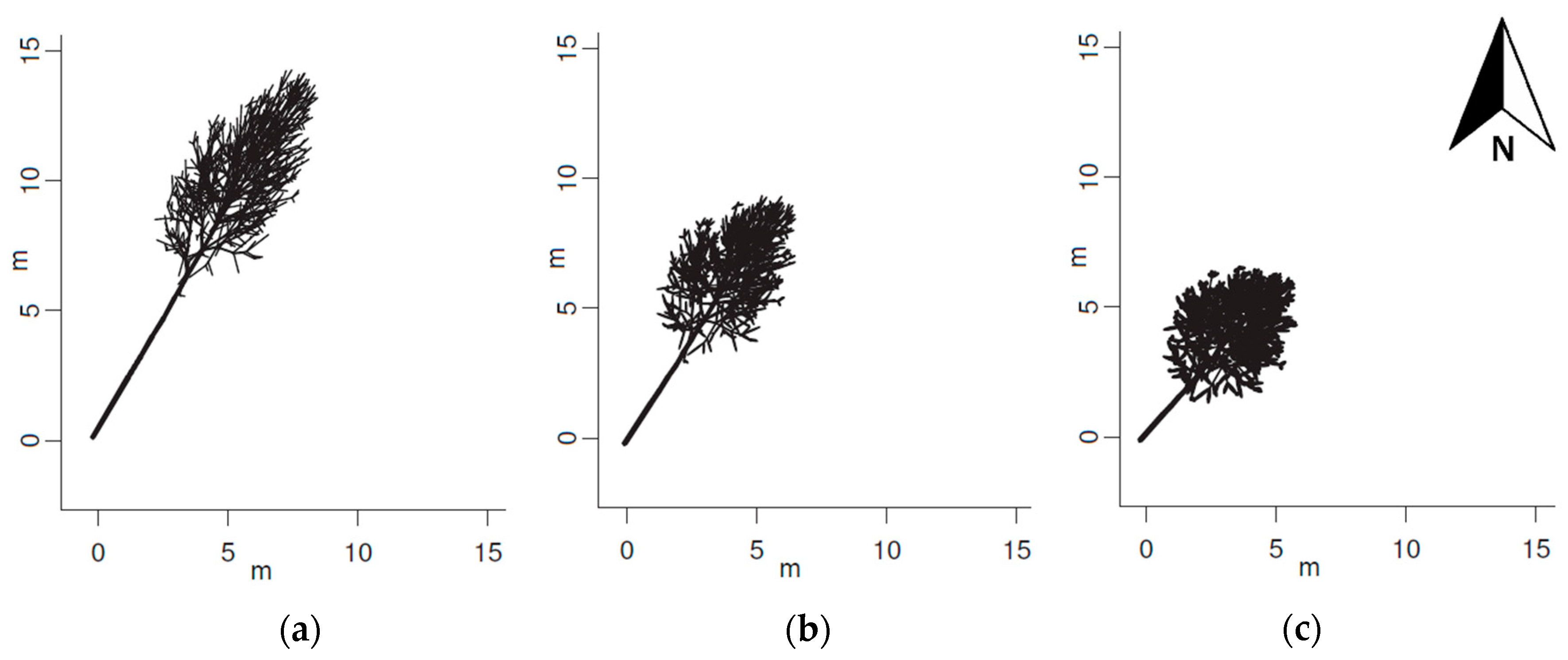
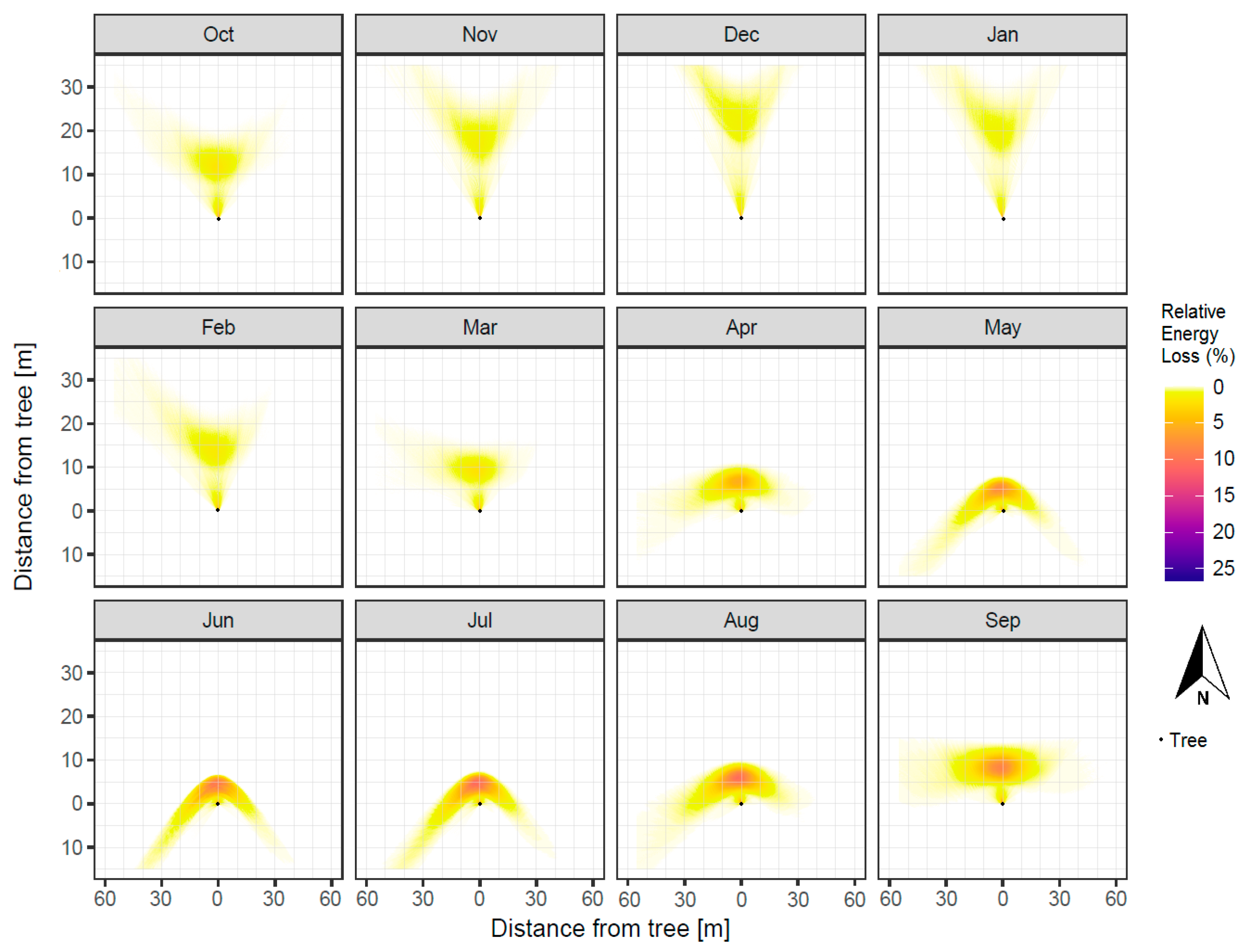
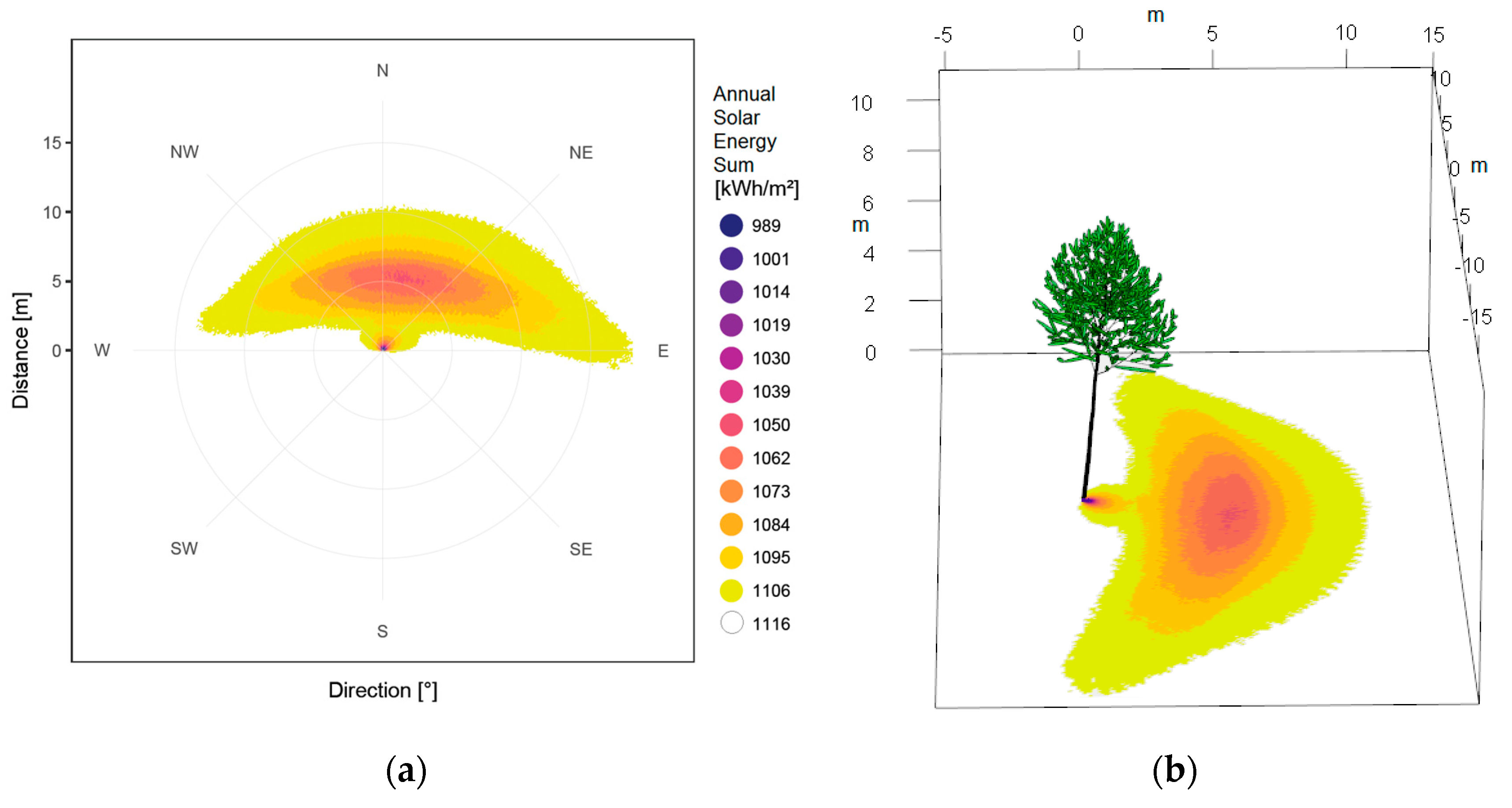
3. Results
4. Discussion
5. Conclusions
6. Outlook
- Improvement of the leaf simulations. Leaf parameters vary between tree species, within the tree crown and throughout the growing season [15,16,17]. Thus, to generate realistic shadow projections of tree crowns, it is crucial to simulate leaves as realistically as possible. At present, our model simulates leaves by adding a single ellipsoid to the end of branches of a radius of less than 0.5 cm, and the ellipsoids increase in their radius each month to simulate leaf growth. We will replace these ellipsoids with more realistic leaf-like polygons, taking also their spatial distribution within tree crowns into account.
- Validation of the results generated by the model by comparing them with on-site light measurements. In case of discrepancies, the model needs to be adapted accordingly.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Editors of Agroforestry Systems. What is Agroforestry? Agrofor. Syst. 1982, 1, 7–12. [Google Scholar] [CrossRef]
- Nair, P.K.R. An Introduction to Agroforestry; Kluwer Academic Publishers (in cooperation with the International Centre for Research in Agroforestry): Dordrecht, The Netherlands, 1993. [Google Scholar]
- Waggoner, P.E.; Pack, A.B.; Reifsnyder, W.E. The Climate of Shade, A Tobacco Tent and A Forest Stand Compared to Open Fields. Available online: http://www.ct.gov/caes/lib/caes/documents/publications/bulletins/b626.pdf (accessed on 24 May 2017).
- Muschler, R.G. Shade improves coffee quality in a sub-optimal coffee-zone of Costa Rica. Agrofor. Syst. 2001, 51, 131–139. [Google Scholar] [CrossRef]
- Stathers, R.J.; Bailey, W.G. Energy receipt and partitioning in a ginseng shade canopy and mulch environment. Agric. For. Meteorol. 1986, 37, 1–14. [Google Scholar] [CrossRef]
- Dupraz, C.; Liagre, F. Agroforesterie. In Des Arbres et des Cultures, 2nd ed.; Éditions France Agricole: Paris, France, 2011. [Google Scholar]
- Talbot, G.; Dupraz, C. Simple models for light competition within agroforestry discontinuous tree stands: Are leaf clumpiness and light interception by woody parts relevant factors? Agrofor. Syst. 2012, 84, 101–116. [Google Scholar] [CrossRef]
- Oker-Blom, P. Photosynthetic radiation regime and canopy structure in modeled forest stands. Acta For. Fenn. 1986, 197, 1–44. [Google Scholar] [CrossRef]
- Sinoquet, H.; Sonohat, G.; Phattaralerphong, J.; Godin, C. Foliage randomness and light interception in 3-D digitized trees: An analysis from multiscale discretization of the canopy. Plant Cell Environ. 2005, 28, 1158–1170. [Google Scholar] [CrossRef]
- Cifuentes, R.; Van der Zande, D.; Salas, C.; Tits, L.; Farifteh, J.; Coppin, P. Modeling 3D canopy structure and transmitted PAR using terrestrial LiDAR. Can. J. Remote Sens. 2017, 43, 124–139. [Google Scholar] [CrossRef]
- Artru, S.; Garré, S.; Dupraz, C.; Hiel, M.-P.; Blitz-Frayret, C.; Lassois, L. Impact of spatio-temporal shade dynamics on wheat growth and yield, perspectives for temperate agroforestry. Eur. J. Agron. 2017, 82, 60–70. [Google Scholar] [CrossRef]
- Stadt, K.J.; Lieffers, V.J. MIXLIGHT: A flexible light transmission model for mixed-species forest stands. Agric. For. Meteorol. 2000, 102, 235–252. [Google Scholar] [CrossRef]
- Oshio, H.; Asawa, T. Estimating the solar transmittance of urban trees using airborne LiDAR and radiative transfer simulation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5483–5492. [Google Scholar] [CrossRef]
- Dauzat, J.; Madelaine-Antin, C.; Heurtebize, J.; Lavalley, C.; Vincent, G. How Much Commercial Timber in Your Plot, How Much Carbon Sequestrated in The Trees, How Much Light Available for Undercrops? Terrestrial Lidar is The Right Technology for Addressing These Questions. Available online: http://agritrop.cirad.fr/580646/1/ID580646.pdf (accessed on 24 May 2017).
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Muys, B.; Coppin, P. Assessment of light environment variability in broadleaved forest canopies using terrestrial laser scanning. Remote Sens. 2010, 2, 1564–1574. [Google Scholar] [CrossRef]
- Grau, E.; Durrieu, S.; Fournier, R.; Gastellu-Etchegorry, J.P.; Yin, T. Estimation of 3D vegetation density with Terrestrial Laser Scanning data using voxels. A sensitivity analysis of influencing parameters. Remote Sens. Environ. 2017, 191, 373–388. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.L.; Fournier, R.A.; Côté, J.F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial LiDAR measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Hackenberg, J.; Morhart, C.; Sheppard, J.; Spiecker, H.; Disney, M. Highly accurate tree models derived from terrestrial laser scan data: A method description. Forests 2014, 5, 1069–1105. [Google Scholar] [CrossRef]
- Morhart, C.; Sheppard, J.P.; Schuler, J.K.; Spiecker, H. Above-ground woody biomass allocation and within tree carbon and nutrient distribution of wild cherry (Prunus avium L.)—A case study. For. Ecosyst. 2016, 3, 1–15. [Google Scholar] [CrossRef]
- Hackenberg, J.; Spiecker, H.; Calders, K.; Disney, M.; Raumonen, P. SimpleTree—An efficient open source tool to build tree models from TLS clouds. Forests 2015, 6, 4245–4294. [Google Scholar] [CrossRef]
- Corripio, J.G. Insol: Solar Radiation. Available online: http://www.meteoexploration.com/R/insol/ (accessed on 24 May 2017).
- Deutscher Wetterdienst (DWD). CDC (Climate Data Center): Hourly Station Observations of Solar Irradiation. Available online: ftp://ftp-cdc.dwd.de/pub/CDC/observations_germany/climate/hourly/solar (accessed on 9 June 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation or Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Zhao, W.; Qualls, R.J.; Berliner, P.R. Modeling of the short wave radiation distribution in an agroforestry system. Agric. For. Meteorol. 2003, 118, 185–206. [Google Scholar] [CrossRef]
- Meloni, S.; Sinoquet, H. Assessment of the spatial distribution of light transmitted below young trees in an agroforestry system. Ann. For. Sci. 1997, 54, 313–333. [Google Scholar] [CrossRef]
- Santos, T.; Gomes, N.; Freire, S.; Brito, M.C.; Santos, L.; Tenedório, J.A. Applications of solar mapping in the urban environment. Appl. Geogr. 2014, 51, 48–57. [Google Scholar] [CrossRef]
- Li, T.; Yang, Q. Advantages of diffuse light for horticultural production and perspectives for further research. Front. Plant Sci. 2015, 6, 704. [Google Scholar] [CrossRef] [PubMed]
- Freitas, S.; Catita, C.; Redweik, P.; Brito, M.C. Modelling solar potential in the urban environment: State-of-the-art review. Renew. Sustain. Energy Rev. 2015, 41, 915–931. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosskopf, E.; Morhart, C.; Nahm, M. Modelling Shadow Using 3D Tree Models in High Spatial and Temporal Resolution. Remote Sens. 2017, 9, 719. https://doi.org/10.3390/rs9070719
Rosskopf E, Morhart C, Nahm M. Modelling Shadow Using 3D Tree Models in High Spatial and Temporal Resolution. Remote Sensing. 2017; 9(7):719. https://doi.org/10.3390/rs9070719
Chicago/Turabian StyleRosskopf, Elena, Christopher Morhart, and Michael Nahm. 2017. "Modelling Shadow Using 3D Tree Models in High Spatial and Temporal Resolution" Remote Sensing 9, no. 7: 719. https://doi.org/10.3390/rs9070719
APA StyleRosskopf, E., Morhart, C., & Nahm, M. (2017). Modelling Shadow Using 3D Tree Models in High Spatial and Temporal Resolution. Remote Sensing, 9(7), 719. https://doi.org/10.3390/rs9070719