2.1. Field Data Collection
The accuracy and precision of the diameter measurements executed on PPC was assessed using 18 loblolly pines (
Pinus taeda Lindl.) from west central Louisiana (
Figure 1a,b). The trees were chosen to describe stands that are ready for a silvicultural prescription (
Figure 1c) (i.e., a thinning or regeneration harvest), and mirror other studies focused on taper modeling [
36,
37,
38]. The selected trees were positioned in the dominant and codominant crown classes, which according to Nyland [
39] receive unobstructed light from above and at least one side (
Figure 1d). Trees located in the upper crown classes (i.e., dominant and codominant) are the focus of active forest management, as they are not only the most valuable trees but also the ones that define the forest stand, and consequently, the ecosystem’s dynamics [
40]. The trees were scheduled for either the first thin (i.e., mechanical thinning) or for final cut (i.e., clearcut). The average d
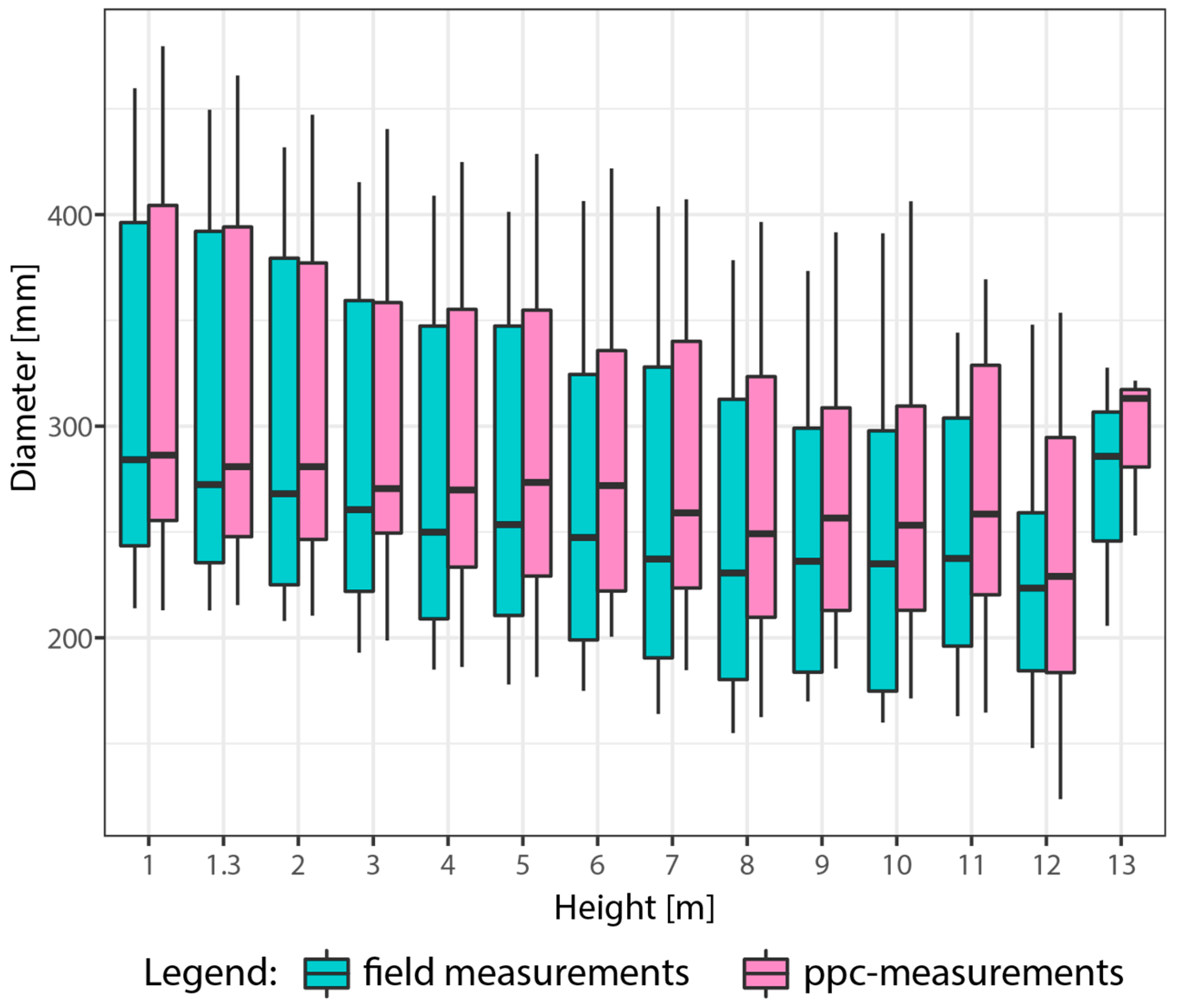
1.3 was on average 306.1 mm (variance 68.5), ranging from 213.0 mm to 449.6 mm. The total height (
H) varied from 15.9 m to 26.8 m, with an average of 22.2 m and a variance of 12.8. The trees grew on productive sites, with site indices ≥60 at base age 25. Each tree was photographed with a Nikon D3200 (i.e., a complementary metal–oxide–semiconductor sensor of 23.2 mm × 15.4 mm) equipped with a Nikkor AF-S DX VR 18–55 mm zoom lens (aperture 3.5–5.6). To capture as much as possible from the tree, the images were acquired at the focal length of 18 mm. For calibration, each tree had the d
1.3 painted circularly, and on opposite sides of the d
1.3 two metal rods of 304.8 mm (i.e., 1 foot) were freely hanged. Shortly after the images were captured, the trees were felled and the diameter along the stem was measured every meter with a Spencer D-tape starting from d
1.3, which was marked at 1.3 m. The accuracy of measurements was 1 mm for diameters and 10 mm for lengths along the stem (i.e., height). To verify the total length after the tree was felled, the total height was extracted from lidar data. The lidar flight scanning the area was executed in March 2012, at most four months before the trees were photographed and cut. To accommodate for the growth between flight time and field measurements, we considered that trees could have increased their height with at most 1 m. The point density was on average 30 points/m
2.
2.2. Photorammetric Point Cloud Generation and Diameter Measurements
The PPC were generated using SfM implemented in Agisoft PhotoScan ver 1.2 [
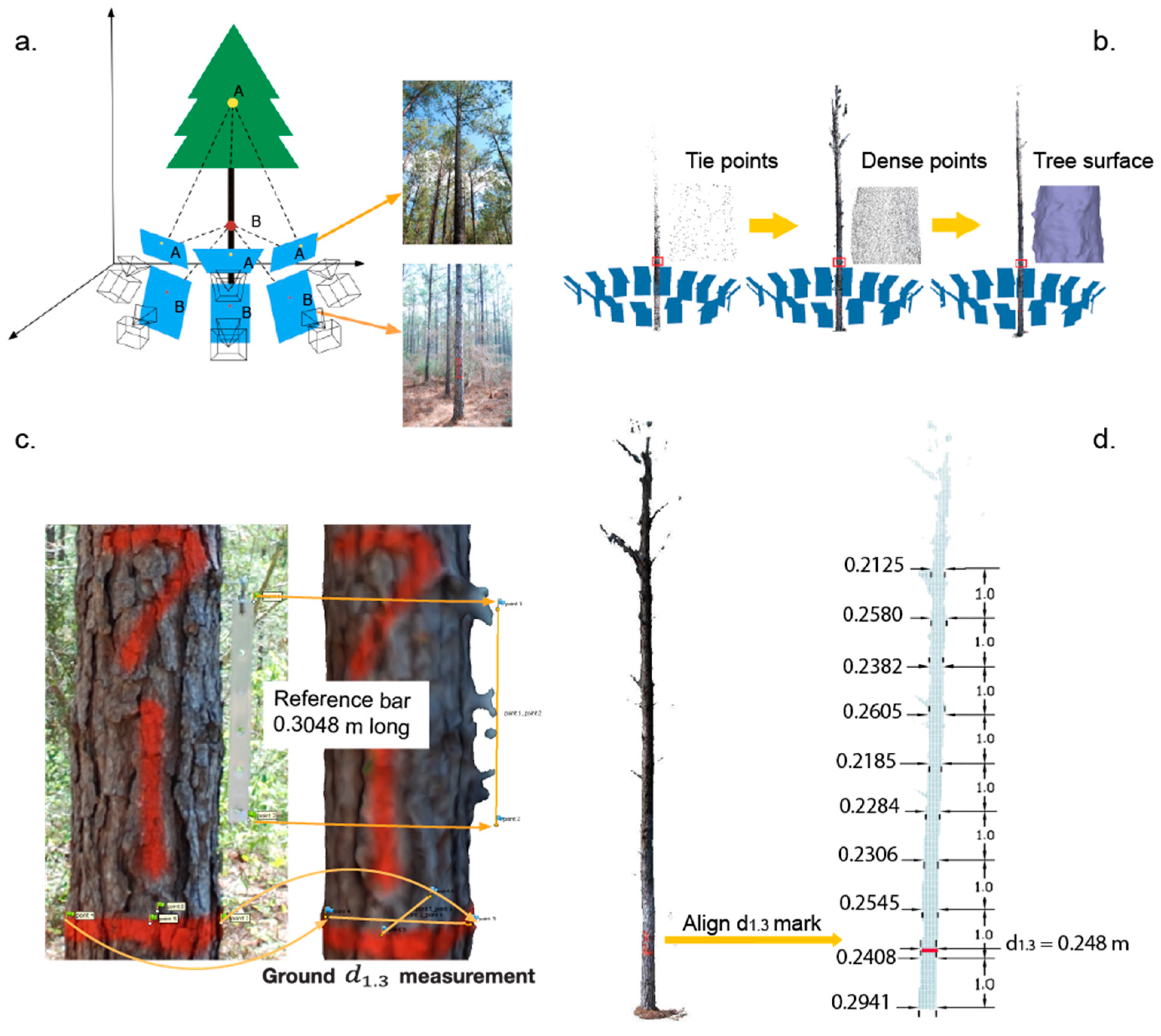
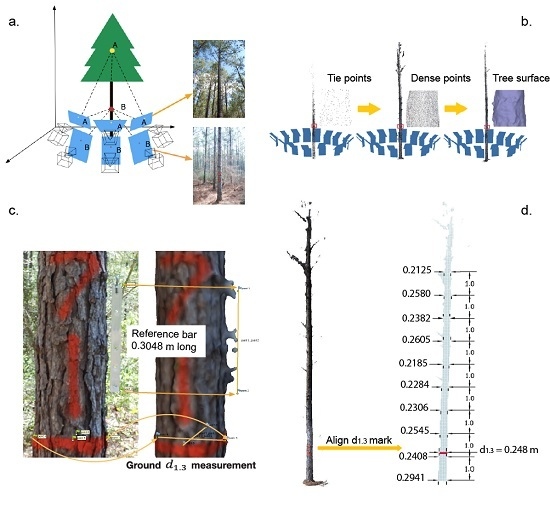
30]. Tree reconstruction and stem diameter measurements from the PPC were executed in four steps (
Figure 2a–d): (1) photo alignment, (2) build the point cloud, (3) scale the point cloud, and (4) measure diameter along the stem. The crucial step of SfM is concerned with the alignment of images, which if not completed properly will render an unusable PPC. Depending on computational power (i.e., the microprocessor), the amount of detail existing inside the image (i.e., the number of pixels), and the time available for processing the alignment can be executed in a few seconds or a few hours. In Agisoft, there are four parameters determining the time and quality of photo alignment: accuracy of camera position, matching detected features across images, the number of key points (i.e., image specific feature points that can represent same entities in multiple images), and tie points (i.e., image specific points used for matching images). Accurate camera locations are obtained when original images are used unaltered, which in Agisoft is coded as “high” [
41]. However, this option is time-consuming; therefore, a lower accuracy can be used [
42], such as medium, which downscales each side of the image by a factor of 2. Liang et al. [
42] obtained good results by a low alignment of photos with a resolution of 5472 × 3648 pixels, which employed only
of the information recorded (i.e., 1368 × 912). In our study, the image resolution was 3872 × 2592 pixels, and we aligned the photos by downscaling the original images by half (i.e., 1936 × 1296). Through experimentation, the maximum number of key points was set to 100,000 and the number of tie-points to 60,000.
Photos were captured around the trees in pairs to cover the lower and higher portions of the stem (
Figure 2a). Each pair overlapped ≥50%, to ensure sufficient common features for successful photo alignment. Georeference provides auxiliary information that helps camera positioning. However, by operating below the canopy no reliable GPS coordinates were acquired; therefore, the photos were aligned by relying only on the presence of the same features on multiple images. At least 10,000 tie-points/image were used for photo alignment and camera positioning.
The second step occurs after photos alignment, and consists in a densification of the tie-points (
Figure 2b). For each tree, the final PPC was created by downscaling the images by a factor of 2, which produced enough points for precise measurements without sacrificing processing time. All trees were described with a PPC of at least 600,000 points (the maximum was approximately 2 million), at least 25,000 points/m
2. To ensure precise measurements, we reconstructed the surface of the trunk with at least 500,000 faces (
Figure 2b). The faces were built with a ratio of 1:5 to the number of points. Compared with previous studies of image-based forest inventories [
34,
35,
42], the selected parameters for SfM in Agisoft (
Table 1) were either similar or provided superior solutions.
Because the images were not georeferenced and no ground control points were present, the PPC is in relative and not absolute units. Therefore, to measure diameters, the PPC and the associated surface had to be scaled. To minimize the errors, scaling was implemented using measurements executed on two perpendicular planes. On the horizontal plane, the ground measured d
1.3 was assigned to the corresponding segment from the PPC. The scale on the vertical plane was carried out by allocating the known length of the metal bar (i.e., 304.8 mm) to the distance between the points delineating the bar inside the PPC (
Figure 2c). After the length of the metal bar was introduced, the d
1.3 on two approximately perpendicular diameters was entered. Based on the tree values, Agisoft computes the scaling error by subtracting the estimated value from the inputted value [
30]. If the scaling error was larger than 5% of the field measured d
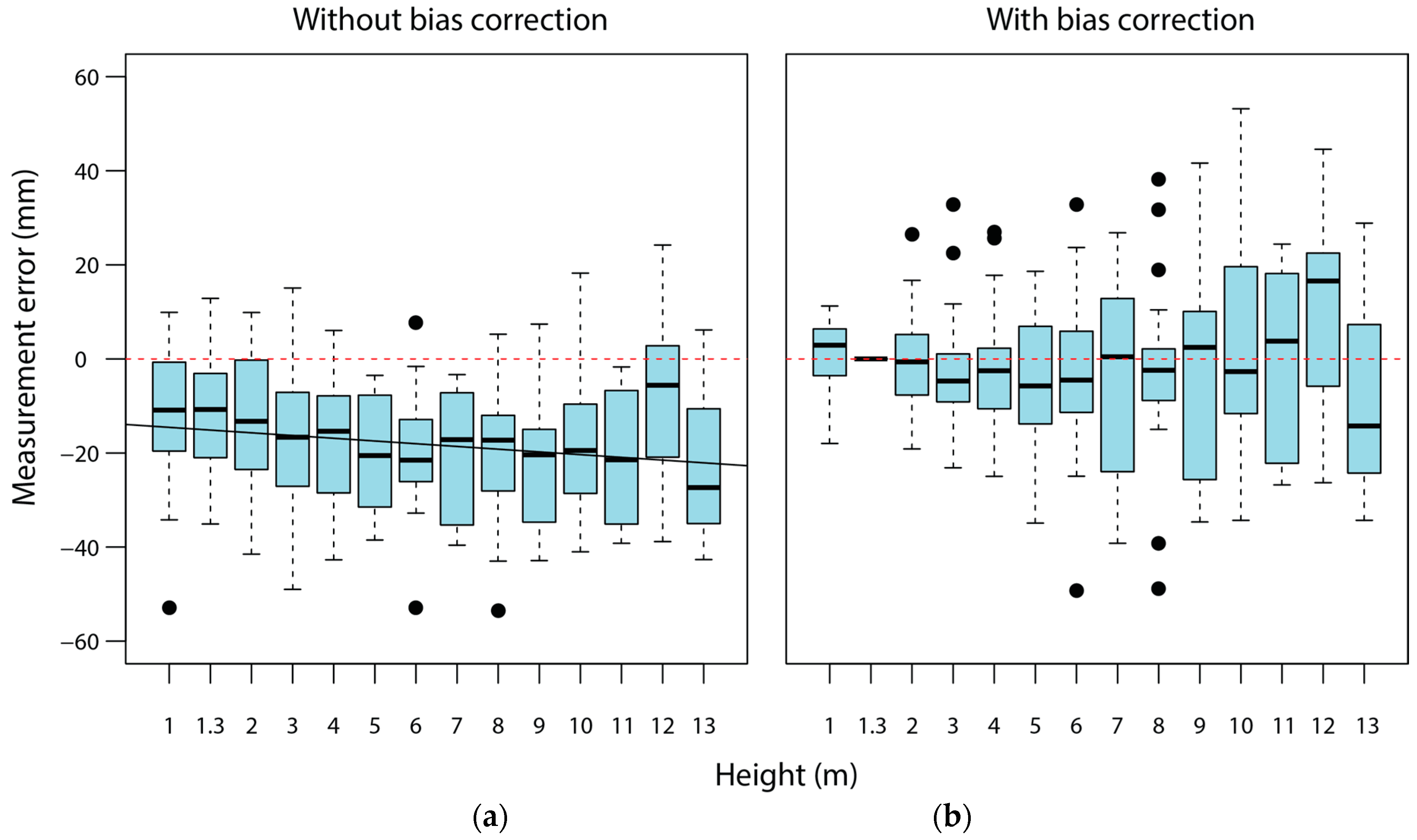
1.3, then the two diameters were re-measured on different positions. Depending on the size of the tree, the root mean square of the error ranged from 6.9 mm to 22.1 mm. Considering that the relationship among points inside the PPC are correct (i.e., are similar to reality) and unchanged, the maximum error that is expected for any linear measurement is 22.1 mm. Scaling is one of the three main sources of errors when PPC are used for actual measurements, and usually increases the magnitude of the investigated attributes with at least one order of magnitude (in our case three orders, from 1 to 1000).
Current guidelines consider field measurements accurate if the difference between the actual and measured d
1.3 is <5% [
43]. The average d
1.3 measured in the field is 306 mm. Because the calibrating metal bar was 304.8 mm (i.e., close to the d
1.3 of measured trees), we considered that a vertical error of 5% is also admissible, even when field measurements for heights accept errors of <10% [
43]. Therefore, the accepted total error for accurate field measurements is 21.6 mm (i.e.,
). For consistency, a similar value could have been used for PPC accuracy, but we decided to tighten the requirements. Consequently, we considered that scaling will have a limited impact on measurements if the total error (i.e., horizontal and vertical) is <10 mm (less than half of the field accepted accuracy).
The last step consists in measuring the diameters every meter along the stem (
Figure 2d), which was executed in AutoCAD Civil 3D [
44]. The second source of PPC measurement error is matching the ground diameters with PPC-estimated diameters. The matching can be implemented in two ways: (1) identify d
1.3 as the middle of the colored band marking the d
1.3 in the PPC, then measure all diameters starting from the identified d
1.3 (i.e., 1.3 m), or (2) identify the ground in the PPC, then measure the diameters with respect to the ground. Both ways offer a check, as either the ground should be at a height (length) of 0 (i.e., former), or d
1.3 should fall inside the colored band (i.e., later). Even when the difference between the d
1.3 identified using the two ways should be minor, its propagation could have a significant impact, particularly for the upper section of the stem. Therefore, diameters were measured in both ways.
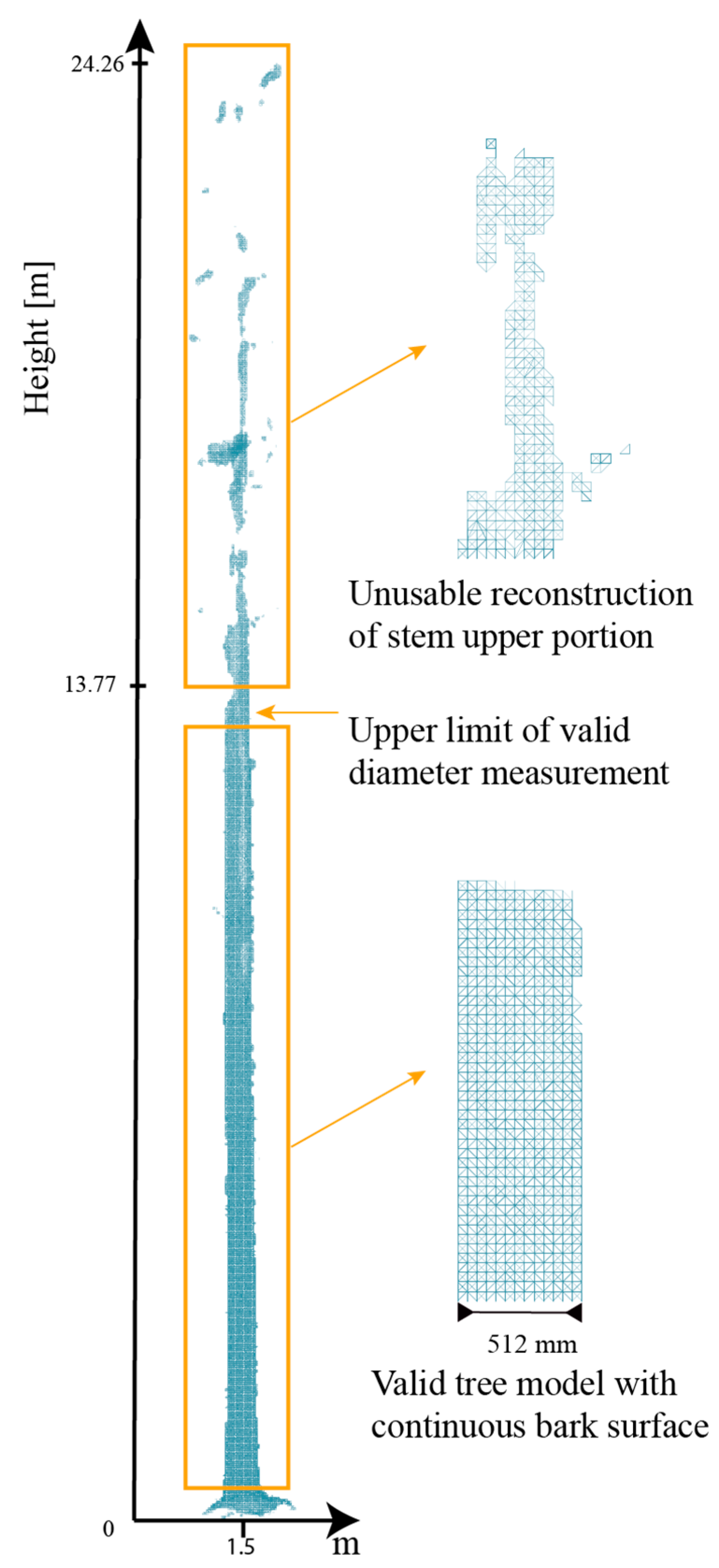
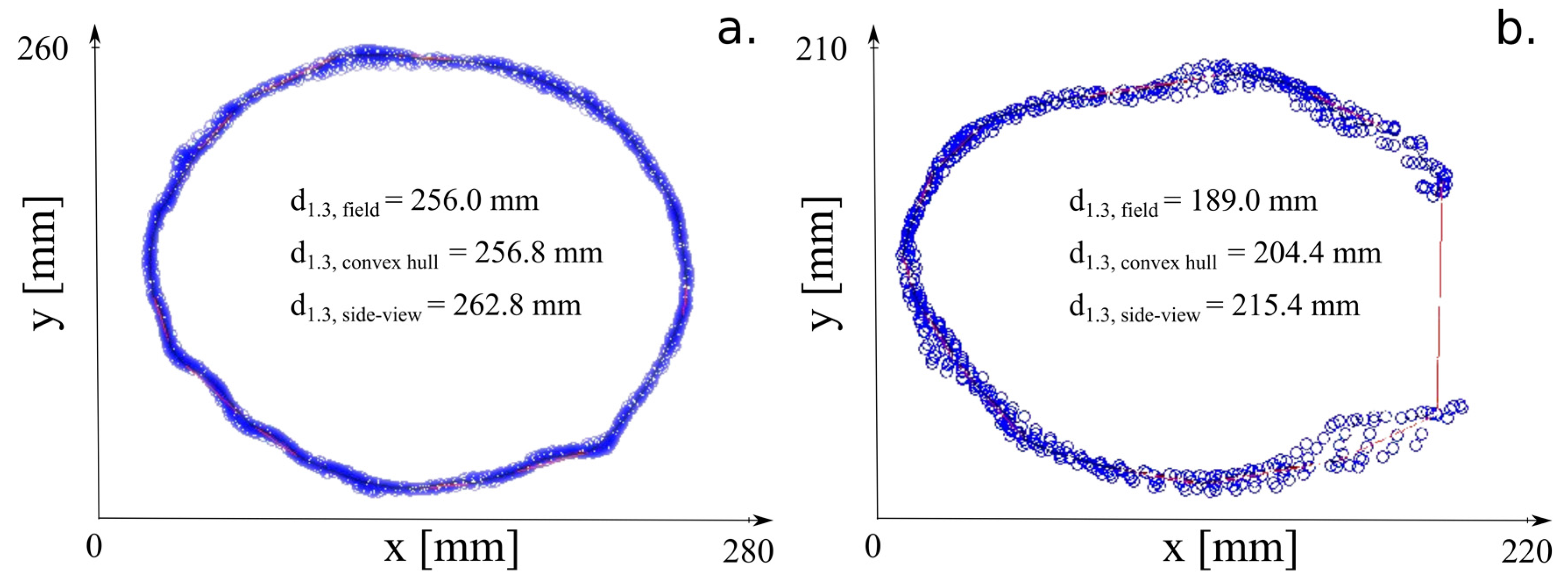
In AutoCAD, the diameters were measured on a plane perpendicular to the axis of the tree. The diameters were measured in two ways: one mirroring the field procedures for taper estimation from the ground (i.e., side view of the stem), and one mirroring the approach of You et al. [
16] (i.e., top view or circumference-based). The side measurement was acquired by averaging four diameters obtained by rotating the stem by approximately 90°. The circumferential measurement was obtained in four steps: (1) section the stem at levels corresponding to the ground measured diameters, (2) eliminate branches and knots, (3) estimate the perimeter with the convex hull algorithm [
45], and (4) compute the diameter by dividing the perimeter by pi. While side measurements depend only on the proper identification of heights on the stem, the circumferential view requires also a minimum number of points for accurate estimations. The smallest number of points evenly distributed along the circumference that estimates pi with 99.9% accuracy is 28. In reality, the points are not uniformly distributed, particularly at larger heights; therefore, we selected based on trial and errors the value 100 for the minimum number of points. To ensure that 100 points are attained, the stem was cross-sectioned not by a plane (i.e., not width) but by two parallel planes, 10 cm apart. The points between the planes were used for diameter estimation. The distance between planes of 10 cm was selected to ensure that 100 points are included in the cross-section, and that the frustum of the stem had virtually no taper (we assumed a constant diameter for any 10 cm along the stem under the canopy). Other studies used smaller distances between the planes (i.e., 5 cm by Maas et al. [
46] or 1 cm by You et al. [
16]), but they were focused on the lower portion of the stem (≤4 m) where enough points existed for constructing the cross-section of the stem. This study focused on the merchantable portion of the stem (i.e., below canopy), which considered larger heights where fewer points exist; therefore, a larger distance was used. The convex hull algorithm was implemented in Matlab version R2017a [
47]. The surfaces generated from PPC (i.e., Agisoft mesh or convex hull), on which the measurements are executed, describes the tree by its outer shape. Therefore, values larger than ground measured values are expected. Measurements on the surface are the third source of error, and probably the largest one. Because the PPC-based diameters likely overestimate the actual diameters, biased estimates are likely.
2.3. Assessment of Measurements and Bias Correction
The main statistics used to assess the accuracy of the PPC-based diameter measurements were the difference between the ground diameter measured at height
h (i.e.,
diameter@h field) and its correspondent from AutoCAD (i.e.,
diameter@h PPC):
Error analysis is necessary not only because overestimates are expected from PPC-based measurements, but also because estimates from SfM could be biased [
48]. Bias is assessed with three statistics, similar to other studies [
49,
50,
51,
52]:
where
errori,h is the PPC-based error at height
h for tree
i that has diameter measured to maximum height
Hi, and
n is the number of trees. It should be noticed that
Hi being an integer number acts as a count, besides being a linear measurement.
If possible, bias would be corrected using a linear function, as it is more robust and parsimonious than nonlinear approaches [
53,
54]. For practicality, the proposed linear model should include variables easy to estimate accurately, either in the field (e.g., d
1.3 or total height) or during processing (e.g., software scaling errors). Furthermore, considering that the images were recorded from the ground, the upper sections of a tree will be described by fewer points than the lower sections, which will render the measurement process less accurate close to the terminal bud. Therefore, we expect that bias will change with height. Consequently, we will be using the following linear model for bias correction (Equation (5)):
where
BCh is the bias correction at height
h,
RH is the relative height,
RH = h/H d1.3 based variable and
scalingbased variable are linear variables derived from d
1.3 and PPC scaling, and
bi,
I = 0, … 4, are coefficients to be estimated.
Preference will be given to a model that has coefficient bi 0 or 1, which are easy to implement. However, this simplistic approach will likely not remove the bias. Nevertheless, if bias is reduced to ≤1% while the root mean square error (RMSE) is larger, the simplification becomes operationally justified.
The common approach of testing bias significance is through the null hypothesis stating that the statistics’ measuring bias are not different than 0 [
52]. Assuming normality and no outliers, a paired
t-test will be used for accepting or rejecting the null hypothesis. However, the
t-test is relatively sensitive to outliers [
53]; therefore, existence of large errors will be investigated with Grubbs’ test [
55]. Grubbs’ test assumes normality, which will be assessed with Kolmogorov–Smirnov test [
56]. When one of the previous two assumptions is violated, the Wilcoxon signed rank test will be used, which is robust to outliers and lack of normality [
57]. All tests were executed in SAS 9.4 [
58].
2.4. Taper Modeling
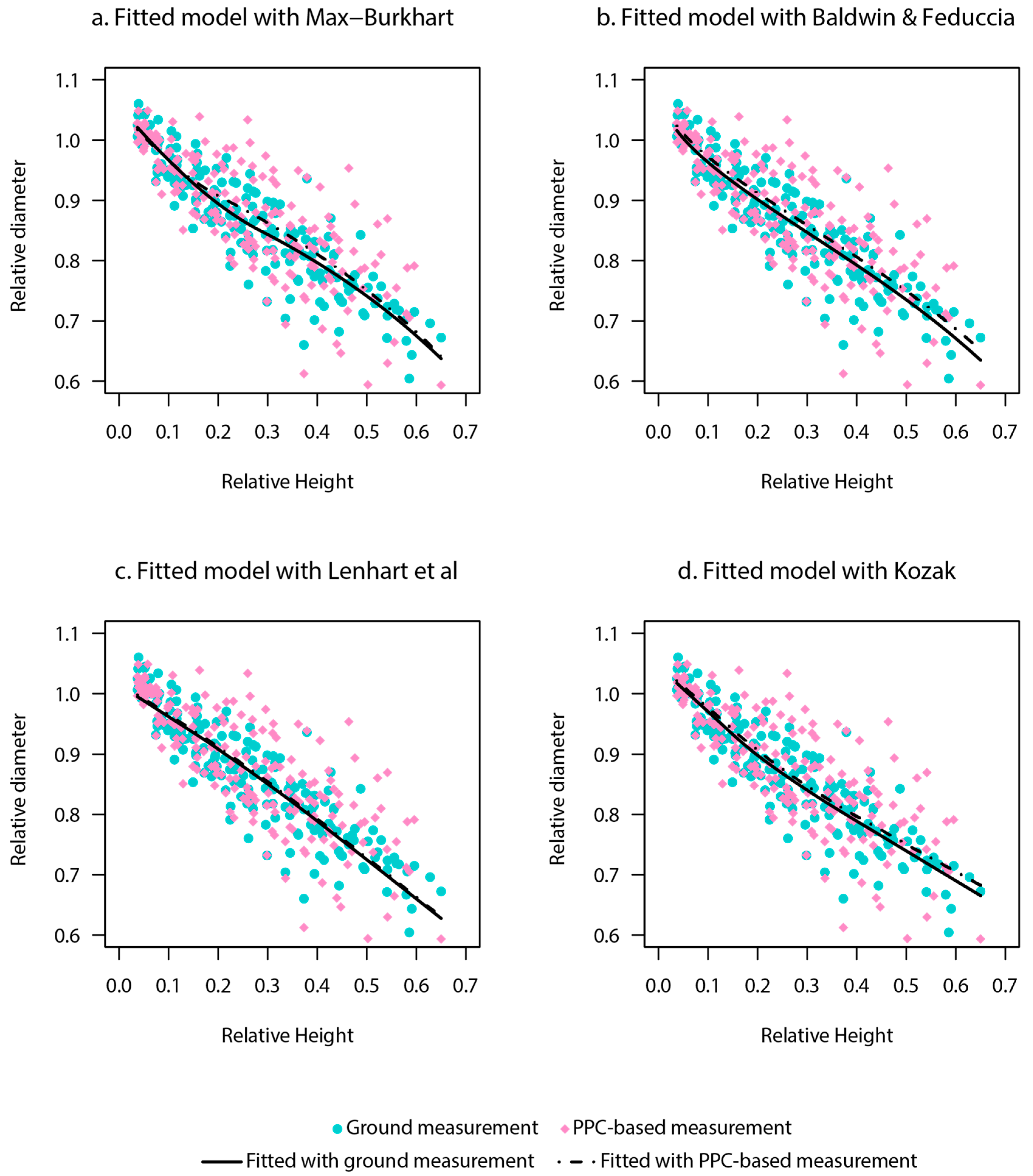
Diameters provide a cross-sectional perspective of a tree, which is also supplied by taper equations. Therefore, it is natural to compare the values obtained from taper models with the PPC-based diameters. The comparison employed four taper models (
Table 2), out of which three are widely used for loblolly pine: Max and Burkhart [
1], Baldwin and Feduccia [
2], Lenhart et al. [
3], and Kozak [
4]. The Max–Burkhart (1976) model has been extensively used to develop compatible taper equations of loblolly pine in central Louisiana and East Texas [
18,
59,
60,
61]. Instead of describing the tree bole with a single equation, the Max–Burkhart partitions the tree bole into two sections. The partitions approximate better the neiloid and paraboloid forms associated with the respective sections of the stem. Comparatively, Kozak’s model 2 (2004) integrates neiloid, paraboloid, and conic forms of the stem as a continuous function by using “changing exponents” [
4]. The Baldwin and Feduccia [
2] and Lenhart et al. [
3] models have a relatively simple model form, and only contain two coefficients. The four models were fit to the field and PPC-based data with the package nls2 [
62] from R version 3.2.4 [
63].
Similar fit statistics used for bias assessment were employed to evaluate the taper models: bias, mean absolute bias (MAB), and root mean square error (RMSE). For the taper models, the error present in the fit statistics is computed as the difference between the measured diameter,
di,h, and the estimated dimeter,
, at height
h for tree
i. Besides the previous three fit statistics, we have included the coefficient of determination
R2 to mirror other taper studies [
64,
65]. Because errors have different signs, bias is usually smaller than the MAB and the RMSE, which are always non-negative. MAB and RMSE are similar in their evaluation power [
66], with the observation that RMSE is slightly higher than MAB, a direct result of the Cauchy–Bunyakovsky–Schwarz inequality [
67].
where
di,h is the PPC–based diameter of tree
i at height
ht,
Hi is the total height of tree
i,
is the diameter predicted from taper equations for tree
i at height
h, and
is the average diameter of tree
i. (A1) was added to the denominator of each statistic to account for the d
1.3 measurement.
The same tests used for assessing the accuracy of PPC measurements (i.e., paired t-test or signed Wilcoxon) were employed to evaluate the performances of the taper models.