Learning-Based Sub-Pixel Change Detection Using Coarse Resolution Satellite Imagery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Learning-Based Approach for Generating Finer Resolution Synthetic Satellite Data
2.1.1. Dictionary Learning
2.1.2. Sparse Representation
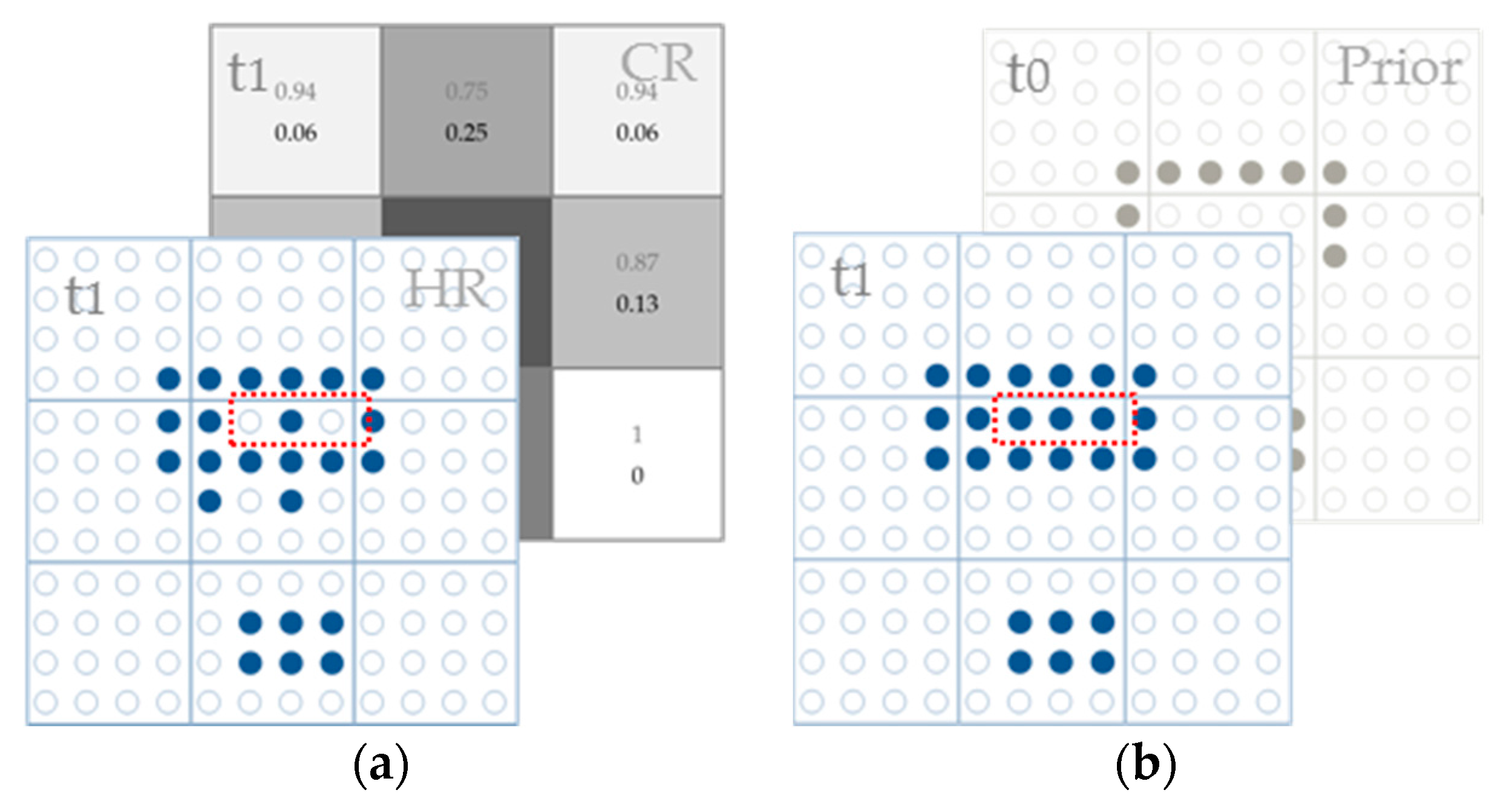
2.2. Sub-Pixel Change Detection with Synthetic Satellite Data
3. Experiments and Result Analysis
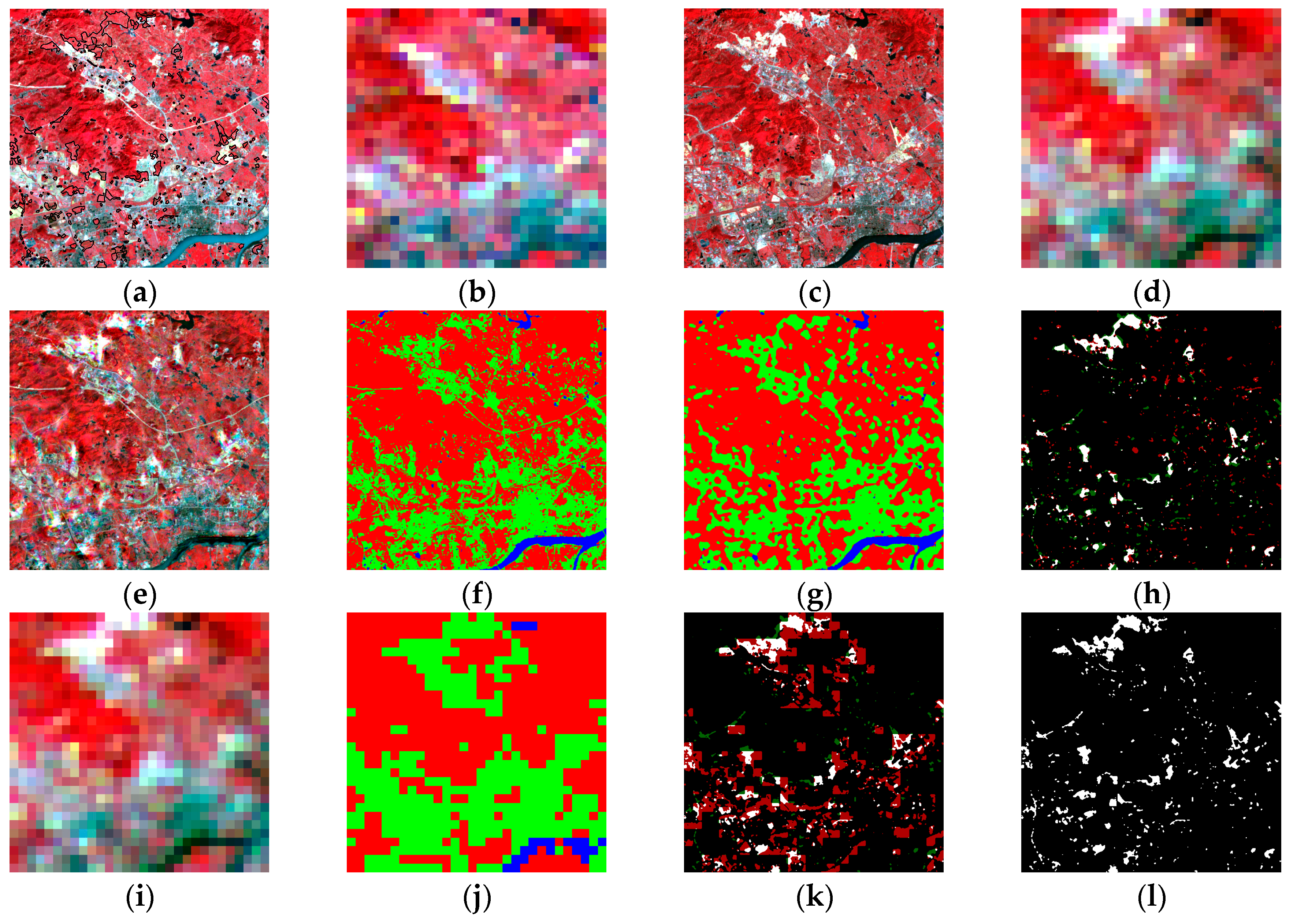
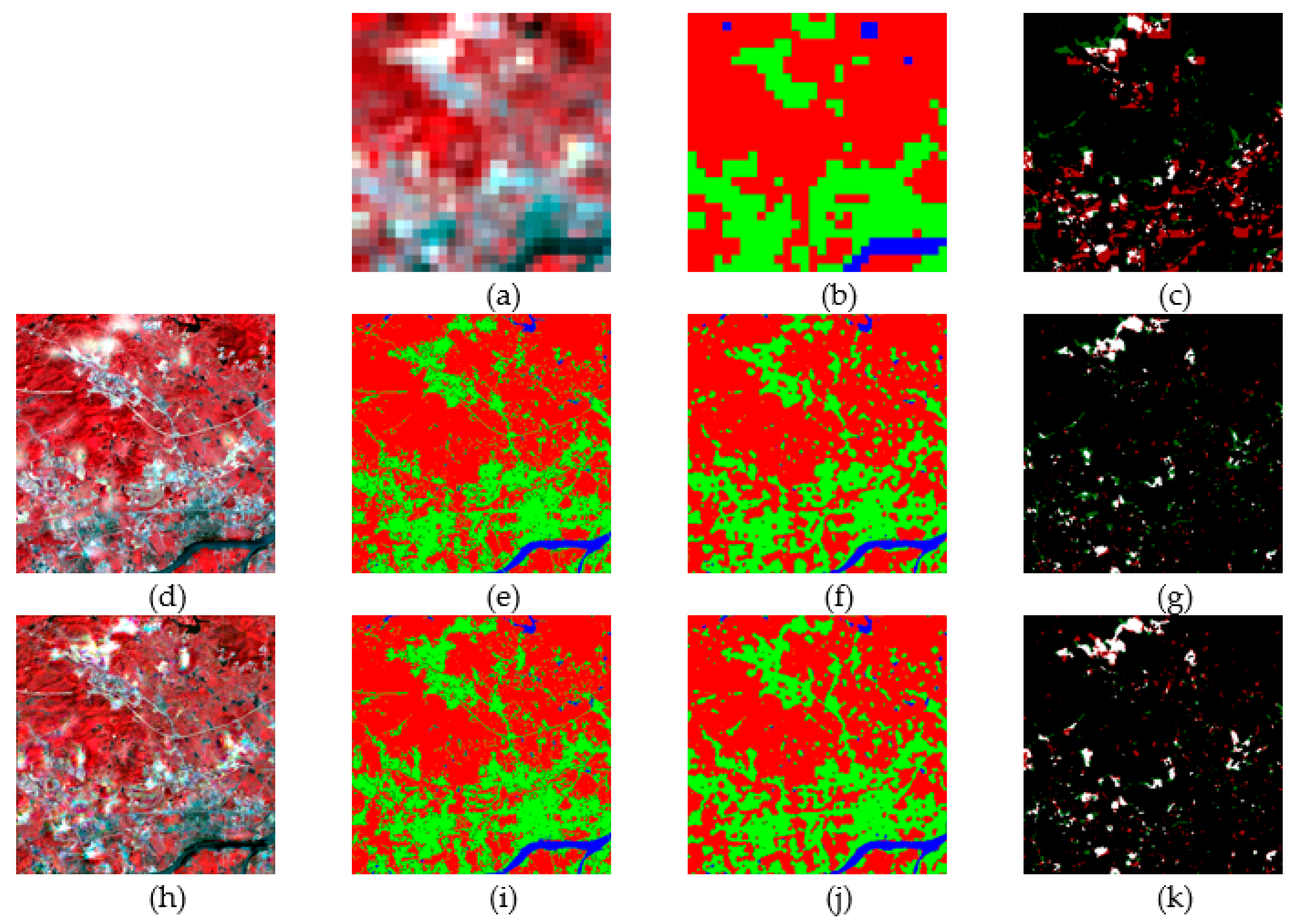
3.1. Synthetic Data Generation and Sub-Pixel Change Detection
3.2. Accuracy Assessment
4. Discussion
4.1. Strengths
4.2. Scale Effect
4.3. Limitations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bruzzone, L.; Prieto, D.F. An adaptive semi-parametric and context-based approach to unsupervised change detection in multitemporal remote-sensing images. IEEE Trans. Image Process. 2002, 11, 452–466. [Google Scholar]
- Xu, Y.; Huang, B. Spatial and temporal classification of synthetic satellite imagery: Land cover mapping and accuracy validation. Geo-Spat. Inf. Sci. 2014, 17, 1–7. [Google Scholar] [CrossRef]
- Singb, A. Digital change detection techniques using remotely sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Fung, T.; LeDrew, E. Application of principal components analysis to change detection. Photogramm. Eng. Remote Sens. 1988, 53, 1649–1658. [Google Scholar]
- Chen, J.; Gong, P.; He, C.; Pu, R.; Shi, P. Land-use/land-cover change detection using improved change-vector analysis. Photogramm. Eng. Remote Sens. 2003, 69, 369–379. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Le Hégarat-Mascle, S.; Ottlé, C.; Guérin, C. Land cover change detection at coarse spatial scales based on iterative estimation and previous state information. Remote Sens. Environ. 2005, 95, 464–479. [Google Scholar] [CrossRef]
- Strugnell, N.C.; Lucht, W.; Schaaf, C. A global albedo data set derived from AVHRR data for use in climate simulations. Geophys. Res. Lett. 2001, 28, 191–194. [Google Scholar] [CrossRef]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Walker, J.J.; De Beurs, K.M.; Wynne, R.H.; Gao, F. Evaluation of Landsat and MODIS data fusion products for analysis of dryland forest phenology. Remote Sens. Environ. 2012, 117, 381–393. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Wu, K.; Du, Q.; Wang, Y.; Yang, Y. Supervised Sub-Pixel Mapping for Change Detection from Remotely Sensed Images with Different Resolutions. Remote Sens. 2017, 9, 284. [Google Scholar] [CrossRef]
- He, D.; Zhong, Y.; Feng, R.; Zhang, L. Spatial-Temporal Sub-Pixel Mapping Based on Swarm Intelligence Theory. Remote Sens. 2016, 8, 894. [Google Scholar] [CrossRef]
- Ling, F.; Li, W.; Du, Y.; Li, X. Land cover change mapping at the subpixel scale with different spatial-resolution remotely sensed imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 182–186. [Google Scholar] [CrossRef]
- Ling, F.; Foody, G.M.; Li, X.; Zhang, Y.; Du, Y. Assessing a temporal change strategy for sub-pixel land cover change mapping from multi-scale remote sensing imagery. Remote Sens. 2016, 8, 642. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Kaiser, G.; Clevers, J.G.P.W.; Schneider, W.; Schaepman, M.E. Downscaling time series of MERIS full resolution data to monitor vegetation seasonal dynamics. Remote Sens. Environ. 2009, 113, 1874–1885. [Google Scholar] [CrossRef]
- Foody, G.M. Approaches for the production and evaluation of fuzzy land cover classifications from remotely-sensed data. Int. J. Remote Sens. 1996, 17, 1317–1340. [Google Scholar] [CrossRef]
- Atkinson, P.M. Sub-pixel target mapping from soft-classified, remotely sensed imagery. Photogramm. Eng. Remote Sens. 2005, 71, 839–846. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial-and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Seitz, N.; White, J.C.; Gao, F.; Masek, J.G.; Stenhouse, G. Generation of dense time series synthetic Landsat data through data blending with MODIS using a spatial and temporal adaptive reflectance fusion model. Remote Sens. Environ. 2009, 113, 1988–1999. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Sun, J.; Xu, Z.; Shum, H.Y. Image super-resolution using gradient profile prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; IEEE: Hoboken, NJ, USA, 2008. [Google Scholar]
- Baker, S.; Kanade, T. Limits on super-resolution and how to break them. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1167–1183. [Google Scholar] [CrossRef]
- Gu, S.; Zuo, W.; Xie, Q.; Meng, D.; Feng, X.; Zhang, L. Convolutional sparse coding for image super-resolution. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1823–1831. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Song, H. Spatiotemporal reflectance fusion via sparse representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, B. A spatio–temporal pixel-swapping algorithm for subpixel land cover mapping. IEEE Geosci. Remote Sens. Lett. 2014, 11, 474–478. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Li, Z. Land cover change detection at subpixel resolution with a Hopfield neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1339–1352. [Google Scholar] [CrossRef]
- Zhang, Y.; Atkinson, P.M.; Li, X.; Ling, F.; Wang, Q.; Du, Y. Learning-Based Spatial–Temporal Superresolution Mapping of Forest Cover with MODIS Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 600–614. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Davis, G.; Mallat, S.; Avellaneda, M. Adaptive greedy approximations. Construc. Approx. 1997, 13, 57–98. [Google Scholar] [CrossRef]
| Actual Data | Simulated Data (S = 16) | |||||
|---|---|---|---|---|---|---|
| Soft | STARFM | Proposed | Soft | STARFM | Proposed | |
| Kappa | 0.45 | 0.46 | 0.47 | 0.46 | 0.49 | 0.50 |
| OA | 83% | 84% | 85% | 83% | 85% | 86% |
| CE | 19% | 18% | 17% | 18% | 17% | 17% |
| OE | 32% | 38% | 37% | 31% | 36% | 30% |
| CC | 0.68 | 0.69 | 0.78 | 0.77 | 0.86 | 0.89 |
| Scale Factor = 4 | Scale Factor = 8 | Scale Factor = 16 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Soft | STARFM | Proposed | Soft | STARFM | Proposed | Soft | STARFM | Proposed | |
| Kappa | 0.53 | 0.60 | 0.61 | 0.52 | 0.53 | 0.55 | 0.46 | 0.49 | 0.50 |
| OA | 86% | 89% | 90% | 85% | 87% | 88% | 83% | 85% | 86% |
| CE | 15% | 13% | 15% | 16% | 15% | 15% | 18% | 17% | 17% |
| OE | 23% | 27% | 16% | 23% | 30% | 26% | 31% | 36% | 30% |
| CC | 0.89 | 0.92 | 0.93 | 0.88 | 0.89 | 0.92 | 0.77 | 0.86 | 0.89 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Lin, L.; Meng, D. Learning-Based Sub-Pixel Change Detection Using Coarse Resolution Satellite Imagery. Remote Sens. 2017, 9, 709. https://doi.org/10.3390/rs9070709
Xu Y, Lin L, Meng D. Learning-Based Sub-Pixel Change Detection Using Coarse Resolution Satellite Imagery. Remote Sensing. 2017; 9(7):709. https://doi.org/10.3390/rs9070709
Chicago/Turabian StyleXu, Yong, Lin Lin, and Deyu Meng. 2017. "Learning-Based Sub-Pixel Change Detection Using Coarse Resolution Satellite Imagery" Remote Sensing 9, no. 7: 709. https://doi.org/10.3390/rs9070709
APA StyleXu, Y., Lin, L., & Meng, D. (2017). Learning-Based Sub-Pixel Change Detection Using Coarse Resolution Satellite Imagery. Remote Sensing, 9(7), 709. https://doi.org/10.3390/rs9070709







