Wavelet-Based Topographic Effect Compensation in Accurate Mountain Glacier Velocity Extraction: A Case Study of the Muztagh Ata Region, Eastern Pamir

Abstract

Glaciers in high mountain regions play an important role in global climate research. Glacier motion, which is the main characteristic of glacier activity, has attracted much interest and has been widely studied, because an accurate ice motion field is crucial for both glacier activity analysis and ice avalanche prediction. Unfortunately, the serious topographic effects associated with the complex terrain in high mountain regions can result in errors in ice movement estimation. Thus, according to the different characteristics of the results of pixel tracking in the wavelet domain after random sample consensus (RANSAC)-based global deformation removal, a wavelet-based topographic effect compensation operation is presented in this paper. The proposed method is then used for ice motion estimation in the Muztagh Ata region, without the use of synthetic-aperture radar (SAR) imaging geometry parameters. The results show that the proposed method can effectively improve the accuracy of glacier motion estimation by reducing the mean and standard deviation values from 0.32 m and 0.4 m to 0.16 m and 0.23 m, respectively, in non-glacial regions, after precisely compensating the topographic effect with Advanced Land Observing Satellite–Phased Array-type L-band Synthetic Aperture Radar (ALOS–PALSAR) imagery. Therefore, the presented wavelet-based topographic effect compensation method is also effective without requiring the SAR imaging geometry parameters and has the potential to be widely used in the accurate estimation of mountain glacier velocity.

1. Introduction

Glaciers are extremely sensitive indicators of climate change [1,2]. Most of the ice bodies in the world have been shrinking in recent decades, partly reflecting the increase in global temperatures observed during this period [3,4,5,6]. Thus, in addition to the glaciers and ice sheets of the High Arctic zone and Greenland, the ice in the high mountain regions in low and middle latitudes such as Tibet or Central Asia has also been attracting considerable attention. The widespread melting of ice in response to global warming can further accelerate glacier flow and potentially lead to significant loss of glacier mass [6,7,8,9]. Therefore, glacier surface velocity is a crucial parameter for estimating ice volume variation in response to global warming, as well as glacial disaster prediction [6,10].

Due to the difficulty of directly monitoring ice motion in remote regions, the feature-tracking and differential interferometry approaches based on remote sensing imagery have been employed for ice motion detection [2,6,11,12]. Compared with the results of in-situ observations that are limited in spatial and temporal resolutions, techniques based on remotely sensed data can provide spatially dense displacement maps at a relatively low cost [7,13]. Among the different remote sensing techniques, the intensity feature tracking method relying on SAR intensity has been demonstrated to be very effective, and has been widely used for routine ice motion observation. Large-scale spatial and temporal coverage can be achieved due to the SAR instrument’s capability of operating day and night, independent of weather conditions and coherence [14]. Its advantages have also been employed in other applications, such as earthquake, flood, and landslide studies [15,16].

High-accuracy ice motion observation plays an important role in studies of ice dynamics, climate change and disaster prediction [1,3,17]. Unfortunately, the complex terrain in high mountain regions often results in errors in ice motion estimation. Many different approaches have been presented in previous studies to compensate for the impact of rugged terrain [18,19,20]. Through precise SAR imaging geometry information, the effect of the terrain can be removed with the help of an external digital elevation model (DEM). However, the data processing requires many parameters, some of which cannot be directly obtained from the affiliated SAR data files. Furthermore, assumptions have to be made in the formula derivation. Indeed, correct retrieval of the displacements of mountain glaciers is strongly dependent on the imaging geometry and the matching parameters [14,18]. Therefore, the SAR imaging geometry parameters and the corresponding spatial baseline and orbital cross angle between two SAR images need to be carefully estimated. Unfortunately, the SAR imaging parameters are sometimes missing or cannot be accurately obtained, which results in a problem for the topography-related value estimation. To solve the problem and obtain accurate ice velocity information in high mountain regions, without considering orbit geometry directly, we present the wavelet-based topographic effect compensation approach.

Wavelet analysis has been widely used in signal processing, filtering, and data compression [21,22,23]. In this paper, a wavelet-based method is first used for topography-related signal removal. By using the correlation information as a proxy, the topography compensation operation can be computed without precise imaging geometry information, thus improving efficiency and reducing the computational cost, and avoiding the complex computation of the imaging parameters. Therefore, the wavelet-based statistical method is efficient and needs fewer parameters, which reduces the difficulty of the computation.

In this paper, we first briefly introduce the study area and datasets. We then present the random sample consensus (RANSAC)-based global deformation estimation method, the wavelet-based topographic effect compensation method, and the corresponding data processing flowchart of the improved intensity feature tracking method. Finally, we present and analyze the results obtained by the proposed method and provide a general conclusion.

2. Study Area and Datasets

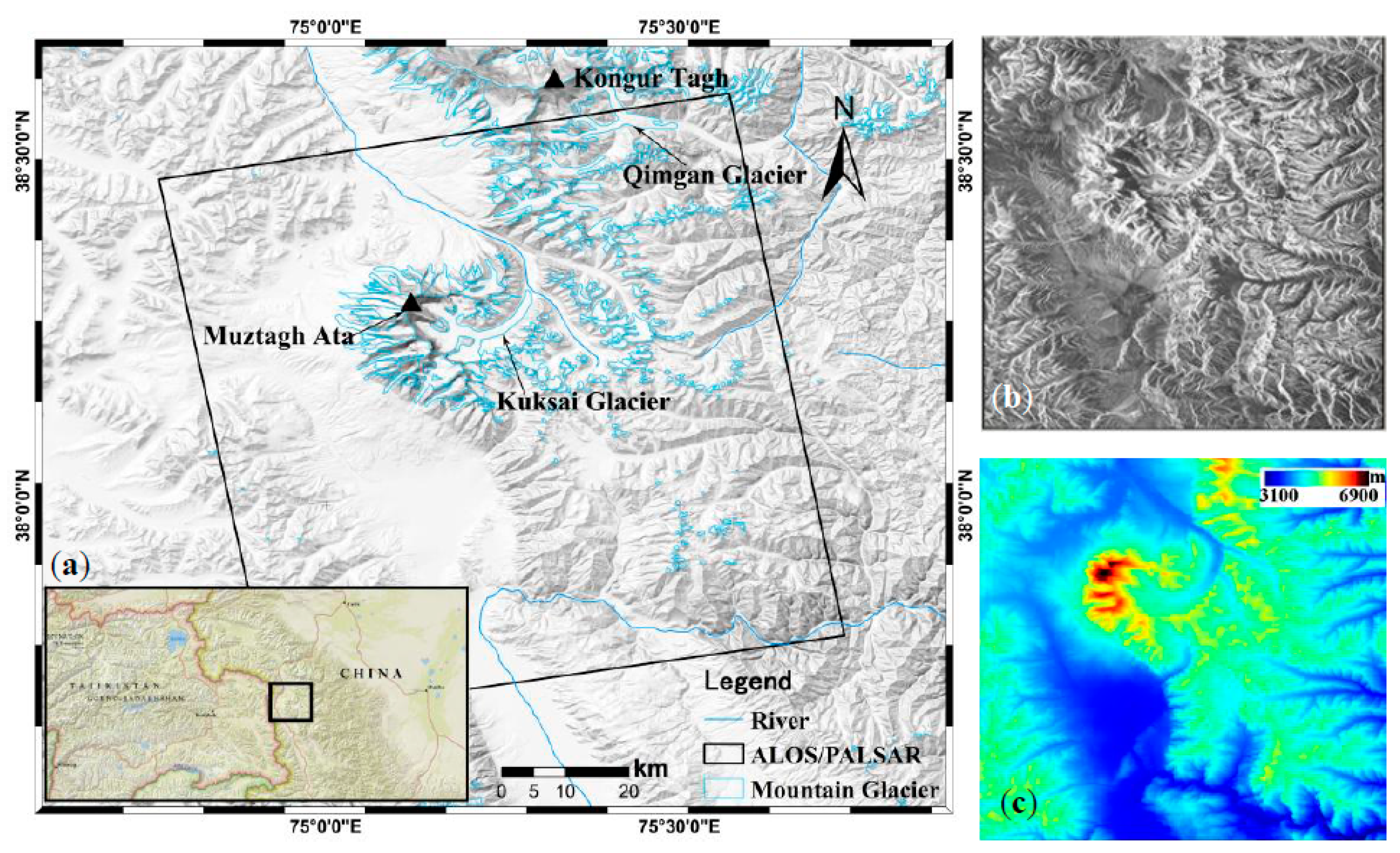
The Muztagh Ata region is a mountainous region located on the eastern Pamir Plateau, on the boundary of Akto County and Taxkorgan County in Xinjiang, China (Figure 1). It features a number of valley glaciers which descend from the ice caps, with a snowline elevation of 5300–5700 m [24]. Kuksai Glacier is the largest glacier in the study area, with a length of about 18 km and a maximum width of 4 km. The melt water from the glaciers in this region feed the Taxkogan River and Kaxgar River. In recent decades, glaciers in the study area have experienced an overall loss of ice mass [25]. A recent study in eastern Pamir, based on the first and second Chinese glacier inventories, indicated that the area of glaciers in the region had decreased by 10.8 + 1.1% from 1963–2009 [26].

Glacier surges in high mountain regions have also become more common and have sometimes caused significant loss of life and property [27,28]. Ice motion, as an important proxy for understanding glacier status, is of vital importance for ice-motion-related disaster prediction [29].

This study used 46-day temporal interval L-band SAR images acquired by ALOS–PALSAR in fine beam single polarization (FBS) mode for the ice motion extraction in the study area (

Table 1. Characteristics of the SAR imagery used for the ice motion estimation.

Date	Satellite	Orbit	Season	Perpendicular Baseline (m)	Temporal Baseline (Days)
14 January 2009	ALOS–PALSAR	Ascending	Winter	250	46
1 March 2009

). Compared with C- or X-band SAR imagery, the L-band images can provide a relatively high correlation and are not seriously affected by snow precipitation, as a result of the deep SAR signal penetration. Therefore, the glacier surface velocity field could be efficiently computed in the region. The SRTM 90-m Digital Elevation Dataset v4 was also employed in this study.

3. Method

The intensity feature tracking method is a widely used alternative approach for the efficient extraction of ice motion when the differential interferometric synthetic-aperture radar (D-InSAR) technique is limited by the loss of coherence [6,30]. The core essence of offset tracking is the similarity measurement of the SAR images acquired with a temporal baseline. In addition, the intensity feature tracking method can yield ice motion in both the range and azimuth directions, rather than only the line-of-sight (LOS) direction of the D-InSAR technique. The maximum detectable displacement for offset tracking depends on the size of the search window used for the normalized cross-correlation (NCC) estimation, i.e., larger displacements can be detected with larger search windows. Search window size is set by considering the size of the glacier, in particular glacier width, and the spatial resolution of the SAR data. An accuracy of tenths of the pixel size can usually be achieved by the use of sub-pixel registration techniques [31,32]. Therefore, high-resolution SAR systems allow us to measure relative displacement at the centimeter level in both the range and azimuth directions.

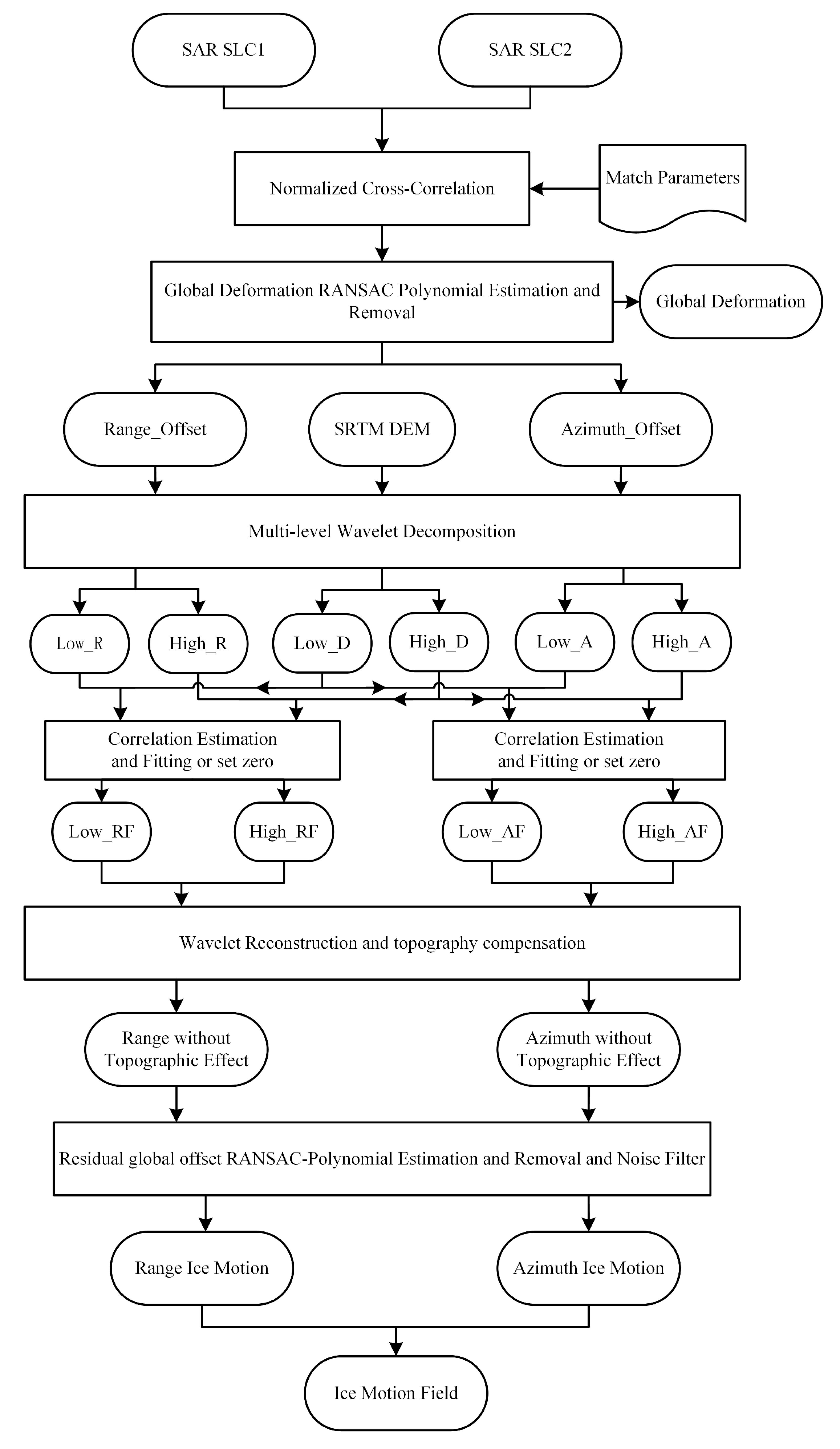
In addition to the glacier-motion-related signals, imaging geometry and topography also contribute to the intensity feature tracking results. In order to obtain accurate ice motion in high mountain regions, the non-glacial-motion-related signals need to be precisely estimated and removed. The initial results of pixel tracking $O_a$ can be divided into four parts, as shown in the following equation:

$$O_a=O_g+O_t+O_i+O_n$$

(1)

where $O_i$ is the offset corresponding to the ice motion value; and $O_g$, $O_t$, and $O_n$ are the non-glacial-related signals that need to be removed from $O_a$. Generally, $O_g$ is the long-wavelength signal, and $O_t$ is the low-frequency signal highly correlated with the DEM. $O_n$ is the high-frequency signal with a random distribution. In this way, the accurate ice motion $O_i$ can be obtained in the final result. The general data processing steps used in this paper are shown in Figure 2.

Global deformation in the range and azimuth directions can usually be fitted by polynomial functions. The key step is the accurate estimation of the coefficients of the fitting function. In this paper, a RANSAC-based optimized method is applied, which can robustly yield the precise coefficients of the polynomial fitting function [33,34].

According to the characteristics of the ice motion, the offset obtained by pixel tracking is composed of not only the ice-motion- and sensor-attitude-related signals, but also the external signal generated by the topographic effect. Therefore, in order to obtain an accurate result for an active glacier, the topographic effect needs to be considered and compensated in the data processing. Based on fully exploring the characteristics of the topography-related signal, the wavelet-based topographic-effect compensation method is presented and employed in this paper. Only after precisely compensating the non-glacial-related signal can glacier motion be accurately presented in the final results.

3.1. RANSAC-Based Global Offset–Deformation Estimation

The offsets corresponding to the orbit and sensor attitude should first be precisely fitted and removed. Generally, different orbit information between two SAR acquisitions results in deformation across the whole frame of the SAR image, which can be considered as the low-frequency signal with a long wavelength. This can usually be efficiently fitted through the polynomial function [14,31]. In this study, according to the characteristics of the offsets corresponding to the orbit and sensor attitude, the following quadratic polynomial function was employed:

$$\begin{array}{l}{O}_g^R=a_0+a_{1}m+a_{2}n+a_{3}mn+a_4{m}^2+a_5{n}^2\\ O_g^A=b_0+b_{1}m+b_{2}n+b_{3}mn+b_4{m}^2+b_5{n}^2\end{array}$$

(2)

where $a_i$ and $b_i$ ($i=0\cdot \cdot \cdot 5$) are the coefficients of the polynomial function, and $m$ and $n$ are the positions of the sample points in the SAR imaging geometry. $O_g^R$ and $O_g^A$ are the global offsets related to the orbit and sensor attitude, which is usually the low-frequency signal. Because of the assumption of stability in the non-glacial region in the intensity feature tracking method, the offset value of an ice-free region can be considered to be the result caused by the difference in orbit and attitude between the two acquisitions. The coefficients of the polynomial functions $a$ and $b$ can then be estimated by least squares (LS) or weighted least squares (WLS) from $m$ and $n$, using only the initial offsets generated by the SAR patch match procedure [33]. As this approach is seriously affected by noise or errors in the offset values, a mask file must be provided to reduce the negative effect of the incorrect offsets or the ice-motion-related offsets, which complicates the computation and reduces the accuracy of the estimated parameters.

In order to improve the efficiency and accuracy of the global deformation fitting and removal, a RANSAC-based parameter estimation method is employed in this paper. The RANSAC algorithm was first presented by Martin and Robert [34]. Due to its strong robustness, the mask file—which is usually used to filter out points with a low signal-to-noise ratio (SNR) in glacial regions—can be ignored, without any negative effect on the accuracy of the parameters of the global polynomial fitting, even when the percentage of outliers reaches 50% of the entire dataset [34,35]. Therefore, RANSAC can efficiently improve the accuracy of the parameter estimation and reduce the negative effect of noise (coregistration error) by rejecting them in the set of inliers, which would be used for coefficient computation of the quadratic polynomial function. Furthermore, after the topographic effect compensation, the RANSAC algorithm can also be used in the residual global-deformation-fitting operation, if residual global deformation still exists in the results. The RANSAC algorithm is essentially composed of two steps that are repeated in an iterative fashion (hypothesize-and-test framework), whose proof and detailed procedure can be found in many previous optimization studies [33,34,36,37].

3.2. Wavelet-Based Topographic Effect Compensation

Following the global offset fitting and removal operation with the quadratic polynomial function, the phenomenon of the topographic effect can usually be clearly observed in the results. Yan et al. [18] presented an accurate approach for topographic effect compensation in ice motion extraction with spaceborne SAR data based on the corresponding imaging geometry. However, the precise satellite orbit and the imaging geometry parameters are required, which seriously limits its wide usage in mountain glacier motion estimation.

In order to efficiently remove the topographic effect, the correlation between the DEM and the residual offsets after the global deformation compensation can be used as a proxy for removing the topography in the final ice motion results. Therefore, in this paper, the wavelet-based method is explored and employed in the identification and compensation of the topography-related part of the residual offset field, because wavelet-based multi-resolution analysis can be efficiently used in image processing and complex signal analysis [22,23].

The ice motion field with topographic effect can be considered the combined result of the topography- and ice-motion-related signals. Compared to the ice motion signal, the topographic-effect-related offset can be considered as the low-frequency signal, which is highly correlated with the corresponding part of the terrain. Therefore, the topographic effect can be compensated by the wavelet decomposition and reconstruction method, with the help of an external DEM. The low-frequency parts of the topography can be replaced with the values computed by the correlation between the low-frequency parts of the topography and the ice motion field; the high-frequency parts are usually set to zero in a reconstruction. The topographic-effect value can finally be obtained by the wavelet decomposition and reconstruction method. Without requiring the complex computation of the imaging parameters, which is a requirement of the previous methods [18,19], the proposed approach can efficiently compensate the offset value caused by the rugged terrain. A detailed data processing flowchart is shown in Figure 2.

The ice motion with topographic effect can be decomposed into different parts in the wavelet domain using multi-resolution analysis [22]. The choice of the wavelet family was empirically derived to achieve a balance between computation time and the wavelet support length that best fits the spatial wavelength of the topography [38]. However, identifying an optimum wavelet function requires a comprehensive numerical and theoretical analysis, which is beyond the scope of this paper. The number of levels for the wavelet decomposition can be roughly determined by the correlation between the low-frequency parts of the ice field and the corresponding DEM. The low-frequency part of the DEM can be removed with a band-pass filter, which can filter out the value corresponding to the topography, leaving only the ice motion value.

$O$ is the offset field with a size of $m$ × $n$, and it can be decomposed in the wavelet domain using multi-resolution analysis as follows:

$$O={\displaystyle \sum _{i_x}^{m-1}{\displaystyle \sum _{i_y}^{n-1}{v}_{i_x{i}_y}{\mathrm{\Phi }}_{J{i}_x{i}_y}}}+{\displaystyle \sum _{j^{\prime }}^{J-1}{\displaystyle \sum _{i_x}^{m-1}{\displaystyle \sum _{i_y}^{n-1}{\displaystyle \sum _{\epsilon }^3{w}_{j^{\prime }{i}_x{i}_y}^{\epsilon }{\mathrm{\Psi }}_{j^{\prime }{i}_x{i}_y}^{\epsilon }}}}}=L^J+{\displaystyle \sum _{j^{\prime }}^{J-1}{\displaystyle \sum _{\epsilon }^3{H}_{\epsilon }^{j^{\prime }}}}$$

(3)

where $v$ and $\omega$ denote the smoothing and wavelet coefficients, respectively; $\mathrm{\Phi }$ and $\mathrm{\Psi }$ are the smoothing and the mother wavelet functions, respectively; $J$ is the number of wavelet scales; and $L$ and $H$ are the low- (long wavelength) and high-frequency (short wavelength) components, respectively.

The purpose of wavelet decomposition and the corresponding correlation is to discriminate between the components that contribute to the ice motion and the topographic effect signals. The same operations apply for the DEM and ice motion. As the level of decomposition increases, the correlation between the long-wavelength–low-frequency signals from the ice field and DEM increase. Once the correlation is large enough, the low- and high-frequency parts of the DEM are replaced by the values $L_D^{\prime }$ and $H_D^{\prime \epsilon }$, which are obtained by the following equations:

$$\{\begin{array}{c}{L}_O=f_L(L_D)\to L_D^{\prime }=f_L(L_D)\\ H_O^{\epsilon }=f_S^{\epsilon }(H_D^{\epsilon })\to H_D^{\prime \epsilon }=f_S^{\epsilon }(H_D^{\epsilon }),\epsilon =1,2,3\end{array}$$

(4)

where $L$ is the approximation coefficient of the topography or DEM signal, corresponding to the part of the signal with low frequency; and $H$ denotes the vertical, horizontal, and diagonal coefficients, corresponding to the part of the signal with high frequency.

Once the correlation between $L_O$ and $L_D$ reaches the given threshold, the relation function $f_L(\cdot )$ between $L_O$ and $L_D$ can be obtained and used in the long-wavelength signal $L_D^{\prime }$ estimation. The same operation is also employed in the correlated short-wavelength signal estimation, and $H_D^{\prime \epsilon }$ is calculated. Finally, the topography-related signal can be obtained by multi-resolution wavelet reconstruction operations with the calculated $L_D^{\prime }$ and $H_D^{\prime \epsilon }$. The topography signal is composed of signals with different wavelengths. In order to reduce the effect of the high-frequency part, we usually set the wavelet coefficients of the high-frequency part to zero.

3.3. Filtering Operation

After the global and topography-related offset removal, a filtering operation for reducing the noise in the ice velocity field was used, which was based on the assumption that the ice flow field is continuous in direction and magnitude, because the glacier behaves like a quasi-plastic solid [24]. After the noise-filtering operation, the offset value caused by the coregistration error was eliminated and the ice motion pattern of the glacier was much more reasonable.

4. Results and Analysis

Due to the complexity of both the ground surface and the traditional intensity feature tracking algorithm, parameter choice for the intensity feature tracking approach is important for ice motion extraction in high mountain regions. Compared with the ice sheets in Antarctica, the width and length of glaciers in high mountain regions are usually limited. Therefore, the search window parameters for the intensity feature tracking operation should be carefully chosen according to the spatial scale of the glacier and the spatial resolution of the SAR imagery. The interval time also needs to be considered during the parameter setting, because the correlation coefficient decreases greatly as the temporal interval increases, especially when the surface scatter characteristics change.

In this paper, considering the size of the glaciers in this region and the general principles described above, the parameters were experimentally chosen as follows: 32 × 32 pixels for the patch window and 64 × 64 pixels for the search window, which could theoretically cover the maximum motion of about 60 m with the spatial resolution of ALOS–PALSAR (4.68 m in range, 3.15 m in azimuth). These parameters depend on the expected maximum displacement produced by the phenomenon being investigated, which needs to be roughly estimated from external data or previous studies. The window step size was set to 4 × 12 pixels, according to the different resolutions of PALSAR data in the slant-range and azimuth directions. The pixel tracking results can thus be presented in a reasonable geometry with the same spatial resolutions in the slant-range and azimuth directions, which is suitable for visual interpretation.

We applied the strategy proposed in this paper to an ALOS–PALSAR imagery pair separated by 46 days between 16 December 2009, and 31 January 2010. NCC similarity estimation processing was performed using the AMPCOR Fortran routine provided in the ROI_PAC software, with the parameters as mentioned above. The initial results are shown in Figure 3.

From the initial results, it can be seen that the total offset caused by all the different factors (orbit, sensor attitude, topography, and ice motion) can be clearly observed in the results of the intensity feature tracking approach. From the offset maps shown in Figure 3, it can be observed that the ice-motion-related signal is very much buried in the offset values caused by the non-glacial-related signals. Only after the orbit and sensor attitude signals had been removed with the presented RANSAC-based global deformation polynomial fitting algorithm were the ice motion and topography-related signals able to be seen, as shown in Figure 3.

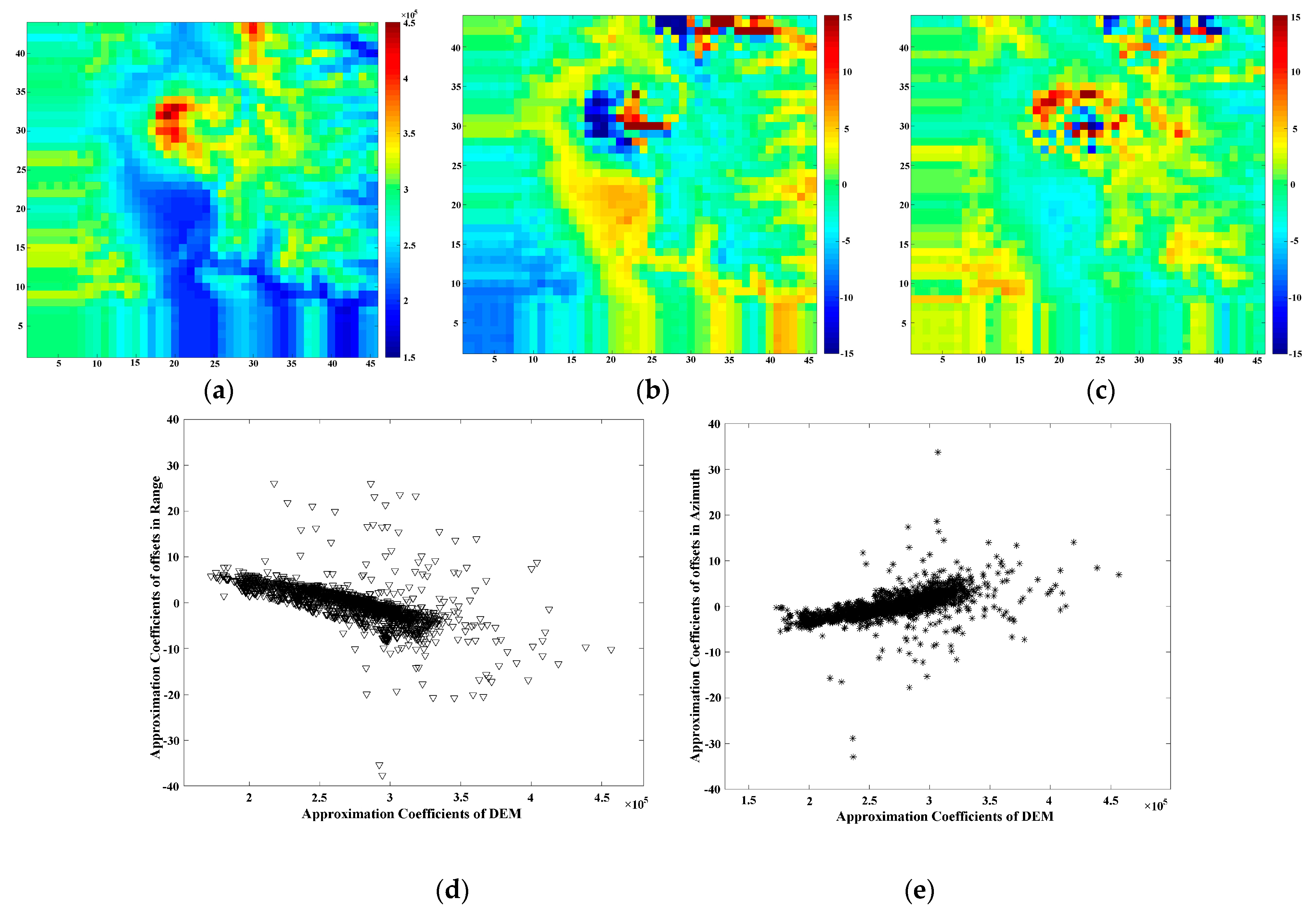
Following the precise global deformation estimation and compensation, only the topography and ice motion signals remain, along with the noise. In order to measure the ice motion, the topographic effect must be efficiently and accurately estimated and compensated with the wavelet-based decomposition–reconstruction method. According to the data processing flowchart in Section 2, the appropriate coefficient signals for the terrain and offset field are presented in Figure 4, corresponding to the low-frequency signal parts of the wavelet decomposition operation. Once the correlation between the approximate parts of the terrain and ice motion is high enough, the wavelet decomposition operation can be stopped and followed by the fitting and replacement operation at the corresponding wavelet decomposition level. In this paper, the Daubechies 6 (db6) wavelet was chosen and the decomposition operation was ended when the correlation of the low-frequency part was large enough. Finally, the multi-resolution analysis performed using db6 at six levels of decomposition was able to satisfy the threshold for the following procedure. Figure 4 shows the (approximate) reconstructed low-frequency components at level 6.

The relationship between the appropriate coefficients of the DEM and the offset field of the slant-range or azimuth can be observed in Figure 4d,e. Moreover, from the correlation maps in Figure 4, a linear function was deemed to be good enough to fully describe the relationship between the appropriate coefficients of the DEM and the offset fields. Thus, the robust linear fitting approach was applied to the reconstructed coefficient signal corresponding to the topographic effect in the ice motion field. Following the fitting and replacement of the topographic effect in the offset fields, the wavelet reconstruction provided the offsets caused by the topographic effect (Figure 5), which could be removed from the offset fields.

We removed the outliers by utilizing the SNR and the constraint of the continuous assumption of the ice motion amplitude and flow directions. By combining the ice motion in the slant-range and azimuth directions, detailed information for the overall glacier surface was obtained, as presented in the ice motion field map in Figure 6. Overall, the motion distribution indicates that the ice motion decreases gradually to zero at the terminus, although the motion is more complex in the upper section of the large-scale glacier.

In order to directly show the effect of the presented wavelet-based topographic effect compensation algorithm with the intensity feature tracking method, the surface motion without the topographic effect compensation is also shown in Figure 6. The comparison indicates that the accuracy of the ice motion field appears to have been greatly improved by the topographic effect compensation.

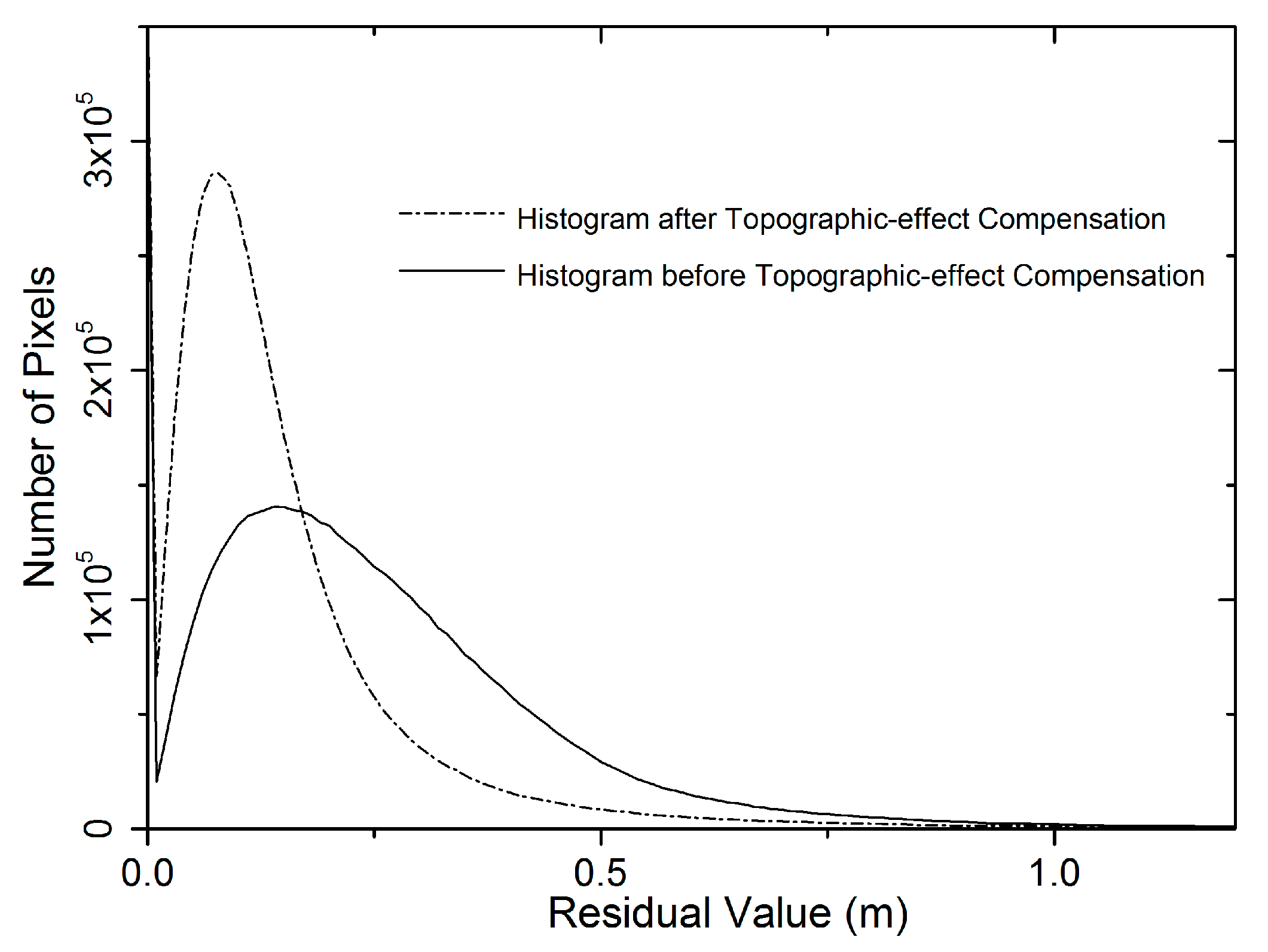
The lack of ground truth for the velocity measurements hampered the simple evaluation of the results. In order to assess the quality of the measurements obtained in this study, several regions were chosen at random. We then calculated the statistical characteristics of the residual values on the ice-free regions. According to the assumption of the intensity feature tracking method, accuracy can be determined by the statistical characteristic of the residual offset in the ice-free regions. We calculated the mean and standard deviation values in the non-glacial regions, which changed from 0.32 m and 0.4 m to 0.16 m and 0.23 m after the topographic effect compensation. The associated histograms of the residual values are shown in Figure 7. Clearly, the proposed approach can reach the accuracy level of a glacier motion estimation using the traditional topographic compensation method, without the imaging geometry parameters, and with less computational cost.

The maximum ice motion value can also be determined from the obtained ice motion field. The Qimgan Glacier surface showed a maximum ice velocity of 24.8 m over the 46 days, which occurred in the upstream part. This indicates that the glacier is more active in this region, which was also seen in the glacier surge that occurred in 2015 [27]. In addition, it can also be observed that rapid ice motion took place in the small-scale glaciers. The average ice motion of the large-scale glaciers was less than that of the small-scale glaciers, which suggests that the large-scale glaciers are more stable. This indicates that the large-scale glaciers are less sensitive to short-term temperature variation than glaciers with a small area [6,39].

5. Discussion

The topographic effect can be clearly observed in the offset field after the global removal of deformations with the RANSAC-based polynomial fitting algorithm proposed in this paper. Based on the correlation between the approximation coefficients in the DEM and ice movement fields, the wavelet-based topographic effect compensation approach was employed for mountain glacier surface motion estimation using SAR imagery. This study also indicated that the topographic effect compensation operation is of great benefit in a glacial region with complex terrain.

The wavelet-based multi-resolution analysis approach is suitable for use with the intensity feature tracking technique, and can be used to analyze surface motions at different scales. It can be considered a statistically-based compensation method, unlike the traditional method which requires precise imaging geometry. The proposed approach can achieve the same accuracy as the traditional topographic compensation method, but it would effectively remove the topographic signal from glacier velocity produced by SAR intensity feature tracking without the complex parameters related to the SAR imaging geometry. Thus, it could easily extend the range of the intensity feature tracking technique, especially into areas with rugged terrain.

Debris cover is helpful for ice motion extraction with the intensity feature tracking method. However, snow cover in the upper sections causes difficulty for the intensity feature tracking method. Therefore, the noise is usually much higher than in the middle and downstream parts. Furthermore, the snow amounts can change the surface characteristics, but the L-band can penetrate the snow. Thus, SAR imagery with a relatively long wavelength is much more suitable for ice motion studies than that with a short wavelength due to its strong penetrative ability, although it is also sometimes heavily influenced by serious melt conditions, which usually cause a loss of correlation and an inability to derive glacier velocities, especially in summer [40].

6. Conclusions

We determined an accurate ice motion field by the use of 46-day temporal interval ALOS–PALSAR imagery of the Muztagh Ata region with RANSAC-based global deformation fitting and wavelet-based topographic effect compensation algorithms. After the precise fitting and removal of the global deformation, a topography-related signal can be observed in the ice motion field. This signal acts as an external error in the results of the intensity feature tracking method, lowering the accuracy and seriously limiting ice motion detection. Therefore, we have presented a new strategy for topographic effect compensation for high mountain regions, with the help of wavelet theory and an external DEM, without requiring the imaging geometry parameters.

With the advantages of the multi-resolution analysis characteristic in wavelet domain operation, the correlation between the terrain and ice field after removing the global deformation was fully explored and efficiently employed in the topographic effect estimation and compensation. The DEM of the study area was considered as the proxy for the topographic effect compensation operations, avoiding the requirement for precise SAR imaging geometry parameters and a complex and time-consuming operation. In this paper, the final ice motion distribution results for the Muztagh Ata glacial region clearly confirm the efficiency of the presented RANSAC-based global fitting and wavelet-based topographic effect compensation algorithms for pixel tracking method. The corresponding ice motion is accurate enough to replace that obtained by the traditional DEM-assisted intensity feature tracking method, which is seriously dependent on SAR imaging geometry.

The final accurate estimation provides deep insight into the complex motion of the glaciers of the Muztagh Ata region in eastern Pamir. Flow velocities of about 196 m/y were found in the upper stream of the Qimgan Glacier, and a low velocity was observed at the terminus of most glaciers. The proposed approach was able to efficiently cover the widely varied ice motion, which will be helpful in the study of ice dynamics and motion prediction. The ice motion distribution of the largest glacier surface in this region was clearly and accurately yielded by the presented method, and the activities of tributaries can also be observed in the final results. Therefore, the wavelet-based topographic effect compensation method and the corresponding accurate motion field could be used to support the analysis and prediction of ice motion in mountain regions with complex terrain. Additionally, the observation result could help to improve the knowledge of ice motion, for an understanding of the status of the glaciers in the region.