Abstract
Fully polarimetric synthetic aperture radar (SAR) can provide detailed information on scattering mechanisms that could enable the target or structure to be identified. This paper presents a method to detect underwater topography in coastal areas using high resolution fully polarimetric SAR data, while less prior information is required. The method is based on the shoaling and refraction of long surface gravity waves as they propagate shoreward. First, the surface scattering component is obtained by polarization decomposition. Then, wave fields are retrieved from the two-dimensional (2D) spectra by the Fast Fourier Transformation (FFT). Finally, shallow water depths are estimated from the dispersion relation. Applicability and effectiveness of the proposed methodology are tested by using C-band fine quad-polarization mode RADARSAT-2 SAR data over the near-shore area of the Hainan province, China. By comparing with the values from an official electronic navigational chart (ENC), the estimated water depths are in good agreement with them. The average relative error of the detected results from the scattering mechanisms based method and single polarization SAR data are 9.73% and 11.53% respectively. The validation results indicate that the scattering mechanisms based methodology is more effective than only using the single polarization SAR data for underwater topography detection, and will inspire further research on underwater topography detection with fully polarimetric SAR data.
1. Introduction
Underwater features and ocean bathymetry is an indispensable information for coastal engineering and management and coastal resources exploitation and protection [1,2]. For example, safely navigating, offshore fishery and aquaculture, research on tide and biodiversity, planning for seawalls and wharf and other human activities are carried out in these areas where water depths less than 100 m. Detailed knowledge of water depth is very useful for them. Conventionally, water depth surveying are carried out by sonar measurements from dedicated vessels, which are accurate for point-measurement, but are not only expensive and time consuming but also difficult in shallow water areas, especially in some special water areas where routine surveying cannot be achieved [2,3].
Synthetic aperture radar (SAR) is an active microwave remote sensor that has the ability to image targets on the earth in both day and night, and for almost all weather conditions [1,4]. Therefore, SAR is widely applied in earth observation, especially in ocean observation. SAR polarimetry is the science of acquiring, processing and analyzing the polarization state of an electromagnetic field that will improve both the ability to characterize physical properties of objects and the retrieval of bio—or geophysical properties of the earth’s surface and subsurface [5,6]. Fully polarimetric (HH, HV, VH and VV) SAR can provide detailed information on scattering mechanisms (single bounce scattering, double bounce scattering and triple—and higher-order bouncing scattering) that could enable the target or the structure to be identified [5]. Under favorable conditions, sea floor topographic features in shallow water areas can be detected from SAR image intensity directly or other features in SAR image indirectly [3,4,7,8,9,10,11,12,13,14]. Therefore, SAR based method that needs less cost and labor and will enrich the means for underwater topographic surveying and mapping.
Underwater topography is conventionally detected by variations of the SAR image intensity which relies on the presence of a current, along with the presence of small-scale waves on the sea surface to provide the radar back scatter [1,3,8,10,14,15]. The typical of this method is Bathymetry Assessment System (BAS) which was based on the theory of imaging processes of underwater bottom topography by SAR proposed by Alpers and Hennings [3,14]. Li et al. shown that sand ridges parallel to tidal currents can also be imaged by SAR [16]. Bi et al. applied polarization information for underwater topography detection [17]. Under special conditions, deep-water (>500 m) bathymetry features can also be imaged by SAR [11]. However, the intensity variations based method depends on some real-time or near-real-time data (such as sea surface wind field and current field) and the calculation procedure of the algorithm is very complicated.
In contrast, swell patterns has been suggested to be applied in the detection of underwater topography. It relies on refraction of long surface gravity waves as they propagate shoreward and requires the assumption that the same wave train exists throughout the image [18]. Although this method has been used since World War II to estimate water depths based on changes in observable wave characteristics, approaches to detect bathymetry from swell patterns in SAR images have been proposed in the past two decades [4,7,9,12,13,18,19,20,21,22]. Pleskachevsky et al. explored bathymetry by the synergetic use of multiple remote sensed data resources (radar data from TerraSAR-X and optical data from QuickBird satellite) for coastal areas. Water depth between 20 m and 60 m is obtained with accuracy in order of 15% from SAR-based method. Water depth less than 20 m is detected by the optical-based method using sunlight reflection analysis. The depths in the range of 20 m up to 10 m represent the domain where the synergy of data from both sources arises [12]. Bian et al. estimated shallow water depth in coastal region where water depth is less than 10 m using HJ-1C (Huan Jing-1C, Huan Jing means environment in Chinese) SAR in S band [7]. In addition, this methodology had been developed by data processing [22] and using modulation transfer function (MTF) to account for the dependence of the strength of radar signatures of ocean waves on their wavenumber and propagation direction relative to the radar look direction [18]. Applicability of linear dispersion relationship and detected algorithm has been applied and discussed [7,21]. Comparing to the intensity variations based method, the swell patterns based method is simple and requires little prior information, but sharp water depths cannot be detected because they are filtered by the algorithm. Although the swell patterns based applications has been proposed and developed for bathymetry estimation using different band (L-band, S-band, C-band and X-band) spaceborne SAR data, they used single polarization data within the allowable error range.
The aim of this study is to develop a detection method based on swell patterns and scattering mechanism using fully polarimetric SAR data. First, different scattering components are obtained by polarization decomposition. Subsequently, shoaling waves are tracked by fixed grid from open sea to shoreline. Wavelength and wave direction can be retrieved by means of the Fast Fourier Transformation (FFT) computation from the dominant scattering component image. Finally, shallow water depth can be estimated using the linear dispersion relationship of ocean waves [1,21]. Moreover, this paper analyzes viability and potential performance for the case of application.
This paper is organized as follows. Section 2 describes materials and the swell patterns based method. Section 3 presents the detection results with one case study in Sanya coastal region, Hainan province, China. Section 4 discusses the proposed method for the application. In the end, conclusions are presented in Section 5.
2. Materials and Methods
2.1. SAR Data and Auxiliary Data
The fully polarimetric datasets of single look complex (SLC) fine quad-polarization C-band full-resolution RADARSAT-2 SAR data are collected for underwater topography detection. They are acquired on 18 September 2009 at 10:50:44 UTC over Sanya coastal region with coverage of 25 km by 25 km, Hainan province, China. Figure 1a–d shows the amplitude images of HH-polarized, HV-polarized, VV-polarized and color-coded image of the Freeman-Durden target decomposition: red, Ps; green, Pd; and blue, Pv with pixel spacing of 5 m respectively. In the monostatic backscattering case, the reciprocity constrains the scattering matrix to be symmetrical, that is, HV = VH. Therefore, VH-polarized image is not given. RADARSAT-2 satellite operates from a sun-synchronous orbit at a height of 798 km, and its platform velocity () is about 7.46 km/s. Acquisition parameters for the collected SAR datasets are given in Table 1.
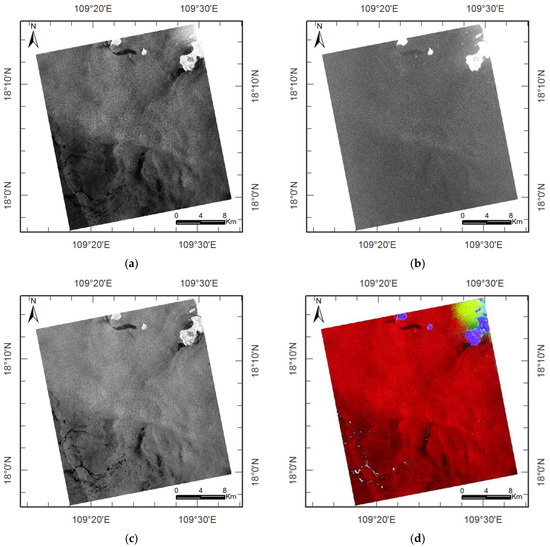
Figure 1.
The C-band fine quad-polarization RADARSAT-2 images and the polarization decomposition result in Sanya coastal region, Hainan province, China, acquired on September 18, 2009 at 10:50:44 UTC. RADARSAT-2 Data and Product © MacDonald, Dettwiler and Associates Ltd., All Rights Reserved. (a) HH-polarized image; (b) HV-polarized image; (c) VV-polarized image; (d) Color-coded image of the Freeman-Durden decomposition red, Ps; green, Pd; and blue, Pv.

Table 1.
RADARSAT-2 quad-polarization SAR data acquisition parameters.
Two different auxiliary data are used in this paper. For water depth information, the ENC (http://map.enclive.cn/) with different scale from the Navigation Guarantee Department (NGD) of the Chinese Navy Headquarter (CNH) is used for comparing and analyzing the detected results. Figure 2 shows low scale of water depth map from the ENC. For sea state, a wind vectors map from microwave scatterometer QuikSCAT and a photo was taken before the start time of the collected RADARSAT-2 data sets as shown in Figure 3 are used for estimating cut-off wavelength.
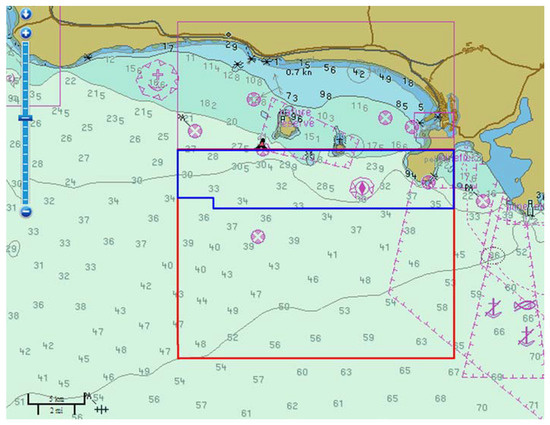
Figure 2.
Water depth map from electronic navigational chart via map.enclive.cn. The unit of water depth in this image is the meter. Low scale of water depths (46 pairs) in the red box are collected for comparison. High scale of water depths (305 pairs) in the blue polygon are also collected for comparison, but they are not presented in this figure. Water depth map © www.enclive.cn, All Rights Reserved.
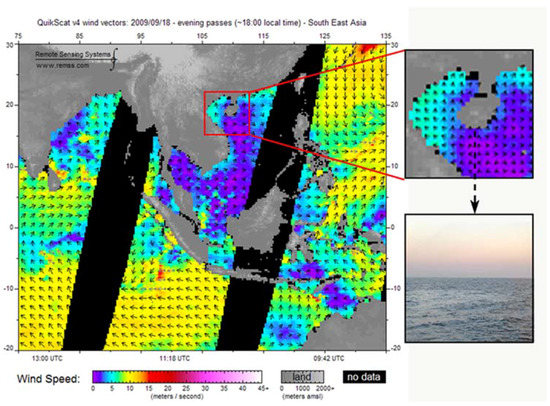
Figure 3.
A wind vectors map from microwave scatterometer QuikSCAT at 18:00 (local time) on 18 September 2009. The study area is outlined in red box. The lower-right portion is a photo of sea state over the study area before the start time of the collected RADARSAT-2 datasets.
2.2. Methods
2.2.1. SAR Imaging of Waves
SAR transmits radar signals and receives backscattered returns whose levels are directly dependent on ocean surface roughness. Ocean roughness is comprised of the mean surface slope, dominated by the long-wavelength field, and the short-scale waves that range between capillary and short-gravity waves. With incidence angle between 20° and 60°, Bragg scattering is the dominant backscatter mechanism, but not under all wind and wave states [1,4,23,24,25]. Under Bragg scattering, the normalized radar cross section (NRCS) of ocean is proportional to the amplitude of the small-scale waves called Bragg waves. Bragg waves are ocean surface waves which have wavelength equal to the projection of the SAR electromagnetic wavelength onto the local ocean surface and which are propagating either directly toward or away from the look direction of SAR [1]. It is expressed by the follow relation:
where is the wavelength of the Bragg wave, is the SAR electromagnetic wavelength, and is the local incidence angle. For incidence angle less than 15°, the specular scattering takes a significant contribution in the radar backscatter, while for incidence angle larger than 70°,the wedge scattering is most prevalent [1,26].
The combination of Bragg scattering with the two-scale approximation is used to describe the interaction of short and long waves, but not under all wind and wave states and radar system configurations. When imaging ocean surface waves, the main modulation mechanisms have been identified as three modulation mechanisms: title modulation, hydrodynamic modulation and velocity bunching modulation [1,6,27]. Title modulation means the longer waves change the local slope of the shorter wave fields. It is strongest for waves travelling in the range direction. Hydrodynamic modulation means the longer waves change the distribution of the shorter wave fields. Velocity bunching modulation means the motion of the long waves alters the SAR imaging process that is unique to SAR imaging systems. If the azimuth shift is less than a wavelength, azimuth-traveling waves are linearly mapped in the SAR imagery. On the contrary, when the displacements are greater than a wavelength, the mapping of waves on the imagery will be nonlinear and distorted. It is greatest for waves travelling in the azimuth direction. When long waves are propagating in a direction perpendicular to the SAR platform, title modulation and hydrodynamic modulation have the strongest effects on the SAR returns [1,28].
Under specific conditions, the imaging mechanism of sea surface can be assumed linear. In general, the imaging mechanism of sea surface by SAR is not linear [1,23]. Therefore, a SAR image cannot be interpreted as a picture of the surface because the orbital motion of longer ocean waves with azimuth component allows the waves to be imaged through the velocity bunching mechanism, the random motions of the ocean surface caused by the short scale waves introduce random position shifts in the azimuth direction that in turn degrade the azimuth resolution and thus limits the detectable ocean wavelengths [1,4,23]. Even though the SAR image contains swell patterns, it may not be suitable for underwater topography detection. However, linear imaging can be assumed under specific conditions, such as not extreme wind speed and sea state, absence of currents, and swell patterns characterized by wavelengths that are greater than cut-off conditions. In other words, the image modulation of azimuth-travelling waves by velocity bunching is linear if the ratio of wave height to wavelength is small. The cut-off wavelength can be estimated by a simple empirical relationship:
where is the slant range, is the platform velocity, is the significant wave height. The lower the satellite orbit and the smaller the wave height, the shorter shoaling waves will be detected. When these conditions are satisfied, the swell wavelengths imaged by SAR represent an unbiased estimate of the true swell wavelengths [21].
2.2.2. Freeman-Durden Decomposition
The Freeman-Durden decomposition is a technique for fitting a physically based, three-component mechanism model to the polarimetric SAR observations, without utilizing any ground truth measurements [5,29]. The mechanisms are a canopy scatter from a cloud of randomly oriented dipoles, even—or double-bounce scatter from a pair of orthogonal surfaces with different dielectric constants, and Bragg scattering from a moderately rough surface [5]. This model can be used to determine to first order, what are the dominant scattering mechanisms that give rise to observed backscatter in polarimetric SAR data. The contribution of each scattering mechanism from Freeman-Durden three-component decomposition can be estimated to the span, following:
where is the power of surface scattering component, is the power of double-bounce scattering component, and is the power of volume scattering component.
Unlike ground covers, backscattering from ocean surface is considerably homogeneous in scattering mechanism, and can be, in most cases, characterized by a two-scale titled Bragg scattering model. The contribution of Bragg surface scattering is given by
where corresponds to the contribution of the single-bounce scattering to the components, with
2.2.3. Wave Shoaling and Refraction
Shoaling and refraction of waves occur when the waves are in shallow water. If the water depth is less than half of the wavelength, then the wave is considered to be in shallow water. As waves travel from deep to shallow water, their shape alters, for example, wave height increase, speed decrease, and length decrease as wave orbits become asymmetrical. This process is called shoaling. Wave refraction is the process by which wave crests realign themselves as a result of decreasing water depths. Varying depths along a wave crest cause the crest to travel at different phase speeds, with those parts of the wave in deeper water moving faster than those in shallow water [1]. This process continues until the crests become parallel to depth contours or the wave breaks regardless of the original direction in deeper water.
Phenomena of swell wave shoaling and refraction due to underwater morphology start appearing in intermediate water depth because surface waves begin to “feel” the bottom when sea water depth is shorter than about half of the swell wavelength. It means that bathymetry through swell wave modulation can be performed only for water depth values lower than half the swell wavelength, that is, the limit water depth value [21].
2.2.4. Linear Dispersion Relationship
The linear dispersion relationship is based on the Airy wave theory. For freely propagating ocean waves, the wave number, wave frequency and water depth are not independent, but are linked by the wave dispersion relation [2,30]. If the effect of current can be neglected, the linear dispersion relation is given by:
where is the angular wave frequency (, is the wave period), is the gravitational acceleration (9.8 m/s2), is the wave number (, is wavelength ), is the water depth in the range between and .
Using Equation (6), water depth can be written as Equation (7).
2.2.5. Description of the Algorithm for Underwater Topography Detection
In this paper, an algorithm based on swell patterns and scattering mechanism using fully polarimetric SAR data is presented for underwater topography detection. Because microwave signals emitted by SAR are able to penetrate into just a few centimeters, they are unable to reach the seabed [1,21]. Therefore, underwater topography is detected indirectly. In the near-shore region, surface waves can “feel” the bottom, causing changes in the wave’s length and direction of wave propagation. Shoaling waves are tracked by FFT computation. Shallow water depth can be estimated due to the fact that SAR images are able to image swell waves in the ocean and their wavelength can be connected to the local depth. There are four steps in underwater topography detection from fully polarimetric SAR data:
(1) Obtaining dominant scattering component. Under moderate wind conditions and at intermediate incidence angle, sea surface scattering which calls for Bragg scattering is a single-reflection and dominant scattering mechanism [5]. Therefore, the Bragg scattering component from polarimetric decompositions can be used for underwater topography detection. In this paper, Freeman-Durden three-component decomposition is used.
(2) Estimation of angular wave frequency. The angular wave frequency can be calculated from other sources or first guesses of initial water depth or wave period. Firstly, the collected SAR images are analyzed. Only those have obvious swell wave features over the shallow water may be used to estimate water depth. Then wavelength and direction of the swell waves are calculated and analyzed. How to estimate swell wave parameters will be given in the next step in detail. Sub images over the isobaths are chosen for the initial angular wave frequency estimation, whereas sub images over different depth are chosen for swell patterns analyzing. Finally, the angular wave frequency is calculated by the linear dispersion relation (Equation (6)) from first guesses of initial water depth or water depth from other resources [4,12]. It can also be calculated by wave period from other resources (buoys, weather services).
If swell wave belongs to shallow water domain (the water depth is less than half of the wavelength), where it can be influenced by the underwater topography. The threshold minimum peak period () for the peak wavelength () is used to distinguish the specified swell wavelength belongs to deep water domain or shallow water domain. It is obtained from deep water relation:
where is the gravitational acceleration. For water depth estimation, the wave period should be greater than peak period. If the wave period is smaller than peak period, the wave belongs to deep water domain.
(3) Retrieval of wave fields. The swell wave parameters for shallow water depth estimation are calculated by FFT computation from the dominant scattering component image. By means of the FFT for the selected sub image, a two-dimensional (2D) image spectrum in wave number space is obtained. The peak in the 2D spectrum marks wavelength and wave direction of all waves visible in the sub image. The wavelength and direction of swell wave can be estimated from the following formula [4,12,31]:
where is the wavelength, is the wave direction with respect to the sub image, and are the peak coordinates in the wave number space. The retrieved directions have an ambiguity of 180°due to the static nature of a SAR image [4]. This ambiguity can be solved with information from the cross spectrum or first guess information from other sources. In shallow water where wave shoaling and refraction appear, the ambiguity problem can be solved by manual inspection. In most case, waves can be considered propagating toward the costal line or propagating along the direction that the water becomes shallower.
Swell wave fields map can be retrieved by ray tracing mode, fixed grid mode or the integrated mode [7]. Ray tracing mode tracks the long wave in the wave direction with the distance related to the wavelength. The distance between the neighboring wave rays is fixed. In this way, the wave can be tracked from the open sea to the shoreline and the change in wavelength and direction can be measured. Fixed grid mode tracks the long wave not in the wave direction but at a constant specified shift. In this way, the wave can also be tracked from the open sea to the shoreline uniformly and the change in wavelength can be measured. Integrated mode tracks the long wave by two modes mentioned above. In this paper, wavelength and wave direction are retrieved by fixed grid using FFT.
Starting from the open ocean, FFT-box (e.g., 1024 × 1024) is moved with a constant specified shift (dx and dy, e.g., dx = dy = 30), then a new FFT is computed. The same process repeats until the FFT box reaches both row edge and column edge of the image for the fixed grid mode. After swell wave tracking, a uniform wave field map is produced.
(4) Detection of underwater topography. By inserting the known wave frequency from step 2 and the wave fields map from step 3, shallow water depths are estimated from the linear dispersion relation for ocean gravity waves. In the end, all estimated shallow water depths are analyzed and abnormal data (e.g., water depth over the land and island, water depth from the FFT-box image has invisibility swell patterns) will be removed.
3. Results
Based on the assumption of the presence of a single wave system in the SAR image of the study area, the shallow water depths map from the quad-polarization SAR data is presented. Results are compared with the values from an official ENC to evaluate the quality of the proposed method.
3.1. Underwater Topography Results
Figure 4 shows the obtained Bragg scattering component image and image spectra. Before shallow water depth estimation, the fully polarimetric datasets of SLC fine quad-polarization RADARSAT-2 SAR data are processed by PolSARpro version 5.0.4. Data processing includes SLC data import, coherency matrix T3 extraction and geometric rectification. Then dominant scattering component is obtained by the Freeman-Durden decomposition which adopts 5 × 5 average window size. There are 12 different subset areas (1024 × 1024 pixels, a to l) are used for image spectrum analyzing and swell wave parameters estimation.
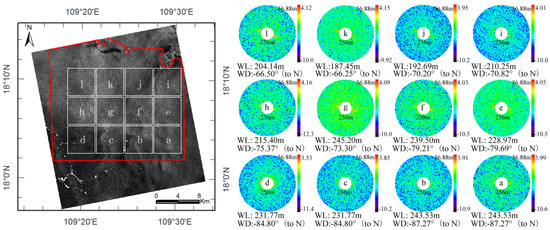
Figure 4.
Image spectra (to be scaled and converted to bytes) for the subscenes of Bragg scattering component image from Freeman-Durden decomposition divided by three rows (in azimuth direction ) and four columns (in opposite range direction) labeled a to l. The red polygon is used to create a buffer polygon with distance 1.28 km. Results outside the inner line are removed. Each spectrum corresponds to a subscene (1024 × 1024 pixels) of 5.12 km by 5.12 km. In order to display back ground as white value, some features in the down left corner of the image are changed to display as white color. Actually, some of them are biogenic film that should display as black color. The corresponding wavelength (WL) and wave direction (WD) are on the right for wave parameters estimation and analyzing.
By computing the FFT, wavelength and propagation direction of these areas are estimated from the 2D spectrum (wavelength between 56.88 m and 256 m are kept and wind streaks are removed based on analysis of image spectra). The wavelength and the relative deep water depth of the region labeled a (Figure 4) are about 243.53 m and 65.0 m (Figure 2). Accordingly, the angular wave frequency () computed by the dispersion relationship (from Equation (6)) is about 0.48556 rad/s and wave period () is about 12.94 s. The ratio of water depth (65 m) and wavelength (243.53 m) is less than 0.3 that means these areas belong to shallow water domain. The island and coastal line is on the top of the study area where topography is relatively flat. In general, obtained wavelengths both from east to west and south to north direction are decreasing and the corresponding water depth is becoming lower. Therefore, problem of the 180° ambiguity of the swell wave direction is resolved and swell waves can be considered propagating toward the costal line.
Figure 5 shows wave tracking results. According to the surface swell patterns in the study area, wave field map is tracked by the fixed grid mode. Every arrow means a FFT-box. Its length means three times of wavelength and direction means the propagating direction of wave. Waves over or near the island are removed from the map by buffer polygon with distance 1.28 km from the red polygon as shown in Figure 4. The distance between the tracked FFT-boxes is set to 1600 m. The change in both wavelength and direction caused by wave shoaling and refraction are clearly visible in Figure 5.
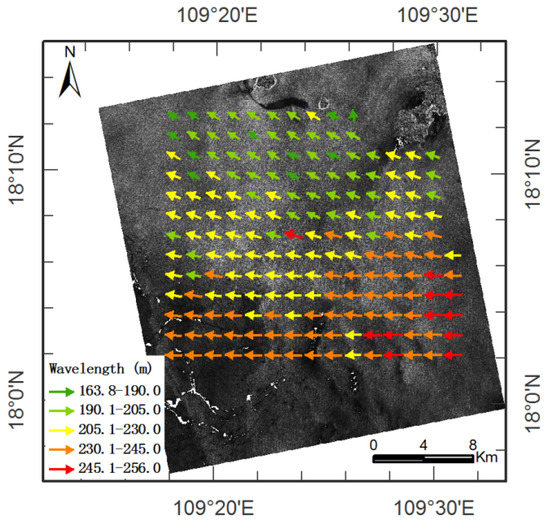
Figure 5.
Wave fields map by fixed grid mode. Each arrow corresponds to a subscene of 1024 × 1024 pixels. The distance between two arrows is 1.6 km (320 pixels). Its length means three times of wavelength and direction means the propagating direction of swell waves.
The longest tracked wavelength () is 256 m as shown in Figure 5. Accordingly, the threshold minimum peak period ( from Equation (8)) is 12.81 s. The obtained wave period (12.94 s) is greater than minimum peak period (12.81 s) that is also show the study area belongs to shallow water domain.
Figure 6 shows underwater topography results from the Freeman-Durden decomposition component of Bragg scattering image. Swell wave fields are tracked by the fixed grid mode which the distance between the tracked FFT-boxes with size of 1024 × 1024 is set to 150 m. The obtained swell wave fields of each FFT-box are sorted from smallest to largest and the last three are averaged as final wavelength. Shallow water depths are estimated from the averaged wavelengths and the estimated wave period (12.90 s) by the linear dispersion relationship (Equation (7)) based on the assumption of the presence of a single wave system in the SAR image. During the calculation, if water depth is greater than 65 m, it will be replaced by 65 m. The estimated water depths where absolute error of the estimated depth is more than 10 m (nearly 25% of the average water depth) are replaced with the value from the nearest location of the ENC as shown in Figure 2. By comparing Figure 2 with Figure 6, the estimated results have accordance well with water depth map from the ENC and have higher spatial resolution, that is, have more detailed underwater topography.

Figure 6.
Three-dimensional of underwater topography with resolution of 150 m by 150 m. The estimated water depths where absolute error of the estimated depth is more than 10 m are replaced with the value from the nearest location of the ENC as shown in Figure 2.
3.2. Comparing with ENC
In order to validate the detected results, there are 46 pairs of the depth estimated from the Bragg scattering component image are selected according to the nearest neighbor distance of the low scale of ENC as shown in Figure 2. When wave period is set to 12.9 s, the average absolute error is about 3.93 m and the average relative error is about 9.73%. The scatter plot as shown in Figure 7 is presented to show the general agreement of the detected results and the water depths from low scale of ENC.
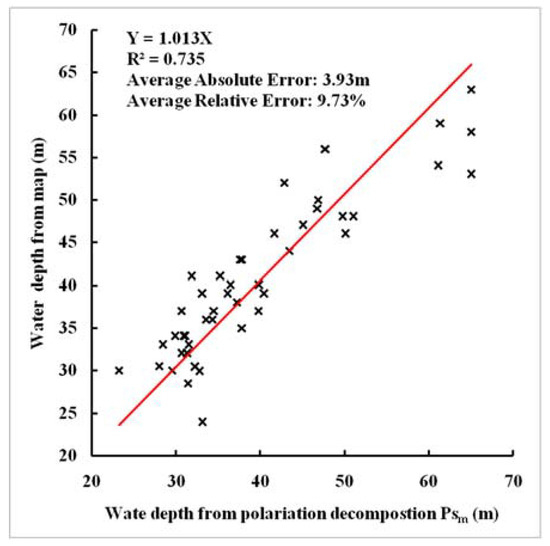
Figure 7.
Scatter plot of the estimated results and water depths from low scale of ENC, for a wave period of 12.90 s.
For further evaluation, there are 305 pairs of water depth from local high scale of ENC in the blue polygon are also collected for comparison. For local comparison, the average absolute error is about 2.57 m and the average relative error is about 8.76%. Results show that the proposed algorithm is feasible and keep more detailed underwater topography. If water depths from ENC are not obsolete, the estimated water depth can be adjusted that will improve the underwater topography detection accuracy.
In order to evaluate whether some of SAR data pre-processing procedures and the introduced detected algorithm will affect the accuracy of the detected accuracy, speckle filtering, different pixel spacing, different subscene size of FFT box and different input images are used for comparing. In this section, wave period is set to 12.9 s and the distance between two FFT-boxes is set to 150 m unless they are specially explained. For smooth filtering, results of comparison between estimated water depths from SAR image and ENC are shown in Table 2. VVsm and HHsm means smoothed VV-polarized and HH-polarized SAR data with pixel spacing of 5 m respectively. Table 3 presents errors of estimated water depths with different pixel spacing (12.5 m, 10 m, 8 m, 5 m). For example, VV5 means VV-polarized image with pixel spacing of 5 m. Table 4 presents errors of estimated water depths with different subscene size of VV-polarized image (256, 512, 1024) for FFT-box. Take for example, VV256 means the size of FFT-box is 256. Table 5 shows comparison results from different input image. VVm, Psm and Ysm means wavelengths from VV-polarized image, surface scattering component image from Freeman-Durden decomposition and Yamaguchi decomposition are the average of the top three wavelengths respectively.

Table 2.
Errors of estimated water depths from single polarization SAR image.

Table 3.
Errors of estimated water depths with different pixel spacing of VV-polarized image.

Table 4.
Errors of estimated water depths with different subscene size of VV-polarized image.

Table 5.
Errors of estimated water depths with different input image.
4. Discussion
A method is proposed which is based on swell patterns and dominant scattering component from polarization decomposition. The new method uses fully polarimetric SAR data for underwater topography detection indicates that it will improve the accuracy of detection. For underwater topography detection, the proposed method and SAR image intensity variations based method are not independent but complementary. Although both of them may be not precisely accurate, they can provide general information about depth changes, especially in coastal areas where underwater topography could not easily be detected by other means.
Comparing to conventional amplitude/intensity images, the proposed method is based on scattering component from polarization decomposition that aims at providing more information for applications. Although advances in the high-resolution SAR technology provide the capability of obtaining detailed target signatures, interpreting SAR images of some special targets or structures or estimating parameters are always being a challenge, especially for single polarization SAR. Experimental results as shown in Table 5 indicate that the dominant scattering mechanism based methodology is more effective than only using the single polarization SAR data for underwater topography detection. They also show single polarization SAR image can be used for shallow water depth estimation using linear dispersion relationship with some accuracy that confirm former studies on the swell patterns based method [4,7,18,19,21,22]. For single polarization SAR data, errors from VV-polarized (VV) SAR data are better than from HH-polarized SAR data, but all relative errors are above 10%. Cross-polarization (HV and VH) SAR data do not discuss here because the investigations have demonstrated that the cross-polarization radar backscatter is not sensitive to incidence angle, but is dependent on wind speed especially under high sea states [32,33]. The Freeman-Durden decomposition results as shown in Figure 1 shows that color red is dominant. It confirms that the surface scattering is the dominant backscatter mechanism with incidence angle between 20–60°, but not under all wind and wave states. Errors from the Bragg scattering component (Ps) by Freeman-Duren decomposition are better than from single polarization SAR data. For fully polarimetric SAR data, errors from the Bragg scattering component by processed wavelengths (Psm) is better than unprocessed wavelengths, and is also better than processed wavelength from VV-polarized SAR data (VVm). The dominant scattering mechanism based method produces good results and reduces the average relative errors to less than 10% that indicates fully polarimetric SAR data can be used for underwater topography detection with good accuracy. In addition, the proposed method is simple but model-based and needs less prior information (even nothing) than the variations of the SAR image intensity based method, especially for relative flat underwater topography. In the test case, we only used one referenced water depth as input parameter, but large covered underwater topography with acceptable errors is obtained. Since ocean wave parameters (e.g., wave height) and other environmental parameters (e.g., wind speed) can be estimated from SAR image [6,31,33,34,35], the proposed algorithm can be developed in the future.
Results as shown in Table 2 imply that speckle filtering will improve the detected accuracy. Although errors of local high resolution from the filtered VV-polarized data is a little higher than other results, in general, errors from smoothed data (VVsm and HHsm) are better than initial data (HH and VV) that supports view of speckle filtering will improve the detected accuracy. For a given SAR data, different pixel spacing can affect the accuracy of wave detection. Nominal resolution of fine beam modes of RADARSAT-2 is 8 m and sampled pixel spacing of the collected SLC data is 4.73 m. Table 3 presents errors of estimated water depths with different pixel spacing. It shows that pixel spacing larger than 10 m will reduce the accuracy of water depth detection. Consequently, pixel spacing should be set near the nominal resolution. The scale of sea surface waves is usually between 100 m and 600 m [1]. If pixel spacing is set too small, it will take up more processing time and not improve the accuracy. Generally, the size of FFT-box is set to 512 or multiples of 512. Results as shown in Table 4 indicate that the larger the size, the higher the accuracy will get. When the size of FFT-box is changed from 1024 to 512, errors are more than doubled. Although errors from 512 are also better than from 256 that may keep some detailed underwater topography, but the averaged relative error larger than 20% is unacceptable. Meanwhile, the size of FFT-box should not be set too large that will take up processing time and reduce some detailed underwater topography.
The sea state over the study area as shown in Figure 3 is not high [36]. It is supposed that the significant wave height () is set to 1.0 m and wind speed (10 m over sea) is set to 5.0 m/s. For a given incidence angle (the near range, 32.353 deg), the cut-off wavelength can be estimated from Equation (2) with slant range () of 919.8 km as 123.3 m. It is less than the minimum of the detectable wavelengths (163.8 m) that means the estimated results are plausible.
For ocean waves, under the Bragg scattering conditions, backscattered signals in general are from single bounce. The single bounce returns from the ocean surface possess the typical Bragg resonant scattering characteristic. Although single polarization amplitude/intensity images keep some swell patterns, the surface scattering component image keeps swell patterns more visible than them and the other two components (the double-bounce and volume scattering components). Results from Freeman-Durden three-component scattering decomposition indicate that the surface scattering component is the dominant scattering over the sea in our test area. However, Freeman-Durden decomposition contains two important assumptions (the assumed three-component scattering model is not always applicable and reflection symmetry) which limit its applicability [5]. Yamaguchi decomposition is used to check the applicability of the surface scattering component from Freeman-Durden decomposition [37]. The results confirm that the surface scattering is the dominant scattering and the surface scattering component image keeps the detailed swell patterns, and as shown in Table 5, indicate that the dominant scattering component based method is applicable in our test area, and both absolute error and relative error are nearly in the same error range. It should be noted that this study has examined only one scene fully polarimetric SAR data. In the future, the dominant scattering component based method will be tested and developed, and further research on underwater topography detection with fully polarimetric SAR data may be inspired.
5. Conclusions
In this paper, an underwater topography detection algorithm based on swell patterns is developed. In comparison to methods published previously, the proposed method depends on the Bragg scattering component which is the dominant scattering of sea surface in most common cases. One scene of fully polarimetric RADARSAT-2 SAR data covering the near shore water of Hainan Island is used in this investigation, and the ENC are used for comparing and analyzing. The average absolute error is within 4.0 m with the average relative error less than 10.0%. For local comparison, the average relative error is less than 9.0%. Due to full polarimetric system provided the most extensive multi-parameter ocean data, fully polarimetric SAR data can be used for feature extraction and information retrieval. Furthermore, the conventional SAR image intensity variations based method is of limited use under less current condition. Therefore, the proposed method can be used for underwater topography detection with less initial input parameters and better accuracy than single polarization SAR data. Although fully polarimetric SAR data have limited swath coverage, they provide unique information on sea surface scattering mechanisms that can be used for underwater topography detection and other applications. As GF-3 Satellite was launched successfully, we may acquire more fully polarimetric SAR data that can be used to verify and develop the proposed method in the future. The dominant scattering component based method can, potentially, be developed for further into fully operational algorithms. The improved method may be used for further underwater topographic mapping with higher temporal resolution and spatial resolution.
Acknowledgments
This study is jointly supported by the National Science Foundation of China (Grant No. 41431174), the National Key Research and Development Program of China (Grant No. 2016YFB0502504) and the National Science Foundation of China (Grant No. 61471358). The authors would like to thank the three anonymous reviewers and the editors for their comments and suggestions that improved the manuscript.
Author Contributions
Xiaolin Bian, Yun Shao, Wei Tian and Chunyan Zhang conceived and designed the research. Xiaolin Bian and Chunyan Zhang performed the experiments. Xiaolin Bian and Yun Shao analyzed the data and results. Wei Tian and Chunyan Zhang conducted validation. Shiang Wang, Xiaochen Wang and Zhixin Zhang contributed materials. Xiaolin Bian wrote the paper. All authors read and approved the final version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jackson, C.R.; Apel, J.R. Synthetic Aperture Radar Marine User's Manual; NOAA: Washington, DC, USA, 2004. [Google Scholar]
- Holland, T.K. Application of the linear dispersion relation with respect to depth inversion and remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2319. [Google Scholar] [CrossRef]
- Calkoen, C.J.; Hesselmans, G.H.F.M.; Wensink, G.J.; Vogelzang, J. The bathymetry assessment system: Efficient depth mapping in shallow seas using radar images. Int. J. Remote Sens. 2001, 22, 2973–2998. [Google Scholar] [CrossRef]
- Brusch, S.; Held, P.; Lehner, S.; Rosenthal, W.; Pleskachevsky, A. Underwater bottom topography in coastal areas from TerraSAR-X data. Int. J. Remote Sens. 2011, 32, 4527–4543. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: London, UK, 2009. [Google Scholar]
- Schuler, D.L.; Lee, J.S.; Kasilingam, D.; Pottier, E. Measurement of ocean surface slopes and wave spectra using polarimetric SAR image data. Remote Sens. Environ. 2004, 91, 198–211. [Google Scholar] [CrossRef]
- Bian, X.; Shao, Y.; Tian, W.; Zhang, C. Estimation of shallow water depth using HJ-1C S-band SAR data. J. Navig. 2016, 69, 113–126. [Google Scholar] [CrossRef]
- Fan, K.; Huang, W.; Lin, H.; Pan, J.; Fu, B.; Gu, Y. Shallow water depth retrieval from space-borne SAR imagery. J. Oceanogr. 2011, 67, 405–413. [Google Scholar] [CrossRef]
- Fan, K.; Huang, W.; He, M.; Fu, B.; Zhang, B.; Chen, X. Depth inversion in coastal water based on SAR image of waves. Chin. J. Oceanol. Limn. 2008, 26, 434–439. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J.; Meng, J. Underwater topography detection of Taiwan Shoal with SAR images. Chin. J. Oceanol. Limn. 2010, 28, 636–642. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Zheng, Q.; Pietrafesa, L.J.; Pichel, W.G.; Li, Z.; Li, X. Deep-water bathymetric features imaged by spaceborne SAR in the Gulf Stream region. Geophys. Res. Lett. 2010, 37, 96–104. [Google Scholar] [CrossRef]
- Pleskachevsky, A.; Lehner, S.; Heege, T.; Mott, C. Synergy and fusion of optical and synthetic aperture radar satellite data for underwater topography estimation in coastal areas. Ocean Dynam. 2011, 61, 2099–2120. [Google Scholar] [CrossRef]
- Wackerman, C.; Lyzenga, D.; Ericson, E.; Walker, D. Estimating Near-Shore Bathymetry Using SAR. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing Symposium, Seattle, WA, USA, 6–10 July 1998; pp. 1668–1670. [Google Scholar]
- Alpers, W.; Ingo, H. A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar. J. Geophys. Res. Oceans 1984, 89, 10529–10546. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J.; Meng, J. A detection model of underwater topography with a series of SAR images acquired at different time. Acta Oceanol. Sin. 2010, 29, 28–37. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Xu, Q.; Pichel, W.G. Sea surface manifestation of along-tidal-channel underwater ridges imaged by SAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2467–2477. [Google Scholar]
- Bi, X.; Meng, J.; Yang, J.; Liu, Q. Application of SAR polarization information for detection of underwater topography. J. Remot. Sens. 2013, 17, 34–45. (In Chinese) [Google Scholar]
- Monteiro, F. Advanced Bathymetry Retrieval from Swell Patterns in High-Resolution SAR Images. Master Thesis, University of Miami, Coral Gables, FL, USA, December 2013. [Google Scholar]
- Mishra, M.K.; Ganguly, D.; Chauhan, P.; Ajai. Estimation of coastal bathymetry using RESAT-1 C-band microwave SAR data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 671–675. [Google Scholar] [CrossRef]
- Li, X.; Lehner, S.; Rosenthal, W. Investigation of ocean surface wave refraction using TerraSAR-X data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 830–840. [Google Scholar]
- Boccia, V. Linear dispersion relation and depth sensitivity to swell parameters: Application to synthetic aperture radar imaging and bathymetry. Sci. World J. 2015, 2015, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Boccia, V.; Renga, A.; Moccia, A.; Zoffoli, S. Tracking of coastal swell fields in SAR images for sea depth retrieval: Application ALOS L-band data. IEEE J. Sele. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3532–3540. [Google Scholar] [CrossRef]
- Hasselmann, K.; Raney, R.K.; Plant, W.J.; Alpers, W.; Shuchman, R.A.; Lyzenga, D.R.; Rufenach, C.L.; Tucker, M.J. Theory of synthetic aperture radar ocean imaging: A MARSEN view. J. Geophys. Res. Atmos. 1985, 90, 4659–4686. [Google Scholar] [CrossRef]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound. Lay. Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Romeiser, R.; Alpers, W. An improved composite surface model for the radar backscattering cross section of the ocean surface: 2. Model response to surface roughness variations and the radar imaging of underwater bottom topography. J. Geophys. Res. Atmos. 1997, 102, 25251–25267. [Google Scholar] [CrossRef]
- Ouchi, K. A theory on the distribution function of backscatter radar cross section from ocean waves of individual wavelength. IEEE Trans. Geosci. Remote Sens. 2000, 38, 811–822. [Google Scholar] [CrossRef]
- Alpers, W.; Ross, D.B.; Rufenach, C.L. On the detectability of ocean surface waves by real and synthetic aperture radar. J. Geophys. Res. Atmos. 1981, 86, 6481–6498. [Google Scholar] [CrossRef]
- Zheng, Q.; Li, L.; Guo, X.; Yong, G.; Zhu, D.; Li, C. SAR imaging and hydrodynamic analysis of ocean bottom topographic waves. J.Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Kirbya, J.T.; Dalrympleb, R.A. An approximate model for nonlinear dispersion in monochromatic wave propagation models. Coast. Eng. 1986, 9, 545–561. [Google Scholar] [CrossRef]
- Collard, F.; Ardhuin, F.; Chapron, B. Extraction of coastal ocean wave fields from SAR images. IEEE J. Oceanic Eng. 2005, 30, 526–533. [Google Scholar] [CrossRef]
- Tian, W.; Shao, Y.; Yuan, J.; Wang, S. An experiment for oil spill recognition using RADARSAT-2 image. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HA, USA, 25–30 July 2010; pp. 2761–2764. [Google Scholar]
- Vachon, P.W.; Wolfe, J. C-band cross-polarization wind speed retrieval. IEEE Geosci. Remote Sens. Lett. 2011, 8, 456–459. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.; Perrie, W.; He, Y. Synergistic measurements of ocean winds and waves from SAR. J. Geophys. Res. Oceans 2015, 120, 6164–6184. [Google Scholar] [CrossRef]
- Shao, W.; Zhang, Z.; Li, X.; Li, H. Ocean wave parameters retrieval from Sentinel-1 SAR imagery. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Vachon, P.W.; Li, X.; Pichel, W.G.; Guo, J.; He, Y. Ocean vector winds retrieval from c-band fully polarimetric SAR measurements. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4252–4261. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).