Hyperspectral Target Detection via Adaptive Joint Sparse Representation and Multi-Task Learning with Locality Information
Abstract
:1. Introduction
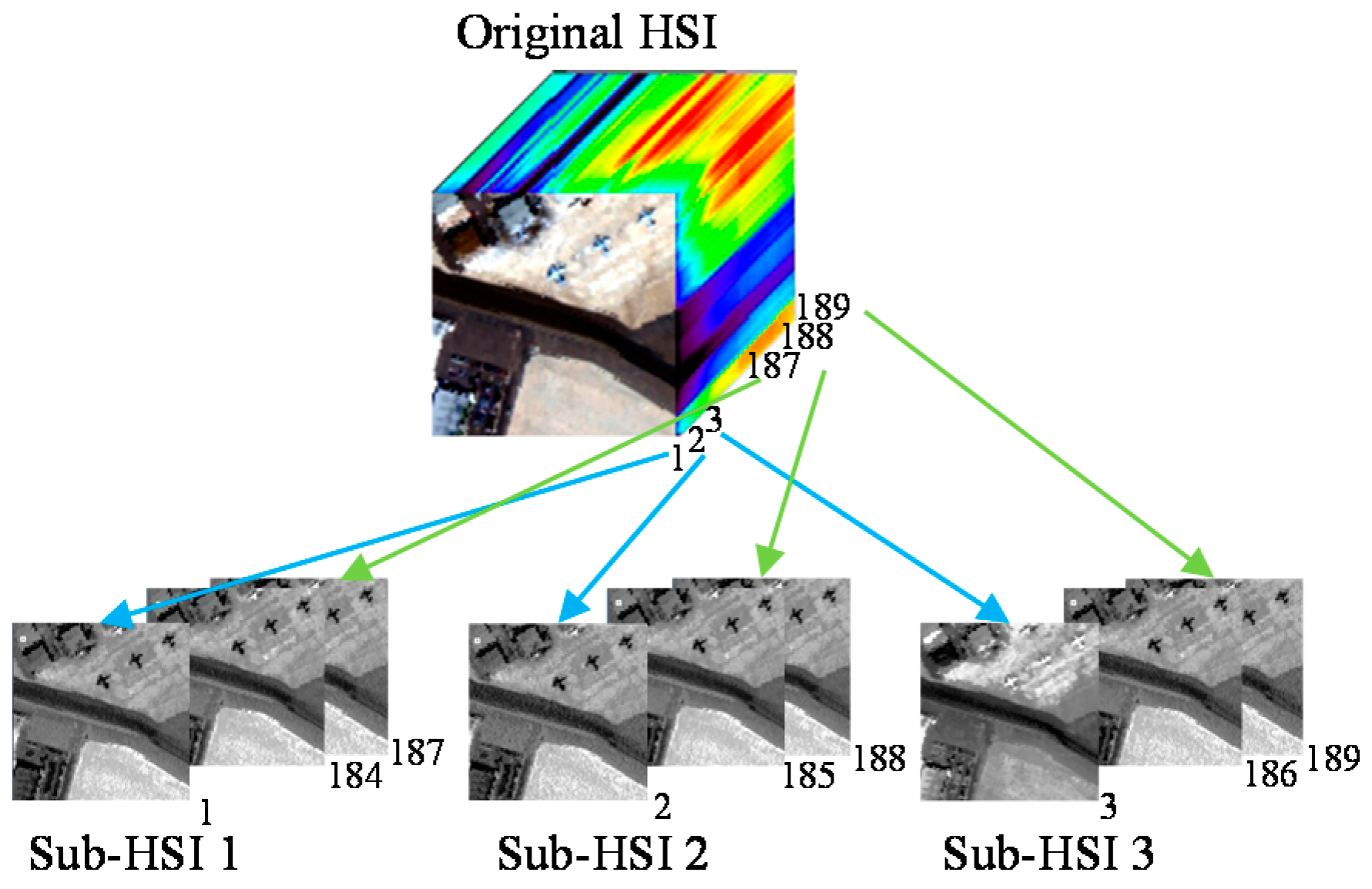
2. Brief Introduction to the JSR-MTL Method
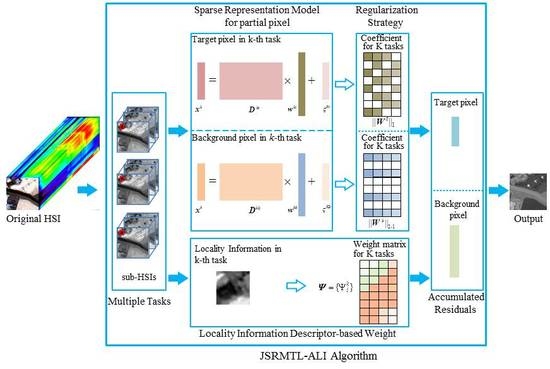
3. Adaptive JSR-MTL with Locality Information Detector
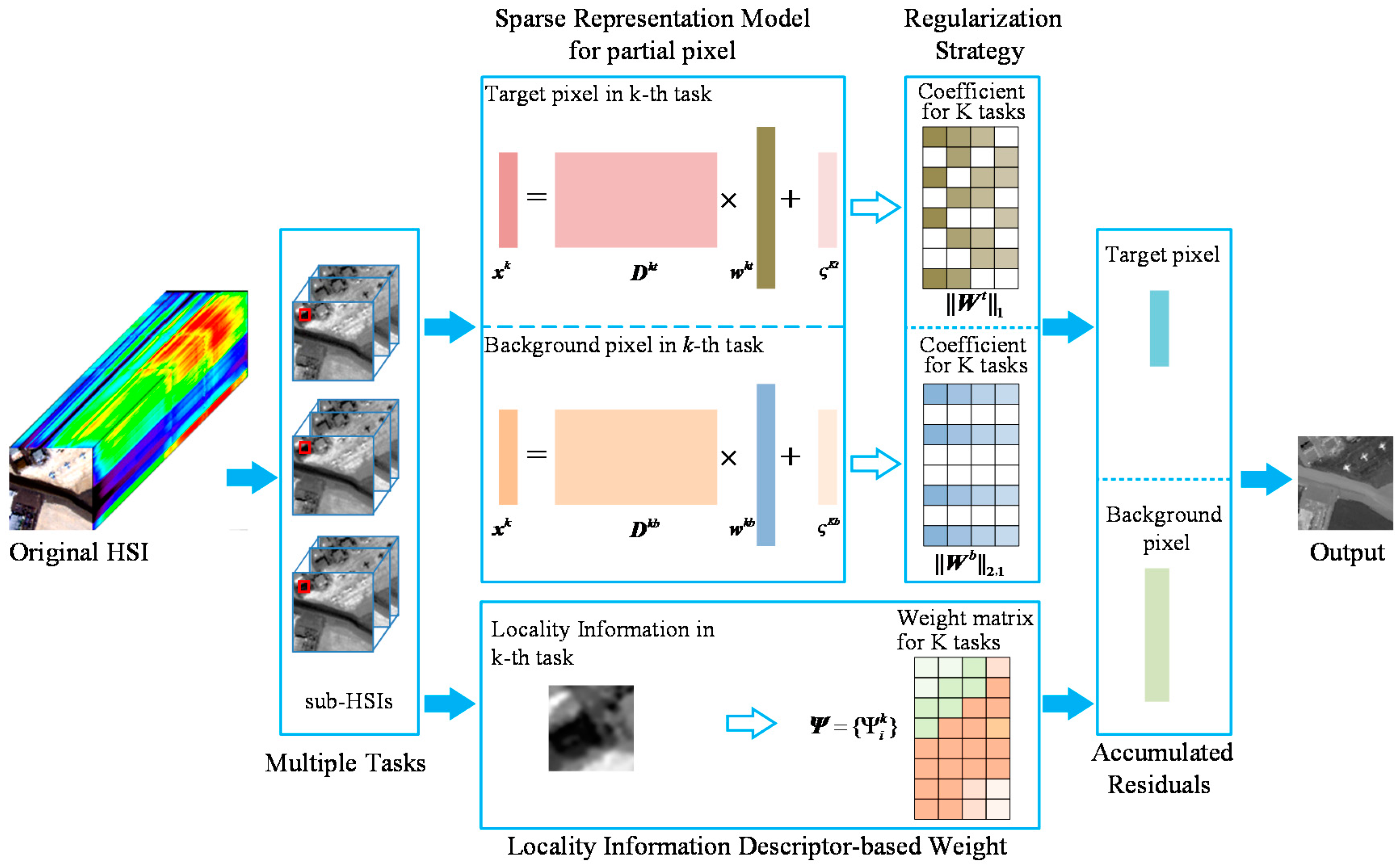
3.1. Adaptive JSR-MTL Model
3.2. Locality Information Descriptor-Based Weight
3.3. Model Optimization
| Algorithm 1. The Coefficients over Target Dictionary Optimization Algorithm. |
| Input: Data , regularization parameter Output: Coefficient vectors Step (1): Initialization: , , , Step (2): Repeat {Main loop} a) b) c) , d) Until: convergence is attained |
| Algorithm 2. The Coefficients over Background Dictionary Optimization Algorithm. |
| Input: Data , regularization parameter , locality information descriptor Output: Coefficient vectors Step (1): Initialization: , , , Step (2): Repeat {Main loop} a) b) c) , d) Until: convergence is attained |
3.4. Final Sketch of the JSRMTL-ALI Detector
4. Experiments and Analysis
4.1. Dataset Description
4.2. Evaluation of JSRMTL-ALI Model
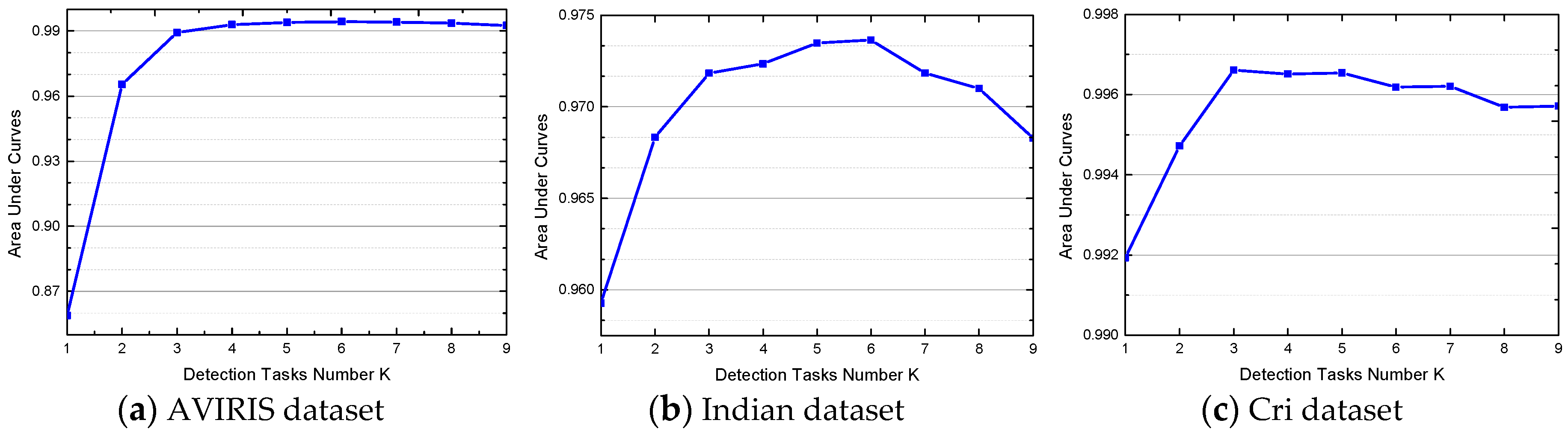
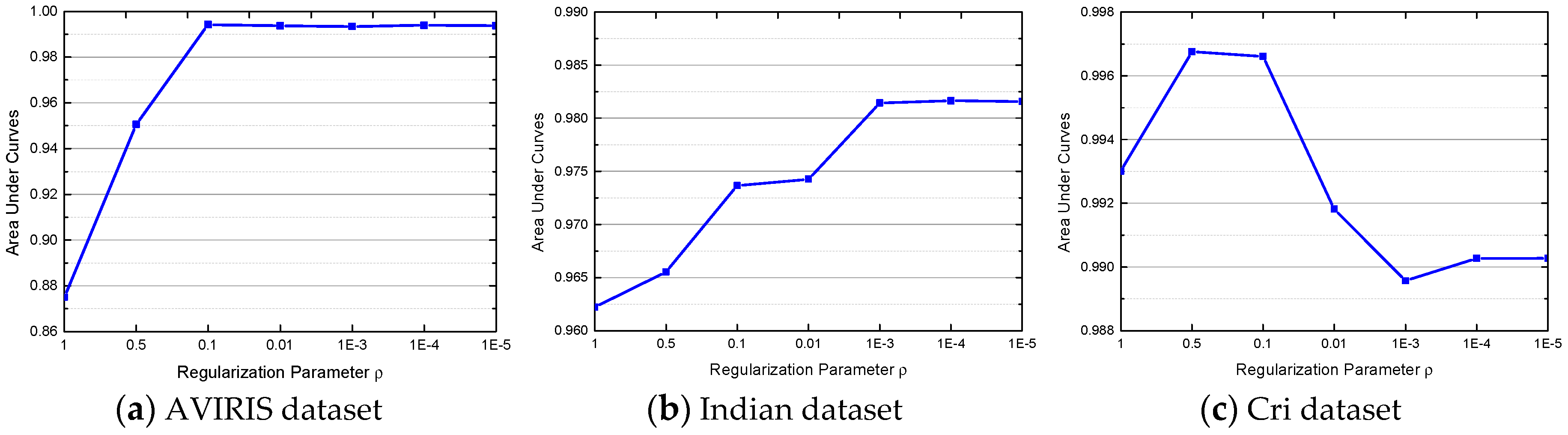
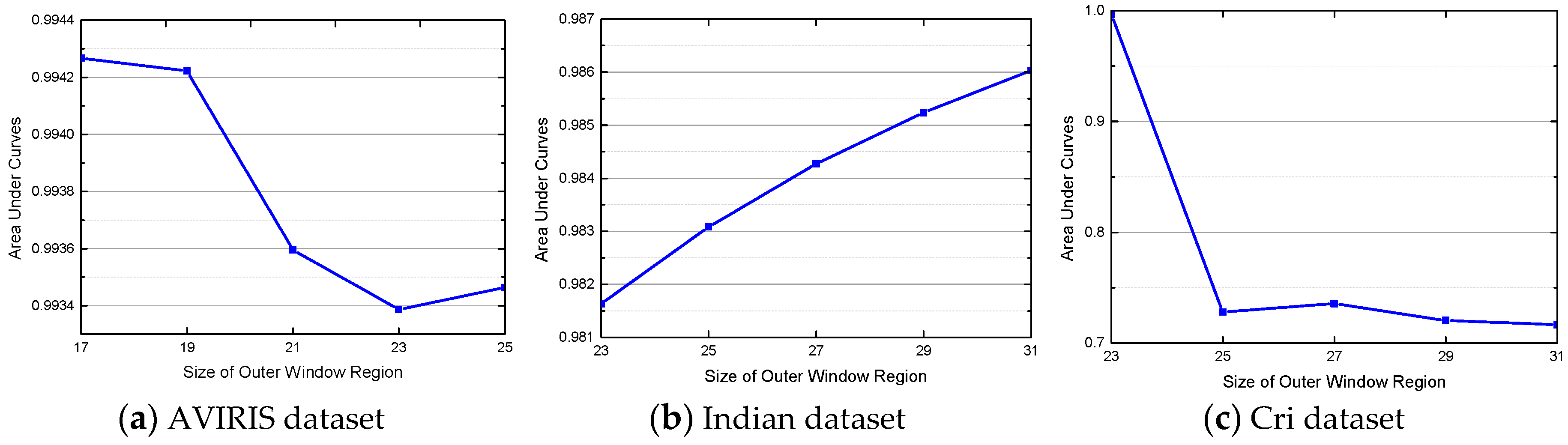
4.3. Parameter Analysis for the JSRMTL-ALI Algorithm
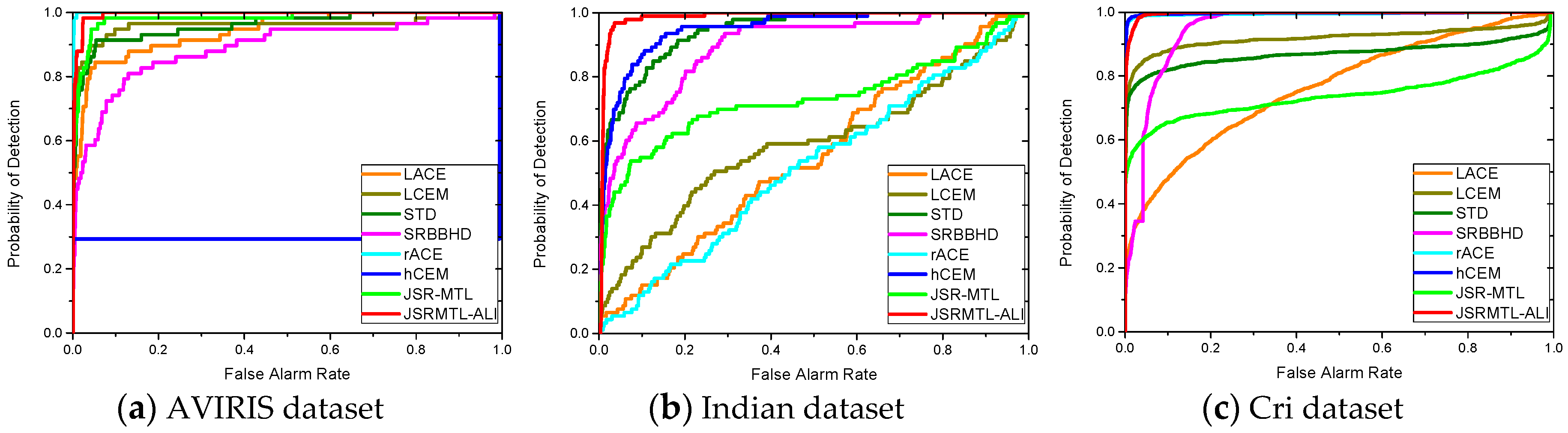
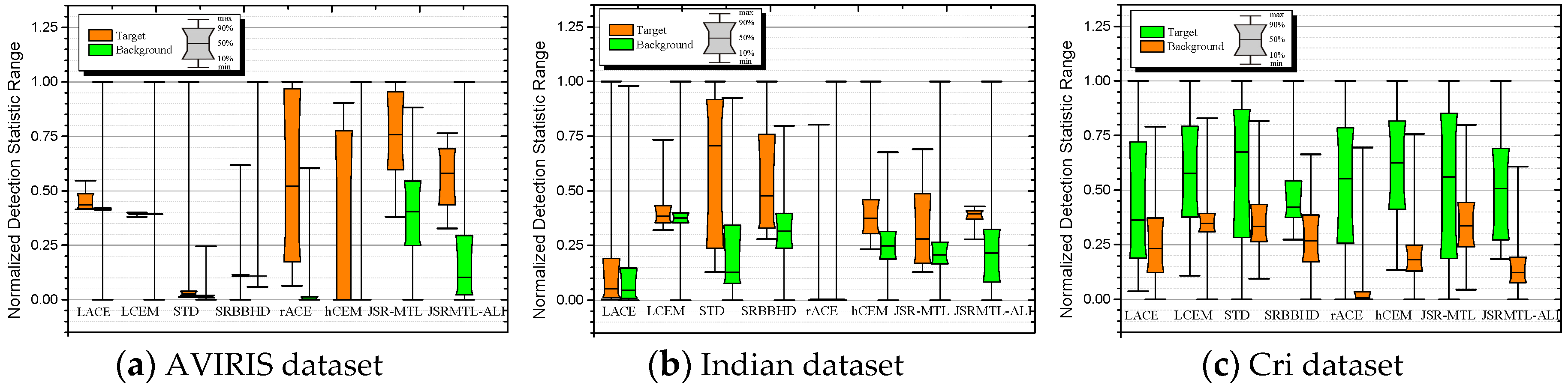
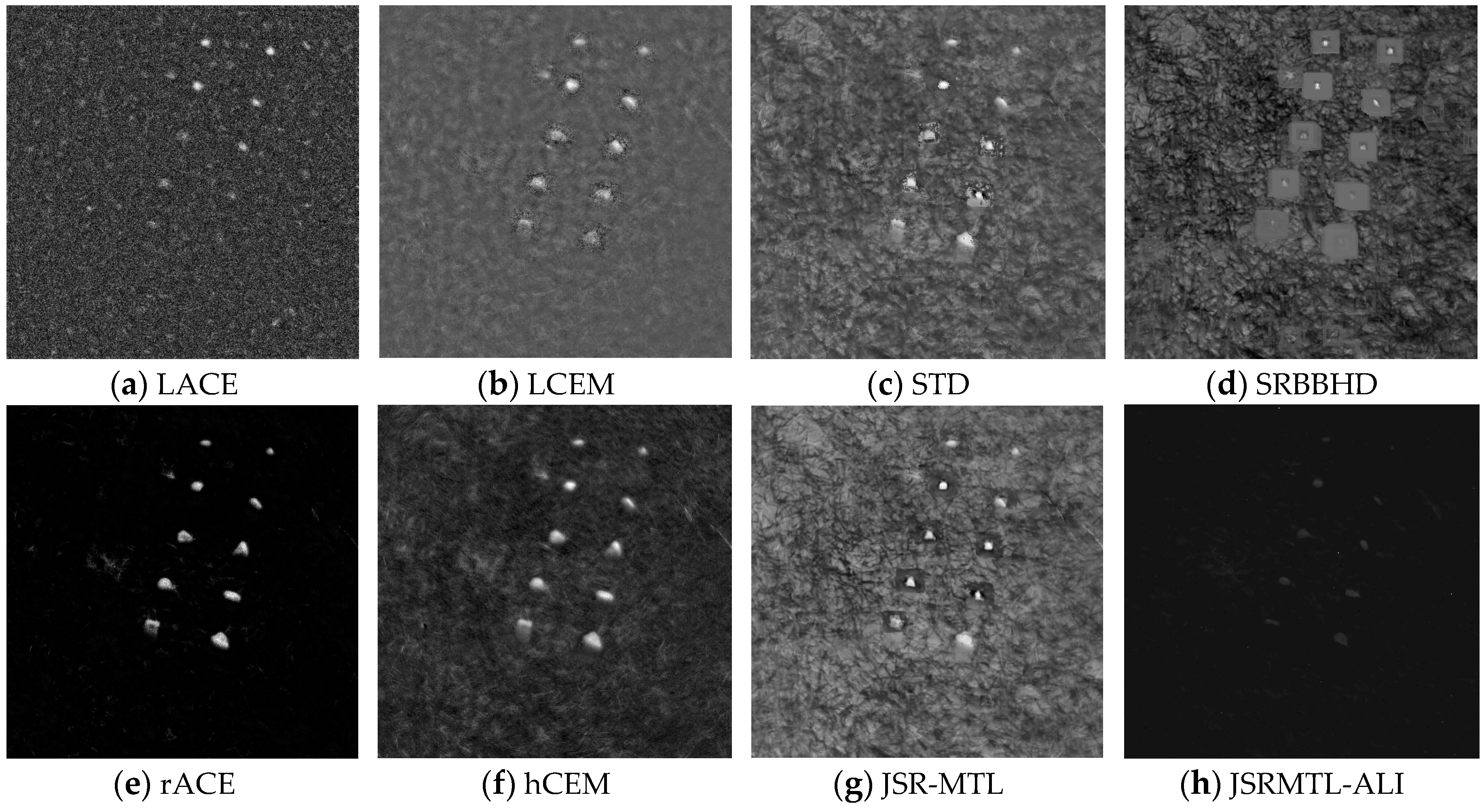
4.4. Detection Performance
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T.; Brueggeman, M. Detection Algorithms in Hyperspectral Imaging Systems: An Overview of Practical Algorithms. IEEE Signal Process. Mag. 2014, 31, 24–33. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral Target Detection: An Overview of Current and Future Challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature Extraction of Hyperspectral Images with Image Fusion and Recursive Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3742–3752. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral Image Data Analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Yuan, Y.; Ma, D.; Wang, Q. Hyperspectral Anomaly Detection by Graph Pixel Selection. IEEE Trans. Cybern. 2016, 46, 3123–3134. [Google Scholar] [CrossRef] [PubMed]
- Stefanou, M.S.; Kerekes, J.P. Image-derived prediction of spectral image utility for target detection applications. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1827–1833. [Google Scholar] [CrossRef]
- Datt, B.; McVicar, T.R.; Niel, T.G.V.; Jupp, D.L.B.; Pearlman, J.S. Preprocessing EO-1 Hyperion hyperspectral data to support the application of agricultural indexes. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1246–1259. [Google Scholar] [CrossRef]
- Eismann, M.T.; Stocker, A.D.; Nasrabadi, N.M. Automated hyperspectral cueing for civilian search and rescue. Proc. IEEE 2009, 97, 1031–1055. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral Image Processing for Automatic Target Detection Applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Wang, T.; Du, B.; Zhang, L. An automatic robust iteratively reweighted unstructured detector for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2367–2382. [Google Scholar] [CrossRef]
- Gao, L.; Yang, B.; Du, Q.; Zhang, B. Adjusted Spectral Matched Filter for Target Detection in Hyperspectral Imagery. Remote Sens. 2015, 7, 6611–6634. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, G.; Gu, Y. Tensor Matched Subspace Detector for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2017, 54, 1967–1974. [Google Scholar] [CrossRef]
- Geng, X.; Ji, L.; Sun, K.; Zhao, Y. CEM: More Bands, Better Performance. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1876–1880. [Google Scholar] [CrossRef]
- Zou, Z.; Shi, Z. Hierarchical Suppression Method for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 330–342. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral Image Classification and Dimensionality Reduction: An Orthogonal Subspace Projection Approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, Z.; Yang, S. Nonlocal Similarity Regularized Sparsity Model for Hyperspectral Target Detection. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1532–1536. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse representation for target detection in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. A Sparse Representation Based Binary Hypothesis Model for Target Detection in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1346–1354. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, B. Extracting Target Spectrum for Hyperspectral Target Detection: An Adaptive Weighted Learning Method Using a Self-Completed Background Dictionary. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1604–1617. [Google Scholar] [CrossRef]
- Farrell, M.D.; Mersereau, R.M. On the impact of PCA dimension reduction for hyperspectral detection of difficult targets. IEEE Geosci. Remote Sens. Lett. 2005, 2, 192–195. [Google Scholar] [CrossRef]
- Fowler, J.E.; Du, Q. Anomaly Detection and Reconstruction from Random Projections. IEEE Trans. Image Process. 2012, 21, 184–195. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Lin, J.; Yuan, Y. Salient Band Selection for Hyperspectral Image Classification via Manifold Ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Binol, H.; Ochilov, S.; Alam, M.S.; BaI, A. Target oriented dimensionality reduction of hyperspectral data by Kernel Fukunaga—Koontz Transform. Opt. Laser Eng. 2016, 89, 123–130. [Google Scholar] [CrossRef]
- Sun, K.; Geng, X.; Ji, L. A New Sparsity-Based Band Selection Method for Target Detection of Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2015, 12, 329–333. [Google Scholar] [CrossRef]
- Jalali, A.; Ravikumar, P.; Sanghavi, S.; Ruan, C. A Dirty Model for Multi-task Learning. In Proceedings of the Neural Information Processing Systems Conference, Hyatt Regency, Vancouver, BC, Canada, 6–11 December 2010. [Google Scholar]
- Yuan, X.; Liu, X.; Yan, S. Visual classification with multi-task joint sparse representation. IEEE Trans. Image Process. 2012, 21, 4349–4360. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Lin, J.; Wang, Q. Hyperspectral Image Classification via Multi-Task Joint Sparse Representation and Stepwise MRF Optimization. IEEE Trans. Cybern. 2016, 46, 2966–2977. [Google Scholar] [CrossRef] [PubMed]
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. Joint Sparse Representation with Multitask Learning for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2017, 55, 894–906. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Ben-David, S.; Schuller, R. Exploiting task relatedness for multiple task learning. In Proceedings of the Conference on Computational Learning Theory, Washington, DC, USA, 24–27 August 2003. [Google Scholar]
- Chen, X.; Pan, W.; Kwok, J.; Garbonell, J. Accelerated gradient method for multi-task sparse learning problem. In Proceedings of the IEEE International Conference on Data Mining, Miami, FL, USA, 6–9 December 2009; pp. 746–751. [Google Scholar]
- Tseng, P. On accelerated proximal gradient methods for convex-concave optimization. SIAM J. Optim. 2008. submitted. [Google Scholar]
- Kang, X.; Li, S.; Fang, L.; Benediktsson, J.A. Intrinsic Image Decomposition for Feature Extraction of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2241–2253. [Google Scholar] [CrossRef]






© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wu, K.; Du, B.; Zhang, L.; Hu, X. Hyperspectral Target Detection via Adaptive Joint Sparse Representation and Multi-Task Learning with Locality Information. Remote Sens. 2017, 9, 482. https://doi.org/10.3390/rs9050482
Zhang Y, Wu K, Du B, Zhang L, Hu X. Hyperspectral Target Detection via Adaptive Joint Sparse Representation and Multi-Task Learning with Locality Information. Remote Sensing. 2017; 9(5):482. https://doi.org/10.3390/rs9050482
Chicago/Turabian StyleZhang, Yuxiang, Ke Wu, Bo Du, Liangpei Zhang, and Xiangyun Hu. 2017. "Hyperspectral Target Detection via Adaptive Joint Sparse Representation and Multi-Task Learning with Locality Information" Remote Sensing 9, no. 5: 482. https://doi.org/10.3390/rs9050482
APA StyleZhang, Y., Wu, K., Du, B., Zhang, L., & Hu, X. (2017). Hyperspectral Target Detection via Adaptive Joint Sparse Representation and Multi-Task Learning with Locality Information. Remote Sensing, 9(5), 482. https://doi.org/10.3390/rs9050482