Niche Modeling of Dengue Fever Using Remotely Sensed Environmental Factors and Boosted Regression Trees
Abstract
:1. Introduction
- (i)
- Which environmental factors have the highest relative influence in association with Dengue fever?
- (ii)
- What is the spatial distribution of the risk of Dengue Fever based on these environmental factors?
- (iii)
- What are the differences between using presence/absence and case counts of DF in this type of analysis?
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Explanatory Variables
2.4. Data Preprocessing
2.5. Boosted Regression Tree Analysis
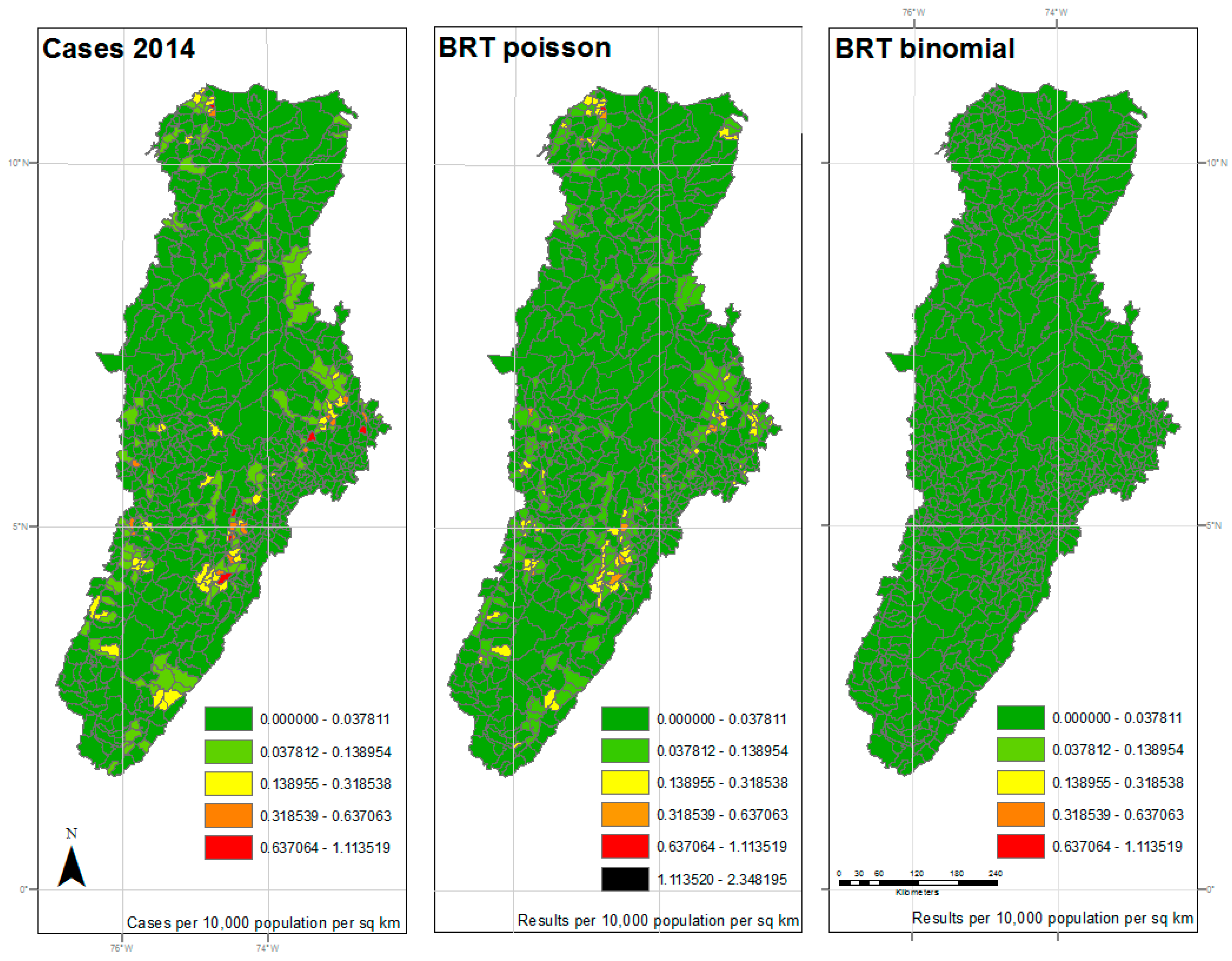
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Codebook
| Variable | XX | Y | Z |
| LST Night | LN | Min is 1 | Min is A |
| LST Day | LD | Max is 2 | Max is B |
| Precipitation | PR | Mean is 3 | Mean is C |
| Vegetation | VE | ||
| Elevation | EL | ||
| Land Cover–Barren | BA | ||
| Land Cover–Cropland | CR | ||
| Land Cover–Forest | FO | ||
| Land Cover–Savanna | SA | ||
| Land Cover–Shrubland | SH | ||
| Land Cover–Snowice | SN | ||
| Land Cover–Urban | UR | ||
| Land Cover–Wetland | WE | ||
| Population Density | POP_DEN |
| Code | Description |
| BA1 | barren minimum municipality |
| BA2 | barren maximum municipality |
| BA3 | barren mean municipality |
| CR1 | cropland minimum municipality |
| CR2 | cropland maximum municipality |
| CR3 | cropland mean municipality |
| EL1 | elevation minimum municipality |
| EL2 | elevation maximum municipality |
| EL3 | elevation mean municipality |
| FO1 | forest minimum municipality |
| FO2 | forest maximum municipality |
| FO3 | forest mean municipality |
| LD1A | daytime LST minimum annual minimum municipality |
| LD1B | daytime LST minimum annual maximum municipality |
| LD1C | daytime LST minimum annual mean municipality |
| LD2A | daytime LST maximum annual minimum municipality |
| LD2B | daytime LST maximum annual maximum municipality |
| LD2C | daytime LST maximum annual mean municipality |
| LD3A | daytime LST mean annual minimum municipality |
| LD3B | daytime LST mean annual maximum municipality |
| LD3C | daytime LST mean annual mean municipality |
| LN1A | nighttime LST minimum annual minimum municipality |
| LN1B | nighttime LST minimum annual maximum municipality |
| LN1C | nighttime LST minimum annual mean municipality |
| LN2A | nighttime LST maximum annual minimum municipality |
| LN2B | nighttime LST maximum annual maximum municipality |
| LN2C | nighttime LST maximum annual mean municipality |
| LN3A | nighttime LST mean annual minimum municipality |
| LN3B | nighttime LST mean annual maximum municipality |
| LN3C | nighttime LST mean annual mean municipality |
| POP_DEN | population density |
| PR1A | precipitation minimum annual minimum municipality |
| PR1B | precipitation minimum annual maximum municipality |
| PR1C | precipitation minimum annual mean municipality |
| PR2A | precipitation maximum annual minimum municipality |
| PR2B | precipitation maximum annual maximum municipality |
| PR2C | precipitation maximum annual mean municipality |
| PR4A | precipitation total annual minimum municipality |
| PR4B | precipitation total annual maximum municipality |
| PR4C | precipitation total annual mean municipality |
| SA1 | savannah minimum municipality |
| SA2 | savannah maximum municipality |
| SA3 | savannah mean municipality |
| SH1 | shrubland minimum municipality |
| SH2 | shrubland maximum municipality |
| SH3 | shrubland mean municipality |
| SN1 | snow and ice minimum municipality |
| SN2 | snow and ice maximum municipality |
| SN3 | snow and ice mean municipality |
| UR1 | urban minimum municipality |
| UR2 | urban maximum municipality |
| UR3 | urban mean municipality |
| VE1A | vegetation minimum annual minimum municipality |
| VE1B | vegetation minimum annual maximum municipality |
| VE1C | vegetation minimum annual mean municipality |
| VE2A | vegetation maximum annual minimum municipality |
| VE2B | vegetation maximum annual maximum municipality |
| VE2C | vegetation maximum annual mean municipality |
| VE3A | vegetation mean annual minimum municipality |
| VE3B | vegetation mean annual maximum municipality |
| VE3C | vegetation mean annual mean municipality |
| WE1 | wetland minimum municipality |
| WE2 | wetland maximum municipality |
| WE3 | wetland mean municipality |
References
- Meentemeyer, R.K.; Haas, S.E.; Vaclavik, T. Landscape epidemiology of emerging infectious diseases in natural and human-altered ecosystems. Annu. Rev. Phytopathol. 2012, 50, 379–402. [Google Scholar] [CrossRef] [PubMed]
- Dengue. Available online: http://www.cdc.gov/dengue/index.html (accessed on 10 August 2016).
- Kaushal, M. Epidemiology of Dengue. Available online: http://www.slideshare.net/menaalkaushal/dengue-epidemiology-case-management-26937383 (accessed on 3 August 2016).
- Messina, J.P.; Kraemer, M.U.; Brady, O.J.; Pigott, D.M.; Shearer, F.M.; Weiss, D.J.; Golding, N.; Ruktanonchai, C.W.; Gething, P.W.; Cohn, E.; et al. Mapping global environmental suitability for Zika virus. eLife 2016, 5, e15272. [Google Scholar] [CrossRef] [PubMed]
- Castro Rodriguez, R.; Carrasquilla, G.; Porras, A.; Galera-Gelvez, K.; Lopez Yescas, J.G.; Rueda-Gallardo, J.A. The Burden of Dengue and the Financial Cost to Colombia, 2010–2012. Am. J. Trop. Med. Hyg. 2016, 94, 1065–1072. [Google Scholar] [CrossRef] [PubMed]
- Instituto Nacional de Salud (INS) Programa SIVIGILA. Entidad Adscrita al Ministerio de Salud y Protección Social de Colombia. 2014. Available online: http://www.ins.gov.co/lineas-de-accion/Subdireccion-Vigilancia/sivigila/Paginas/vigilancia-rutinaria.aspx (accessed on 12 August 2016).
- Hay, S.I. An overview of remote sensing and geodesy for epidemiology and public health application. Adv. Parasitol. 2000, 47, 1–35. [Google Scholar] [PubMed]
- Moreno-Madriñán, M.; Crosson, W.; Eisen, L.; Estes, S.; Estes, M., Jr.; Hayden, M.; Hemmings, S.; Irwin, D.; Lozano-Fuentes, S.; Monaghan, A.; et al. Correlating remote sensing data with the abundance of pupae of the dengue virus mosquito vector, Aedes aegypti, in central Mexico. ISPRS Int. J. Geo-Inf. 2014, 3, 732–749. [Google Scholar] [CrossRef]
- Machault, V.; Yébakima, A.; Etienne, M.; Vignolles, C.; Palany, P.; Tourre, Y.M.; Guérécheau, M.; Lacaux, J.P. Mapping entomological dengue risk levels in Martinique using high-resolution remote-sensing environmental data. ISPRS Int. J. Geo-Inf. 2014, 3, 1352–1371. [Google Scholar] [CrossRef]
- Aertsen, W.; Kint, V.; de Vos, B.; Deckers, J.; van Orshoven, J.; Muys, B. Predicting forest site productivity in temperate lowland from forest floor, soil and litterfall characteristics using boosted regression trees. Plant Soil 2012, 354, 157–172. [Google Scholar] [CrossRef]
- Carty, D.; Young, T.; Zaretzki, R.; Petutschnigg, A. Predicting and Correlating the Strength Properties of Wood Composite Process Parameters by Use of Boosted Regression Tree Models. For. Prod. J. 2015, 65, 365–371. [Google Scholar] [CrossRef]
- Shah, D.A.; De Wolf, E.D.; Paul, P.A.; Madden, L.V. Predicting Fusarium Head Blight Epidemics with Boosted Regression Trees. Phytopathology 2014, 104, 702–714. [Google Scholar] [CrossRef] [PubMed]
- De’Ath, G.; Fabricius, K.E. Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology 2000, 81, 3178–3192. [Google Scholar] [CrossRef]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, R.; Bunn, A.; Powell, S.; Zambon, M. Classification of remotely sensed imagery using stochastic gradient boosting as a refinement of classification tree analysis. Remote Sens. Environ. 2004, 90, 331–336. [Google Scholar] [CrossRef]
- Pigott, D.M.; Bhatt, S.; Golding, N.; Duda, K.A.; Battle, K.E.; Brady, O.J.; Messina, J.P.; Balard, Y.; Bastien, P.; Pratlong, F.; et al. Global distribution maps of the leishmaniases. eLife 2014, 3, e35671. [Google Scholar] [CrossRef] [PubMed]
- Messina, J.P.; Pigott, D.M.; Golding, N.; Duda, K.A.; Brownstein, J.S.; Weiss, D.J.; Gibson, H.; Robinson, T.P.; Gilbert, M.; William Wint, G.R.; et al. The global distribution of Crimean-Congo hemorrhagic fever. Trans. R. Soc. Trop. Med. Hyg. 2015, 109, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Cheong, Y.L.; Leitão, P.J.; Lakes, T. Assessment of land use factors associated with dengue cases in Malaysia using boosted regression trees. Spat. Spatiotemporal. Epidemiol. 2014, 10, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Gubler, D.J. Dengue, Urbanization and Globalization: The Unholy Trinity of the 21(st) Century. Trop. Med. Health 2011, 39, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Chareonviriyaphap, T.; Akratanakul, P.; Nettanomsak, S.; Huntamai, S. Larval habitats and distribution patterns of Aedes aegypti (Linnaeus) and Aedes albopictus (Skuse), in Thailand. Southeast. Asian J. Trop. Med. Public Health 2003, 34, 529–535. [Google Scholar] [PubMed]
- Wan-Norafikah, O.; Nazni, W.A.; Noramiza, S.; Shafa’ar-Ko’ohar, S.; Heah, S.K.; Nor-Azlina, A.H.; Khairul-Asuad, M.; Lee, H.L. Distribution of Aedes mosquitoes in three selected localities in Malaysia. Sains Malays. 2012, 41, 1309–1313. [Google Scholar]
- Delmelle, A.P.E.; Kanaroglou, P. (Eds.) Spatial Analysis in Health Geography; Ashgate Publishing, Ltd.: Farnham, UK, 2015. [Google Scholar]
- Heymann, D.L. Control of Communicable Diseases Manual; American Public Health Association: Washington, DC, USA, 2008. [Google Scholar]
- Morin, C.W.; Comrie, A.C.; Ernst, K. EHP—Climate and Dengue Transmission: Evidence and Implications. Environ. Health Perspect. 2013, 1264, 1264–1272. [Google Scholar]
- De la Hoz, F.; Martínez-Duran, M.; Pacheco-García, O.; Quijada-Bonilla, H. Protocolo de Vigilancia en Salud Pública: Dengue. In Public Health Surveillance Protocol. Dengue; Instituto Nacional de Salud: Bogotá, Colombia, 2014. [Google Scholar]
- Departamento Administrativo Nacional de Estadística (DANE). Gobierno de Colombia. 2014. Available online: http://www.dane.gov.co/ (accessed on 19 July 2014).
- Ramon Solano, R.; Didan, K.; Jacobson, A.; Huete, A. Modis Vegetation Index User’s Guide; The University of Arizona: Tucson, AZ, USA, 2010. [Google Scholar]
- ArcGIS for Desktop. Available online: http://www.esri.com/software/arcgis/arcgis-for-desktop (accessed on 3 November 2016).
- LP DAAC: NASA Land Data Products and Services. Land Cover Type Yearly L3 Global 500 m SIN Grid. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1 (accessed on 5 November 2016).
- Ruiz-Lopez, F.; Gonzalez-Mazo, A.; Velez-Mira, A.; Gomez, G.F.; Zuleta, L.; Uribe, S.; Velez-Bernal, I.D. Presence of Aedes (Stegomyia) aegypti (Linnaeus, 1762) and its natural infection with dengue virus at unrecorded heights in Colombia. Biomedica 2016, 36, 303–308. [Google Scholar] [CrossRef] [PubMed]
- Lima, A.; Lovin, D.D.; Hickner, P.V.; Severson, D.W. Evidence for an overwintering population of Aedes aegypti in Capitol Hill Neighborhood, Washington, DC. Am. J. Trop. Med. Hyg. 2016, 94, 231–235. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Statistics 2011, 29, 1189–1232. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Leathwick, J.R.; Elith, J.; Francis, M.P.; Hastie, T.; Taylor, P. Variation in demersal fish species richness in the oceans surrounding New Zealand: An analysis using boosted regression trees. Mar. Ecol. Prog. Ser. 2006, 321, 267–281. [Google Scholar] [CrossRef]
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, M.U.G.; Sinka, M.E.; Duda, K.A.; Mylne, A.Q.N.; Shearer, F.M.; Barker, C.M.; Moore, C.G.; Carvalho, R.G.; Coelho, G.E.; Van Bortel, W.; et al. The global distribution of the arbovirus vectors Aedes aegypti and Ae. Albopictus. eLife 2015, 4, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Liu, X.; Kok, S.-Y.; Rajarethinam, J.; Liang, S.; Yap, G.; Chong, C.-S.; Lee, K.-S.; Tan, S.S.Y.; Chin, C.K.Y.; et al. Three-Month Real-Time Dengue Forecast Models: An Early Warning System for Outbreak Alerts and Policy Decision Support in Singapore. Environ. Health Perspect. 2015. [Google Scholar] [CrossRef] [PubMed]
- Dhang, C.; Benjamin, S.; Saranum, M.; Fook, C.; Lim, L.; Ahmad, N.; Sofian-Azirun, M. Dengue vector surveillance in urban residential and settlement areas in Selangor, Malaysia. Trop. Biomed. 2005, 22, 39–43. [Google Scholar]
- Lounibos, L.P. Invasions by insect vectors of human disease. Annu. Rev. Entomol. 2002, 47, 233–266. [Google Scholar] [CrossRef] [PubMed]
- Brady, O.J.; Golding, N.; Pigott, D.M.; Kraemer, M.U.G.; Messina, J.P.; Reiner, R.C.; Scott, T.W.; Smith, D.L.; Gething, P.W.; Hay, S.I. Global temperature constraints on Aedes aegypti and Ae. Albopictus persistence and competence for dengue virus transmission. Parasites Vectors 2014, 7, 338. [Google Scholar] [CrossRef] [PubMed]
- Rueda, L.; Patel, K.; Axtell, R.; Stinner, R. Temperature-Dependent Development and Survival Rates of Culex quinquefasciatus and Aedes aegypti. J. Med. Entomol. 1990, 27, 892–898. [Google Scholar] [CrossRef] [PubMed]
- Lozano-Fuentes, S.; Hayden, M.H.; Welsh-Rodriguez, C.; Ochoa-Martinez, C.; Tapia-Santos, B.; Kobylinski, K.C.; Uejio, C.K.; Zielinski-Gutierrez, E.; Delle Monache, L.; Monaghan, A.J.; et al. The dengue virus mosquito vector Aedes aegypti at high elevation in México. Am. J. Trop. Med. Hyg. 2012, 87, 902–909. [Google Scholar] [CrossRef] [PubMed]
- Ibanez-Bernal, S. New altitudinal record of Aedes(Stegomyia) aegypti(Linnaeus, 1762)(Diptera: Culicidae) in Mexico.). Folia Entomol. Mex. 1987, 72, 163–164. [Google Scholar]
- Suárez, M.F.; Nelson, M.J. Registro de altitud del Aedes aegypti en Colombia. Biomédica 1981, 1, 225. [Google Scholar] [CrossRef]
- Rogers, D.J.; Wilson, A.J.; Hay, S.I.; Graham, A.J. The global distribution of yellow fever and dengue. Adv. Parasitol. 2006, 62, 181–220. [Google Scholar] [PubMed]
- Stanforth, A.; Moreno-Madriñán, M.J.; Ashby, J. Exploratory Analysis of Dengue Fever Niche Variables within the Rio Magdalena Watershed. Remote Sens. 2016, 8, 770. [Google Scholar] [CrossRef]
- Moreno-Madriñán, M.J.; Turell, M.J. Factors of concern regarding Zika and other Aedes aegypti-transmitted viruses in the U.S. J. Med. Entomol. 2017. [Google Scholar] [CrossRef]
- Ridgeway, G. Generalized Boosted Models: A Guide to the gbm Package. 2007. Available online: http://www.saedsayad.com/docs/gbm2.pdf (accessed on 3 August 2007).
- Hagenlocher, M.; Delmelle, E.; Casas, I.; Kienberger, S. Assessing socioeconomic vulnerability to dengue fever in Cali, Colombia: Statistical vs expert-based modeling. Int. J. Health Geogr. 2013, 12, 36. [Google Scholar] [CrossRef] [PubMed]
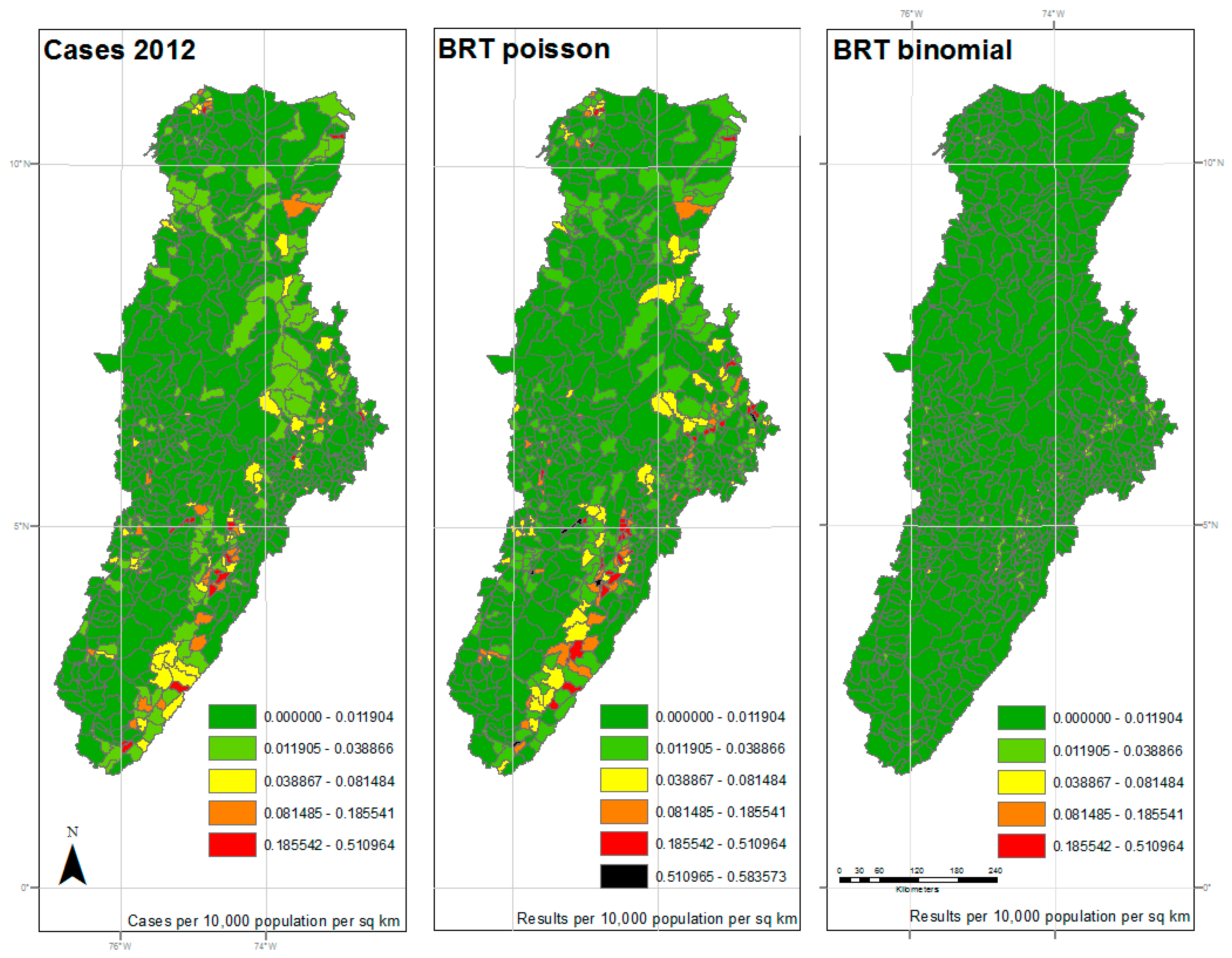
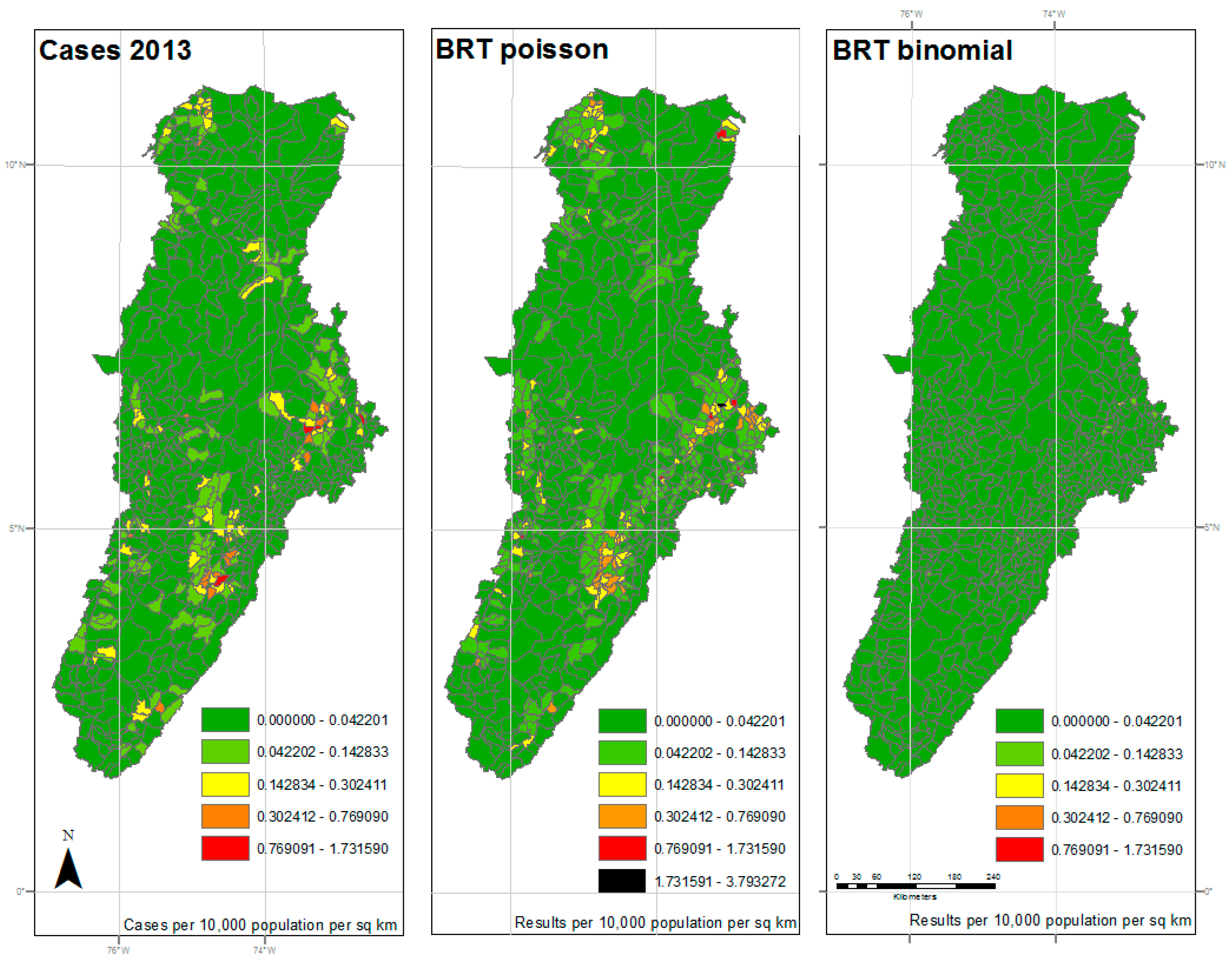
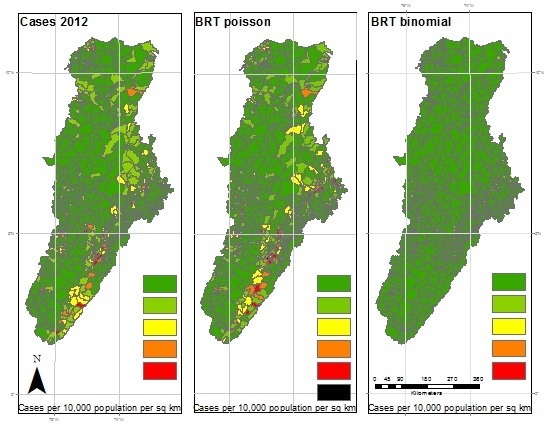
| Year | Poisson | Bernoulli | ||||
|---|---|---|---|---|---|---|
| RMSE | Pearson r | p-Value | RMSE | Pearson r | p-Value | |
| 2012 | 18.013 | 0.956 | <0.001 | 62.703 | 0.298 | <0.001 |
| 2013 | 31.535 | 0.979 | <0.001 | 152.992 | 0.202 | <0.001 |
| 2014 | 35.253 | 0.986 | <0.001 | 80.500 | 0.278 | <0.001 |
| Poisson Model | Bernoulli Model | ||||
|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | 2012 | 2013 | 2014 |
| LD3B (52.45%) | POP_DEN (56.57%) | POP_DEN (60.22%) | POP_DEN (16.01%) | LD1B (12.67%) | LD1B (27.26%) |
| LD2B (16.42%) | LD3B (14.7%) | LD1B (11.09%) | EL3 (12.56%) | EL3 (11.46%) | LN1B (11.3%) |
| LD1B (8.28%) | UR3 (13.86%) | UR3 (8.71%) | LN3B (8.26%) | VE2B (6.63%) | POP_DEN (9.28%) |
| POP_DEN (5.97%) | LD1B (11.91%) | LD3B (3.97%) | LN3C (6.14%) | POP_DEN (6.61%) | LN2C (5.41%) |
| VE1A (4.15%) | LN1B (0.4%) | LD1A (1.96%) | LD2B (4.63%) | LN1B (5.68%) | LN1C (4.92%) |
| LD1A (2.67%) | FO3 (0.34%) | LN1A (1.83%) | LN2C (4.03%) | SA3 (4.64%) | VE2A (4.75%) |
| FO3 (1.49%) | LN1A (0.31%) | FO3 (1.61%) | LD1B (4.02%) | PR4A (4.54%) | SA3 (4.69%) |
| UR3 (1.39%) | LD2B (0.29%) | VE2A (1.47%) | UR3 (3.87%) | LN1A (4.46%) | EL3 (4.12%) |
| LN3B (1.05%) | VE2A (0.27%) | LN2C (1.33%) | LD1A (3.78%) | LD3B (4.21%) | LD1A (3.88%) |
| LN1B (1.03%) | VE2B (0.23%) | LD2B (1.33%) | VE1A (3.61%) | LN1C (4%) | PR4A (3.48%) |
| VE1B (0.87%) | LD1A (0.22%) | LN3B (1.27%) | FO3 (3.17%) | VE2C (3.99%) | LN3B (3.44%) |
| VE3B (0.84%) | VE2C (0.2%) | VE2C (0.9%) | LN1C (3.09%) | FO3 (3.82%) | FO3 (2.8%) |
| VE3A (0.77%) | LN3B (0.19%) | LN1B (0.84%) | LD3B (3.04%) | LN3B (3.76%) | UR3 (2.69%) |
| VE1C (0.7%) | LN1C (0.12%) | EL3 (0.79%) | PR4A (2.99%) | LD2B (3.68%) | VE2B (2.53%) |
| EL3 (0.42%) | EL3 (0.09%) | VE2B (0.66%) | LN1B (2.86%) | LN2C (3.65%) | LN3C (2.14%) |
| SA3 (0.35%) | SA3 (0.08%) | PR4A (0.55%) | EL1 (2.79%) | UR3 (3.37%) | LD3B (1.72%) |
| LN1A (0.35%) | LN2C (0.07%) | LN1C (0.53%) | VE3A (2.77%) | VE2A (3.29%) | VE2C (1.64%) |
| LN1C (0.28%) | EL1 (0.06%) | EL1 (0.51%) | SA3 (2.39%) | LD1A (3.26%) | LN1A (1.54%) |
| EL1 (0.22%) | PR4A (0.04%) | LN3C (0.25%) | VE3B (2.32%) | LN3C (3.2%) | EL1 (1.39%) |
| PR4A (0.12%) | LN3C (0.04%) | SA3 (0.2%) | VE3C (2.23%) | EL1 (3.08%) | LD2B (1.02%) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashby, J.; Moreno-Madriñán, M.J.; Yiannoutsos, C.T.; Stanforth, A. Niche Modeling of Dengue Fever Using Remotely Sensed Environmental Factors and Boosted Regression Trees. Remote Sens. 2017, 9, 328. https://doi.org/10.3390/rs9040328
Ashby J, Moreno-Madriñán MJ, Yiannoutsos CT, Stanforth A. Niche Modeling of Dengue Fever Using Remotely Sensed Environmental Factors and Boosted Regression Trees. Remote Sensing. 2017; 9(4):328. https://doi.org/10.3390/rs9040328
Chicago/Turabian StyleAshby, Jeffrey, Max J. Moreno-Madriñán, Constantin T. Yiannoutsos, and Austin Stanforth. 2017. "Niche Modeling of Dengue Fever Using Remotely Sensed Environmental Factors and Boosted Regression Trees" Remote Sensing 9, no. 4: 328. https://doi.org/10.3390/rs9040328
APA StyleAshby, J., Moreno-Madriñán, M. J., Yiannoutsos, C. T., & Stanforth, A. (2017). Niche Modeling of Dengue Fever Using Remotely Sensed Environmental Factors and Boosted Regression Trees. Remote Sensing, 9(4), 328. https://doi.org/10.3390/rs9040328