Evaluating Water Controls on Vegetation Growth in the Semi-Arid Sahel Using Field and Earth Observation Data
Abstract
:1. Introduction
2. Field Sites
2.1. Demokeya, Sudan
2.2. Wankama, Niger
2.3. Dahra, Senegal
3. Data and Methods
3.1. Field Data
3.1.1. Eddy Covariance Gross Primary Productivity
3.1.2. Climatic Variables
3.2. Earth Observation Data
3.3. Methodology
3.3.1. Plant-Available Water
3.3.2. Vapor Pressure Deficit
3.3.3. Antecedent Precipitation Index
3.3.4. Enhanced Vegetation Index
3.3.5. Statistical Analysis
4. Results and Discussion
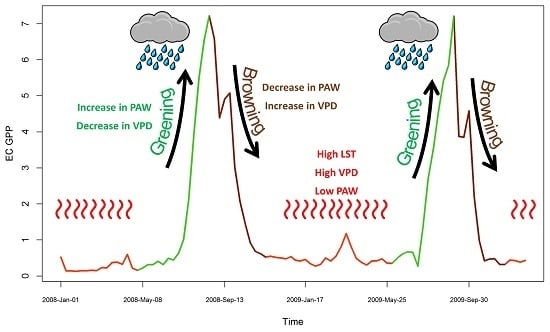
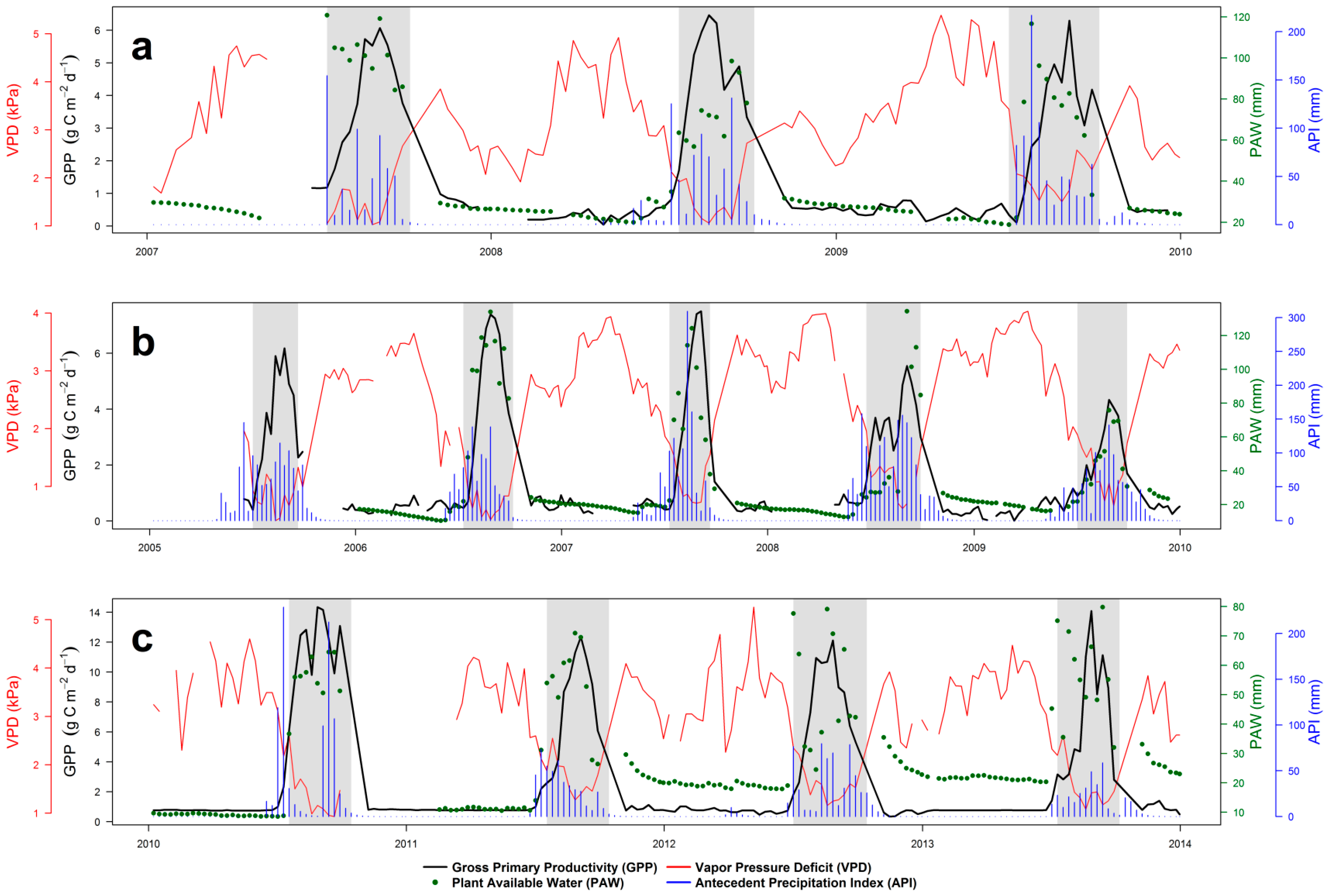
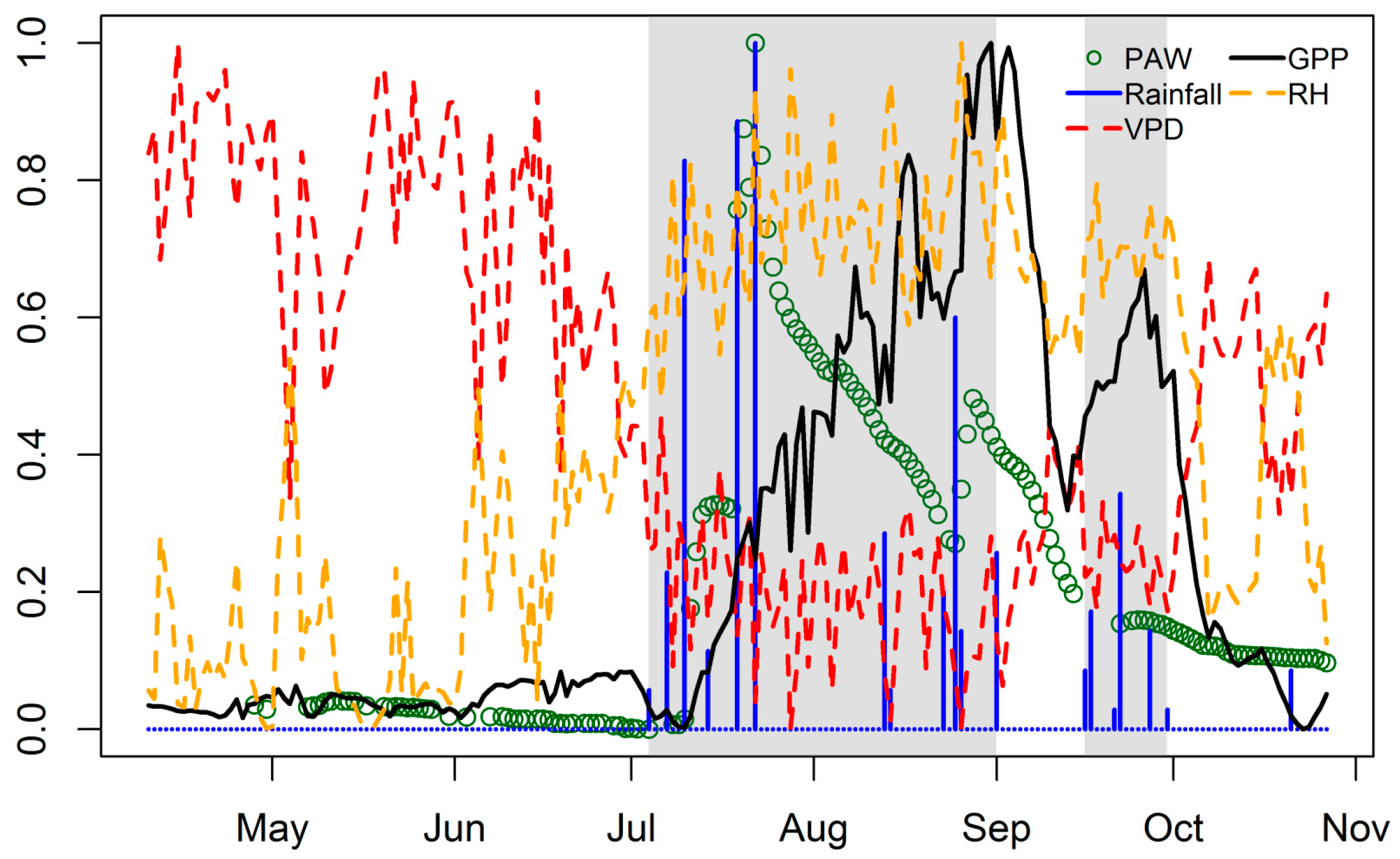
4.1. Seasonal Dynamics and Inter-Annual Variability of EC GPP, PAW, VPD and API
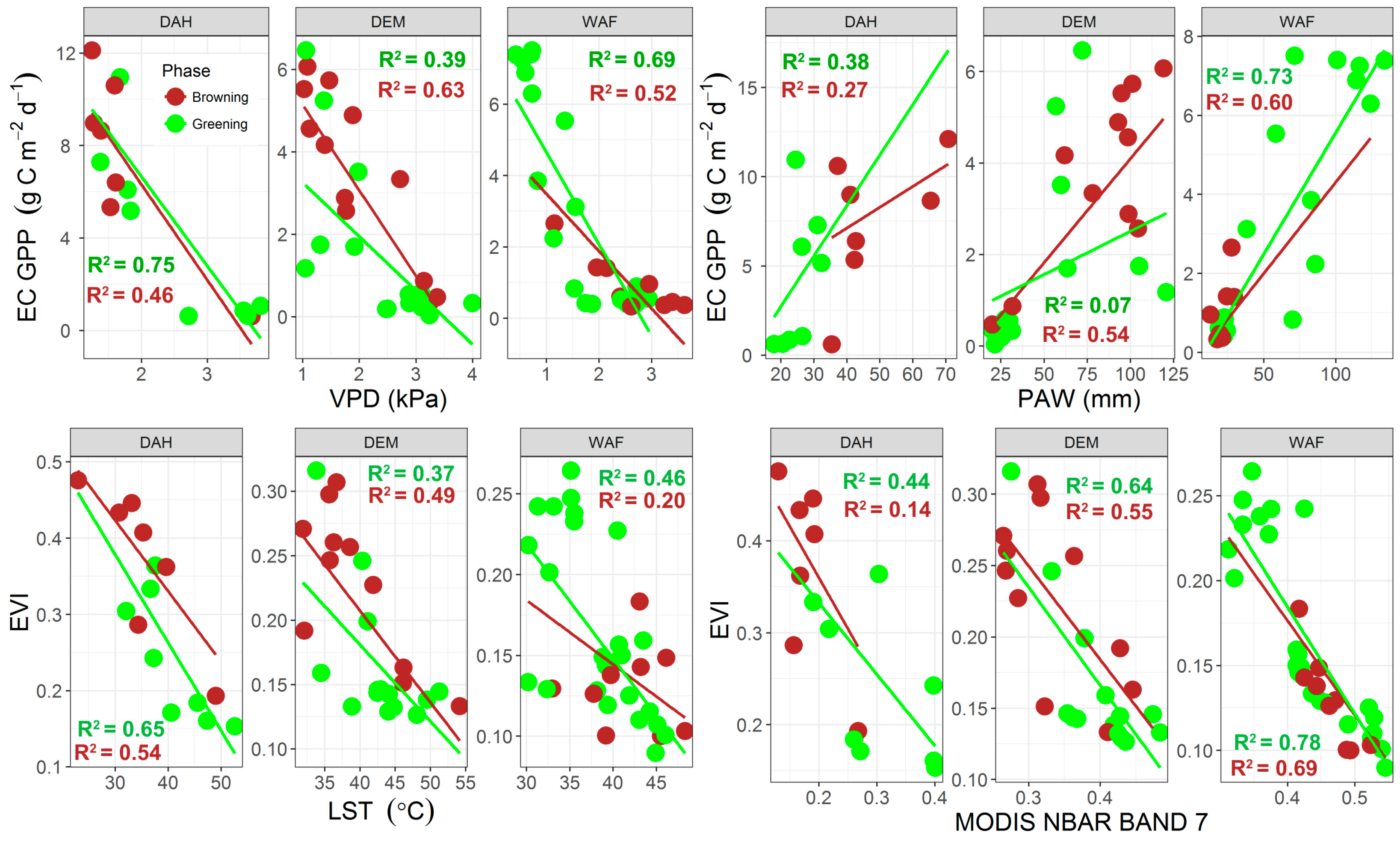
4.2. Relationship between EC GPP, PAW, VPD, and API
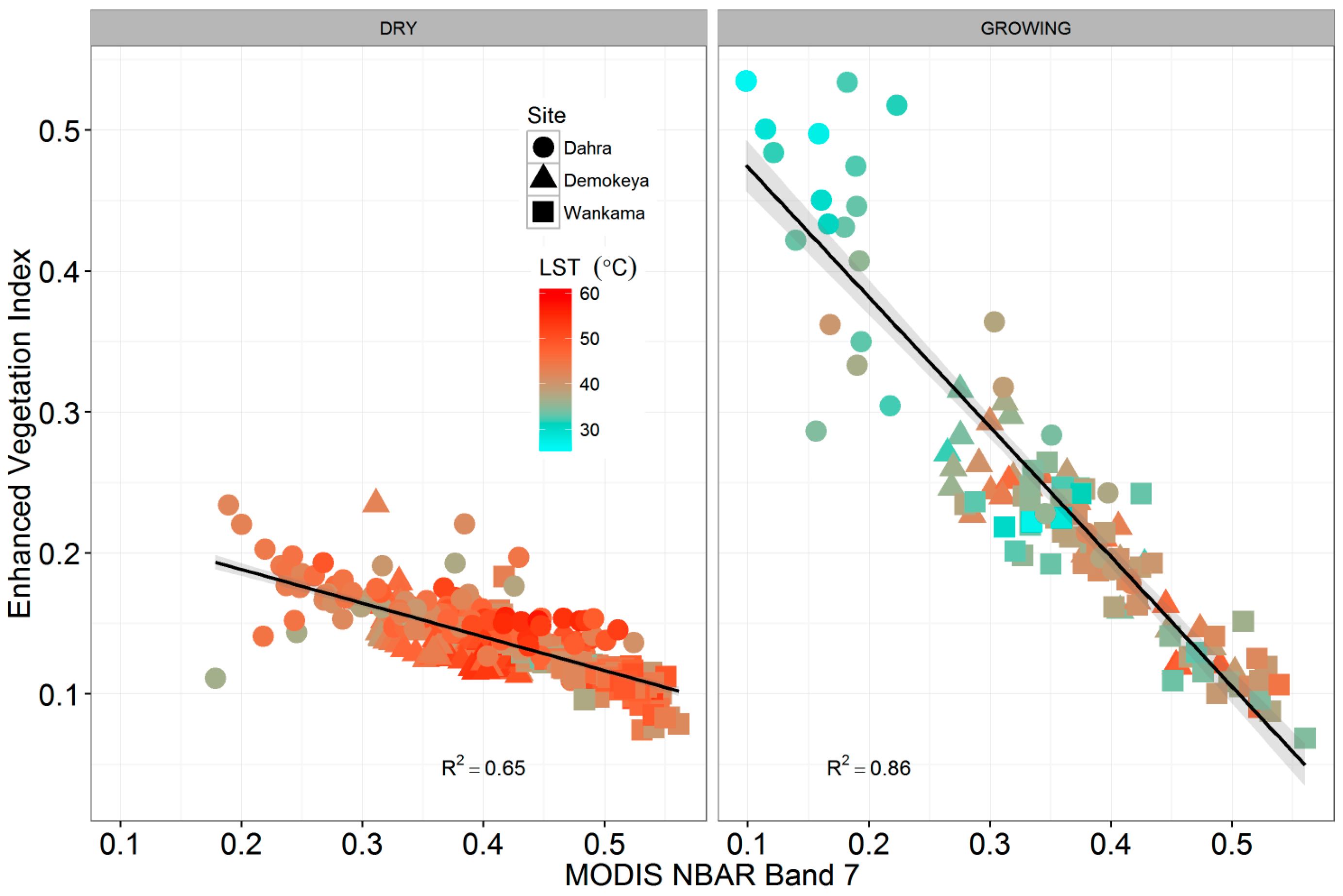
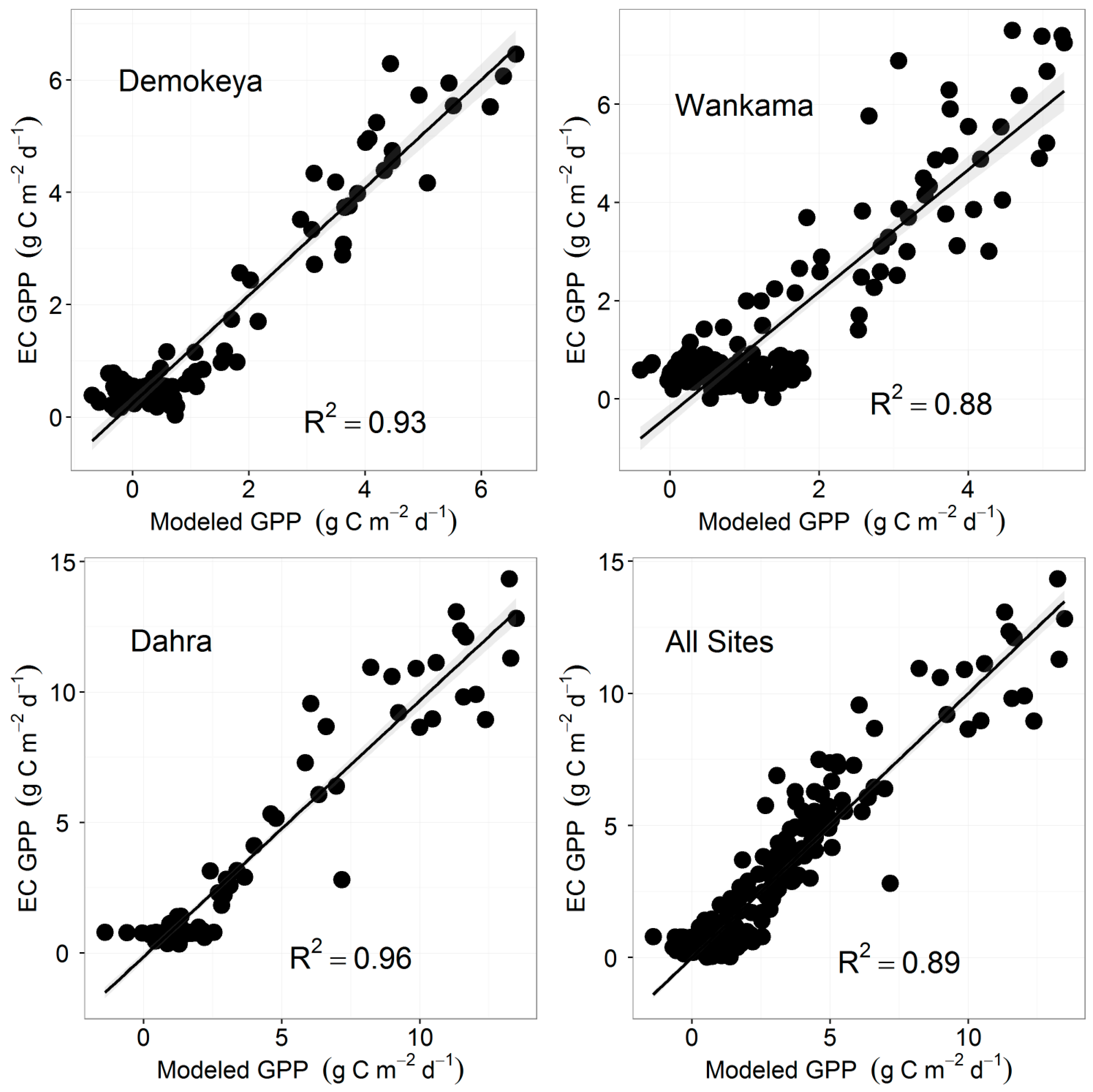
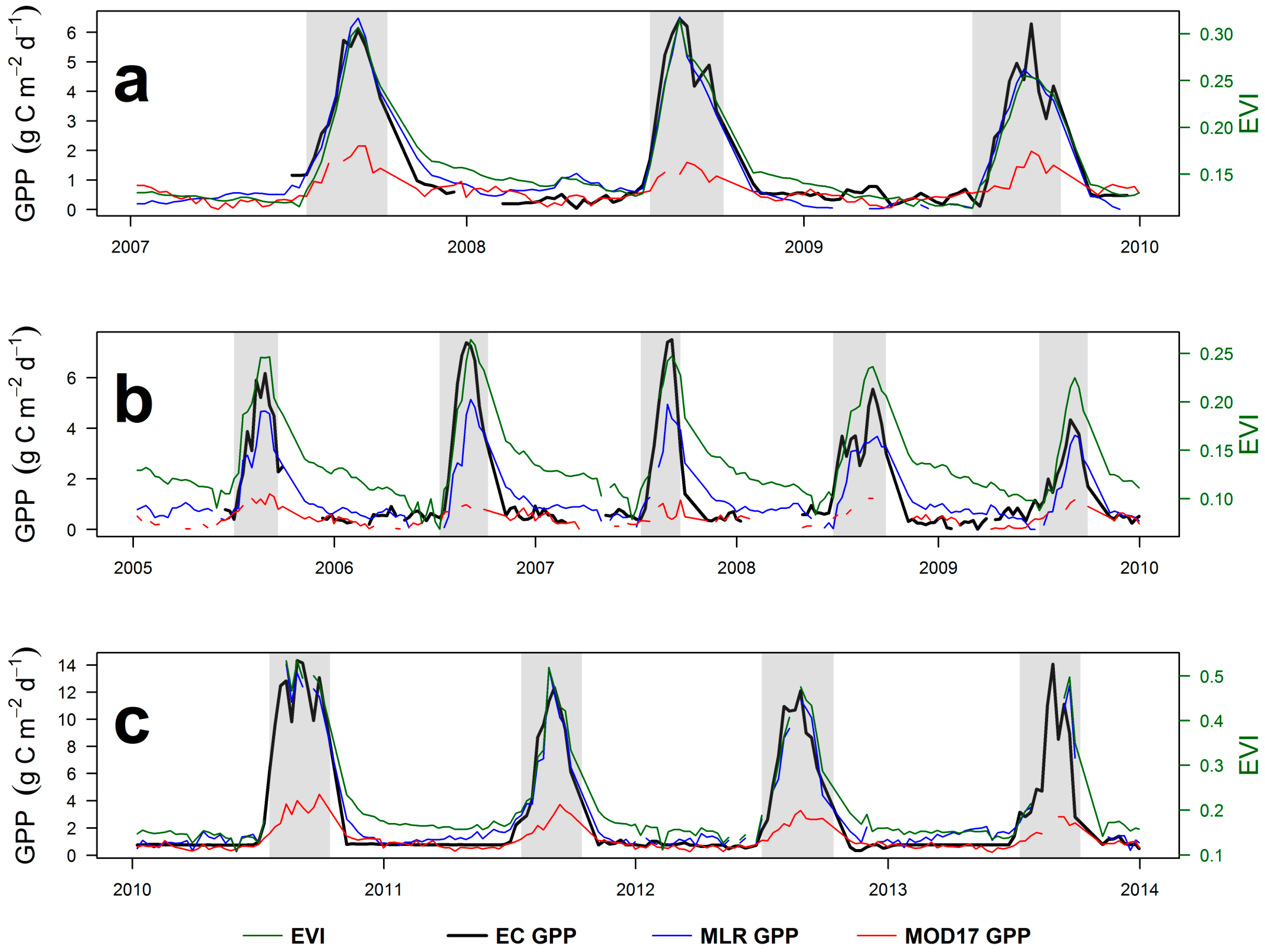
4.3. Eddy Covariance Gross Primary Productivity and MODIS-Derived Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ellis, J.; Galvin, K.A. Climate patterns and land-use practices in the dry zones of Africa. BioScience 1994, 44, 340–349. [Google Scholar] [CrossRef]
- Eklundh, L.; Olsson, L. Vegetation index trends for the African Sahel 1982–1999. Geophys. Res. Lett. 2003, 30, 1430. [Google Scholar] [CrossRef]
- Olsson, L.; Eklundh, L.; Ardö, J. A recent greening of the Sahel—Trends, patterns and potential causes. J. Arid Environ. 2005, 63, 556–566. [Google Scholar] [CrossRef]
- Dardel, C.; Kergoat, L.; Hiernaux, P.; Mougin, E.; Grippa, M.; Tucker, C.J. Re-greening Sahel: 30 years of remote sensing data and field observations (Mali, Niger). Remote Sens. Environ. 2014, 140, 350–364. [Google Scholar] [CrossRef]
- Brandt, M.; Mbow, C.; Diouf, A.A.; Verger, A.; Samimi, C.; Fensholt, R. Ground- and satellite-based evidence of the biophysical mechanisms behind the greening Sahel. Glob. Chang. Biol. 2015, 21, 1610–1620. [Google Scholar] [CrossRef] [PubMed]
- Seaquist, J.; Olsson, L.; Ardö, J.; Eklundh, L. Broad-scale increase in NPP quantified for the African Sahel, 1982–1999. Int. J. Remote Sens. 2006, 27, 5115–5122. [Google Scholar] [CrossRef]
- Hickler, T.; Eklundh, L.; Seaquist, J.W.; Smith, B.; Ardö, J.; Olsson, L.; Sykes, M.T.; Sjöström, M. Precipitation controls Sahel greening trend. Geophys. Res. Lett. 2005, 32, L21415. [Google Scholar] [CrossRef]
- Abdi, A.M.; Seaquist, J.; Tenenbaum, D.E.; Eklundh, L.; Ardo, J. The supply and demand of net primary production in the Sahel. Environ. Res. Lett. 2014, 9, 094003. [Google Scholar] [CrossRef]
- Vrieling, A.; de Leeuw, J.; Said, M. Length of growing period over Africa: Variability and trends from 30 years of NDVI time series. Remote Sens. 2013, 5, 982–1000. [Google Scholar] [CrossRef]
- Philippon, N.; Martiny, N.; Camberlin, P.; Hoffman, M.T.; Gond, V. Timing and patterns of the ENSO signal in Africa over the last 30 years: Insights from normalized difference vegetation index data. J. Clim. 2014, 27, 2509–2532. [Google Scholar] [CrossRef]
- Nicholson, S.E. Dryland Climatology; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Le Houérou, H.N. Definition, geographical limits, contacts with other ecoclimatic zones. In The Grazing Land Ecosystems of the African Sahel; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–16. [Google Scholar]
- Tagesson, T.; Fensholt, R.; Cappelaere, B.; Mougin, E.; Horion, S.; Kergoat, L.; Nieto, H.; Mbow, C.; Ehammer, A.; Demarty, J.; et al. Spatiotemporal variability in carbon exchange fluxes across the Sahel. Agric. For. Meteorol. 2016, 226, 108–118. [Google Scholar] [CrossRef]
- Hiernaux, P.; Le Houérou, H.N. Les parcours du Sahel. Sci. Chang. Planét/Sécheresse 2006, 17, 51–71. [Google Scholar]
- Brandt, M.; Hiernaux, P.; Rasmussen, K.; Mbow, C.; Kergoat, L.; Tagesson, T.; Ibrahim, Y.Z.; Wélé, A.; Tucker, C.J.; Fensholt, R. Assessing woody vegetation trends in Sahelian drylands using MODIS based seasonal metrics. Remote Sens. Environ. 2016, 183, 215–225. [Google Scholar] [CrossRef]
- Tucker, C.J.; Vanpraet, C.; Boerwinkel, E.; Gaston, A. Satellite remote sensing of total dry matter production in the Senegalese Sahel. Remote Sens. Environ. 1983, 13, 461–474. [Google Scholar] [CrossRef]
- Prince, S.D. Satellite remote sensing of primary production: Comparison of results for Sahelian grasslands 1981–1988. Int. J. Remote Sens. 1991, 12, 1301–1311. [Google Scholar] [CrossRef]
- Verhoef, A.; Allen, S.J.; Bruin, H.A.R.; Jacobs, C.M.J.; Heusinkveld, B.G. Fluxes of carbon dioxide and water vapour from a Sahelian savanna. Agric. For. Meteorol. 1996, 80, 231–248. [Google Scholar] [CrossRef]
- Moncrieff, J.B.; Monteny, B.; Verhoef, A.; Friborg, T.; Elbers, J.; Kabat, P.; de Bruin, H.; Soegaard, H.; Jarvis, P.G.; Taupin, J.D. Spatial and temporal variations in net carbon flux during HAPEX-Sahel. J. Hydrol. 1997, 188, 563–588. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Tucker, C.J.; Ba, M. Desertification, drought, and surface vegetation: An example from the West African Sahel. Bull. Am. Meteorol. Soc. 1998, 79, 815–830. [Google Scholar] [CrossRef]
- Sjöström, M.; Ardö, J.; Arneth, A.; Boulain, N.; Cappelaere, B.; Eklundh, L.; De Grandcourt, A.; Kutsch, W.; Merbold, L.; Nouvellon, Y. Exploring the potential of MODIS EVI for modeling gross primary production across African ecosystems. Remote Sens. Environ. 2011, 115, 1081–1089. [Google Scholar] [CrossRef]
- Merbold, L.; Ardö, J.; Arneth, A.; Scholes, R.; Nouvellon, Y.; De Grandcourt, A.; Archibald, S.; Bonnefond, J.; Boulain, N.; Brueggemann, N. Precipitation as driver of carbon fluxes in 11 African ecosystems. Biogeosciences 2009, 6, 1027–1041. [Google Scholar] [CrossRef]
- Nutini, F.; Boschetti, M.; Candiani, G.; Bocchi, S.; Brivio, P. Evaporative fraction as an indicator of moisture condition and water stress status in semi-arid rangeland ecosystems. Remote Sens. 2014, 6, 6300. [Google Scholar] [CrossRef]
- Velluet, C.; Demarty, J.; Cappelaere, B.; Braud, I.; Issoufou, H.B.A.; Boulain, N.; Ramier, D.; Mainassara, I.; Charvet, G.; Boucher, M.; et al. Building a field- and model-based climatology of local water and energy cycles in the cultivated Sahel—Annual budgets and seasonality. Hydrol. Earth Syst. Sci. 2014, 18, 5001–5024. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Hanan, N.; Kabat, P.; Lesch, L. A Remote sensing study of the NDVI-Ts relationship and the transpiration from sparse vegetation in the sahel based on high-resolution satellite data. Remote Sens. Environ. 1999, 69, 224–240. [Google Scholar] [CrossRef]
- Ago, E.E.; Serça, D.; Agbossou, E.K.; Galle, S.; Aubinet, M. Carbon dioxide fluxes from a degraded woodland in West Africa and their responses to main environmental factors. Carbon Balance Manag. 2015, 10, 22. [Google Scholar] [CrossRef] [PubMed]
- Ardö, J. Increasing the confidence of African carbon cycle assessments. In Proceedings of the EGU General Assembly 2016, Vienna, Austria, 17–22 April 2016.
- Running, S.W.; Thornton, P.E.; Nemani, R.R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the Earth Observing System. In Methods in Ecosystem Science; Sala, O.E., Mooney, H.A., Howarth, R.W., Eds.; Springer: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Sjöström, M.; Zhao, M.; Archibald, S.; Arneth, A.; Cappelaere, B.; Falk, U.; de Grandcourt, A.; Hanan, N.; Kergoat, L.; Kutsch, W.; et al. Evaluation of MODIS gross primary productivity for Africa using eddy covariance data. Remote Sens. Environ. 2013, 131, 275–286. [Google Scholar] [CrossRef]
- Sadeghi, M.; Jones, S.B.; Philpot, W.D. A linear physically-based model for remote sensing of soil moisture using short wave infrared bands. Remote Sens. Environ. 2015, 164, 66–76. [Google Scholar] [CrossRef]
- Liang, S.; Zhong, B.; Fang, H. Improved estimation of aerosol optical depth from MODIS imagery over land surfaces. Remote Sens. Environ. 2006, 104, 416–425. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P. Moisture Effects on Soil Reflectance. Soil Sci. Soc. Am. J. 2002, 66, 722–727. [Google Scholar] [CrossRef]
- Weidong, L.; Baret, F.; Xingfa, G.; Qingxi, T.; Lanfen, Z.; Bing, Z. Relating soil surface moisture to reflectance. Remote Sens. Environ. 2002, 81, 238–246. [Google Scholar] [CrossRef]
- Tian, J.; Philpot, W.D. Relationship between surface soil water content, evaporation rate, and water absorption band depths in SWIR reflectance spectra. Remote Sens. Environ. 2015, 169, 280–289. [Google Scholar] [CrossRef]
- Ardö, J.; Molder, M.; El-Tahir, B.A.; Elkhidir, H.A. Seasonal variation of carbon fluxes in a sparse savanna in semi arid Sudan. Carbon Balance Manag. 2008, 3, 7. [Google Scholar] [CrossRef] [PubMed]
- Cappelaere, B.; Descroix, L.; Lebel, T.; Boulain, N.; Ramier, D.; Laurent, J.P.; Favreau, G.; Boubkraoui, S.; Boucher, M.; Bouzou Moussa, I.; et al. The AMMA-CATCH experiment in the cultivated Sahelian area of south-west Niger—Investigating water cycle response to a fluctuating climate and changing environment. J. Hydrol. 2009, 375, 34–51. [Google Scholar] [CrossRef]
- Tagesson, T.; Fensholt, R.; Guiro, I.; Rasmussen, M.O.; Huber, S.; Mbow, C.; Garcia, M.; Horion, S.; Sandholt, I.; Holm-Rasmussen, B.; et al. Ecosystem properties of semiarid savanna grassland in West Africa and its relationship with environmental variability. Glob. Chang. Biol. 2015, 21, 250–264. [Google Scholar] [CrossRef] [PubMed]
- Olsson, L.; Ardö, J. Soil carbon sequestration in degraded semiarid agro-ecosystems-perils and potentials. AMBIO J. Hum. Environ. 2002, 31, 471–477. [Google Scholar] [CrossRef]
- Boulain, N.; Cappelaere, B.; Ramier, D.; Issoufou, H.B.A.; Halilou, O.; Seghieri, J.; Guillemin, F.; Oï, M.; Gignoux, J.; Timouk, F. Towards an understanding of coupled physical and biological processes in the cultivated Sahel—2. Vegetation and carbon dynamics. J. Hydrol. 2009, 375, 190–203. [Google Scholar] [CrossRef]
- Tagesson, T.; Fensholt, R.; Cropley, F.; Guiro, I.; Horion, S.; Ehammer, A.; Ardö, J. Dynamics in carbon exchange fluxes for a grazed semi-arid savanna ecosystem in West Africa. Agric. Ecosyst. Environ. 2015, 205, 15–24. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Sjöström, M.; Ardö, J.; Eklundh, L.; El-Tahir, B.; El-Khidir, H.; Hellström, M.; Pilesjö, P.; Seaquist, J. Evaluation of satellite based indices for gross primary production estimates in a sparse savanna in the Sudan. Biogeosciences 2009, 6, 129–138. [Google Scholar] [CrossRef]
- Tagesson, T.; Fensholt, R.; Huber, S.; Horion, S.; Guiro, I.; Ehammer, A.; Ardö, J. Deriving seasonal dynamics in ecosystem properties of semi-arid savanna grasslands from in situ-based hyperspectral reflectance. Biogeosciences 2015, 12, 4621–4635. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Jägermeyr, J.; Gerten, D.; Lucht, W.; Hostert, P.; Migliavacca, M.; Nemani, R. A high-resolution approach to estimating ecosystem respiration at continental scales using operational satellite data. Glob. Chang. Biol. 2014, 20, 1191–1210. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, H.; Dungan, J.L.; White, M.A.; Yang, F.; Michaelis, A.R.; Running, S.W.; Nemani, R.R. Satellite-based estimation of surface vapor pressure deficits using MODIS land surface temperature data. Remote Sens. Environ. 2008, 112, 142–155. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; et al. A new model of gross primary productivity for North American ecosystems based solely on the enhanced vegetation index and land surface temperature from MODIS. Remote Sens. Environ. 2008, 112, 1633–1646. [Google Scholar] [CrossRef]
- Pappas, C.; Fatichi, S.; Leuzinger, S.; Wolf, A.; Burlando, P. Sensitivity analysis of a process-based ecosystem model: Pinpointing parameterization and structural issues. J. Geophys. Res. Biogeosci. 2013, 118, 505–528. [Google Scholar] [CrossRef]
- Zotarelli, L.; Dukes, M.D.; Morgan, K.T. Interpretation of Soil Moisture Content to Determine Soil Field Capacity and Avoid Over-Irrigating Sandy Soils Using Soil Moisture Sensors; UF/IFAS Extension: Gainesville, FL, USA, 2010. [Google Scholar]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Leenaars, J.; van Oostrum, A.; Ruiperez Gonzalez, M. Africa Soil Profiles Database, Version 1.2. A Compilation of Geo-Referenced and Standardised Legacy Soil Profile Data for Sub-Saharan Africa (with Dataset); ISRIC—World Soil Information: Wageningen, The Netherlands, 2014. [Google Scholar]
- Dingman, S.L. Physical Hydrology, 3rd ed.; Waveland Press: Long Grove, IL, USA, 2015. [Google Scholar]
- Anderson, D.B. Relative humidity or vapor pressure deficit. Ecology 1936, 17, 277–282. [Google Scholar] [CrossRef]
- Maroco, J.P.; Pereira, J.S.; Chaves, M.M. Stomatal responses to leaf-to-air vapour pressure deficit in sahelian species. Funct. Plant Biol. 1997, 24, 381–387. [Google Scholar] [CrossRef]
- Ward, A.D.; Trimble, S.W.; Burckhard, S.R.; Lyon, J.G. Environmental Hydrology, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Kohler, M.; Linsley, R. Predicting the Runoff from Storm Rainfall; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1951. [Google Scholar]
- Choudhury, B.J.; Golus, R.E. Estimating soil wetness using satellite data. Int. J. Remote Sens. 1988, 9, 1251–1257. [Google Scholar] [CrossRef]
- Heggen, R.J. Normalized Antecedent Precipitation Index. J. Hydrol. Eng. 2001, 6, 377–381. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.F.; Hossain, F.; Curtis, S.; Huffman, G.J. A first approach to global runoff simulation using satellite rainfall estimation. Water Resour. Res. 2007, 43, W08502. [Google Scholar] [CrossRef]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical–biophysical relationships of vegetation spectra without background contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Ma, X.; Huete, A.; Yu, Q.; Coupe, N.R.; Davies, K.; Broich, M.; Ratana, P.; Beringer, J.; Hutley, L.B.; Cleverly, J.; et al. Spatial patterns and temporal dynamics in savanna vegetation phenology across the North Australian Tropical Transect. Remote Sens. Environ. 2013, 139, 97–115. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Zhao, W.; Ji, X. Spatio-temporal variation in transpiration responses of maize plants to vapor pressure deficit under an arid climatic condition. J. Arid Land 2016, 8, 409–421. [Google Scholar] [CrossRef]
- Kutsch, W.L.; Hanan, N.; Scholes, B.; McHugh, I.; Kubheka, W.; Eckhardt, H.; Williams, C. Response of carbon fluxes to water relations in a savanna ecosystem in South Africa. Biogeosciences 2008, 5, 1797–1808. [Google Scholar] [CrossRef]
- Schwinning, S.; Sala, O.E.; Loik, M.E.; Ehleringer, J.R. Thresholds, memory, and seasonality: Understanding pulse dynamics in arid/semi-arid ecosystems. Oecologia 2004, 141, 191–193. [Google Scholar] [CrossRef] [PubMed]
- Shinoda, M.; Yamaguchi, Y. Influence of soil moisture anomaly on temperature in the Sahel: A Comparison between wet and dry decades. J. Hydrometeorol. 2003, 4, 437–447. [Google Scholar] [CrossRef]
- Tagesson, T.; Ardö, J.; Guiro, I.; Cropley, F.; Mbow, C.; Horion, S.; Ehammer, A.; Mougin, E.; Delon, C.; Galy-Lacaux, C.; et al. Very high CO2 exchange fluxes at the peak of the rainy season in a West African grazed semi-arid savanna ecosystem. Geograf. Tidsskr. Dan. J. Geogr. 2016, 116, 93–109. [Google Scholar] [CrossRef]
- Steiner, A.L.; Pal, J.S.; Rauscher, S.A.; Bell, J.L.; Diffenbaugh, N.S.; Boone, A.; Sloan, L.C.; Giorgi, F. Land surface coupling in regional climate simulations of the West African monsoon. Clim. Dyn. 2009, 33, 869–892. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S.; Diedhiou, A. The West African Monsoon Dynamics. Part I: Documentation of Intraseasonal Variability. J. Clim. 2003, 16, 3389–3406. [Google Scholar] [CrossRef]
- Browne, N.A.K.; Sylla, M.B. Regional climate model sensitivity to domain size for the simulation of the West African summer monsoon rainfall. Int. J. Geophys. 2012, 2012, 1–17. [Google Scholar] [CrossRef]
- Messager, C.; Gallée, H.; Brasseur, O. Precipitation sensitivity to regional SST in a regional climate simulation during the West African monsoon for two dry years. Clim. Dyn. 2004, 22, 249–266. [Google Scholar] [CrossRef]
- Gargallo-Garriga, A.; Sardans, J.; Pérez-Trujillo, M.; Rivas-Ubach, A.; Oravec, M.; Vecerova, K.; Urban, O.; Jentsch, A.; Kreyling, J.; Beierkuhnlein, C.; et al. Opposite metabolic responses of shoots and roots to drought. Sci. Rep. 2014, 4, 6829. [Google Scholar] [CrossRef] [PubMed]
- Otieno, D.O.; K’Otuto, G.O.; Maina, J.N.; Kuzyakov, Y.; Onyango, J.C. Responses of ecosystem carbon dioxide fluxes to soil moisture fluctuations in a moist Kenyan savanna. J. Trop. Ecol. 2010, 26, 605–618. [Google Scholar] [CrossRef]
- Hasibeder, R.; Fuchslueger, L.; Richter, A.; Bahn, M. Summer drought alters carbon allocation to roots and root respiration in mountain grassland. New Phytol. 2015, 205, 1117–1127. [Google Scholar] [CrossRef] [PubMed]
- Murray-Tortarolo, G.; Friedlingstein, P.; Sitch, S.; Seneviratne, S.I.; Fletcher, I.; Mueller, B.; Greve, P.; Anav, A.; Liu, Y.; Ahlström, A.; et al. The dry season intensity as a key driver of NPP trends. Geophys. Res. Lett. 2016, 43, 2632–2639. [Google Scholar] [CrossRef]
- Ardö, J.; Olsson, L. Soil carbon sequestration in traditional farming in sudanese dry lands. Environ. Manag. 2004, 33, S318–S329. [Google Scholar] [CrossRef]
- De Bie, S.; Ketner, P.; Paasse, M.; Geerling, C. Woody plant phenology in the West Africa savanna. J. Biogeogr. 1998, 25, 883–900. [Google Scholar] [CrossRef]
- Fontaine, B.; Louvet, S.; Roucou, P. Fluctuations in annual cycles and inter-seasonal memory in West Africa: Rainfall, soil moisture and heat fluxes. Theor. Appl. Climatol. 2007, 88, 57–70. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Schlosser, C.A.; Brubaker, K.L. Precipitation, recycling, and land memory: An integrated analysis. J. Hydrometeorol. 2009, 10, 278–288. [Google Scholar] [CrossRef]
- Hiernaux, P.; Cissé, M.; Diarra, L.; De Leeuw, P. Fluctuations saisonnières de la feuillaison des arbres et des buissons sahéliens. Conséquences pour la quantification des ressources fourragères. Revue D'élevage Médecine Vétérinaire Des Pays Tropicaux 1994, 47, 117–125. [Google Scholar]
- Ma, X.; Huete, A.; Yu, Q.; Restrepo-Coupe, N.; Beringer, J.; Hutley, L.B.; Kanniah, K.D.; Cleverly, J.; Eamus, D. Parameterization of an ecosystem light-use-efficiency model for predicting savanna GPP using MODIS EVI. Remote Sens. Environ. 2014, 154, 253–271. [Google Scholar] [CrossRef]
- Ahlström, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K.; et al. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef] [PubMed]
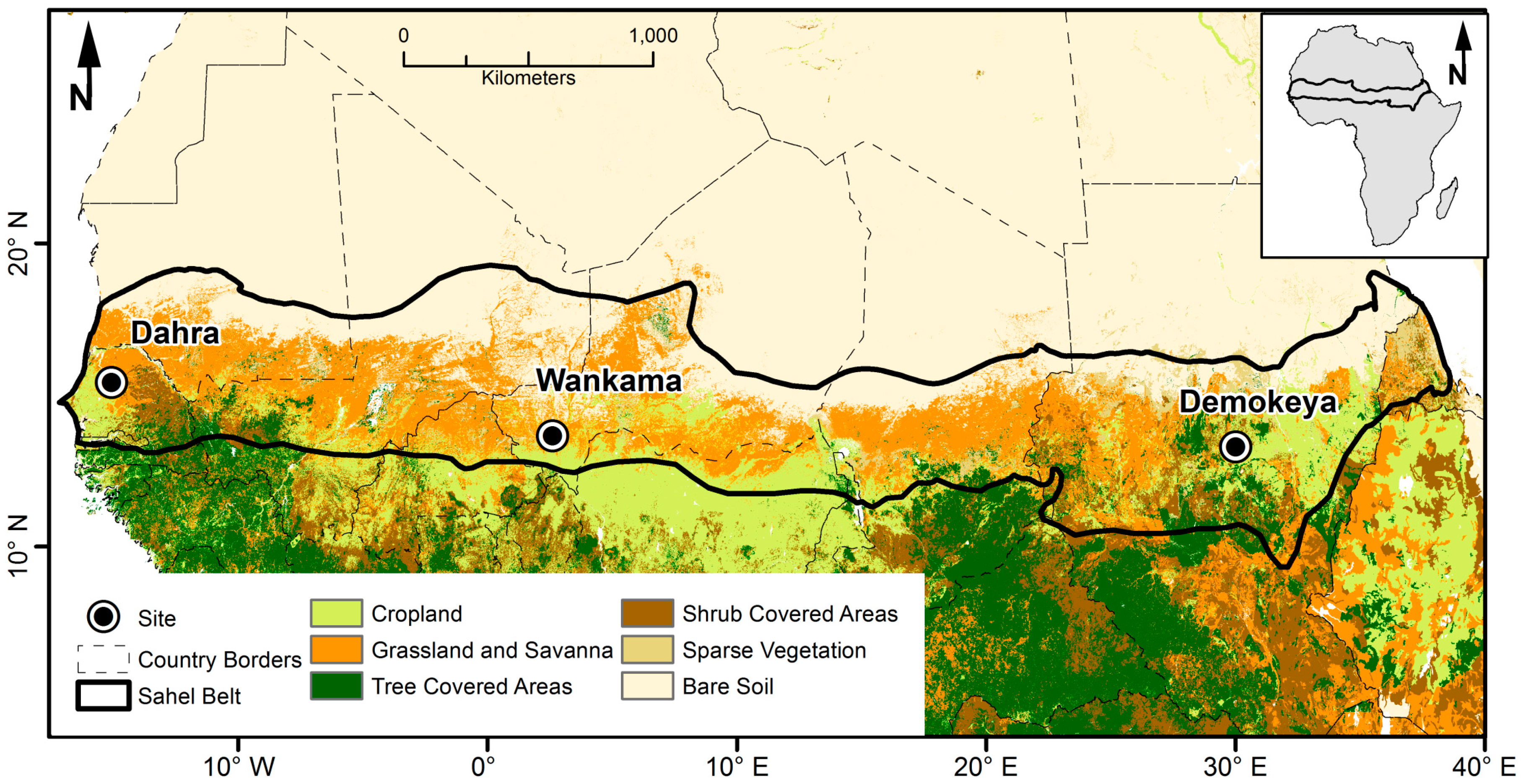


| Site, Country | Longitude, Latitude (DD) | Vegetation Type | Soil Type | MAP (mm) | MAT (°C) | Measurement Years | Rel. Hum. DS/GS (%) | Ref. |
|---|---|---|---|---|---|---|---|---|
| Demokeya, Sudan | 30.47, 13.28 | Sparse acacia savanna | Cambic Arenosols | 320 | 30 | 2007–2009 | 16/57 | [36] |
| Wankama, Niger | 2.63, 13.64 | Fallow shrubland | Sandy Ferruginous Arenosols | 479 | 30 | 2005–2009 | 28/75 | [37] |
| Dahra, Senegal | −15.43, 15.40 | Open woody savanna | Luvic Arenosols | 416 | 29 | 2010–2013 | 9/63 | [38] |
| Site | Field Capacity, % | Soil Texture, % (Sand/Silt/Clay) | Permanent Wilting Point, % | ||
|---|---|---|---|---|---|
| 0–30 cm | 30–100 cm | 0–30 cm | 30–100 cm | ||
| Demokeya | 15 | 89/6/5 | 90/5/5 | 2 | 3 |
| Wankama Fallow | 16 | 90/5/5 | 88/5/7 | 3 | 3 |
| Dahra | 7 | 89/6/5 | 89/5/6 | 2 | 4 |
| Response = EC GPP | Statistics | |||
|---|---|---|---|---|
| Demokeya | RMSE | R2 | n | BIC |
| API | 1.61 | 0.28 | 97 | 382.04 |
| VPD | 1.22 | 0.59 | 95 | 321.88 |
| PAW | 1.19 | 0.62 | 89 | 298.27 |
| VPD + API | 1.22 | 0.59 | 95 | 326.36 |
| API + PAW | 1.19 | 0.62 | 89 | 301.82 |
| PAW + VPD | 1.12 | 0.66 | 89 | 291.87 |
| Wankama Fallow | RMSE | R2 | n | BIC |
| API | 1.54 | 0.33 | 159 | 605.44 |
| VPD | 0.96 | 0.74 | 157 | 448.70 |
| PAW | 0.91 | 0.76 | 132 | 365.07 |
| VPD + API | 0.94 | 0.75 | 156 | 445.64 |
| API + PAW | 0.91 | 0.77 | 131 | 366.92 |
| PAW + VPD | 0.77 | 0.83 | 129 | 318.23 |
| Dahra | RMSE | R2 | n | BIC |
| API | 2.91 | 0.38 | 161 | 815.93 |
| PAW | 2.51 | 0.59 | 154 | 736.34 |
| VPD | 1.99 | 0.75 | 146 | 631.43 |
| API + PAW | 2.28 | 0.64 | 147 | 680.49 |
| VPD + API | 1.92 | 0.77 | 146 | 624.80 |
| VPD + PAW | 1.88 | 0.77 | 139 | 590.21 |
| All Sites | RMSE | R2 | n | BIC |
| API | 2.37 | 0.33 | 417 | 1888.05 |
| PAW | 2.27 | 0.36 | 375 | 1780.69 |
| VPD | 2.21 | 0.43 | 398 | 1779.50 |
| VPD + API | 2.22 | 0.44 | 390 | 1697.36 |
| API + PAW | 2.18 | 0.45 | 367 | 1652.43 |
| PAW + VPD | 2.06 | 0.47 | 364 | 1624.53 |
| Response = EC GPP | Greening Phase n = 106 | Browning Phase n = 75 | ||||
|---|---|---|---|---|---|---|
| rs | ts | p | rs | ts | p | |
| PAW | 0.44 | 4.950 | <0.01 | 0.16 | 0.156 | 0.18 |
| VPD | −0.24 | −2.525 | 0.01 | −0.52 | −0.523 | <0.01 |
| EVI | 0.61 | 7.776 | <0.05 | 0.60 | 6.289 | <0.01 |
| LST | −0.28 | −2.957 | <0.05 | −0.34 | −3.074 | <0.01 |
| BAND 7 | 0.32 | 3.426 | <0.05 | 0.22 | 1.920 | 0.06 |
| Response = EC GPP | Statistics | |||
|---|---|---|---|---|
| Demokeya | RMSE | R2 | n | BIC |
| BAND 7 | 1.70 | 0.20 | 97 | 392.13 |
| LST | 1.44 | 0.40 | 94 | 349.51 |
| EVI | 0.60 | 0.89 | 97 | 184.09 |
| MOD17 GPP | 0.89 | 0.77 | 95 | 262.10 |
| EVI + LST | 0.58 | 0.89 | 94 | 180.95 |
| EVI + BAND 7 | 0.51 | 0.93 | 97 | 161.24 |
| EVI + BAND7 + LST | 0.48 | 0.93 | 94 | 155.54 |
| Wankama Fallow | RMSE | R2 | n | BIC |
| LST | 1.55 | 0.33 | 155 | 592.58 |
| BAND 7 | 1.36 | 0.50 | 158 | 559.78 |
| EVI | 0.96 | 0.74 | 158 | 450.78 |
| MOD17 GPP | 1.43 | 0.44 | 123 | 452.12 |
| EVI + LST | 0.94 | 0.76 | 154 | 444.33 |
| EVI + BAND 7 | 0.90 | 0.78 | 158 | 435.56 |
| EVI + BAND7 + LST | 0.67 | 0.88 | 154 | 344.91 |
| Dahra | RMSE | R2 | n | BIC |
| BAND 7 | 2.73 | 0.38 | 156 | 772.01 |
| LST | 2.35 | 0.58 | 163 | 747.90 |
| EVI | 1.00 | 0.91 | 156 | 459.54 |
| MOD17 GPP | 1.35 | 0.86 | 166 | 587.48 |
| EVI + LST | 0.96 | 0.92 | 153 | 442.79 |
| EVI + BAND 7 | 0.93 | 0.93 | 156 | 440.53 |
| EVI + BAND7 + LST | 0.85 | 0.96 | 153 | 414.90 |
| All Sites | RMSE | R2 | n | BIC |
| BAND 7 | 2.18 | 0.32 | 411 | 1826.60 |
| LST | 2.03 | 0.42 | 412 | 1767.47 |
| EVI | 1.04 | 0.83 | 411 | 1220.91 |
| MOD17 GPP | 1.39 | 0.76 | 384 | 1362.45 |
| EVI + LST | 0.96 | 0.86 | 401 | 1131.69 |
| EVI + BAND 7 | 0.91 | 0.88 | 411 | 1112.77 |
| EVI + BAND7 + LST | 0.84 | 0.89 | 401 | 1023.90 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdi, A.M.; Boke-Olén, N.; Tenenbaum, D.E.; Tagesson, T.; Cappelaere, B.; Ardö, J. Evaluating Water Controls on Vegetation Growth in the Semi-Arid Sahel Using Field and Earth Observation Data. Remote Sens. 2017, 9, 294. https://doi.org/10.3390/rs9030294
Abdi AM, Boke-Olén N, Tenenbaum DE, Tagesson T, Cappelaere B, Ardö J. Evaluating Water Controls on Vegetation Growth in the Semi-Arid Sahel Using Field and Earth Observation Data. Remote Sensing. 2017; 9(3):294. https://doi.org/10.3390/rs9030294
Chicago/Turabian StyleAbdi, Abdulhakim M., Niklas Boke-Olén, David E. Tenenbaum, Torbern Tagesson, Bernard Cappelaere, and Jonas Ardö. 2017. "Evaluating Water Controls on Vegetation Growth in the Semi-Arid Sahel Using Field and Earth Observation Data" Remote Sensing 9, no. 3: 294. https://doi.org/10.3390/rs9030294
APA StyleAbdi, A. M., Boke-Olén, N., Tenenbaum, D. E., Tagesson, T., Cappelaere, B., & Ardö, J. (2017). Evaluating Water Controls on Vegetation Growth in the Semi-Arid Sahel Using Field and Earth Observation Data. Remote Sensing, 9(3), 294. https://doi.org/10.3390/rs9030294