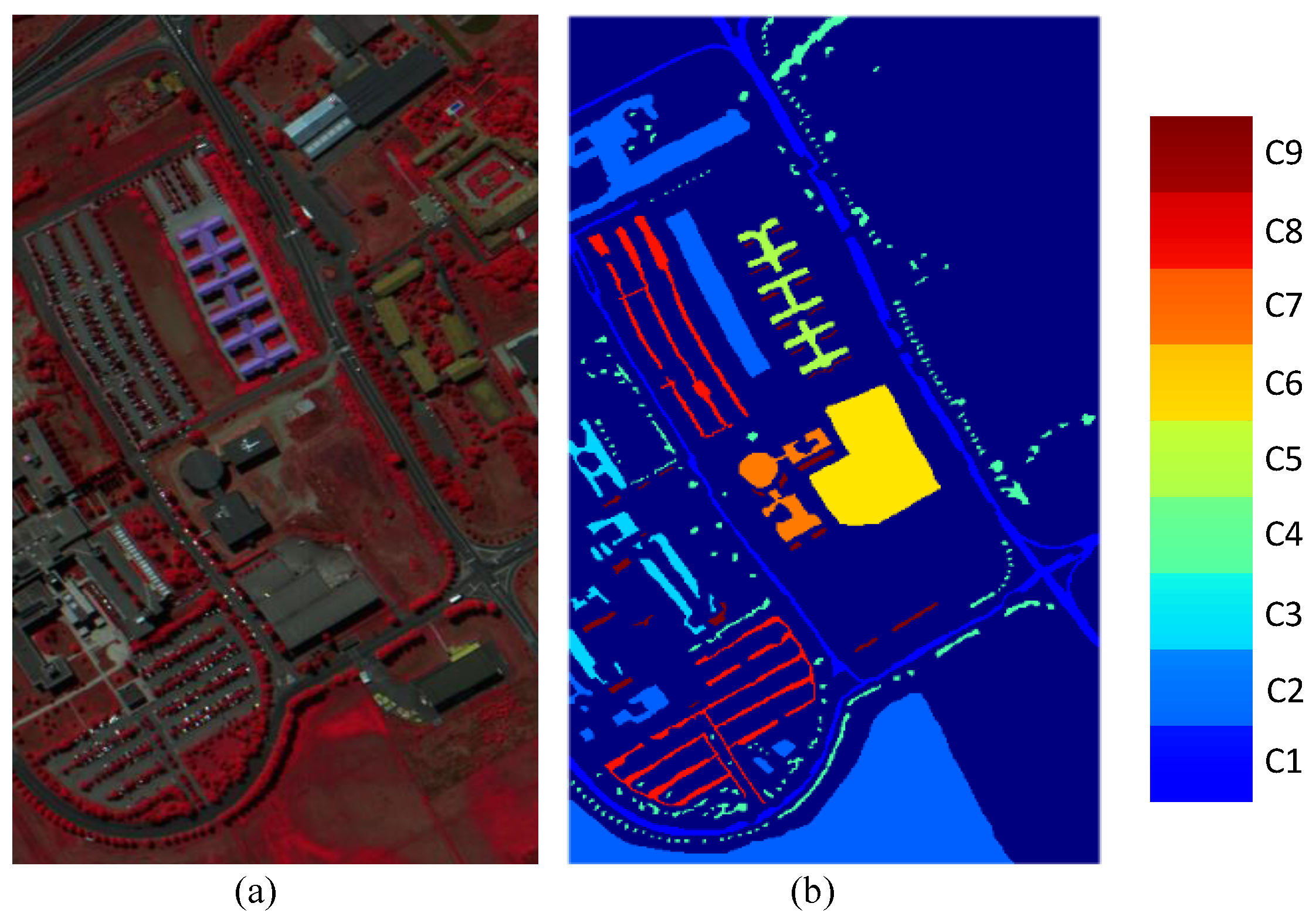
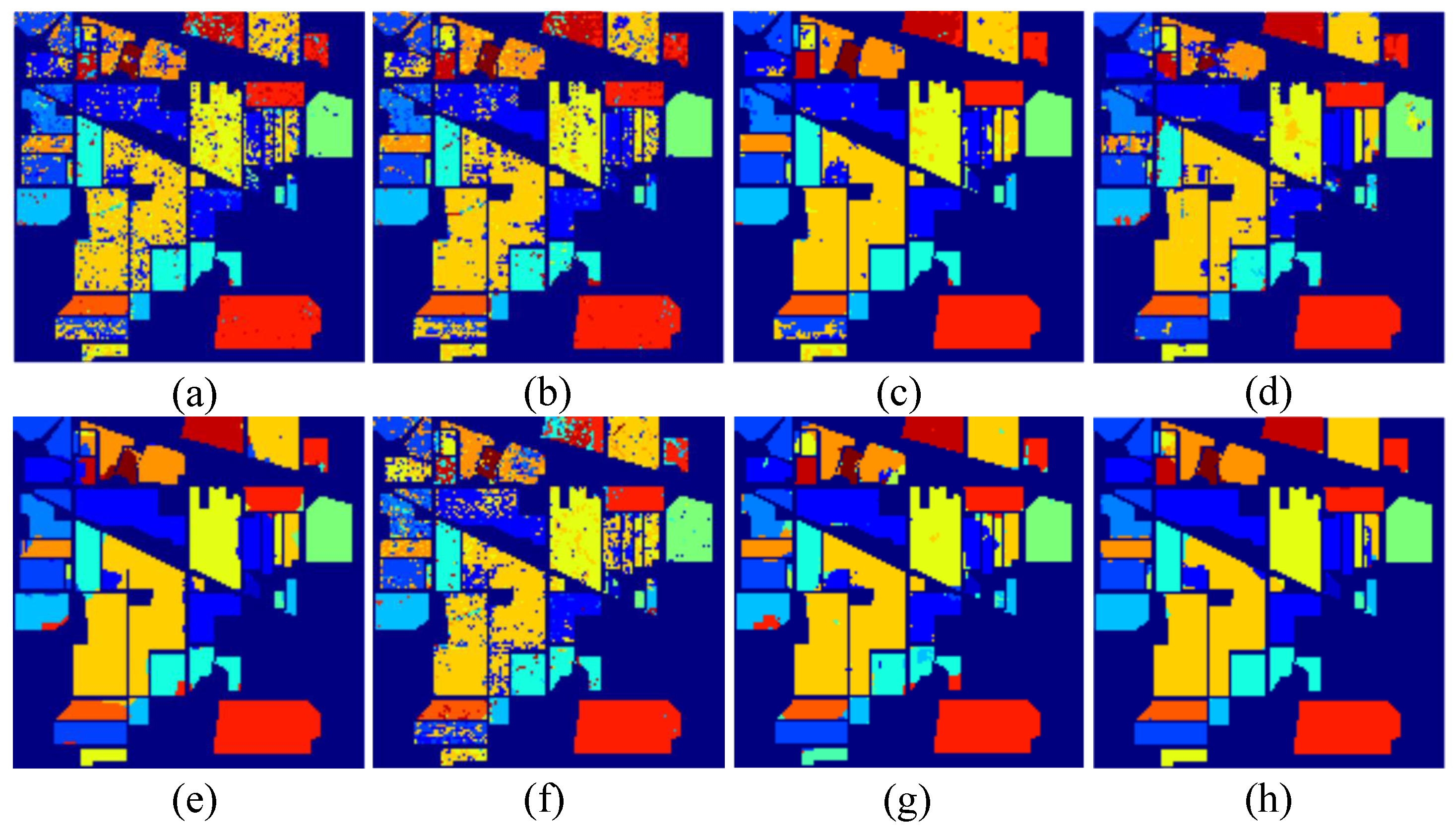
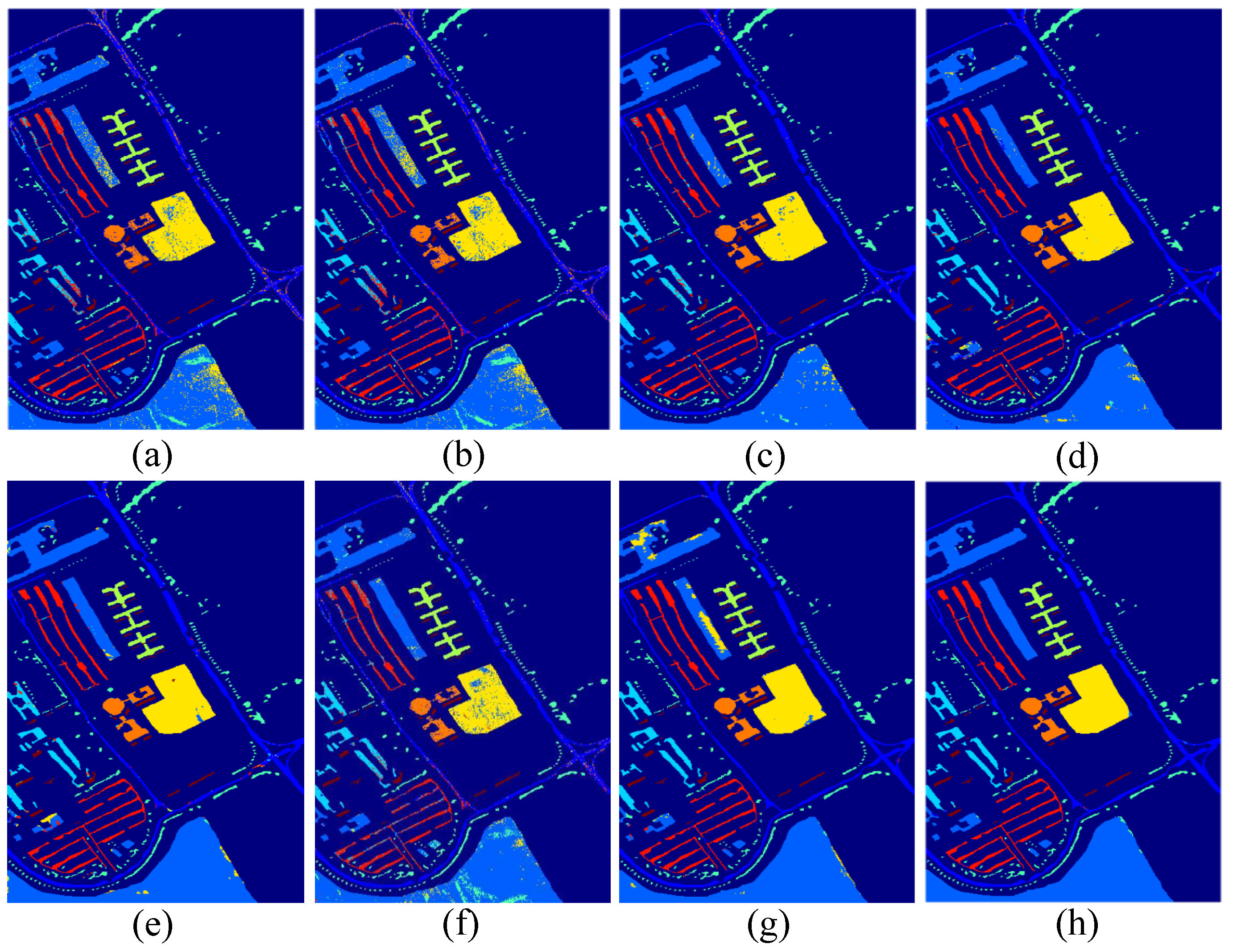
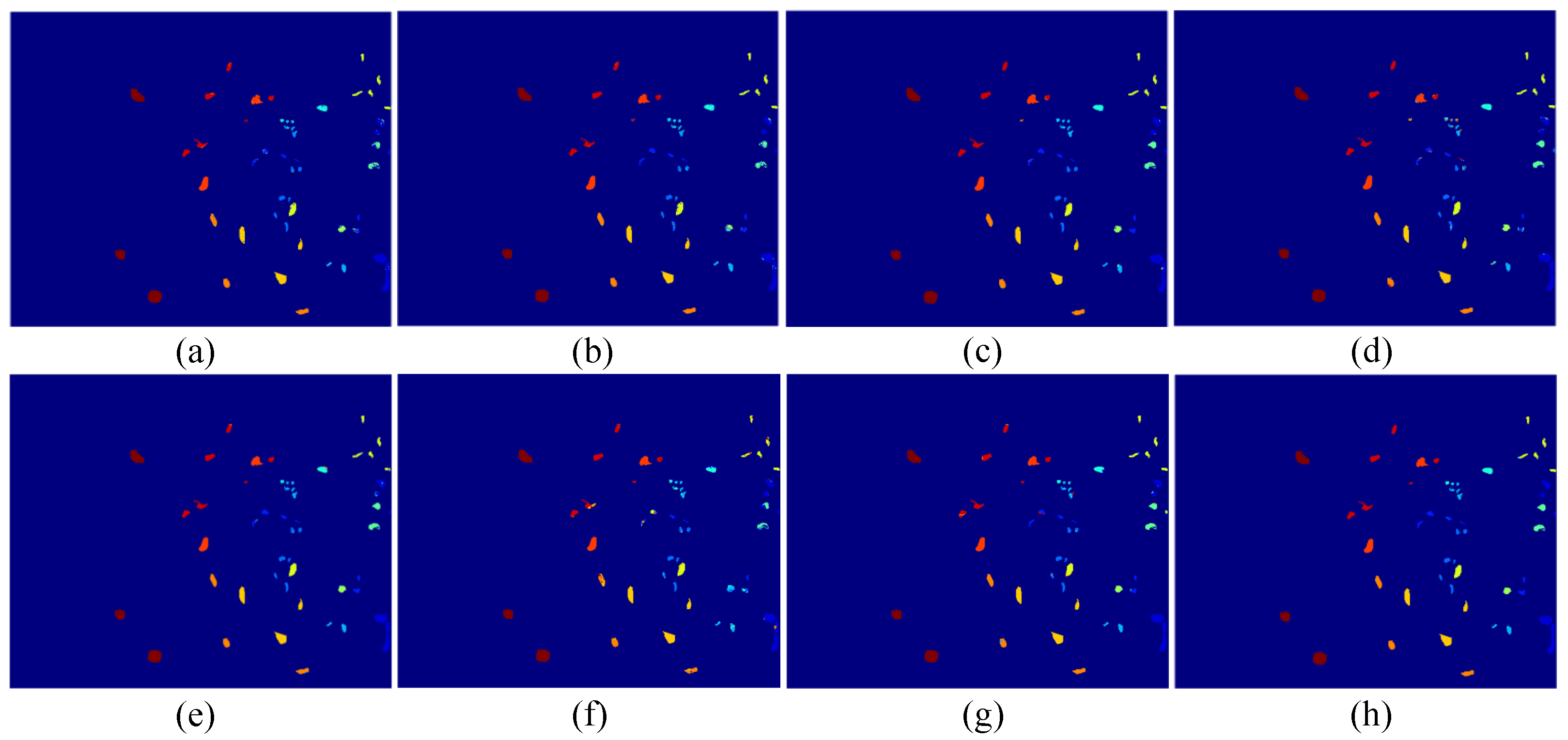
1. Introduction
Current hyperspectral sensors can acquire images with high spectral and spatial resolutions simultaneously. For example, the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor covers 224 continuous spectral bands across the electromagnetic spectrum with a spatial resolution of 3.7 m. Such rich information has been successfully used in various applications such as national defense, urban planning, precision agriculture and environment monitoring [
1].
For these applications, an essential step is image classification, whose purpose is to identify the label of each pixel. Hyperspectral image (HSI) classification is a challenging task. Two important issues exist [
2,
3]. The first one is the curse of dimensionality. HSI provides very high-dimensional data with hundreds of spectral channels ranging from the visible to the short wave-infrared region of the electromagnetic spectrum. These high-dimensional data with limited numbers of training samples can easily result in the Hughes phenomenon [
4], which means that the classification accuracy starts to decrease when the number of features exceeds a threshold. The other one is the use of spatial information. The improvement of spatial resolutions may increase spectral variations among intra-class pixels while decreasing spectral variations among inter-class pixels [
5,
6]. Thus, only using spectral information is not enough to obtain a satisfying result.
To solve the first issue, a widely used method is to project the original data into a low-dimensional subspace, in which most of the useful information can be preserved. In the existing literature, large amounts of works have been proposed [
7,
8,
9,
10]. They can be roughly divided into two categories: unsupervised feature extraction (FE) methods and supervised ones. The unsupervised methods attempt to reveal low-dimensional data structures without using any label information of training samples. These methods retain overall structure of data and do not focus on separating information of samples. Typical methods include but are not limited to principal component analysis (PCA) [
7], neighborhood preserving embedding (NPE) [
11], and independent component analysis (ICA) [
12]. Different from these, the aim of supervised learning methods is to explore the information of labeled data to learn a discriminant subspace. One typical method is linear discriminant analysis (LDA) [
13,
14], which aims to maximize the inter-class distance and minimize the intra-class distance. In [
8], a non-parametric weighted FE (NWFE) method was proposed. NWFE extends LDA by integrating nonparametric scatter matrices with training samples around the decision boundary [
8]. Local Fisher discriminant analysis (LFDA) was proposed in [
15], which extends the LDA by assigning greater weights to closer connecting samples.
To address the second issue, many works have been proposed to incorporate the spatial information into the spectral information [
16,
17,
18]. This is because the coverage area of one kind of material or one object usually contains more than one pixel. Current spatial-spectral feature fusion methods can be categorized into three classes: feature-level fusion, decision-level fusion, and regularization-level fusion [
3]. For feature-level fusion, one often extracts the spatial features and the spectral features independently and then concatenates them into a vector [
5,
19,
20,
21]. However, the direct concatenation will lead to a high-dimensional feature space. For decision-level fusion, multiple results are first derived using the spatial and spectral information, respectively, and then combined according to some strategies such as the majority voting strategy [
22,
23,
24]. For regularization-level fusion, a regularizer representing the spatial information is incorporated into the original object function. For example, in [
25,
26], Markov random field (MRF) modeling, the joint prior probabilities of each pixel and its spatial neighbors were incorporated into the Bayesian classifier as a regularizer. Although this method works well in capturing the spatial information, optimizing the objective function in MRF is time-consuming, especially on high-resolution data.
Recently, deep learning (DL) has attracted much attention in the field of remote sensing [
27,
28,
29,
30]. The core idea of DL is to automatically learn high-level semantic features from data itself in a hierarchical manner. In [
31,
32], the autoencoder model has been successfully used for HSI classification. In general, the inputs of the autoencoder model are a high-dimensional vector. Thus, to learn the spatial features from HSIs, an alternative method is flattening a local image patch into a vector and then feeding it into the model. However, this method may destroy the two-dimensional (2D) structure of images, leading to the loss of spatial information. Similar issues can be found in the deep belief network (DBN) [
33]. To address this issue, convolutional neural network (CNN) based deep models have been popularly used [
2,
34]. They directly take the original image or the local image patch as network inputs, and use local-connected and weight sharing structure to extract the spatial features from HSIs. In [
2], the authors designed a CNN network with three convolutional layers and one fully-connected layer. In addition, the input of the network is the first principal component of HSIs extracted by PCA. Although the experimental results demonstrate that this model can successfully learn the spatial feature of HSIs, it may fail to extract the spectral features. Recently, a three-dimensional (3D) CNN model was proposed in [
34]. In order to extract the spectral-spatial features from HSIs, the authors consider the 3D image patches as the input of the network. This complex structure will inevitably increase the amount of parameters, easily leading to the overfitting problem with a limited number of training samples.
In this paper, we propose a bidirectional-convolutional long short term memory (Bi-CLSTM) network to address the spectral-spatial feature learning problem. Specifically, we regard all the spectral bands as an image sequence, and model their relationships using a powerful LSTM network [
35]. Similar to other fully-connected networks such as autoencoder and DBN, LSTM can not capture the spatial information of HSIs. Inspired from [
36], we replace the fully-connected operators in the network by convolutional operators, resulting in a convolutional LSTM (CLSTM) network. Thus, CLSTM can simultaneously learn the spectral and spatial features. In addition, LSTM assumes that previous states affect future states, while the spectral channels in the sequence are correlated with each other. To address this issue, we further propose a Bi-CLSTM network. During the training process of the Bi-CLSTM network, we adopt two tricks to alleviate the overfitting problem. They are dropout and data augmentation operations.
To sum up, the main contributions of this paper are as follows. First, we consider images in all the spectral bands as an image sequence, and use LSTM to effectively model their relationships; second, considering the specific characteristics of hyperspectral images, we further propose a unified framework to combine the merits of LSTM and CNN for spectral-spatial feature extraction.
2. Review of RNN and LSTM
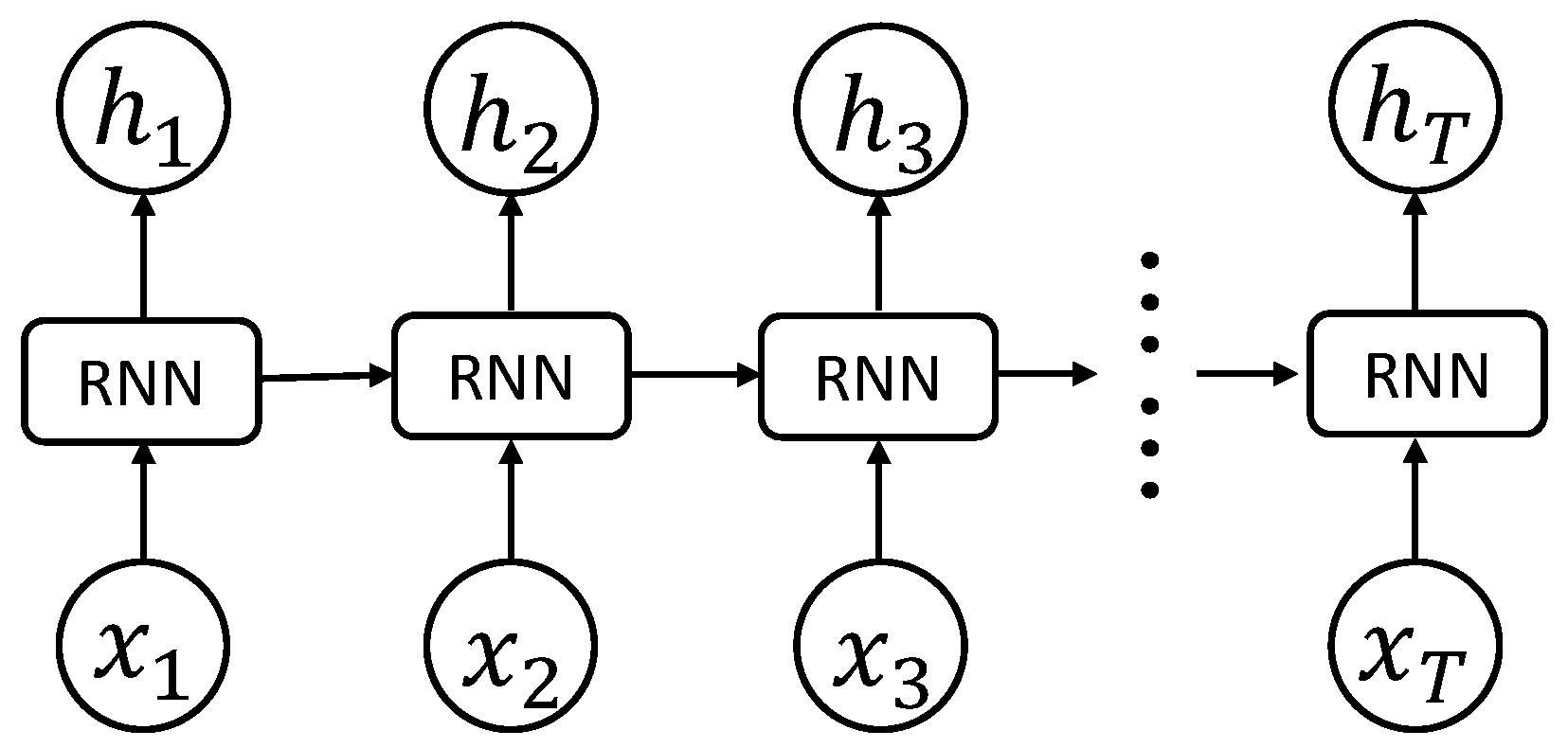
Recurrent neural network (RNN) [
37,
38] is an extension of traditional neural networks and used to address the sequence learning problem. Unlike the feedforward neural network, RNN adds recurrent edges to connect the neuron to itself across time so that it can model a probability distribution over sequence data.
Figure 1 demonstrates an example of RNN. The input of the network is a sequence data
. The node updates its hidden state
, given its previous state
and present input
, by
where
is the weight between the input node and the recurrent hidden node,
is the weight between the recurrent hidden node and itself from the previous time step, and
b and
are bias and nonlinear activation function, respectively.
As an important branch of the deep learning family, RNNs have recently shown promising results in many machine learning and computer vision tasks [
39,
40]. However, it has been observed that training RNN models to model the long-term sequence data is difficult. As can be seen from Equation (
1), the contribution of recurrent hidden node
at time
m to itself
at time
n may approach infinity or zero as the time interval increases whether
or
. This will lead to the gradient vanishing and exploding problem [
41]. To address this issue, Hochreiter and Schmidhuber proposed LSTM to replace the recurrent hidden node by a memory cell. The memory cell contains a node with a self-connected recurrent edge of a fixed weight one, ensuring that the gradient can pass across many time steps without vanishing or exploding. The LSTM unit consists of four important parts: input gate
, output gate
, forget gate
, and candidate cell value
. Based on these parts, memory cell and output can be computed by:
where
is the logistic sigmoid function, ‘·’ is a matrix multiplication operator, ‘∘’ is a dot product operator, and
,
,
as well as
are bias terms. The weight matrix subscripts have obvious meanings. For instance,
is the hidden-input gate matrix, and
is the input-output gate matrix etc.
3. Methodology
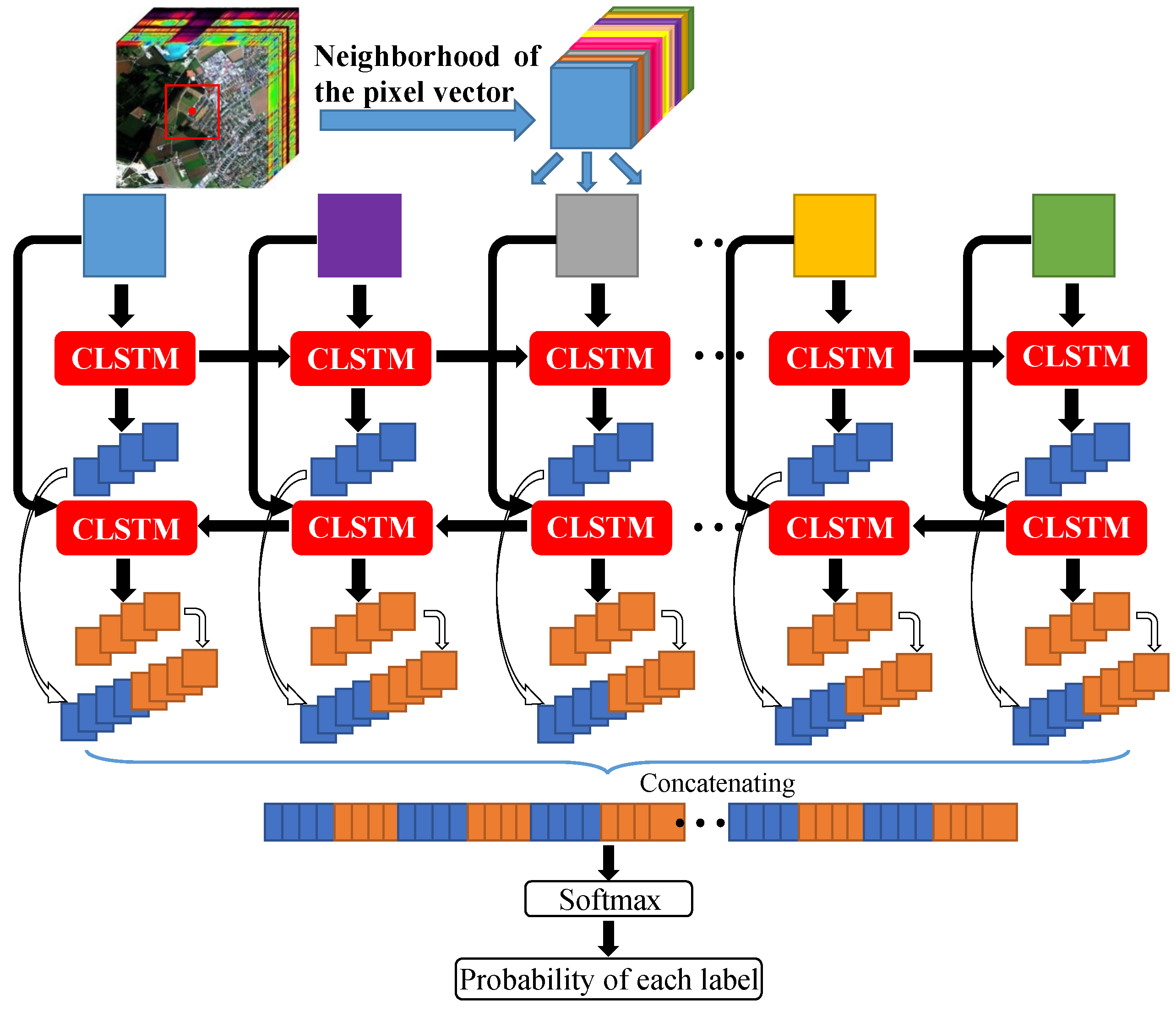
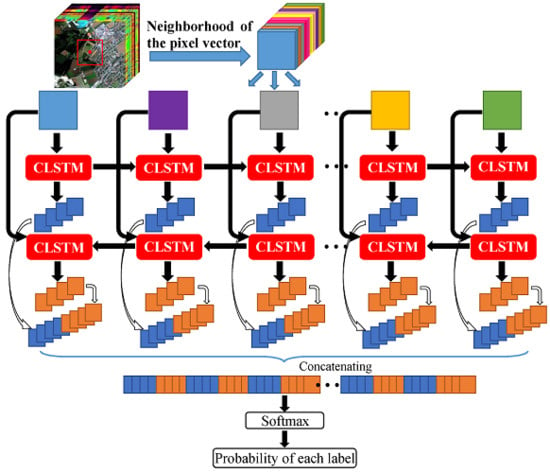
The flowchart of the proposed Bi-CLSTM model is shown in
Figure 2. Suppose an HSI can be represented as a 3D matrix
with
pixels and
l spectral channels. Given a pixel at the spatial position
where
and
, we can choose a small sub-cube
centered at it. The goal of Bi-CLSTM is to learn the most discriminative spectral-spatial information from
. Such information is the final feature representation for the pixel at the spatial position
. If we split the sub-cube across the spectral channels, then
can be considered as an
l-length sequence
. The image patches in the sequence are fed into the CLSTM one by one to extract the spectral feature via a recurrent operator and the spatial feature via a convolution operator simultaneously.
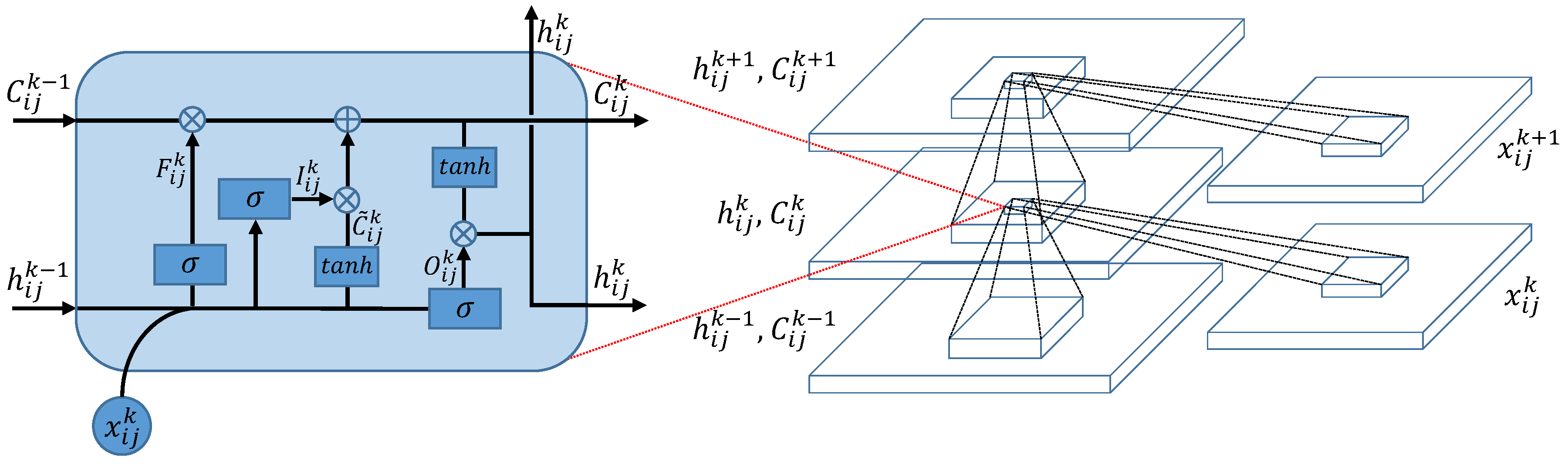
CLSTM is a modification of LSTM, which replaces the fully-connected operators by convolutional operators [
36]. The structure of CLSTM is shown in
Figure 3, where the left side zooms in its core computation unit, called a memory cell. In the memory cell, ‘⊗’ and ‘⊕’ represent dot product and matrix addition, respectively. For the
k-th image patch
in the sequence
, CLSTM firstly decides what information to throw away from the previous cell state
via the forget gate
. The forget gate pays attention to
and
, and outputs a value between 0 and 1 after an activation function. Here, 1 represents “keep the whole information” and 0 represents “throw away the information completely”. Secondly, CLSTM needs to decide what new information to store in the current cell state
. This includes two parts: first, the input gate
decides what information to update by the same way as forget gate; second, the memory cell creates a candidate value
computed by
and
. After finishing these two parts, CLSTM multiplies the previous memory cell state
by
, adds the product to
, and updates the information
. Finally, CLSTM decides what information to output via the cell state
and output gate
. The above process can be formulated as the following equations:
where
is the logistic sigmoid function, ‘∗’ is a convolutional operator, ‘∘’ is a dot product, and
and
are bias terms. The weight matrix subscripts have the obvious meaning. For example,
is the hidden-input gate matrix, and
is the input-output gate matrix etc. To implement the convolutional and recurrent operator in CLSTM simultaneously, the spatial size of
and
must be the same as that of
(we use zero-padding [
42] to ensure that input will keep the original spatial size after convolution operation).
In the existing literature [
43,
44,
45], LSTM has been well acknowledged as a powerful network to address the orderly sequence learning problem based on the assumption that previous states will affect future states. However, different from the traditional sequence learning problem, the spectral channels in the sequence are correlated with each other. In [
46], bidirectional recurrent neural networks (Bi-RNN) was proposed to use both latter and previous information to model sequential data. Motivated by it, we use a Bi-CLSTM network shown in
Figure 2 to sufficiently extract the spectral feature. Specifically, the image patches are fed into the CLSTM network one by one with a forward and a backward sequence, respectively. After that, we can acquire two spectral-spatial feature sequences. In the classification stage, they are concatenated into a vector denoted as
G and a Softmax layer is used to obtain the probability of each class that the pixel belongs to. Softmax function ensures the activation of each output unit sums to 1, so that we can deem the output as a set of conditional probabilities. Given the vector
G, the probability that the input belongs to category
c equals
where
W and
b are weights and biases of the Softmax layer and the summation is over all the output units. The pseudocode for the Bi-CLSTM model is given in Algorithm 1, where we use simplified variables to make the procedure clear.
It is well known that the performance of DL algorithms depends on the number of training samples. However, there often exists a small number of available samples in HSIs. To this end, we adopt two data augmentation methods. They are flipping and rotating operators. Specifically, we rotate the HSI patches by 90, 180, and 270 degrees anticlockwise and flip them horizontally and vertically. Furthermore, we rotate the horizontally and vertically flipped patches by 90 degrees separately.
Figure 4 shows some examples of flipping and rotating operators. As a result, the number of training samples can be increased by eight times. In addition, the data augmentation method, dropout [
47] is also used to improve the performance of Bi-CLSTM. We set some outputs of neurons to zeros, which means that these neurons do not propagate any information forward or participate in the back-propagation learning algorithm. Every time an input is sampled, network drops neurons randomly to form different structures. In the next section, we will validate the effectiveness of data augmentation and dropout methods.
| Algorithm 1: Algorithm for the Bi-CLSTM model. |
![Remotesensing 09 01330 i001]() |