MODIS-Based Estimation of Terrestrial Latent Heat Flux over North America Using Three Machine Learning Algorithms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Machine Learning Algorithms
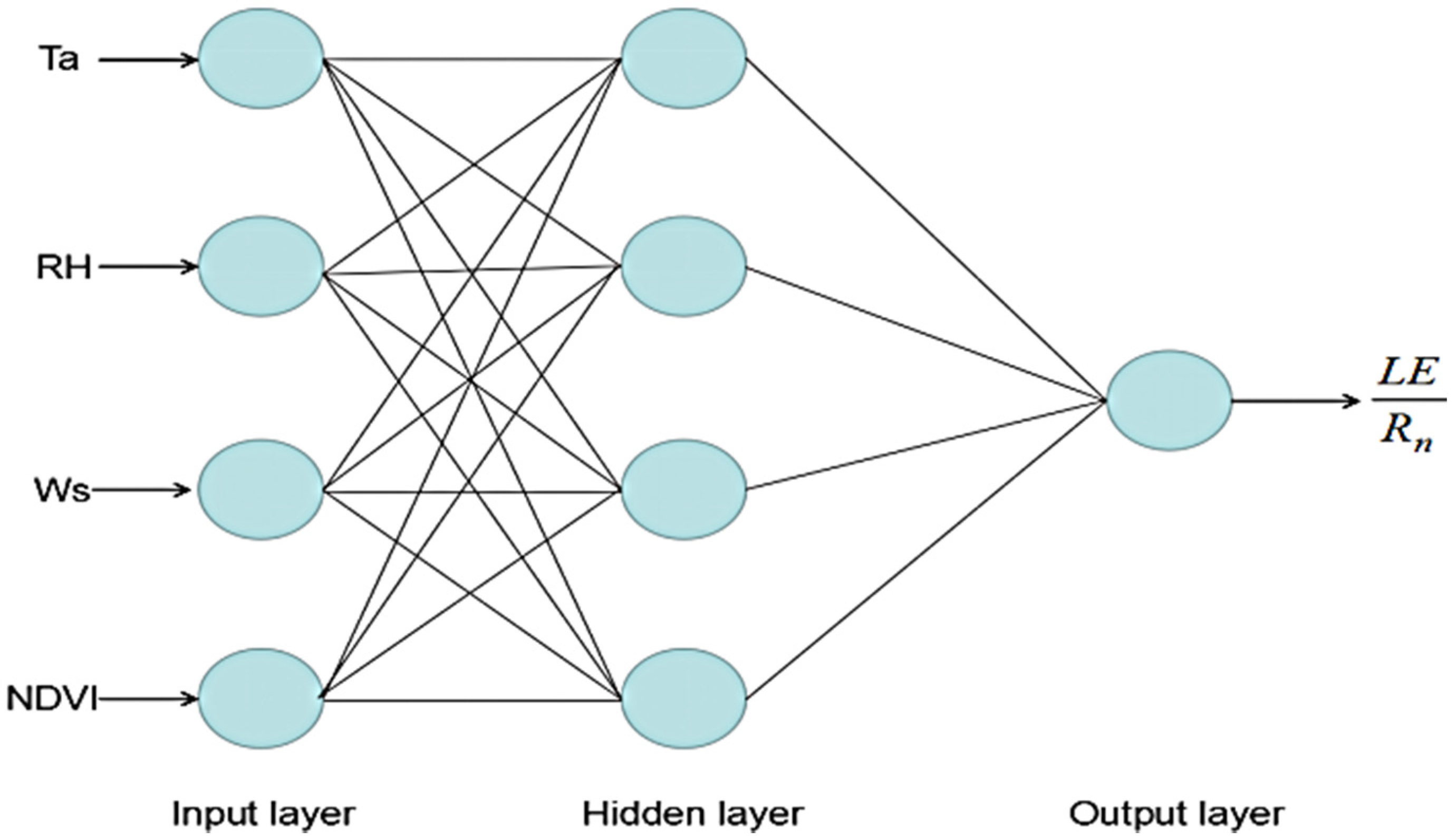
2.1.1. Artificial Neural Network
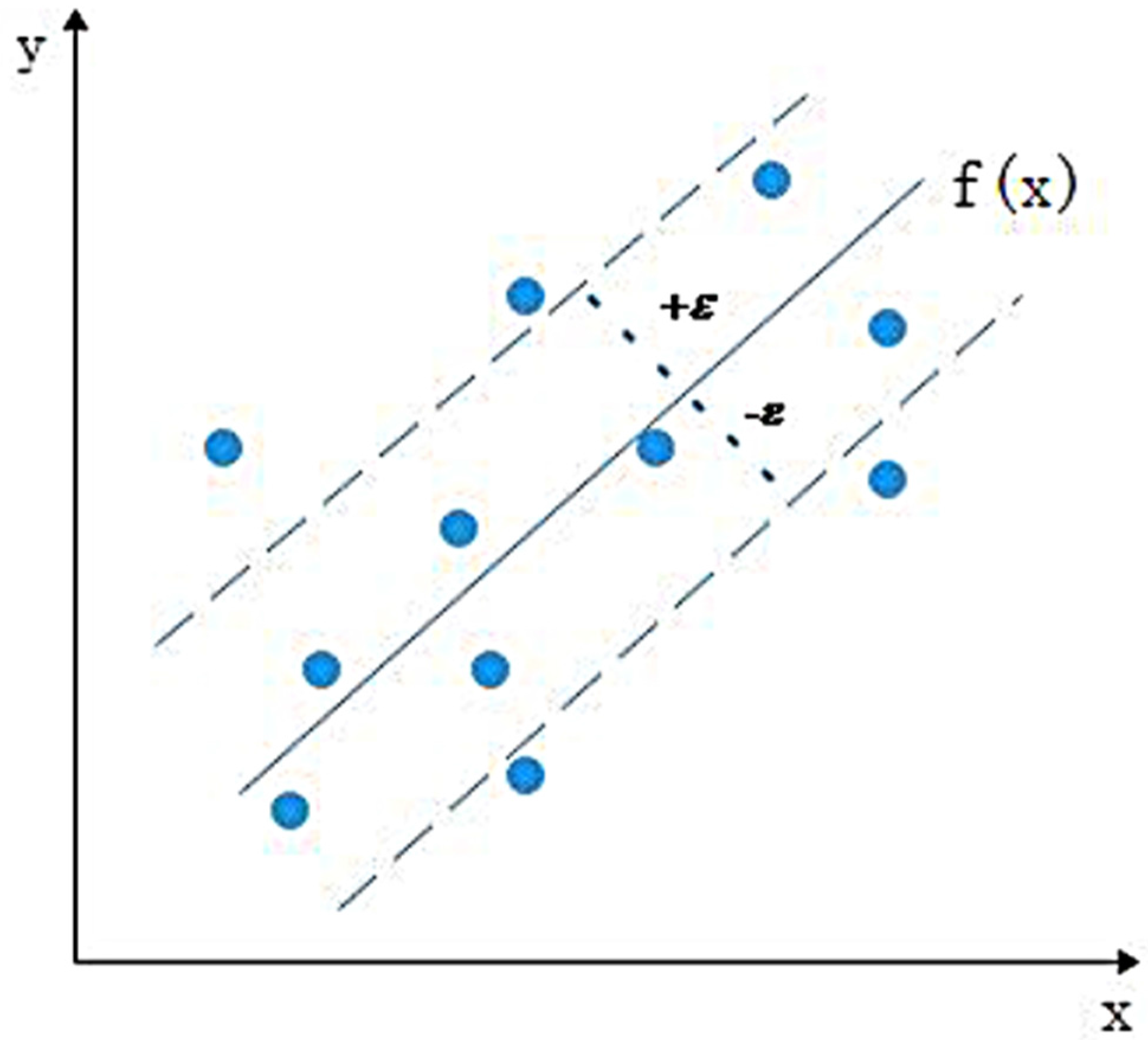
2.1.2. Support Vector Machine
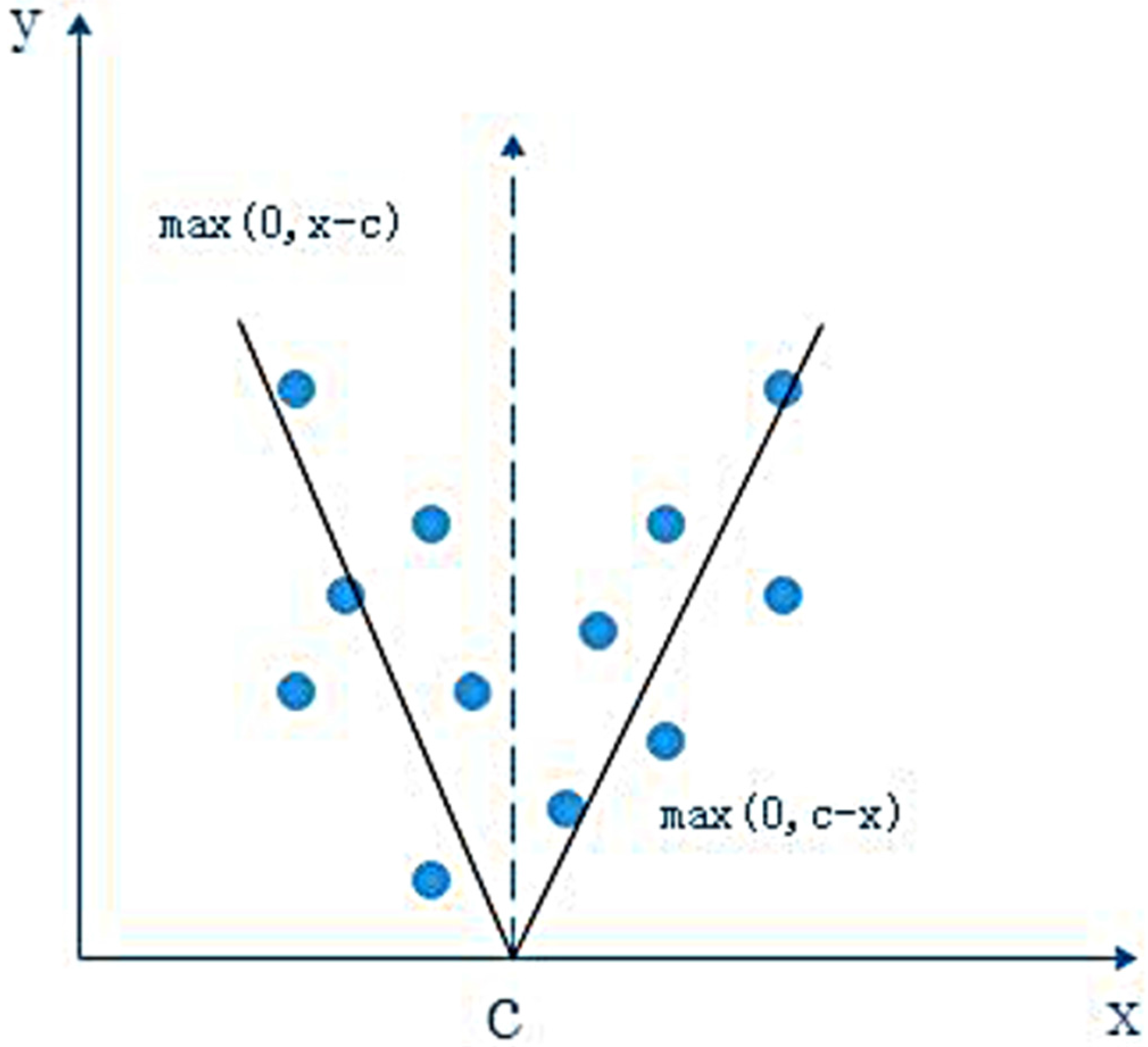
2.1.3. Multivariate Adaptive Regression Spline
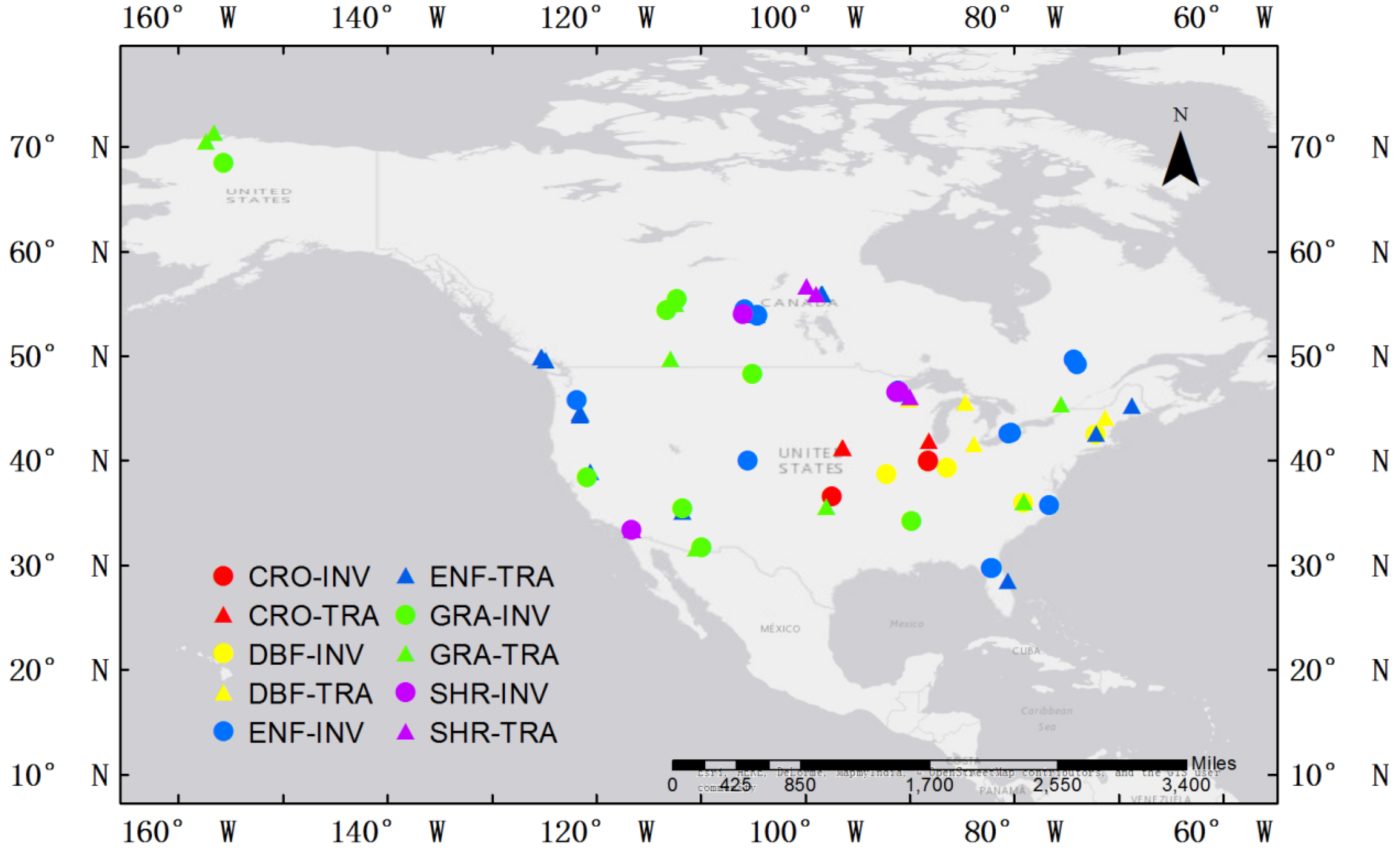
2.2. Experimental and Simulated Data
2.2.1. Eddy Covariance Observations
2.2.2. MODIS and MERRA Data
2.2.3. Criteria of Evaluation
2.2.4. Experimental Setup
3. Results
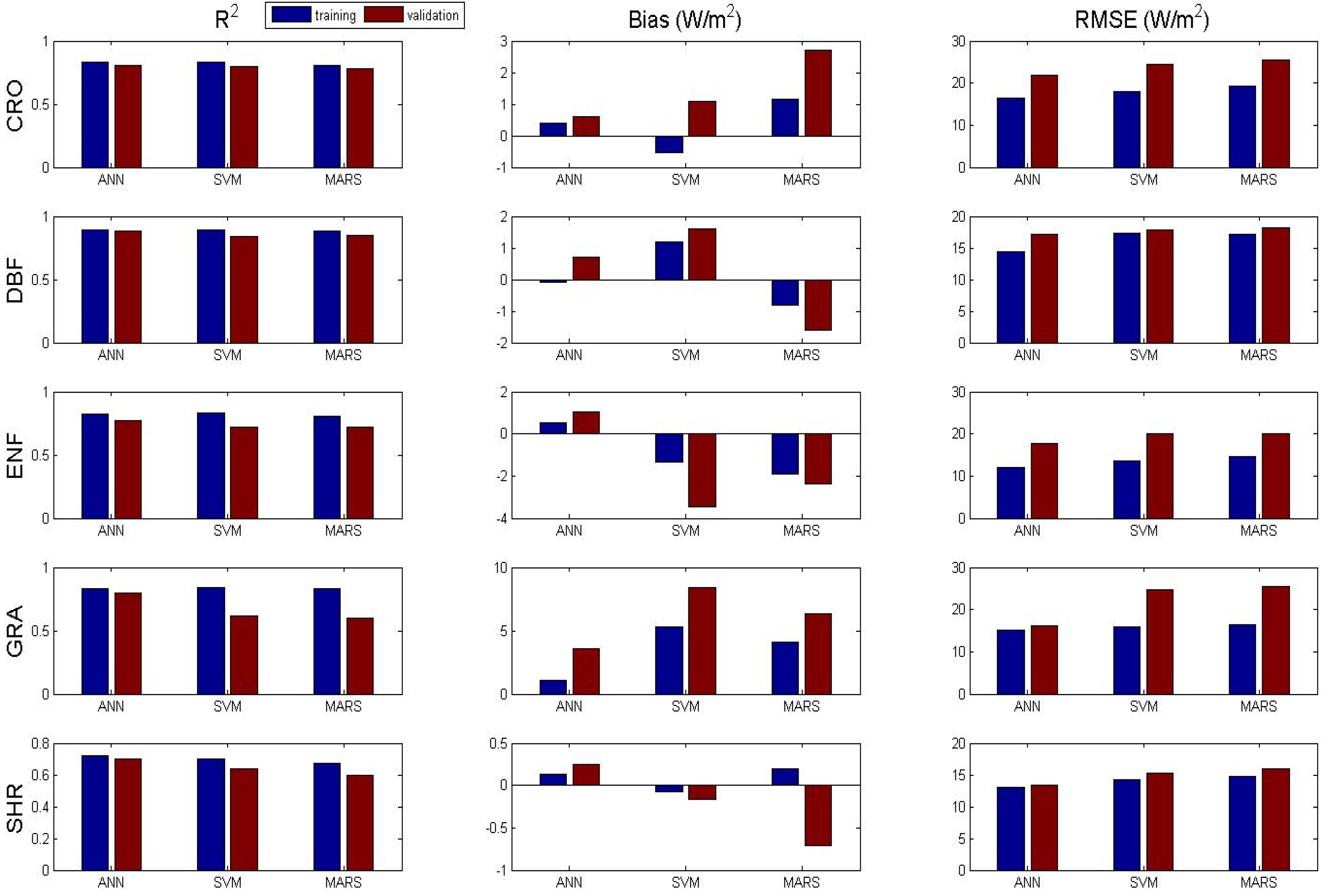
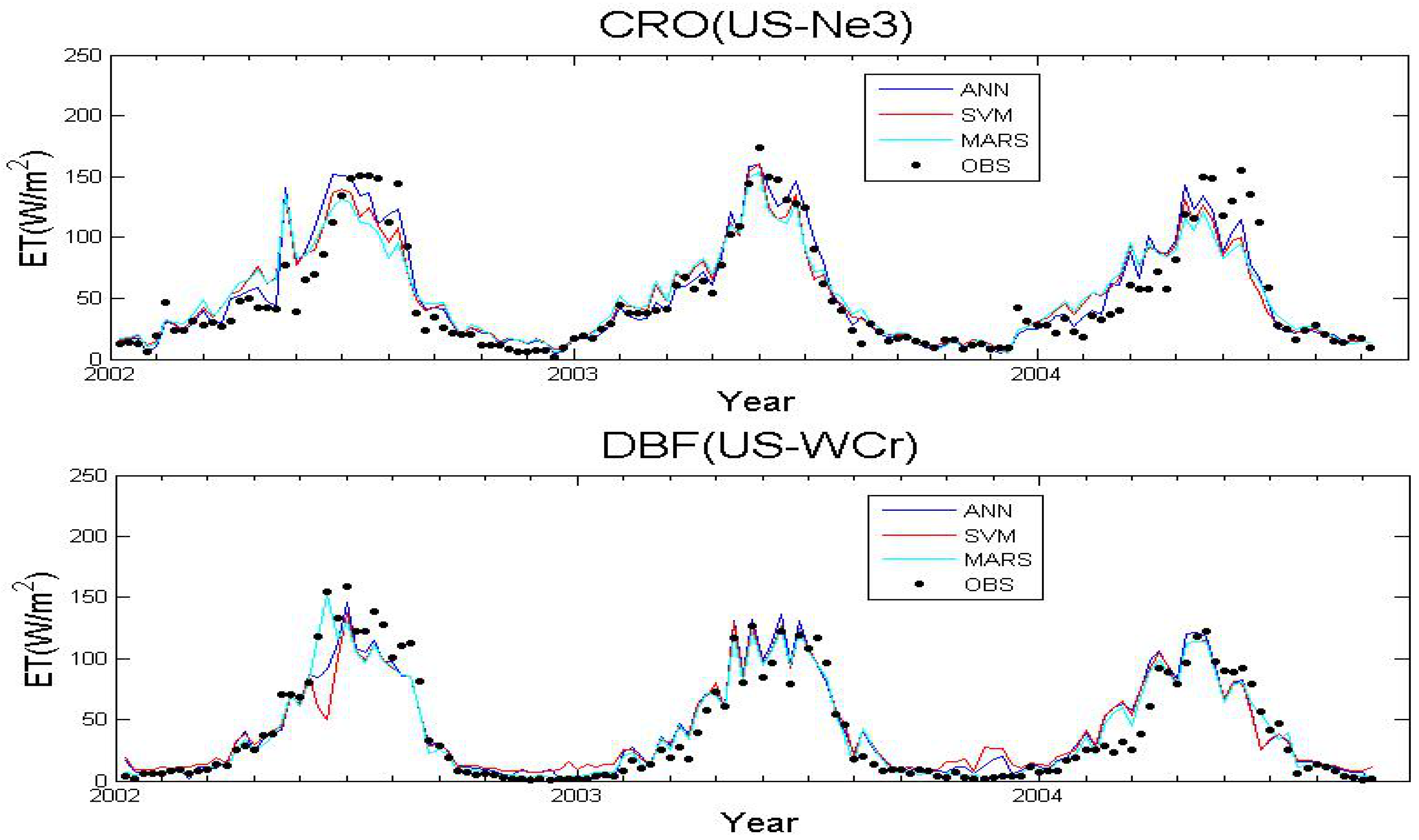
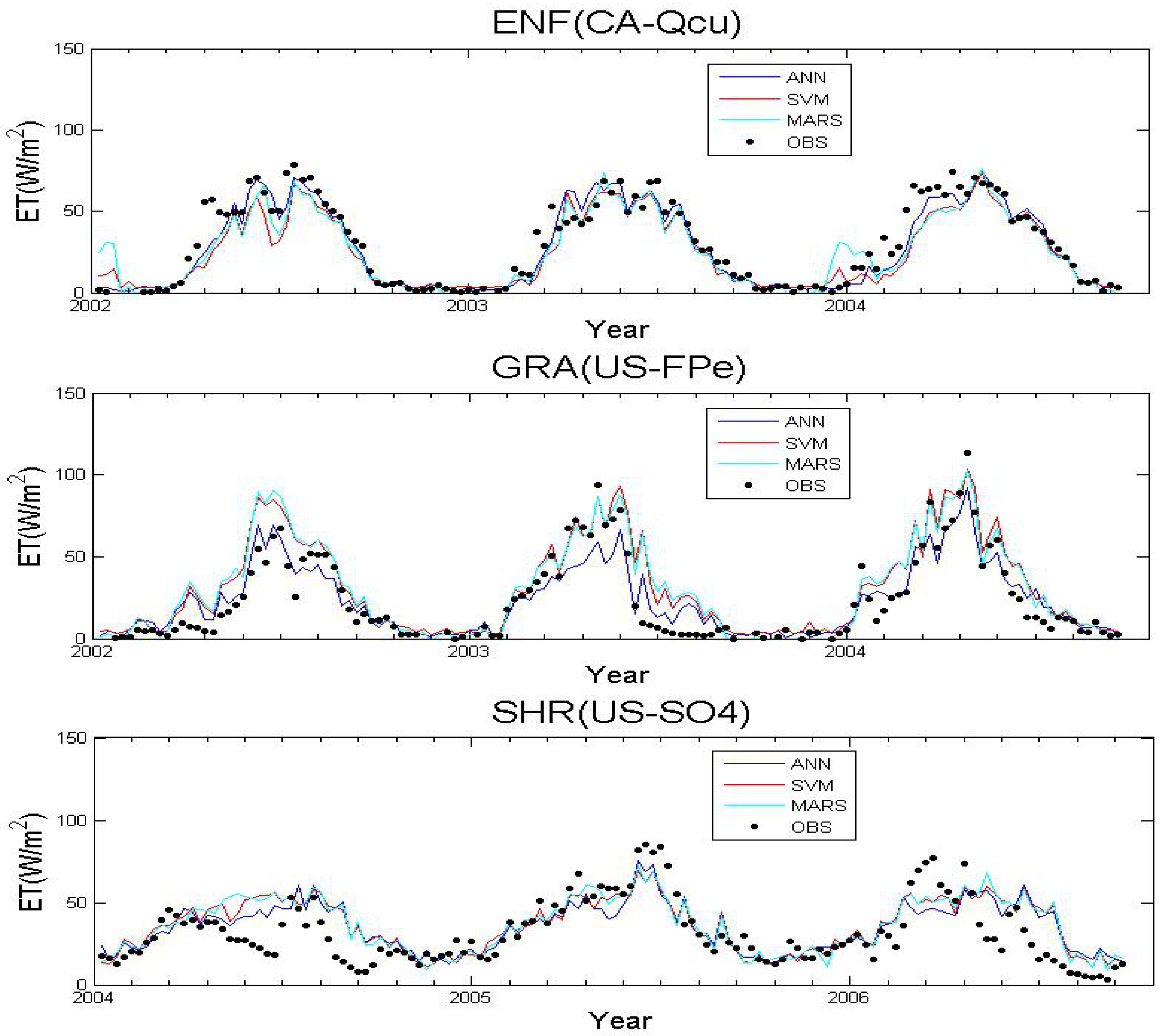
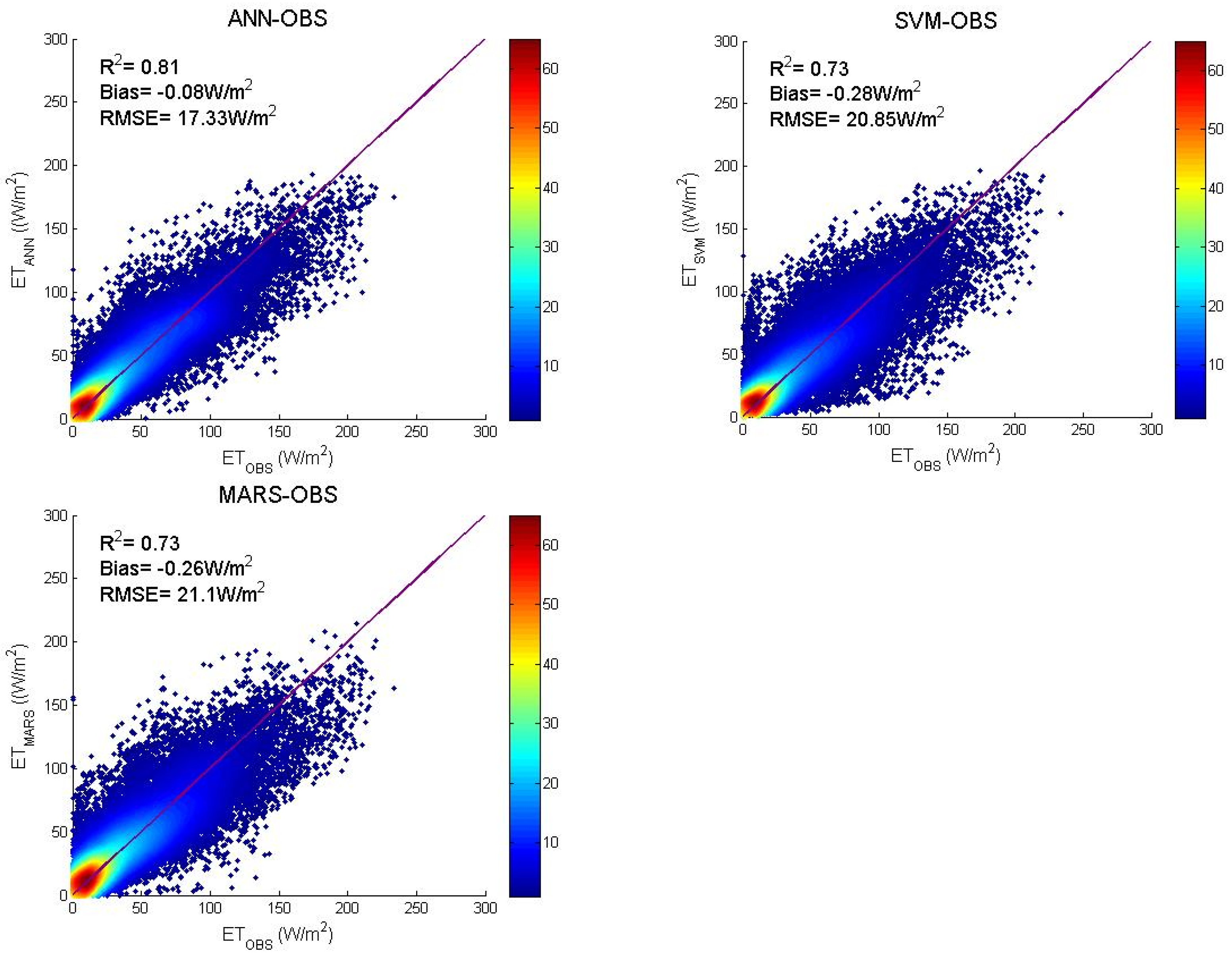
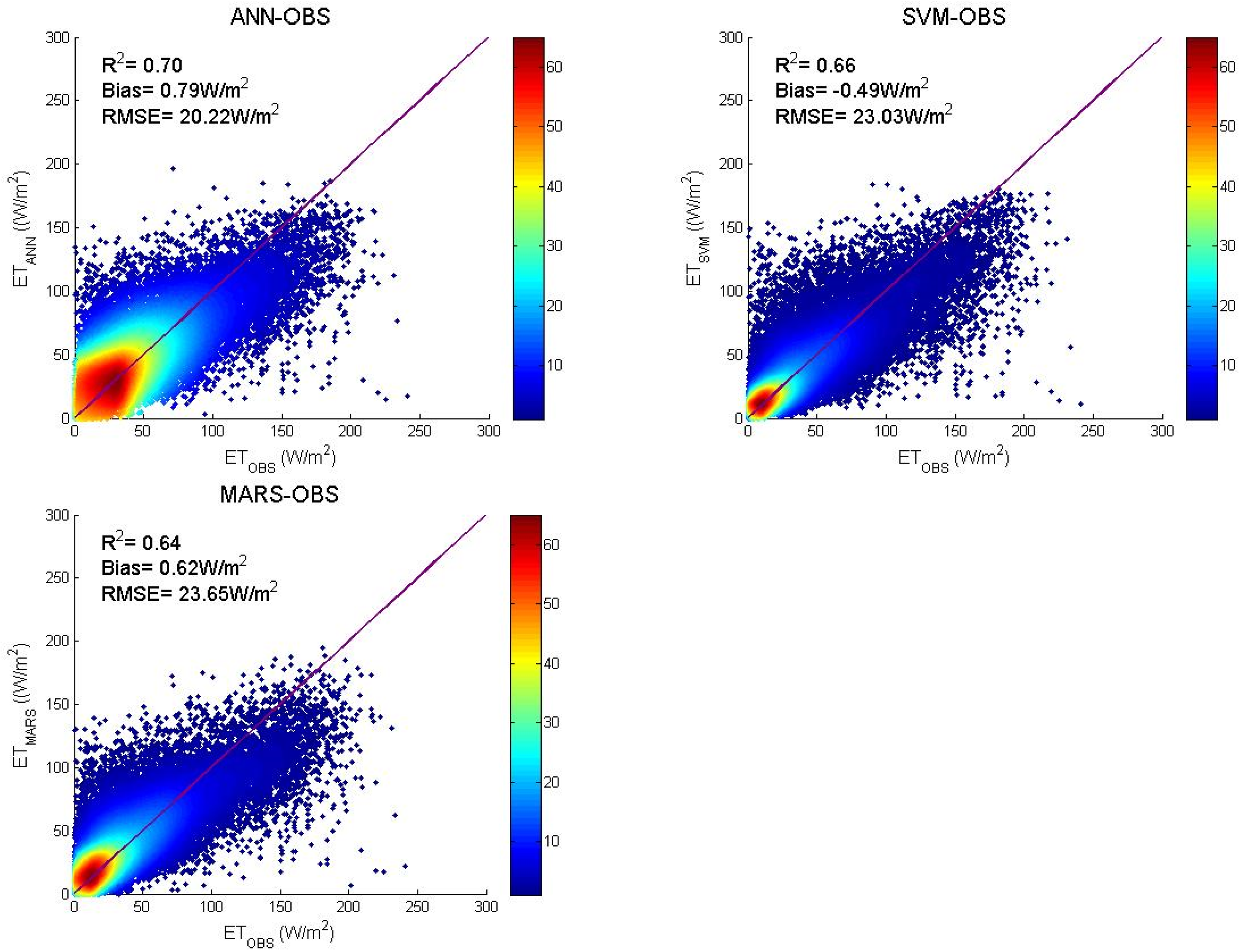
3.1. Algorithms Evaluation Based on Specific Site Data
3.2. Algorithms Evaluation Based on MERRA Data
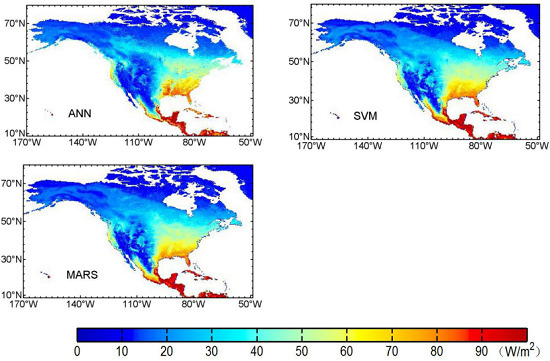
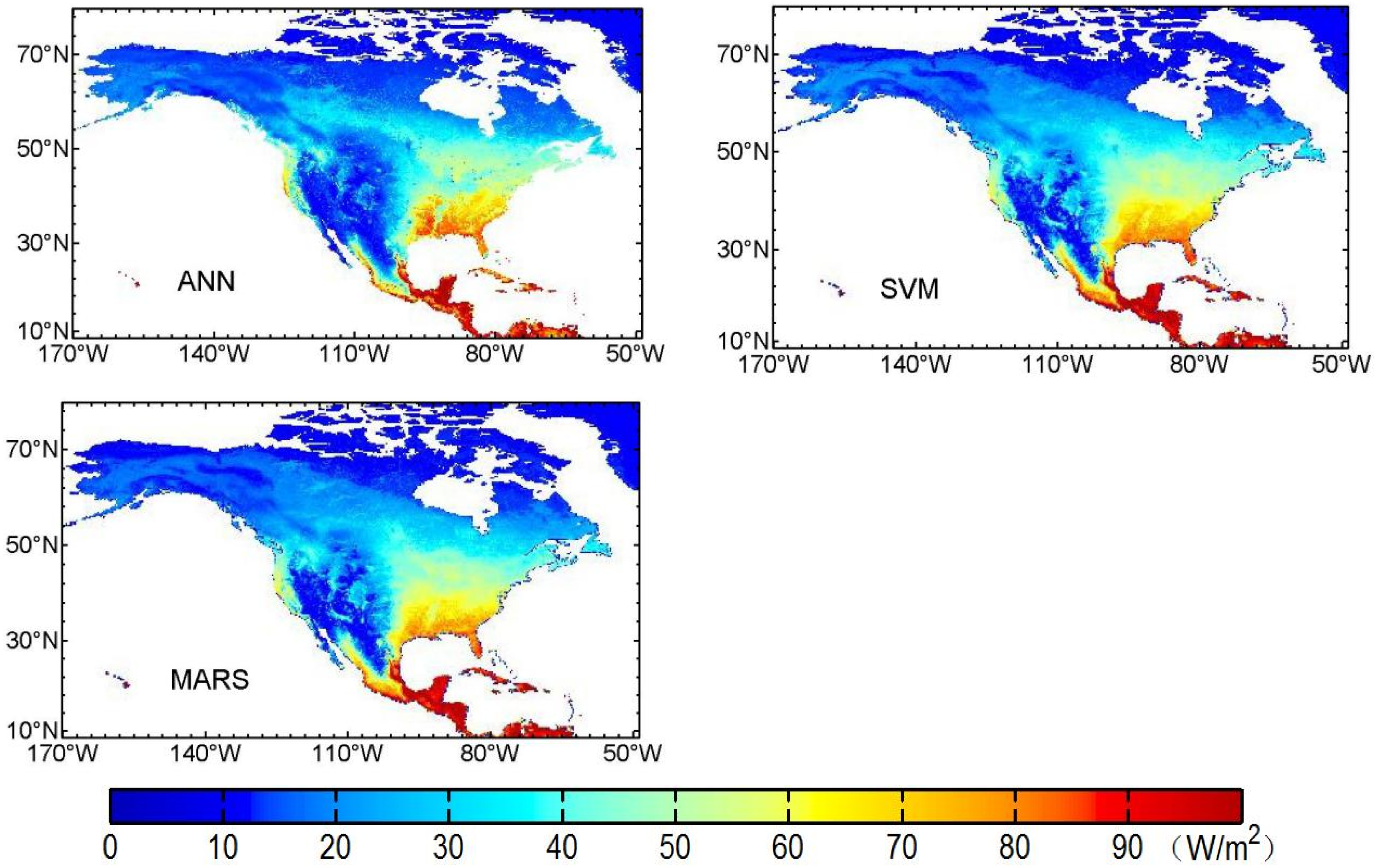
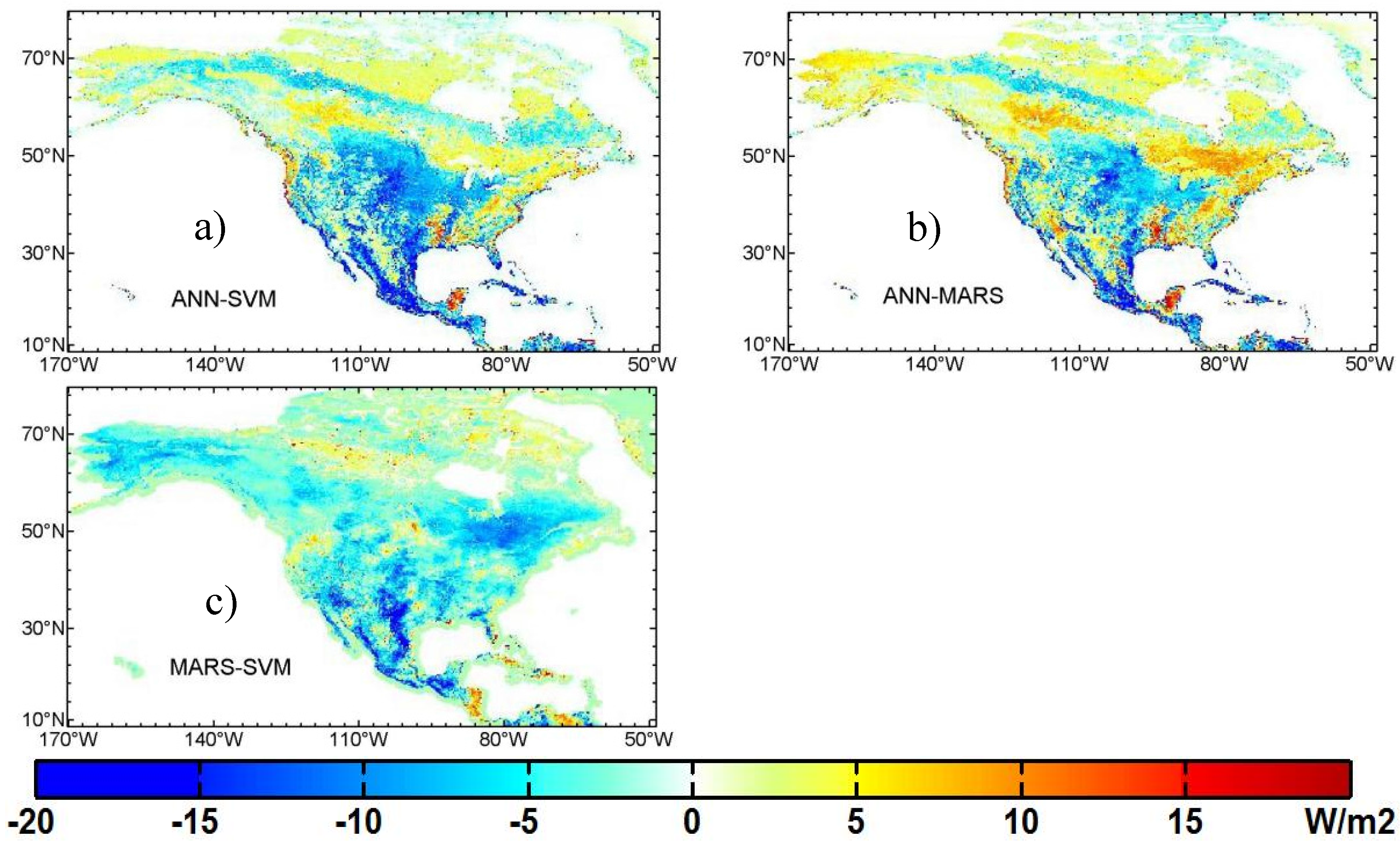
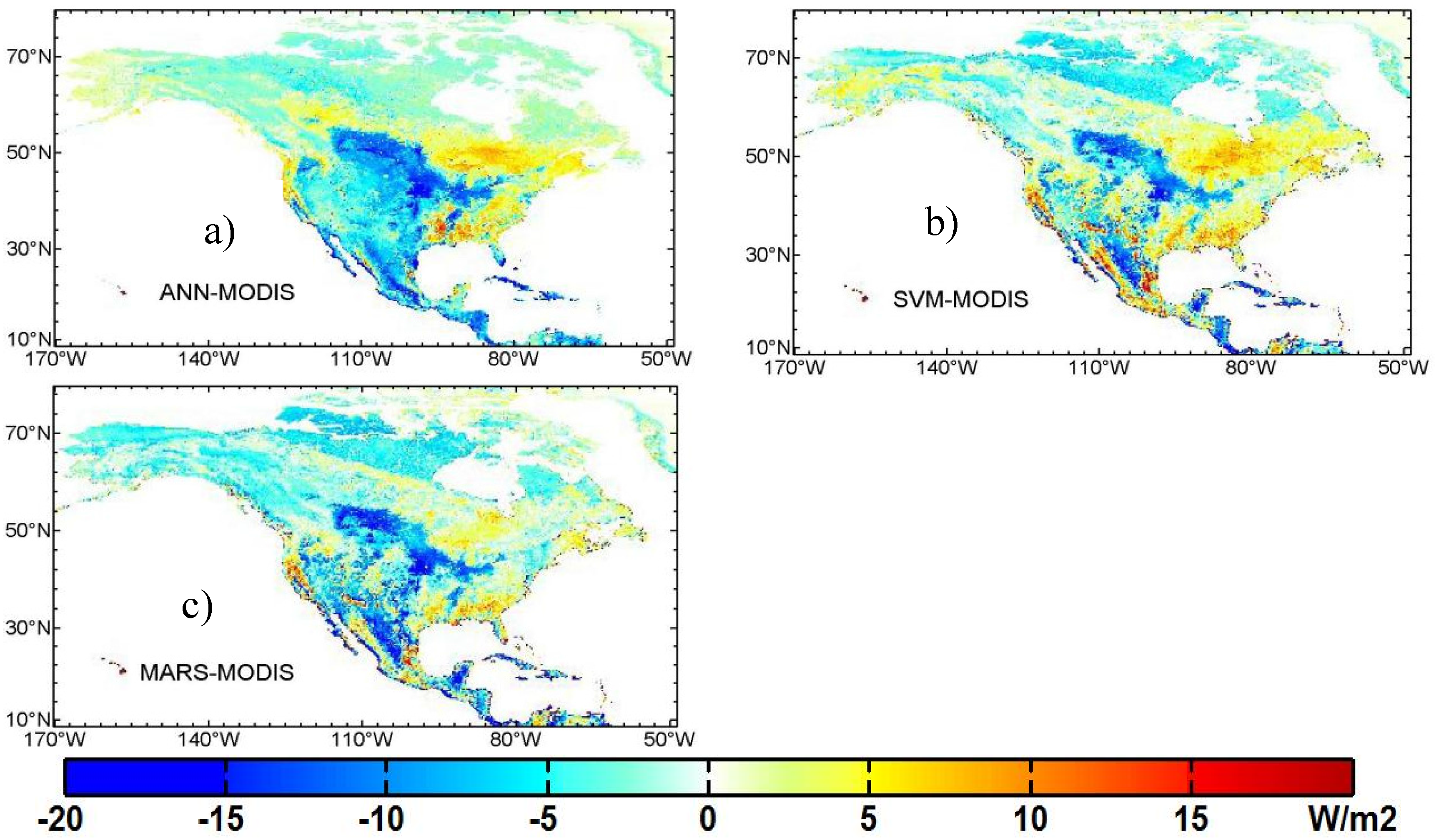
3.3. Mapping of Terrestrial LE Using Three Machine Learning Algorithms
4. Discussion
4.1. Performance of the Machine Learning Algorithms
4.2. Comparison between Different LE Products
4.3. Limitations and Recommendations for Future Research
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper No 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurement, remote sensing and model simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R.; Wallender, W.W.; Pruitt, W.O. Estimating evapotranspiration using artificial neural network. J. Irrig. Drain. Eng. 2002, 128, 224–233. [Google Scholar] [CrossRef]
- Los, S.O.; Collatz, G.J.; Sellers, P.J.; Malmström, C.M.; Pollack, N.H.; Defries, R.S.; Bounoua, L.; Parris, M.T.; Tucker, C.J.; Dazlich, D.A. A global 9-yr biophysical land surface dataset from noaa avhrr data. J. Hydrometeorol. 2000, 1, 183–199. [Google Scholar] [CrossRef]
- Jin, Y.; Randerson, J.T.; Goulden, M.L. Continental-scale net radiation and evapotranspiration estimated using modis satellite observations. Remote Sens. Environ. 2011, 115, 2302–2319. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a modis global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on modis and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205. [Google Scholar] [PubMed]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 2009, 100, 81–92. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and modis satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Wang, K.; Wang, P.; Li, Z.; Cribb, M.; Sparrow, M. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature. J. Geophys. Res. Atmos. 2007, 112, D15107. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.Q.; Jeu, R.D. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Liang, S.; Qin, Q.; Wang, K.; Zhao, S. Monitoring global land surface drought based on a hybrid evapotranspiration model. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 447–457. [Google Scholar] [CrossRef]
- Qin, Q. Simple method to determine the priestley-taylor parameter for evapotranspiration estimation using albedo-vi triangular space from modis data. J. Appl. Remote Sens. 2011, 5, 3505. [Google Scholar]
- Xu, T.; Liang, S.; Liu, S. Estimating turbulent fluxes through assimilation of geostationary operational environmental satellites data using ensemble kalman filter. J. Geophys. Res. Atmos. 2011, 116, 644. [Google Scholar] [CrossRef]
- Xu, T.; Liu, S.; Liang, S.; Qin, J. Improving predictions of water and heat fluxes by assimilating modis land surface temperature products into the common land model. J. Hydrometeorol. 2010, 12, 227–244. [Google Scholar] [CrossRef]
- Jiménez, C.; Prigent, C.; Mueller, B.; Seneviratne, S.I.; Mccabe, M.F.; Wood, E.F.; Rossow, W.B.; Balsamo, G.; Betts, A.K.; Dirmeyer, P.A. Global intercomparison of 12 land surface heat flux estimates. J. Geophys. Res. Atmos. 2011, 116, 3–25. [Google Scholar] [CrossRef]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of modis 16 global terrestrial evapotranspiration products in various climates and land cover types in asia. KSCE J. Civ. Eng. 2012, 16, 229–238. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, ipcc ar4 simulations. Clim. Dyn. 2008, 31, 79–105. [Google Scholar] [CrossRef]
- Bruton, J.M.; Mcclendon, R.W.; Hoogenboom, G. Estimating daily pan evaporation with artificial neural networks. Am. Soc. Agric. Biol. Eng. 2000, 43, 491–496. [Google Scholar] [CrossRef]
- El-Shafie, A.; Alsulami, H.M.; Jahanbani, H.; Najah, A. Multi-lead ahead prediction model of reference evapotranspiration utilizing ann with ensemble procedure. Stoch. Environ. Res. Risk Assess. 2013, 27, 1423–1440. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Shukla, S. Support vector machine based modeling of evapotranspiration using hydro-climatic variables in a sub-tropical environment. Bioresour. Technol. 2013, 128, 351. [Google Scholar] [CrossRef]
- Deo, R.C.; Samui, P.; Kim, D. Estimation of monthly evaporative loss using relevance vector machine, extreme learning machine and multivariate adaptive regression spline models. Stoch. Environ. Res. Risk Assess. 2016, 30, 1769–1784. [Google Scholar] [CrossRef]
- Yang, F.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.X.; Nemani, R.R. Prediction of continental-scale evapotranspiration by combining modis and ameriflux data through support vector machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
- Adnan, M.; Latif, M.A.; Abaid-ur-Rehman; Nazir, M. Estimating evapotranspiration using machine learning techniques. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 108–113. [Google Scholar]
- Tabari, H.; Marofi, S.; Sabziparvar, A.A. Estimation of daily pan evaporation using artificial neural network and multivariate non-linear regression. Irrig. Sci. 2010, 28, 399–406. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; pp. 988–999. [Google Scholar]
- Nurmemet, I.; Ghulam, A.; Tiyip, T.; Elkadiri, R.; Ding, J.L.; Maimaitiyiming, M.; Abliz, A.; Sawut, M.; Zhang, F.; Abliz, A. Monitoring soil salinization in keriya river basin, northwestern China using passive reflective and active microwave remote sensing data. Remote Sens. 2015, 7, 8803–8829. [Google Scholar] [CrossRef]
- Dibike, Y.B.; Velickov, S.; Solomatine, D.; Abbott, M.B. Model induction with support vector machines: Introduction and applications. J. Comput. Civ. Eng. 2001, 15, 208–216. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Butte, N.F.; Wong, W.W.; Adolph, A.L.; Puyau, M.R.; Vohra, F.A.; Zakeri, I.F. Validation of cross-sectional time series and multivariate adaptive regression splines models for the prediction of energy expenditure in children and adolescents using doubly labeled water. J. Nutr. 2010, 140, 1516. [Google Scholar] [CrossRef] [PubMed]
- Veaux, R.D.D.; Ungar, L.H. Multicollinearity: A Tale of Two Nonparametric Regressions; Springer: New York, NY, USA, 2007; pp. 393–402. [Google Scholar]
- Adamowski, J.; Chan, H.; Prasher, S.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in montreal, Canada. Water Resour. Res. 2012, 48, 1528. [Google Scholar] [CrossRef]
- Sephton, P. Forecasting Recessions: Can We Do Better on Mars? Federal Reserve Bank of St. Louis: Washington, DC, USA, 2001; Volume 83. [Google Scholar]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the hai river basin, China. J. Geophys. Res. Atmos. 2012, 117, 13113. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Teyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the modis vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the modis terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Friedl, M.A.; Mciver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A. Global land cover mapping from modis: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Intelligent formulation of structural engineering systems. In Proceedings of the Seventh MIT Conference on Computational Fluid and Solid Mechanics—Focus: Multipgysics & Multiscale, Cambridge, MA, USA, 12–14 June 2013. [Google Scholar]
- Cristau, H.-J.; Cellier, P.P.; Spindler, J.F.; Taillefer, M. Highly efficient and mild copper-catalyzed N- and C-arylations with aryl bromides and iodides. Chemistry 2004, 10, 5607–5622. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. Libsvm: A Library for Support Vector Machines; ACM: New York, NY, USA, 2011; pp. 1–27. [Google Scholar]
- Meyer, D. Support vector machines the interface to libsvm in package e1071. R News 2013, 1, 1–3. [Google Scholar]
- Lu, X.L.; Zhuang, Q.L. Evaluating evapotranspiration and water-use efficiency of terrestrial ecosystems in the conterminous united states using modis and ameriflux data. Remote Sens. Environ. 2010, 114, 1924–1939. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly avhrr and islscp-ii data, validated at 16 fluxnet sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Meynadier, R.; Sheffield, J.; Wood, E.F. Multi-model, multi-sensor estimates of global evapotranspiration: Climatology, uncertainties and trends. Hydrol. Process. 2011, 25, 3993–4010. [Google Scholar] [CrossRef]
- Yebra, M.; Dijk, A.V.; Leuning, R.; Huete, A.; Guerschman, J.P. Evaluation of optical remote sensing to estimate actual evapotranspiration and canopy conductance. Remote Sens. Environ. 2013, 129, 250–261. [Google Scholar] [CrossRef]
- Demarty, J.; Chevallier, F.; Friend, A.; Viovy, N.; Piao, S.; Ciais, P. Assimilation of Global Modis Leaf Area Index Retrievals within a Terrestrial Biosphere Model. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yao, Y.; Wang, Z.; Jia, K.; Zhang, X.; Zhang, Y.; Wang, X.; Xu, J.; Chen, X. Satellite-derived spatiotemporal variations in evapotranspiration over northeast China during 1982–2010. Remote Sens. 2017, 9, 1140. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of moderate resolution imaging spectroradiometer (modis) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. Biogeosci. 2006, 111, 338–356. [Google Scholar] [CrossRef]
- Baldocchi, D. Breathing of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Liu, S.; Jia, K.; Zhang, X.; Xiao, Z.; Fisher, J.B.; Mu, Q. Improving global terrestrial evapotranspiration estimation using support vector machine by integrating three process-based algorithms. Agric. For. Meteorol. 2017, 242, 55–74. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Yu, J.; Zhao, S.; Lin, Y.; Jia, K.; Zhang, X.; Cheng, J.; Xie, X.; Sun, L. Differences in estimating terrestrial water flux from three satellite-based priestley-taylor algorithms. Int. J. Appl. Earth Obs. Geoinf. 2017, 56, 1–12. [Google Scholar] [CrossRef]

| R2 | Bias (W/m2) | RMSE (W/m2) | |||||
|---|---|---|---|---|---|---|---|
| PFT | Algorithms | Train | Test | Train | Test | Train | Test |
| CRO | ANN | 0.83 | 0.81 | 0.4 | 0.6 | 16.47 | 21.86 |
| SVM | 0.83 | 0.8 | −0.54 | 1.1 | 17.92 | 24.37 | |
| MARS | 0.81 | 0.78 | 1.15 | 2.7 | 19.23 | 25.38 | |
| DBF | ANN | 0.89 | 0.88 | −0.08 | 0.7 | 14.48 | 17.17 |
| SVM | 0.89 | 0.84 | 1.19 | 1.6 | 17.25 | 17.91 | |
| MARS | 0.88 | 0.85 | −0.8 | −1.6 | 17.15 | 18.19 | |
| ENF | ANN | 0.82 | 0.77 | 0.55 | 1.05 | 12.15 | 17.74 |
| SVM | 0.83 | 0.72 | −1.35 | −3.47 | 13.69 | 20.02 | |
| MARS | 0.81 | 0.72 | −1.88 | −2.36 | 14.63 | 20.05 | |
| GRA | ANN | 0.83 | 0.8 | 1.1 | 3.55 | 15.05 | 16.14 |
| SVM | 0.84 | 0.62 | 5.3 | 8.37 | 15.81 | 24.76 | |
| MARS | 0.83 | 0.6 | 4.12 | 6.35 | 16.45 | 25.39 | |
| SHR | ANN | 0.72 | 0.7 | 0.13 | 0.25 | 13.05 | 13.35 |
| SVM | 0.7 | 0.64 | −0.08 | −0.17 | 14.24 | 15.22 | |
| MARS | 0.67 | 0.6 | 0.2 | −0.71 | 14.78 | 15.95 | |
| R2 | Bias (W/m2) | RMSE (W/m2) | |||||
|---|---|---|---|---|---|---|---|
| PFT | Algorithms | Train | Test | Train | Test | Train | Test |
| CRO | ANN | 0.81 | 0.77 | −0.6 | 1.4 | 23.2 | 25.9 |
| SVM | 0.63 | 0.57 | −1.8 | 2.1 | 20.83 | 29.22 | |
| MARS | 0.58 | 0.53 | 0.9 | 1.7 | 25.35 | 30.33 | |
| DBF | ANN | 0.88 | 0.85 | 1.3 | 2.1 | 13.25 | 17.45 |
| SVM | 0.75 | 0.72 | 2.82 | 3.06 | 22.42 | 28.39 | |
| MARS | 0.79 | 0.76 | −1.03 | −1.19 | 19.92 | 23.44 | |
| ENF | ANN | 0.78 | 0.75 | 1.06 | 2.05 | 13.34 | 16.18 |
| SVM | 0.77 | 0.74 | −2.81 | −3.95 | 16.13 | 17.31 | |
| MARS | 0.76 | 0.72 | −1.9 | −2.65 | 14.12 | 18 | |
| GRA | ANN | 0.73 | 0.67 | −0.35 | 3.75 | 20.85 | 23.3 |
| SVM | 0.72 | 0.66 | 5.27 | 6.37 | 21.01 | 23.68 | |
| MARS | 0.66 | 0.63 | 4.8 | 5.35 | 21.68 | 24.43 | |
| SHR | ANN | 0.69 | 0.65 | 0.22 | 0.61 | 12.08 | 14.85 |
| SVM | 0.68 | 0.63 | −1.81 | −1.04 | 11.22 | 15.63 | |
| MARS | 0.69 | 0.62 | −0.31 | −1.5 | 16.21 | 17.1 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yao, Y.; Zhao, S.; Jia, K.; Zhang, X.; Zhang, Y.; Zhang, L.; Xu, J.; Chen, X. MODIS-Based Estimation of Terrestrial Latent Heat Flux over North America Using Three Machine Learning Algorithms. Remote Sens. 2017, 9, 1326. https://doi.org/10.3390/rs9121326
Wang X, Yao Y, Zhao S, Jia K, Zhang X, Zhang Y, Zhang L, Xu J, Chen X. MODIS-Based Estimation of Terrestrial Latent Heat Flux over North America Using Three Machine Learning Algorithms. Remote Sensing. 2017; 9(12):1326. https://doi.org/10.3390/rs9121326
Chicago/Turabian StyleWang, Xuanyu, Yunjun Yao, Shaohua Zhao, Kun Jia, Xiaotong Zhang, Yuhu Zhang, Lilin Zhang, Jia Xu, and Xiaowei Chen. 2017. "MODIS-Based Estimation of Terrestrial Latent Heat Flux over North America Using Three Machine Learning Algorithms" Remote Sensing 9, no. 12: 1326. https://doi.org/10.3390/rs9121326
APA StyleWang, X., Yao, Y., Zhao, S., Jia, K., Zhang, X., Zhang, Y., Zhang, L., Xu, J., & Chen, X. (2017). MODIS-Based Estimation of Terrestrial Latent Heat Flux over North America Using Three Machine Learning Algorithms. Remote Sensing, 9(12), 1326. https://doi.org/10.3390/rs9121326