Multipath Interferences in Ground-Based Radar Data: A Case Study
Abstract
:1. Introduction
1.1. KAPRI Instrument Details
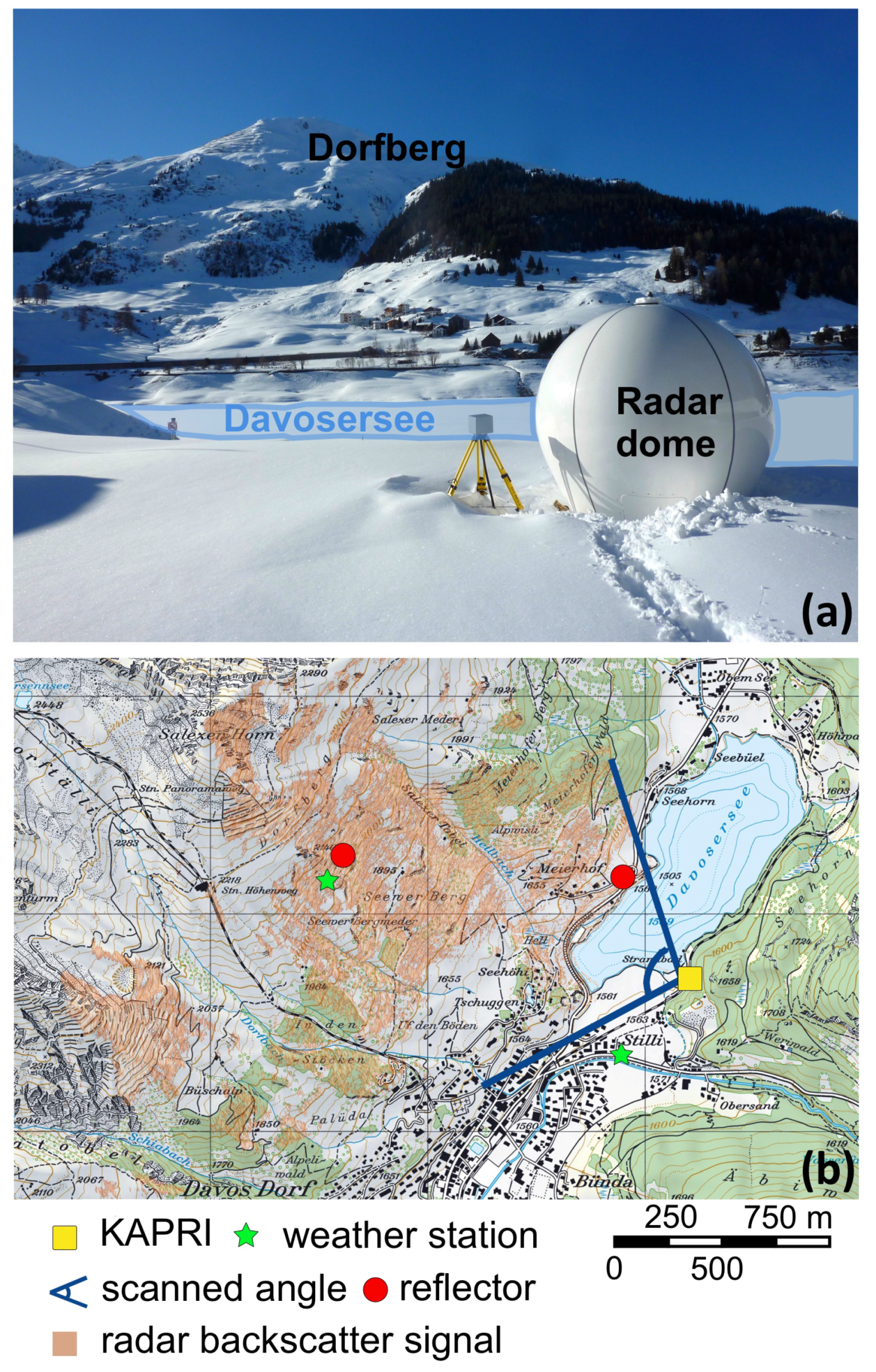
1.2. Test Sites and Datasets
1.2.1. Davos Strandbad
1.2.2. ETH Hönggerberg
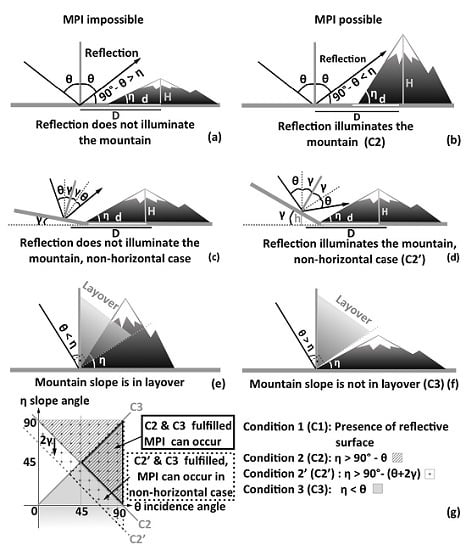
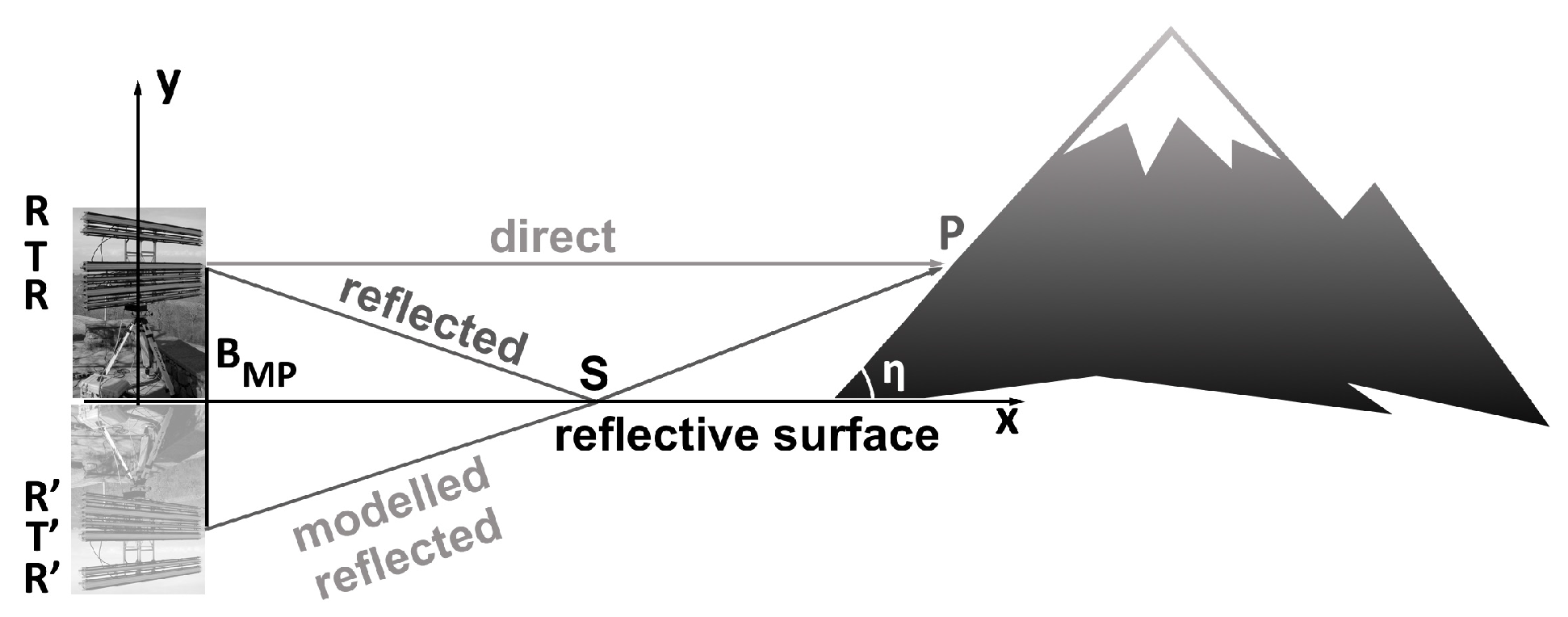
2. Model
2.1. Model Description
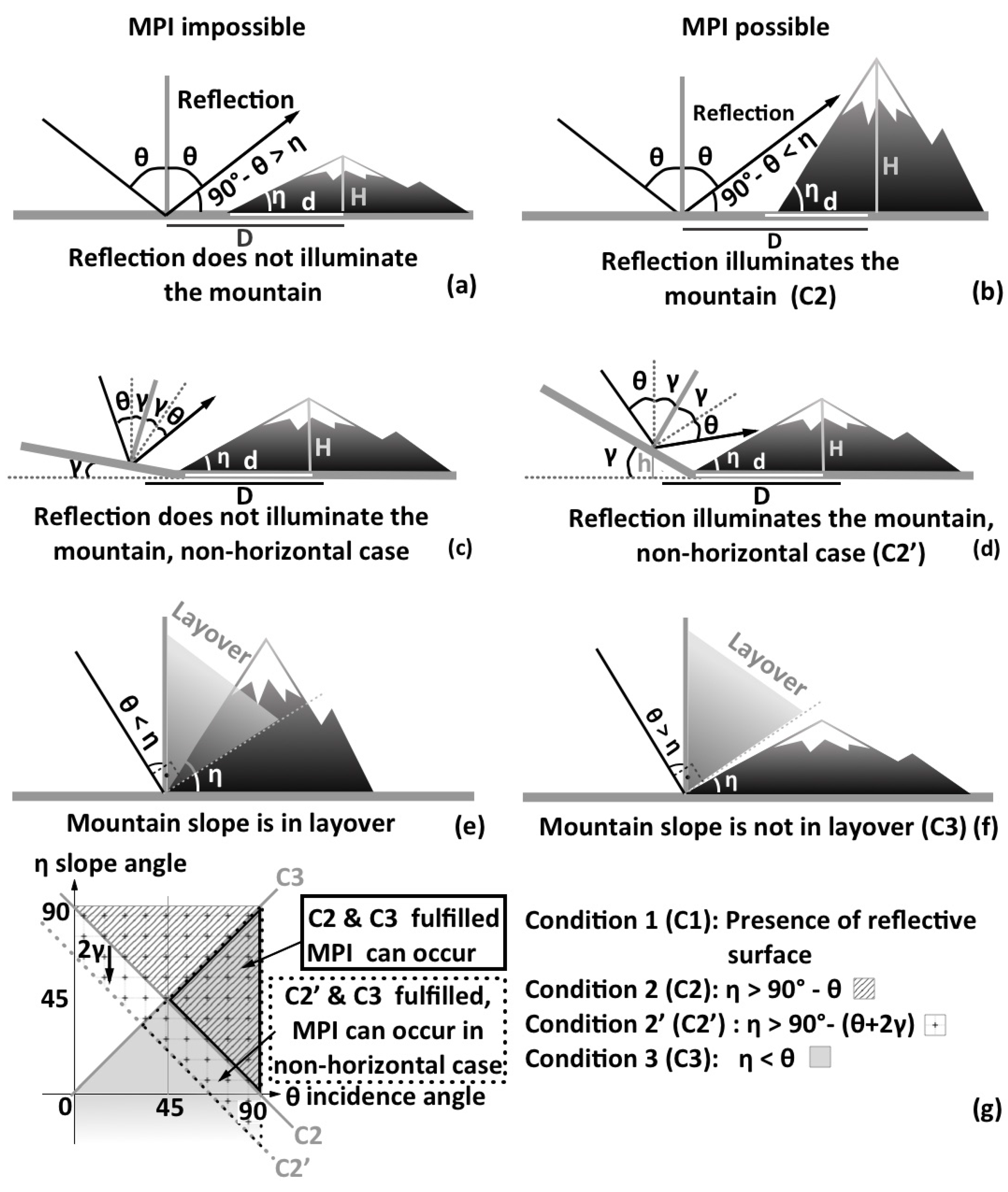
2.2. Theoretical Considerations
2.3. Application of the Model
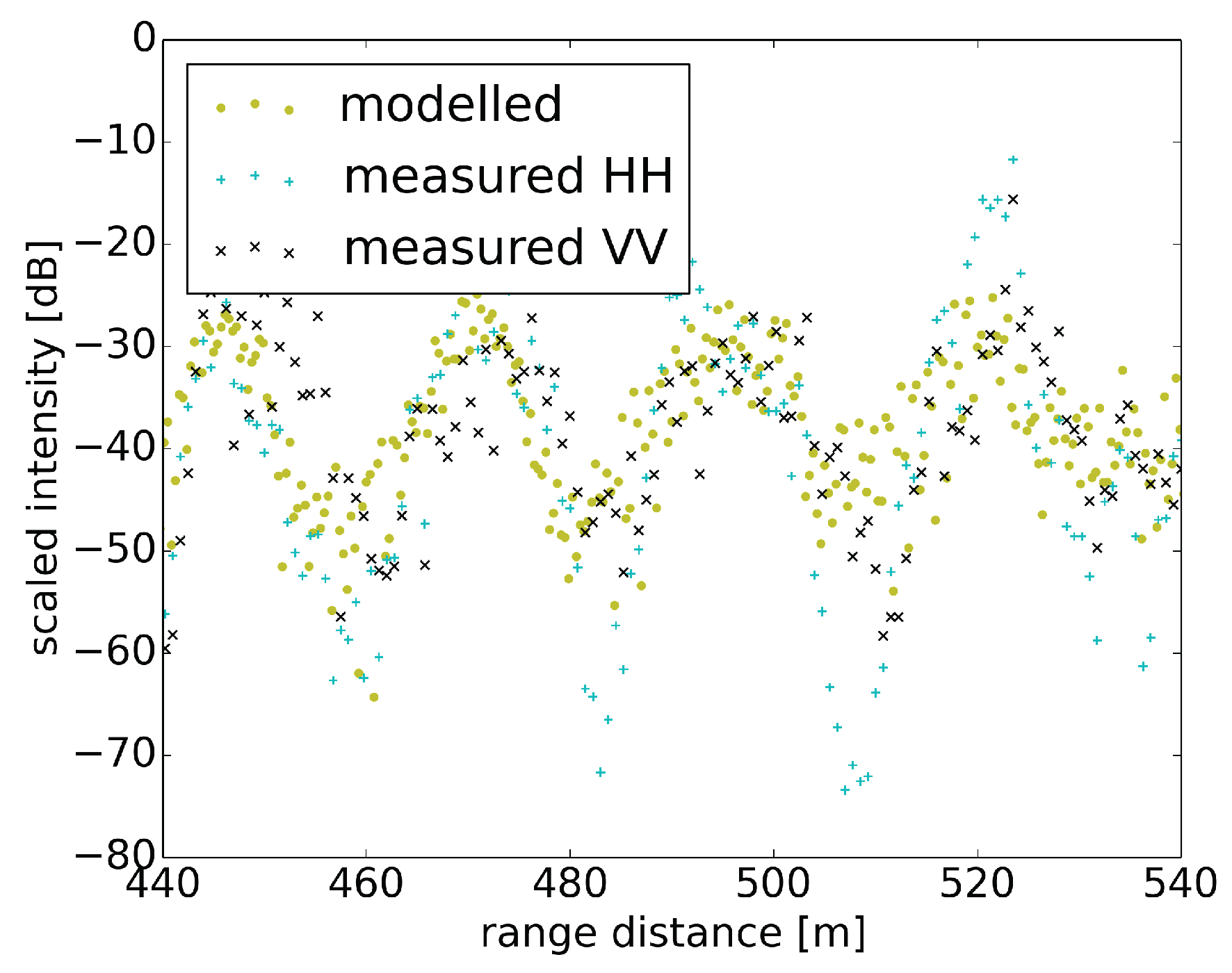
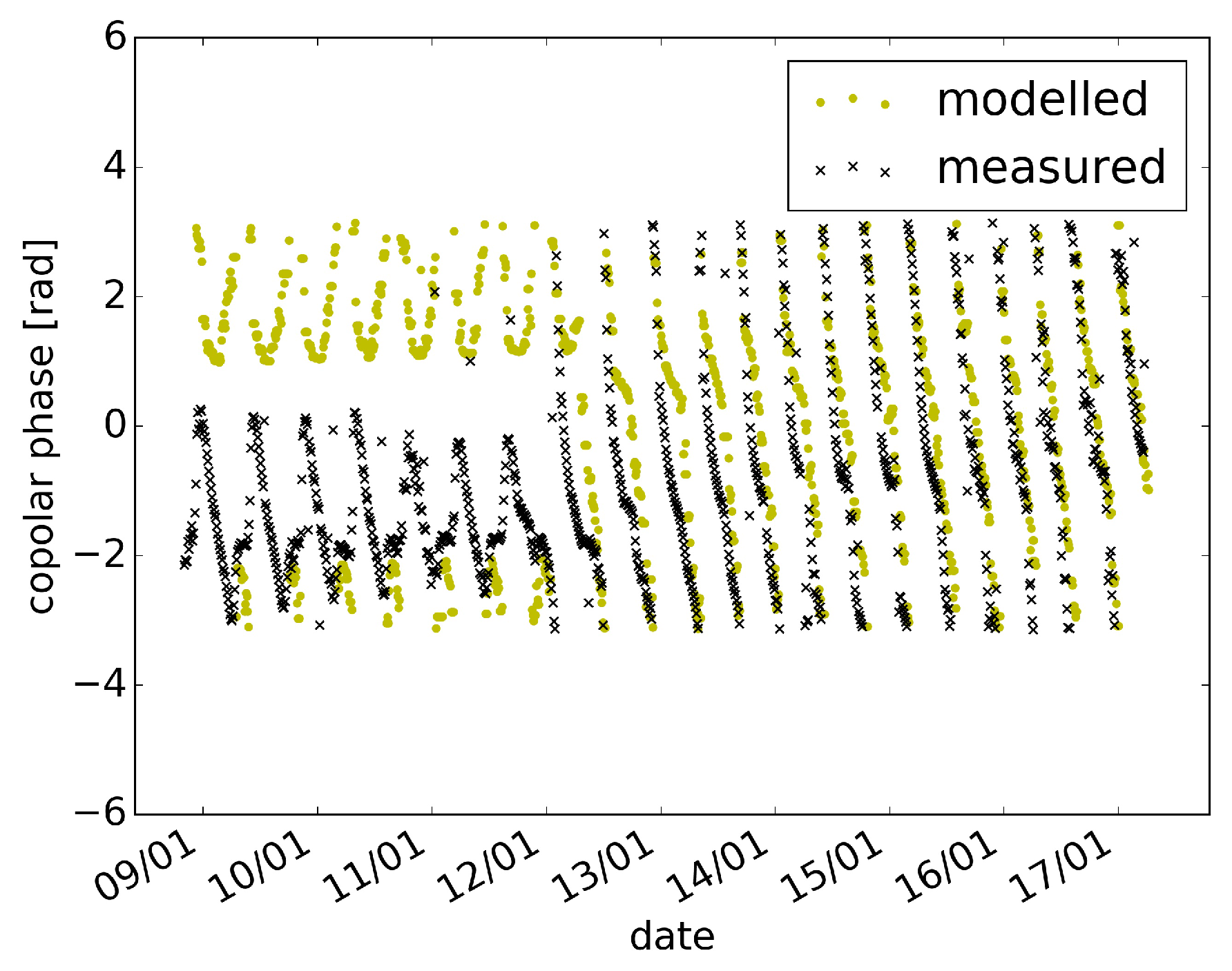
3. Results: Measured and Modelled Multipath Interferences
3.1. Influence of Polarisation and Slope Angle
3.2. Influence of the Reflection Surface Scattering Properties
3.3. Influence of Changing Multipath Baseline
3.3.1. First Order Effects Visible in the Backscatter Intensity Data
3.3.2. Second Order Effects Visible in the Interferometric and Polarimetric Data
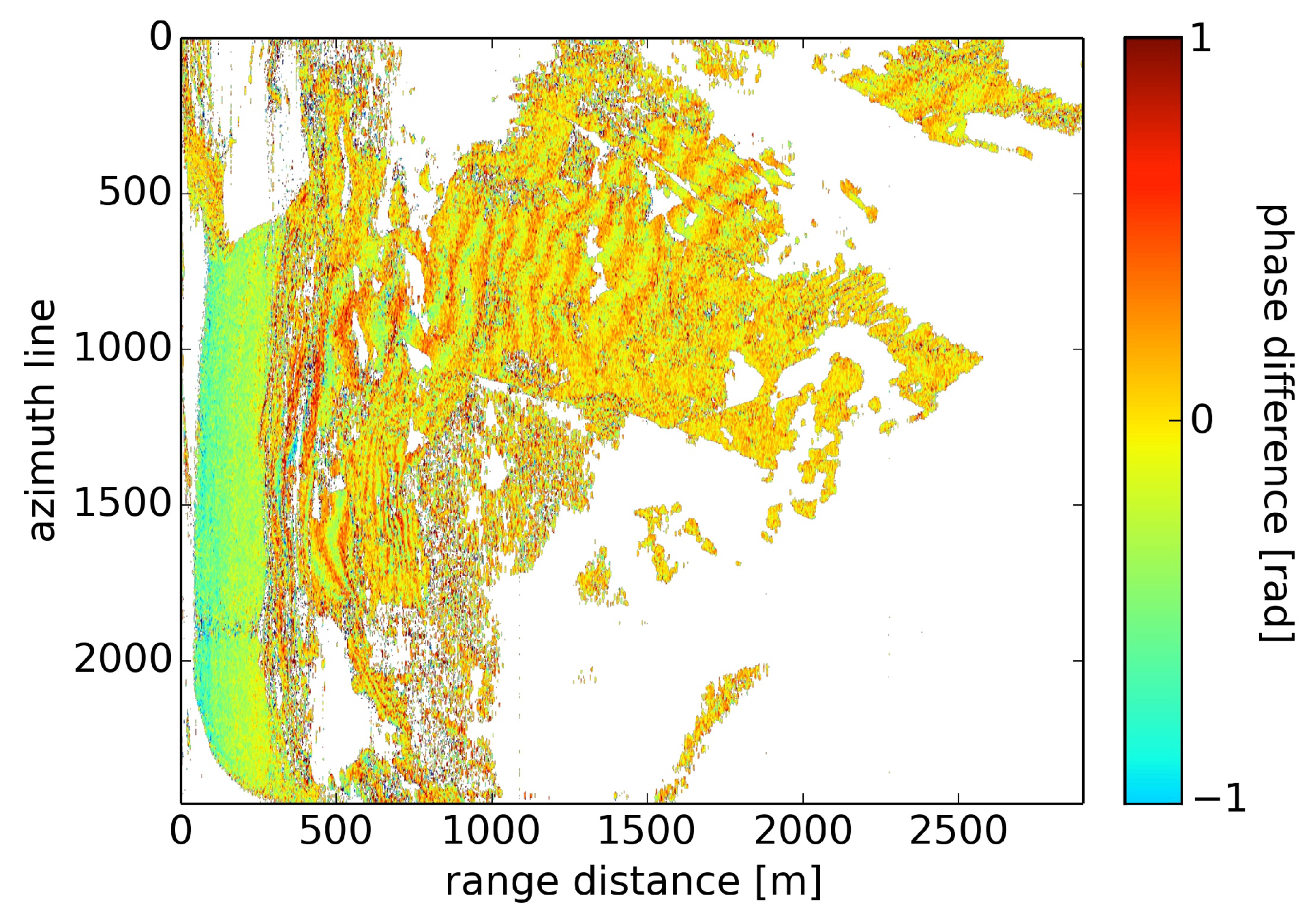
3.3.3. Fourth Order Effects Visible in the Difference of Single Pass Interferograms
4. Discussion
4.1. Occurence of MPI in Satellite- and Ground-Based Radar Data
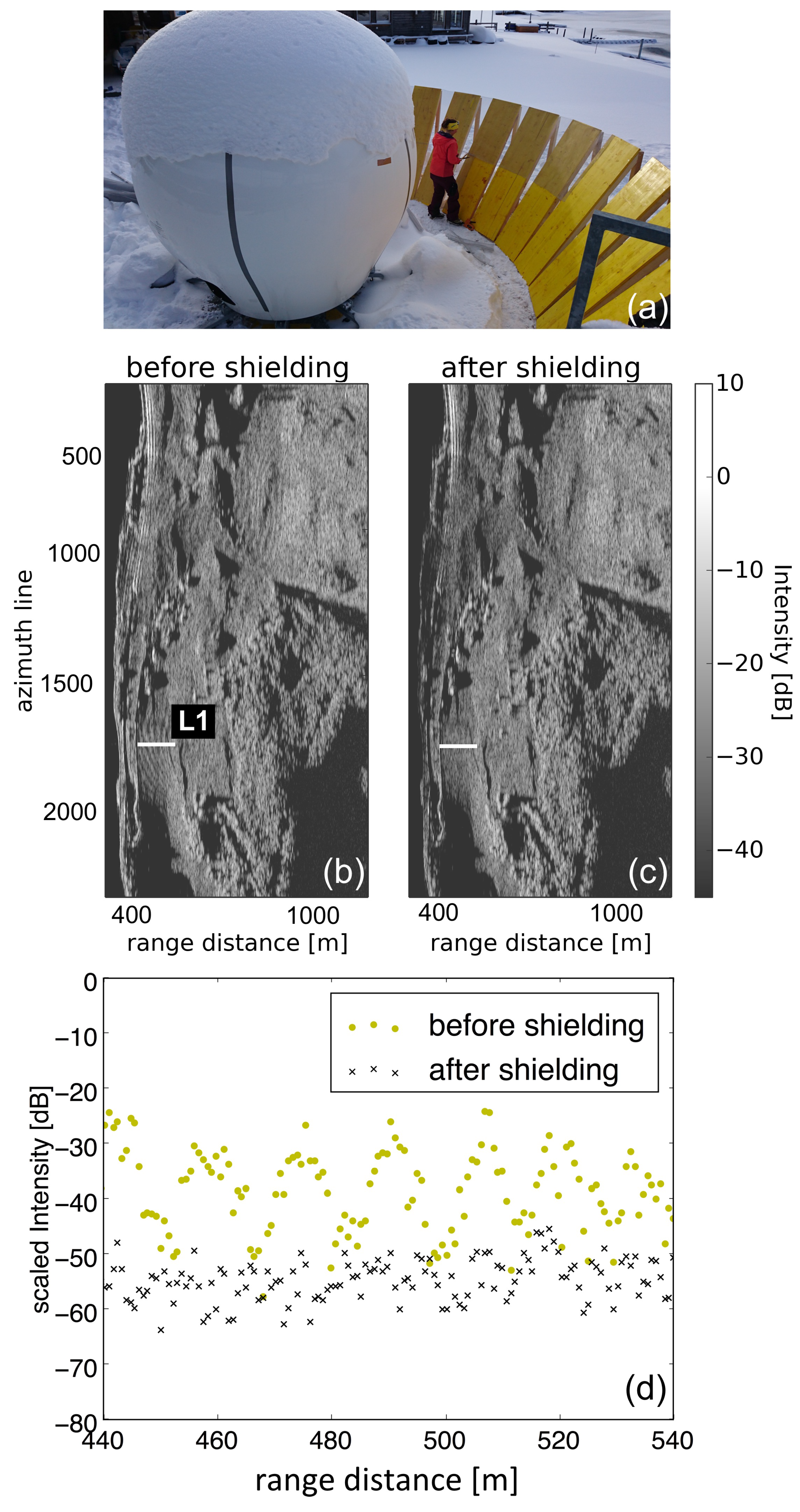
4.2. Avoiding MPI
4.3. Limitations of the Model
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Antonello, G.; Casagli, N.; Farina, P.; Leva, D.; Nico, G.; Sieber, A.J.; Tarchi, D. Ground-based SAR interferometry for monitoring mass movements. Landslides 2004, 1, 21–28. [Google Scholar] [CrossRef]
- Calabro, M.D.; Schmidt, D.A.; Roering, J.J. An examination of seasonal deformation at the Portuguese Bend landslide, Southern California, using radar interferometry. J. Geophys. Res. 2010, 115, 1–10. [Google Scholar] [CrossRef]
- Casagli, N.; Catani, F.; Del Ventisette, C.; Luzi, G. Monitoring, prediction, and early warning using ground-based radar interferometry. Landslides 2010, 7, 291–301. [Google Scholar] [CrossRef]
- Leva, D.; Nico, G.; Tarchi, D.; Fortuny-Guasch, J. Temporal analysis of a landslide by means of a ground-based SAR interferometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 745–752. [Google Scholar] [CrossRef]
- Mazzanti, P.; Brunetti, A. Assessing rockfall susceptibility by Terrestrial SAR Interferometry. In Proceedings of the Mountain Risks International Conference, Firenze, Italy, 24–26 November 2010; pp. 109–114. [Google Scholar]
- Pieraccini, M.; Casagli, N.; Luzi, G.; Tarchi, D.; Mecatti, D.; Noferini, L.; Atzeni, C. Landslide monitoring by ground-based radar interferometry: A field test in Valdarno (Italy). Int. J. Remote Sens. 2003, 24, 1385–1391. [Google Scholar] [CrossRef]
- Tarchi, D. Monitoring landslide displacements by using ground-based synthetic aperture radar interferometry: Application to the Ruinon landslide in the Italian Alps. J. Geophys. Res. 2003, 108, 2387. [Google Scholar] [CrossRef]
- Tarchi, D.; Antonello, G.; Casagli, N.; Farina, P.; Fortuny-Guasch, J.; Guerri, L.; Leva, D. On the use of ground-based SAR interferometry for slope failure early warning: The Cortenova Rock Slide (Italy). In Landslides: Risk Analysis and Sustainable Disaster Management; Springer: Berlin/Heidelberg, Germany, 2005; pp. 337–342. [Google Scholar]
- Del Ventisette, C.; Intrieri, E.; Luzi, G.; Casagli, N.; Fanti, R.; Leva, D. Using ground based radar interferometry during emergency: The case of the A3 motorway (Calabria Region, Italy) threatened by a landslide. Nat. Hazards Earth Syst. Sci. 2011, 11, 2483–2495. [Google Scholar] [CrossRef]
- Rödelsperger, S.; Läufer, G.; Gerstenecker, C.; Becker, M. Monitoring of displacements with ground-based microwave interferometry: IBIS-S and IBIS-L. J. Appl. Geodesy 2010, 4, 41–54. [Google Scholar] [CrossRef]
- Severin, J.; Eberhardt, E.; Leoni, L.; Fortin, S. Use of Ground-Based Synthetic Aperture Radar to Investigate Complex 3-D Pit Slope Kinematics. In Proceedings of the Slope Stability 2011: International Symposium on Rock Slope Stability in Open Pit Mining and Civil Engineering, Vancouver, BC, Canada, 18–21 September 2011; pp. 1991–1996. [Google Scholar]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Macaluso, G.; Tamburini, A.; Atzeni, C. Monitoring of an alpine glacier by means of ground-based SAR interferometry. IEEE Geosci. Remote Sens. Lett. 2007, 4, 495–499. [Google Scholar] [CrossRef]
- Riesen, P.; Strozzi, T.; Bauder, A.; Wiesmann, A.; Funk, M. Short-term surface ice motion variations measured with a ground-based portable real aperture radar Interferometer. J. Glaciol. 2011, 57, 53–60. [Google Scholar] [CrossRef]
- Leinss, S.; Wiesmann, A.; Lemmetyinen, J.; Hajnsek, I. Snow Water Equivalent of Dry Snow Measured by Differential Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3773–3790. [Google Scholar] [CrossRef]
- Caduff, R.; Wiesmann, A.; Bühler, Y.; Pielmeier, C. Continuous monitoring of snowpack displacement at high spatial and temporal resolution with terrestrial radar interferometry. Geophys. Res. Lett. 2015, 42, 813–820. [Google Scholar] [CrossRef]
- Caduff, R.; Wiesmann, A.; Bühler, Y.; Bieler, C.; Limpach, P. Terrestrial radar interferometry for snow glide activity monitoring and its potential as precursor of wet snow. In Proceedings of the 13th Congress Interpraevent, Lucerne, Switzerland, 30 May–2 June 2016; pp. 239–248. [Google Scholar]
- Martinez-Vazquez, A.; Fortuny-Guasch, J. A GB-SAR processor for snow avalanche identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3948–3956. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. DEM by ground-based SAR interferometry. IEEE Geosci. Remote Sens. Lett. 2007, 4, 659–663. [Google Scholar] [CrossRef]
- Strozzi, T.; Werner, C.; Wiesmann, A.; Wegmuller, U. Topography mapping with a portable real-aperture radar interferometer. IEEE Geosci. Remote Sens. Lett. 2012, 9, 277–281. [Google Scholar] [CrossRef]
- Caduff, R.; Schlunegger, F.; Kos, A.; Wiesmann, A. A review of terrestrial radar interferometry for measuring surface change in the geosciences. Earth Surf. Process. Landf. 2015, 40, 208–228. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef]
- Lloyd, H. On a New Case of Interference of the Rays of Light. Trans. R. Ir. Acad. 1831, 17, 171–177. [Google Scholar]
- Bolton, J. Radio astronomy at Dover Heights. Proc. Astron. Soc. Aust. 1982, 4, 349–358. [Google Scholar] [CrossRef]
- Mrstik, A.; Smith, P. Multipath limitations on low-angle radar tracking. IEEE Trans. Aerosp. Electron. Syst. 1978, 14, 85–102. [Google Scholar] [CrossRef]
- Werner, C.; Andreas, W.; Strozzi, T.; Kos, A.; Caduff, R.; Wegmuller, U. The GPRI Multi-mode Differential Interferometric Radar for Ground-based Observations. In Proceedings of the 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012. [Google Scholar]
- Baffelli, S.; Frey, O.; Werner, C.; Hajnsek, I. System Characterization and Polarimetric Calibration of the Ku-Band Advanced Polarimetric Interferometer. In Proceedings of the 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–6. [Google Scholar]
- Hecht, E. Optics, 4th ed.; Addison-Wesley: San Francisco, CA, USA, 2002; Volume 3. [Google Scholar]
- Graham, L.C. Synthetic Interferometer Radar For Topographic Mapping. Proc. IEEE 1974, 62, 763–768. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-Dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]





| Parameter | Value | Unit |
|---|---|---|
| center frequency: fc | 17.2 | GHz |
| bandwidth: | 200 | MHz |
| azimuth beamwidth | 0.385 | deg |
| elevation beamwidth | 35 | deg |
| range resolution: r | 0.75 | m |
| az at 1 km range distance | 7.0 | m |
| az at 2 km range distance | 14.0 | m |
| polarisation | HH, VV, HV, VH | |
| maximal baseline Bmax | 0.36 | m |
| HoA at 1 km range distance | 52 | m |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucas, C.; Leinss, S.; Bühler, Y.; Marino, A.; Hajnsek, I. Multipath Interferences in Ground-Based Radar Data: A Case Study. Remote Sens. 2017, 9, 1260. https://doi.org/10.3390/rs9121260
Lucas C, Leinss S, Bühler Y, Marino A, Hajnsek I. Multipath Interferences in Ground-Based Radar Data: A Case Study. Remote Sensing. 2017; 9(12):1260. https://doi.org/10.3390/rs9121260
Chicago/Turabian StyleLucas, Célia, Silvan Leinss, Yves Bühler, Armando Marino, and Irena Hajnsek. 2017. "Multipath Interferences in Ground-Based Radar Data: A Case Study" Remote Sensing 9, no. 12: 1260. https://doi.org/10.3390/rs9121260
APA StyleLucas, C., Leinss, S., Bühler, Y., Marino, A., & Hajnsek, I. (2017). Multipath Interferences in Ground-Based Radar Data: A Case Study. Remote Sensing, 9(12), 1260. https://doi.org/10.3390/rs9121260