Estimating Land Surface Temperature from Feng Yun-3C/MERSI Data Using a New Land Surface Emissivity Scheme
Abstract
:1. Introduction
2. Data
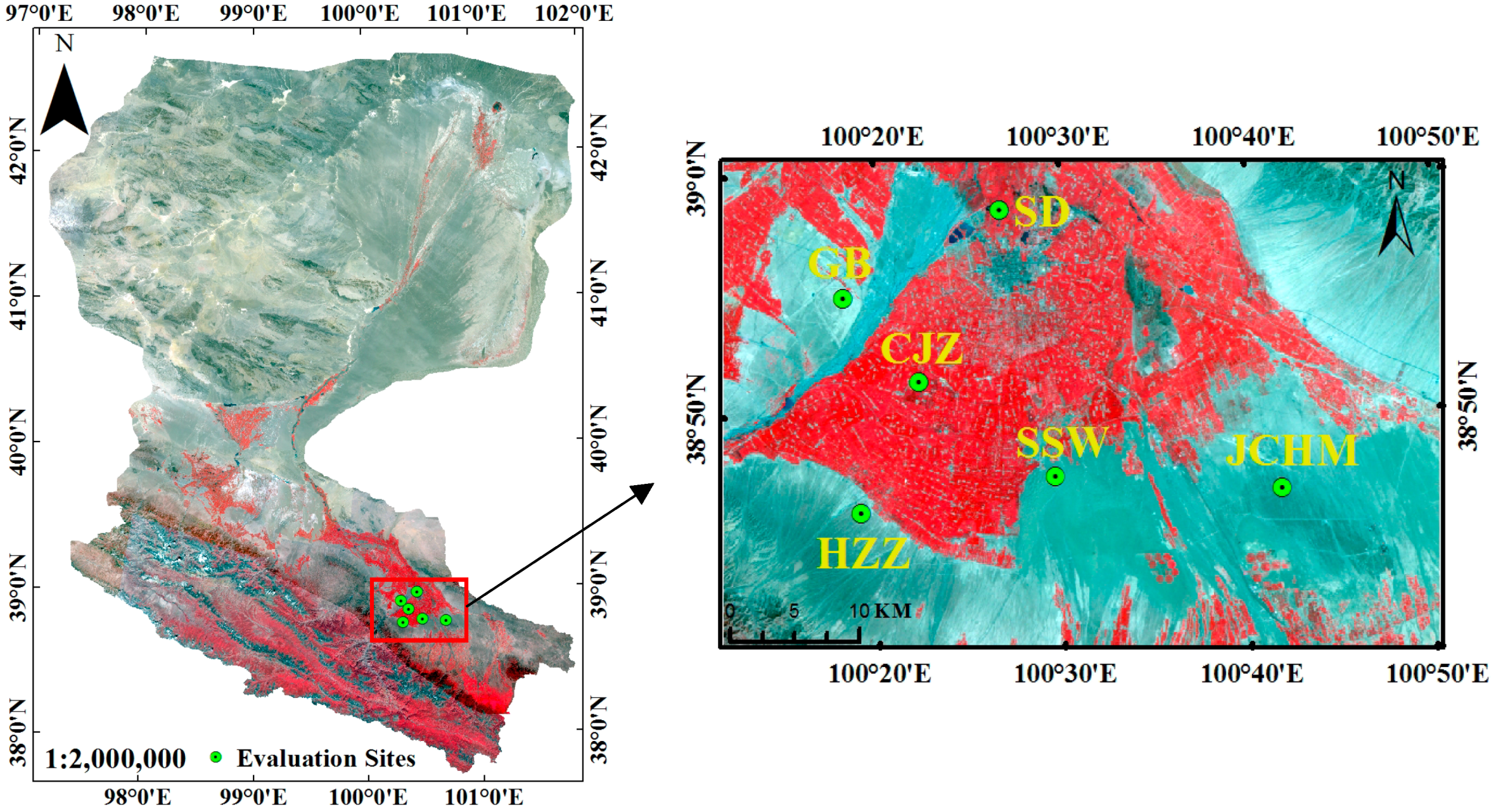
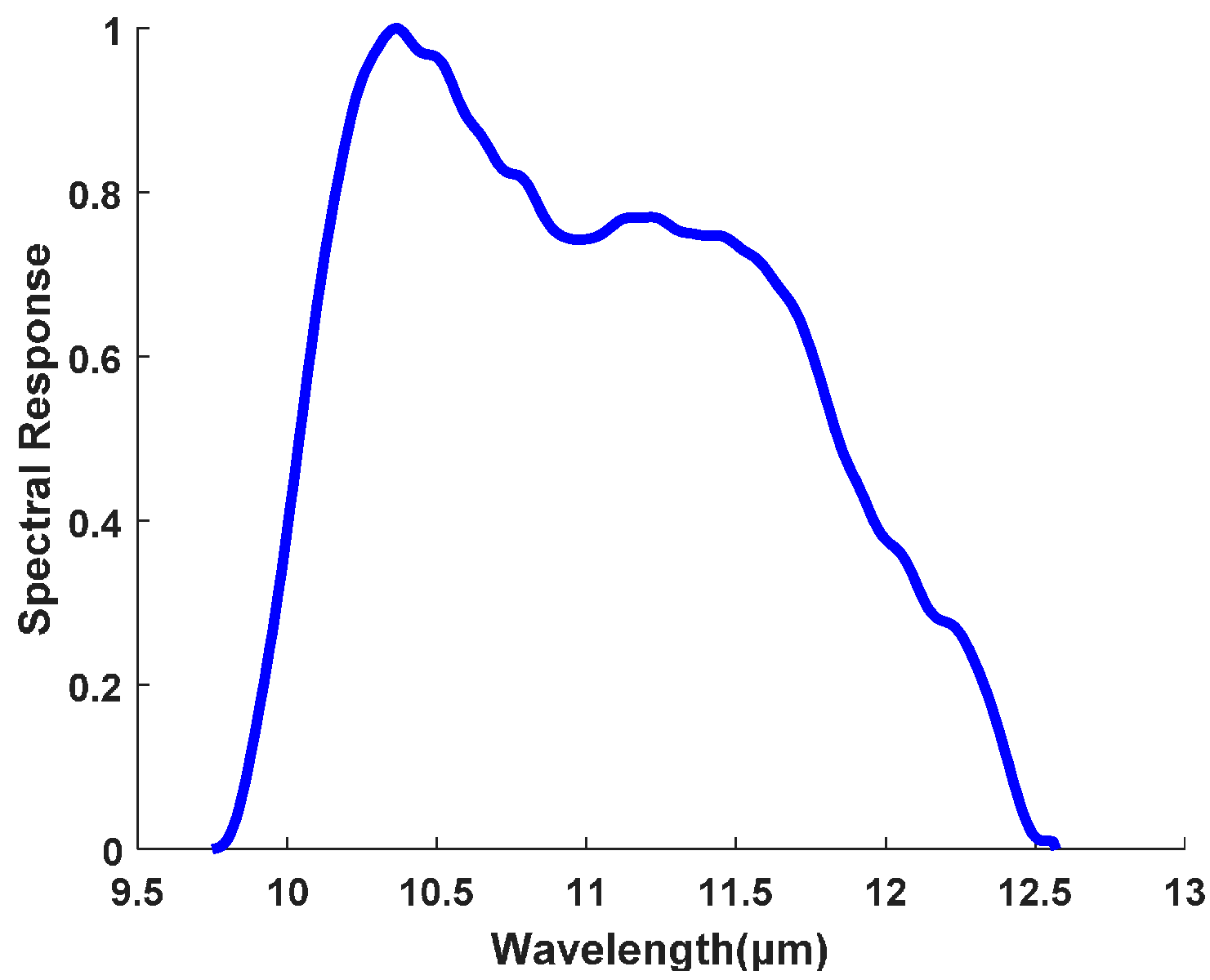
2.1. Satellite Products
2.2. Ground Measurements
3. Methods
3.1. Algorithms Used for Estimating the LSTs
3.1.1. The Radiative Transfer Equation (RTE) Algorithm
3.1.2. The Generalized Single-Channel (GSC) Algorithm
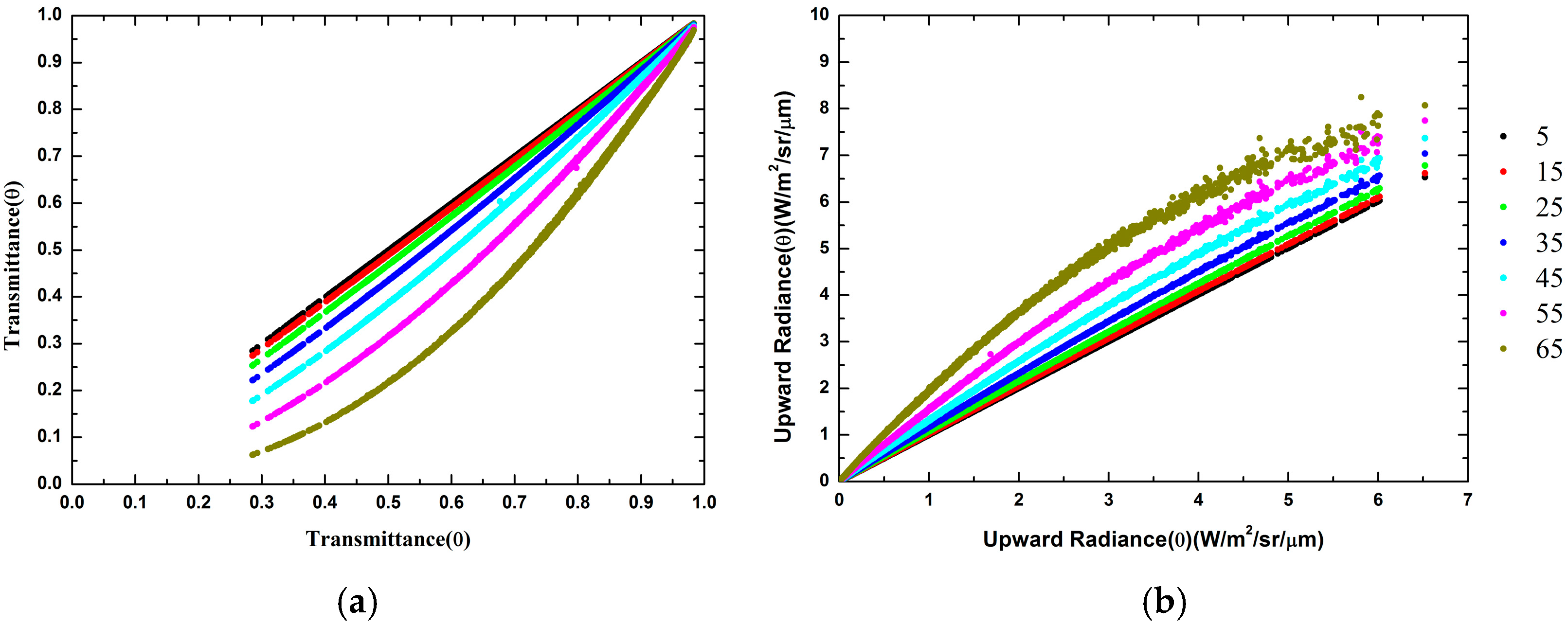
3.2. Angular Dependent Atmospheric Correction
3.3. A New Scheme for Determining Land Surface Emissivity
4. Results and Analysis
4.1. Coefficients for Atmospheric Correction
4.2. Evaluation with the In Situ LSE
4.3. Sensitivity Analysis of Emissivity
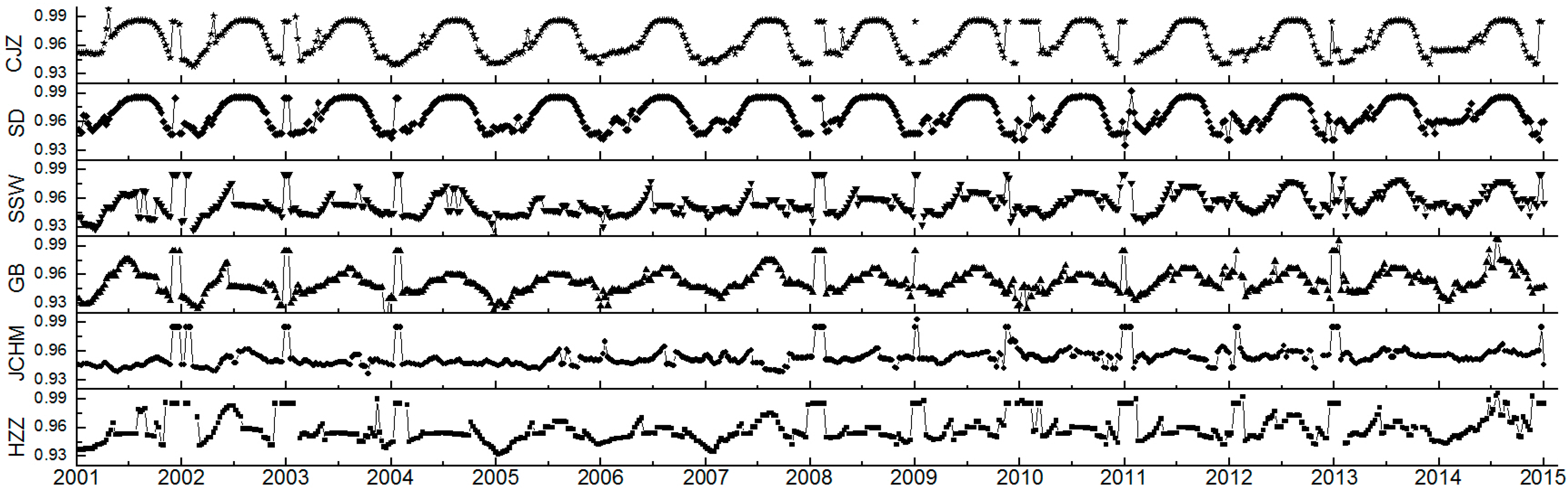
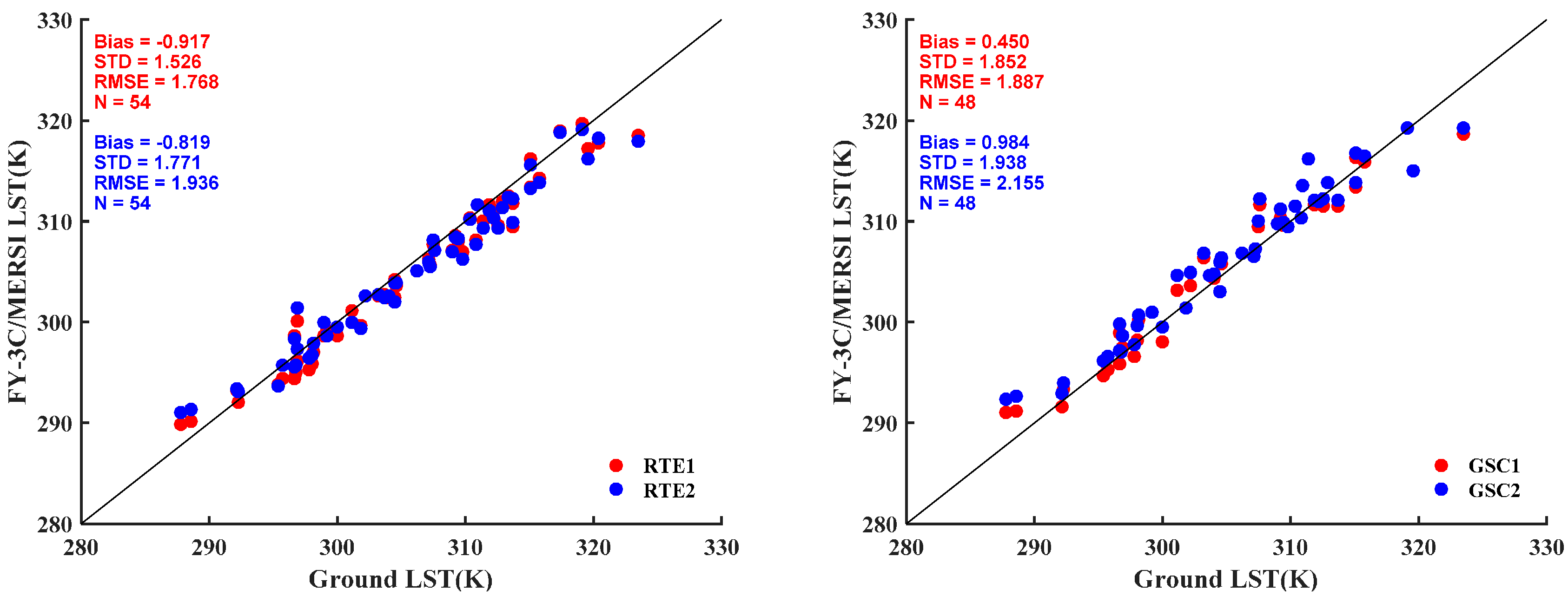
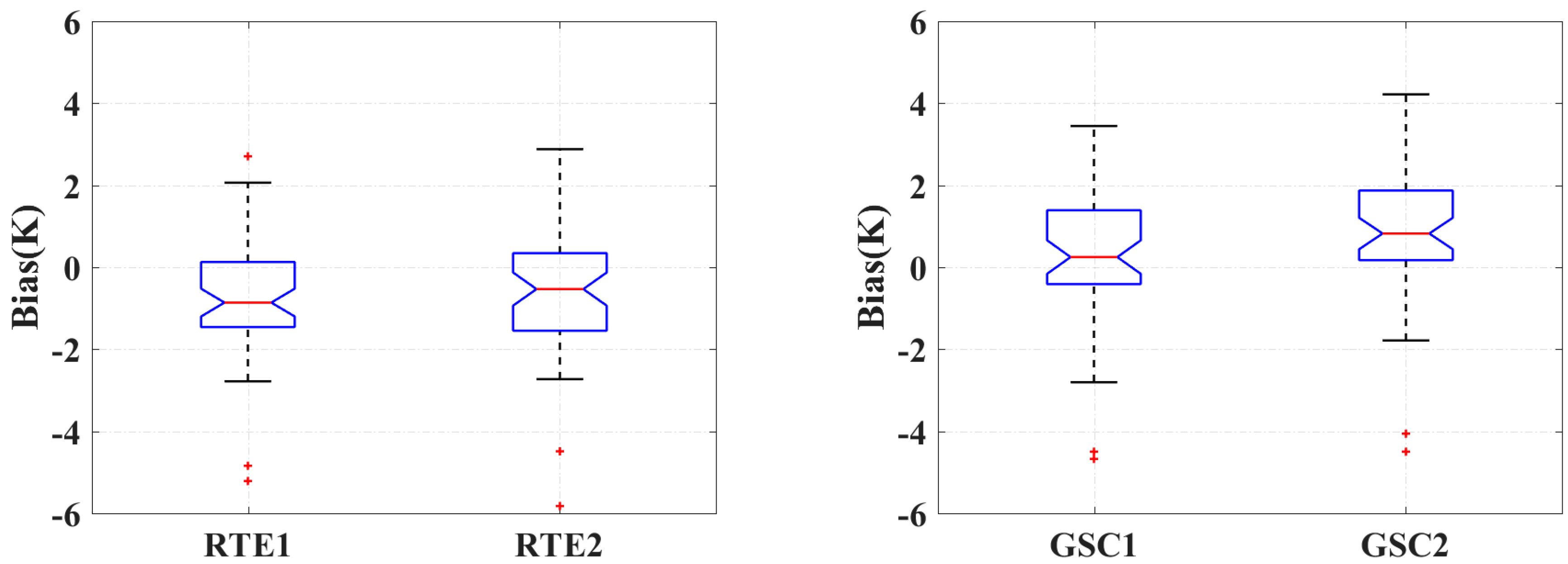
4.4. Validation of Retrieved LST from FY-3C/MERSI with In Situ LST
5. Discussion
5.1. Comparison with LST Derived from ASTER Emissivity Product
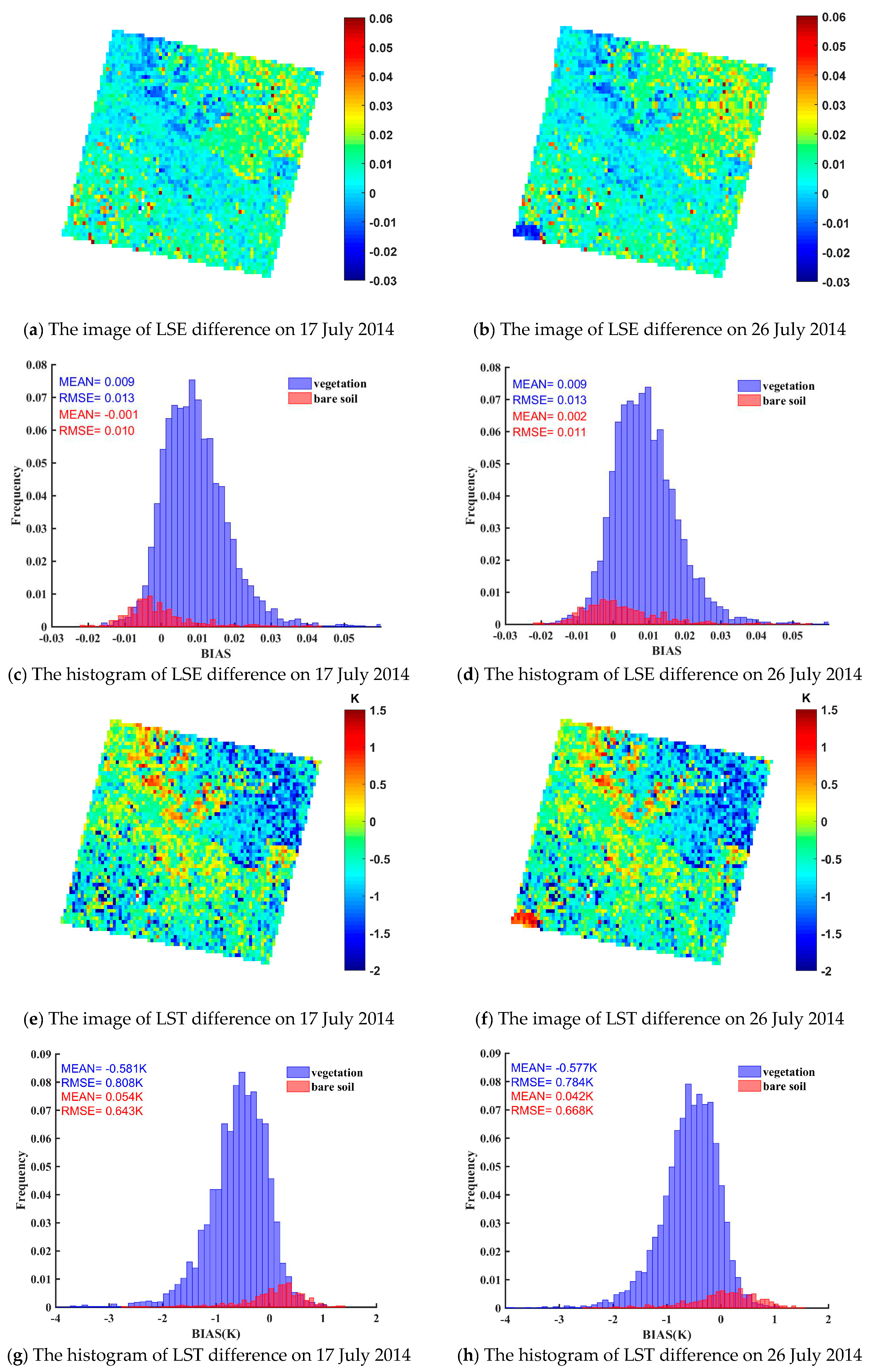
5.2. Effects of Spatial Scale on the LST and LSE Evaluation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Mannstein, H. Surface Energy Budget, Surface Temperature and Thermal Inertia. In Remote Sensing Applications in Meteorology and Climatology; Vaughan, R.A., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 1987; pp. 391–410. [Google Scholar]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to european, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Wang, J.; Li, X. A stepwise refining algorithm of temperature and emissivity separation for hyperspectral thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1588–1597. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.-M.; Tang, B.-H.; Yan, G.-J. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from landsat tm data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar]
- Jiménez-Muñoz, J.C. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Ellicott, E.; Vermote, E.; Petitcolin, F.; Hook, S.J. Validation of a new parametric model for atmospheric correction of thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2008, 47, 295–311. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Yu, Y.; Privette, J.L.; Pinheiro, A.C. Evaluation of split-window land surface temperature algorithms for generating climate data records. IEEE Trans. Geosci. Remote Sens. 2008, 46, 179–192. [Google Scholar] [CrossRef]
- Yunyue, Y.; Tarpley, D.; Privette, J.L.; Goldberg, M.D.; Rama Varma Raja, M.K.; Vinnikov, K.Y.; Hui, X. Developing algorithm for operational GOES-R land surface temperature product. IEEE Trans. Geosci. Remote Sens. 2009, 47, 936–951. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; De Feis, I.; Amoroso, M.; Venafra, S.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from geostationary infrared radiances. Atmos. Meas. Tech. 2013, 6, 3613–3634. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Valor, E.; Niclòs, R.; Sánchez, J.M.; Galve, J.M.; Mira, M. Temperature and emissivity separation from ASTER data for low spectral contrast surfaces. Remote Sens. Environ. 2007, 110, 162–175. [Google Scholar] [CrossRef]
- Sobrino, J.; Jimenezmunoz, J.; Balick, L.; Gillespie, A.; Sabol, D.; Gustafson, W. Accuracy of ASTER level-2 thermal-infrared standard products of an agricultural area in Spain. Remote Sens. Environ. 2007, 106, 146–153. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 modis land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Y.; Yu, P.; Göttsche, F.; Trigo, I. Quality assessment of S-NPP VIIRS land surface temperature product. Remote Sens. 2015, 7, 12215–12241. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R.T. Estimation of land surface temperature from a geostationary operational environmental satellite (GOES-8). J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Sun, D.; Yu, Y. Land Surface Temperature (LST) Retrieval from Goes Satellite Observations. In Satellite-based Applications on Climate Change; Qu, J., Powell, A., Sivakumar, M., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2013; pp. 289–334. [Google Scholar]
- Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Göttsche, F.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from seviri infrared channels: A validation and intercomparison study. Atmos. Meas. Tech. 2015, 8, 2981–2997. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature-vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Fee, D.; Matoza, R.S. An overview of volcano infrasound: From hawaiian to plinian, local to global. J. Volcanol. Geotherm. Res. 2013, 249, 123–139. [Google Scholar] [CrossRef]
- Diker, C.; Ulusoy, I. Monitoring Thermal Activity of Eastern Anatolian Volcanoes Using Modis Images. In Proceedings of the European Geosciences Union General Assembly, Vienna, Austria, 27 April–2 May 2014; pp. 375–381. [Google Scholar]
- Ulusoy, İ. Temporal monitoring of radiative heat flux from the craters of tendürek volcano (East Anatolia, Turkey) using ASTER satellite imagery. In Proceedings of the European Geosciences Union General Assembly, Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Guangmeng, Q.; Mei, Z. Using MODIS land surface temperature to evaluate forest fire risk of Northeast China. IEEE Geosci. Remote Sens. Lett. 2004, 1, 98–100. [Google Scholar] [CrossRef]
- ManzoDelgado, L.; SánchezColón, S.; Álvarez, R. Assessment of seasonal forest fire risk using NOAA-AVHRR: A case study in central mexico. Int. J. Remote Sens. 2009, 30, 4991–5013. [Google Scholar] [CrossRef]
- Meng, X.; Li, H.; Du, Y.; Liu, Q.; Zhu, J.; Sun, L. Retrieving land surface temperature from landsat 8 TIRS data using RTTOV and ASTER GED. In Proceedings of the Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 4302–4305. [Google Scholar]
- Yu, X.; Guo, X.; Wu, Z. Land surface temperature retrieval from landsat 8 TIRS—Comparison between radiative transfer equation-based method, split window algorithm and single channel method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef]
- Windahl, E.; Beurs, K.D. An intercomparison of landsat land surface temperature retrieval methods under variable atmospheric conditions using in situ skin temperature. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 11–27. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Cristobal, J.; Sobrino, J.A.; Soria, G.; Ninyerola, M.; Pons, X.; Pons, X. Revision of the single-channel algorithm for land surface temperature retrieval from landsat thermal-infrared data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Zhou, J.; Zhan, W.; Hu, D.; Zhao, X. Improvement of mono-window algorithm for retrieving land surface temperature from HJ-1B satellite data. Chin. Geogr. Sci. 2010, 20, 123–131. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Li, Z.L. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Hulley, G.; Veraverbeke, S.; Hook, S. Thermal-based techniques for land cover change detection using a new dynamic MODIS multispectral emissivity product (MOD21). Remote Sens. Environ. 2014, 140, 755–765. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the VIIRS and MODIS lst products in an arid area of Northwest China. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term global land surface satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Estimating global land surface broadband thermal-infrared emissivity from the advanced very high resolution radiometer optical data. Int. J. Digit. Earth 2013, 6, 34–49. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Estimating the broadband longwave emissivity of global bare soil from the MODIS shortwave albedo product. J. Geophys. Res. Atmos. 2014, 119, 614–634. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the glass leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2013, 52, 209–223. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HIWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HIWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Wang Heshun, L.H.; Cao, B.; Du, Y.; Xiao, Q.; Liu, Q. HIWATER: Dataset of Thermal Infrared Spectrum Observed by BOMEM MR304 in the Middle Reaches of the Heihe River Basin; Institute of Remote Sensing Applications, Chinese Academy of Sciences: Beijing, China, 2012. [Google Scholar]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Tan Junlei, M.M. HIWATER: Dataset of Infrared Temperature in Zhanye Airport Desert; Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences: Beijing, China, 2012. [Google Scholar]
- Ingram, P.M.; Muse, A.H. Sensitivity of iterative spectrally smooth temperature/emissivity separation to algorithmic assumptions and measurement noise. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2158–2167. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Yao, Y.; Ren, B.; Shi, L.; Liu, H. A comparative study of three land surface broadband emissivity datasets from satellite data. Remote Sens. 2013, 6, 111–134. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A. Feasibility of retrieving land-surface temperature from ASTER TIR bands using two-channel algorithms: A case study of agricultural areas. IEEE Geosci. Remote Sens. Lett. 2007, 4, 60–64. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Verhoef, W.; Shi, L.; Liu, Q. Estimating the hemispherical broadband longwave emissivity of global vegetated surfaces using a radiative transfer model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 905–917. [Google Scholar] [CrossRef]
- Barsi, J.A.; Butler, J.J.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a web-based atmospheric correction tool for single thermal band instruments. In Proceedings of the Optics and Photonics, San Diego, CA, USA, 31 July–4 August 2005; Volume 5882, pp. 136–142. [Google Scholar]
- Li, H.; Liu, Q.; Du, Y.; Jiang, J.; Wang, H. Evaluation of the NCEP and MODIS atmospheric products for single channel land surface temperature retrieval with ground measurements: A case study of HJ-1B IRS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1399–1408. [Google Scholar] [CrossRef]
- Cook, M.; Schott, J.; Mandel, J.; Raqueno, N. Development of an operational calibration methodology for the landsat thermal data archive and initial testing of the atmospheric compensation component of a land surface temperature (LST) product from the archive. Remote Sens. 2014, 6, 11244–11266. [Google Scholar] [CrossRef]
- Rivalland, V.; Tardy, B.; Huc, M.; Hagolle, O.; Marcq, S.; Boulet, G. A useful tool for atmospheric correction and surface temperature estimation of landsat infrared thermal data. In Proceedings of the European Geosciences Union General Assembly, Vienna, Austria, 17–22 April 2016; Volume 8, p. 696. [Google Scholar]
- Matricardi, M.; Chevallier, F.; Kelly, G.; Thépaut, J.N. An improved general fast radiative transfer model for the assimilation of radiance observations. Q. J. R. Meteorol. Soc. 2010, 130, 153–173. [Google Scholar] [CrossRef]
- Tonooka, H. Accurate atmospheric correction of ASTER thermal infrared imagery using the WVS method. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2778–2792. [Google Scholar] [CrossRef]
- Jiang, G.M.; Zhou, W.; Liu, R. Development of split-window algorithm for land surface temperature estimation from the VIRR/FY-3A measurements. IEEE Geosci. Remote Sens. Lett. 2013, 10, 952–956. [Google Scholar] [CrossRef]
- Borbas, E.E.; Seemann, S.W.; Huang, H.L.; Li, J.; Menzel, P.W. Global profile training database for satellite regression retrievals with estimates of skin temperature and emissivity. In Proceedings of the International TOVS Study Conference, Beijing, China, 25–31 May 2005. [Google Scholar]
- Galve, J.M.; Coll, C.; Caselles, V.; Valor, E. An atmospheric radiosounding database for generating land surface temperature algorithms. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1547–1557. [Google Scholar] [CrossRef]
- Ren, B.; Cheng, J. Land Surface Temperature Retrieval Algorithm of Single Channel for FY-3A/MERSI; Beijing Normal University: Beijing, China, 2015. [Google Scholar]
- Dong, L.X.; Hu, J.Y.; Tang, S.H.; Min, M. Field validation of glass land surface broadband emissivity database using pseudo-invariant sand dunes sites in Northern China. Int. J. Digit. Earth 2013, 6, 96–112. [Google Scholar] [CrossRef]
- Pandya, M.R.; Shah, D.B.; Trivedi, H.J.; Lunagaria, M.M.; Pandey, V.; Panigrahy, S.; Parihar, J.S. Field measurements of plant emissivity spectra: An experimental study on remote sensing of vegetation in the thermal infrared region. J. Indian Soc. Remote Sens. 2013, 41, 787–796. [Google Scholar] [CrossRef]
- Niclòs, R.; Caselles, V.; Coll, C.; Valor, E. Determination of sea surface temperature at large observation angles using an angular and emissivity-dependent split-window equation. Remote Sens. Environ. 2007, 111, 107–121. [Google Scholar] [CrossRef]
- Yu Wenping, M.M.; Ren, Z.; Tan, J.; Li, Y.; Wang, H. HIWATER: Dataset of Emissivity in the Heihe River Basin; Cold and Arid Regions Science Data Center at Lanzhou: Lanzhou, China, 2013. [Google Scholar]
- Hulley, G.C.; Hughes, C.G.; Hook, S.J. Quantifying uncertainties in land surface temperature and emissivity retrievals from ASTER and MODIS thermal infrared data. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Privette, J.L.; Coudert, B.; Palecki, M.A.; Demarty, J.; Ottlé, C.; Augustine, J.A. Land surface temperature product validation using NOAA’S surface climate observation networks—Scaling methodology for the visible infrared imager radiometer suite (VIIRS). Remote Sens. Environ. 2012, 124, 282–298. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Gillespie, A.; Sabol, D.; Gustafson, W.T. Improved land surface emissivities over agricultural areas using ASTER NDVI. Remote Sens. Environ. 2006, 103, 474–487. [Google Scholar] [CrossRef]
- Coll, C.; Valor, E.; Galve, J.M.; Mira, M.; Bisquert, M.; García-Santos, V.; Caselles, E.; Caselles, V. Long-term accuracy assessment of land surface temperatures derived from the advanced along-track scanning radiometer. Remote Sens. Environ. 2012, 116, 211–225. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Dong, L.; Ren, B.; Shi, L. Validation of the moderate-resolution imaging spectrometer (MODIS) land surface emissivity products over the taklimakan desert. J. Appl. Remote Sens. 2014, 8. [Google Scholar] [CrossRef]


| IGBP Class | Composite Type | Leaf Emissivity | Sources |
|---|---|---|---|
| 1~7 | Forest and Shrubland | 0.967 | Mean of conifer and deciduous emissivity from ASTER spectral library and 24 leaf emissivities from MODIS spectral library and 10 measured leaf emissivities from Wang et al. [43] |
| 8, 9 | Savanna | 0.966 | 50% forest + 50% grassland |
| 10 | Grassland | 0.965 | Mean of green grass emissivity from ASTER spectral library and elephant grass emissivity from Pandya et al. [61] |
| 12, 14 | Cropland | 0.966 | Mean of 9 leaf emissivities from Pandya et al. [61], 4 wheat emissivities of Li et al. [36] and 39 measured leaf emissivities from Wang et al. [43] |
| 16, 254 | Other types | 0.966 | Mean value of above four types |
| Parameters | a1 | a2 | a3 | b1 | b2 | b3 | c1 | c2 | c3 |
|---|---|---|---|---|---|---|---|---|---|
| −0.0111 | −0.0846 | 0.0007 | −0.0955 | 0.9205 | 0.9997 | 0.0189 | −0.0198 | 0.0003 | |
| 0.1077 | 0.721 | −0.0055 | −0.2987 | −0.4775 | 1.0104 | 0.1885 | −0.2376 | −0.005 |
| Station Name | Type Name | Measured Emissivity | Estimated LSE Using the Method in Section 3.3 | Bias |
|---|---|---|---|---|
| CJZ01 | Corn leaf | 0.973 | 0.985 | 0.012 |
| CJZ02 | Chinese cabbage leaf | 0.987 | 0.985 | −0.002 |
| GB01 | Alhagi sparsifolia | 0.976 | 0.960 | −0.016 |
| SSW01 | Sparse vegetation | 0.986 | 0.971 | −0.015 |
| SSW02 | Large cluster sparse vegetation | 0.960 | 0.985 | 0.025 |
| SSW03 | Large cluster sparse vegetation | 0.959 | 0.962 | 0.003 |
| GB02 | Bare soil | 0.957 | 0.960 | 0.003 |
| 17 July 2014 | 26 July 2014 | |||||||
|---|---|---|---|---|---|---|---|---|
| Sites | LSEaster | LSEmersi | LSTaster (K) | LSTmersi (K) | LSEaster | LSEmersi | LSTaster (K) | LSTmersi (K) |
| SD | 0.955 | 0.984 | 300.566 | 298.887 | 0.955 | 0.984 | 302.115 | 300.447 |
| CJZ | 0.963 | 0.985 | 302.865 | 301.524 | 0.963 | 0.985 | 300.360 | 299.062 |
| GB | 0.954 | 0.955 | 312.475 | 312.401 | 0.954 | 0.957 | 315.341 | 315.154 |
| SSW | 0.954 | 0.964 | 317.890 | 317.179 | 0.954 | 0.967 | 318.487 | 317.616 |
| HZZ | 0.971 | 0.968 | 314.886 | 315.099 | 0.971 | 0.968 | 314.020 | 314.224 |
| LST STD (K) | LSE STD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sites | 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 |
| SD | 0.929 | 1.086 | 1.242 | 1.470 | 1.664 | 0.006 | 0.006 | 0.006 | 0.006 | 0.006 |
| CJZ | 0.804 | 1.041 | 1.387 | 1.801 | 1.977 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 |
| GB | 0.435 | 0.625 | 0.776 | 0.842 | 0.887 | 0.003 | 0.004 | 0.004 | 0.005 | 0.005 |
| SSW | 0.671 | 0.829 | 0.942 | 1.121 | 1.485 | 0.004 | 0.004 | 0.005 | 0.005 | 0.005 |
| HZZ | 0.396 | 0.468 | 0.530 | 0.601 | 0.684 | 0.003 | 0.004 | 0.004 | 0.004 | 0.005 |
| JCHM | 0.342 | 0.426 | 0.491 | 0.506 | 0.523 | 0.003 | 0.004 | 0.004 | 0.004 | 0.004 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Cheng, J.; Liang, S. Estimating Land Surface Temperature from Feng Yun-3C/MERSI Data Using a New Land Surface Emissivity Scheme. Remote Sens. 2017, 9, 1247. https://doi.org/10.3390/rs9121247
Meng X, Cheng J, Liang S. Estimating Land Surface Temperature from Feng Yun-3C/MERSI Data Using a New Land Surface Emissivity Scheme. Remote Sensing. 2017; 9(12):1247. https://doi.org/10.3390/rs9121247
Chicago/Turabian StyleMeng, Xiangchen, Jie Cheng, and Shunlin Liang. 2017. "Estimating Land Surface Temperature from Feng Yun-3C/MERSI Data Using a New Land Surface Emissivity Scheme" Remote Sensing 9, no. 12: 1247. https://doi.org/10.3390/rs9121247
APA StyleMeng, X., Cheng, J., & Liang, S. (2017). Estimating Land Surface Temperature from Feng Yun-3C/MERSI Data Using a New Land Surface Emissivity Scheme. Remote Sensing, 9(12), 1247. https://doi.org/10.3390/rs9121247








