Stochastic Models of Very High-Rate (50 Hz) GPS/BeiDou Code and Phase Observations
Abstract
:1. Introduction
2. Methods
2.1. Least-Squares Variance Component Estimation
2.2. Geometry-Based Functional Model Using GNSS Single-Differenced Observations
2.3. Stochastic Model of GNSS Code and Phase Observations
2.3.1. Precisions
2.3.2. Cross Correlations
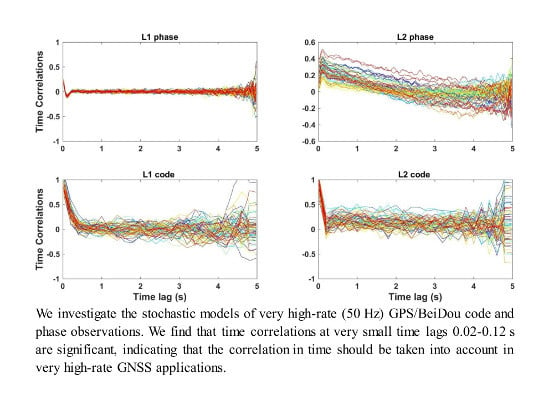
2.3.3. Time Correlations
3. Very-High (50 Hz) Data, VCE Procedure and Results
3.1. Data Description
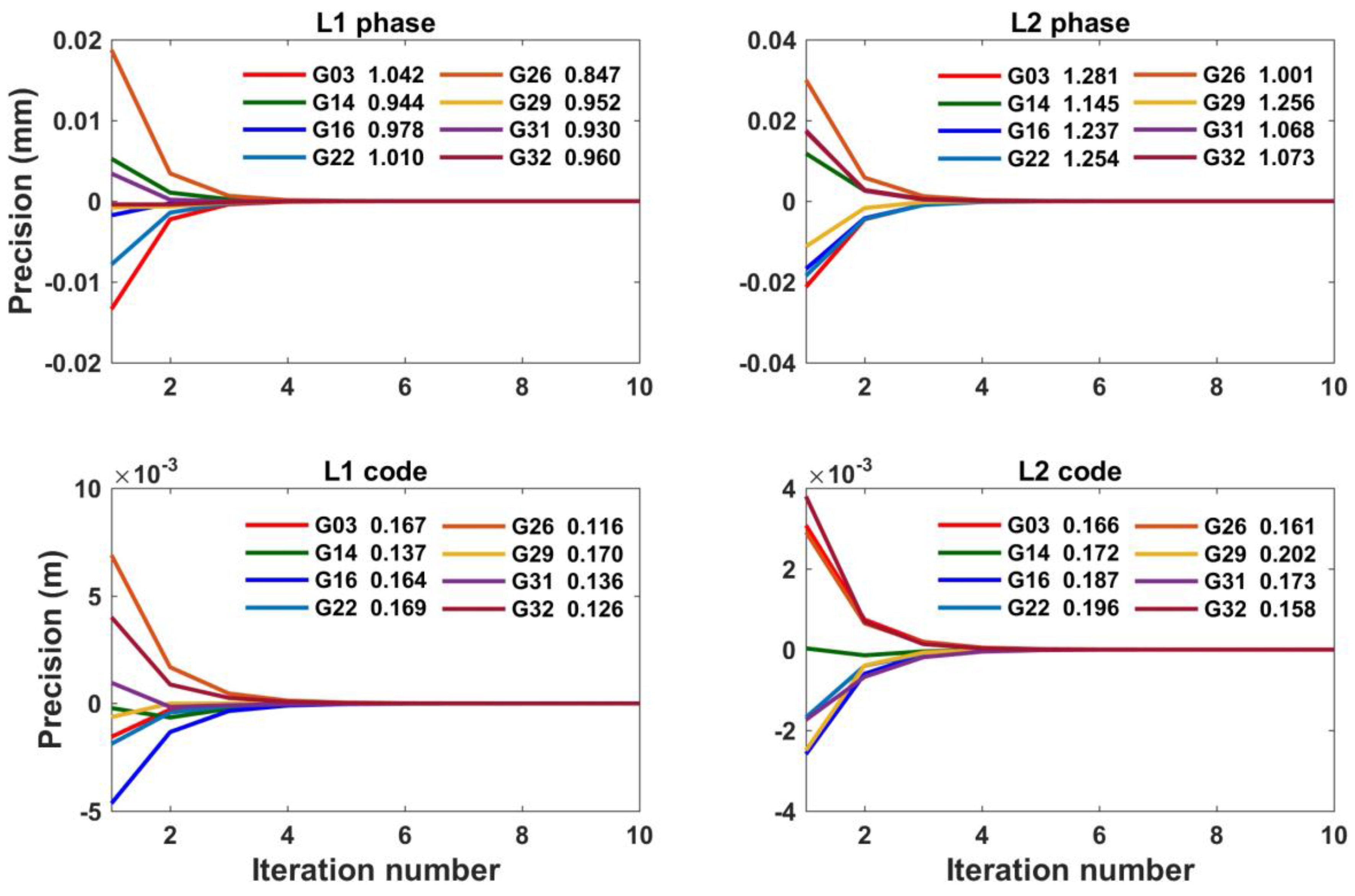
3.2. VCE Procedure
3.3. Results and Analysis
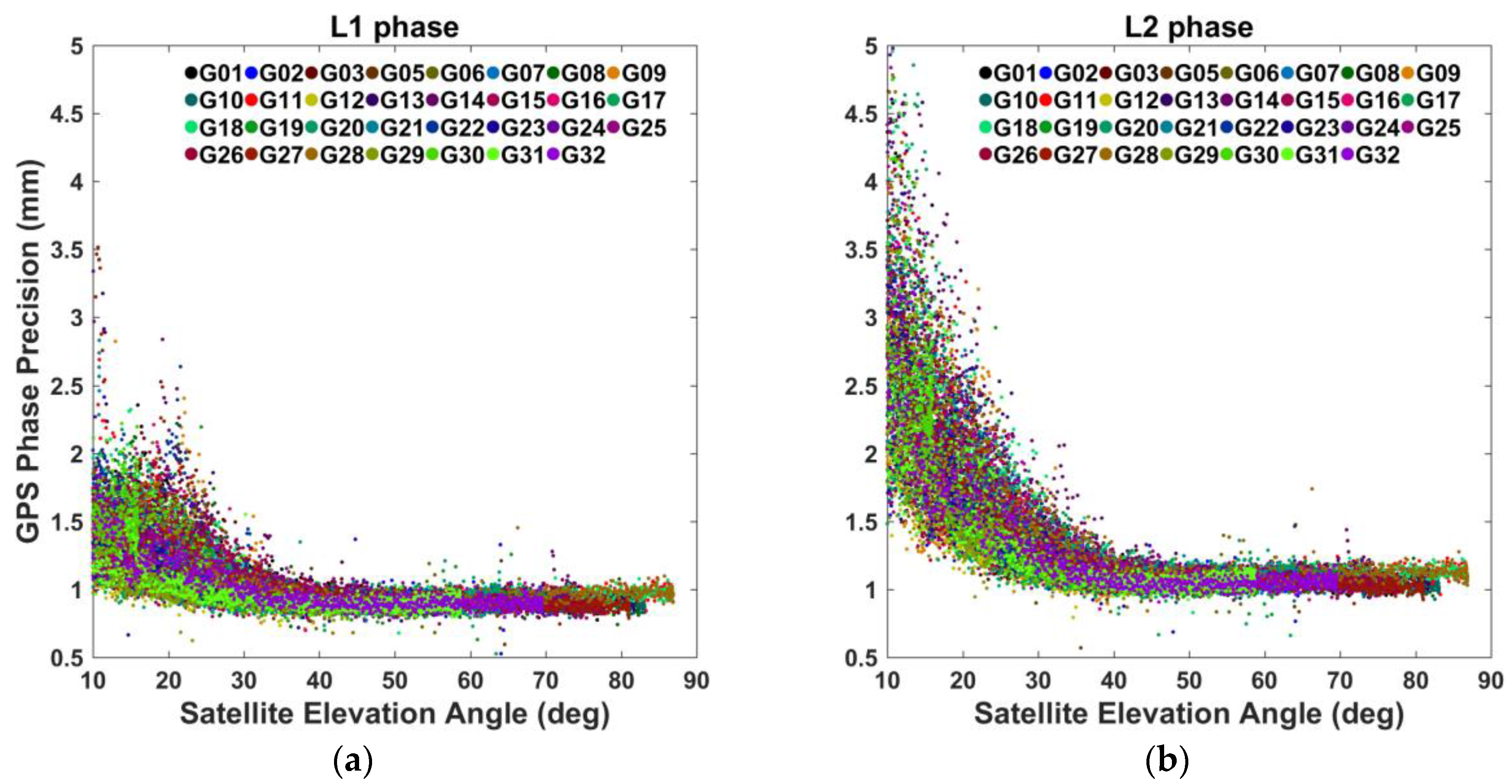
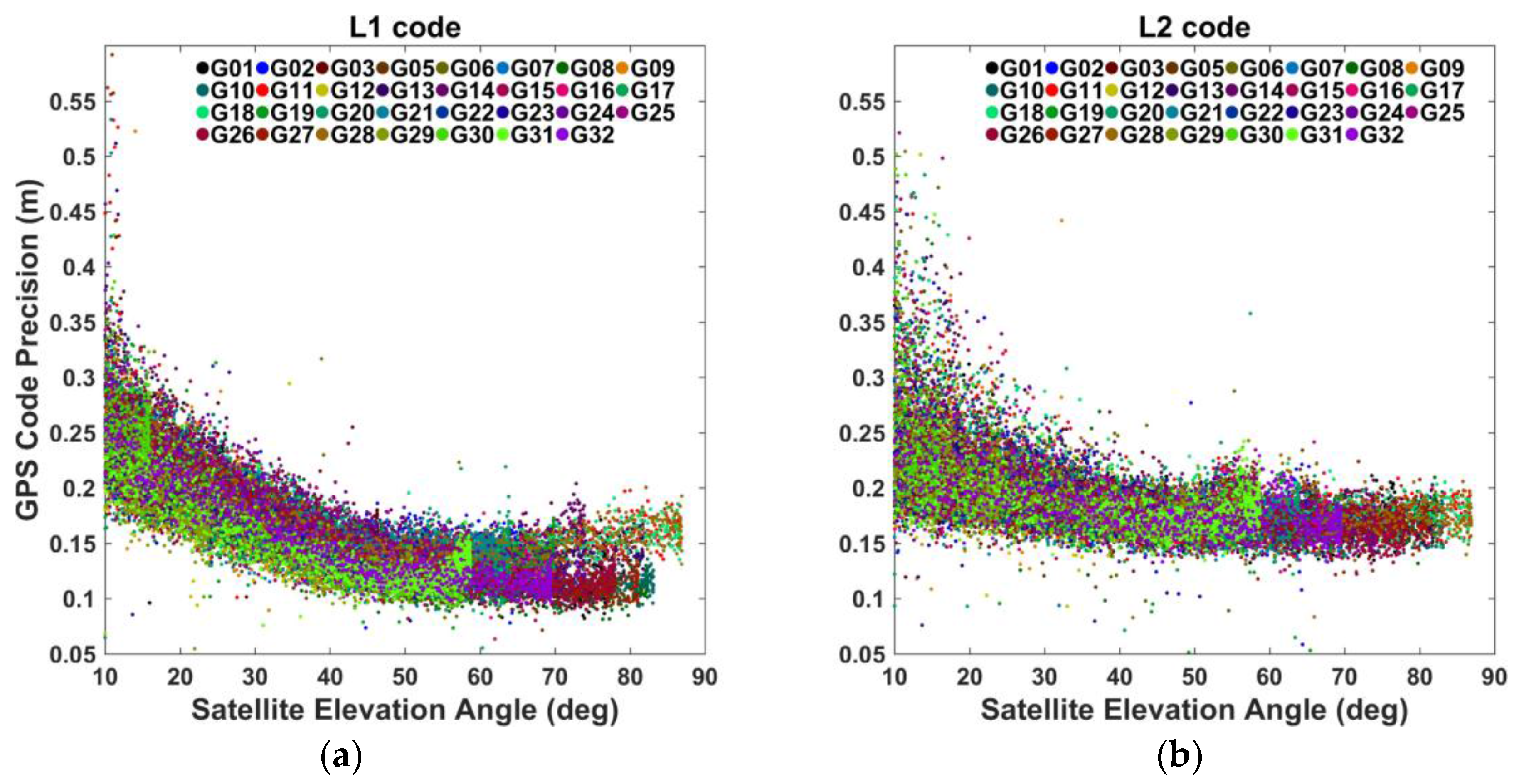
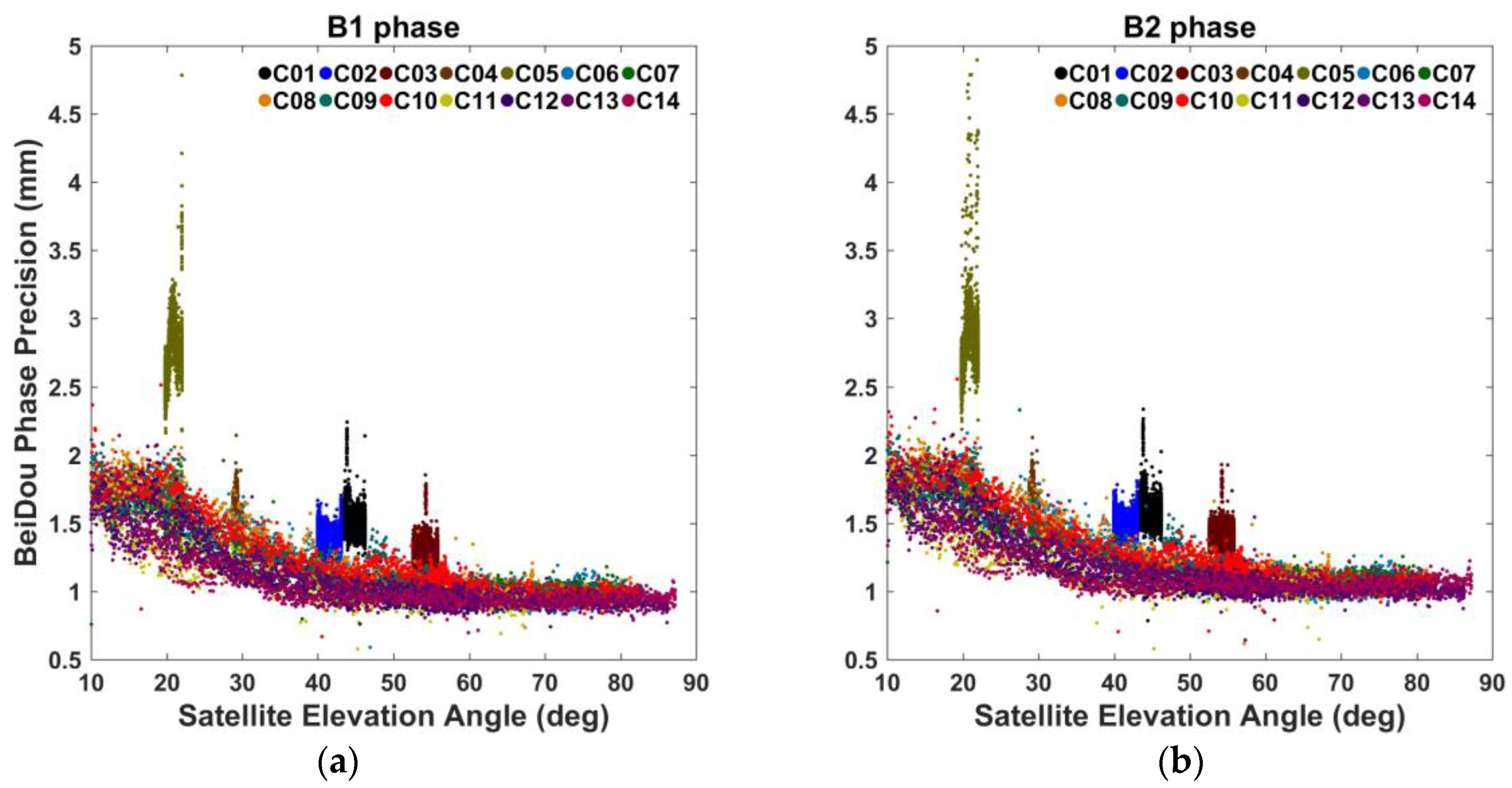
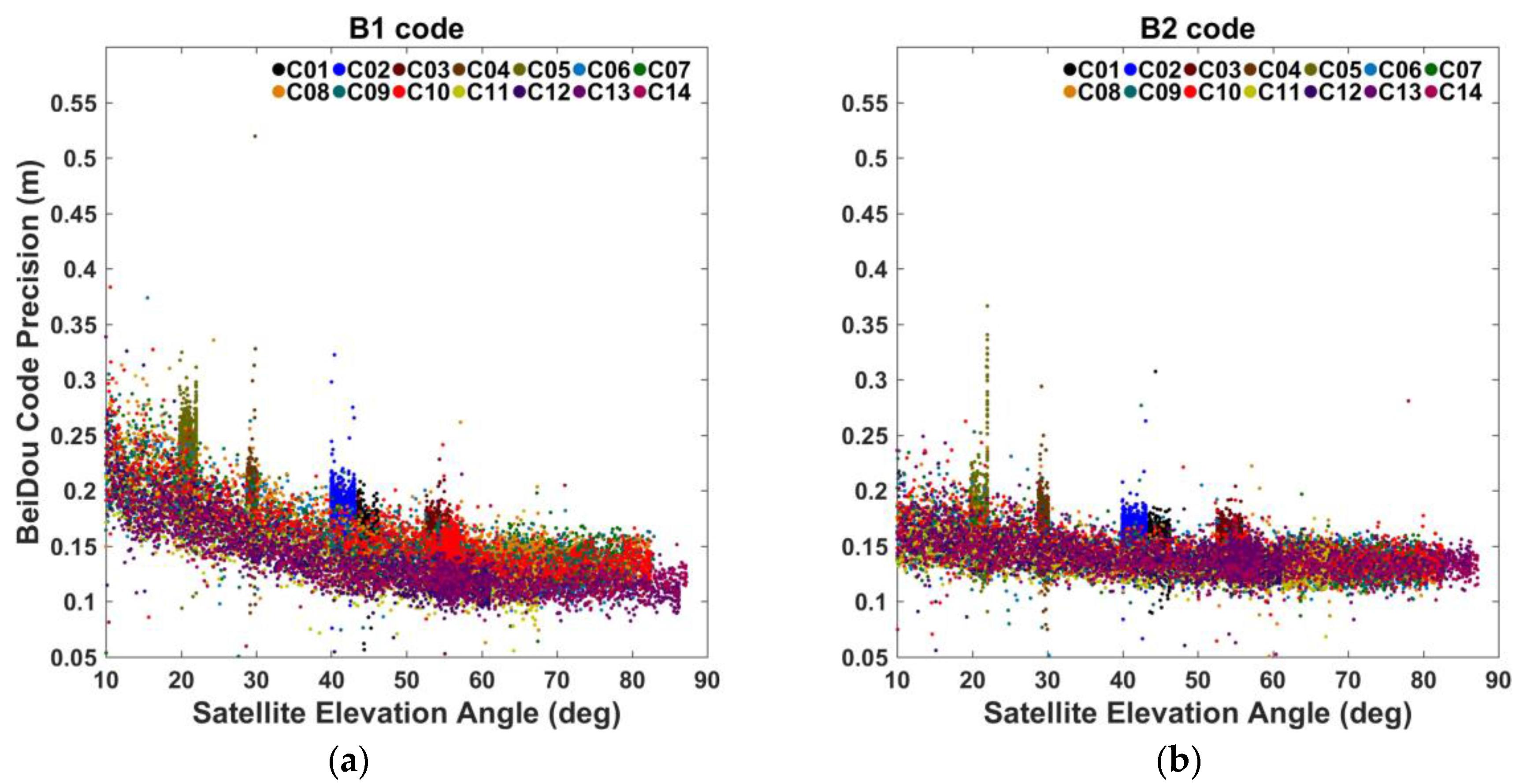
3.3.1. Precisions of GNSS Observations
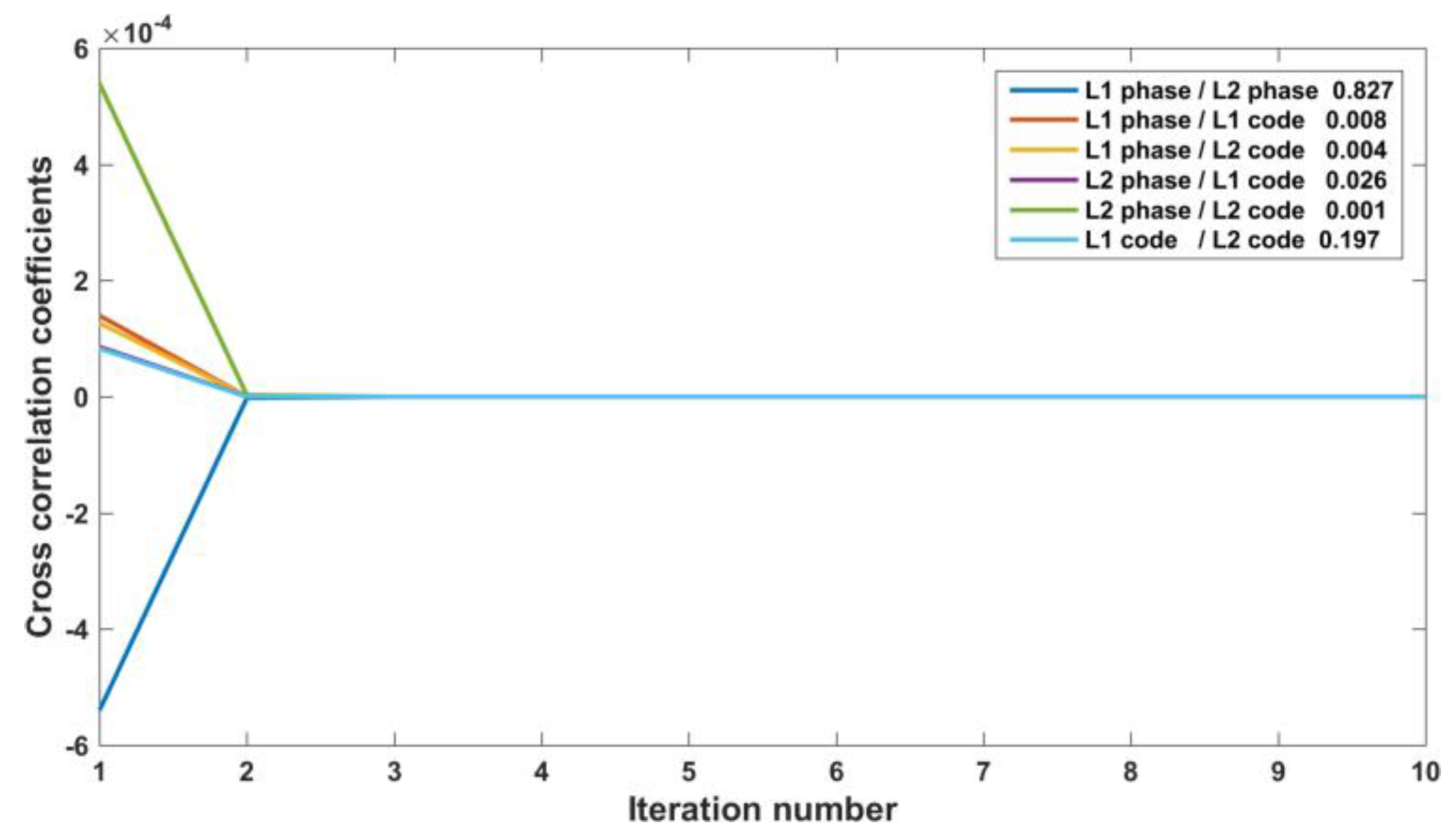
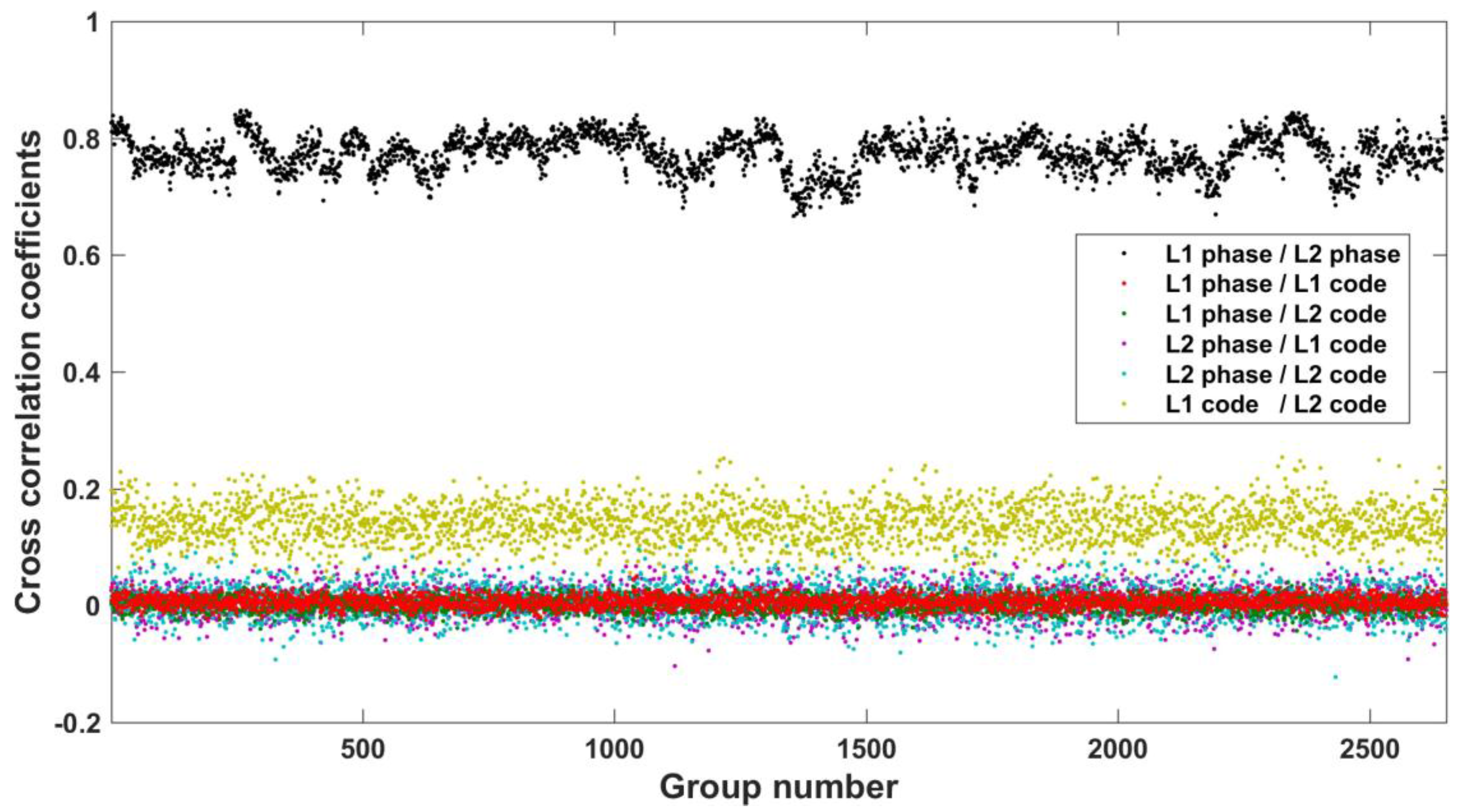
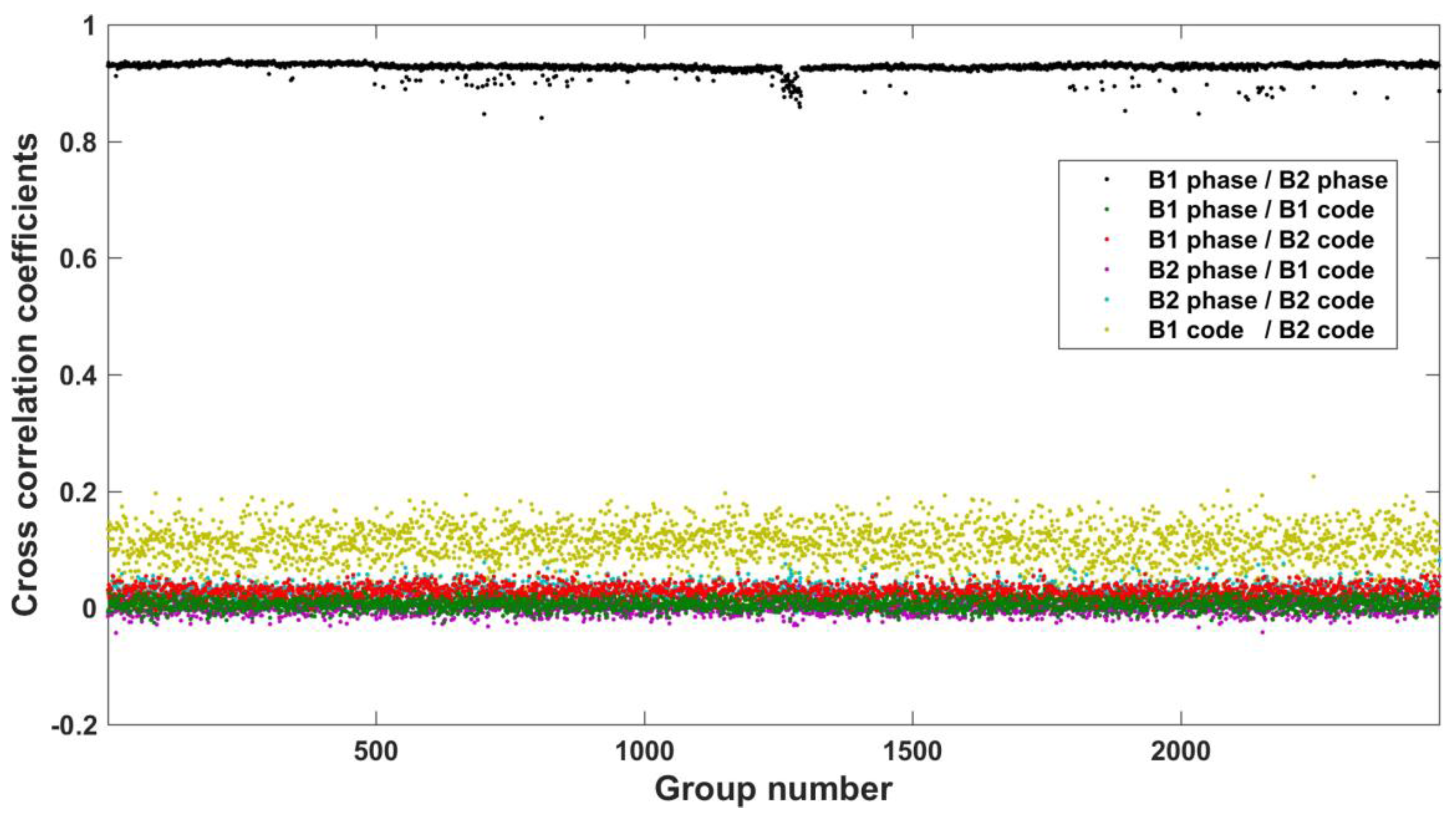
3.3.2. Cross Correlations
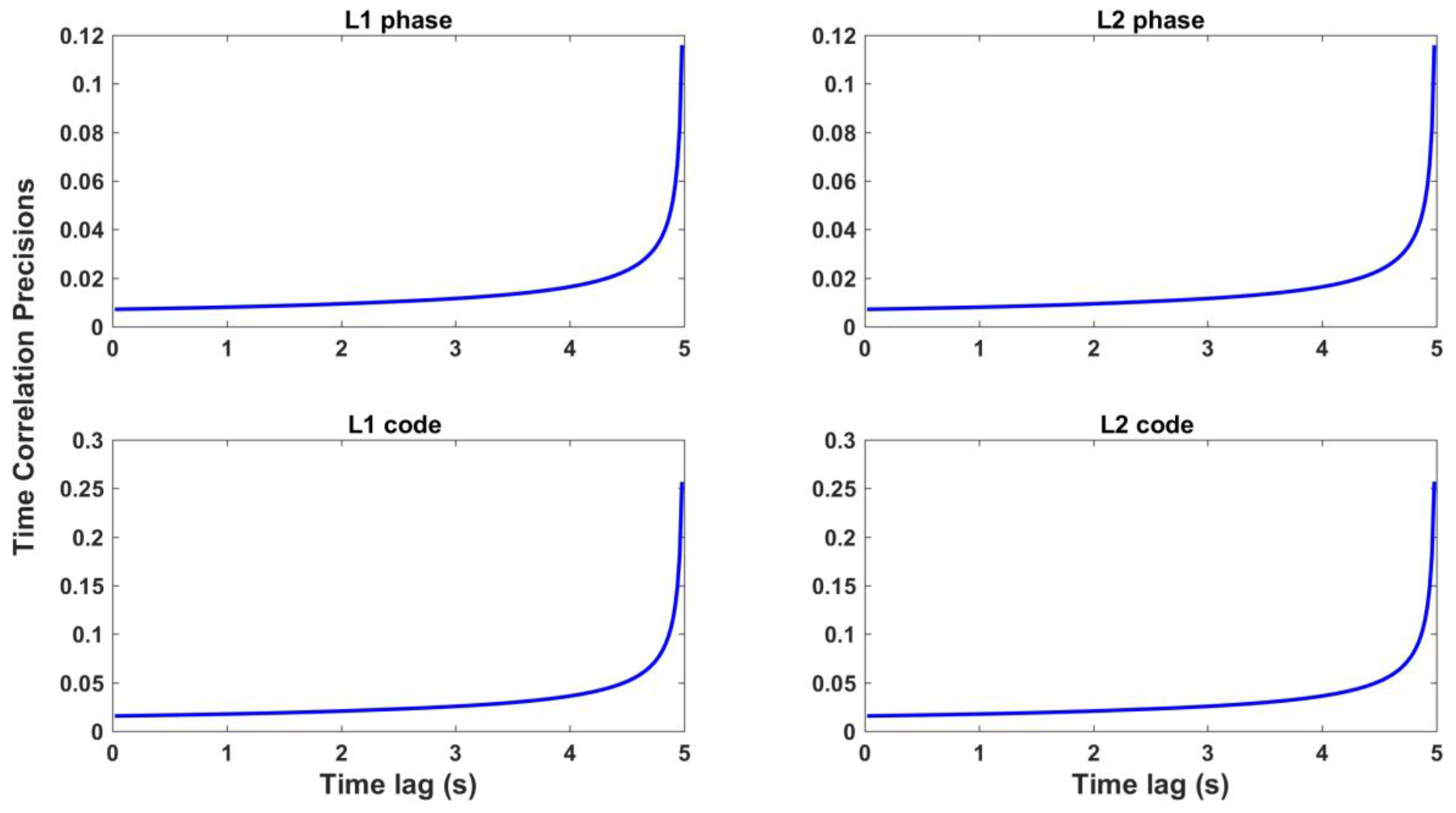
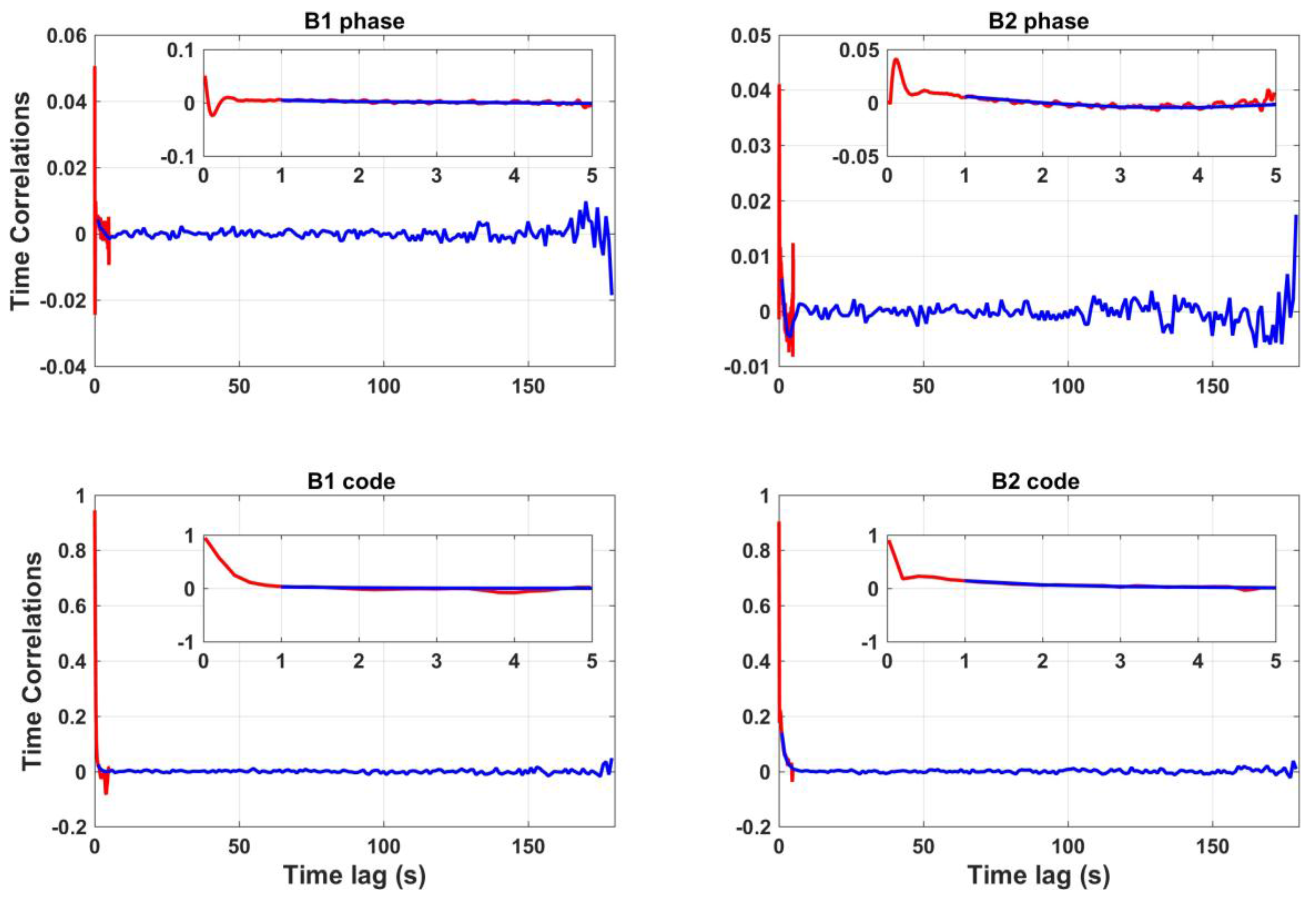
3.3.3. Time Correlations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tiberius, C.C.J.M.; Kenselaar, F. Estimation of the stochastic model for GPS code and phase observables. Surv. Rev. 2000, 35, 441–454. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A. Least-Squares Variance Component Estimation: Theory and GPS Applications; Delft University of Technology: Delft, The Netherlands, 2007. [Google Scholar]
- Eueler, H.-J.; Goad, C.C. On optimal filtering of GPS dual frequency observations without using orbit information. Bull. Geod. 1991, 65, 130–143. [Google Scholar] [CrossRef]
- Gerdan, G.P. A comparison of four methods of weighting double difference pseudorange measurements. Aust. Surv. 1995, 40, 60–66. [Google Scholar] [CrossRef]
- Jin, X.X.; de Jong, C.D. Relationship between satellite elevation and precision of GPS code observations. J. Navig. 1996, 49, 253–265. [Google Scholar]
- Jonkman, N. Integer GPS-Ambiguity Estimation without the Receiver-Satellite Geometry; Delft University of Technology: Delft, The Netherlands, 1998. [Google Scholar]
- Wang, J.; Stewart, M.P.; Tsakiri, M. Stochastic modeling for static GPS baseline data processing. J. Surv. Eng. 1998, 124, 171–181. [Google Scholar] [CrossRef]
- Bona, P. Precision, cross correlation, and time correlation of GPS phase and code observations. GPS Solut. 2000, 4, 3–13. [Google Scholar] [CrossRef]
- Tiberius, C.; Kenselaar, F. Variance component estimation and precise GPS positioning: Case study. J. Surv. Eng. 2003, 129, 11–18. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Xu, P. Assessment of stochastic models for GPS measurements with different types of receivers. Chi. Sci. Bull. 2008, 53, 3219–3225. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Teunissen, P.; Tiberius, C. Application of least-squares variance component estimation to GPS observables. J. Surv. Eng. 2009, 135, 149–160. [Google Scholar] [CrossRef]
- Li, B. Stochastic modeling of triple-frequency BeiDou signals: Estimation, assessment and impact analysis. J. Geod. 2016, 90, 593–610. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Amiri-Simkooei, A.R. Least-squares variance component estimation. J. Geod. 2007, 82, 65–82. [Google Scholar] [CrossRef]
- Avallone, A.; Marzario, M.; Cirella, A.; Piatanesi, A.; Rovelli, A.; Di Alessandro, C.; D′Anastasio, E.; D′Agostino, N.; Giuliani, R.; Mattone, M. Very high rate (10 Hz) GPS seismology for moderate-magnitude earthquakes: The case of the Mw 6.3 L′Aquila (central Italy) event. J. Geophys. Res. 2011, 116, B02305. [Google Scholar] [CrossRef]
- Xu, P.; Shi, C.; Fang, R.; Liu, J.; Niu, X.; Zhang, Q.; Yanagidani, T. High-rate precise point positioning (PPP) to measure seismic wave motions: An experimental comparison of GPS PPP with inertial measurement units. J. Geod. 2013, 87, 361–372. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, W.; Shi, C.; Liu, J. High-rate (1-Hz and 50-Hz) GPS seismology: Application to the 2013 Mw 6.6 Lushan earthquake. J. Asian Earth Sci. 2014, 79, 426–431. [Google Scholar] [CrossRef]
- Shu, Y.; Shi, Y.; Xu, P.; Niu, X.; Liu, J. Error analysis of high-rate GNSS precise point positioning for seismic wave measurement. Adv. Space Res. 2017, 59, 2691–2713. [Google Scholar] [CrossRef]
- Colosimo, G.; Crespi, M.; Mazzoni, A. Real-time GPS seismology with a stand-alone receiver: A preliminary feasibility demonstration. J. Geophys. Res. 2011, 116, B11302. [Google Scholar] [CrossRef]
- Geng, T.; Xie, X.; Fang, R.; Su, X.; Zhao, Q.; Liu, G.; Li, H.; Shi, C.; Liu, J. Real-time capture of seismic waves using high-rate multi-GNSS observations: Application to the 2015 Mw 7.8 Nepal earthquake. Geophys. Res. Lett. 2016, 43, 161–167. [Google Scholar] [CrossRef]
- Meng, X.; Dodson, A.H.; Roberts, G.W. Detecting bridge dynamics with GPS and triaxial accelerometers. Eng. Struct. 2007, 29, 3178–3184. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Gu, M. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge. Mearsurement 2013, 46, 420–432. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic deflections of a stiff footbridge using 100-Hz GNSS and accelerometer data. J. Surv. Eng. 2015, 141, 04015003. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. PLL bandwidth and noise in 100 Hz GPS measurements. GPS Solut. 2014, 19, 173–185. [Google Scholar] [CrossRef]
- Li, M.; Qu, L.Z.; Zhao, Q.L.; Guo, J.; Su, X.; Li, X.T. Precise point positioning with the BeiDou navigation satellite system. Sensors 2014, 14, 927–943. [Google Scholar] [CrossRef] [PubMed]
- Li, X.X.; Zhang, X.H.; Ren, X.D.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation global navigation satellite systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Rao, C.R. Estimation of variance and covariance components—MINQUE theory. J. Multivar. Anal. 1971, 1, 257–275. [Google Scholar] [CrossRef]
- Koch, K. Bayesian inference for variance components. Manuscr. Geod. 1987, 12, 309–313. [Google Scholar]
- Yu, Z. A generalization theory of estimation of variance-covariance components. Manuscr. Geod. 1992, 17, 295. [Google Scholar]
- Yu, Z. A universal formula of maximum likelihood estimation of variance-covariance components. J. Geod. 1996, 70, 233–240. [Google Scholar] [CrossRef]
- Xu, P.; Shen, Y.; Fukuda, Y.; Liu, Y. Variance component estimation in linear inverse ill-posed models. J. Geod. 2006, 80, 69–81. [Google Scholar] [CrossRef]
- Satirapod, C.; Wang, J.; Rizos, C. A simplified MINQUE procedure for the estimation of variance-covariance components of GPS observables. Surv. Rev. 2013, 36, 582–590. [Google Scholar] [CrossRef]
- Xu, P.; Liu, Y.; Shen, Y.; Fukuda, Y. Estimability analysis of variance and covariance components. J. Geod. 2007, 81, 593–602. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Teunissen, P. Towards a Least-Squares Framework for Adjusting and Testing of Both Functional and Stochastic Models; Delft University of Technology: Delft, The Netherlands, 2004. [Google Scholar]
- Förstner, W. Ein verfahren zur schätzung von varianz-und kovarianzkomponenten. Allgemeine Vermessungsnachrichten 1979, 86, 446–453. [Google Scholar]
- Teunissen, P.J.G. A canonical theory for short GPS baselines. Part I: The baseline precision. J. Geod. 1997, 71, 320–336. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. A canonical theory for short GPS baselines. Part II: The ambiguity precision and correlation. J. Geod. 1997, 71, 389–401. [Google Scholar] [CrossRef]
- Teunissen, P. A canonical theory for short GPS baselines. Part III: The geometry of the ambiguity search space. J. Geod. 1997, 71, 486–501. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. A canonical theory for short GPS baselines. Part IV: Precision versus reliability. J. Geod. 1997, 71, 513–525. [Google Scholar] [CrossRef]
- Bradford, P.W.; Spilker, J.; Enge, P. Global Positioning System: Theory and Applications; American Institute of Astronautics: Washington, DC, USA, 1996; pp. 163–164. [Google Scholar]
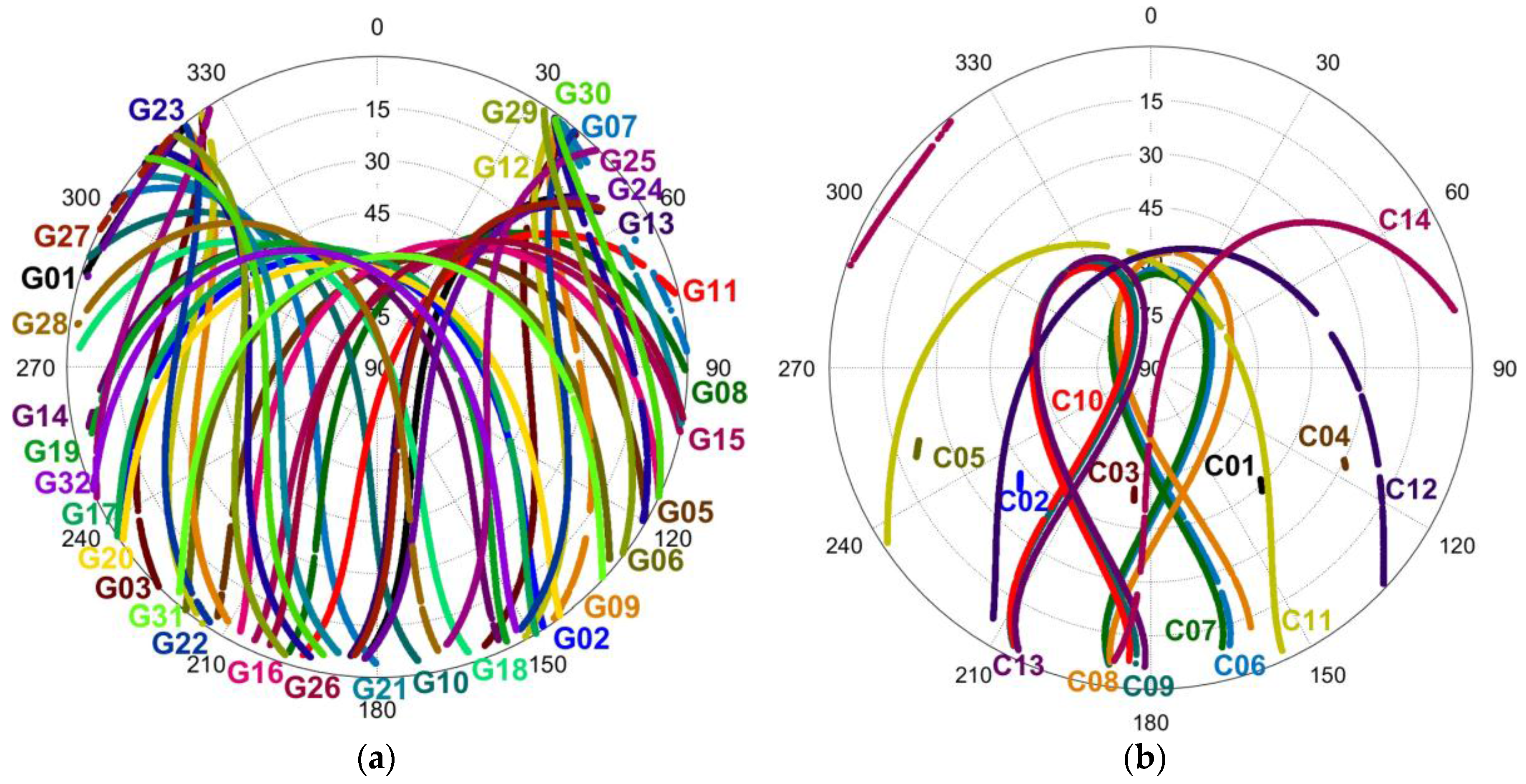


| Constellation | Observation Types | Satellite Types |
| GPS | L1 code (C1) | MEO (G01–32, except G04) |
| L2 code (P2) | ||
| L1 phase | ||
| L2 phase | ||
| BeiDou | B1 code | GEO (C01–05), IGSO (C06–10), MEO (C11–14) |
| B2 code | ||
| B1 phase | ||
| B2 phase |
| GPS | L1 Phase | L2 Phase | L1 Code | L2 Code |
| 0.91 | 1.07 | 131.05 | 172.53 | |
| BeiDou | B1 Phase | B2 Phase | B1 Code | B2 Code |
| 1.16 | 1.26 | 142.23 | 141.22 |
| GPS | L1 Phase/L2 Phase | L1 Phase/L1 Code | L1 Phase/L2 Code | L2 Phase/L1 Code | L2 Phase/L2 Code | L1 Code/L2 Code |
| 0.773 | 0.006 | 0.003 | 0.005 | 0.007 | 0.141 | |
| BeiDou | B1 Phase/B2 Phase | B1 Phase/B1 Code | B1 Phase/B2 Code | B2 Phase/B1 Code | B2 Phase/B2 Code | B1 Code/B2 Code |
| 0.927 | 0.006 | 0.027 | 0.001 | 0.026 | 0.111 |
| Constellation | Obs. Type | Maximum Value (Time Lag) | Value at Time Lag of 1 s | Mean Value over Time Lags 50–150 s |
|---|---|---|---|---|
| GPS | L1 phase | 0.175 (0.02 s) | 0.000 | 0.000 |
| L2 phase | 0.293 (0.12 s) | 0.141 | 0.000 | |
| L1 code | 0.882 (0.02 s) | 0.014 | 0.002 | |
| L2 code | 0.858 (0.02 s) | 0.177 | 0.001 | |
| BeiDou | B1 phase | 0.051 (0.02 s) | 0.005 | 0.000 |
| B2 phase | 0.041 (0.12 s) | 0.005 | 0.000 | |
| B1 code | 0.945 (0.02 s) | 0.032 | 0.000 | |
| B2 code | 0.904 (0.02 s) | 0.139 | 0.000 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, Y.; Fang, R.; Liu, J. Stochastic Models of Very High-Rate (50 Hz) GPS/BeiDou Code and Phase Observations. Remote Sens. 2017, 9, 1188. https://doi.org/10.3390/rs9111188
Shu Y, Fang R, Liu J. Stochastic Models of Very High-Rate (50 Hz) GPS/BeiDou Code and Phase Observations. Remote Sensing. 2017; 9(11):1188. https://doi.org/10.3390/rs9111188
Chicago/Turabian StyleShu, Yuanming, Rongxin Fang, and Jingnan Liu. 2017. "Stochastic Models of Very High-Rate (50 Hz) GPS/BeiDou Code and Phase Observations" Remote Sensing 9, no. 11: 1188. https://doi.org/10.3390/rs9111188
APA StyleShu, Y., Fang, R., & Liu, J. (2017). Stochastic Models of Very High-Rate (50 Hz) GPS/BeiDou Code and Phase Observations. Remote Sensing, 9(11), 1188. https://doi.org/10.3390/rs9111188