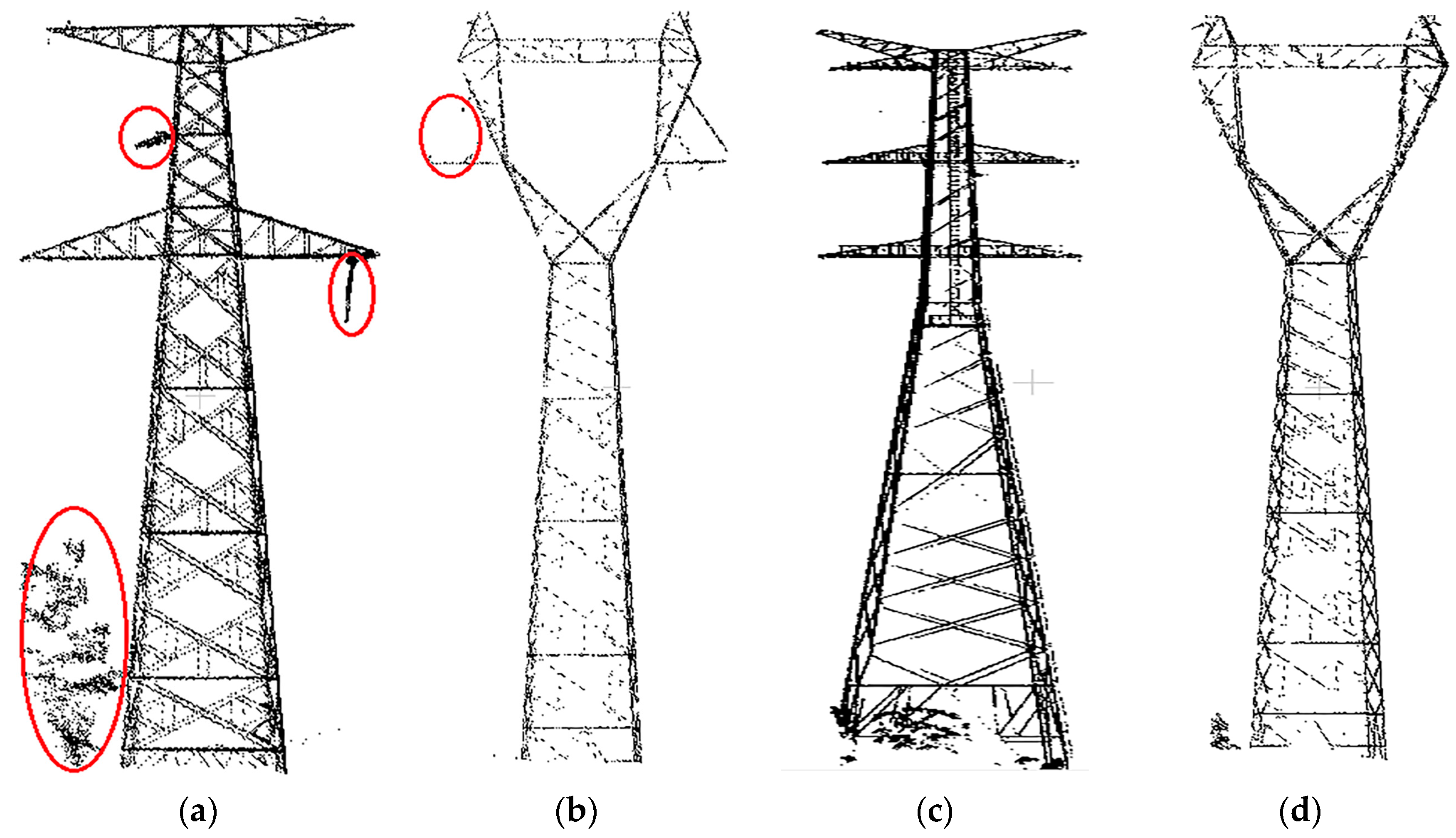
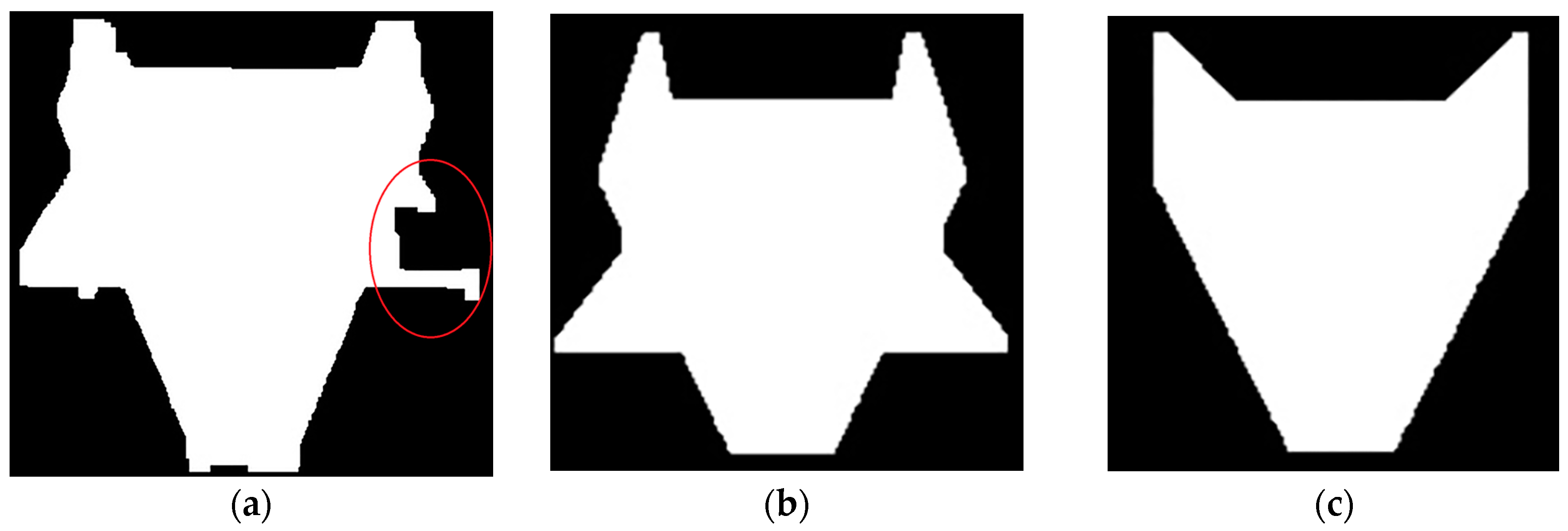
High voltage transmission systems, as the fundamental infrastructure for power transmission in long distance, assume enormous importance in the national economy’s development and daily production. To ensure the safe and stable operation of power systems, it is indispensable to periodically monitor the high-voltage transmission systems. As a key object of high voltage transmission systems, considering the safety of transmission and the uniformity of force, the power pylon is well-designed with specific structures, and its reconstruction is attracting growing attention in the 3D digitalization of transmission corridors. The reconstructed 3D pylon model is not only helpful for disaster management and urban planning, but is also critical to environmental protection, and urban development policy planning [
2]. For example, the accurate positions and parameters of pylons can be obtained through reconstruction, which is meaningful for disaster recovery and radiation testing [
3].
However, limited by rugged field environments and data acquisition technologies, it is hard to obtain high accuracy data of power pylons and reconstruct them automatically. Over the past few decades, the most widely used method for pylon reconstruction has been manual modeling with AutoCAD or 3dmax from draft designs, which cannot well match with the as-built pylons in the field and do not record the structure modifications [
4]. Given the rapid development of LiDAR technology however, the acquisition of high accuracy high density point cloud of power transmission corridor has become easier and cheaper. Advanced LiDAR technology provides an efficient solution for real pylon model reconstruction, but adds complexity to data processing. A highly efficient and precise reconstruction method is desperately needed for administrative departments responsible for power grid systems.
1.1. Related Work
Because of power pylons’ structural complexity and type diversity, few research projects have been devoted to power pylons’ automatic reconstruction from LiDAR point cloud. Han [
5] proposed a data-driven method to model power pylons, where 3D grids were firstly built with a line tracing algorithm on the binary image. However, in this instance, the reconstructed models consisted of only tangled lines without correct topological relations. Chen et al. [
6] proposed a semiautomatic model-driven method to rebuild pylons; this method was further improved by Li and Chen et al. [
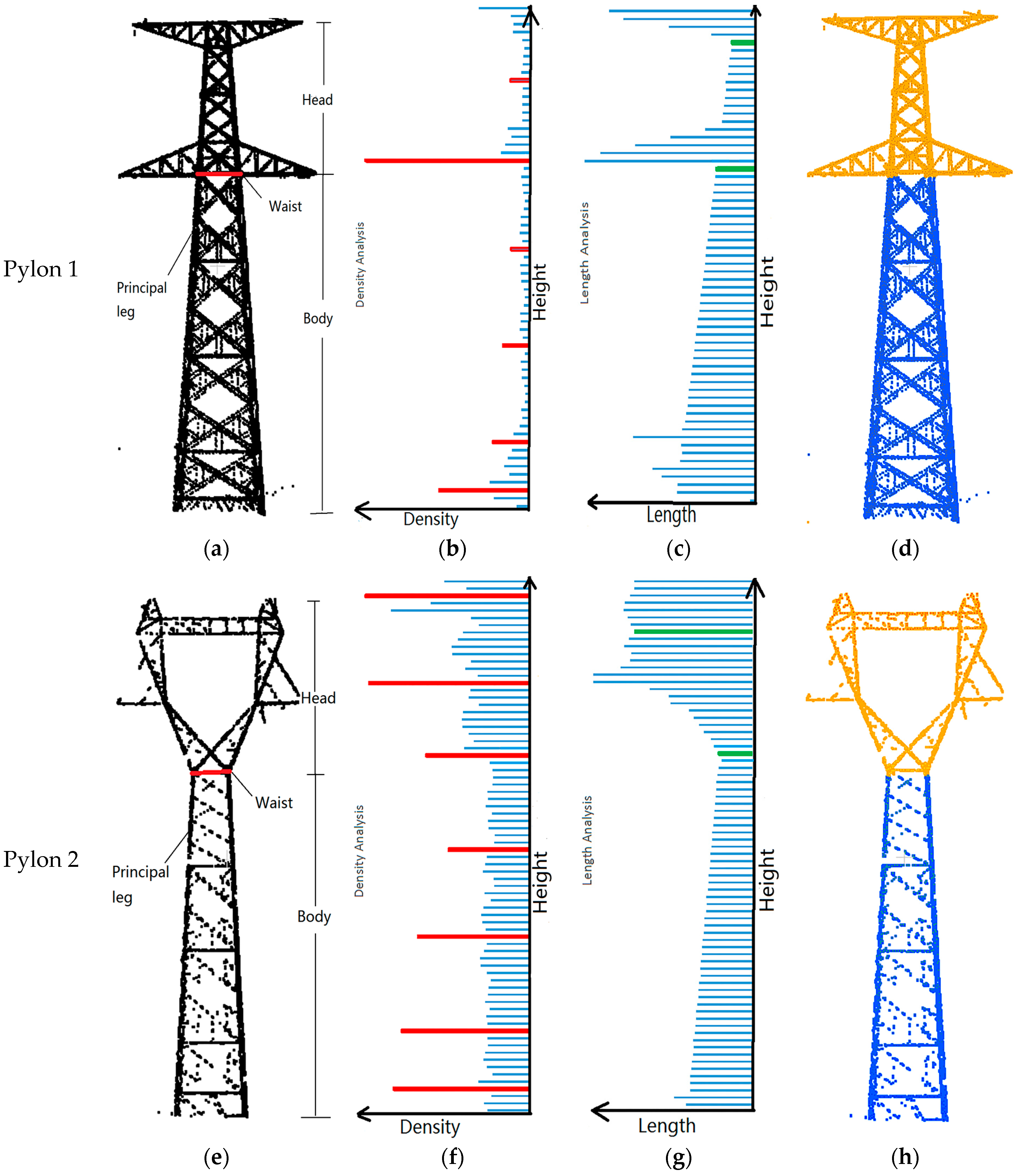
1]. In their work, the point cloud of a pylon was firstly decomposed into three parts according to their density features: legs, body, and head. Then, the pylon body was reconstructed with four principal planes while the pylon head was identified by a SVM (Support Vector Machine) algorithm from a pylon head model library. However, this approach is not fully automatic. The SVM classifier is applied just to classify the head type, and the final head models are manually processed [
2]. In addition, a decomposition method only using the density feature is not feasible for some complex pylons. Kwoczyńska and Dobek [
7] introduced a semiautomatic pylon modeling function on the MicroStation V8i software using special overlays – TerraScan and TerraModeler of Finnish Terrasolid Company, in which extremely simplified pylon templates were used, thus the reconstructed models cannot accurately describe the structure of the original power pylon. To fully automate the pylon reconstruction workflow, Guo et al. [
2] introduced a stochastic geometric method to reconstruct power pylons, in which the type of the pylon and all the parameters of the pylon body and pylon head were solved together by a Reversible Jump Markov Chain Monte Carlo (RJMCMC) sampler with a simulated annealing algorithm. However, this RJMCMC-based method is time-consuming [
8], since a large proportion of iteration times are wasted in recognizing the pylon type. In addition, geometric relations between the pylon parameters are not considered, leading to estimation of redundant parameters.
To seek a better solution for automatic power pylon reconstruction, attentions are firstly turned to technologies for other man-made object reconstruction, and then potentially useful ideas are adopted to improve the processing flow and methods for pylon reconstruction. Although there are many varieties of object reconstruction methods, the most reported methods can be divided into three general categories [
9]: data-driven, model-driven and hybrid-driven.
Data-driven: Generally, data-driven reconstruction methods adopt a bottom-up strategy. They firstly extract basic features, such as planes, lines, or points, and then through a combination of features and their topological relations, a complete model is reconstructed. In buildings, reconstruction usually contains two key processes: building roof edge segmentation and topological reconstruction [
1]. Since plane features of buildings are more stable than point or line features, for complex roof structures with high-density point cloud data, methods based on plane segmentation is first adopted, such as ridge or edge-based and voxel-based region growing [
10,
11], cross-line element growth (CLEG) [
12], RANSAC [
13,
14], classification or feature clustering [
15,
16,
17,
18]; then, point or line features are obtained by intersection of plane features. Reconstruction results of data-driven methods are not limited by the integrity of the model library, and they theoretically allow the generation of a model in any shape [
19]. Data-driven methods provide accurate descriptions of simple objects when the data are complete. For example, Laefer and Truong-Hong [
20] introduced a method to automatically identify structural steel members and generate their geometry from a terrestrial LiDAR data for building information modeling (BIM) usage. Experiments shows that the 3D model can be derived by assembling the 3D sub-models of all individual members. However, deviations or reconstruction failures will occur when raw data are sparse, noisy or partially occluded [
21]. To overcome this problem, more and more multi-platform and multi-view data are fused to improve data integrity. For example, Kedzierski and Fryskowska [
22,
23] integrated data from different laser scanning technologies, such as terrestrial and airborne, to reconstruct buildings more precisely.
Model-driven: Contrary to data-driven methods, model-driven methods use a top-down strategy, which is based on a predefined model library. There are two key steps for model-driven methods: (1) the optimal model matching between existing models in the predefined library and the original data; and (2) the appropriate parameter estimation of the optimal selected model. For most model-driven building reconstruction methods, there is a common assumption that a building is a collection of roof primitives, such as gable roofs and hipped roofs [
24]. Several Monte Carlo Simulation approaches, such as RJMCMC [
25,
26], have been adopted to solve model parameters and great potential has been shown in object reconstruction. Model-driven methods are known to be robust with respect to data quality and suitable for large scenes [
2]. Because topological relations of models are predefined in the model library, it is advantageous for low-density point cloud data, and it can guarantee topological correctness of reconstructed models [
1]. For example, Cheng et al. [
27] proposed a full framework to reconstruct multilayer interchange bridge. An interchange bridge was firstly divided into structure units; then its obscured structures was detected and restored; finally, by modeling each structure unit, the interchange bridge was reconstructed. However, the reconstruction results are limited by the integrity of the predefined model library [
9], and it is can be quite time-consuming, especially when large amounts of parameters need to be estimated.
Hybrid-driven: Because of the complexity in structure and diversity in shape, it is hard to meet the reconstruction requirements of complex objects by merely using either data-driven or model-driven methods. Therefore, hybrid approaches combining both data-driven and model-driven strategies have been put forward in recent years. Construction constraints (e.g., coplanarity, symmetry and parallelism) are brought into the process of object reconstruction to optimize models. For example, Xiong et al. [
28] introduced flexible building primitives for 3D building modeling. In this method, the point cloud of buildings was firstly segmented into roof patches, and then through combining the predefined building primitives, buildings could be well reconstructed. Kwak and Habib [
29] developed a framework for fully-automated building model generation where the building’s approximate boundary was firstly generated by a data-driven method and then integrated by a model-based processing strategy. Zheng et al. [
9] proposed a hybrid approach for generating Level of Detail 2 (LoD2) building models. Buildings could be completely and correctly reconstructed through this method by assembling basic models. Cabaleiro et al. [
4] proposed a method for the detection and automatic 3D modeling of metal frame connections from LiDAR data. In their method, the information of connections was firstly extracted, and then through a parametric model of connections, the geometric model of the frame could be completed. Compared with the single reconstruction strategy, hybrid approaches combine both advantages: on the one hand, it is more flexible than model-driven methods; on the other hand, it is more robust than data-driven methods.
1.2. Contribution
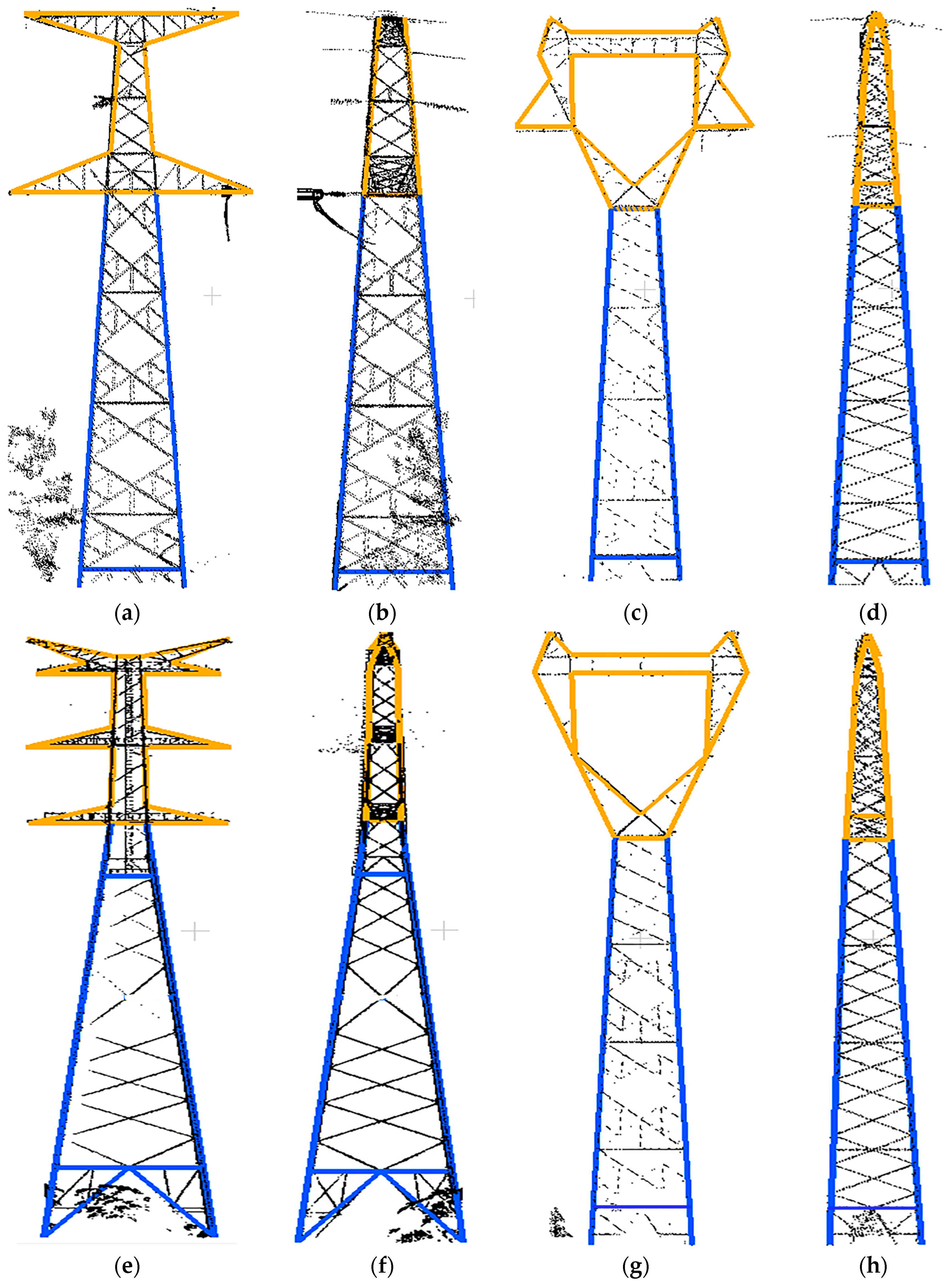
As power pylons are one kind of man-made objects with certain construction constraints, the above three object reconstruction strategies can also apply to power pylons, as data-driven and model-driven strategies have been adopted to reconstruct the whole pylon or its components, for example, Han’s method [
5] belongs to data-driven while Guo’s approach [
2] belongs to model-driven. However, differed from other man-made objects, the power pylon in high voltage systems is well-designed with specific structures, which is much more complex in structure and diverse in type, leading the existing object reconstruction approaches could not be directly applicable for the pylon problem. Thus, this paper focus on power pylons widely used in the high voltage transmission systems in China, and proposes a heuristic method for power pylon reconstruction, combining both data-driven and model-driven strategies.
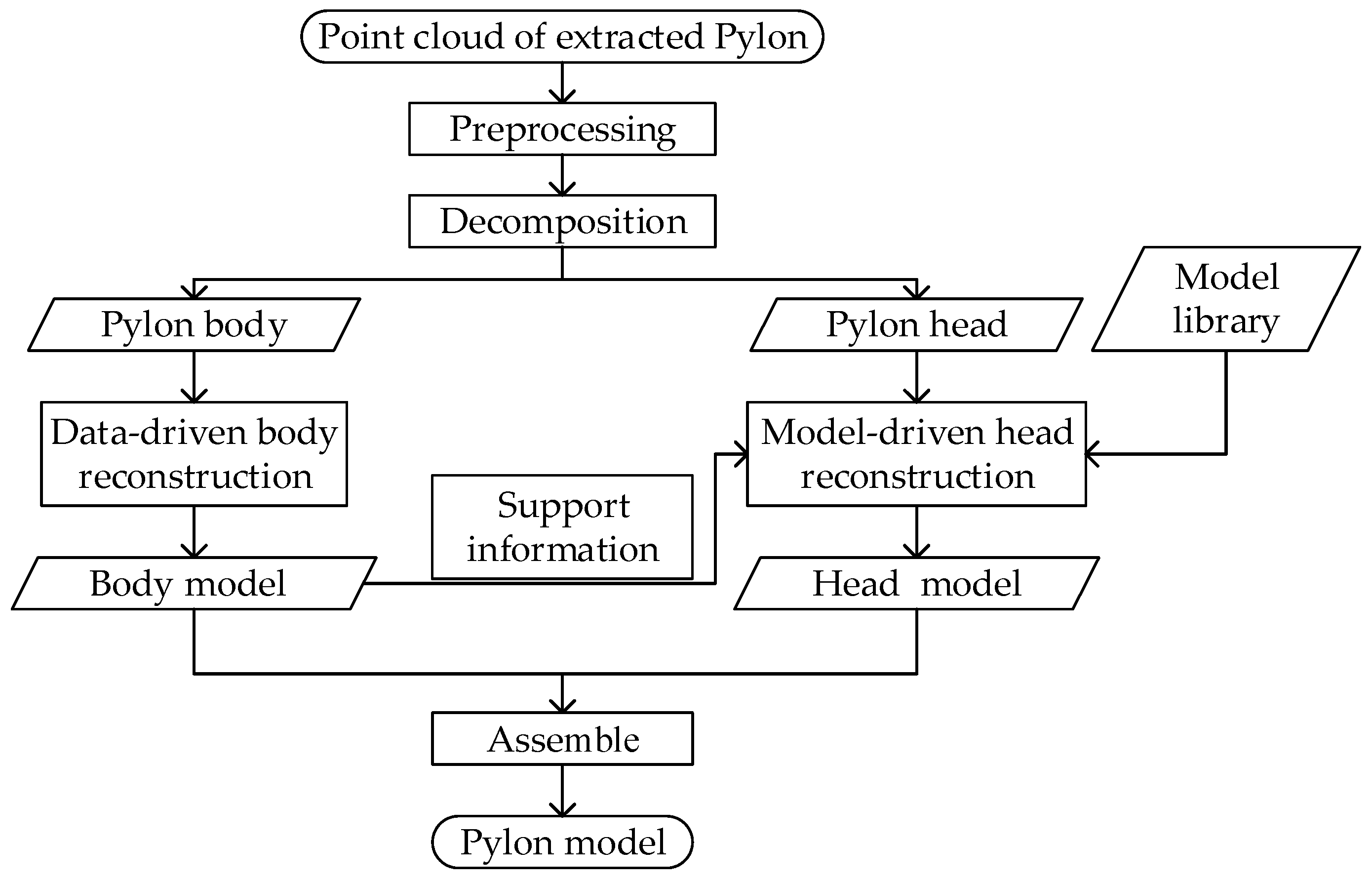
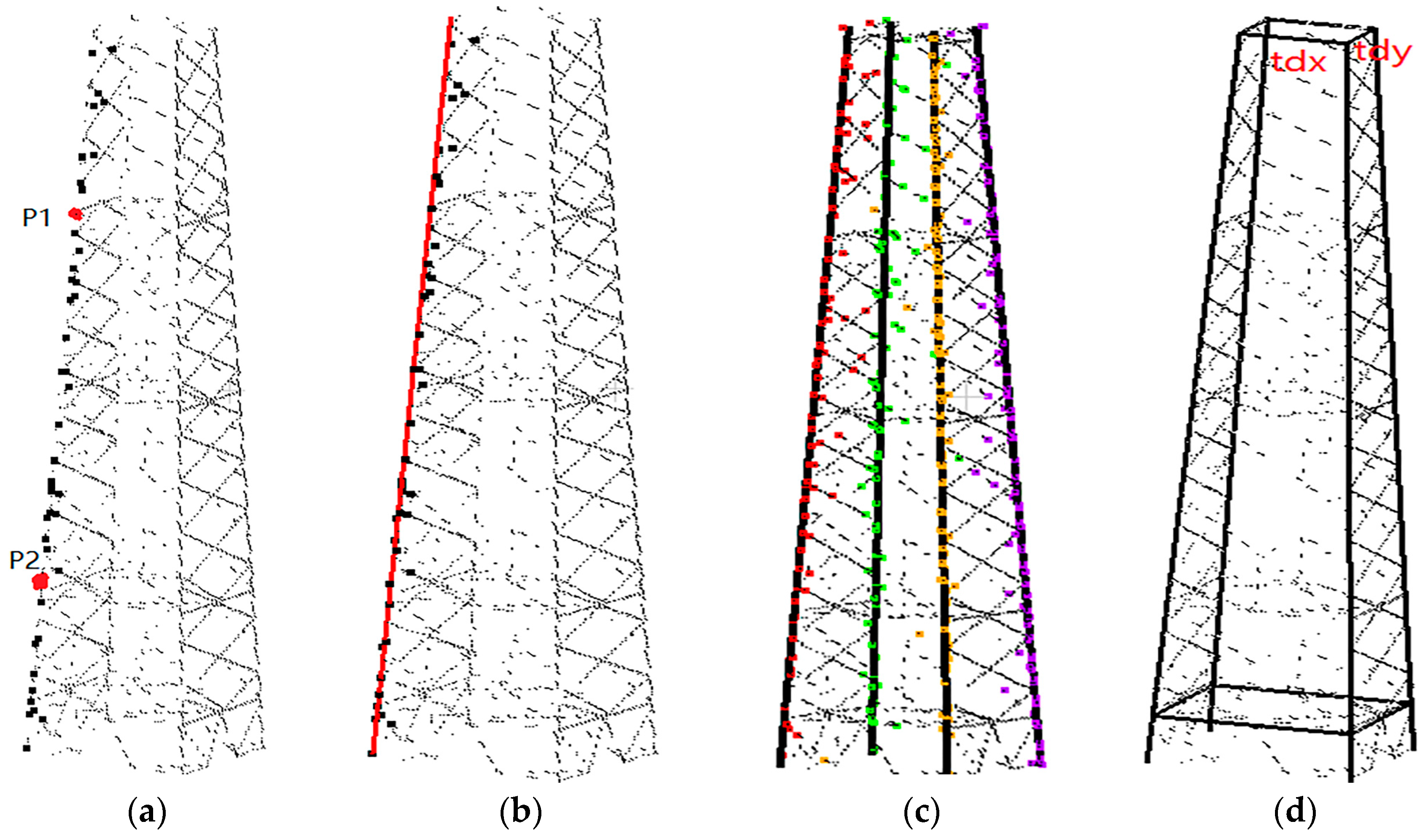
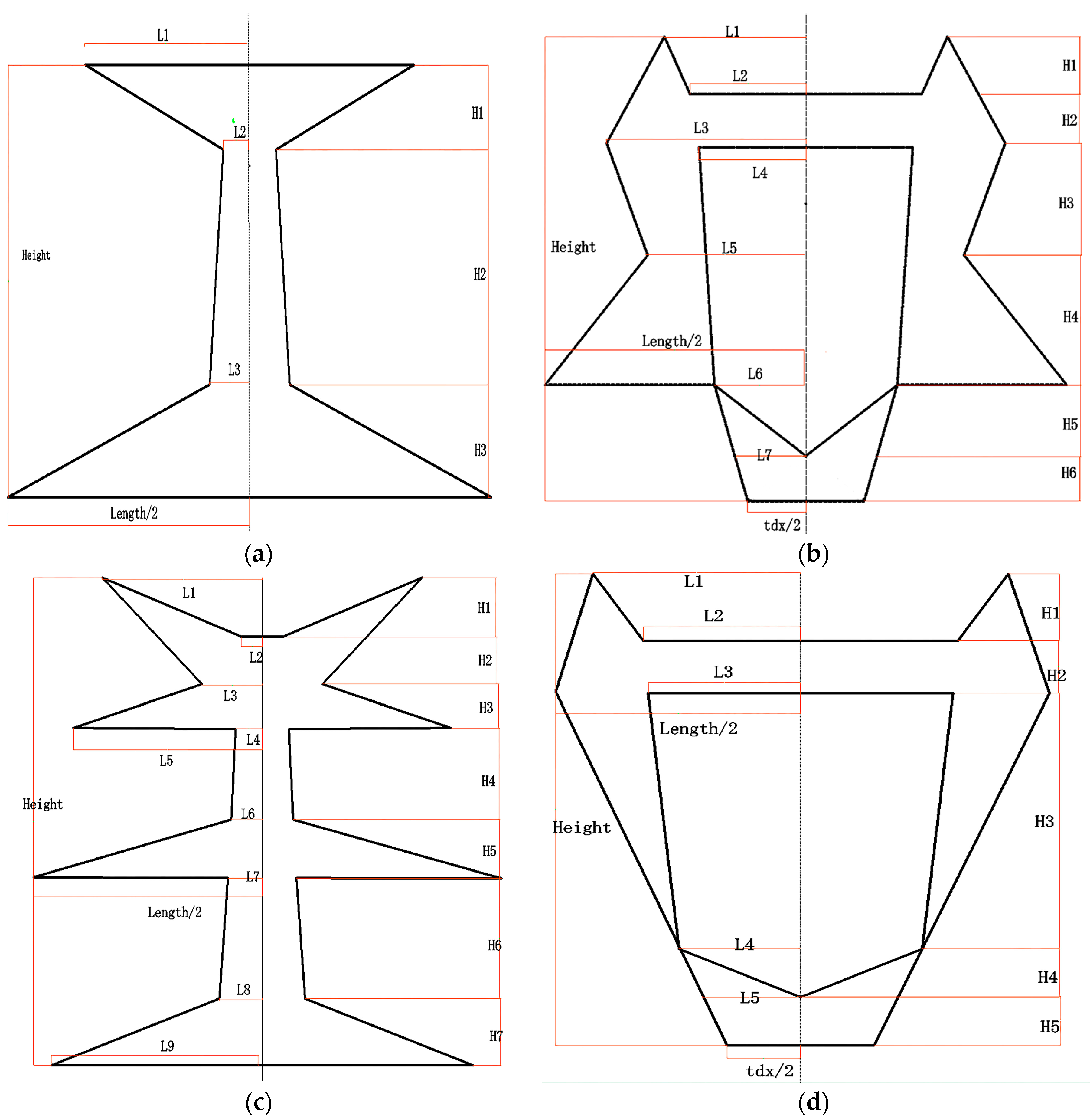
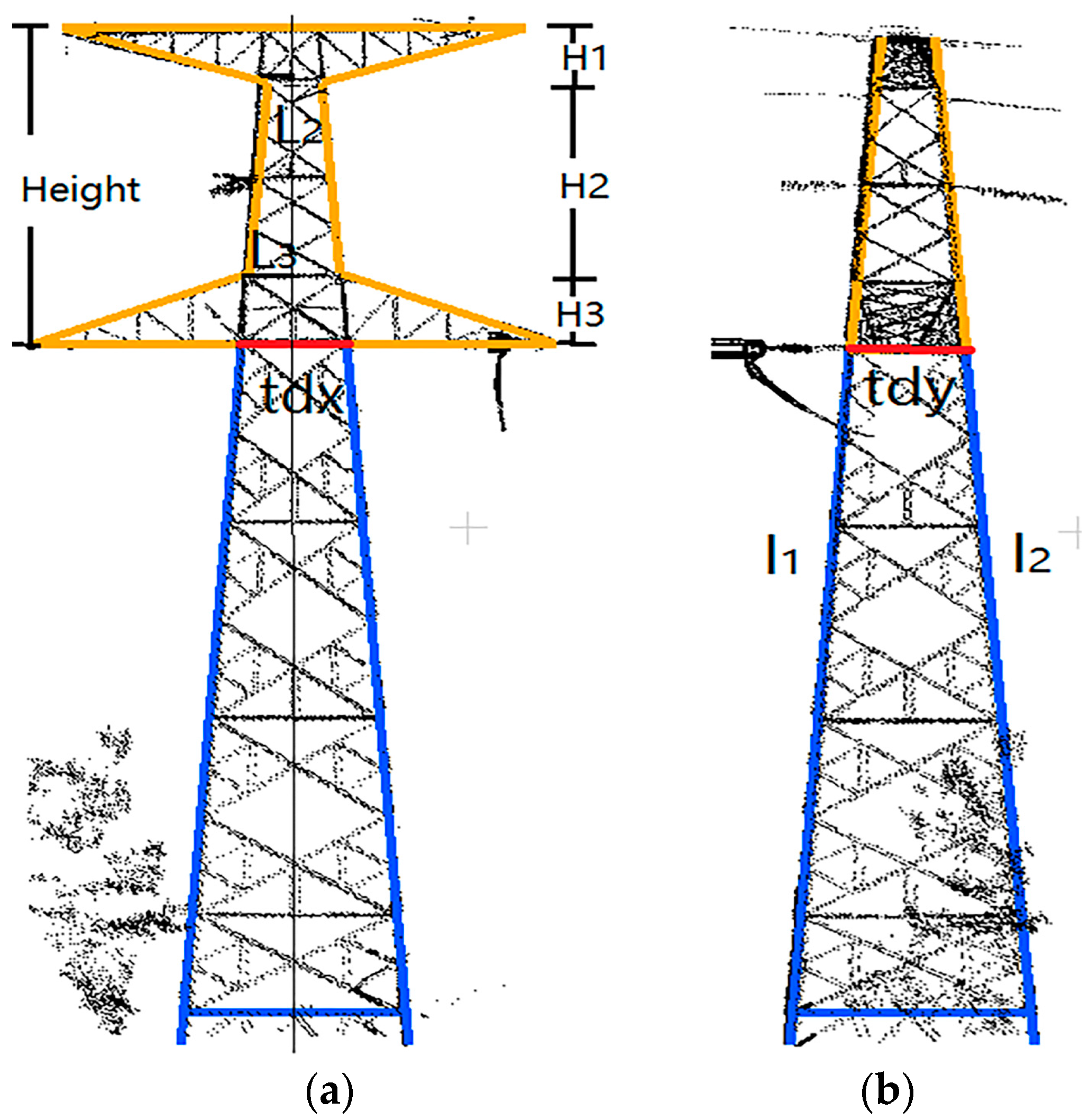
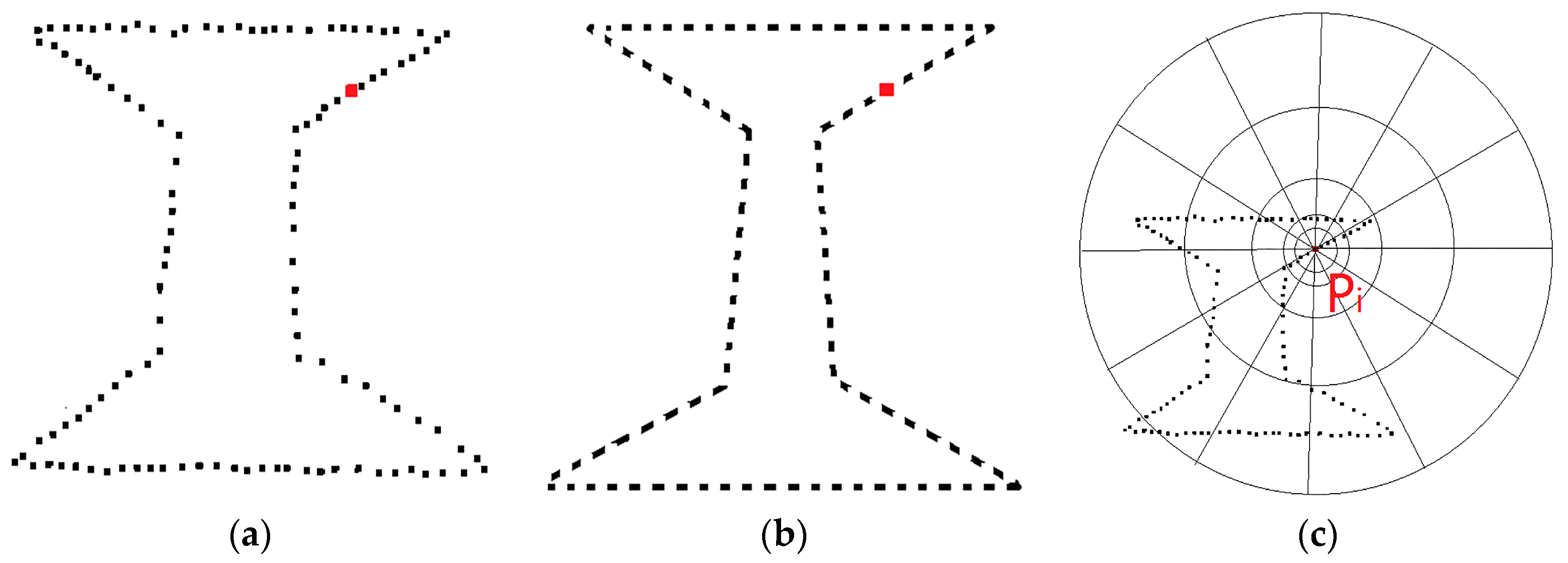
The processing flowchart of the proposed method is shown in
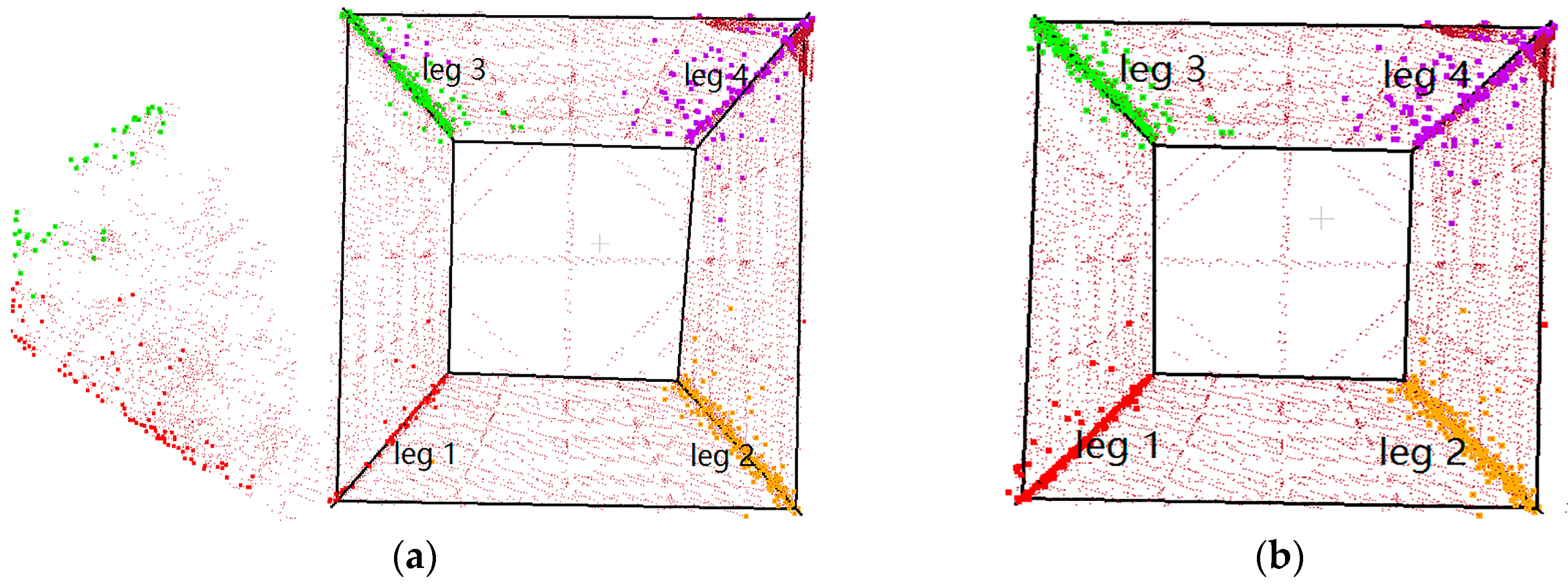
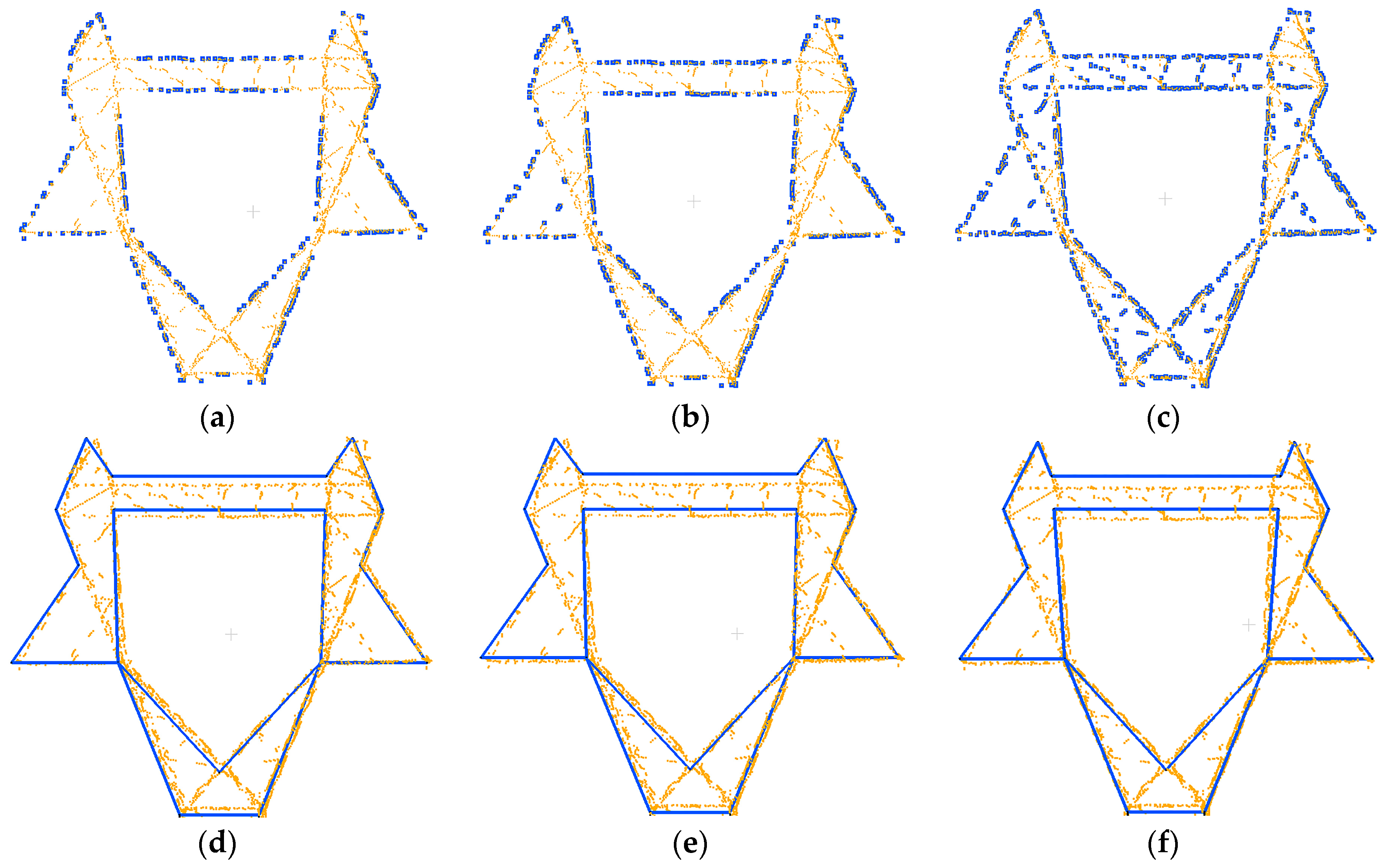
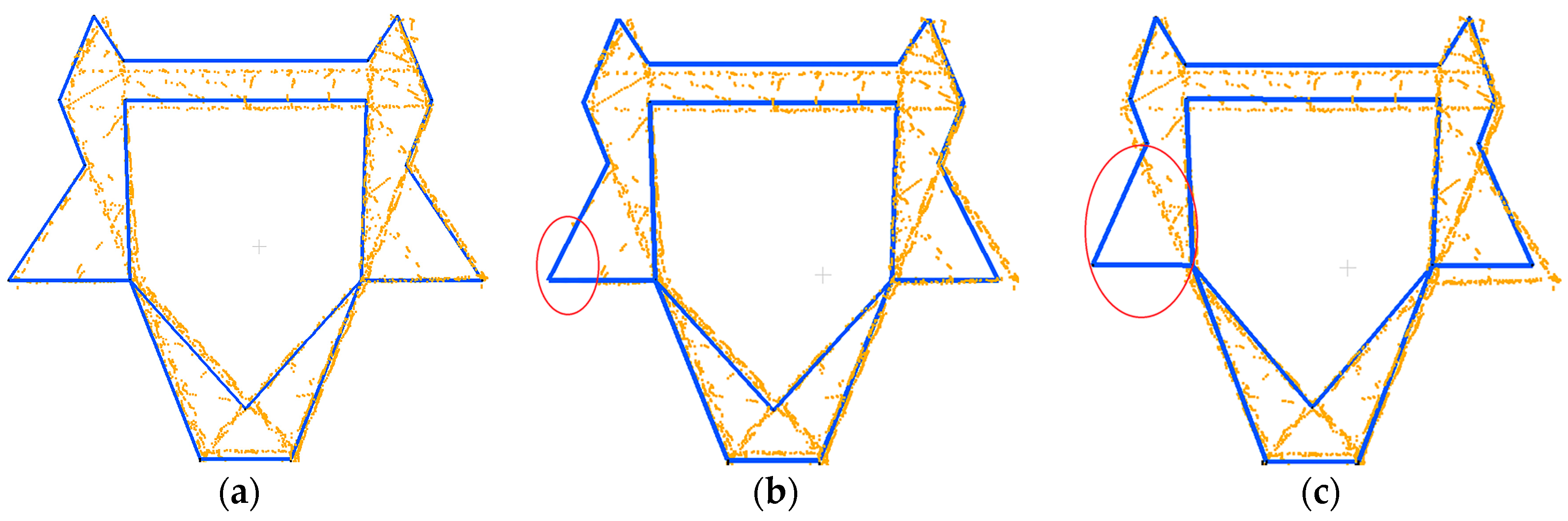
Figure 1. Structurally, a pylon is firstly decomposed into two parts: the pylon body and head. Then, optimal strategies are adopted to reconstruct different pylon parts: for the pylon body with a single type and simple structure whose shape is determined by four principal legs, a data-driven method is applied, where a RANSAC-based algorithm is adopted to fit each principal leg with a 3D line; for the pylon head with various types and complex structures, as they are constructed with regular construction constraints, a model-driven method is applied with a predefined model library, where the pylon head type is recognized by a shape context algorithm, and their parameters are estimated by a Metropolis–Hastings (MH) sampler coupled with a Simulated Annealing (SA) algorithm. Body reconstruction results, information about the original point cloud, and geometric relations between parameters are used in the process of head reconstruction to reduce the number and search space of parameters.