Exploring Subpixel Learning Algorithms for Estimating Global Land Cover Fractions from Satellite Data Using High Performance Computing
Abstract
:1. Introduction
- Perform a comparative analysis of the least squares, sparse regression, signal–subspace and geometrical methods for the subpixel classification of different datasets.
- Develop a method to utilize the abundance maps obtained from subpixel learning algorithms to retrieve fractional land cover (LC) classes representing forest, farmland (including agricultural and herbaceous lands), water, and urban areas.
2. Review of Subpixel Learning Algorithms
2.1. Unconstrained Least Squares (UCLS)
2.2. Fully Constrained Least Squares (FCLS)
2.3. Modified Fully Constrained Least Squares (MFCLS)
2.4. Simplex Projection (SP)
2.5. Sparse Unmixing via Variable Splitting and Augmented Lagrangian (SUnSAL)
2.6. SUnSAL and Total Variation (SUnSAL TV)
2.7. Collaborative SUnSAL (CL SUnSAL)
3. Data
3.1. Computer Simulated Data
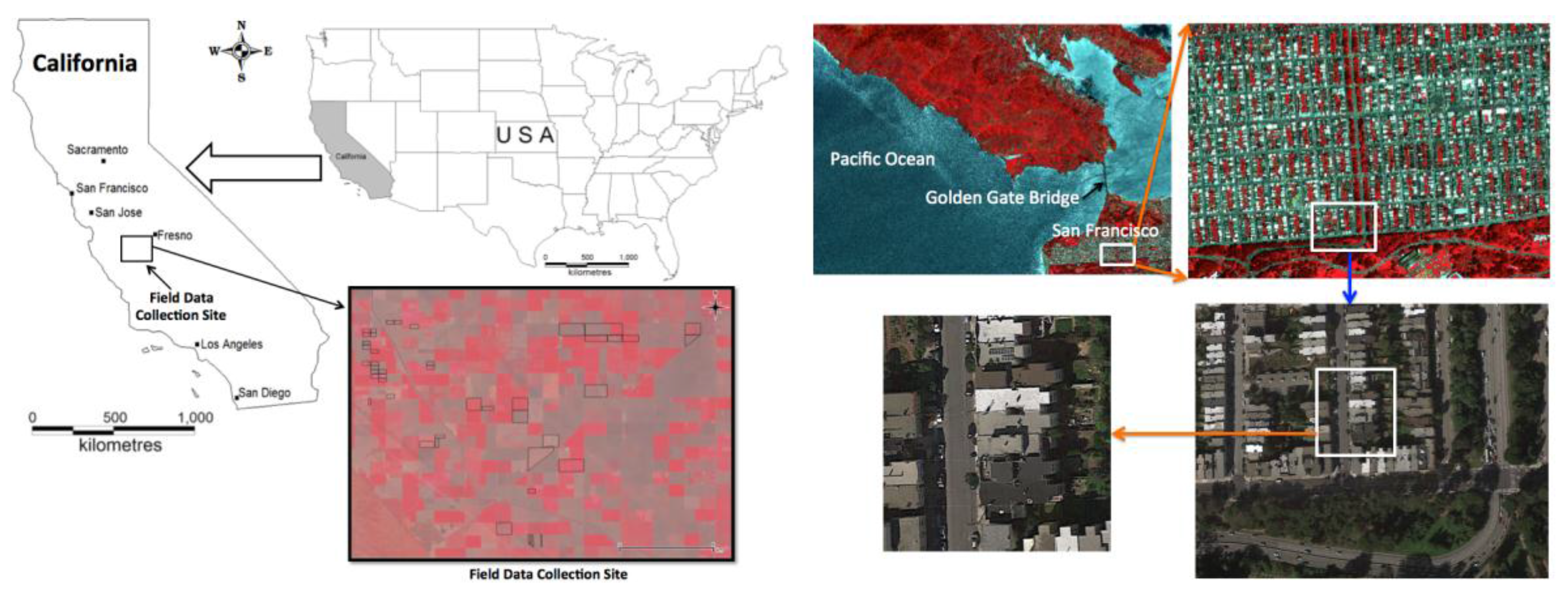
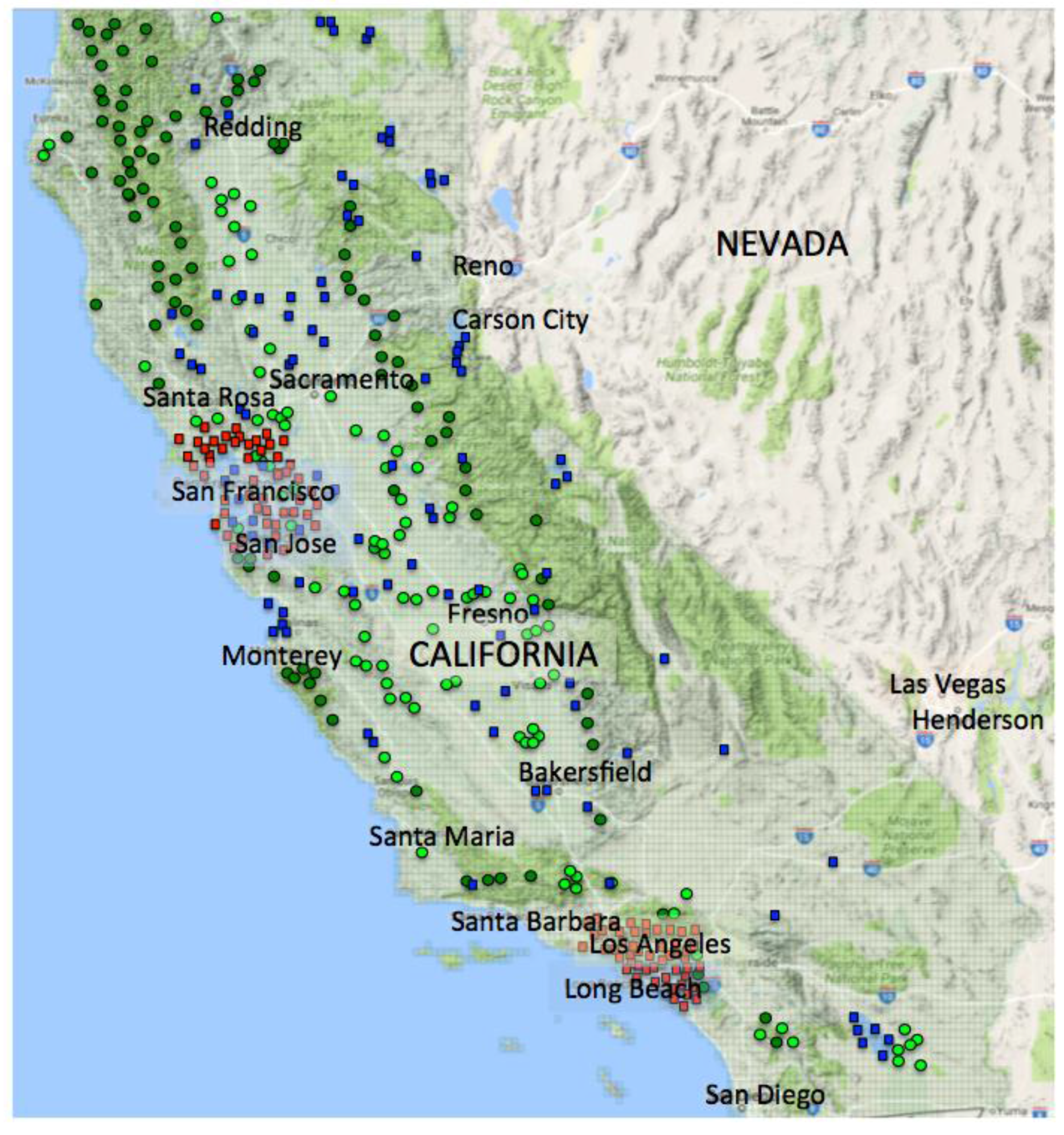
3.2. Landsat Data—An Agricultural Landscape and an Urban Scenario
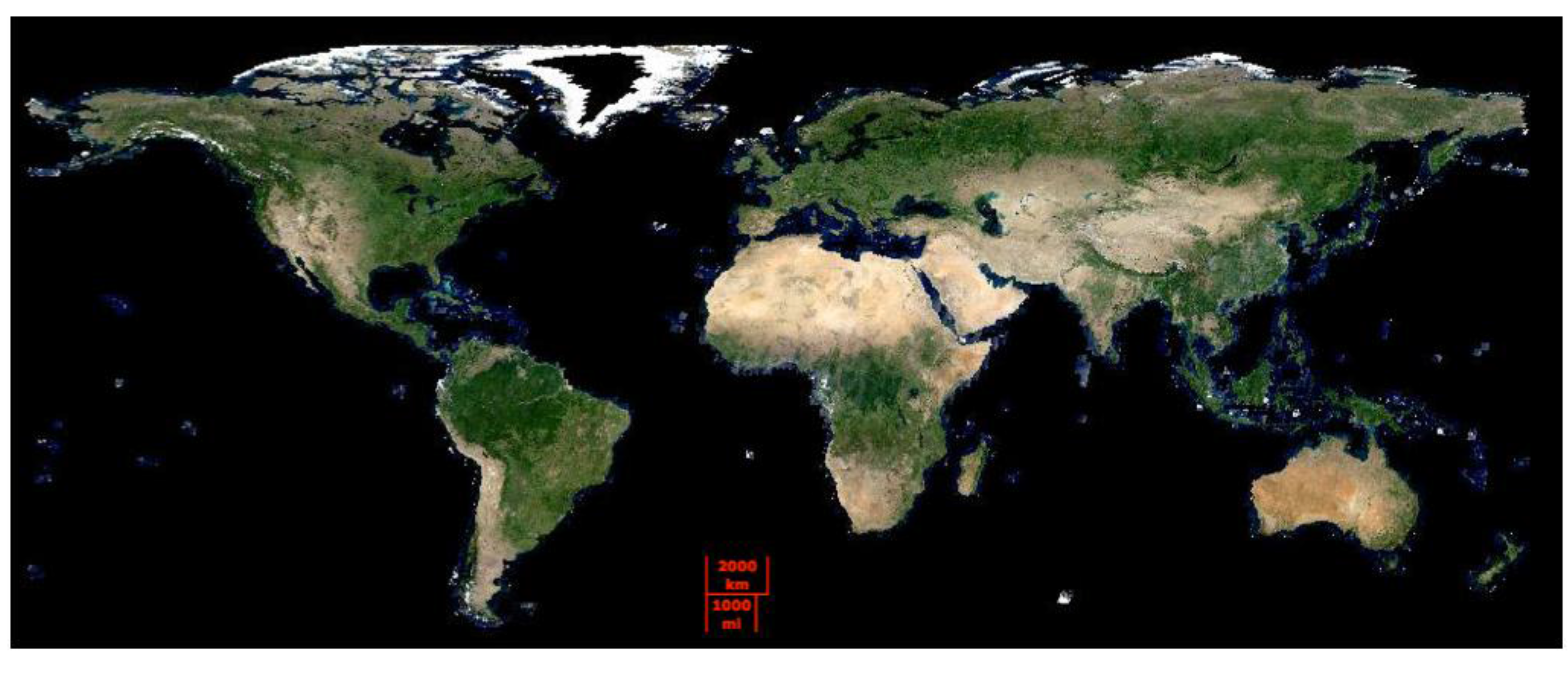
3.3. Global Web-Enabled Landsat Data (WELD)
3.4. Endmember Generation
4. Classification Methods and Validation Approaches
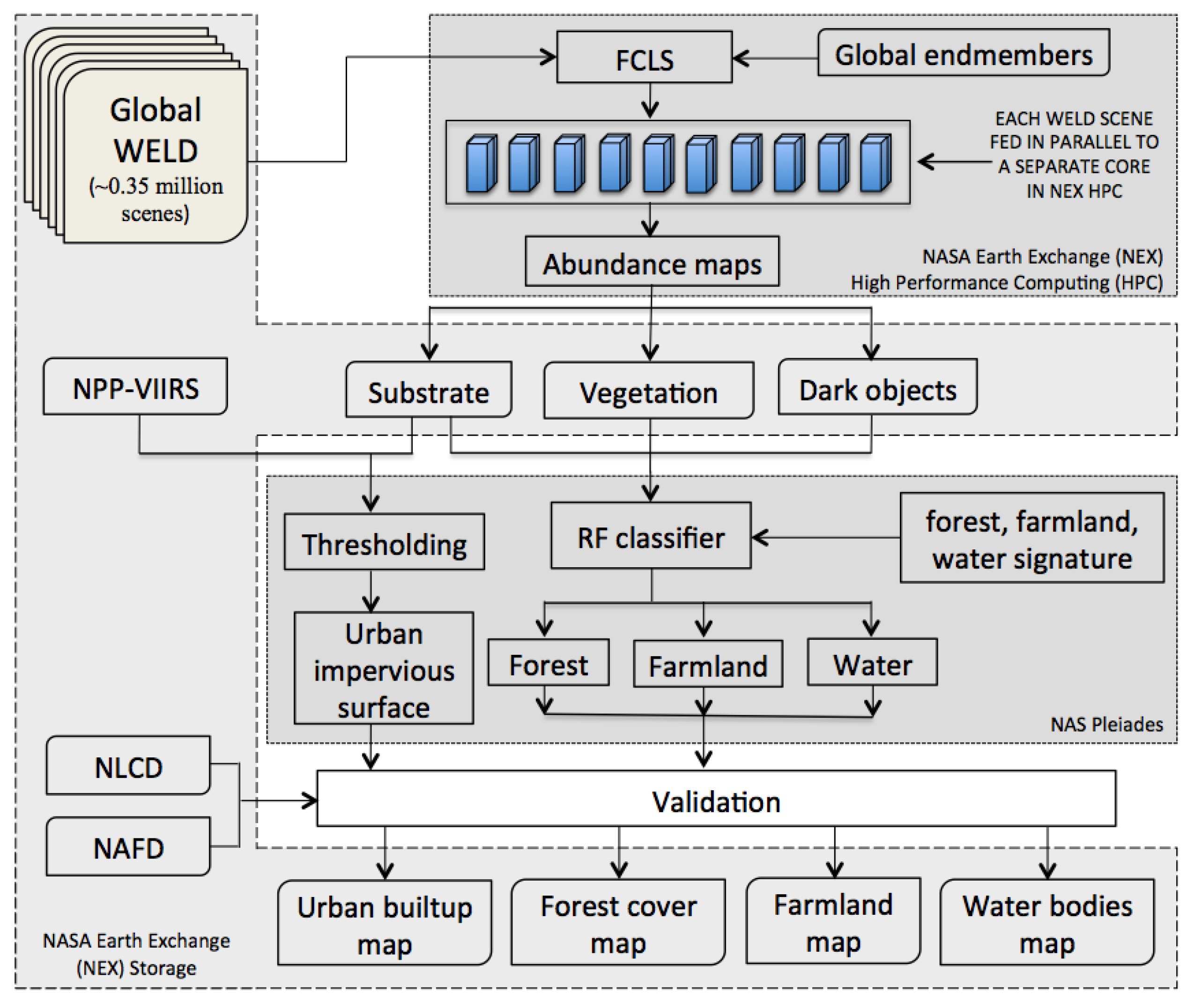
4.1. Land Cover Classification from Abundance Maps
4.2. Validation Methods
4.3. Parameter Settings and Computational Requirements
5. Experimental Results and Discussion
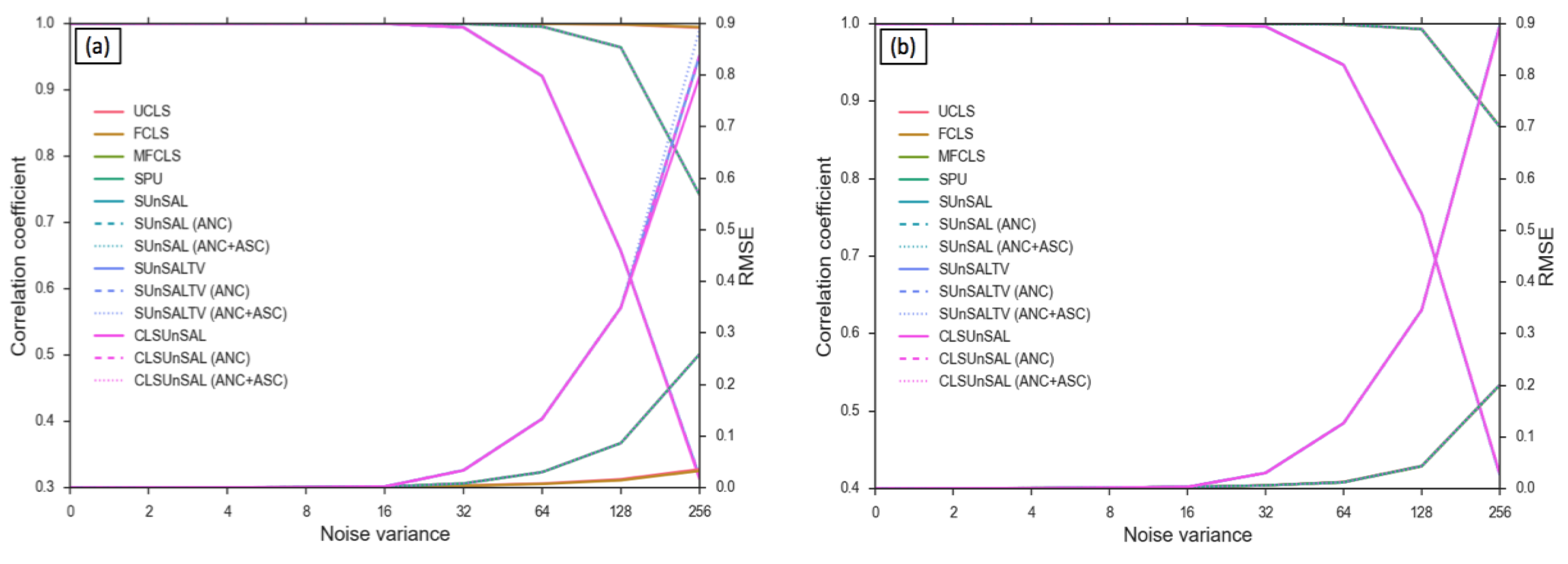
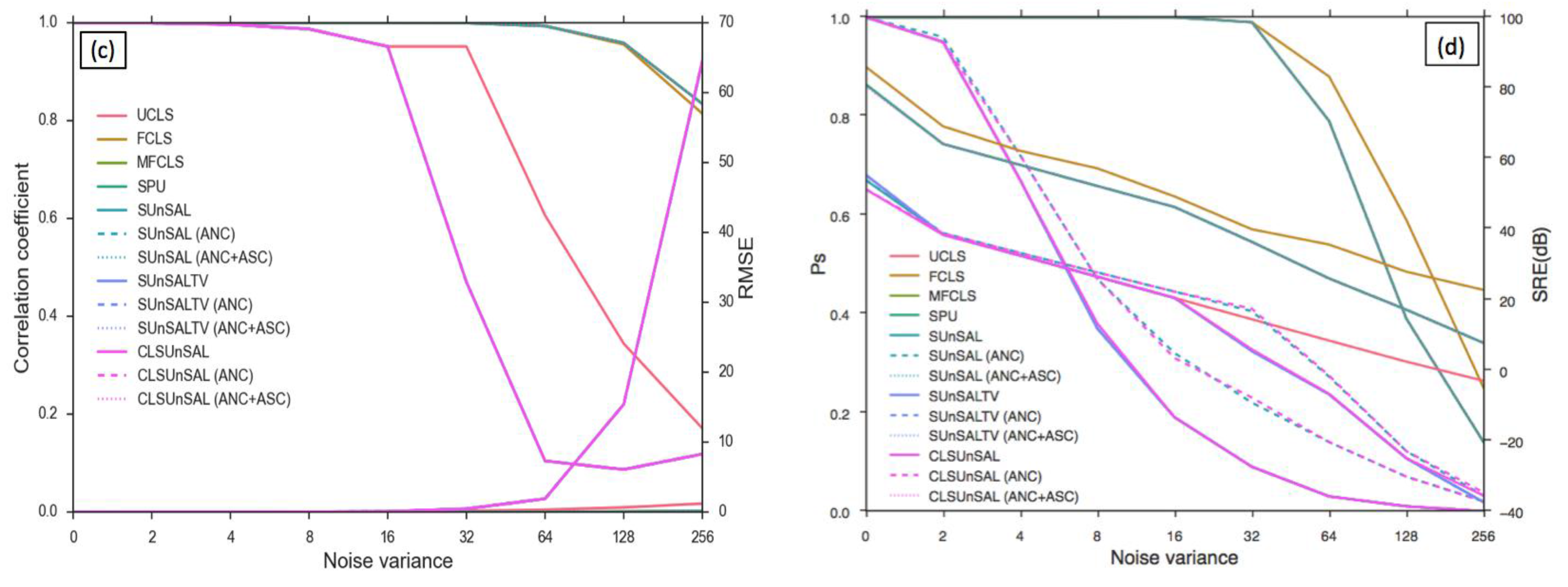
5.1. Computer Simulations
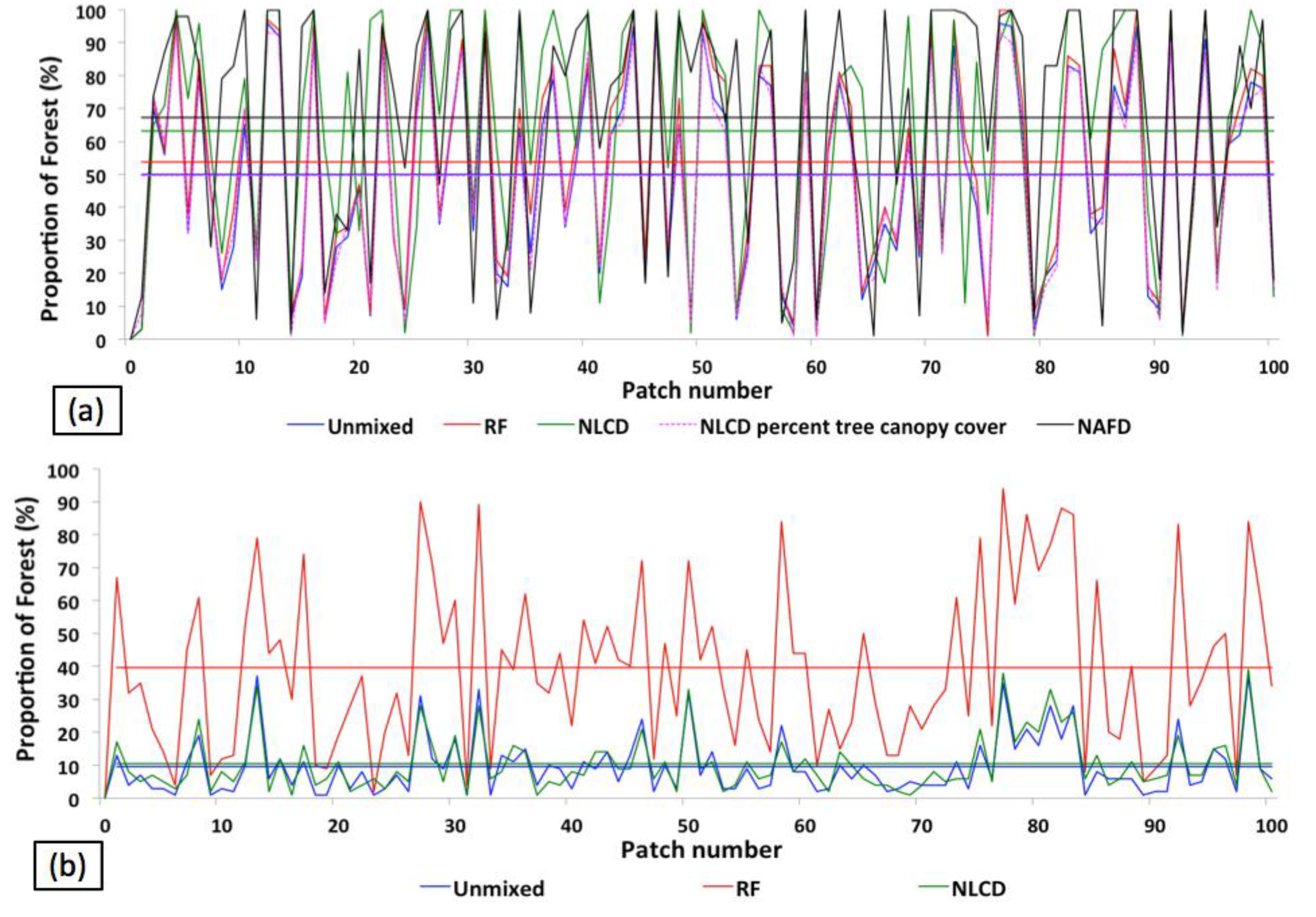
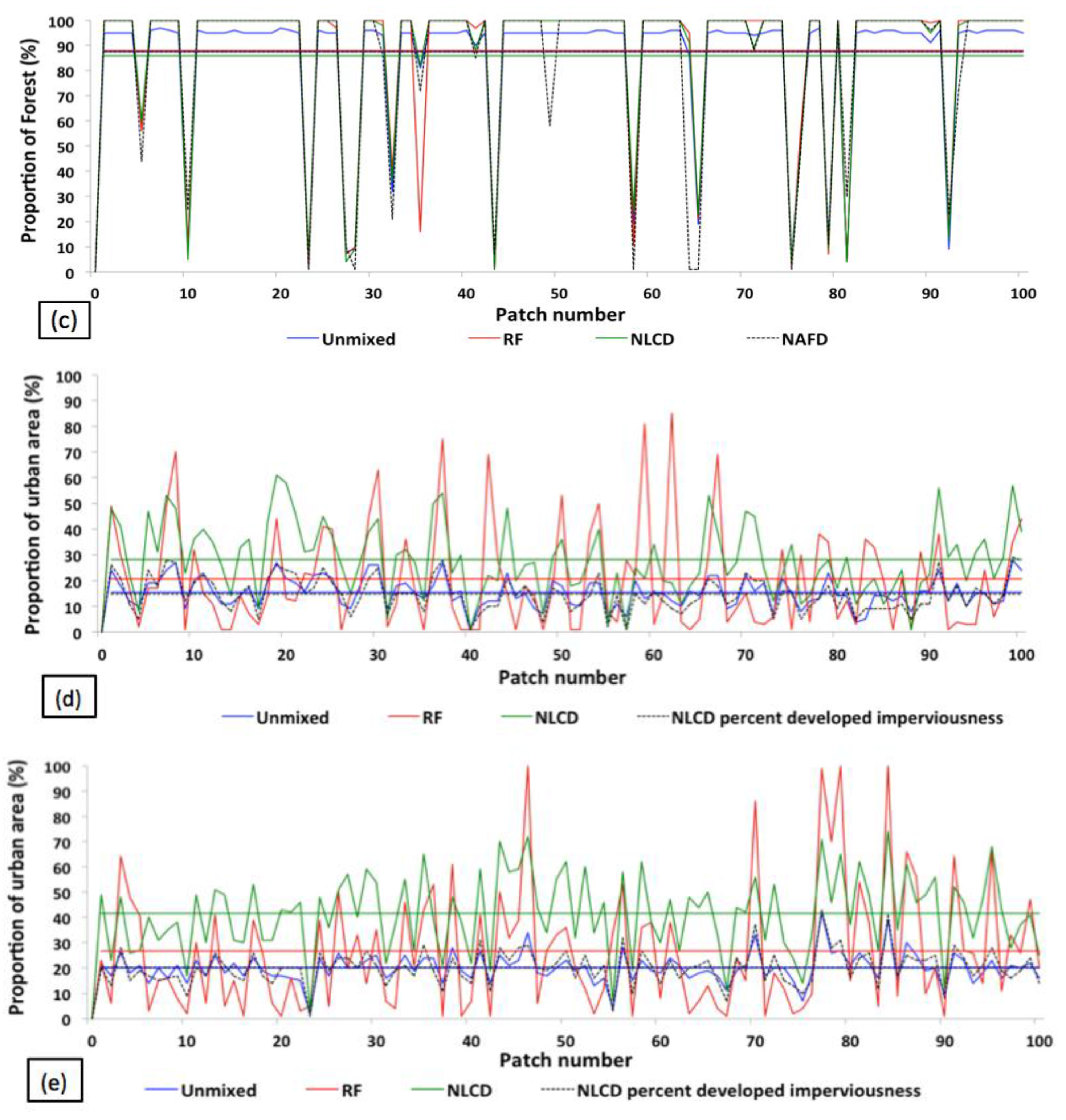
5.2. Landsat Data—An Agritultural Landscape
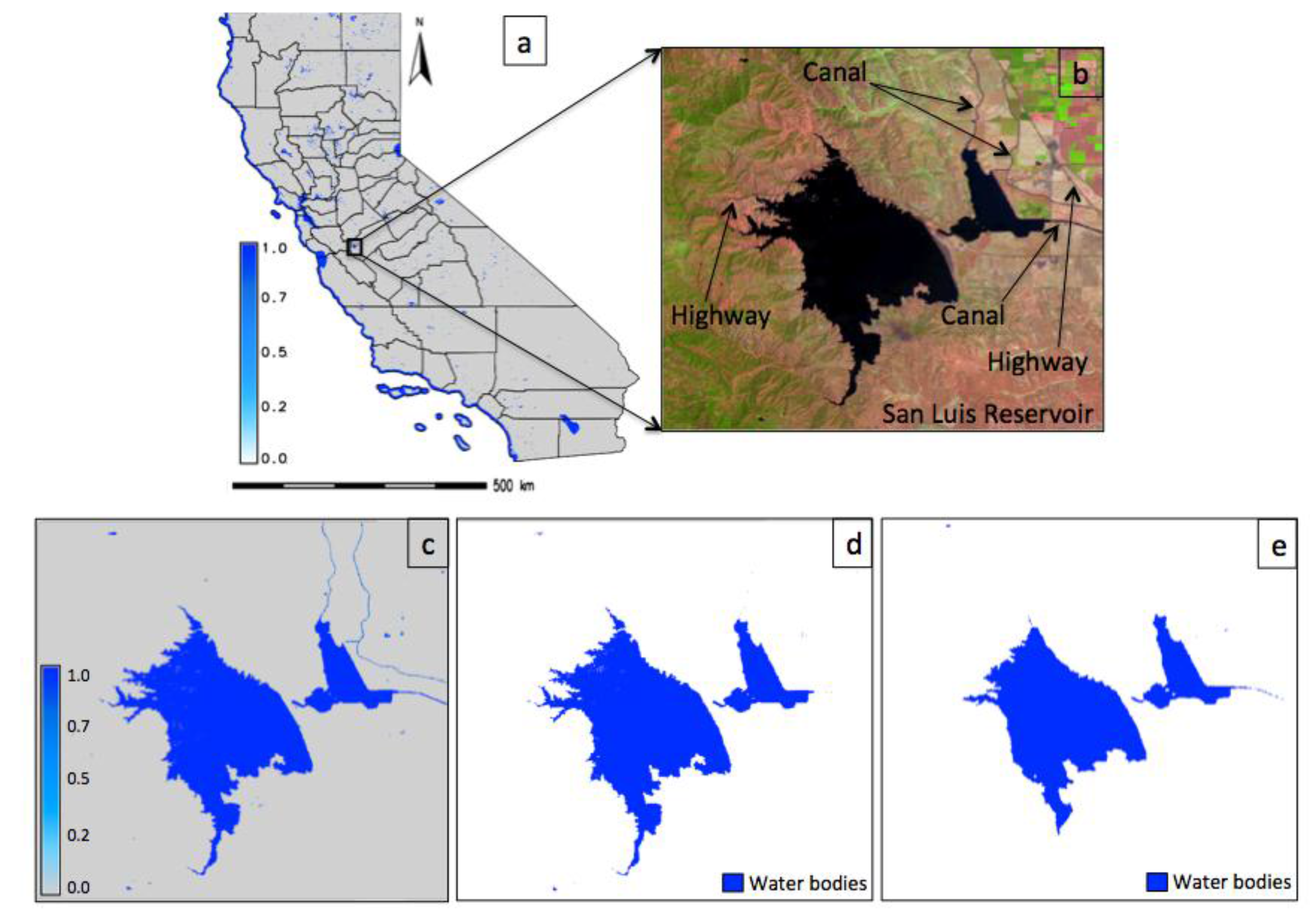
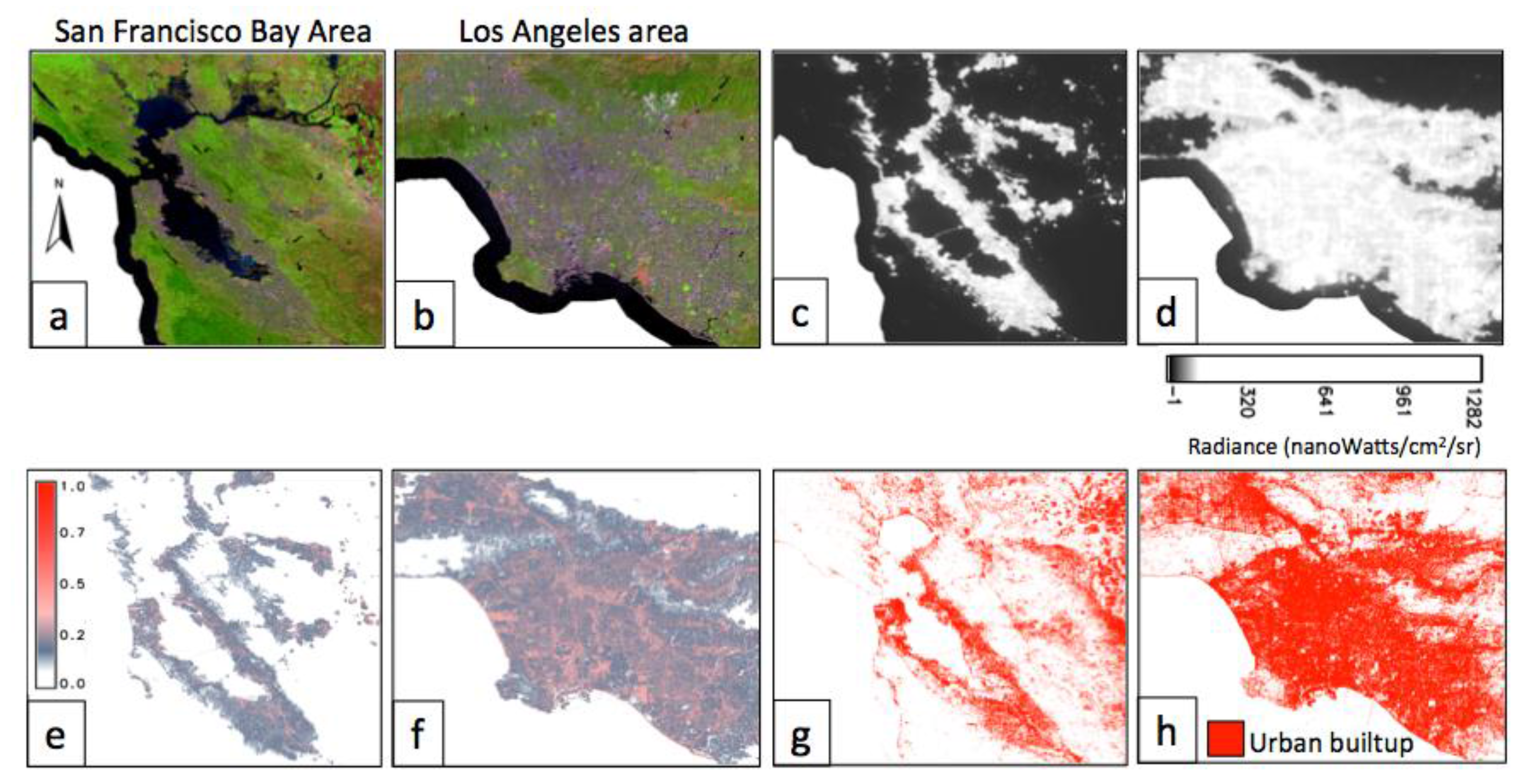
5.3. Landsat Data—An Urban Scenario
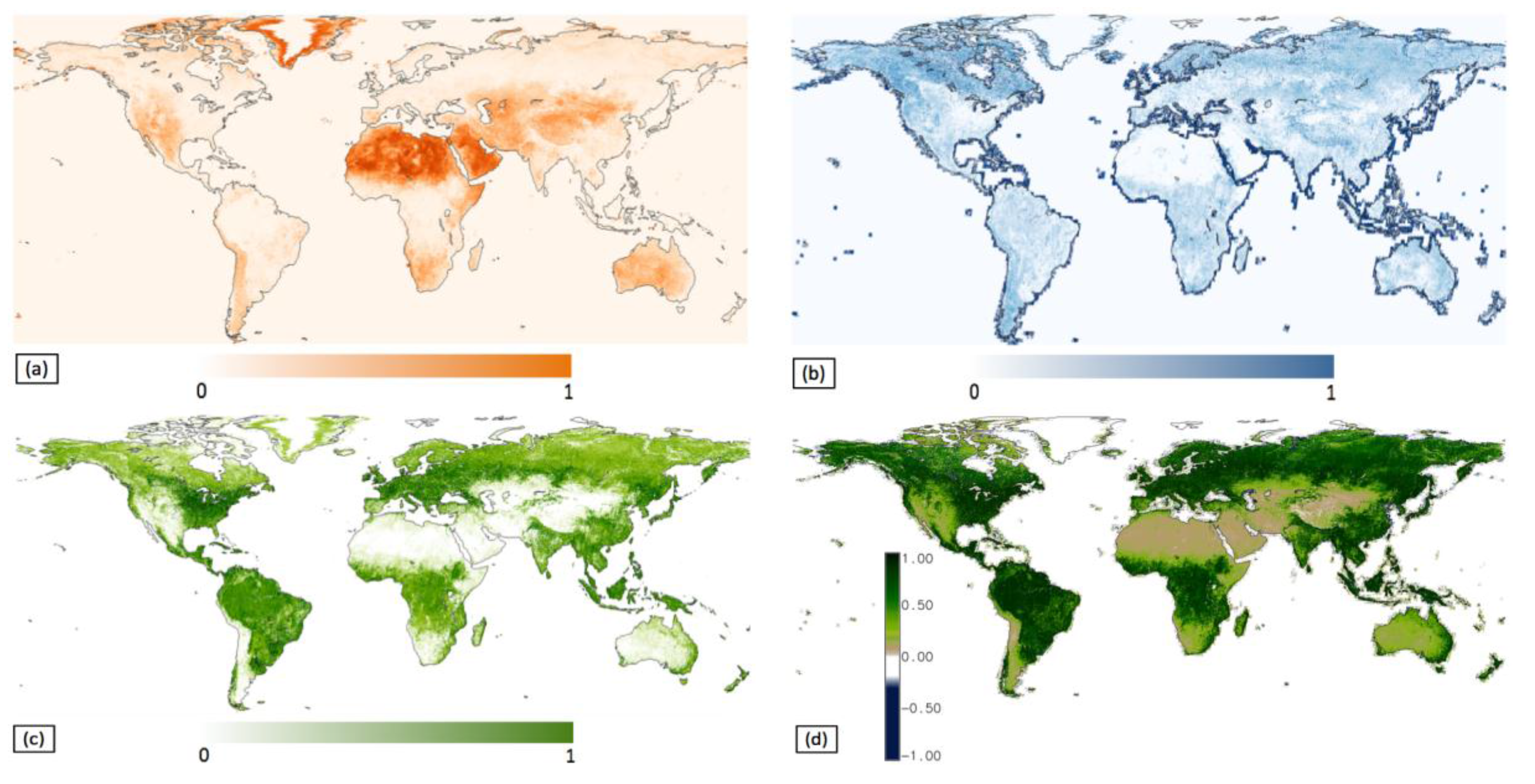
5.4. Global WELD Subpixel Classification
5.5. Subpixel Land Cover Classification
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Plaza, A.; Du, Q.; Bioucas-Dias, J.M.; Jia, X.; Kruse, F. Foreword to the special issue on spectral unmixing of remotely sensed data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4103–4110. [Google Scholar] [CrossRef]
- Heylen, R.; Burazerovi´c, D.; Scheunders, P. Fully Constrained Least Squares Spectral Unmixing by Simplex Projection. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4112–4122. [Google Scholar] [CrossRef]
- Hapke, B.W. Bidirectional reflectance spectroscopy. I. Theory. J. Geophys. Res. 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y.; Richard, C.; Bermudez, J.C.M.; McLaughlin, S.; Hero, A.O. Nonlinear unmixing of hyperspectral images: Models and algorithms. IEEE Signal Process. Mag. 2014, 31, 82–94. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A. Hyperspectral unmixing: Geometrical, statistical, and sparse regression-based approaches. In Proceedings of the SPIE Image and Signal Processing and Remote Sensing XVI, Toulouse, France, 20–23 September 2010; Volume 7830, pp. 1–15. [Google Scholar]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Kumar, U.; Kumar Raja, S.; Mukhopadhyay, C.; Ramachandra, T.V. A neural network based hybrid mixture model to extract information from non-linear mixed pixels. Information 2012, 3, 420–441. [Google Scholar] [CrossRef]
- Parente, M.; Plaza, A. Survey of geometric and statistical unmixing algorithms for hyperspectral images. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, Iceland, 14–16 June 2010. [Google Scholar]
- Iordache, M.-D.; Bioucas-Dias, J.M.; Plaza, A. Collaborative sparse regression for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 341–354. [Google Scholar] [CrossRef]
- Kumar, U.; Kerle, N.; Ramachandra, T.V. Contrained Linear Spectral Unmixing Technique for Regional Land Cover Mapping Using MODIS Data. In Innovations and Advanced Techniques in Systems, Computing Sciences and Software Engineering; Elleithy, K., Ed.; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Ju, J.; Kolaczyk, E.D.; Gopal, S. Gaussian mixture discriminant analysis and sub-pixel land cover characterization in remote sensing. Remote Sens. Env. 2003, 84, 550–560. [Google Scholar] [CrossRef]
- Olthof, I.; Fraser, R.H. Mapping northern land cover fractions using Landsat ETM+. Remote Sens. Env. 2007, 107, 496–509. [Google Scholar] [CrossRef]
- Immitzer, M.; Bock, S.; Einzmann, K.; Vuolo, F.; Pinnel, N.; Wallner, A.; Atzberger, C. Fractional cover mapping of spruce and pine at 1 ha resolution combining very high and medium spatial resolution satellite imagery. Remote Sens. Env. 2017. Available online: http://dx.doi.org/10.1016/j.rse.2017.09.031 (accessed on 27 March 2017).
- Karoui, M.S.; Deville, Y.; Hosseini, S.; Ouamri, A. Blind unmixing of remote sensing data with some pure pixels: Extension and comparison of spatial methods exploiting sparsity and nonnegativity properties. In Proceedings of the 2013 8th International Workshop on Systems, Signal Processing and their Applications (WoSSPA), Algiers, Algeria, 12–15 May 2013. [Google Scholar]
- Pu, H.; Xia, W.; Wang, B.; Jiang, G.-M. A Fully Constrained Linear Spectral Unmixing Algorithm Based on Distance Geometry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1157–1176. [Google Scholar] [CrossRef]
- Zhang, B.; Zhuang, L.; Gao, L.; Luo, W.; Ran, Q.; Du, Q. PSO-EM: A Hyperspectral Unmixing Algorithm Based On Normal Compositional Model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7782–7792. [Google Scholar] [CrossRef]
- Chang, C.-I. Hyperspectral Imaging Techniques for Spectral Detection and Classification; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Chang, C.-I. Orthogonal Subspace Projection (OSP) Revisited: A Comprehensive Study and Analysis. IEEE Trans. Geosci. Remote Sens. 2005, 43, 502–518. [Google Scholar]
- Ball, J.E.; Bruce, L.M.; Younan, N.H. Hyperspectral Pixel Unmixing via Spectral Band Selection and DC-Insensitive Singular Value Decomposition. IEEE Geosci. Remote Sens. Lett. 2007, 4, 382–386. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A. Analysis of Image Spectrometer Data Using–Dimensional Geometry and a Mixture-Tuned Matched Filtering Approach. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4138–4152. [Google Scholar] [CrossRef]
- Kumar, U.; Milesi, C.; Nemani, R.R.; Kumar Raja, S.; Wang, W.; Ganguly, S. Partially and Fully Constrained Least Squares Linear Spectral Mixture Model for Subpixel Land Cover Classification using Landsat Data. Int. J. Sig. Proc. Sys. 2016, 4, 245–251. [Google Scholar]
- AVIRIS Data. Available online: http://aviris.jpl.nasa.gov/data/ (accessed on 27 March 2017).
- US Army Corps of Engineers. Available online: http://www.agc.army.mil (accessed on 27 March 2017).
- Chang, C.-I.; Ren, H. An Experiment-Based Quantitative and Comparative Analysis of Target Detection and Image Classification Algorithms for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1044–1063. [Google Scholar] [CrossRef]
- USGS Digital Spectral Library. Available online: http://speclab.cr.usgs.gov/spectral-lib.html (accessed on 27 March 2017).
- ASTER Spectral Library. Available online: http://speclib.jpl.nasa.gov/ (accessed on 27 March 2017).
- Lobell, D.B.; Asner, G.P. Cropland distribution from temporal unmxixing of MODIS data. Remote Sens. Env. 2004, 87, 412–422. [Google Scholar] [CrossRef]
- Lu, D.; Moran, E.; Batistella, M. Linear mixture model applied to Amazon vegetation classificaiton. Remote Sens. Env. 2003, 87, 456–469. [Google Scholar] [CrossRef] [Green Version]
- Pacheco, A.; McNairn, H. Evaluating multispectral remote sensing and spectral unmixing analysis for crop residue mapping. Remote Sens. Env. 2010, 114, 2219–2228. [Google Scholar] [CrossRef]
- Kumar, U.; Milesi, C.; Kumar Raja, S.; Ganguly, S.; Nemani, R.R. Unconstrained Linear Spectral Mixture Models for Spatial Information Extraction: A Comparative Study. In Proceedings of the IEEE Conference on Information Reuse and Integration (IRI), San Francisco, CA, USA, 13–15 August 2015. [Google Scholar] [CrossRef]
- Kumar, U.; Ganguly, S.; Milesi, C.; Nemani, R.R. Fully Constrained Linear Subpixel Classification Algorithms: A Comparative Analysis Based on Heuristic. In Proceedings of the World Congress on Engineering and Computer Science (WCECS), San Francisco, CA, USA, 21–23 October 2015. [Google Scholar]
- Heinz, D.C.; Chang, C.-I. Fully Constrained Least Squares Linear Spectral Mixture Analysis Method for Material Quantification in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Lawson, L.; Hanson, R.J. Solving Least Squares Problems; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Bro, R.; Jong, S.D. A fast nonnegativity-constrained least squares algorithm. J. Chemom. 1997, 115, 393–401. [Google Scholar] [CrossRef]
- Kumar, U.; Milesi, C.; Ganguly, S.; Kumar Raja, S.; Nemani, R.R. Simplex Projection for Land Cover Information Mining from Landsat-5 TM Data. In Proceedings of the IEEE International Conference on Information Reuse and Integration (IRI), San Francisco, CA, USA, 13–15 August 2015. [Google Scholar] [CrossRef]
- Iordache, M.-D.; Bioucas-Dias, J.M.; Plaza, A. Sparse Unmixing of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef]
- Kumar, U.; Milesi, C.; Nemani, R.R.; Kumar Raja, S.; Ganguly, S.; Wang, W. Sparse Unmixing via Variable Splitting and Augmented Lagrangian For Vegetation and Urban Area Classification Using Landsat Data. In Proceedings of the 2015 International Workshop on Image and Data Fusion, The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Kona, HI, USA, 21–23 July 2015; Volume XL-7/W4, pp. 59–65. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, Iceland, 14–16 June 2010. [Google Scholar]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Kumar, U.; Milesi, C.; Kumar Raja, S.; Nemani, R.R.; Ganguly, S.; Wang, W. Land cover fraction estimation with global endmembers using collaborative SUnSAL. In Proceedings of the SPIE Optics + Photonics, Remote Sensing and Modeling of Ecosystems for Sustainability XII, San Diego, CA, USA, 9–13 August 2015. [Google Scholar]
- Afonso, M.; Bioucas-Dias, J.M.; Figueiredo, M. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 2011, 20, 681–695. [Google Scholar] [CrossRef] [PubMed]
- Stuckens, J.; Somers, B.; Delalieux, S.; Verstraeten, W.W.; Coppin, P. The impact of common assumptions on canopy radiative transfer simulations: A case study in citrus orchards. J. Quantitative Spectroscopy and Radiative Transfer. 2009, 110, 1–21. [Google Scholar] [CrossRef]
- Somers, B.; Cools, K.; Delalieux, S.; Stuckens, J.; Van der Zande, D.; Verstraeten, W.W.; Coppin, P. Nonlinear Hyperspectral Mixture Analysis for tree cover estimates in orchards. Remote Sens. Env. 2009, 113, 1183–1193. [Google Scholar] [CrossRef]
- Global Landsat. 2012. Available online: http://www.LDEO.columbia.edu/~small/GlobalLandsat/ (accessed on 27 March 2017).
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Env. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Johnson, L.; Trout, T. Satellite-assisted monitoring of vegetable crop evapotranspiration in California’s San Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Kline, K.; Scaramuzza, P.L.; Kovalskyy, V.; Hansen, M.C.; Loveland, T.R.; Vermote, E.F.; Zhang, C. Web-enabled Landsat Data (WELD): Landsat ETM+ Composited Mosaics of the Conterminous United States. Remote Sens. Env. 2010, 114, 35–49. [Google Scholar] [CrossRef]
- Small, C. The Landsat ETM plus spectral mixing space. Remote Sens. Env. 2004, 93, 1–17. [Google Scholar] [CrossRef]
- Small, C.; Milesi, C. Multi-scale Standardized Spectral Mixture Models. Remote Sens. Env. 2013, 136, 442–454. [Google Scholar] [CrossRef]
- Huang, C.; Song, K.; Kim, S.; Townshend, J.R.G.; Davis, P.; Masek, J.G.; Goward, S.N. Use of a dark object concept and support vector machines to automate forest cover change analysis. Remote Sens. Env. 2008, 112, 970–985. [Google Scholar] [CrossRef]
- Liaw, A.; Weiner, M. Classification and Regression by Random Forests. R News 2002, 2, 18–22. Available online: http://CRAN.R-project.org/doc/Rnews/ (accessed on 27 March 2017).
- He, C.Y.; Shi, P.J.; Li, J.G.; Chen, J.; Pan, Y.Z.; Li, J.; Zhuo, L.; Ichinose, T. Restoring Urbanization Process in China in the 1990s by using Non-Radiance Calibrated DMSP/OLS Nighttime Light Imagery and Statistical Data. Chin. Sci. Bull. 2006, 51, 1614–1620. [Google Scholar] [CrossRef]
- Shu, S.; Yu, B.; Wu, J.; Liu, H. Methods for Deriving Urban Built-Up Area Using Night-Light Data: Assessment and Application. Remote Sens. Tech. App. 2011, 26, 169–176. [Google Scholar]
- Homer, C.G.; Dewitz, J.A.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.D.; Wickham, J.D.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States-Representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Xian, G.; Homer, C.; Dewitz, J.; Fry, J.; Hossain, N.; Wickham, J. The change of impervious surface area between 2001 and 2006 in the conterminous United States. Photogramm. Engg. Remote Sens. 2011, 77, 758–762. [Google Scholar]
- Goward, S.N.; Huang, C.; Zhao, F.; Schleeweis, K.; Rishmawi, K.; Lindsey, M.; Dungan, J.L.; Michaelis, A. NACP NAFD Project: Forest Disturbance History from Landsat, 1986–2010. ORNL DAAC: Oak Ridge, TN, USA, 2015. Available online: http://dx.doi.org/10.3334/ORNLDAAC/1290 (accessed on 3 March 2017).
- Huang, C.; Goward, S.N.; Masek, J.F.; Thomas, N.; Zhu, Z.; Vogelmann, J.E. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Env. 2010, 114, 183–198. [Google Scholar] [CrossRef]
- Nemani, R.R.; Hashimoto, H.; Votava, P.; Melton, F.; Wang, W.; Michaelis, A.; Mutch, L.; Milesi, C.; Hiatt, S.; White, M. Monitoring and forecasting ecosystem dynamics using the Terrestrial Observation and Prediction System (TOPS). Remote Sens. Env. 2009, 113, 1497–1509. [Google Scholar] [CrossRef]
- Nowak, D.J.; Greenfield, E.J. Evaluating The National Land Cover Database Tree Canopy and Impervious Cover Estimates Across the Conterminous United States: A Comparison with Photo-Interpreted Estimates. Environ. Manag. 2010, 46, 378–390. [Google Scholar] [CrossRef] [PubMed]
- Small, C.; Lu, J.W.T. Estimation and vicarious validation of urban vegetation abundance by spectral mixture analysis. Remote Sens. Env. 2006, 100, 441–456. [Google Scholar] [CrossRef]
- Kumar, U.; Kumar Raja, S.; Mukhopadhyay, C.; Ramachandra, T.V. Assimilation of Endmember Variability in Spectral Mixture Analysis for Urban Land Cover Extraction. Adv. Space Res. 2013, 52, 2015–2033. [Google Scholar] [CrossRef]
- Basu, S.; Ganguly, S.; Nemani, R.R.; Mukhopadhyay, S.; Zhang, G.; Milesi, C.; Michaelis, A.; Votava, P.; Dubayah, R.; Duncanson, L.; et al. A semi-automated probabilistic framework for tree cover delineation from 1-m NAIP imagery using a high performance computing architecture. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1–19. [Google Scholar] [CrossRef]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; Dibiano, R.; Karki, M.; Nemani, R.R. DeepSat—A Learning framework for Satellite Imagery. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM SIGSPATIAL), Seattle, WA, USA, 3–6 November 2015. [Google Scholar] [CrossRef]


| Forest | Farmland | Water | Urban (SF) | Urban (LA) | Overall | |
|---|---|---|---|---|---|---|
| Total samples | 200,000 | 200,000 | 200,000 | 100,000 | 100,000 | 800,000 |
| Class samples | 100,000 | 100,000 | 100,000 | 50,000 | 50,000 | 400,000 |
| Non-class samples | 100,000 | 100,000 | 100,000 | 50,000 | 50,000 | 400,000 |
| Unmixing TPR * | 93.87 | 90.29 | 92.65 | 89.81 | 90.83 | 91.49 |
| Unmixing FPR * | 3.46 | 4.12 | 0.5 | 4.99 | 8.17 | 4.25 |
| RF TPR * | 88.86 | 85.19 | 88.27 | 83.33 | 79.91 | 85.11 |
| RF FPR * | 5.12 | 8.21 | 2.17 | 12.71 | 15.13 | 8.67 |
| RF | Unmixing Based Classification | |||||
|---|---|---|---|---|---|---|
| Class | PA ** | UA ** | PA ** | UA ** | ||
| Forest | 87.97 | 88.69 | 91.17 | 95.29 | ||
| Farmland | 85.11 | 86.75 | 94.87 | 85.63 | ||
| Water | 89.87 | 87.43 | 89.65 | 95.12 | ||
| Urban (SF) | 84.24 | 83.19 | 85.33 | 94.31 | ||
| Urban (LA) | 76.52 | 83.39 | 88.67 | 92.96 | ||
| Average | 84.74 | 85.89 | 89.94 | 92.66 | ||
| OA ** | 85.31 | 91.30 | ||||
| kappa | 0.83 | 0.89 | ||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, U.; Ganguly, S.; Nemani, R.R.; Raja, K.S.; Milesi, C.; Sinha, R.; Michaelis, A.; Votava, P.; Hashimoto, H.; Li, S.; et al. Exploring Subpixel Learning Algorithms for Estimating Global Land Cover Fractions from Satellite Data Using High Performance Computing. Remote Sens. 2017, 9, 1105. https://doi.org/10.3390/rs9111105
Kumar U, Ganguly S, Nemani RR, Raja KS, Milesi C, Sinha R, Michaelis A, Votava P, Hashimoto H, Li S, et al. Exploring Subpixel Learning Algorithms for Estimating Global Land Cover Fractions from Satellite Data Using High Performance Computing. Remote Sensing. 2017; 9(11):1105. https://doi.org/10.3390/rs9111105
Chicago/Turabian StyleKumar, Uttam, Sangram Ganguly, Ramakrishna R. Nemani, Kumar S Raja, Cristina Milesi, Ruchita Sinha, Andrew Michaelis, Petr Votava, Hirofumi Hashimoto, Shuang Li, and et al. 2017. "Exploring Subpixel Learning Algorithms for Estimating Global Land Cover Fractions from Satellite Data Using High Performance Computing" Remote Sensing 9, no. 11: 1105. https://doi.org/10.3390/rs9111105
APA StyleKumar, U., Ganguly, S., Nemani, R. R., Raja, K. S., Milesi, C., Sinha, R., Michaelis, A., Votava, P., Hashimoto, H., Li, S., Wang, W., Kalia, S., & Gayaka, S. (2017). Exploring Subpixel Learning Algorithms for Estimating Global Land Cover Fractions from Satellite Data Using High Performance Computing. Remote Sensing, 9(11), 1105. https://doi.org/10.3390/rs9111105






