Angular Resolution Enhancement Provided by Nonuniformly-Spaced Linear Hydrophone Arrays in Ocean Acoustic Waveguide Remote Sensing
Abstract
:1. Introduction
2. Methods and Materials
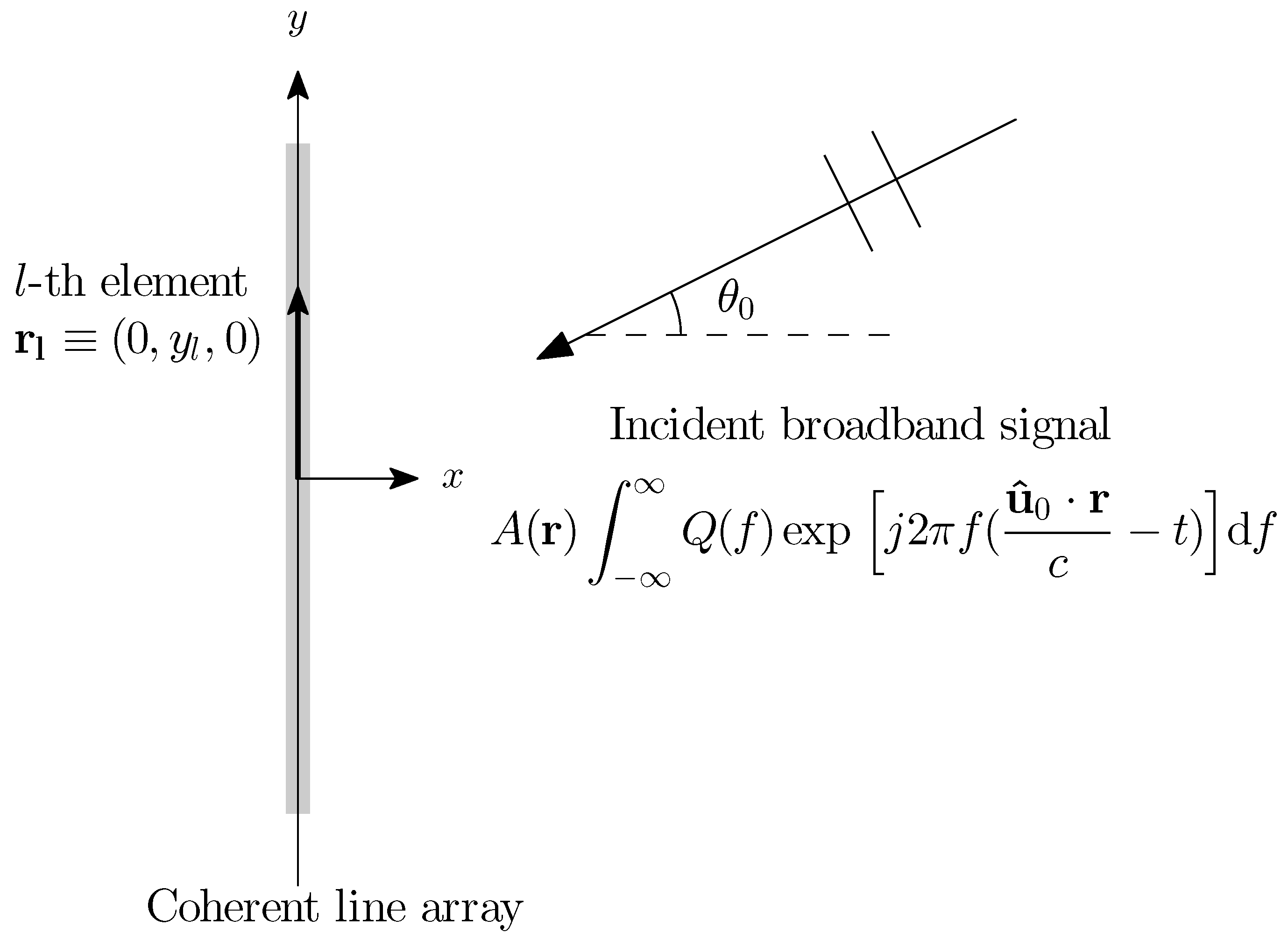
2.1. Theory: Linear Discrete Array Beamformer
2.2. Experimental Acoustic Data Collection with a Coherent Discrete Hydrophone Array
3. Illustrative Examples
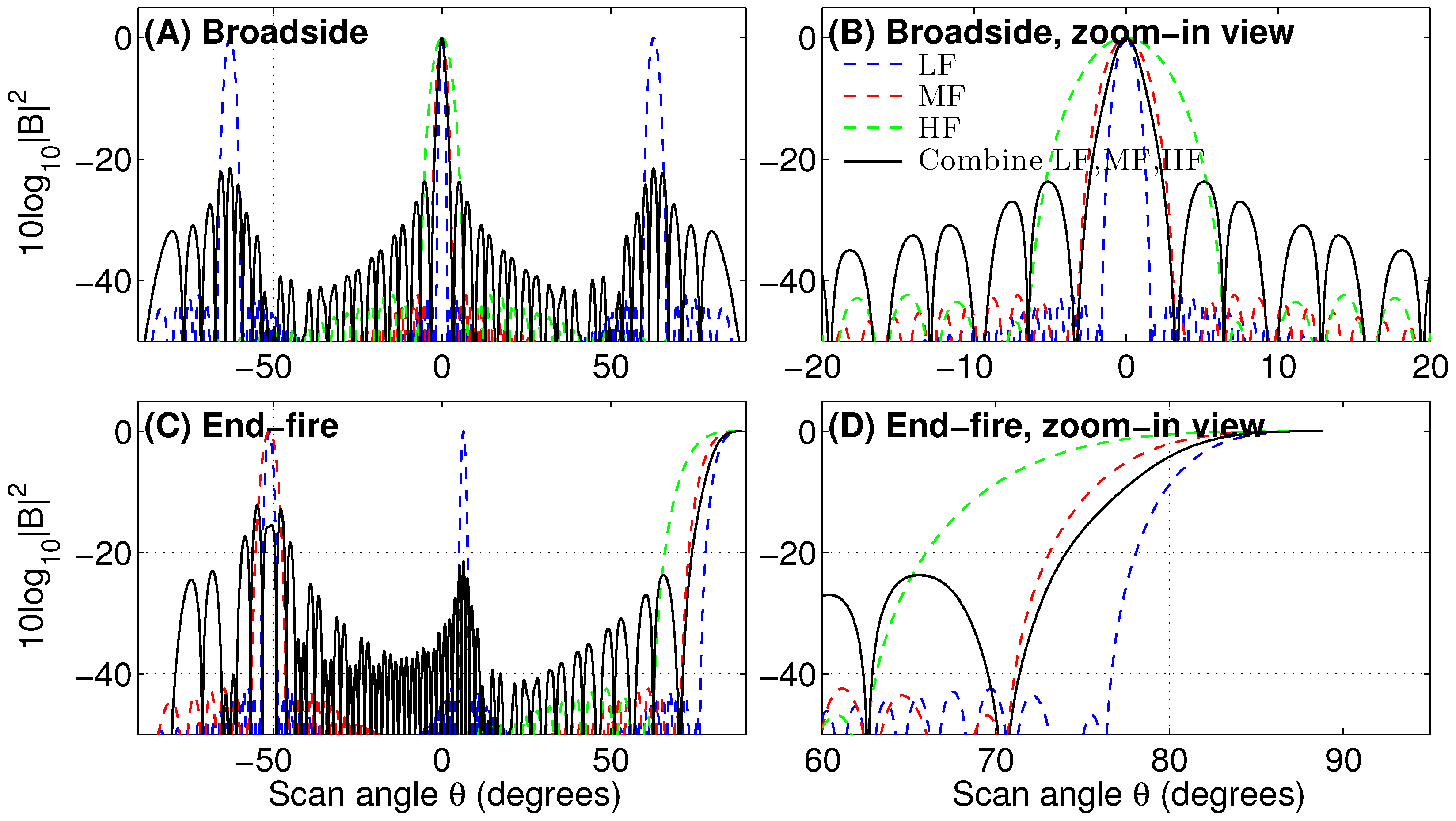
3.1. Theoretical Results
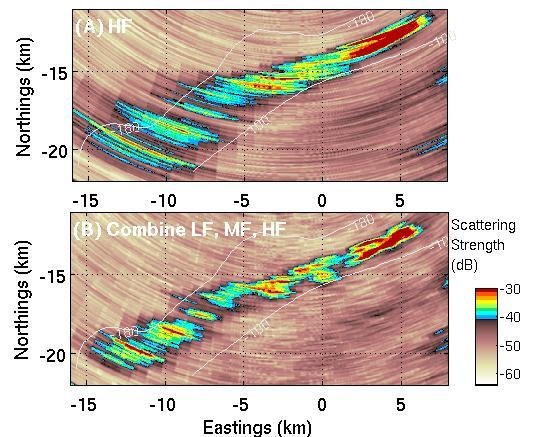
3.2. OAWRS Scattering Strength Images of Shoaling Fish Populations
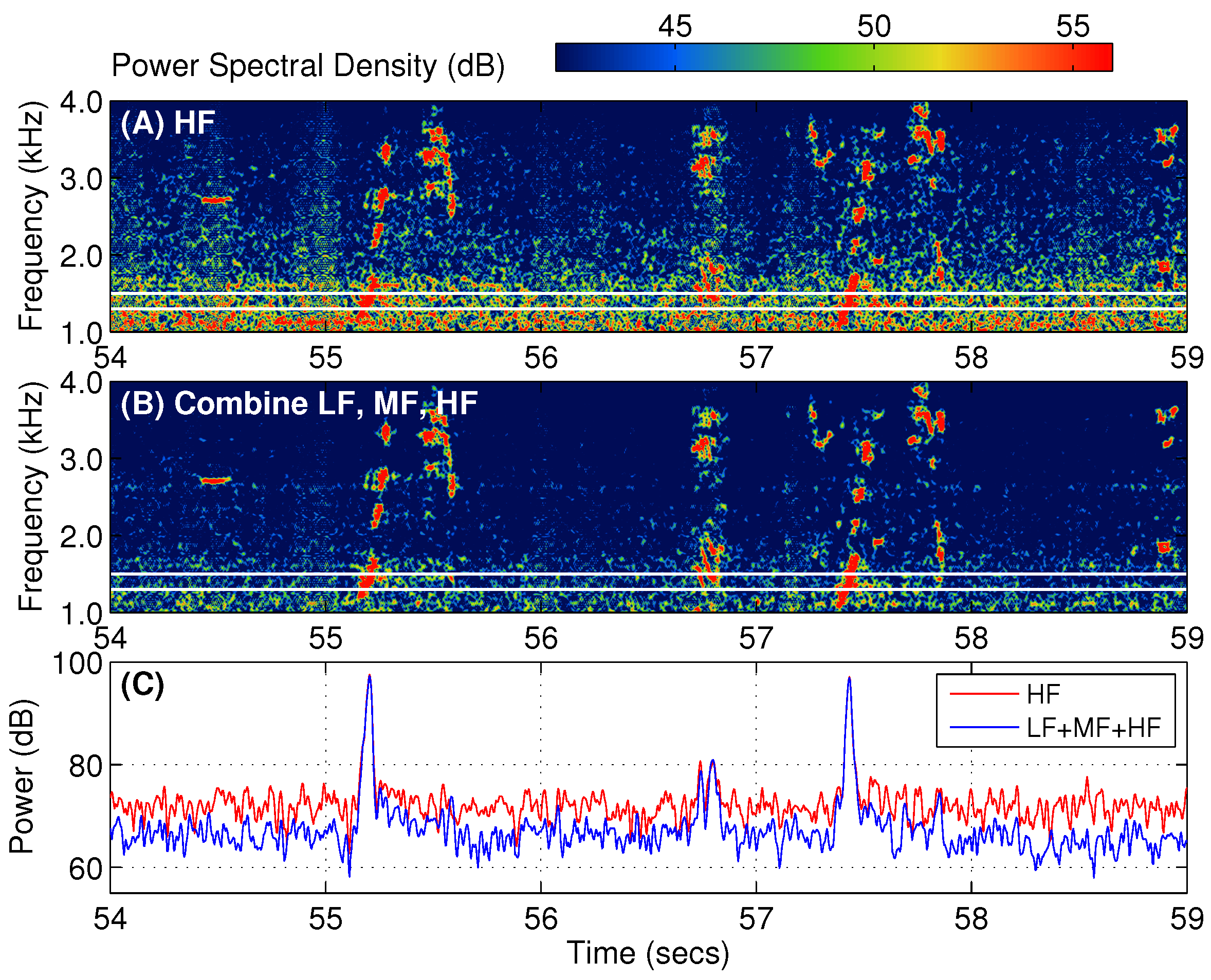
3.3. POAWRS Beamformed Spectrogram of Marine Mammal Vocalizations and Ship Tonals
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SNR | signal-to-noise ratio |
| ONR-FORA | Office of Naval Research Five Octave Research Array |
| OAWRS | ocean acoustic waveguide remote sensing |
| POAWRS | passive ocean acoustic waveguide remote sensing |
| GOME06 | Gulf of Maine 2006 Experiment |
| LFM | linear frequency modulated |
| PSD | power spectral density |
| ULF | ultra low frequency |
| LF | low frequency |
| MF | mid frequency |
| HF | high frequency |
References
- Wang, D.; Garcia, H.; Huang, W.; Tran, D.D.; Jain, A.D.; Yi, D.H.; Gong, Z.; Jech, J.M.; Godø, O.R.; Makris, N.C.; et al. Vast assembly of vocal marine mammals from diverse species on fish spawning ground. Nature 2016, 531, 366–370. [Google Scholar] [CrossRef] [PubMed]
- Makris, N.C.; Ratilal, P.; Jagannathan, S.; Gong, Z.; Andrews, M.; Bertsatos, I.; Godø, O.R.; Nero, R.W.; Jech, J.M. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 2009, 323, 1734–1737. [Google Scholar] [CrossRef] [PubMed]
- Makris, N.C.; Ratilal, P.; Symonds, D.T.; Jagannathan, S.; Lee, S.; Nero, R.W. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science 2006, 311, 660–663. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Huang, W.; Garcia, H.; Ratilal, P. Vocalization source level distributions and pulse compression gains of diverse baleen whale species in the Gulf of Maine. Remote Sens. 2016, 8, 881. [Google Scholar] [CrossRef]
- Huang, W.; Wang, D.; Ratilal, P. Diel and Spatial Dependence of Humpback Song and Non-Song Vocalizations in Fish Spawning Ground. Remote Sens. 2016, 8, 712. [Google Scholar] [CrossRef]
- Huang, W.; Wang, D.; Garcia, H.; Godø, O.R.; Ratilal, P. Continental Shelf-Scale Passive Acoustic Detection and Characterization of Diesel-Electric Ships Using a Coherent Hydrophone Array. Remote Sens. 2017, 9, 772. [Google Scholar] [CrossRef]
- Jagannathan, S.; Küsel, E.T.; Ratilal, P.; Makris, N.C. Scattering from extended targets in range-dependent fluctuating ocean-waveguides with clutter from theory and experiments. J. Acoust. Soc. Am. 2012, 132, 680–693. [Google Scholar] [CrossRef] [PubMed]
- Jagannathan, S.; Bertsatos, I.; Symonds, D.; Chen, T.; Nia, H.T.; Jain, A.D.; Andrews, M.; Gong, Z.; Nero, R.; Ngor, L.; et al. Ocean acoustic waveguide remote sensing (OAWRS) of marine ecosystems. Mar. Ecol. Prog. Ser. 2009, 395, 137–160. [Google Scholar] [CrossRef]
- Makris, N.C.; Berkson, J.M. Long-range backscatter from the Mid-Atlantic Ridge. J. Acoust. Soc. Am. 1994, 95, 1865–1881. [Google Scholar] [CrossRef]
- Makris, N.C.; Avelino, L.Z.; Menis, R. Deterministic reverberation from ocean ridges. J. Acoust. Soc. Am. 1995, 97, 3547–3574. [Google Scholar] [CrossRef]
- Gong, Z.; Ratilal, P.; Makris, N.C. Simultaneous localization of multiple broadband non-impulsive acoustic sources in an ocean waveguide using the array invariant. J. Acoust. Soc. Am. 2015, 138, 2649–2667. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Jain, A.D.; Tran, D.; Yi, D.H.; Wu, F.; Zorn, A.; Ratilal, P.; Makris, N.C. Ecosystem scale acoustic sensing reveals humpback whale behavior synchronous with herring spawning processes and re-evaluation finds no effect of sonar on humpback song occurrence in the Gulf of Maine in Fall 2006. PLoS ONE 2014, 9, e104733. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Andrews, M.; Jagannathan, S.; Patel, R.; Jech, J.M.; Makris, N.C.; Ratilal, P. Low-frequency target strength and abundance of shoaling Atlantic herring (Clupea harengus) in the Gulf of Maine during the Ocean Acoustic Waveguide Remote Sensing 2006 Experiment. J. Acoust. Soc. Am. 2010, 127, 104–123. [Google Scholar] [CrossRef] [PubMed]
- Ratilal, P.; Lai, Y.; Symonds, D.T.; Ruhlmann, L.A.; Preston, J.R.; Scheer, E.K.; Garr, M.T.; Holland, C.W.; Goff, J.A.; Makris, N.C. Long range acoustic imaging of the continental shelf environment: The Acoustic Clutter Reconnaissance Experiment 2001. J. Acoust. Soc. Am. 2005, 117, 1977–1998. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Cho, S.; Kang, T.; Hodgkiss, W.; Preston, J. Long-range acoustic communication in deep water using a towed array. J. Acoust. Soc. Am. 2011, 129, EL71–EL75. [Google Scholar] [CrossRef] [PubMed]
- Preston, J.R.; Ellis, D.D.; Gauss, R.C. Geoacoustic parameter extraction using reverberation data from the 2000 Boundary Characterization Experiment on the Malta Plateau. IEEE J. Ocean. Eng. 2005, 30, 709–732. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing Vol. II: Detection Theory; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Johnson, D.H.; Dudgeon, D.E. Array Signal Processing: Concepts and Techniques; Prentice Hall PTR: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Urick, R. Principles of Underwater Sound; McGraw Hill: New York, NY, USA, 1983. [Google Scholar]
- Tolstoy, I.; Clay, C. Ocean Acoustics: Theory and Experiment in Underwater Sound; American Institute of Physics: New York, NY, USA, 1987. [Google Scholar]
- Kuperman, W.A.; Collins, M.D.; Perkins, J.S.; Davis, N. Optimal time-domain beamforming with simulated annealing including application of apriori information. J. Acoust. Soc. Am. 1990, 88, 1802–1810. [Google Scholar] [CrossRef]
- Collins, M.D.; Berkson, J.M.; Kuperman, W.A.; Makris, N.C.; Perkins, J.S. Applications of optimal time-domain beamforming. J. Acoust. Soc. Am. 1993, 93, 1851–1865. [Google Scholar] [CrossRef]
- Aidala, V.; Hammel, S. Utilization of modified polar coordinates for bearings-only tracking. IEEE Trans. Autom. Control 1983, 28, 283–294. [Google Scholar] [CrossRef]
- Gong, Z.; Tran, D.D.; Ratilal, P. Comparing passive source localization and tracking approaches with a towed horizontal receiver array in an ocean waveguide. J. Acoust. Soc. Am. 2013, 134, 3705–3720. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Makris, N.C. The array invariant. J. Acoust. Soc. Am. 2006, 119, 336–351. [Google Scholar] [CrossRef] [PubMed]
- Becker, K.; Preston, J. The ONR five octave research array (FORA) at Penn State. In Proceedings of the IEEE OCEANS 2003, San Diego, CA, USA, 22–26 September 2003; Volume 5, pp. 2607–2610. [Google Scholar]
- Van Trees, H. Detection, Estimation, and Modulation Theory, Part IV Optimum Array Processing; Detection, Estimation, and Modulation Theory; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Etter, R.J.; Cutbirth, J.M.; Ceccio, S.L.; Dowling, D.R.; Perlin, M. High reynolds number experimentation in the US navy’s William B Morgan Large Cavitation Channel. Meas. Sci. Technol. 2005, 16, 1701–1709. [Google Scholar] [CrossRef]
- Maguer, A.; Dymond, R.; Mazzi, M.; Biagini, S.; Fioravanti, S.; Guerrini, P. SLITA: A new slim towed array for AUV applications. J. Acoust. Soc. Am. 2008, 123, 141–146. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P. Nested arrays in two dimensions, part I: Geometrical considerations. IEEE Trans. Signal Process. 2012, 60, 4694–4705. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Martino, G.D.; Iodice, A. Passive beamforming with coprime arrays. IET Radar Sonar Navig. 2017, 11, 964–971. [Google Scholar] [CrossRef]
- Adhikari, K.; Buck, J.R.; Wage, K.E. Beamforming with extended co-prime sensor arrays. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 4183–4186. [Google Scholar]
- Adhikari, K.; Buck, J.R.; Wage, K.E. Extending coprime sensor arrays to achieve the peak side lobe height of a full uniform linear array. EURASIP J. Adv. Signal Process. 2014, 148. [Google Scholar] [CrossRef]
- Cen, L.; Ser, W.; Yu, Z.L.; Rahardja, S. An improved genetic algorithm for aperiodic array synthesis. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2008), Las Vegas, NV, USA, 31 March–4 April 2008; pp. 2465–2468. [Google Scholar]
- Barott, W.C.; Steffes, P.G. Grating lobe reduction in aperiodic linear arrays of physically large antennas. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 406–408. [Google Scholar] [CrossRef]
- Spence, T.G.; Werner, D.H. Design of broadband planar arrays based on the optimization of aperiodic tilings. IEEE Trans. Antennas Propag. 2008, 56, 76–86. [Google Scholar] [CrossRef]
- Trucco, A.; Martelli, S.; Crocco, M. Low-cost acoustic cameras for underwater wideband passive imaging. IEEE J. Ocean. Eng. 2015, 40, 929–937. [Google Scholar] [CrossRef]
- Trucco, A.; Martelli, S.; Crocco, M. Passive underwater imaging through optimized planar arrays of hydrophones. In Proceedings of the 2014 Oceans-St. John’s, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–5. [Google Scholar]
- Trucco, A.; Murino, V. Stochastic optimization of linear sparse arrays. IEEE J. Ocean. Eng. 1999, 24, 291–299. [Google Scholar] [CrossRef]
- McGehee, D.; Jaffe, J.S. Beamforming with dense random arrays: The development of a spatially shaded polyvinylidene fluoride acoustic transducer. J. Acoust. Soc. Am. 1994, 95, 318–323. [Google Scholar] [CrossRef]
- Yang, H.; Chen, H.; Xu, L. Beamforming with nonsinusoidal signal for grating lobes suppression in underwater acoustic imaging. In Proceedings of the OCEANS 2015-Genova, Genoa, Italy, 18–21 May 2015; pp. 1–5. [Google Scholar]
- Camacho, J.; Parrilla, M.; Fritsch, C. Phase coherence imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56. [Google Scholar] [CrossRef] [PubMed]
- Camacho, J.; Parrilla, M.; Fritsch, C. Grating-lobes reduction by application of phase coherence factors. In Proceedings of the 2009 IEEE International Ultrasonics Symposium (IUS), Rome, Italy, 20–23 September 2009; pp. 341–344. [Google Scholar]
- Torbatian, Z.; Adamson, R.; Bance, M.; Brown, J. Transmit beamforming techniques for suppressing grating lobes in large pitch ultrasonic phased arrays. Proc. SPIE 2011, 7968, 79680R. [Google Scholar]
- Torbatian, Z.; Adamson, R.; Bance, M.; Brown, J.A. A split-aperture transmit beamforming technique with phase coherence grating lobe suppression. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2588–2595. [Google Scholar] [CrossRef] [PubMed]
- Preston, J.R.; Ellis, D.D. Extracting bottom information from towed-array reverberation data: Part I: Measurement methodology. J. Mar. Syst. 2009, 78, S359–S371. [Google Scholar] [CrossRef]
- McEachern, J.F.; McConnell, J.A.; Jamieson, J.; Trivett, D. ARAP—Deep Ocean Vector Sensor Research Array. In Proceedings of the OCEANS 2006, Boston, MA, USA, 18–21 September 2006; pp. 1–5. [Google Scholar]
- Tran, D.; Andrews, M.; Ratilal, P. Probability distribution for energy of saturated broadband ocean acoustic transmission: Results from Gulf of Maine 2006 experiment. J. Acoust. Soc. Am. 2012, 132, 3659–3672. [Google Scholar] [CrossRef] [PubMed]
- Center, N. Atlantic herring stock assessment for 2012. In Proceedings of the 54th Northeast Regional Stock Assessment Workshop (54th SAW), Woods Hole, MA, USA, 5–9 June 2012. [Google Scholar]
- Jech, J.M.; Stroman, F. Aggregative patterns of pre-spawning Atlantic herring on Georges Bank from 1999–2010. Aquat. Living Resour. 2012, 25, 1–14. [Google Scholar] [CrossRef]
- Overholtz, W.J.; Jacobson, L.D.; Melvin, G.D.; Cieri, M.; Power, M.; Libby, D.; Clark, K. Stock Assessment of the Gulf of Maine–Georges Bank Atlantic Herring Complex, 2003. In Northeast Fisheries Science Center References Document 04-06; Northeast Fisheries Science Center: Woods Hole, MA, USA, 2004; 290p. [Google Scholar]
- Jech, J.M.; Price, V.; Chavez-Rosales, S.; Michaels, W. Atlantic herring (Clupea harengus) demographics in the Gulf of Maine from 1998 to 2012. J. Northwest Atl. Fish. Sci. 2015, 47, 57–74. [Google Scholar] [CrossRef]
- Andrews, M.; Gong, Z.; Ratilal, P. High resolution population density imaging of random scatterers with the matched filtered scattered field variance. J. Acoust. Soc. Am. 2009, 126, 1057–1068. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.D.; Makris, N.C. Maximum Likelihood Deconvolution of Beamformed Images with Signal-Dependent Speckle Fluctuations from Gaussian Random Fields: With Application to Ocean Acoustic Waveguide Remote Sensing (OAWRS). Remote Sens. 2016, 8, 694. [Google Scholar] [CrossRef]
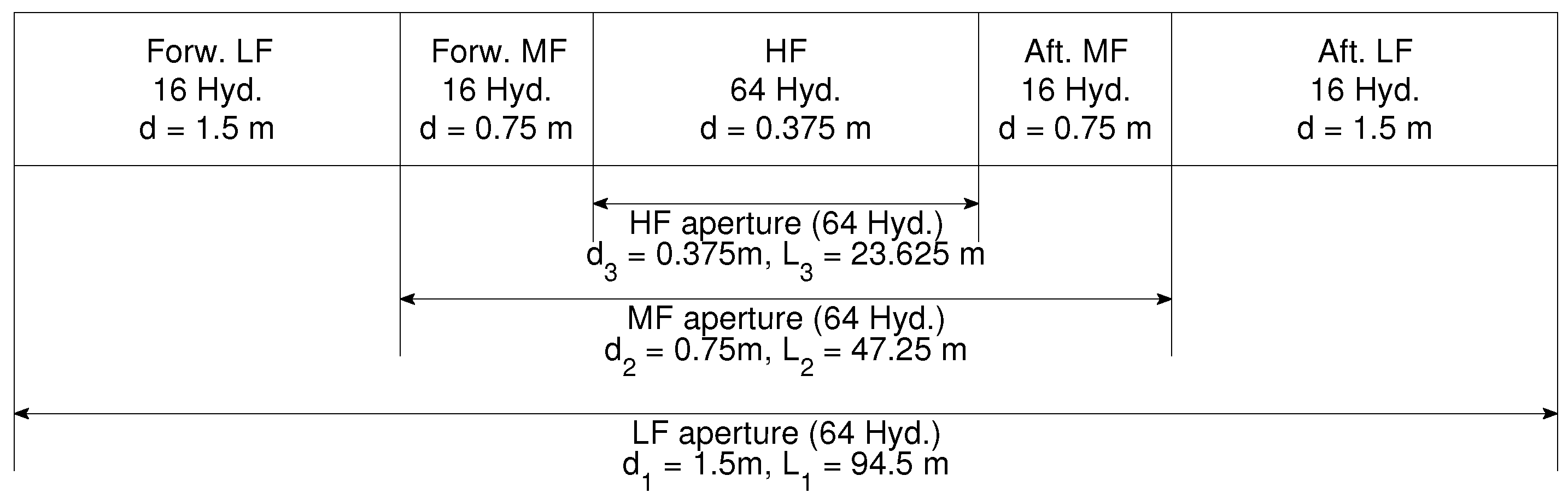
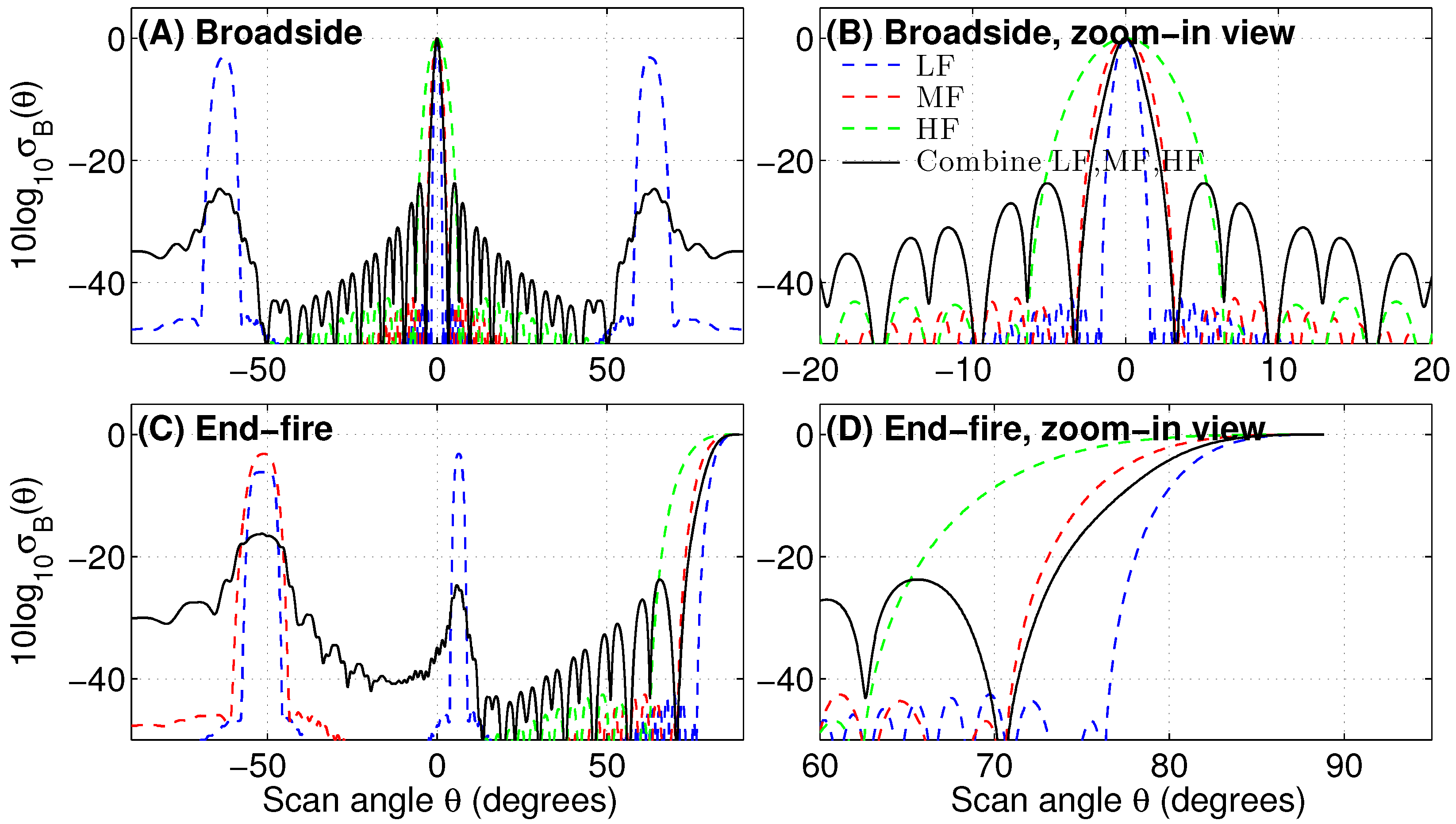
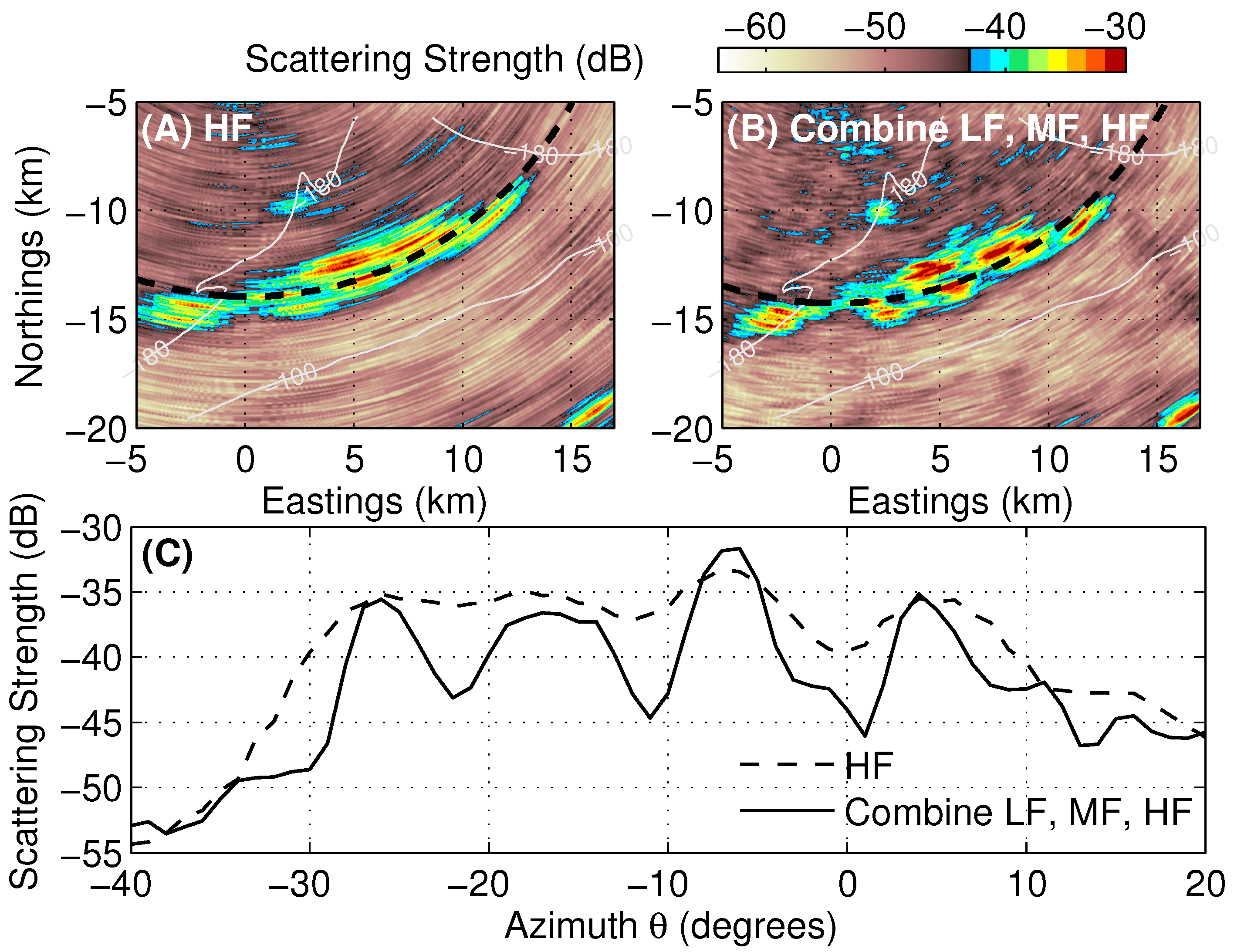
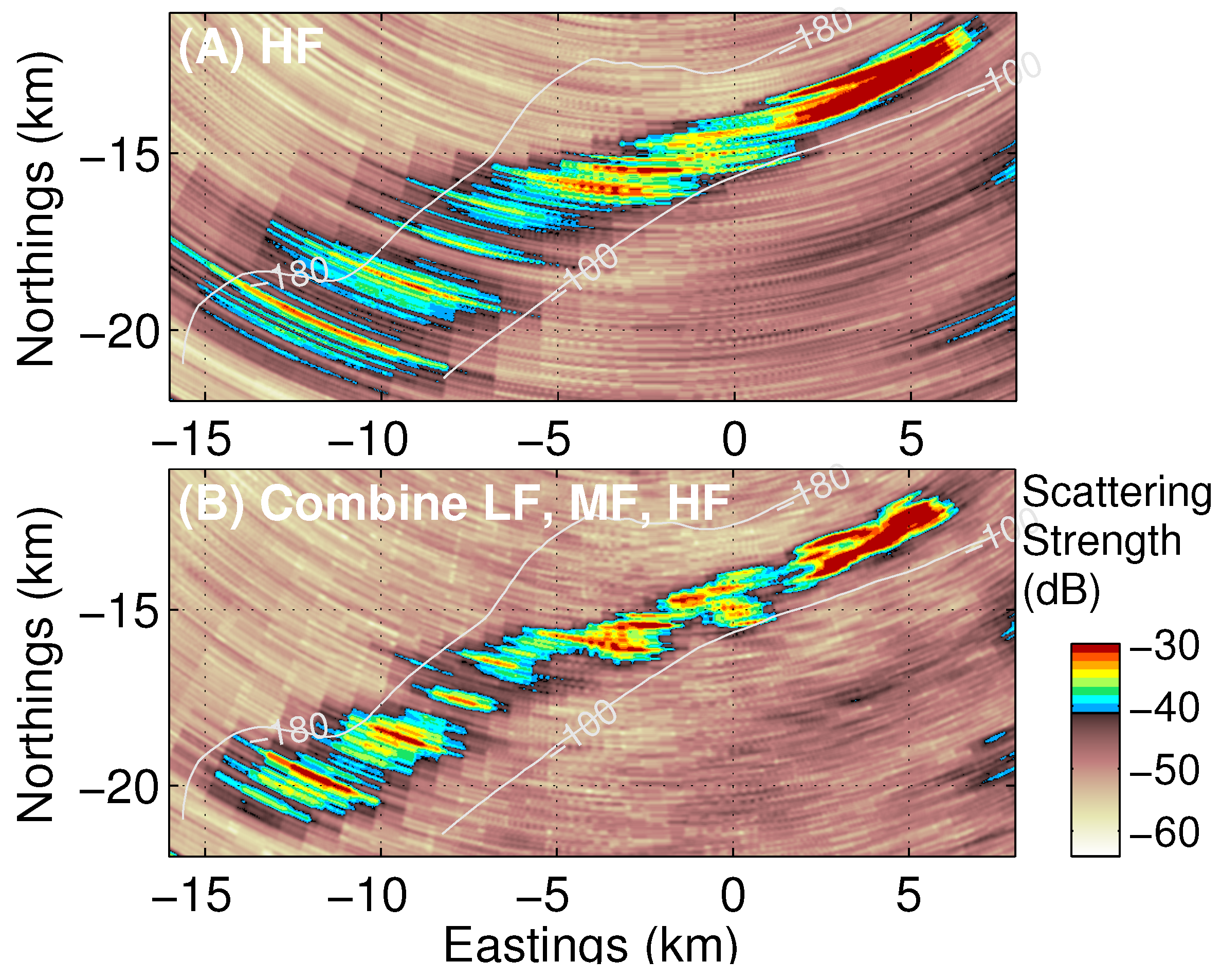
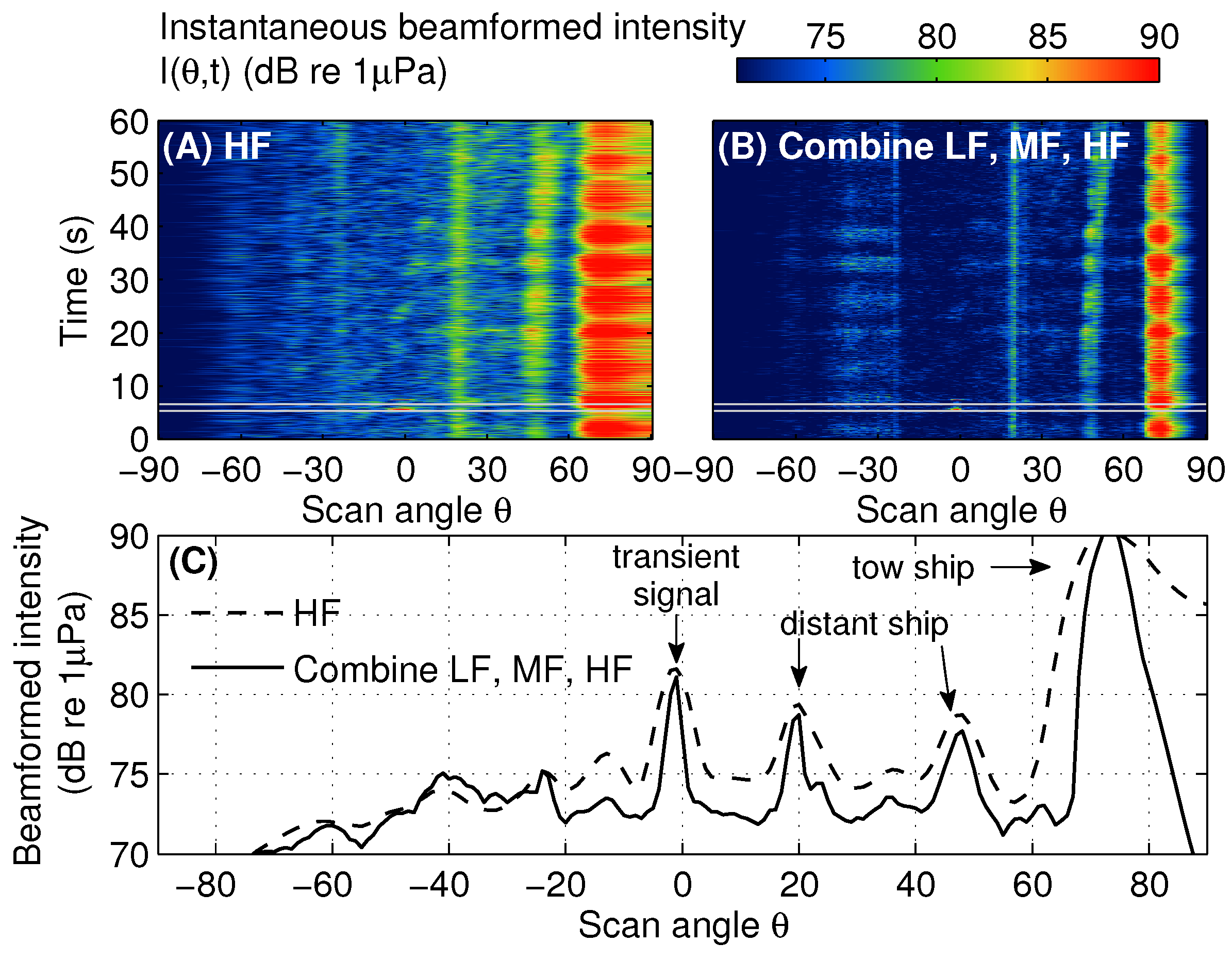
| Subaperture | LF | MF | HF | LF + MF | LF + MF + HF | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | 64 | 64 | 64 | 96 | 128 | |||||
| L (m) | 94.5 | 47.25 | 23.625 | 94.5 | 94.5 | |||||
| d (m) | 1.5 | 0.75 | 0.375 | variable | variable | |||||
| (Hz) | 950 | 1125 | 950 | 1125 | 950 | 1125 | 950 | 1125 | 950 | 1125 |
| (dB) | 19.45 | 15.42 | 16.44 | 17.18 | 13.43 | 14.17 | 18.75 | 19.29 | 17.71 | 18.37 |
| (deg) | 1.26 | 1.05 | 2.50 | 2.11 | 4.97 | 4.19 | 1.44 | 1.21 | 1.74 | 1.47 |
| (dB) | −3.92 | −3.21 | −42.64 | −3.21 | −42.64 | −42.59 | −21.39 | −5.75 | −24.88 | −16.21 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Ratilal, P. Angular Resolution Enhancement Provided by Nonuniformly-Spaced Linear Hydrophone Arrays in Ocean Acoustic Waveguide Remote Sensing. Remote Sens. 2017, 9, 1036. https://doi.org/10.3390/rs9101036
Wang D, Ratilal P. Angular Resolution Enhancement Provided by Nonuniformly-Spaced Linear Hydrophone Arrays in Ocean Acoustic Waveguide Remote Sensing. Remote Sensing. 2017; 9(10):1036. https://doi.org/10.3390/rs9101036
Chicago/Turabian StyleWang, Delin, and Purnima Ratilal. 2017. "Angular Resolution Enhancement Provided by Nonuniformly-Spaced Linear Hydrophone Arrays in Ocean Acoustic Waveguide Remote Sensing" Remote Sensing 9, no. 10: 1036. https://doi.org/10.3390/rs9101036
APA StyleWang, D., & Ratilal, P. (2017). Angular Resolution Enhancement Provided by Nonuniformly-Spaced Linear Hydrophone Arrays in Ocean Acoustic Waveguide Remote Sensing. Remote Sensing, 9(10), 1036. https://doi.org/10.3390/rs9101036